kRadar++: Coarse-to-Fine FMCW Scanning Radar Localisation
Simple Summary
Abstract
1. Introduction
2. Related Work
2.1. Vision- and LiDAR-Based Lifelong Navigation
2.2. Radar-Based Mapping and Localisation
2.3. Hierarchical Localisation
3. Preliminaries
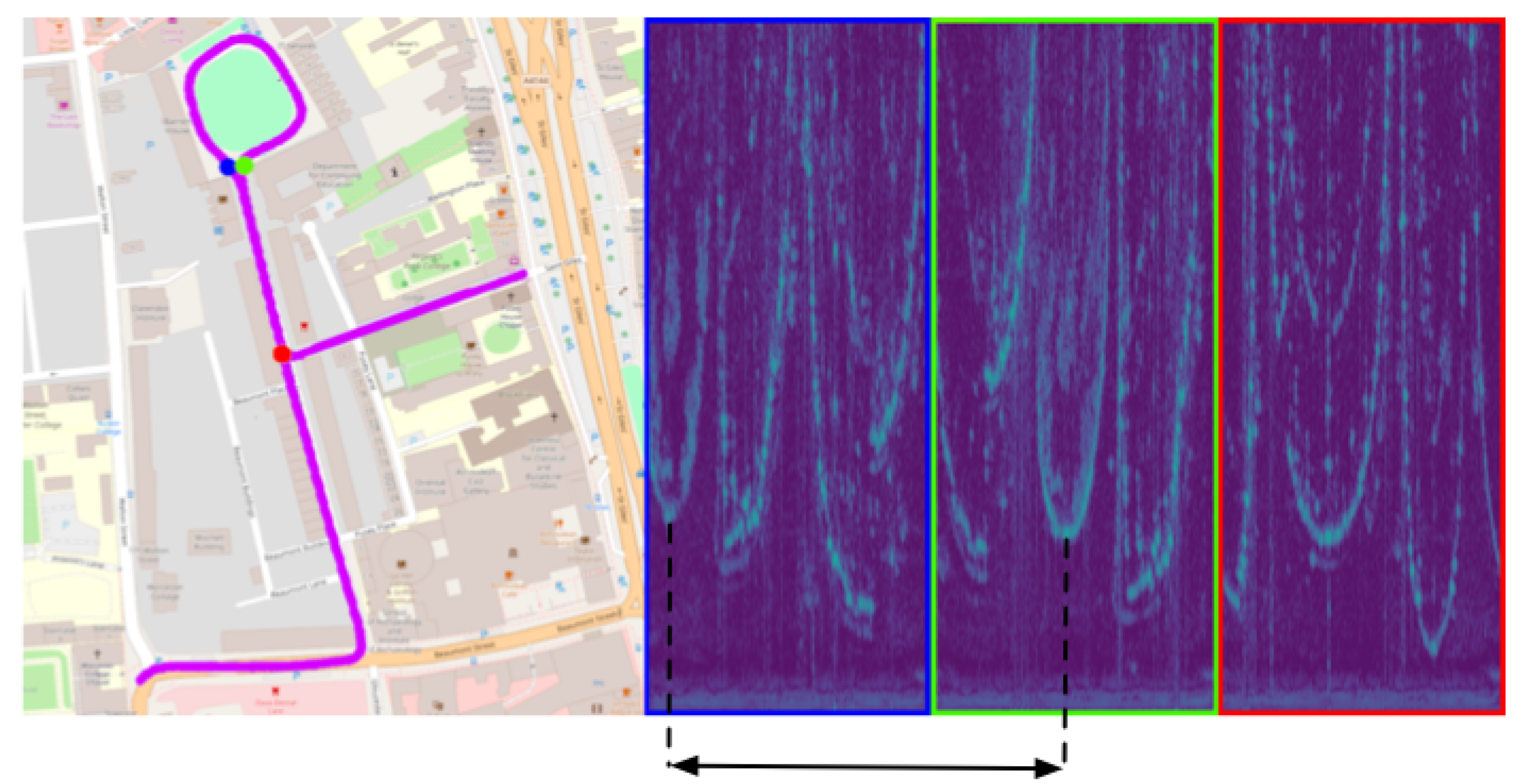
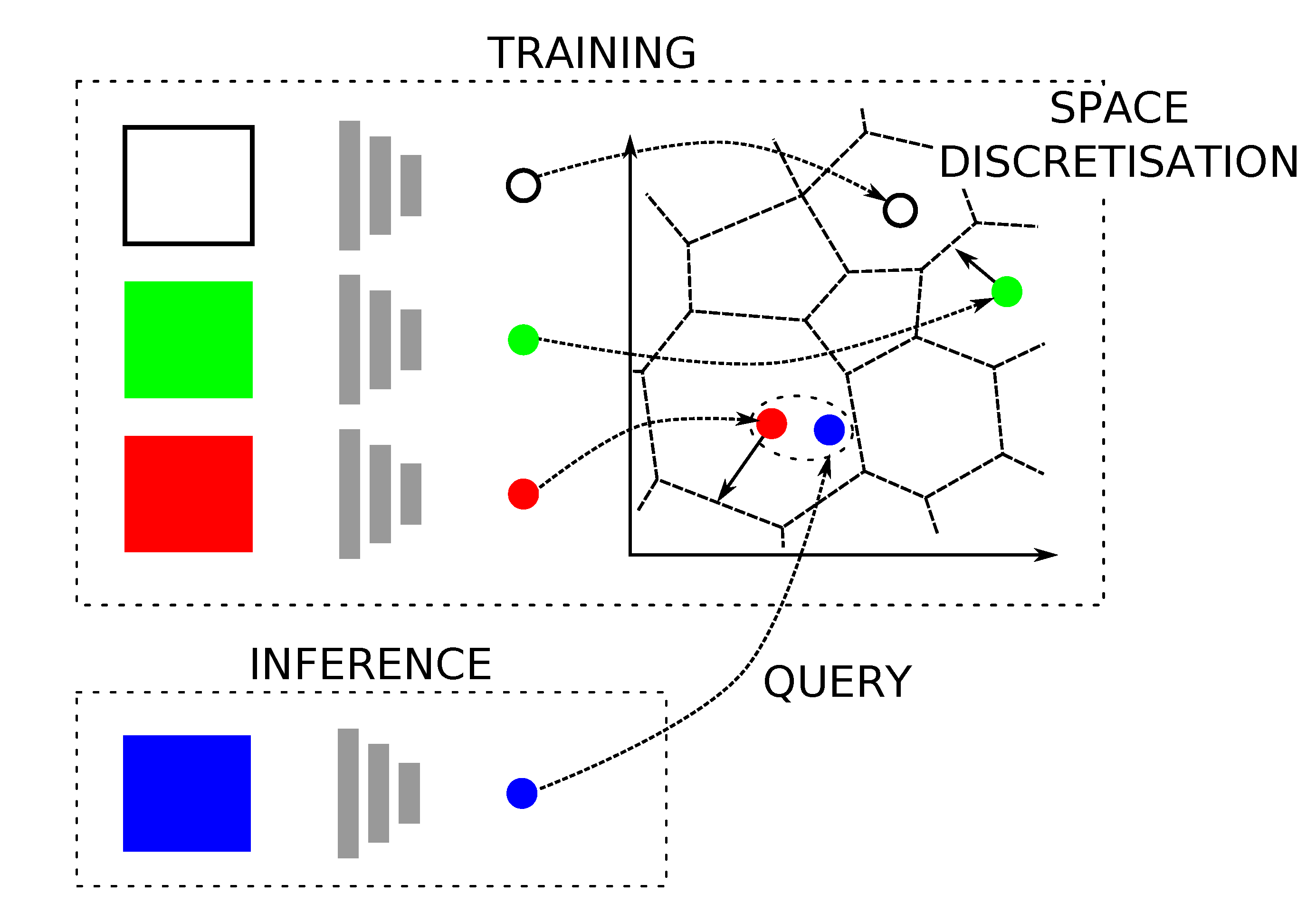
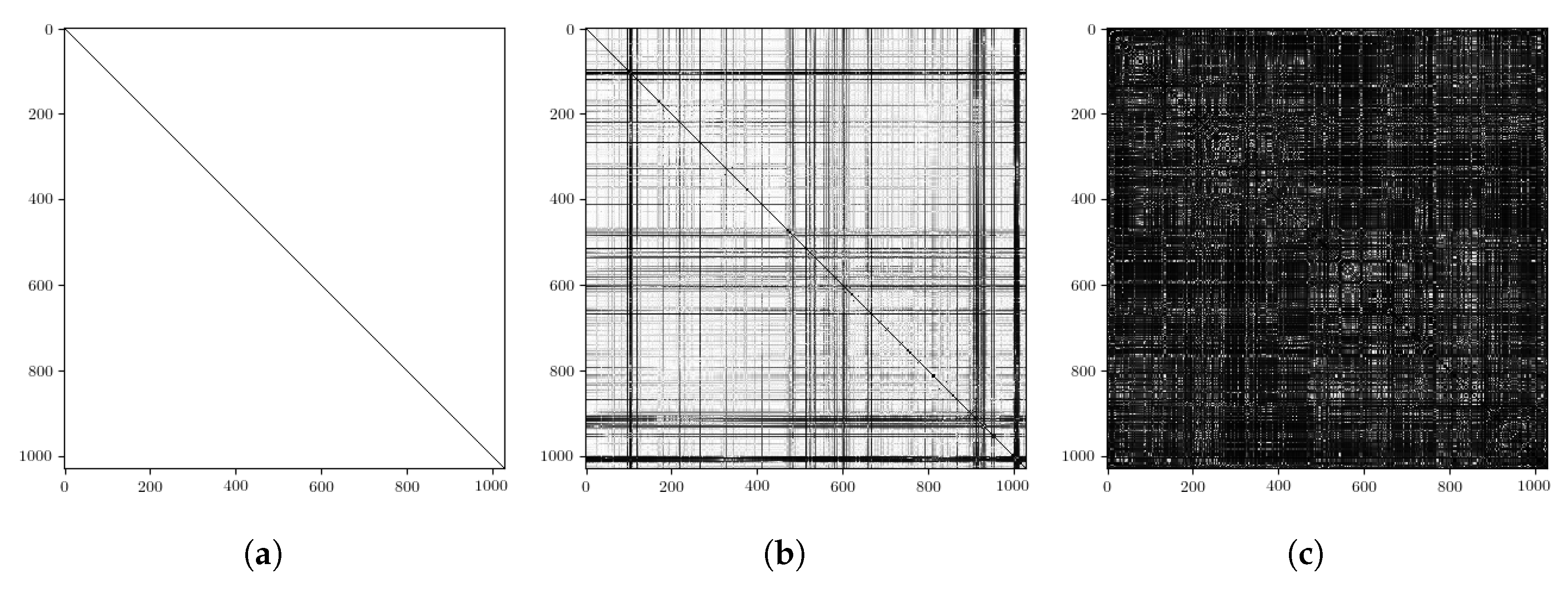
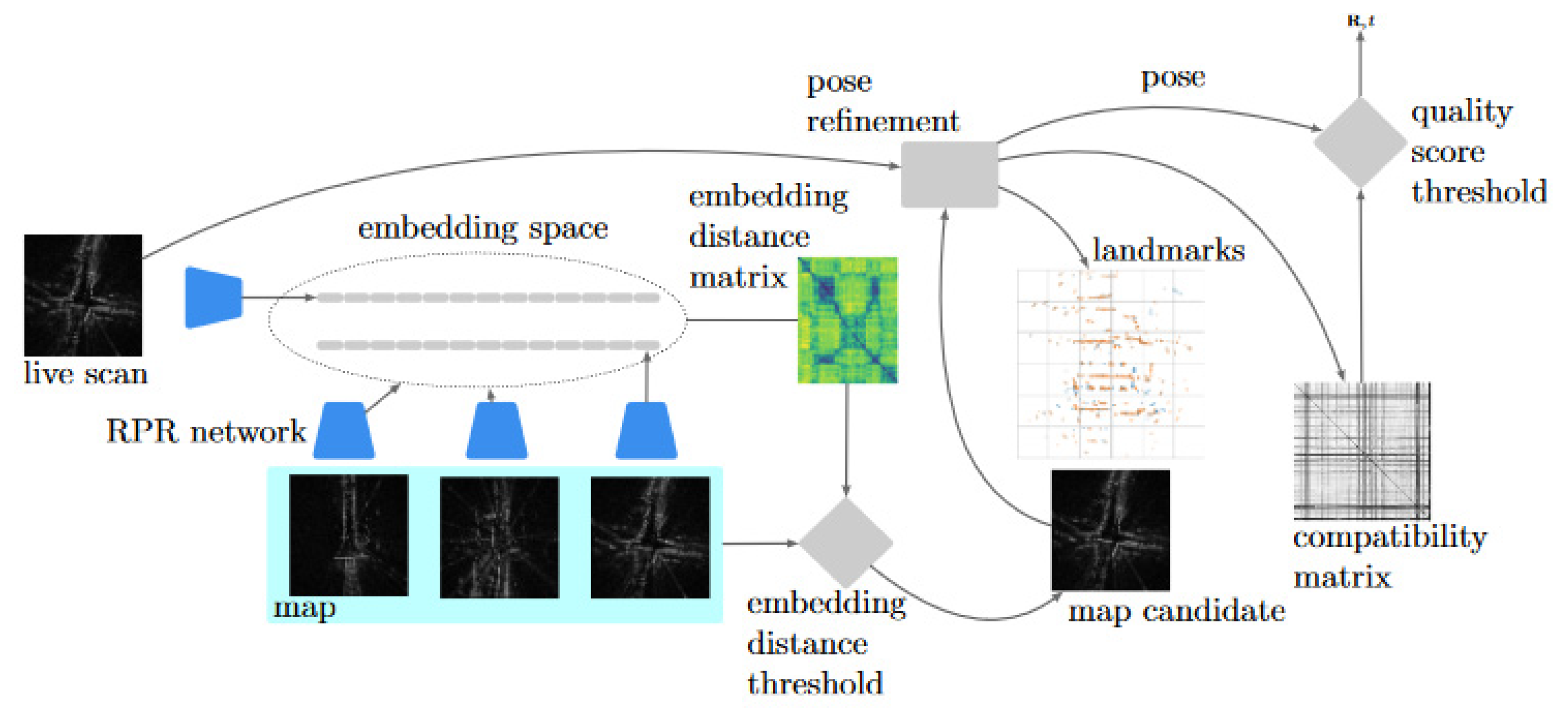
3.1. Radar Place Recognition (RPR)
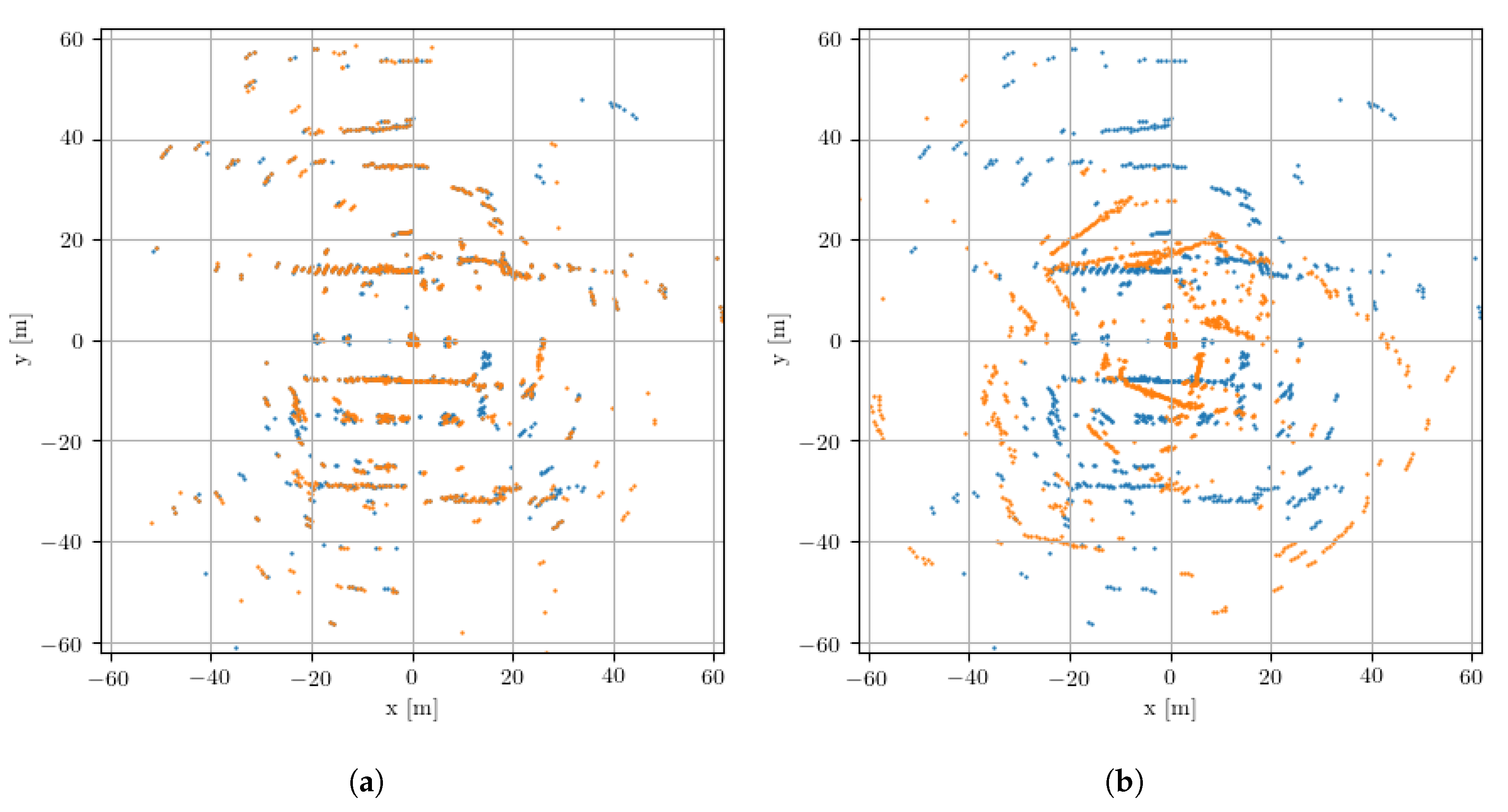
3.2. Pose Refinement
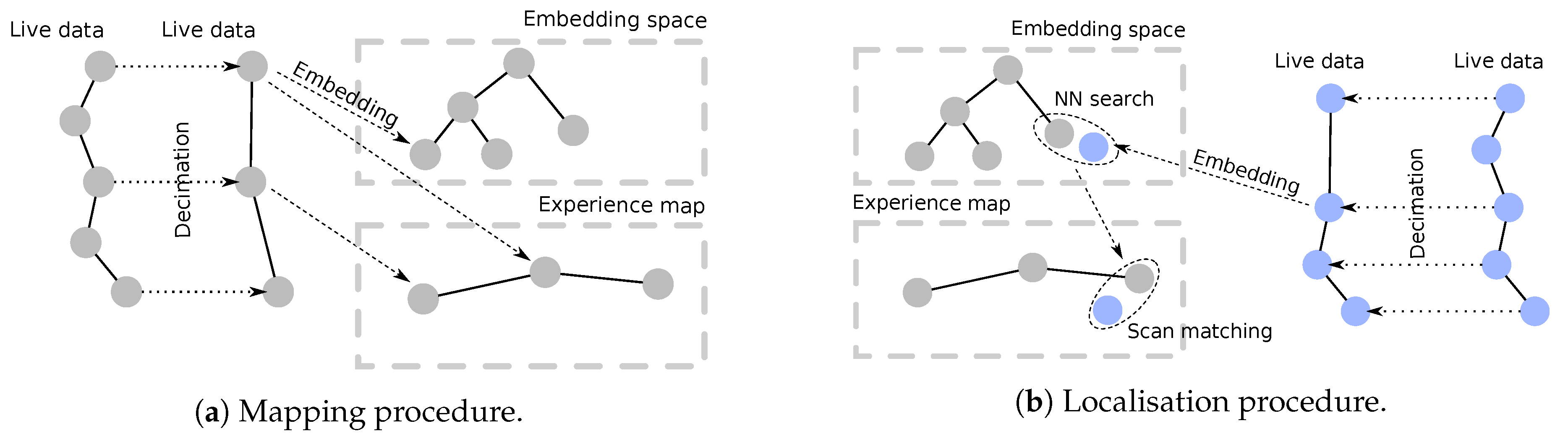
4. Hierarchical Radar Localisation
4.1. Mapping
4.2. Localisation
5. Experimental Design
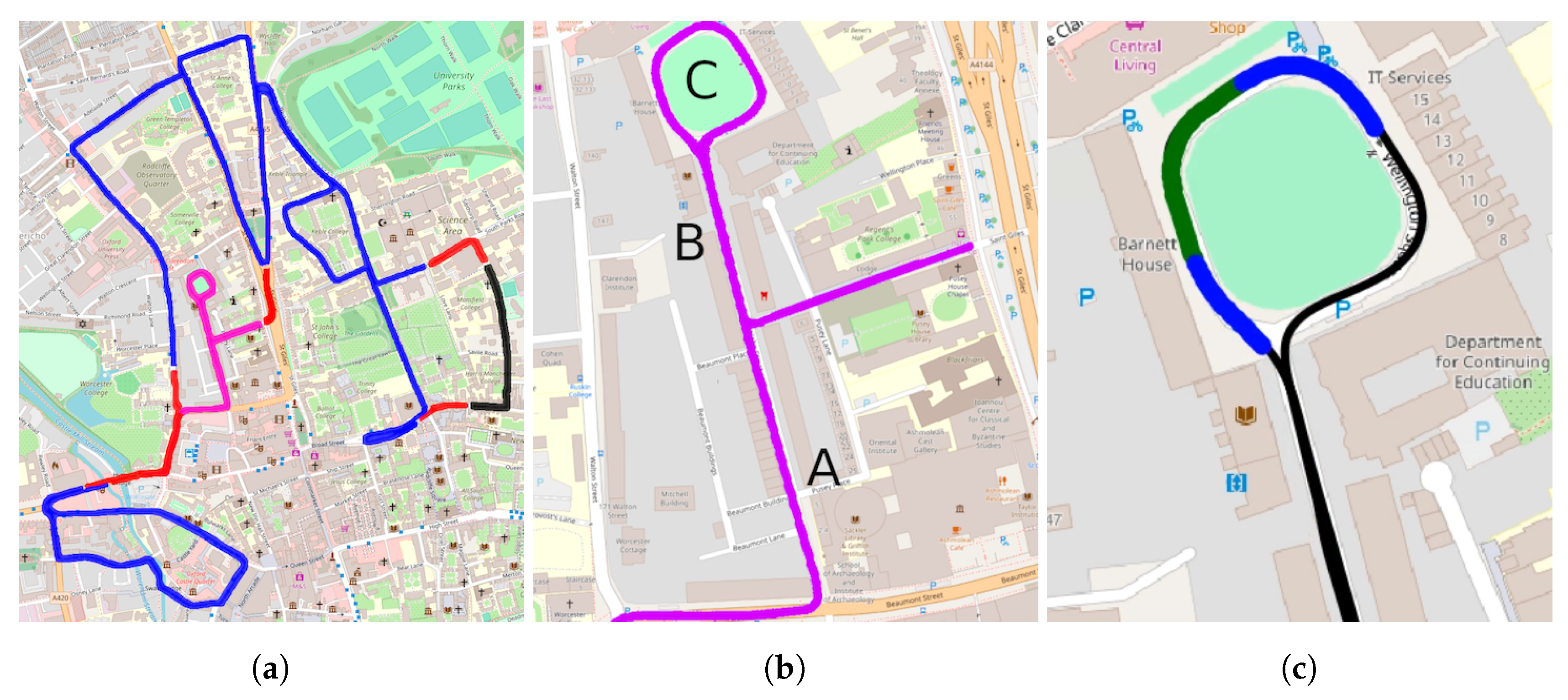
5.1. Dataset
- 2 forays for training,
- 2 forays for hyperparameter tuning,
- 1 foray for mapping, and
- 25 forays for localisation.
5.2. Localisation Performance Requirements
5.3. Online Requirements
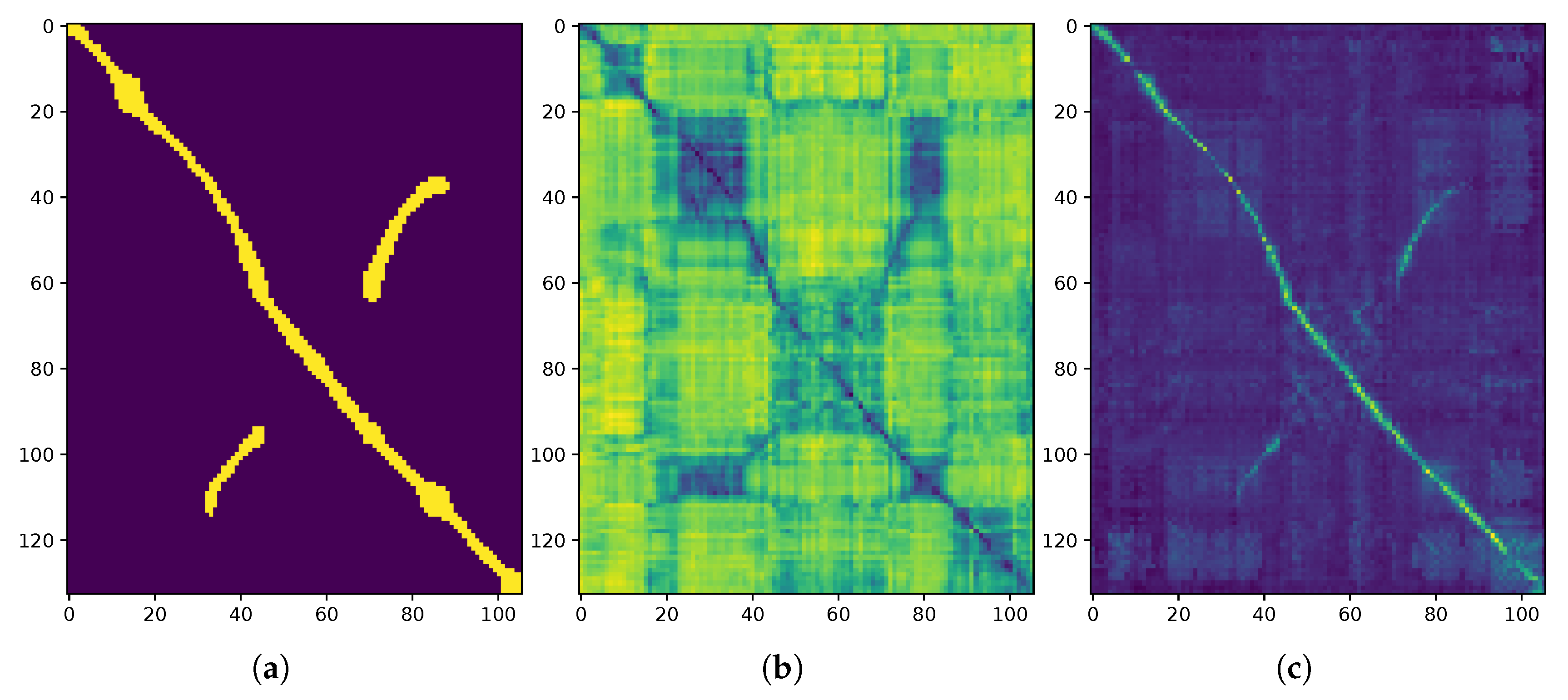
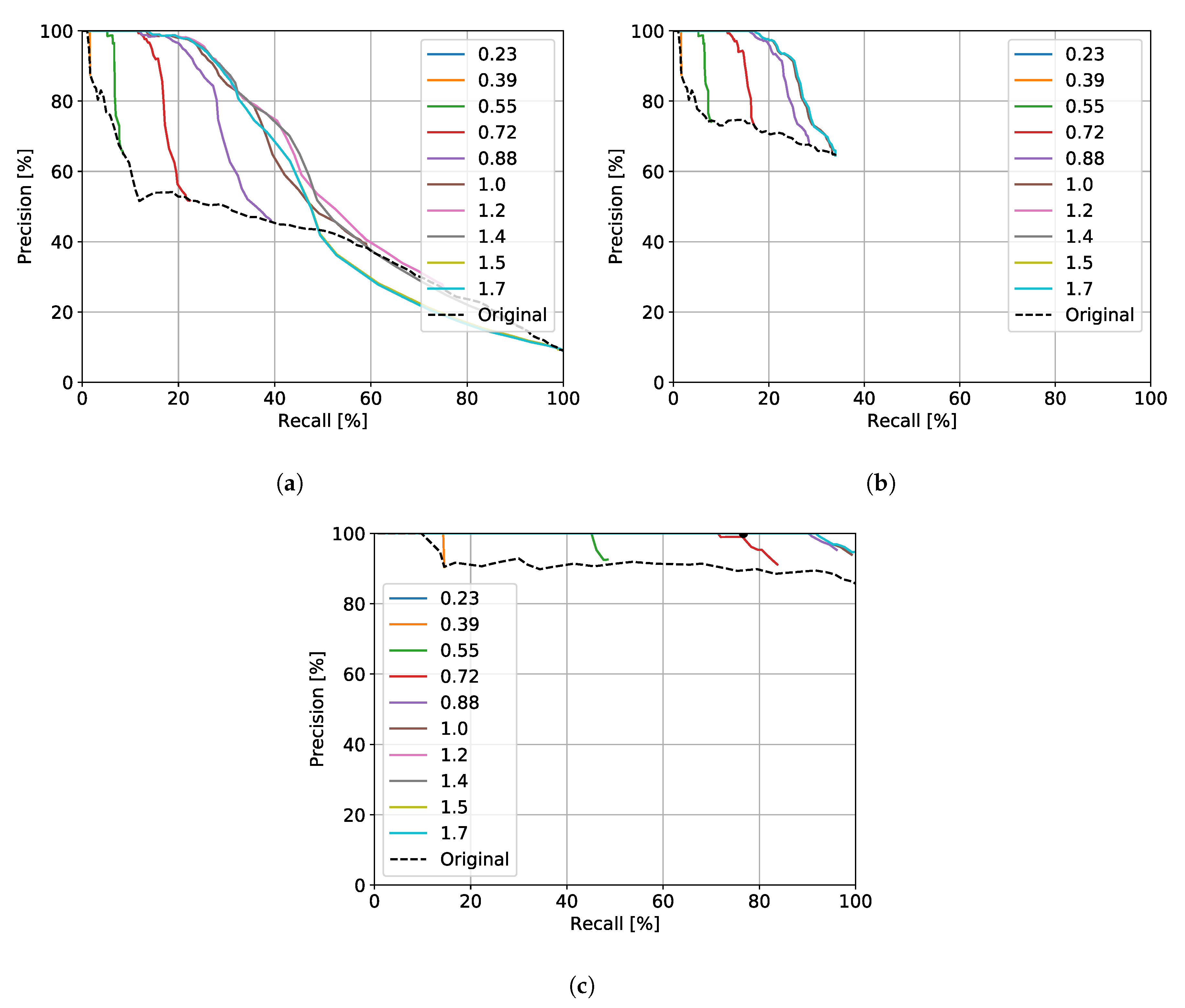
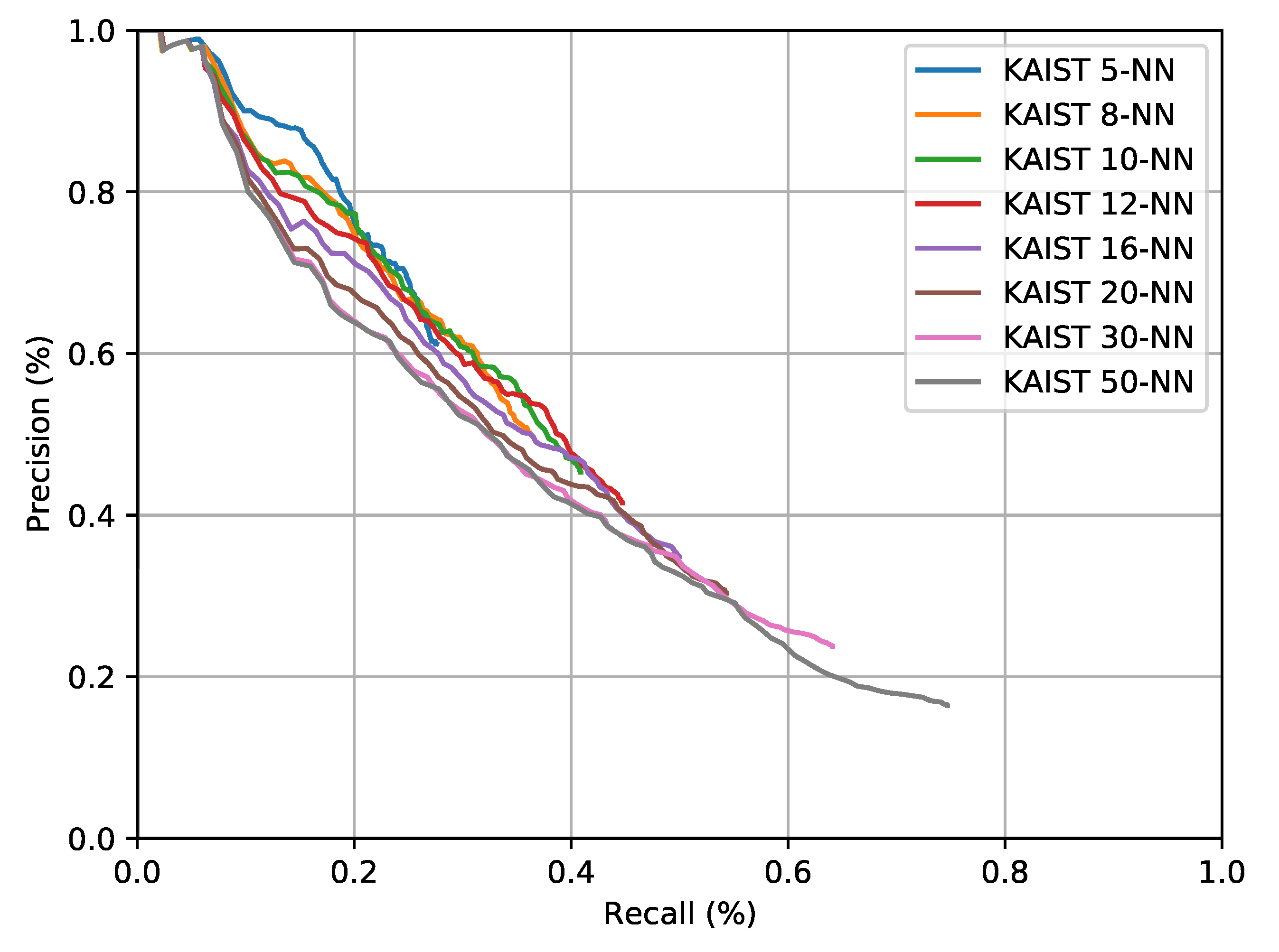
6. Hyperparameter Tuning
7. Localisation Performance
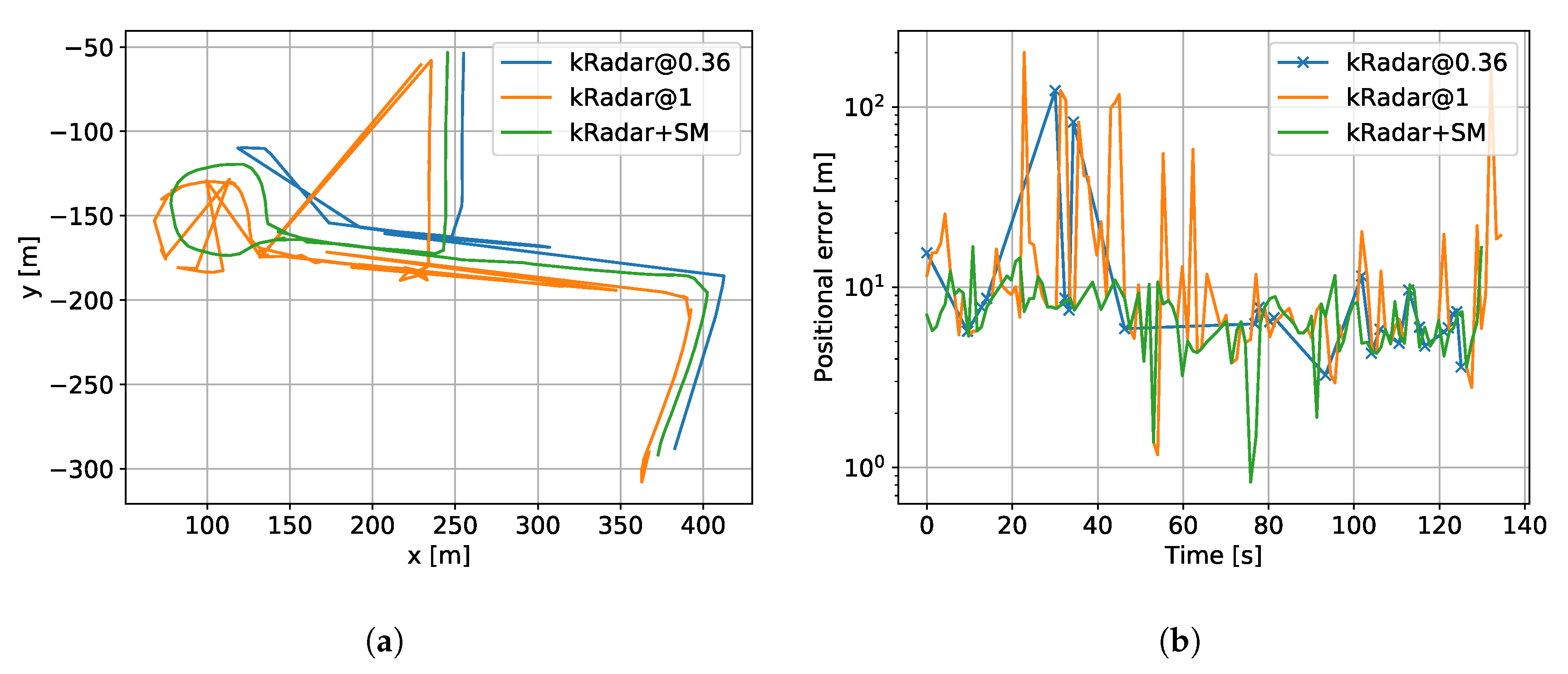
7.1. Localisation of a Single Experience
7.2. Month-Long Localisation
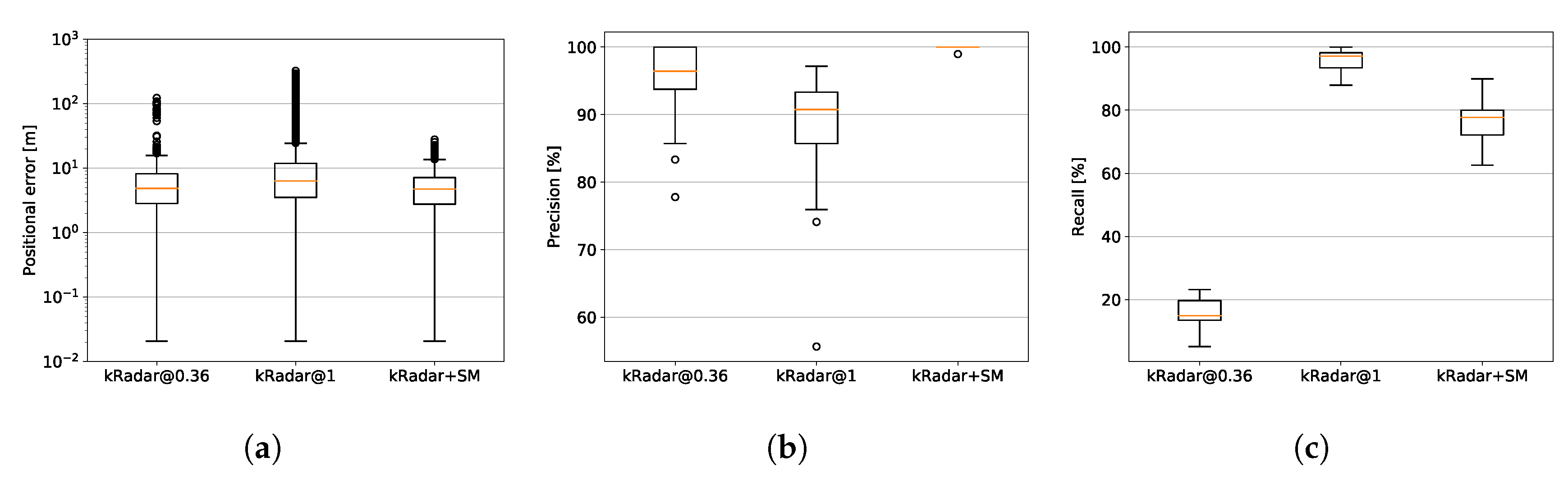
8. Benchmark Comparison
9. Conclusions
- can be used to bolster the performance of topological localisation by geometric verification,
- reports accurate poses in a TR scenario,
- maintains localisation performance over long time scales, and
- lends itself well to lifelong navigation techniques for improving localisation.
10. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| fmcw | Frequency-Modulated Continuous-Wave |
| rtr | radar teach-and-repeat |
| cnn | Convolutional Neural Network |
| vlad | Vector of Locally Aggregated Descriptors |
| dl | Deep Learning |
| wsl | Weakly-Supervised Learning |
| vo | Visual Odometry |
| gps | Global Positioning System |
| ro | Radar Odometry |
| uwb | Ultra Wide Band |
| fft | Fast Fourier Transform |
| slam | Simultaneous Localisation and Mapping |
| mmw | Millimetre-Wave |
| fcnn | Fully Convolutional Neural Network |
| lidar | Light Detection and Ranging |
| nn | nearest neighbour |
| auc | Area-under-Curve |
| fov | field-of-view |
| pr | precision and recall |
| tr | teach-and-repeat |
| svd | Singular-Value Decomposition |
| vtr | visual teach-and-repeat |
| av | autonomous vehicle |
| ebn | Experience-based Navigation |
| vpr | visual place recognition |
| rpr | radar place recognition |
| tdof | three degree-of-freedom |
| mcl | Montecarlo Localisation |
References
- Sibley, G.; Mei, C.; Reid, I.; Newman, P. Vast-scale outdoor navigation using adaptive relative bundle adjustment. Int. J. Robot. Res. 2010, 29, 958–980. [Google Scholar] [CrossRef]
- Cen, S.H.; Newman, P. Precise ego-motion estimation with millimeter-wave radar under diverse and challenging conditions. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Cen, S.H.; Newman, P. Radar-only ego-motion estimation in difficult settings via graph matching. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 298–304. [Google Scholar]
- Aldera, R.; De Martini, D.; Gadd, M.; Newman, P. Fast Radar Motion Estimation with a Learnt Focus of Attention using Weak Supervision. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 1190–1196. [Google Scholar]
- Aldera, R.; De Martini, D.; Gadd, M.; Newman, P. What Could Go Wrong? Introspective Radar Odometry in Challenging Environments. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Barnes, D.; Weston, R.; Posner, I. Masking by Moving: Learning Distraction-Free Radar Odometry from Pose Information. In Proceedings of the Conference on Robot Learning (CoRL), Osaka, Japan, 30 October–1 November 2019. [Google Scholar]
- Barnes, D.; Posner, I. Under the Radar: Learning to Predict Robust Keypoints for Odometry Estimation and Metric Localisation in Radar. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Săftescu, S.; Gadd, M.; De Martini, D.; Barnes, D.; Newman, P. Kidnapped Radar: Topological Radar Localisation using Rotationally-Invariant Metric Learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Gadd, M.; De Martini, D.; Newman, P. Look Around You: Sequence-based Radar Place Recognition with Learned Rotational Invariance. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Tang, T.Y.; De Martini, D.; Barnes, D.; Newman, P. RSL-Net: Localising in Satellite Images From a Radar on the Ground. IEEE Robot. Autom. Lett. 2020, 5, 1087–1094. [Google Scholar] [CrossRef]
- Kim, G.; Park, Y.S.; Cho, Y.; Jeong, J.; Kim, A. Mulran: Multimodal range dataset for urban place recognition. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Hong, Z.; Petillot, Y.; Wang, S. RadarSLAM: Radar based Large-Scale SLAM in All Weathers. arXiv 2020, arXiv:2005.02198. [Google Scholar]
- Weston, R.; Cen, S.; Newman, P.; Posner, I. Probably Unknown: Deep Inverse Sensor Modelling Radar. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5446–5452. [Google Scholar]
- Williams, D.; De Martini, D.; Gadd, M.; Marchegiani, L.; Newman, P. Keep off the Grass: Permissible Driving Routes from Radar with Weak Audio Supervision. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Rhodes, Greece, 20–23 September 2020. [Google Scholar]
- Kaul, P.; De Martini, D.; Gadd, M.; Newman, P. RSS-Net: Weakly-Supervised Multi-Class Semantic Segmentation with FMCW Radar. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020. [Google Scholar]
- Sattler, T.; Havlena, M.; Radenovic, F.; Schindler, K.; Pollefeys, M. Hyperpoints and fine vocabularies for large-scale location recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2102–2110. [Google Scholar]
- Furgale, P.; Barfoot, T.D. Visual teach and repeat for long-range rover autonomy. J. Field Robot. 2010, 27, 534–560. [Google Scholar] [CrossRef]
- Krajník, T.; Majer, F.; Halodová, L.; Vintr, T. Navigation without localisation: Reliable teach and repeat based on the convergence theorem. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1657–1664. [Google Scholar]
- Sprunk, C.; Tipaldi, G.D.; Cherubini, A.; Burgard, W. Lidar-based teach-and-repeat of mobile robot trajectories. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3144–3149. [Google Scholar]
- Churchill, W.; Newman, P. Experience-based navigation for long-term localisation. Int. J. Robot. Res. 2013, 32, 1645–1661. [Google Scholar] [CrossRef]
- Sibley, G.; Mei, C.; Reid, I.; Newman, P. Planes, trains and automobiles—Autonomy for the modern robot. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 285–292. [Google Scholar]
- Strasdat, H.; Davison, A.J.; Montiel, J.M.; Konolige, K. Double window optimisation for constant time visual SLAM. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2352–2359. [Google Scholar]
- Maddern, W.; Pascoe, G.; Newman, P. Leveraging experience for large-scale LIDAR localisation in changing cities. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1684–1691. [Google Scholar]
- Reina, G.; Johnson, D.; Underwood, J. Radar sensing for intelligent vehicles in urban environments. Sensors 2015, 15, 14661–14678. [Google Scholar] [CrossRef] [PubMed]
- Mielle, M.; Magnusson, M.; Lilienthal, A.J. A comparative analysis of radar and lidar sensing for localization and mapping. In Proceedings of the European Conference on Mobile Robotics (ECMR), Prague, Czech Republic, 4–6 September 2019. [Google Scholar]
- Vivet, D.; Checchin, P.; Chapuis, R. Localization and mapping using only a rotating FMCW radar sensor. Sensors 2013, 13, 4527–4552. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Park, T.H. Extended Kalman Filter (EKF) Design for Vehicle Position Tracking Using Reliability Function of Radar and Lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef] [PubMed]
- Tang, T.Y.; De Martini, D.; Wu, S.; Newman, P. Self-Supervised Localisation between Range Sensors and Overhead Imagery. arXiv 2020, arXiv:2006.02108. [Google Scholar]
- Fariña, B.; Toledo, J.; Estevez, J.I.; Acosta, L. Improving Robot Localization Using Doppler-Based Variable Sensor Covariance Calculation. Sensors 2020, 20, 2287. [Google Scholar] [CrossRef] [PubMed]
- Middelberg, S.; Sattler, T.; Untzelmann, O.; Kobbelt, L. Scalable 6-dof localization on mobile devices. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 268–283. [Google Scholar]
- Garcia-Fidalgo, E.; Ortiz, A. Hierarchical place recognition for topological mapping. IEEE Trans. Robot. 2017, 33, 1061–1074. [Google Scholar] [CrossRef]
- Sarlin, P.E.; Cadena, C.; Siegwart, R.; Dymczyk, M. From coarse to fine: Robust hierarchical localization at large scale. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019; pp. 12716–12725. [Google Scholar]
- Sarlin, P.E.; Debraine, F.; Dymczyk, M.; Siegwart, R.; Cadena, C. Leveraging deep visual descriptors for hierarchical efficient localization. In Proceedings of the 2nd Annual Conference on Robot Learning, Zürich, Switzerland, 29–31 October 2018. [Google Scholar]
- Chen, X.; Läbe, T.; Milioto, A.; Röhling, T.; Vysotska, O.; Haag, A.; Behley, J.; Stachniss, C.; Fraunhofer, F. OverlapNet: Loop Closing for LiDAR-based SLAM. In Proceedings of the Robotics: Science and Systems (RSS), Freiburg, Germany, 12–16 July 2020. [Google Scholar]
- Kim, G.; Kim, A. Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4802–4809. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5297–5307. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Wang, T.H.; Huang, H.J.; Lin, J.T.; Hu, C.W.; Zeng, K.H.; Sun, M. Omnidirectional CNN for Visual Place Recognition and Navigation. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2341–2348. [Google Scholar]
- Zhang, R. Making Convolutional Networks Shift-Invariant Again. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 7324–7334. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Cieslewski, T.; Choudhary, S.; Scaramuzza, D. Data-efficient decentralized visual SLAM. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2466–2473. [Google Scholar]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 437–478. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Leordeanu, M.; Hebert, M. A spectral technique for correspondence problems using pairwise constraints. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1, Beijing, China, 17–21 October 2005; Volume 2, pp. 1482–1489. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Nguyen Mau, T.; Inoguchi, Y. Locality-Sensitive Hashing for Information Retrieval System on Multiple GPGPU Devices. Appl. Sci. 2020, 10, 2539. [Google Scholar] [CrossRef]
- Churchill, W.; Newman, P. Practice Makes Perfect? Managing and Leveraging Visual Experiences for Lifelong Navigation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MA, USA, 14–18 May 2012; pp. 4525–4532. [Google Scholar]
- Maddern, W.; Pascoe, G.; Linegar, C.; Newman, P. 1 Year, 1000 km: The Oxford RobotCar Dataset. Int. J. Robot. Res. 2017, 36, 3–15. [Google Scholar] [CrossRef]
- Barnes, D.; Gadd, M.; Murcutt, P.; Newman, P.; Posner, I. The Oxford Radar RobotCar Dataset: A Radar Extension to the Oxford RobotCar Dataset. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Kyberd, S.; Attias, J.; Get, P.; Murcutt, P.; Prahacs, C.; Towlson, M.; Venn, S.; Vasconcelos, A.; Gadd, M.; De Martini, D.; et al. The Hulk: Design and Development of a Weather-proof Vehicle for Long-term Autonomy in Outdoor Environments. In Proceedings of the International Conference on Field and Service Robotics (FSR), Tokyo, Japan, 29–31 August 2019. [Google Scholar]
- Gadd, M.; De Martini, D.; Marchegiani, L.; Kunze, L.; Newman, P. Sense-Assess-eXplain (SAX): Building Trust in Autonomous Vehicles in Challenging Real-World Driving Scenarios. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Workshop on Ensuring and Validating Safety for Automated Vehicles (EVSAV), Las Vegas, NV, USA, 20 October 2020. [Google Scholar]
- MacTavish, K.; Paton, M.; Barfoot, T.D. Visual triage: A bag-of-words experience selector for long-term visual route following. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2065–2072. [Google Scholar]
- Dequaire, J.; Tong, C.H.; Churchill, W.; Posner, I. Off the Beaten Track: Predicting Localisation Performance in Visual Teach and Repeat. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
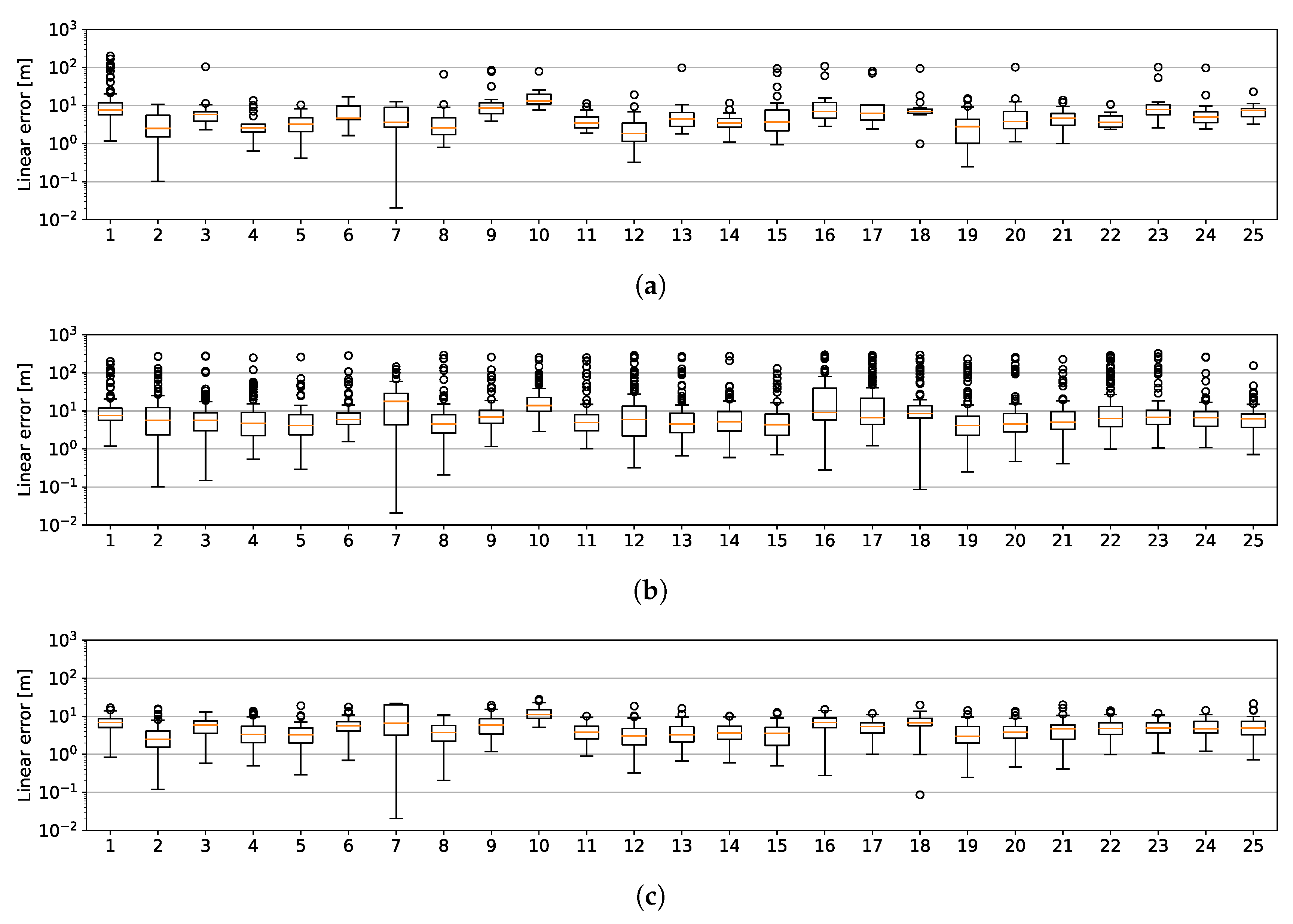
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martini, D.; Gadd, M.; Newman, P. kRadar++: Coarse-to-Fine FMCW Scanning Radar Localisation. Sensors 2020, 20, 6002. https://doi.org/10.3390/s20216002
De Martini D, Gadd M, Newman P. kRadar++: Coarse-to-Fine FMCW Scanning Radar Localisation. Sensors. 2020; 20(21):6002. https://doi.org/10.3390/s20216002
Chicago/Turabian StyleDe Martini, Daniele, Matthew Gadd, and Paul Newman. 2020. "kRadar++: Coarse-to-Fine FMCW Scanning Radar Localisation" Sensors 20, no. 21: 6002. https://doi.org/10.3390/s20216002
APA StyleDe Martini, D., Gadd, M., & Newman, P. (2020). kRadar++: Coarse-to-Fine FMCW Scanning Radar Localisation. Sensors, 20(21), 6002. https://doi.org/10.3390/s20216002





