Probabilistic Analysis of a Buffer Overflow Duration in Data Transmission in Wireless Sensor Networks
Abstract
:1. Introduction
2. Model Description
3. Basic Equations for First Buffer Overflow Duration
- the moment r is the arrival time of, at most, the th packet and the next packet enters the system after time i (the buffer does not become saturated before time i);
- the moment r is the arrival time of, at most, the th packet and the next packet enters the system exactly at time i;
- at time r the th packet arrives, so the buffer overflow period begins at time
- the first packet (after the opening of the system) arrives exactly at time i;
- the first packet (after the opening of the system) arrives after time
4. Representation for Solution
5. The Case of Next Buffer Overflows
6. Numerical Study
- -
- the offered traffic load defined as the quotient of the mean service time and the mean interarrival time;
- -
- the number of jobs n accumulated in the buffer before the starting moment;
- -
- the shape of the service (processing) time distribution;
- -
- the buffer size.
- geometric with fixed parameter
- deterministic (constant) of duration
- bounded discrete distribution, where the service time takes on finite number of possible values; dealing with the impact of the distribution skewness we analyze separately the following subcases of this type of distribution:
- –
- symmetric;
- –
- with positive skewness (positive asymmetry);
- –
- with negative skewness (negative asymmetry).
6.1. Impact of the Type of Processing Distribution
6.2. Impact of Skewness Type of the Processing Distribution
- symmetric distribution of the formand otherwise, for which the skewness equals 0;
- distribution with positive skewness (positive asymmetry) of the formand otherwise, for which the skewness equals
- distribution with negative skewness (negative asymmetry) of the formand otherwise, for which the skewness equals
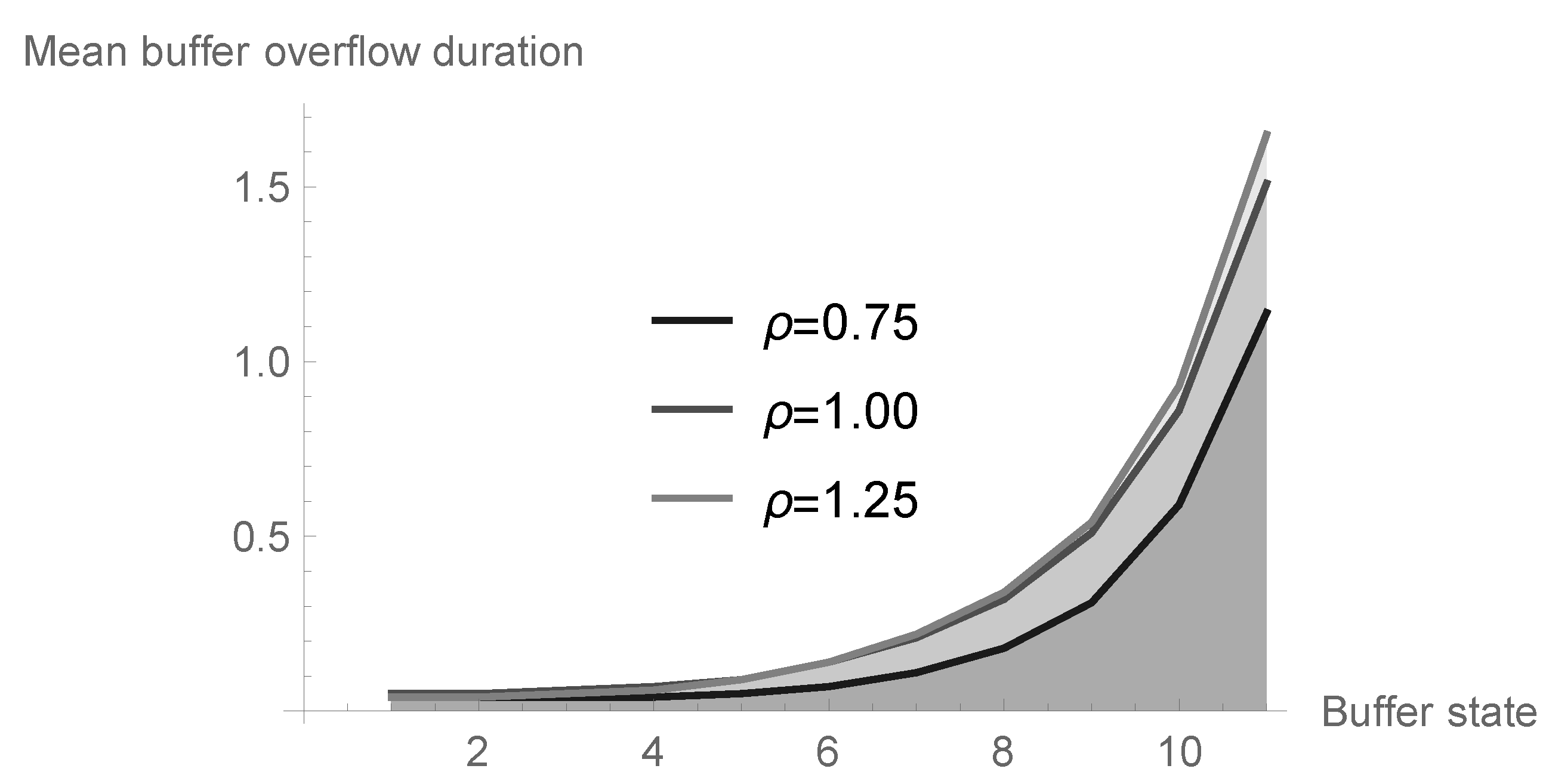
6.3. Mean Buffer Overflow Duration in Dependence on Offered Load and Initial Buffer State
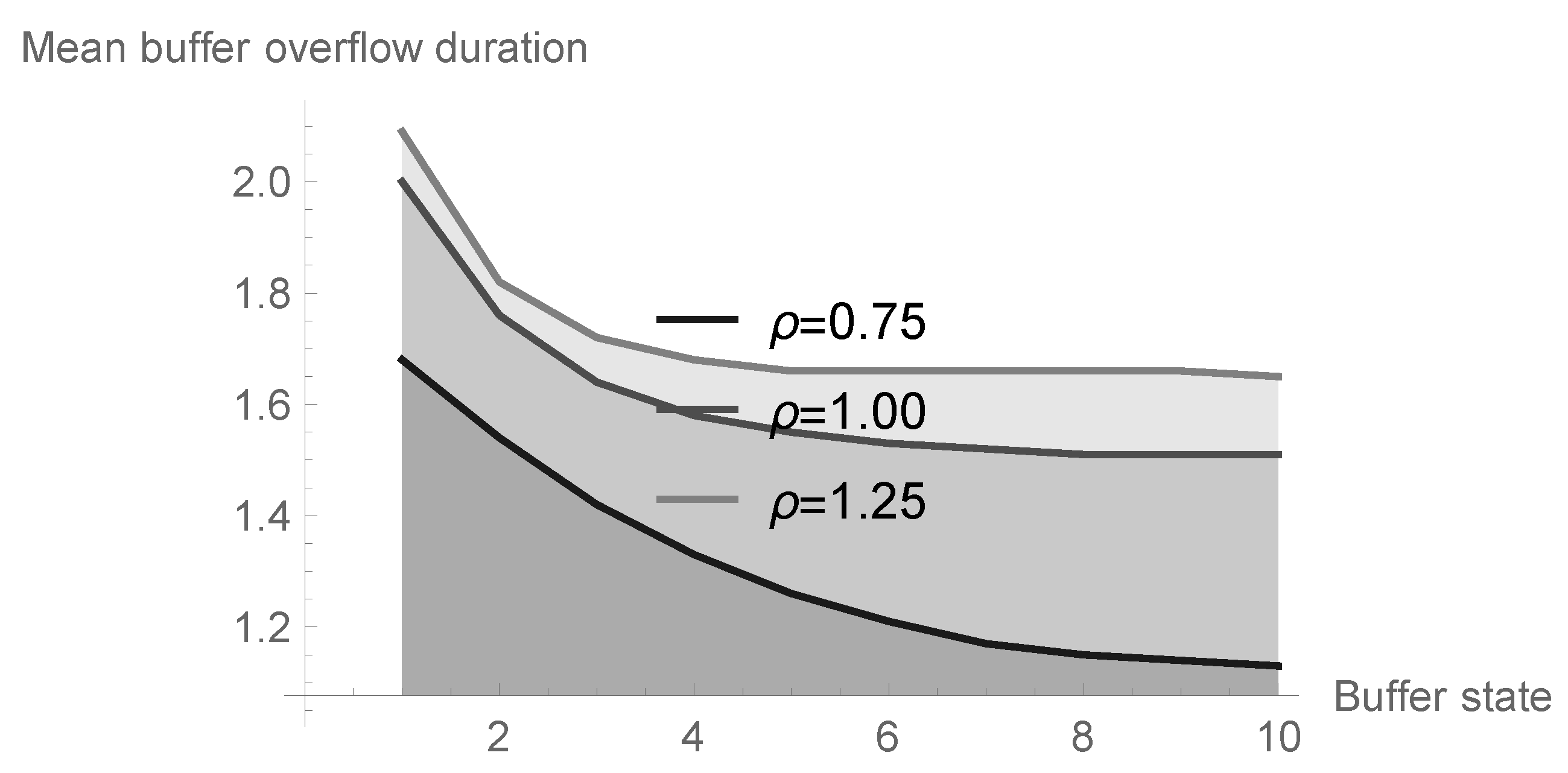
6.4. Impact of System Size
7. Conclusions
Funding
Conflicts of Interest
References
- Sumathi, K.; Venkatesan, M. A survey on congestion control in wireless sensor networks. Int. J. Comput. Appl. 2016, 147, 6. [Google Scholar] [CrossRef]
- Syed, A.S.; Babar, N.; Imran, A.K. Congestion control algorithms in wireless sensor networks: Trends and opportunities. J. King Saud Univ. 2017, 29, 236–245. [Google Scholar]
- Joshi, G.; Dwivedi, S.; Goel, A.; Mulherkar, J.; Ranjan, P. Power and buffer overflow optimization in wireless sensor nodes. In Proceedings of the International Conference on Computer Science and Information Technology, Bangalore, India, 2–4 January 2011; pp. 450–458. [Google Scholar]
- Shwe, H.Y.; Gacanin, H.; Adachi, F. Multi-layer WSN with power efficient buffer management policy. In Proceedings of the 2010 IEEE International Conference on Communication Systems, Singapore, 17–19 November 2010. [Google Scholar]
- de Boer, P.T.; Nicola, V.F.; van Ommeren, J.C.W. The remaining service time upon reaching a high level in M/G/1 queues. Queueing Syst. 2001, 39, 55–78. [Google Scholar] [CrossRef]
- Chae, K.C.; Kim, K.; Kim, N.K. Remarks on the remaining service time upon reaching a target level in the M/G/1 queue. Oper. Res. Lett. 2007, 35, 308–310. [Google Scholar] [CrossRef]
- Chydziński, A. On the remaining service time upon reaching a target level in M/G/1 queues. Queueing Syst. 2004, 47, 71–80. [Google Scholar] [CrossRef]
- Fakinos, D. The expected remaining service time in a single server queue. Oper. Res. 1982, 30, 1014–1018. [Google Scholar] [CrossRef] [Green Version]
- Kempa, W.M. On buffer overflow duration in WSN with a vacation-type power saving mechanism. In Proceedings of the 2017 International Conference on Systems, Signals and Image Processing (IWSSIP), Poznan, Poland, 22–24 May 2017; pp. 87–90. [Google Scholar]
- Kempa, W.M. On buffer overflow duration in a finite-capacity queueing system with multiple vacation policy. In Proceedings of the 43th International Conference Applications of Mathematics in Engineering and Economics (AMEE’17), Sozopol, Bulgaria, 8–13 June 2017; pp. 1–6. [Google Scholar]
- Kempa, W.M. Buffer overflow duration in a model of WSN node with power saving mechanism based on SV policy. In Proceedings of the International Conference on Information and Software Technologies, Druskininkai, Lithuania, 12–14 October 2017; pp. 385–394. [Google Scholar]
- Kempa, W.M. The virtual waiting time for the batch arrival queueing systems. Stoch. Anal. Appl. 2004, 22, 1235–1255. [Google Scholar] [CrossRef]
- Kempa, W.M. Analysis of departure process in batch arrival queue with multiple vacations and exhaustive service. Commun. Stat. Theory Methods 2011, 40, 2856–2865. [Google Scholar] [CrossRef]
- Kempa, W.M.; Marjasz, R. Distribution of the time to buffer overflow in the M/G/1/N-type queueing model with batch arrivals and multiple vacation policy. J. Oper. Res. Soc. 2019, 71, 447–455. [Google Scholar] [CrossRef]
- Kempa, W.M.; Paprocka, I.; Grabowik, C.; Kalinowski, K. Distribution of time to buffer overflow in a finite-buffer manufacturing model with unreliable machine. In Proceedings of the MATEC Web of Conferences, Iasi, Romania, 4 August 2017. [Google Scholar]
- Tikhonenko, O.; Kempa, W.M. The generalization of AQM algorithms for queueing systems with bounded capacity. In Proceedings of the Parallel Processing and Applied Mathematics, 9th International Conference (PPAM 2011), Torun, Poland, 11–14 September 2011; pp. 242–251. [Google Scholar]
- Cao, J.; Ma, Z.; Guo, S.; Yu, X. Performance analysis of non-exhaustive wireless sensor networks based on queueing theory. Int. J. Commun. Netw. Distrib. Sys. 2020, 24, 186–213. [Google Scholar] [CrossRef]
- Ghosh, S.; Unnikrishnan, S. Reduced power consumption in Wireless Sensor Networks using queue based approach. In Proceedings of the 5th IEEE International Conference on Advances in Computing, Communication and Control (ICAC3), Mumbai, India, 1–2 December 2017. [Google Scholar]
- Kempa, W.M. Analytical model of a Wireless Sensor Network (WSN) node operation with a modified threshold-type energy saving mechanism. Sensors 2019, 19, 3114. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-H.; Jung, I.-B. Adaptive-compression based congestion control technique for wireless sensor networks. Sensors 2010, 10, 2919–2945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Li, Q.; Qu, Y.; Zhao, B. An energy-efficient MAC protocol using dynamic queue management for delay-tolerant mobile sensor networks. Sensors 2011, 11, 1847–1864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syafrudin, M.; Alfian, G.; Fitriyani, N.L.; Rhee, J. Performance analysis of IoT-based sensor, big data processing, and machine learning model for real-time monitoring system in automotive manufacturing. Sensors 2018, 18, 2946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Qi, H.; Xu, T.; Hua, Q.Q.; Yin, H.S.; Hua, G. Queue models for wireless sensor networks based on random early detection. Peer Peer Netw. Appl. 2019, 12, 1539–1549. [Google Scholar] [CrossRef]
- Hafidi, S.; Gharbi, N.; Mokdad, L. Queuing and service management for congestion control in Wireless Sensor Networks using Markov chains. In Proceedings of the IEEE Symposium on Computers and Communications ISCC, Murcia, Spain, 27–30 June 2005; pp. 176–181. [Google Scholar]
- Alfa, A.S. An alternative approach for analyzing finite buffer queues in discrete time. Perform. Eval. 2003, 53, 75–92. [Google Scholar] [CrossRef]
- Grassmann, W.; Tavakoli, J. The distribution of the line length in a discrete time GI/G/1 queue. Perform. Eval. 2019, 131, 43–53. [Google Scholar] [CrossRef]
- Kim, B.; Kim, J. Explicit solution for the stationary distribution of a discrete-time finite buffer queue. J. Ind. Manag. Optim. 2016, 12, 1121–1133. [Google Scholar] [CrossRef]
- Zhao, Z.; Elancheziyande, A.; De Oliveira, J.C. Sleeping policy cost analysis for sensor nodes collecting heterogeneous data. In Proceedings of the 43rd IEEE Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 18–20 March 2009; pp. 635–640. [Google Scholar]
- Hoflack, L.; De Vuyst, S.; Wittevrongel, S.; Bruneel, H. System content and packet delay in discrete-time queues with session-based arrivals. In Proceedings of the 5th IEEE International Conference on Information Technology, Las Vegas, NV, USA, 7–9 April 2008; pp. 1053–1058. [Google Scholar]
- Bruneel, H.; Kim, B.G. Discrete-Time Models for Communication Systems Including ATM; Kluwer Academic Publishers: Boston, MA, USA, 1993; pp. 1–48. [Google Scholar]
- Hunter, J.J. Mathematical techniques of applied probability, vol. II. In Discrete-Time Models: Techniques and Applications; Academic Press: New York, NY, USA, 1983; pp. 189–236. [Google Scholar]
- Takagi, H. Queueing analysis—A foundation of performance evaluation, Vol. 3. In Discrete-Time Systems; North-Holland: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Wittevrongel, S.; Bruneel, H. Discrete-time queue with correlated arrivals and constant service times. Comput. Oper. Res. 1999, 20, 93–108. [Google Scholar] [CrossRef]
- Fiems, D.; Steyaert, B.; Bruneel, H. Discrete-time queues with generally distributed service times and renewal-type server interruptions. Perform. Eval. 2005, 35, 277–298. [Google Scholar] [CrossRef]
- Bharath-Kumar, K. Discrete time queueing systems and their networks. IEEE Trans. Commun. 1980, 28, 260–263. [Google Scholar] [CrossRef]
- Korolyuk, V.S. Boundary-value problems for compound Poisson processes. Theor. Probab. Appl. 1974, 19, 1–13. [Google Scholar] [CrossRef]
- Abate, J.; Whitt, W. Numerical inversion of probability generating functions. Oper. Res. Lett. 1992, 12, 245–251. [Google Scholar] [CrossRef]










| k | Symmetry | Negative Skewness | Positive Skewness |
|---|---|---|---|
| 1 | 0.644089 | 0.409344 | 0.418129 |
| 2 | 0.361425 | 0.107254 | 0.142688 |
| 3 | 0.166121 | 4.163336 | 0.030098 |
| 4 | 0.051831 | 6.938894 | 0 |
| 5 | 0.013312 | 5.551115 | 1.110223 |
| 6 | 3.700743 | 9.251859 | 2.312965 |
| Buffer State n | |||
|---|---|---|---|
| 0 | 0.036321 | 0.049755 | 0.038306 |
| 1 | 0.036321 | 0.049755 | 0.038306 |
| 2 | 0.037954 | 0.055577 | 0.045982 |
| 3 | 0.042496 | 0.069353 | 0.062898 |
| 4 | 0.052282 | 0.094659 | 0.092465 |
| 5 | 0.071575 | 0.137233 | 0.140520 |
| 6 | 0.108269 | 0.206258 | 0.216532 |
| 7 | 0.177884 | 0.318161 | 0.337882 |
| 8 | 0.313364 | 0.508249 | 0.544020 |
| 9 | 0.585439 | 0.855341 | 0.925785 |
| 10 | 1.134407 | 1.511127 | 1.654884 |
| System Size N | |||
|---|---|---|---|
| 2 | 1.682303 | 2.000242 | 2.088127 |
| 3 | 1.535842 | 1.762685 | 1.818474 |
| 4 | 1.418714 | 1.639140 | 1.716005 |
| 5 | 1.327611 | 1.577548 | 1.678921 |
| 6 | 1.257000 | 1.545704 | 1.664732 |
| 7 | 1.205492 | 1.528632 | 1.658915 |
| 8 | 1.171707 | 1.519536 | 1.656483 |
| 9 | 1.151613 | 1.514796 | 1.655473 |
| 10 | 1.140419 | 1.512365 | 1.655056 |
| 11 | 1.134407 | 1.511127 | 1.654884 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kempa, W.M. Probabilistic Analysis of a Buffer Overflow Duration in Data Transmission in Wireless Sensor Networks. Sensors 2020, 20, 5772. https://doi.org/10.3390/s20205772
Kempa WM. Probabilistic Analysis of a Buffer Overflow Duration in Data Transmission in Wireless Sensor Networks. Sensors. 2020; 20(20):5772. https://doi.org/10.3390/s20205772
Chicago/Turabian StyleKempa, Wojciech M. 2020. "Probabilistic Analysis of a Buffer Overflow Duration in Data Transmission in Wireless Sensor Networks" Sensors 20, no. 20: 5772. https://doi.org/10.3390/s20205772
APA StyleKempa, W. M. (2020). Probabilistic Analysis of a Buffer Overflow Duration in Data Transmission in Wireless Sensor Networks. Sensors, 20(20), 5772. https://doi.org/10.3390/s20205772





