Variational Channel Estimation with Tempering: An Artificial Intelligence Algorithm for Wireless Intelligent Networks
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Previous Research and Limitations
1.3. Objective
- Modeling of the channel estimation problem into a variational message passing algorithm;
- Evaluation of the performance error bound of our novel CEVTI algorithm;
- Use of a Monte Carlo simulation to verify the bit error rate (BER), convergence rate, and mutual information of the CEVTI approach; and
- Established the efficiency and superiority of our new algorithm, CEVTI.
1.4. Contributions
- The modeling of the OFDM channel estimation problem into a new variational message passing algorithm;
- An evaluation of the performance error bound of our innovative variational tempering channel estimation algorithm; and
- A numerical simulation of the performance of CEVTI to show that in general cases, the proposed CEVTI algorithm performs better than other algorithms.
2. Background
3. Solution Framework
3.1. Mean-Field CEVTI
3.2. Tempered Joint
3.3. Tempered ELBO
3.4. Local Variational
4. The CEVTI Algorithm
Updates
5. Application of CEVTI
5.1. Application of CEVTI for CDMA
5.1.1. Channel Coefficient Estimation
5.1.2. Noise Covariance Estimation
5.1.3. Codeword Distribution Estimation
5.2. Application of CEVTI in Massive MIMO
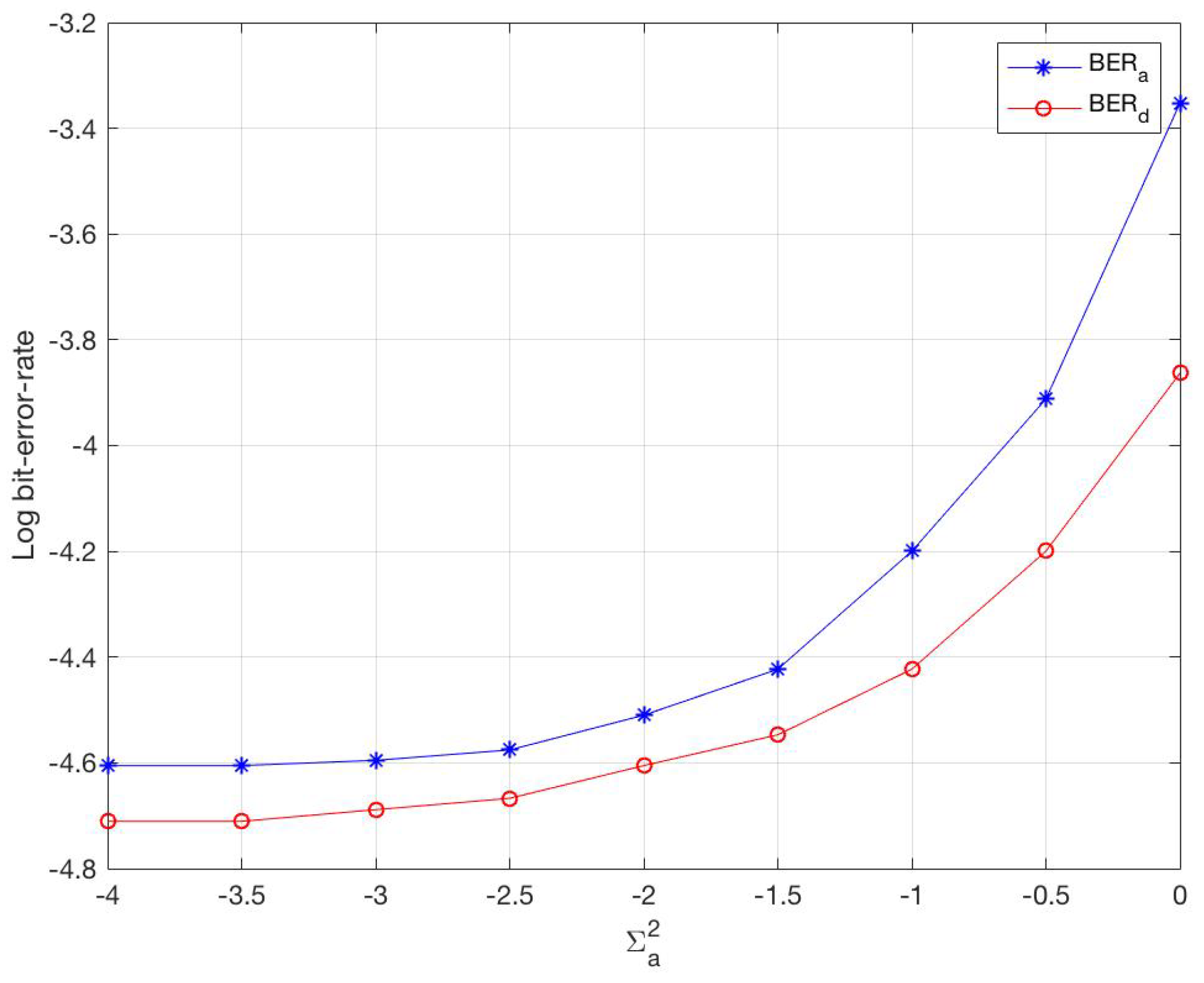
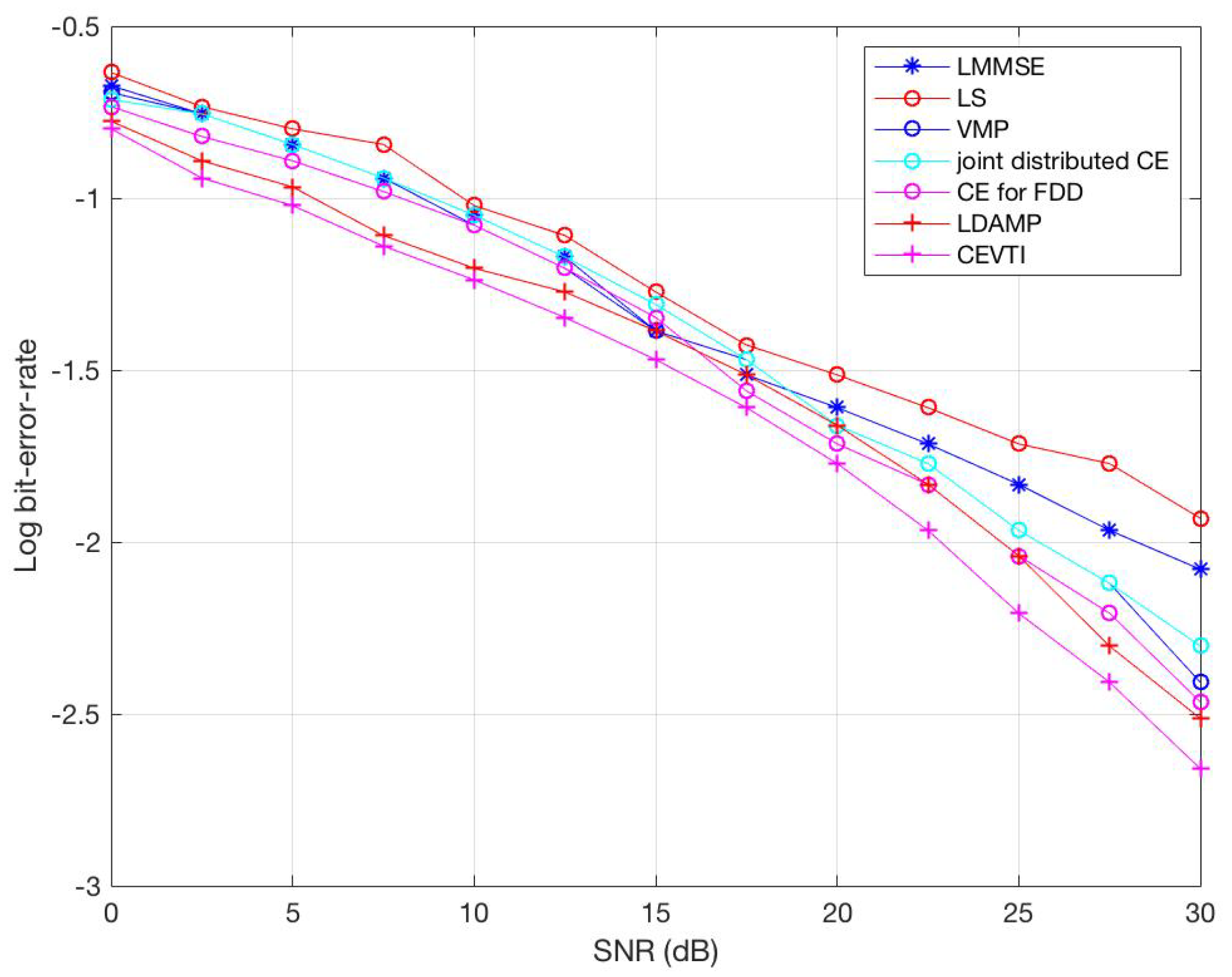
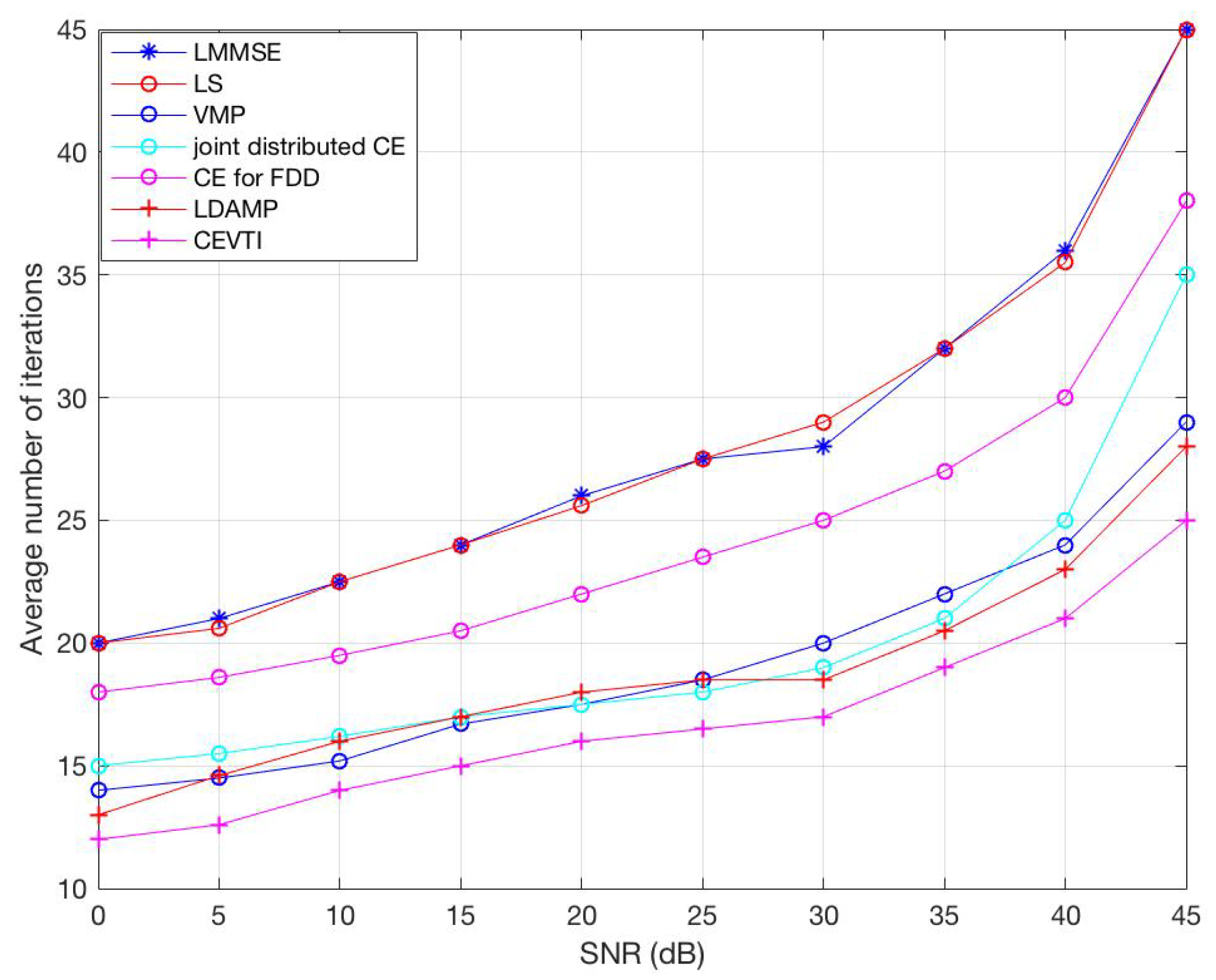
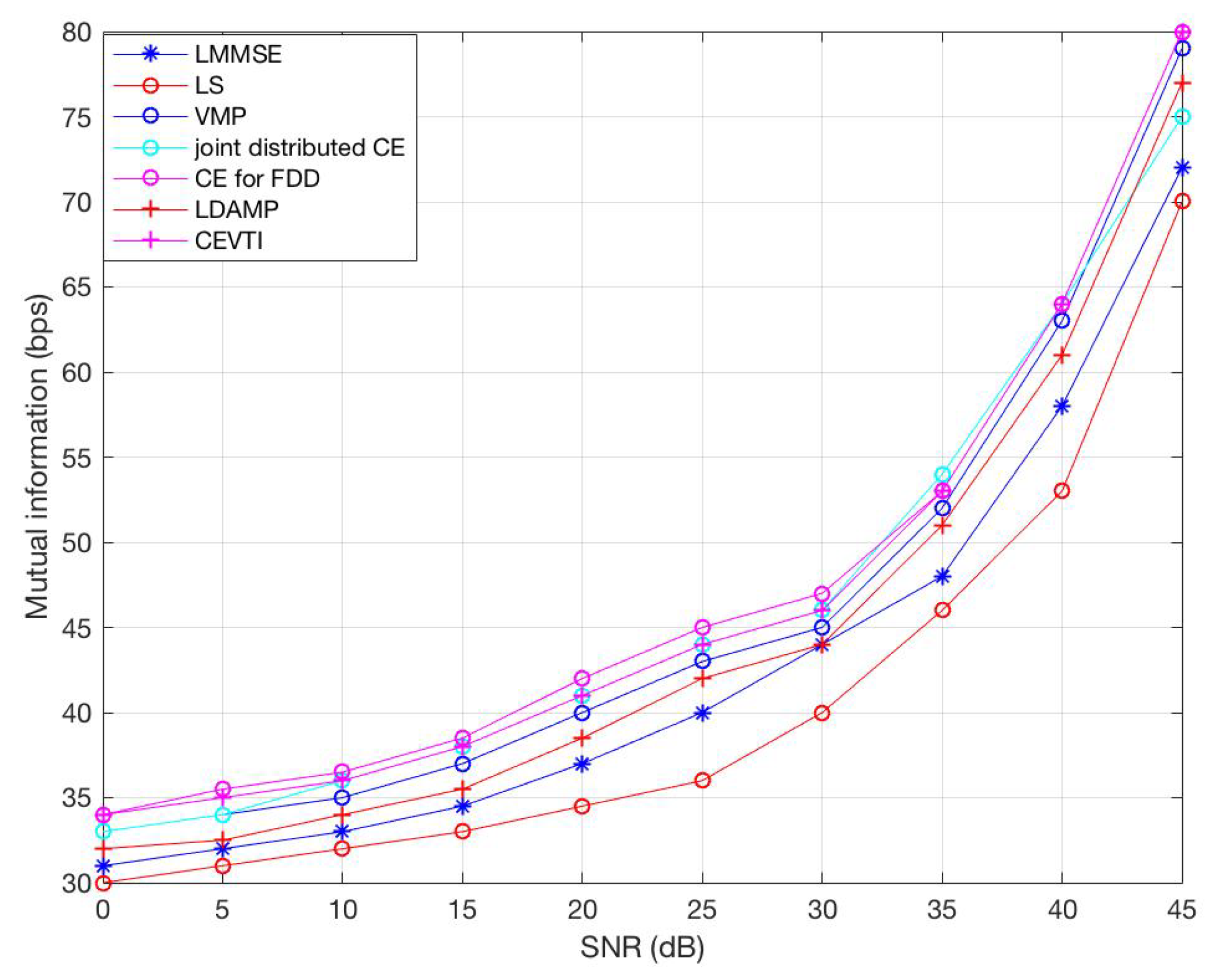
6. Simulations and Results
6.1. Simulations
6.2. Complexity Analysis
6.3. Optimality Guarantee
7. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| WSNs | Wireless Sensor Networks |
| VI | Variational Inference |
| CEVTI | Channel Estimation Variational Tempering Inference |
| CE | Channel Estimation |
| CS | Compressive Sensing |
| CSI | Channel State Information |
| MP | Message Passing |
| ELBO | Evidence Lower Bound |
| MCMC | Monte Carlo Markov Chain |
References
- Alibakhshikenari, M.; Virdee, B.S.; Khalily, M.; Shukla, P.; See, C.H.; Abd-Alhameed, R.; Falcone, F.; Limiti, E. Beam-scanning leaky-wave antenna based on CRLH-metamaterial for millimetre-wave applications. IET Microwaves Antennas Propag. 2019, 13, 1129–1133. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Limiti, E. Compact Single-Layer Traveling-Wave Antenna Design Using Metamaterial Transmission Lines. Radio Sci. 2017, 52, 1510–1521. [Google Scholar] [CrossRef] [Green Version]
- Mallat, N.K.; Ishtiaq, M.; Rehman, A.U.; Iqbal, A. Millimeter-Wave in the Face of 5G Communication Potential Applications. IETE J. Res. 2020, 3, 1–9. [Google Scholar] [CrossRef]
- Mohammadi, M.; Kashani, F.H.; Ghalibafan, J. Backfire-to-endfire scanning capability of a balanced metamaterial structure based on slotted ferrite-filled waveguide. Waves Random Complex Media 2019, 1–15. [Google Scholar] [CrossRef]
- Awan, W.; Hussain, N.; Naqvi, S.; Iqbal, A.; Striker, R.; Mitra, D.; Braaten, B. A Miniaturized Wideband and Multi-band On-Demand Reconfigurable Antenna for Compact and Portable Devices. AEU Int. J. Electron. Commun. 2020, 122, 153266. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; See, C.H.; Abdalhameed, R.; Falcone Lanas, F.J.; Limiti, E. High-gain metasurface in polyimide on-chip antenna based on CRLH-TL for sub-terahertz integrated circuits. Sci. Rep. 2020, 10, 4298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watanabe, K.; Kojima, S.; Akao, T.; Katsuno, M.; Ahn, C.J. Modified Pilot Selection for Systematic Polar Coded MIMO-OFDM Channel Estimation. In Proceedings of the 2018 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS 2018), Okinawa, Japan, 27–30 November 2018; pp. 237–241. [Google Scholar]
- Khan, I.; Singh, D. Efficient compressive sensing based sparse channel estimation for 5G massive MIMO systems. AEU Int. J. Electron. Commun. 2018, 89, 181–190. [Google Scholar] [CrossRef]
- Motade, S.; Kulkarni, A. Channel Estimation and Data Detection Using Machine Learning for MIMO 5G Communication Systems in Fading Channel. Technologies 2018, 6, 72. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Yang, F.; Liu, S.; Song, J.; Han, Z. Sparse Channel Estimation for MIMO-OFDM Systems in High-Mobility Situations. IEEE Trans. Veh. Technol. 2018, 67, 6113–6124. [Google Scholar] [CrossRef]
- Dai, J.; Liu, A.; Lau, V.K.N. FDD Massive MIMO Channel Estimation With Arbitrary 2D-Array Geometry. IEEE Trans. Signal Process. 2018, 66, 2584–2599. [Google Scholar] [CrossRef] [Green Version]
- Nayebi, E.; Rao, B.D. Semi-blind Channel Estimation for Multiuser Massive MIMO Systems. IEEE Trans. Signal Process. 2018, 66, 540–553. [Google Scholar] [CrossRef]
- Qiao, Y.T.; Yu, S.Y.; Su, P.C.; Zhang, L.J. Research on an iterative algorithm of LS channel estimation in MIMO OFDM systems. IEEE Trans. Broadcast. 2005, 51, 149–153. [Google Scholar] [CrossRef]
- Simko, M.; Mehlfuhrer, C.; Wrulich, M.; Rupp, M. Doubly dispersive channel estimation with scalable complexity. In Proceedings of the 2010 International Itg Workshop on Smart Antennas (WSA 2010), Bremen, Germany, 23–24 February 2010; pp. 251–256. [Google Scholar]
- Wang, J.; Chen, H.; Li, S. Soft-output MMSE V-BLAST receiver with MMSE channel estimation under correlated Rician fading MIMO channels. Wirel. Commun. Mob. Comput. 2012, 12, 1363–1370. [Google Scholar] [CrossRef]
- Daasch, R.R.; Shirley, C.G.; Chen, H.; Gao, F.; Ansari, N. Distributed Angle Estimation for Localization in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2013, 12, 527–537. [Google Scholar]
- Wang, X.; Poor, H.V. Iterative (turbo) soft interference cancellation and decoding for coded CDMA. IEEE Trans. Commun. 1999, 47, 1046–1061. [Google Scholar] [CrossRef] [Green Version]
- Rao, X.; Lau, V.K.N. Distributed Compressive CSIT Estimation and Feedback for FDD Multi-User Massive MIMO Systems. IEEE Trans. Signal Process. 2014, 62, 3261–3271. [Google Scholar]
- Tseng, C.C.; Wu, J.Y.; Lee, T.S. Enhanced Compressive Downlink CSI Recovery for FDD Massive MIMO Systems Using Weighted Block -Minimization. IEEE Trans. Commun. 2016, 64, 1055–1067. [Google Scholar] [CrossRef]
- Paskin, M.; Guestrin, C.; McFadden, J. A robust architecture for distributed inference in sensor networks. In Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN 2005), Los Angeles, CA, USA, 24–27 April 2005; pp. 55–62. [Google Scholar]
- Bellili, F.; Sohrabi, F.; Yu, W. Generalized Approximate Message Passing for Massive MIMO mmWave Channel Estimation with Laplacian Prior. IEEE Trans. Commun. 2019, 67, 3205–3219. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.H.F. Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems. IEEE Wirel. Commun. Lett. 2017, 7, 114–117. [Google Scholar] [CrossRef]
- He, H.; Wen, C.-K.; Jin, S.; Li, G.Y. Deep learning-based channel estimation for beamspace mmwave massive mimo systems. IEEE Wirel. Commun. Lett. 2018, 7, 852–855. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, H.; Hua, M.; Li, C.; Huang, Y.; Yang, L. Double Coded Caching in Ultra Dense Networks: Caching and Multicast Scheduling via Deep Reinforcement Learning. IEEE Trans. Commun. 2020, 68, 1071–1086. [Google Scholar] [CrossRef]
- Ahmad, A.; Serpedin, E.; Nounou, H.; Nounou, M. Joint distributed parameter and channel estimation in wireless sensor networks via variational inference. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 830–834. [Google Scholar]
- Hu, B.; Land, I.; Rasmussen, L.; Piton, R.; Fleury, B. A Divergence Minimization Approach to Joint Multiuser Decoding for Coded CDMA. IEEE J. Sel. Areas Commun. 2008, 26, 432–445. [Google Scholar]
- Kirkelund, G.E.; Manchon, C.N.I.; Christensen, L.P.B.; Riegler, E.; Fleury, B.H. Variational Message-Passing for Joint Channel Estimation and Decoding in MIMO-OFDM. In Proceedings of the 2010 IEEE Global Communications Conference (GLOBECOM 2010), Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar]
- Cheng, X.; Sun, J.; Li, S. Channel Estimation for FDD Multi-User Massive MIMO: A Variational Bayesian Inference-Based Approach. IEEE Trans. Wirel. Commun. 2017, 16, 7590–7602. [Google Scholar] [CrossRef]
- Thoota, S.S.; Murthy, C.R.; Annavajjala, R. Quantized Variational Bayesian Joint Channel Estimation and Data Detection for Uplink Massive MIMO Systems with Low resolution ADCS. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP 2019), Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar]
- Mandt, S.; Mcinerney, J.; Abrol, F.; Ranganath, R.; Blei, D. Variational Tempering. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS 2016), Cadiz, Spain, 9–11 May 2016; pp. 704–712. [Google Scholar]
- Buchholz, A. Quasi-Monte Carlo Variational Inference. arXiv 2004, arXiv:1807.01604v1. [Google Scholar]
- Wu, N.; Yuan, W.; Guo, Q.; Kuang, J. A Hybrid BP-EP-VMP Approach to Joint Channel Estimation and Decoding for FTN Signaling over Frequency Selective Fading Channels. IEEE Access 2017, 5, 6849–6858. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic Variational Inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Subrahmanyam, P.V. Brouwer’s Fixed-Point Theorem. In Elementary Fixed Point Theorems; Springer: Berlin, Germany, 2018. [Google Scholar]
- Koller, D.; Friedman, N.; Bach, F. Probabilistic graphical models: Principles and techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
| Parameter | Meaning | Value |
|---|---|---|
| pilot number | 32 | |
| N | number of users | 8 |
| M | number of antennas | 4 |
| receiver j’s signal toward user i | ||
| signal prior | [0.5,1] | |
| user prior | [0.4,0.6] | |
| convergence tolerance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, M.; Chen, Y.; Islam, S.M.N.; Crespi, N. Variational Channel Estimation with Tempering: An Artificial Intelligence Algorithm for Wireless Intelligent Networks. Sensors 2020, 20, 5939. https://doi.org/10.3390/s20205939
Liu J, Li M, Chen Y, Islam SMN, Crespi N. Variational Channel Estimation with Tempering: An Artificial Intelligence Algorithm for Wireless Intelligent Networks. Sensors. 2020; 20(20):5939. https://doi.org/10.3390/s20205939
Chicago/Turabian StyleLiu, Jia, Mingchu Li, Yuanfang Chen, Sardar M. N. Islam, and Noel Crespi. 2020. "Variational Channel Estimation with Tempering: An Artificial Intelligence Algorithm for Wireless Intelligent Networks" Sensors 20, no. 20: 5939. https://doi.org/10.3390/s20205939
APA StyleLiu, J., Li, M., Chen, Y., Islam, S. M. N., & Crespi, N. (2020). Variational Channel Estimation with Tempering: An Artificial Intelligence Algorithm for Wireless Intelligent Networks. Sensors, 20(20), 5939. https://doi.org/10.3390/s20205939






.png)


