Establishment of a New Quantitative Evaluation Model of the Targets’ Geometry Distribution for Terrestrial Laser Scanning
Abstract
1. Introduction
2. Methods
2.1. Registration Model of Two Scans
2.2. Calculation of Rotation Parameters
2.3. Calculation of Translation Parameters
2.4. Quantitative Evaluation Model of TGD
- The values of and represent the amplification of the unit weight variance, which means the lower the values of and , the higher the solution precisions of the rotation parameters and the translation parameters;
- The values of calculated by Equation (19) are related to the coefficient matrix and the weight matrix of , among which is related to TGD (the coordinates of targets ) and the rotation matrix . Namely, when is fixed, the better the quality of TGD, the lower the values of ;
- The values of calculated by Equation (20) are related to the coefficient matrix ; and the weight matrix of , among which is related to TGD (the coordinates of targets ) and the position of scanner i + 1 in Scan i. Namely, the better the quality of TGD and the position of scanner i + 1, the lower the values of ;
- The calculation formula of is identical to the calculation formula of in GPS, so the can be used to evaluate the quality of the received GPS satellites’ distribution. Namely, the and model is a unified evaluation model of the targets’ and GNSS satellites’ geometric distribution.
2.5. Equationuationual Weight Model of and
2.6. Model Application Scheme
2.6.1. The Best Position of Scanner i + 1
- (1)
- Selecting the possible place of scanner i + 1 in Scan i;
- (2)
- Obtaining the coordinates of all targets in Scan i;
- (3)
- Using Equations (11), (12), (20) and (24) to calculate the values of under different possible places of scanner i + 1;
- (4)
- When the value of is the minimum, the corresponding place is the best position of scanner i + 1.
2.6.2. The Best TGD
- (1)
- Selecting the possible place of targets in Scan i;
- (2)
- Obtaining the coordinates of scanner i + 1 in Scan i;
- (3)
- Setting the number k of targets;
- (4)
- Choosing k places from , and using Equations (6), (20) and (25) to calculate the values of ;
- (5)
- When the value of is the minimum, the corresponding places are the optimum positions of targets, namely, the best TGD.
2.6.3. The Best TGD and the Best Position of Scanner i + 1
- (1)
- Selecting the possible place of targets and the possible place of scanner i + 1 in Scan i;
- (2)
- Setting the number k of targets;
- (3)
- Similar to the above, calculating the values of by k different possible places of targets, and selecting the best TGD where the value of is the minimum;
- (4)
- Similar to the above, calculating the values of under different possible places of scanner i + 1, and selecting the best position of scanner i + 1 where the value of is the minimum.
3. Theoretical Analysis
3.1. The Existence Conditions of
3.2. The Existence Conditions of
- All targets are in the plane of Scan i’s coordinate system, and ;
- All targets are in the plane of Scan i’s coordinate system, and ;
- All targets are in the plane of Scan i’s coordinate system, and .
3.3. The Relationship Between and the Number of Targets
3.4. The Relationship Between and the Number of Targets
3.5. Bounds
3.6. Bounds
4. Experimental Verification
4.1. Calculation Method of Registration Precision
4.2. Experiment I
4.3. Experiment II
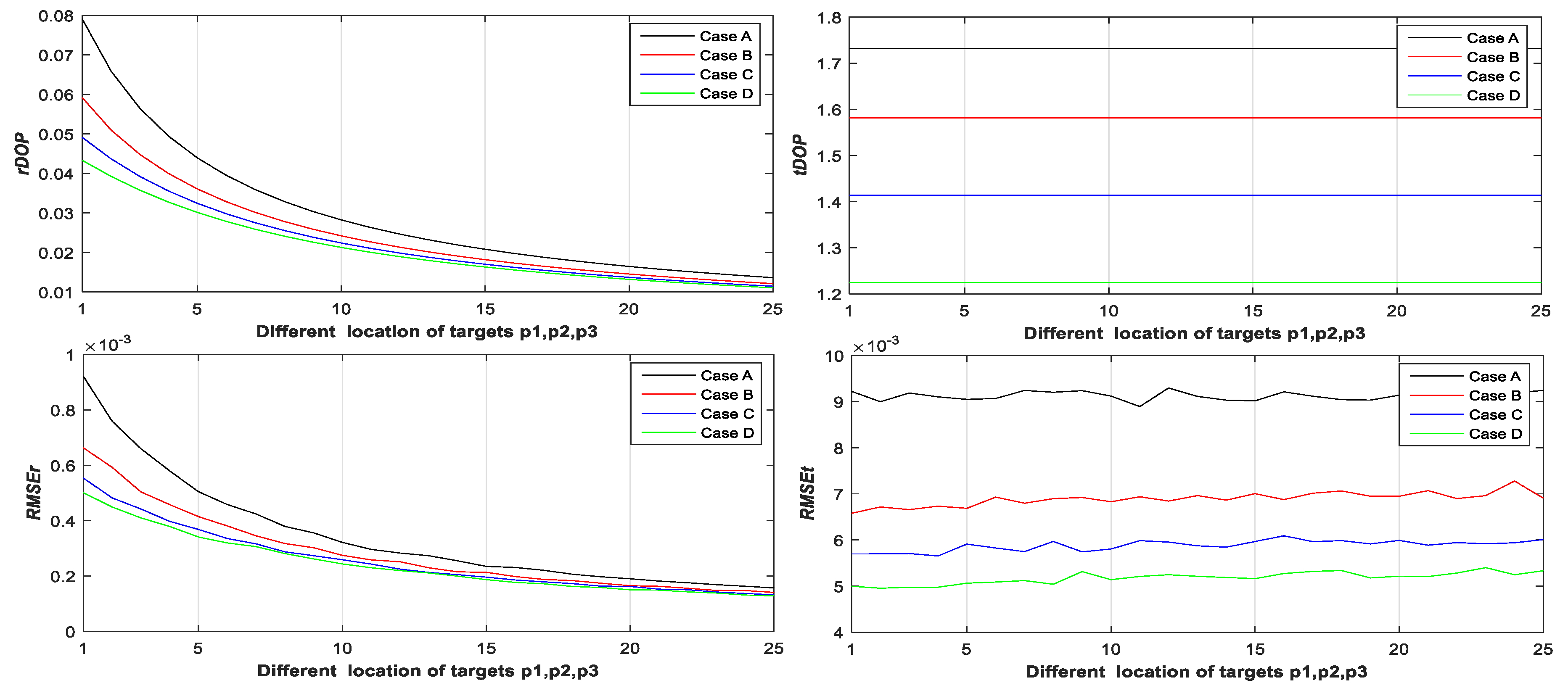
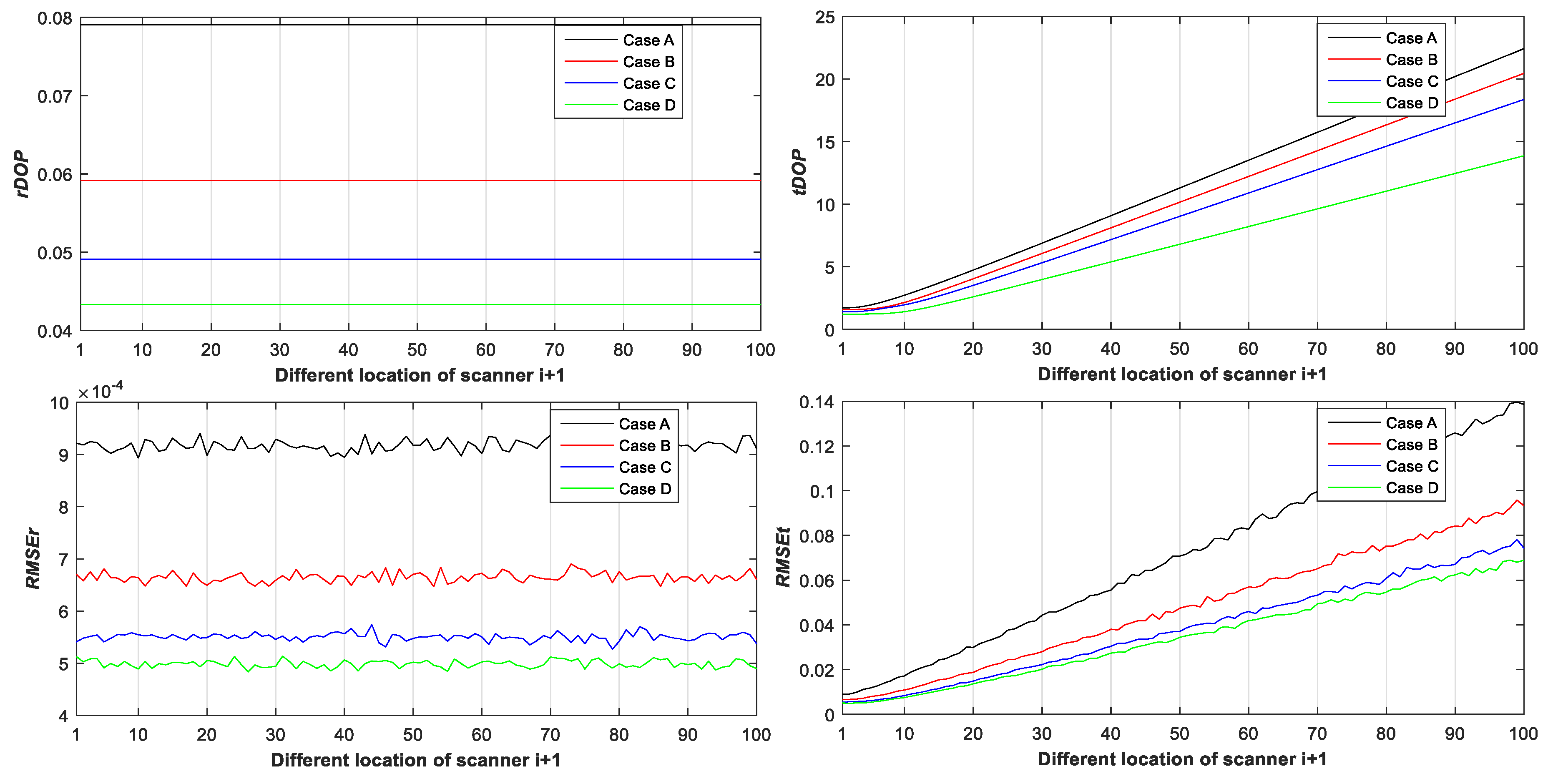
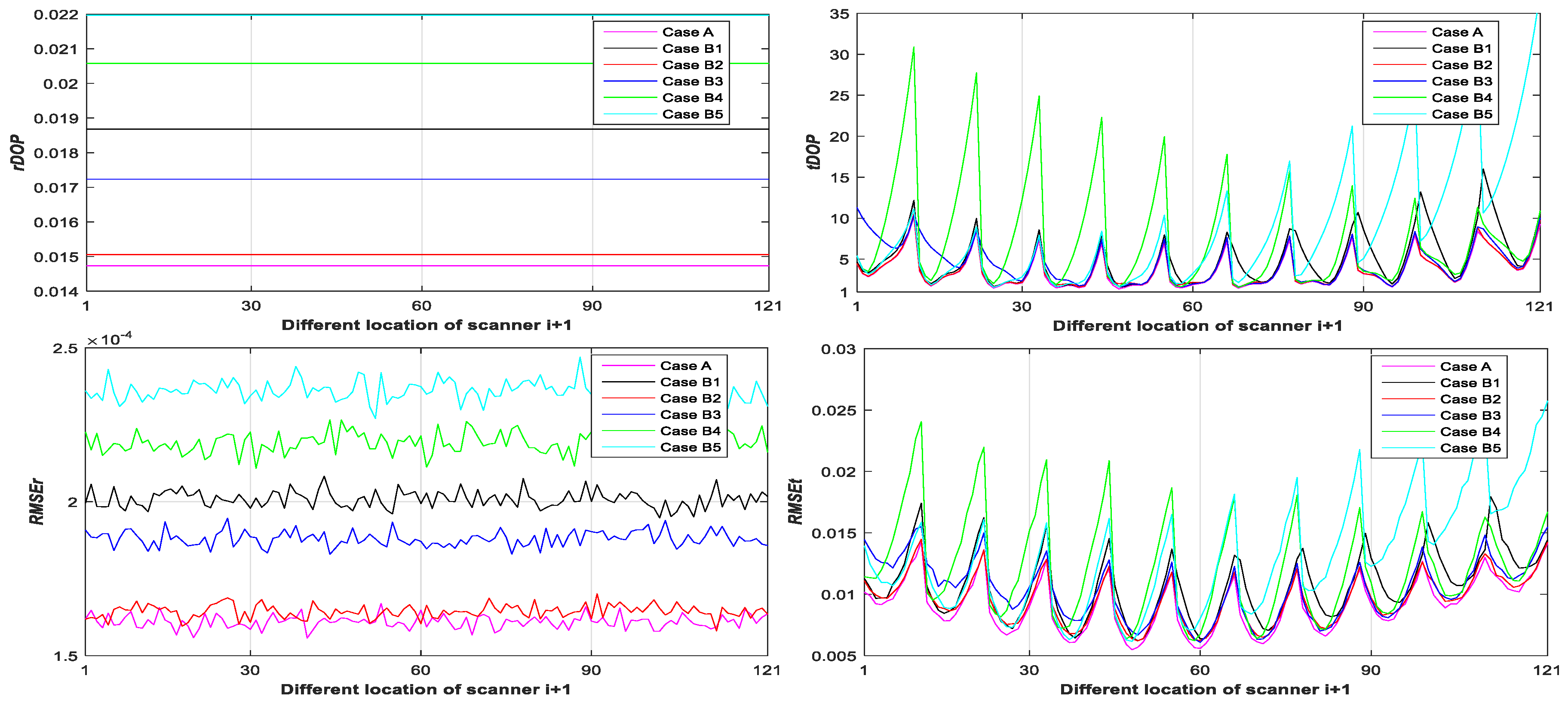
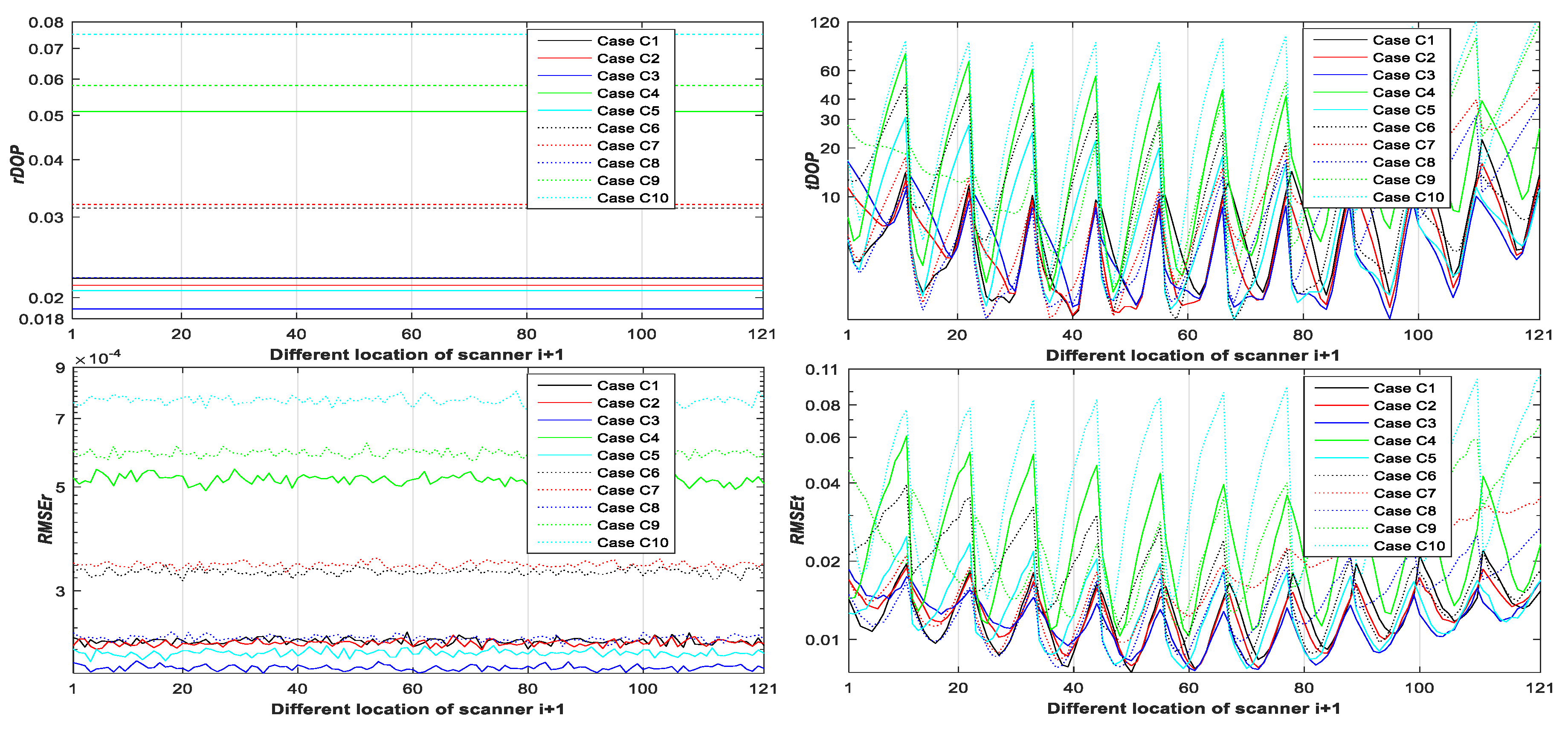
4.4. Results Analysis
- (a)
- (b)
- The farther away the location of scanner i + 1 (with respect to different ), the greater the and in Figure 6;
- (c)
- When the number and position of targets change, but the location of the scanner is unchanged, the value of is a constant, the is around a constant, and different numbers of targets (with respect to Case A, B, C, and D) have different constant valued of and ; the more targets (with respect to Case A, B, C, and D), the smaller the and (see Figure 3, Figure 4 and Figure 5);
- (d)
- (e)
- (f)
- When the location of the scanner changes, but the number and position of targets are unchanged, the value of is a constant, the is around a constant, and different numbers of targets (with respect to Case A, B, C, D, A1, B1–5, and C1–10) have different constant values of and ; the more targets there are (with respect to Case A, B, C, D, A1, B1–5, and C1–10), the smaller the and (see Figure 6, Figure 7 and Figure 8);
- (g)
- The differences between the and the minimum values in cases A1, B1–5, and C1–10 with the minimum are −0.5, −1.6, −1.8, 0.9, −2, −1.7, −1.5, −1.8, −2.1, −1.5, −1.5, −1.6, −1.3, −1.5, −2.0, and −0.8 mm, respectively, which are all less than (half the observation variance, 2.5 mm), so we can use the minimum value with the minimum to represent the minimum value;
- (h)
- We can use and to assess the impact of the targets’ geometry distribution on the rotation parameters and translation parameters, respectively, and use and to help determine the optimal placement location of targets (with respect to the minimum ) and the best location of scanner i + 1 (with respect to the minimum ).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deng, F. Registration Between Multiple Laser Scanner Data Sets, Laser Scanning, Theory and Application; Wang, C.C., Ed.; IntechOpen: London, UK, 2011; pp. 449–472. ISBN 978-953-307-205-0. Available online: http://www.intechopen.com/books/laser-scanning-theory-and-applications/registratioin-between-multiple-laser-scanner-data-sets (accessed on 26 April 2011).
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2009. [Google Scholar]
- Yang, R.H.; Meng, X.L.; Yao, Y.B.; Chen, B.Y.; You, Y.S.; Xiang, Z.J. An analytical approach to evaluate point cloud registration error utilizing targets. ISPRS J. Photogramm. Remote Sens. 2018, 142, 48–56. [Google Scholar] [CrossRef]
- Sharp, G.C.; Lee, S.W.; Wehe, D.K. Multiview registration of 3D scenes by minimizing error between coordinate frames. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1037–1050. [Google Scholar] [CrossRef]
- Eggert, D.W.; Lorusso, A.; Fisher, R.B. Estimating 3-D rigid body transformations: A comparison of four major algorithms. Mach. Vis. Appl. 1997, 9, 272–290. [Google Scholar] [CrossRef]
- Yao, J.L.; Han, B.M.; Yang, Y.X. Research on registration of ground lidar range images. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 12–1119. [Google Scholar]
- Cheng, L.; Chen, S.; Liu, X.Q.; Xu, H.; Wu, Y.; Li, M.C.; Chen, Y.M. Registration of laser scanning point clouds: A review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed]
- Flores-Fuentes, W.; Rivas-Lopez, M.; Sergiyenko, O.; Gonzalez-Navarro, F.F.; Rivera-Castillo, J.; Hernandez-Balbuena, D.; Rodríguez-Quiñonez, J.C. Combined application of power spectrum centroid and support vector machines for measurement improvement in optical scanning systems. Signal Process. 2014, 98, 37–51. [Google Scholar] [CrossRef]
- Rodríguez-Quiñonez, J.C.; Sergiyenko, O.; Flores-Fuentes, W.; Rivera-Castillo, J.; Hernandez-Balbuena, D.; Rascón, R.; Mercorelli, P. Improve a 3D distance measurement accuracy in stereo vision systems using optimization methods’ approach. Opto-Electron. Rev. 2017, 25, 24–32. [Google Scholar] [CrossRef]
- Janßen, J.; Medic, T.; Kuhlmann, H.; Holst, C. Decreasing the uncertainty of the target center estimation at terrestrial laser scanning by choosing the best algorithm and by improving the target design. Remote Sens. 2019, 11, 845. [Google Scholar] [CrossRef]
- Wang, G.L. Research on Registration of Ground Lidar Range Images. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2006. [Google Scholar]
- Fan, L.; Smethurst, J.A.; Atkinson, P.M.; Powrie, W. Error in target-based georeferencing and registration in terrestrial laser scanning. Comput. Geosci. 2015, 83, 54–64. [Google Scholar] [CrossRef]
- Pan, L.X.L. Research on Some Problems of Point Cloud. Master’s Thesis, Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Gordon, S.J.; Lichti, D.D. Terrestrial laser scanners with a narrow field of view: The effect on 3D resection solutions. Surv. Rev. 2004, 37, 292–468. [Google Scholar] [CrossRef]
- Harvey, B.R. Registration and transformation of multiple site terrestrial laser scanning. Geomat. Res. Australas. 2004, 80, 33–50. [Google Scholar]
- Li, Z.C. Research on the Algorithm and Accuracy of Coordinate Conversion. Master’s Thesis, Kuming University of Science and Technology, Kuming, China, 2015. [Google Scholar]
- Liu, K.; Liao, Z.P.; Ding, M.Q.; Xiang, Y.; Cai, C.G. Effects on accuracy of point cloud registration by target setting between the stations. Geotech. Investig. Surv. 2016, 4, 55–58, 67. [Google Scholar]
- Wang, Y.C.; Hu, W.S. Influence caused by public point selection on accuracy of coordinate conversion. Mod. Surv. Mapp. 2008, 31, 5–15. [Google Scholar]
- Zhao, B.F.; Zhang, X.; Jiang, T.C. Effect of coordinate conversion model and the selected common points on the accuracy of conversion results. J. Huaihai Inst. Technol. Nat. Sci. Ed. 2009, 18, 4–56. [Google Scholar]
- Zhang, H.L.; Lin, J.R.; Zhu, J.G. Three-dimensional coordinate transformation accuracy and its influencing factors. Opto-Electron. Eng. 2012, 39, 10–31. [Google Scholar]
- Bornaz, L.; Lingus, A.; Rinaudo, F. Multiple Scan Registration in LiDAR Close-Range Applications. 2003. Available online: https://pdfs.semanticscholar.org/ce10/a74f8de40df362c8a9cc8f54fa0e6484b4f4.pdf (accessed on 18 January 2020).
- Li, Z.H.; Huang, J.S. GPS Surveying Data Processing, 2nd ed.; Wuhan University press: Wuhan, China, 2010; pp. 160–162. [Google Scholar]
- Yang, R.H. Research on Point Cloud Angular Resolution and Processing Model of Terrestrial Laser Scanning. Ph.D. Thesis, Wuhan University, Wuhan, China, 2011. [Google Scholar]
- Cui, X.Z.; Yu, Z.S.; Tao, B.Z.; Liu, D.J.; Yu, Z.L.; Sun, H.Y.; Wang, X.Z. Generalized Surveying Adjustment, 2nd ed.; Wuhan University press: Wuhan, China, 2009; pp. 8–9. [Google Scholar]
- Li, J.W.; Li, Z.H.; Zhou, W.; Si, S.J. Study on the minimum of GDOP in Satellite navigation and its applications. Acta Geodaetica Cartogr. Sin. 2011, 40, 85–88. [Google Scholar]
- Meng, X.; Roberts, G.W.; Dodson, A.H.; Cosser, E.; Barnes, J.; Rizos, C. Impact of GPS satellite and pseudolite geometry on structural deformation monitoring: Analystical and empirical studies. J. Geod. 2004, 77, 12–822. [Google Scholar] [CrossRef]
- Yarlagadda, R.; Ali, I.; Dhahir, N.A.; Hershey, J. GPS DOP Metric. IEEE Proc. Radar Sonar Navig. 2000, 147, 5–264. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influnencing factor on the quanlity of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
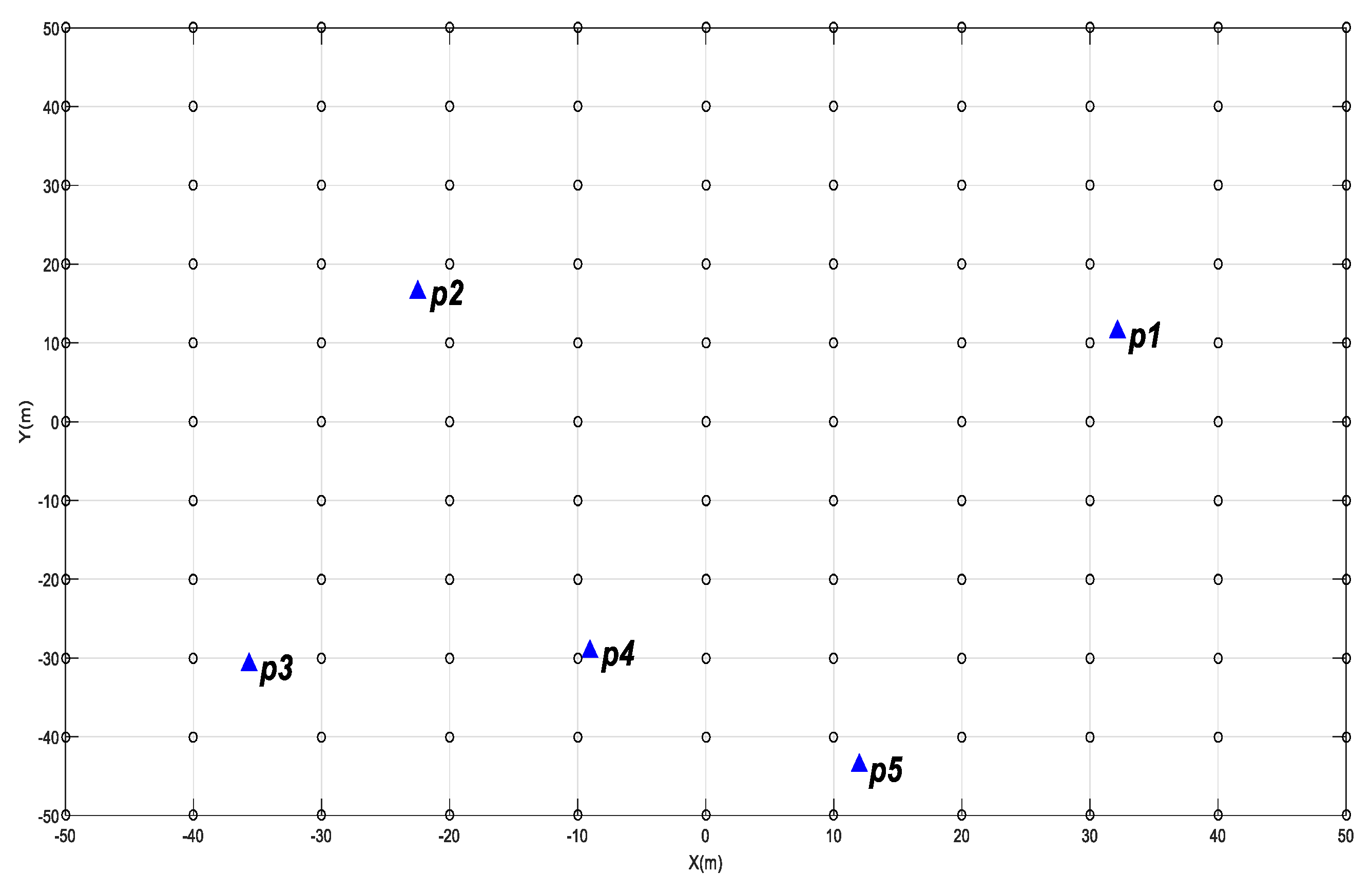


| The Name of Distribution | Including Targets | The Name of Distribution | Including Targets |
|---|---|---|---|
| Case A1 | , , , , | Case C1 | , , |
| Case B1 | , , , | Case C2 | , , |
| Case B2 | , , , | Case C3 | , , |
| Case B3 | , , , | Case C4 | , , |
| Case B4 | , , , | Case C5 | , , |
| Case B5 | , , , | Case C6 | , , |
| Case C7 | , , | ||
| Case C8 | , , | ||
| Case C9 | , , | ||
| Case C10 | , , |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Meng, X.; Xiang, Z.; Li, Y.; You, Y.; Zeng, H. Establishment of a New Quantitative Evaluation Model of the Targets’ Geometry Distribution for Terrestrial Laser Scanning. Sensors 2020, 20, 555. https://doi.org/10.3390/s20020555
Yang R, Meng X, Xiang Z, Li Y, You Y, Zeng H. Establishment of a New Quantitative Evaluation Model of the Targets’ Geometry Distribution for Terrestrial Laser Scanning. Sensors. 2020; 20(2):555. https://doi.org/10.3390/s20020555
Chicago/Turabian StyleYang, Ronghua, Xiaolin Meng, Zejun Xiang, Yingmin Li, Yangsheng You, and Huaien Zeng. 2020. "Establishment of a New Quantitative Evaluation Model of the Targets’ Geometry Distribution for Terrestrial Laser Scanning" Sensors 20, no. 2: 555. https://doi.org/10.3390/s20020555
APA StyleYang, R., Meng, X., Xiang, Z., Li, Y., You, Y., & Zeng, H. (2020). Establishment of a New Quantitative Evaluation Model of the Targets’ Geometry Distribution for Terrestrial Laser Scanning. Sensors, 20(2), 555. https://doi.org/10.3390/s20020555






