Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs
Abstract
1. Introduction
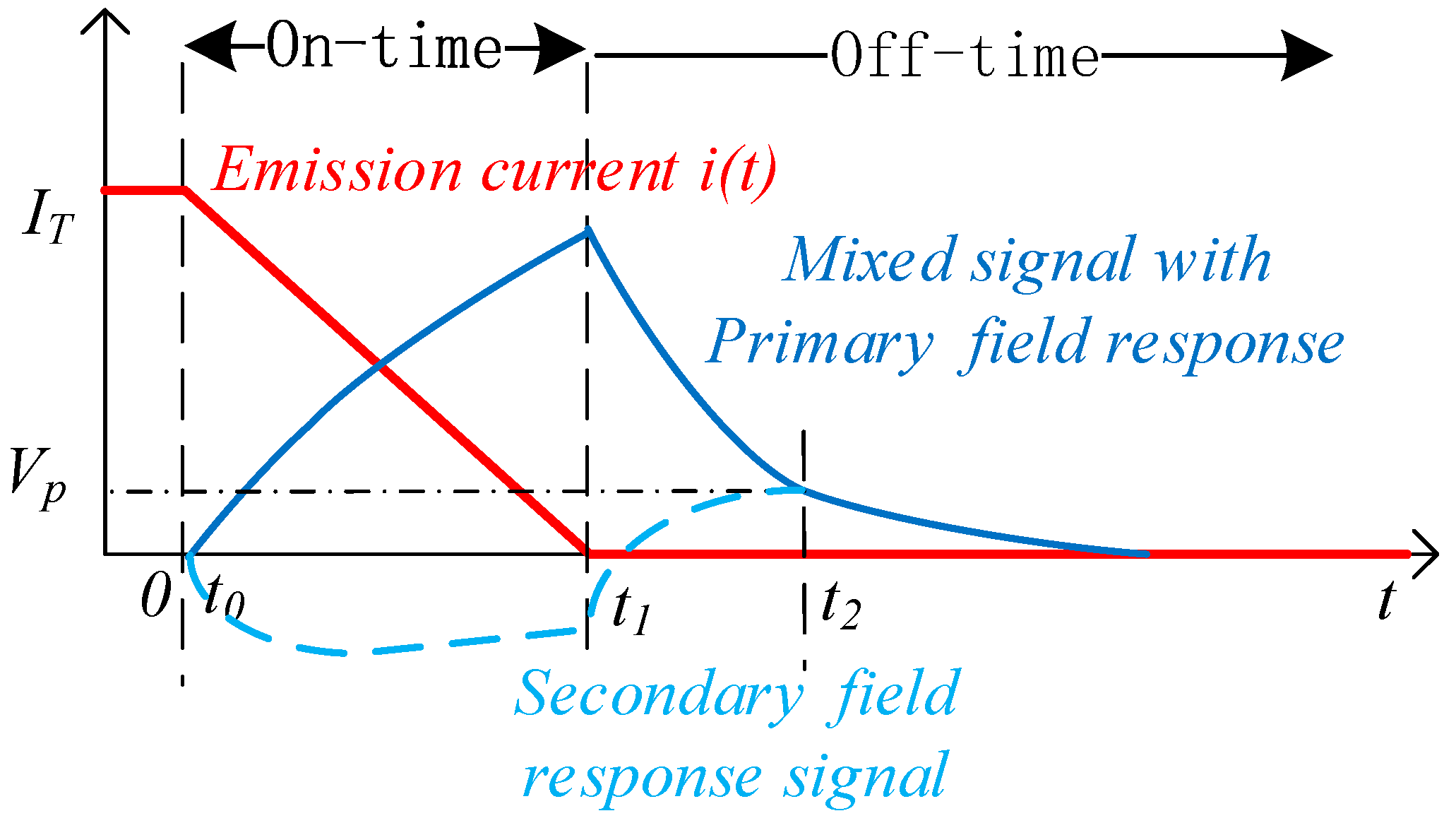
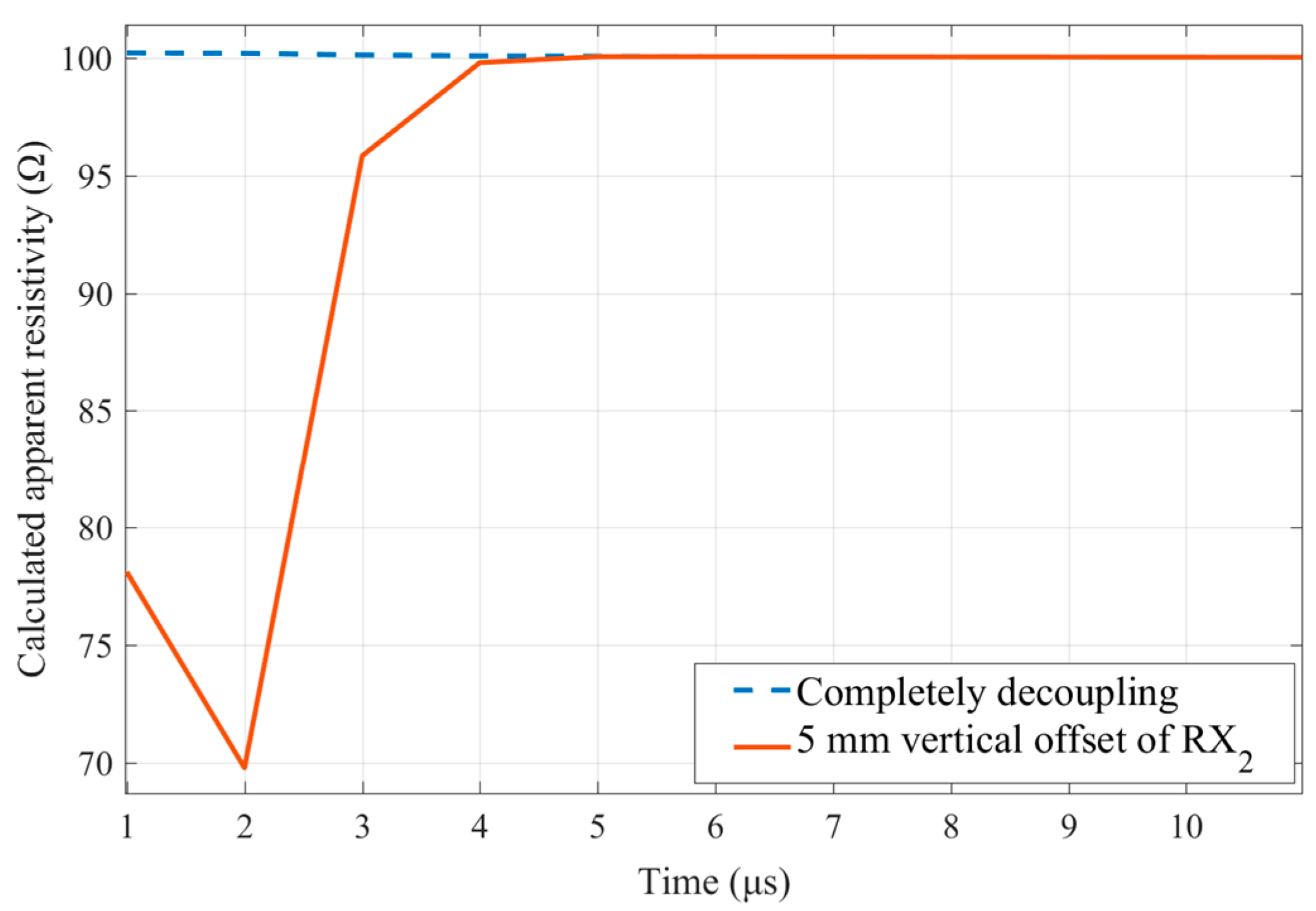
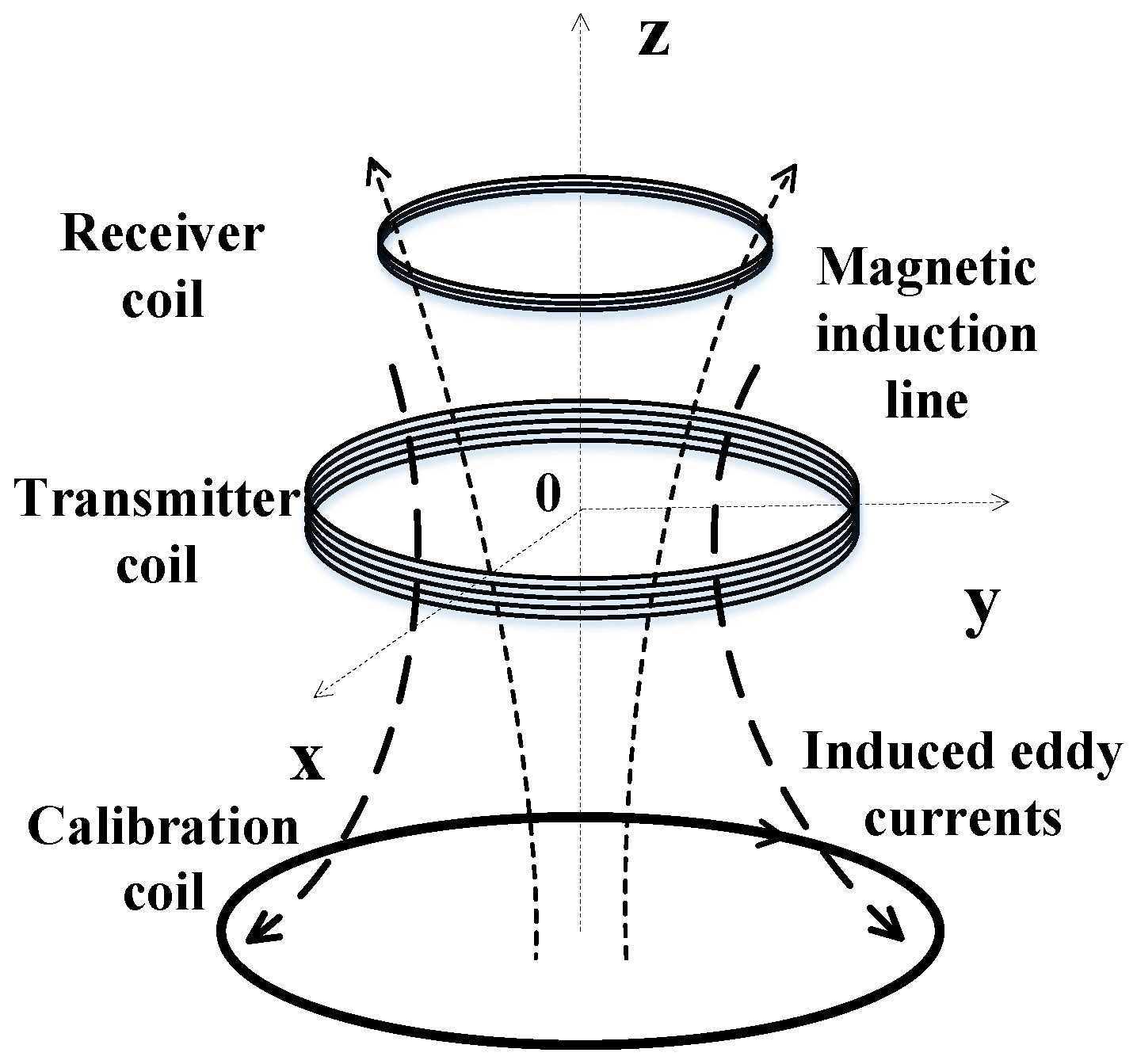
2. The Primary Field Shielding Leakage
3. Shielding Stability to the Primary Field
3.1. Vertical Stability Coefficient
3.2. Horizontal Stability Coefficient
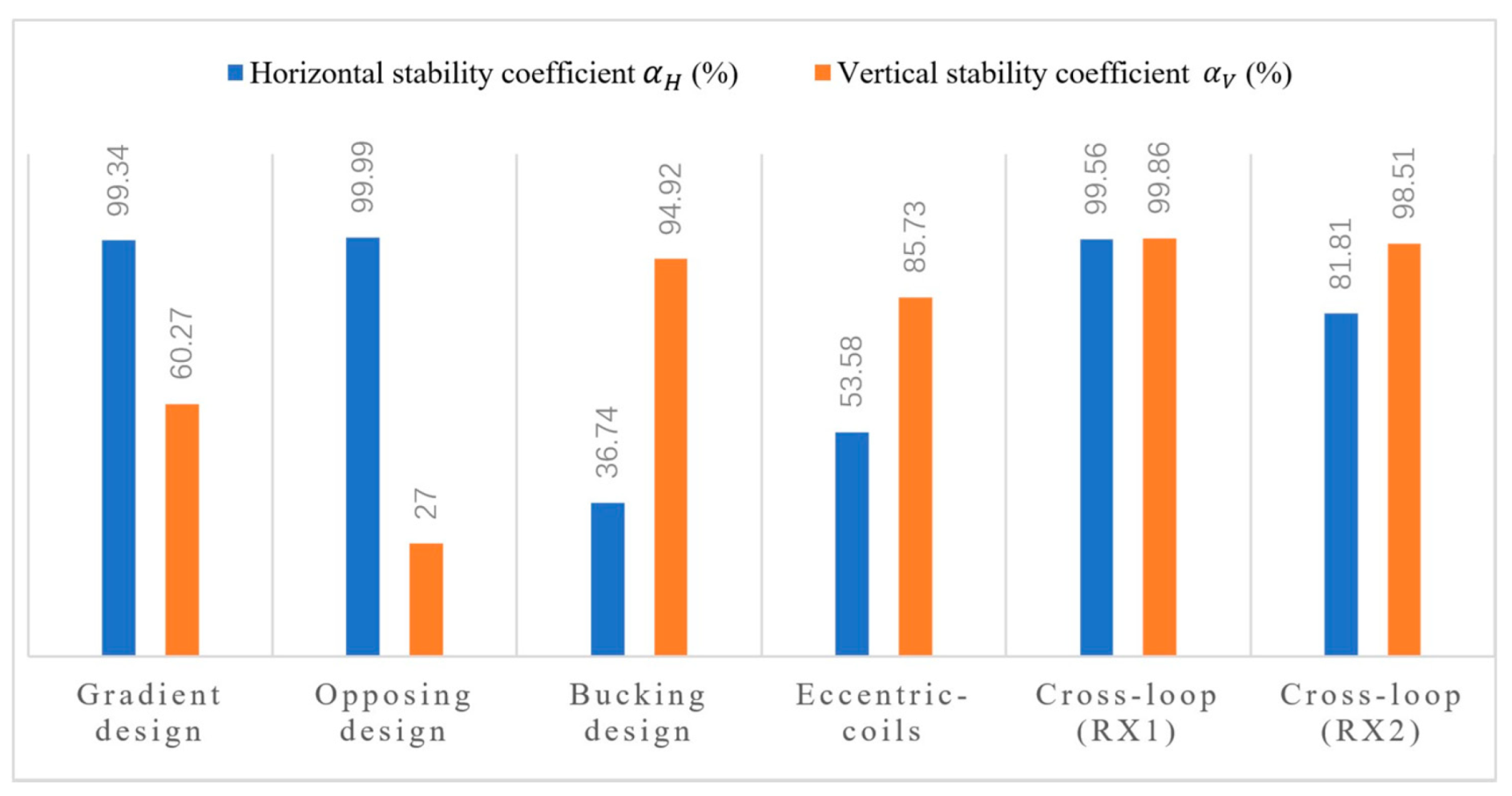
4. Shielding Stability Comparison
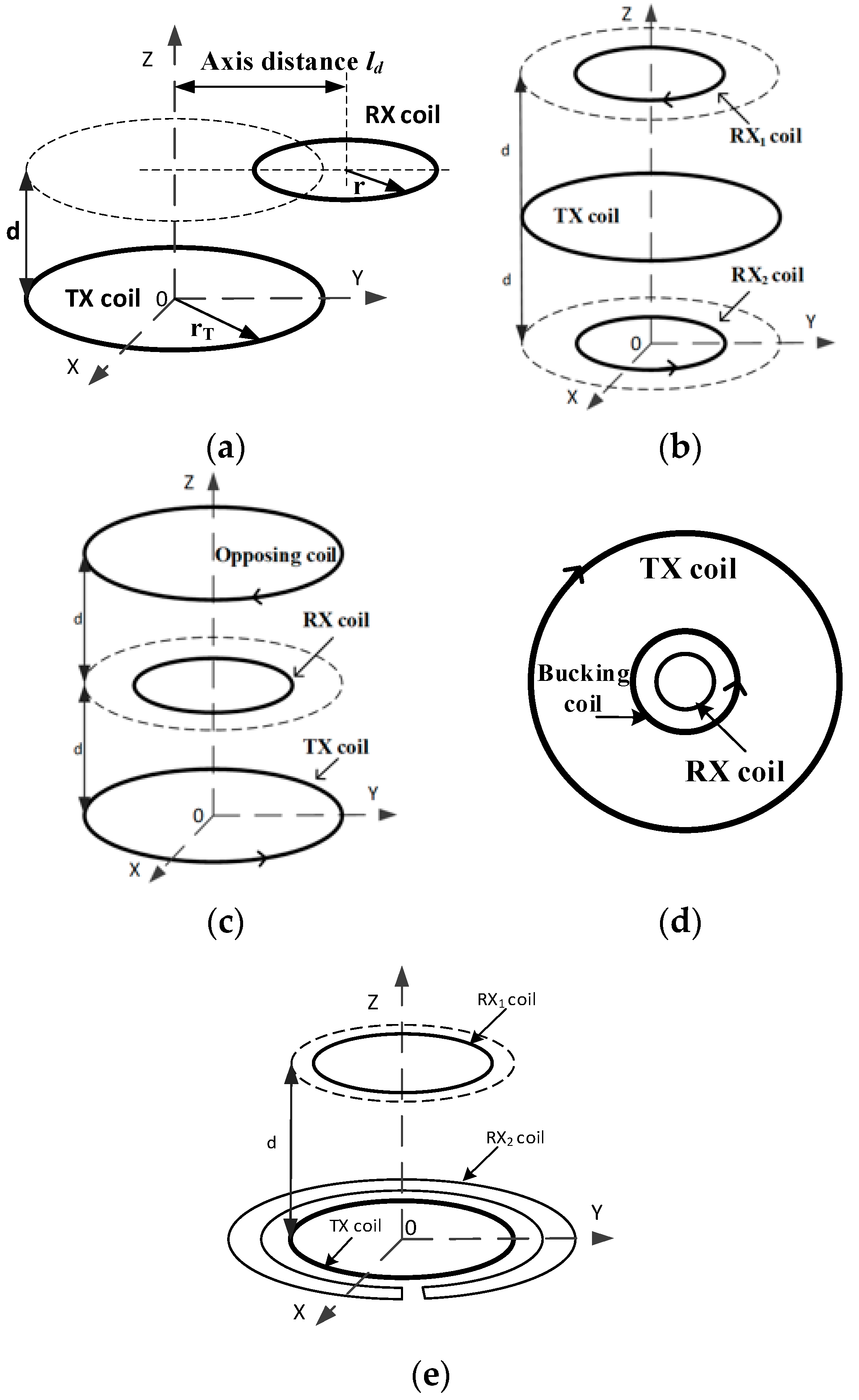
4.1. The Gradient Design
4.2. The Opposing Design
4.3. The Bucking Design
4.4. The Eccentric-Coils
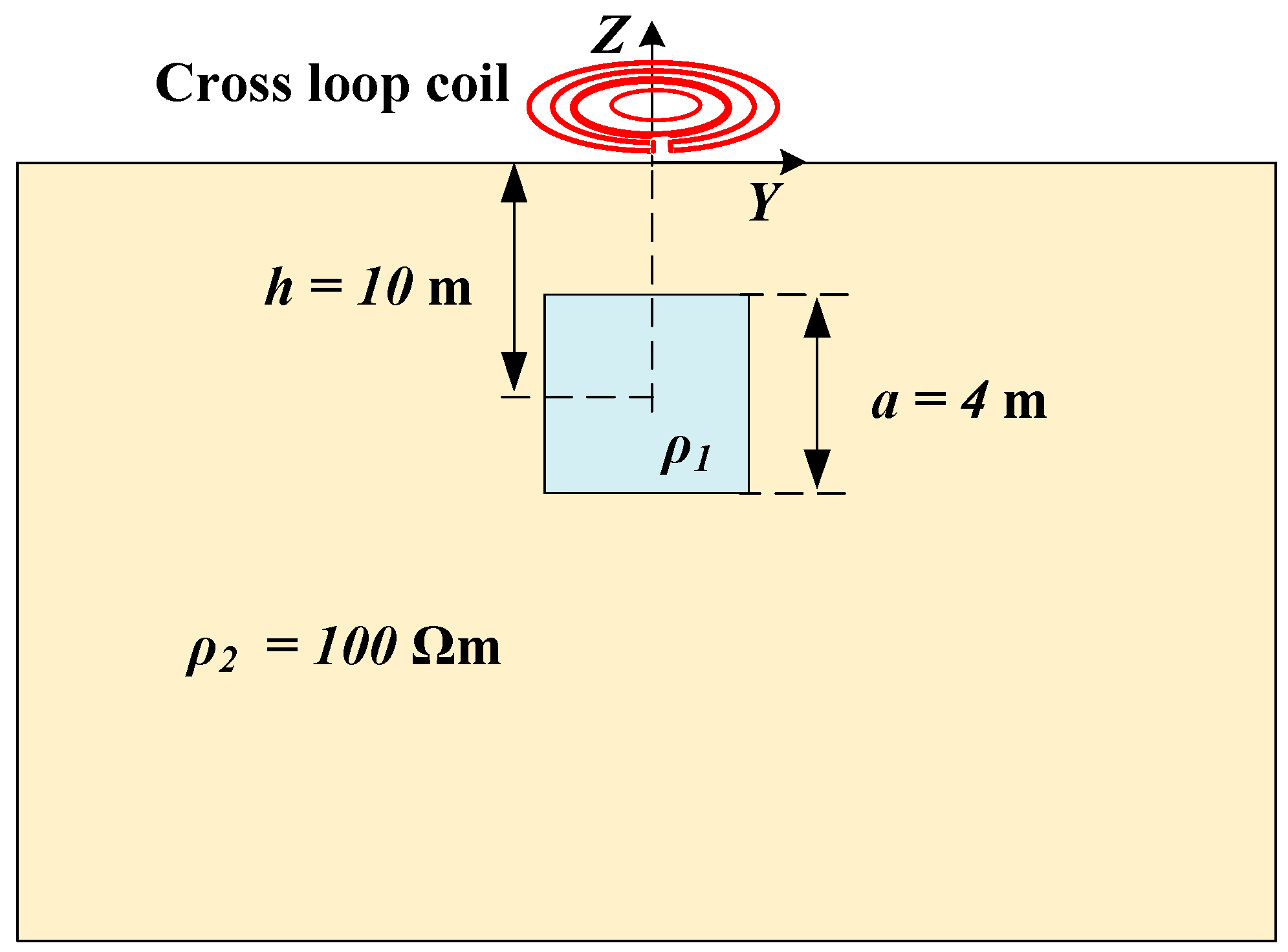
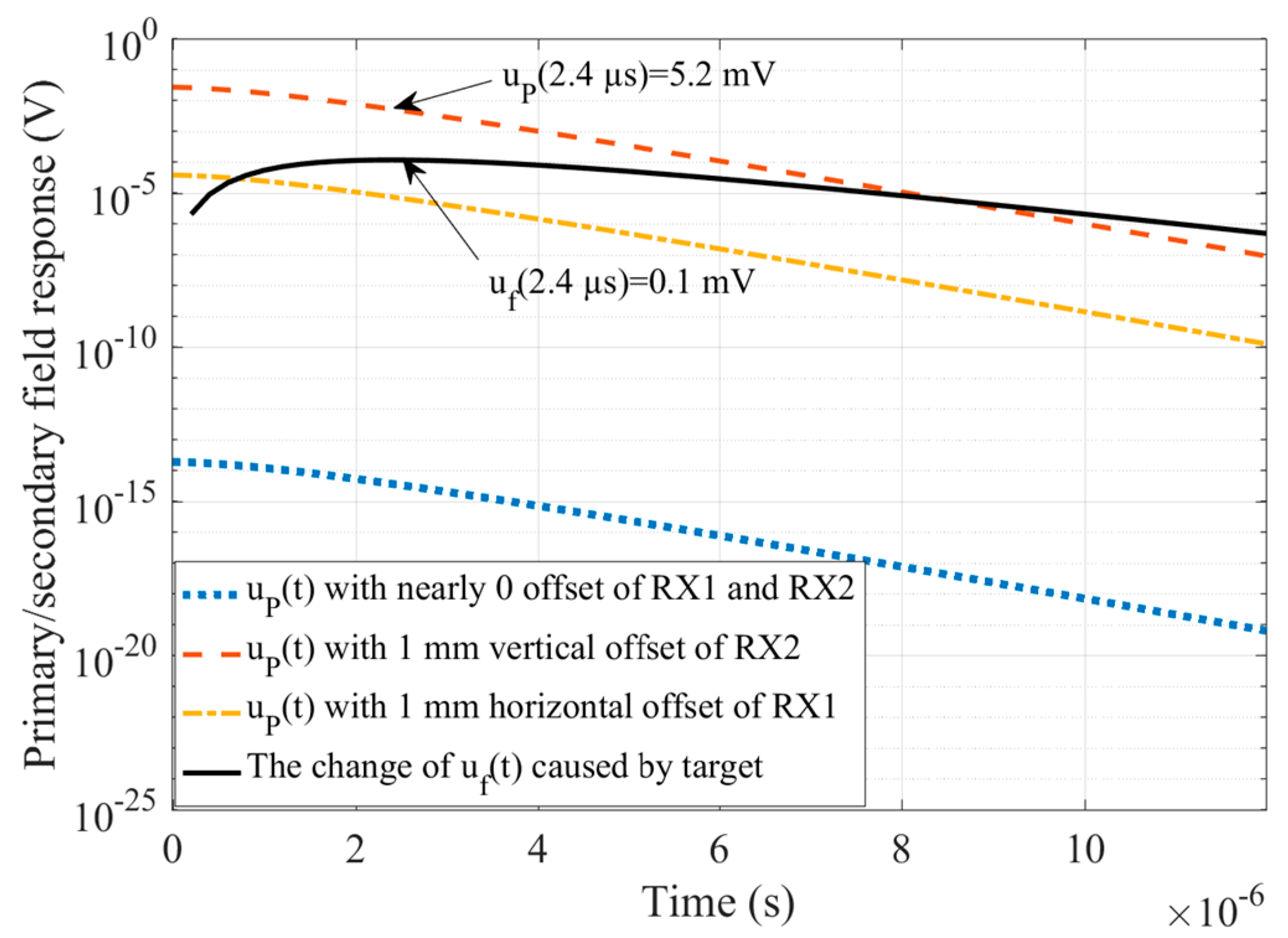
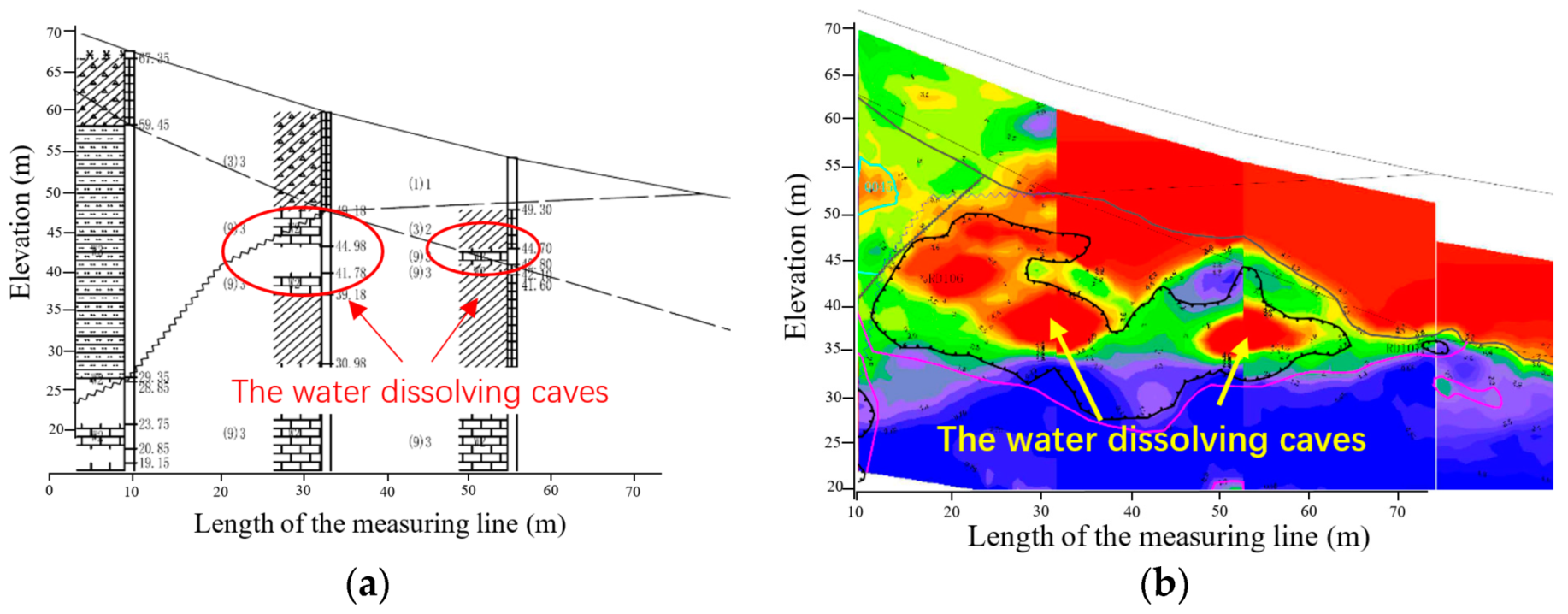
5. Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jun, L.; Lin, W.; Xiao-Guang, W.; Min, C.; Lei, F.; Xin-Lei, S. Research and development on the air-core coil sensor for mine transient electromagnetic exploration. Chin. J. Geophys. 2016, 59, 721–730. [Google Scholar]
- Chen, C.; Liu, F.; Lin, J.; Zhu, K.; Wang, Y. An Optimized Air-Core Coil Sensor with a Magnetic Flux Compensation Structure Suitable to the Helicopter TEM System. Sensors 2016, 16, 508. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Zhang, S.; Chen, S. An optimal transfer characteristic of an air cored transient electromagnetic sensor. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012. [Google Scholar]
- Badewa, E.; Unc, A.; Cheema, M.; Kavanagh, V.; Galagedara, L. Soil Moisture Mapping Using Multi-Frequency and Multi-Coil Electromagnetic Induction Sensors on Managed Podzols. Agronomy 2018, 8, 224. [Google Scholar] [CrossRef]
- Casterad, M.; Herrero, J.; Betrán, J.; Ritchie, G. Sensor-Based Assessment of Soil Salinity during the First Years of Transition from Flood to Sprinkler Irrigation. Sensors 2018, 18, 616. [Google Scholar] [CrossRef] [PubMed]
- Dang, B.; Yang, L.; Liu, C.; Zheng, Y.; Li, H.; Dang, R.; Sun, B. A Uniform Linear Multi-Coil Array-Based Borehole Transient Electromagnetic System for Non-Destructive Evaluations of Downhole Casings. Sensors 2018, 18, 2707. [Google Scholar] [CrossRef] [PubMed]
- Schamper, C.; Auken, E.; Sørensen, K. Coil response inversion for very early time modelling of helicopter-borne time-domain electromagnetic data and mapping of near-surface geological layers. Geophys. Prospect. 2014, 62, 658–674. [Google Scholar] [CrossRef]
- Smith, R.S.; Balch, S.J. Robust estimation of the band-limited inductive limit response from impulse-response TEM measurements taken during the transmitter switch-off and the transmitter off-time. Geophysics 2000, 65, 476–481. [Google Scholar] [CrossRef]
- Walker, S.E.; Rudd, J. Extracting more information from on-time data. Aseg Ext. Abstr. 2009, 1, 1–8. [Google Scholar] [CrossRef]
- Yu, C.G.; Fu, Z.H.; Wang, Q.; Tai, H.M.; Qin, S.Q. A Novel Method for Fault Diagnosis of Grounding Grids. IEEE Trans. Ind. Appl. 2015, 51, 5182–5188. [Google Scholar] [CrossRef]
- Fu, Z.H.; Wang, H.W.; Wang, Y.; Fu, N.Y.; Tai, H.M.; Qin, S.Q. Elimination of Mutual Inductance Effect for Small-Loop Electromagnetic Devices. Geophysics 2019, 84, E143–E154. [Google Scholar] [CrossRef]
- Xi, Z.Z.; Long, X.; Huang, L.; Zhou, S.; Song, G.; Hou, H.T.; Chen, X.P.; Wang, L.; Xiao, W.; Qi, Q.X. Opposing coils transient electromagnetic method focused near-surface resolution. Geophysics 2016, 81, E279–E285. [Google Scholar] [CrossRef]
- Miles, P. Multi-Sensor System for Airborne Geophysical Prospecting and Method. U.S. Patent 9,921,331, 20 March 2018. [Google Scholar]
- Chen, S.D.; Wang, Y.J.; Zhang, S. Bucking coil used in airborne transient electromagnetic survey. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012. [Google Scholar]
- Lawrence, H.; Demontoux, F.; Wigneron, J.P.; Paillou, P.; Wu, T.D.; Kerr, Y.H. Evaluation of a Numerical Modeling Approach Based on the Finite-Element Method for Calculating the Rough Surface Scattering and Emission of a Soil Layer. IEEE Geosci. Remote Sens. Lett. 2011, 8, 953–957. [Google Scholar] [CrossRef]
- Meng, L.; Li, T.; Zheng, D. Numerical simulation of transient electromagnetic response of unfavorable geological body in tunnel. Appl. Mech. Mater. 2011, 90, 37–40. [Google Scholar] [CrossRef]
- Zhu, X.G.; Su, X.F.; Tai, H.M.; Fu, Z.H.; Yu, C.G. Bipolar Steep Pulse Current Source for Highly Inductive Load. IEEE Trans. Power Electron. 2016, 31, 6169–6175. [Google Scholar] [CrossRef]
- Nabighian, M.N. Quasi-static transient response of a conducting half-space—An approximate representation. Geophysics 1979, 44, 1700–1705. [Google Scholar] [CrossRef]


| d (mm) | 0 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| 99.86% | 96.26% | 92.71% | 90.19% | 87.94% |
| d (mm) | 0 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| 98.51% | 98.6% | 98.37% | 98.42% | 98.6% |
| d (mm) | 0 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| 99.56% | 99.57% | 99.67% | 99.81% | 99.95% |
| d (mm) | 0 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| 81.81% | 80.4% | 80.65% | 80.66% | 80.46% |
| Parameter | Gradient Design | Opposing Design | Bucking Design | Eccentric-Coils | Cross-Loop Design |
|---|---|---|---|---|---|
| (A) | 10 | 10 | 10 | 10 | 10 |
| 14 | 14 | 14 | 14 | 14 | |
| d (m) | 0.15 | 0.15 | 0 | 0.15 | 0 |
| (m) | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 |
| (m) | 0.25 | 0.25 | 0.25 | 0.25 | RX1: 0.3 RX2: 0.65, 0.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Wang, H.; Fu, Z.; Fu, W. Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs. Sensors 2020, 20, 519. https://doi.org/10.3390/s20020519
Huang J, Wang H, Fu Z, Fu W. Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs. Sensors. 2020; 20(2):519. https://doi.org/10.3390/s20020519
Chicago/Turabian StyleHuang, Jiangbo, Haowen Wang, Zhihong Fu, and Wei Fu. 2020. "Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs" Sensors 20, no. 2: 519. https://doi.org/10.3390/s20020519
APA StyleHuang, J., Wang, H., Fu, Z., & Fu, W. (2020). Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs. Sensors, 20(2), 519. https://doi.org/10.3390/s20020519




