A Fail-Operational Control Architecture Approach and Dead-Reckoning Strategy in Case of Positioning Failures
Abstract
1. Introduction
- A fail-operational positioning system that comprises a UKF, a virtual sensor, and a monitor system, capable of remaining operative from degraded to total failure of the position reception and warns for fall-back triggering.
- A real-time trajectory planner that defines the lateral and longitudinal references for the DDT fall-back in degraded mode to achieve a minimal risk condition avoiding rear-end collisions.
- A vehicle motion control that executes the planned trajectory, including a lateral reference constraint avoiding undesirable lane departures.
- A case study resembles a real urban scenario demanding a DDT fall-back strategy due to a major positioning failure, working with minimum sensor interface bringing the vehicle to a safe place.
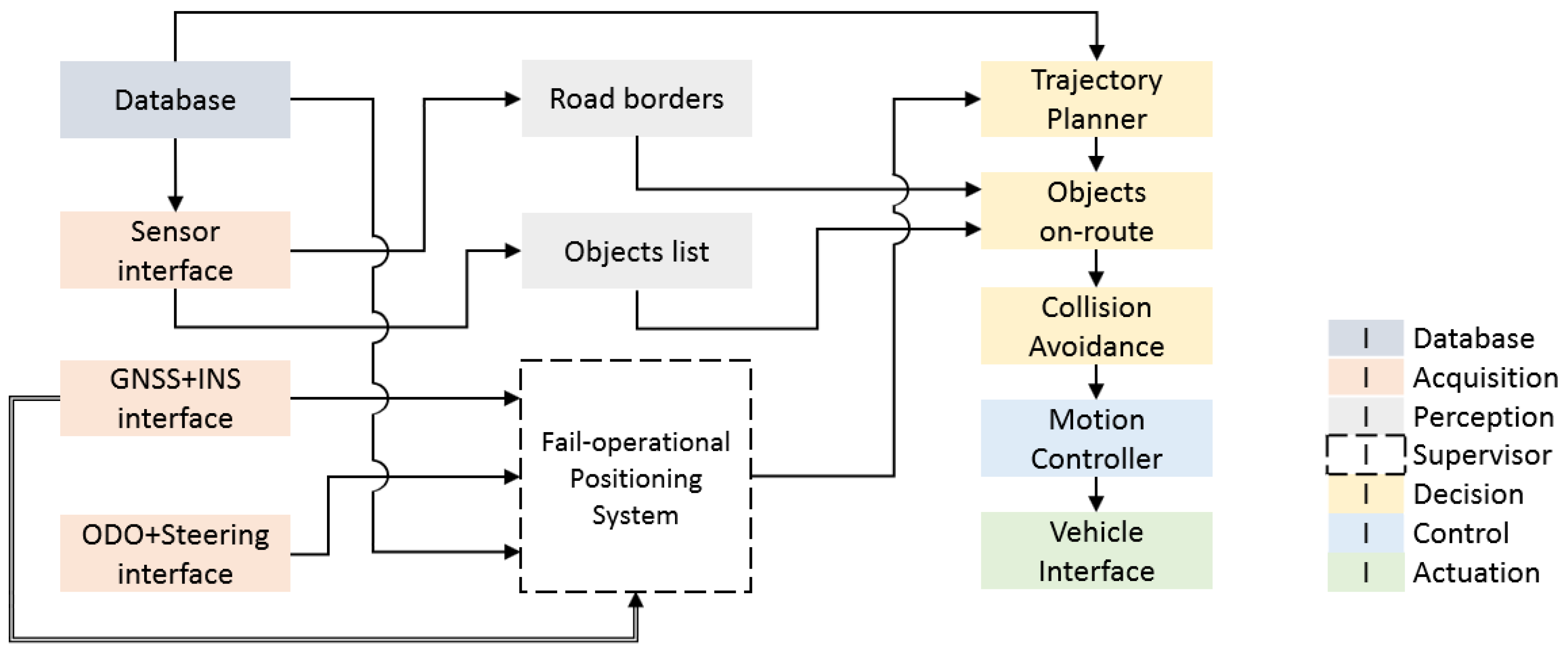
2. Fail-Operational Control Architecture
2.1. Database
2.2. Acquisition
2.3. Perception
2.4. Supervisor. Fail-Operational Positioning System
2.5. Decision
2.6. Control
2.7. Actuation
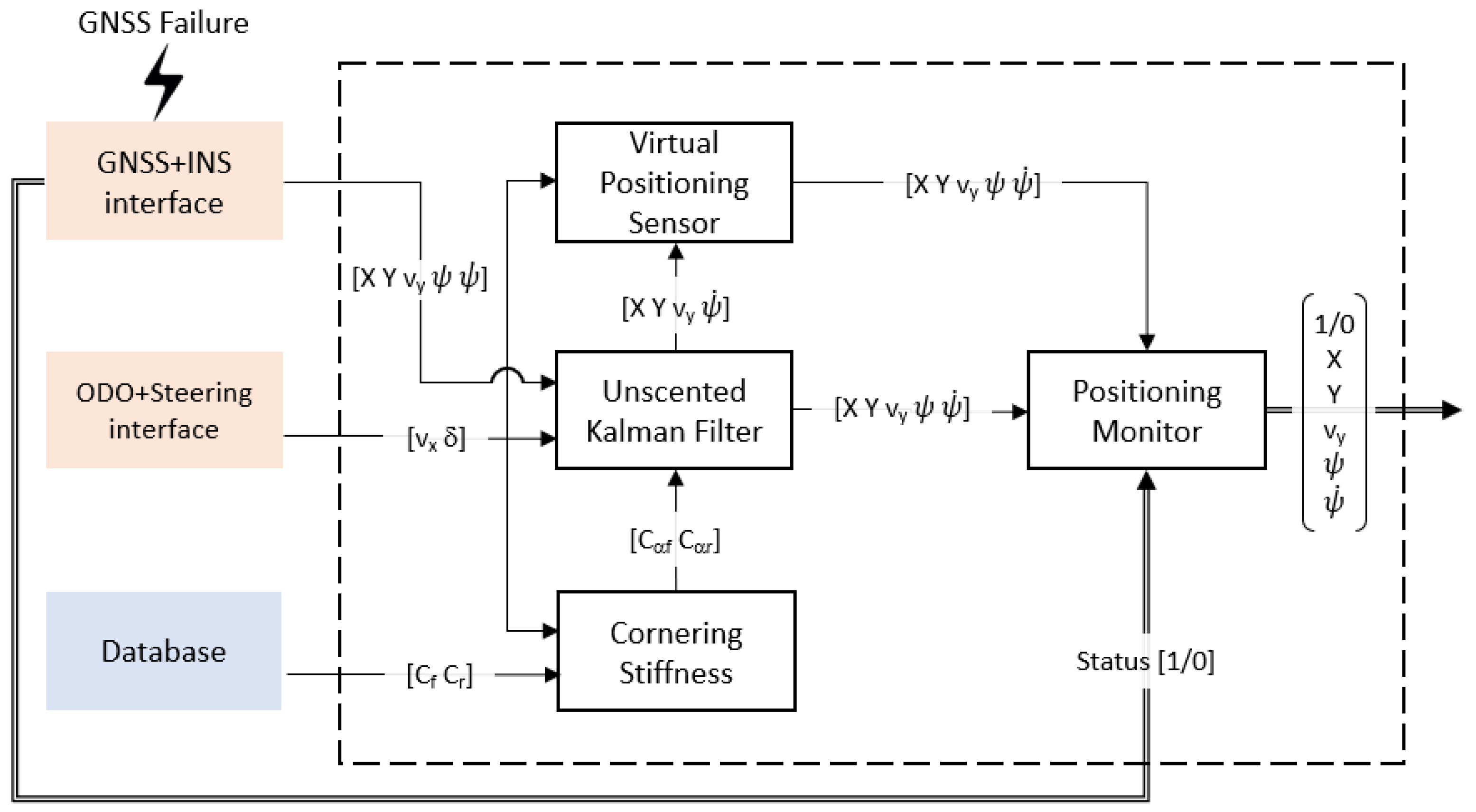
3. Fail-Operational Positioning System
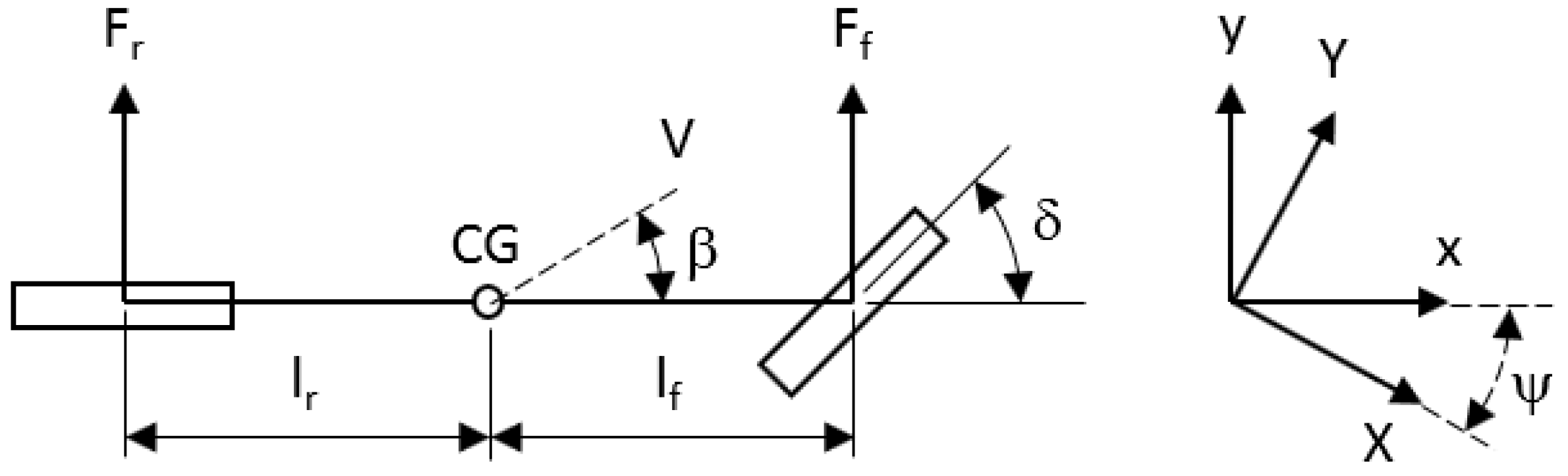
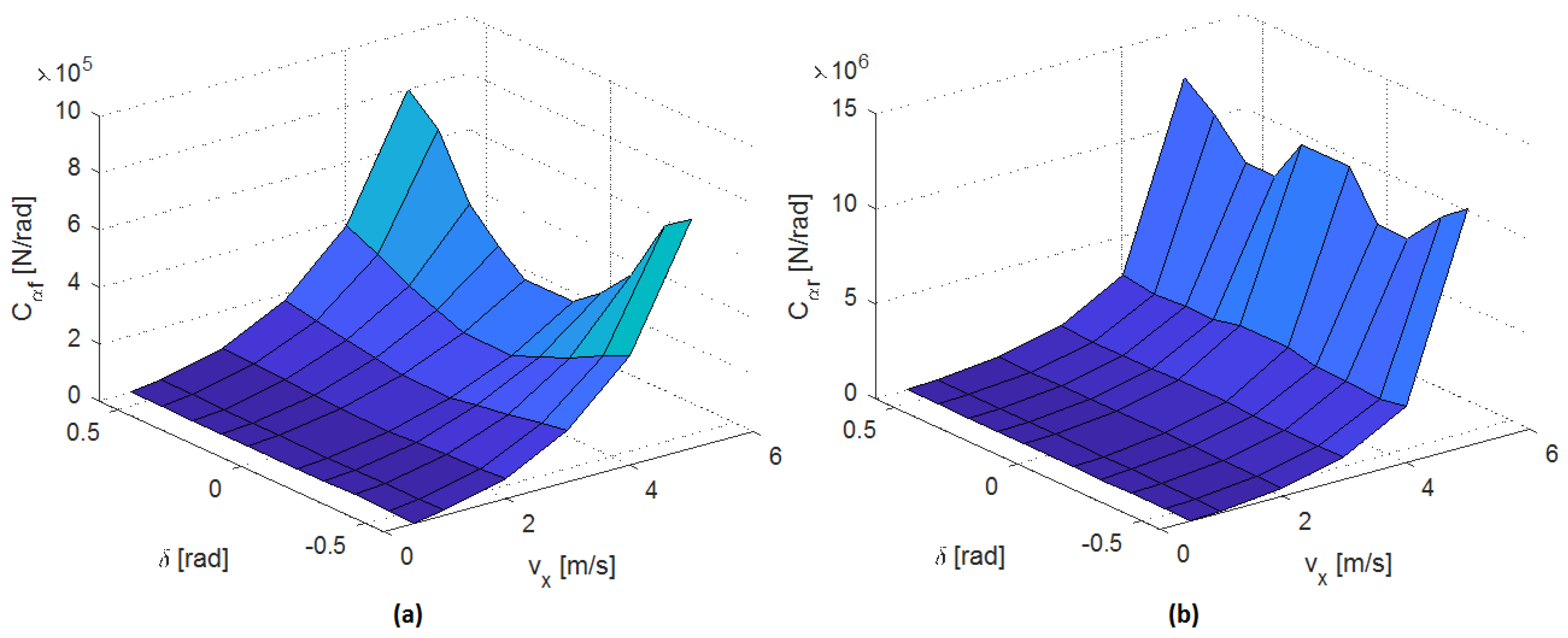
3.1. Vehicle Model and Cornering Stiffness Estimation
3.1.1. The Kinematic and Dynamic Vehicle Models
3.1.2. Cornering Stiffness Estimation
3.2. Adaptive Unscented Kalman Filter
3.3. Virtual Positioning Sensor
3.4. Positioning Monitor
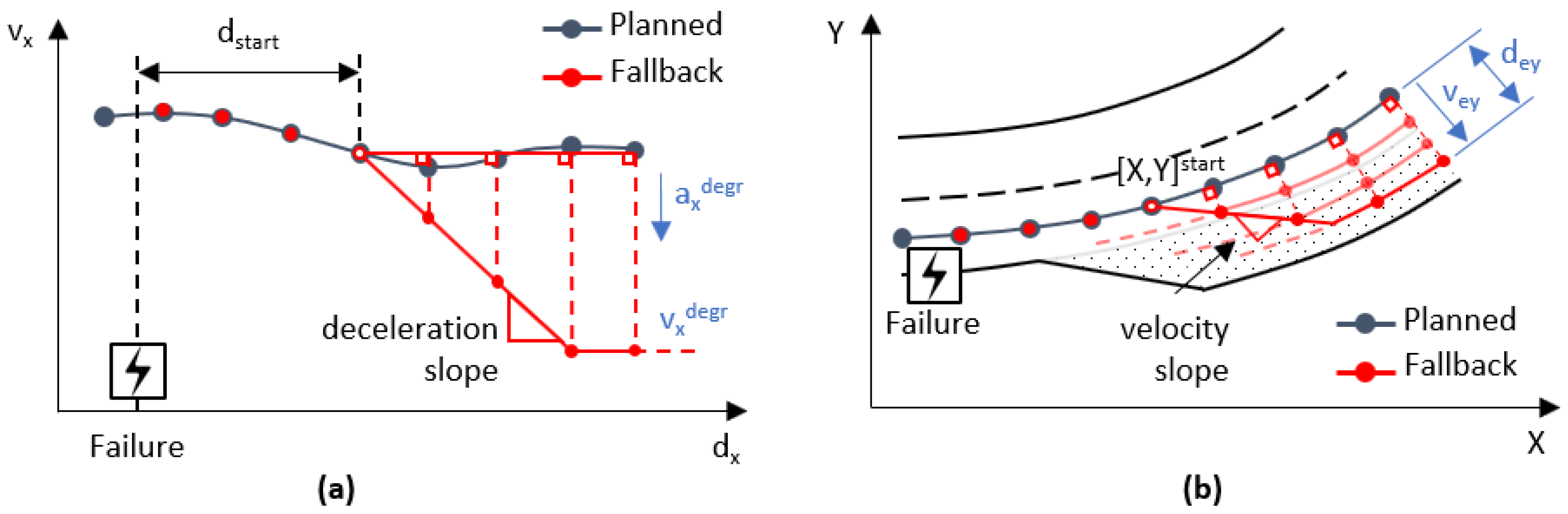
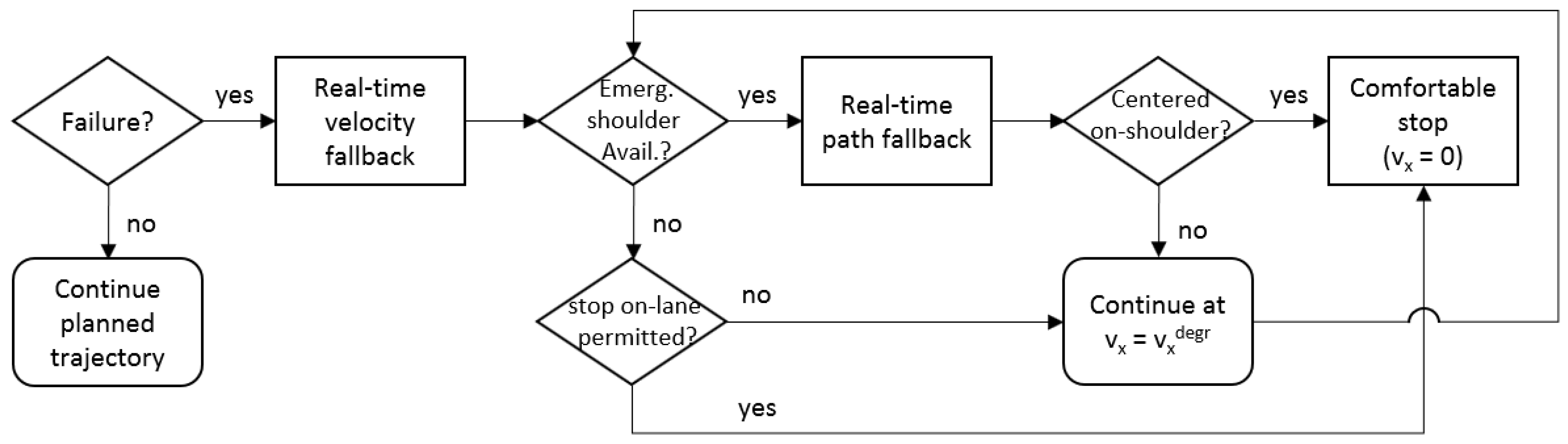
4. Fall-Back Strategies Implementation in the Decision Stage
4.1. Real-Time Trajectory Planner
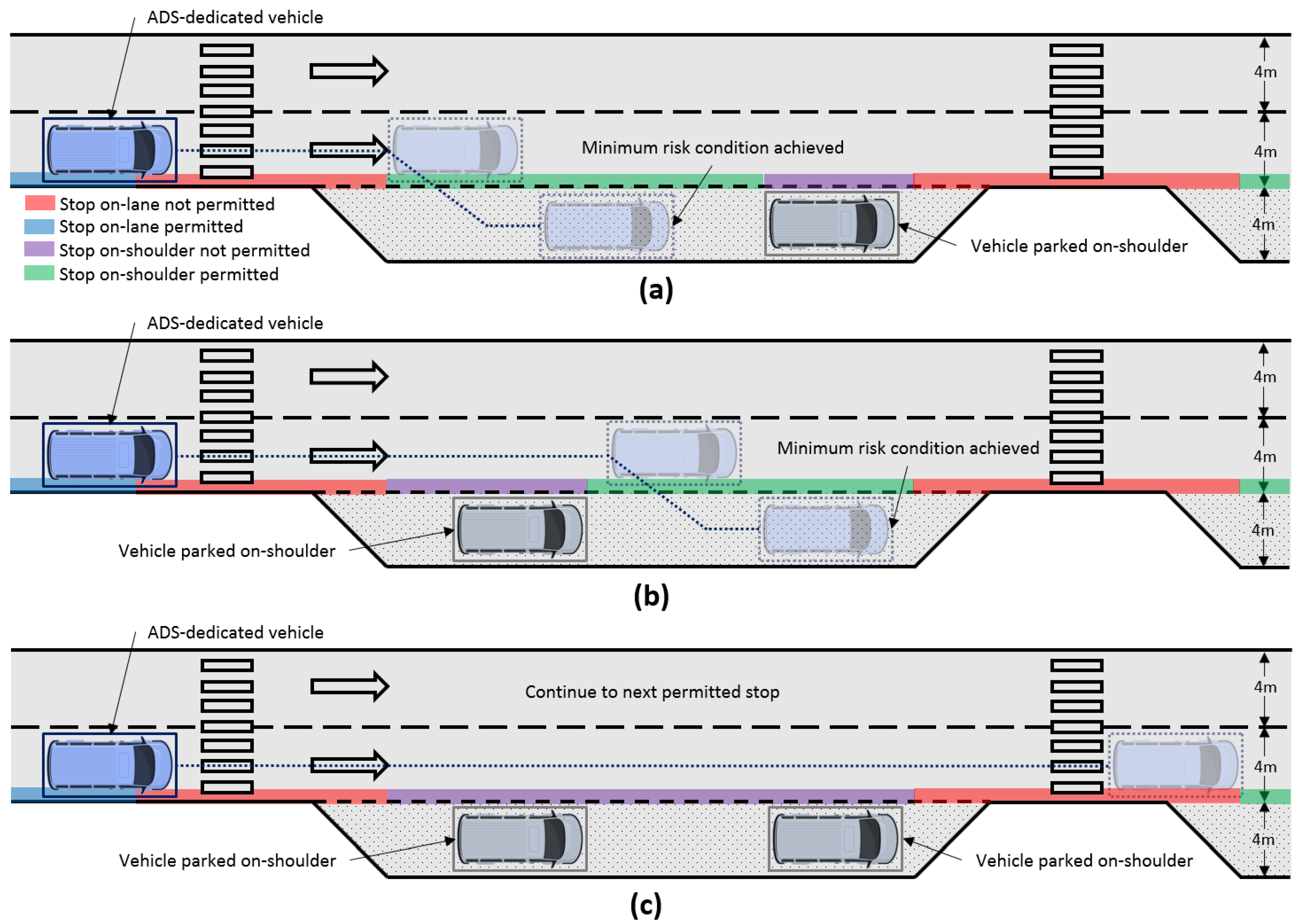
4.2. Rear-End Collision Avoidance
4.3. Vehicle Motion Control
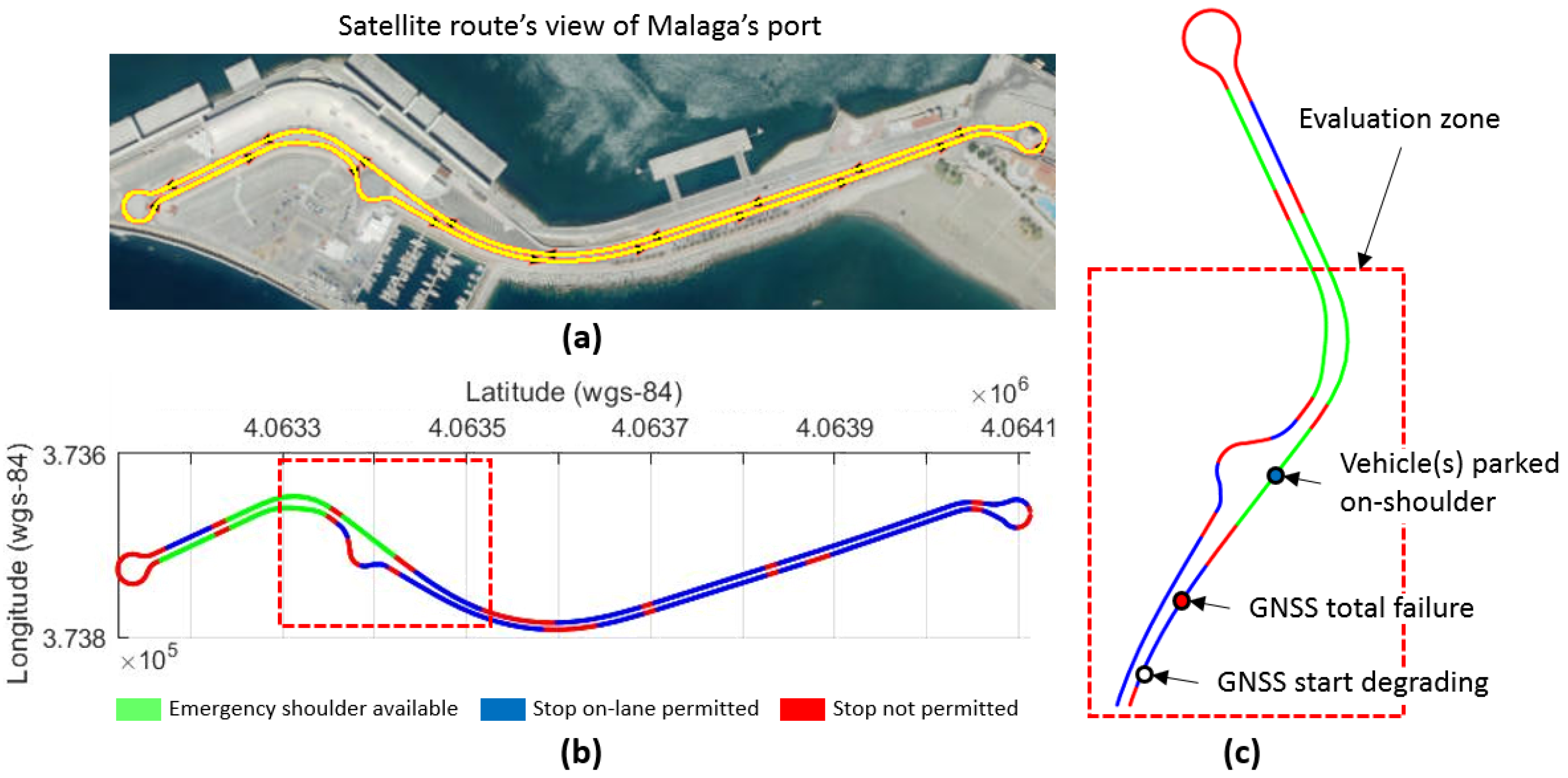
5. Case Study
5.1. Realistic Scenario
5.2. Test Platform
5.3. Parameters
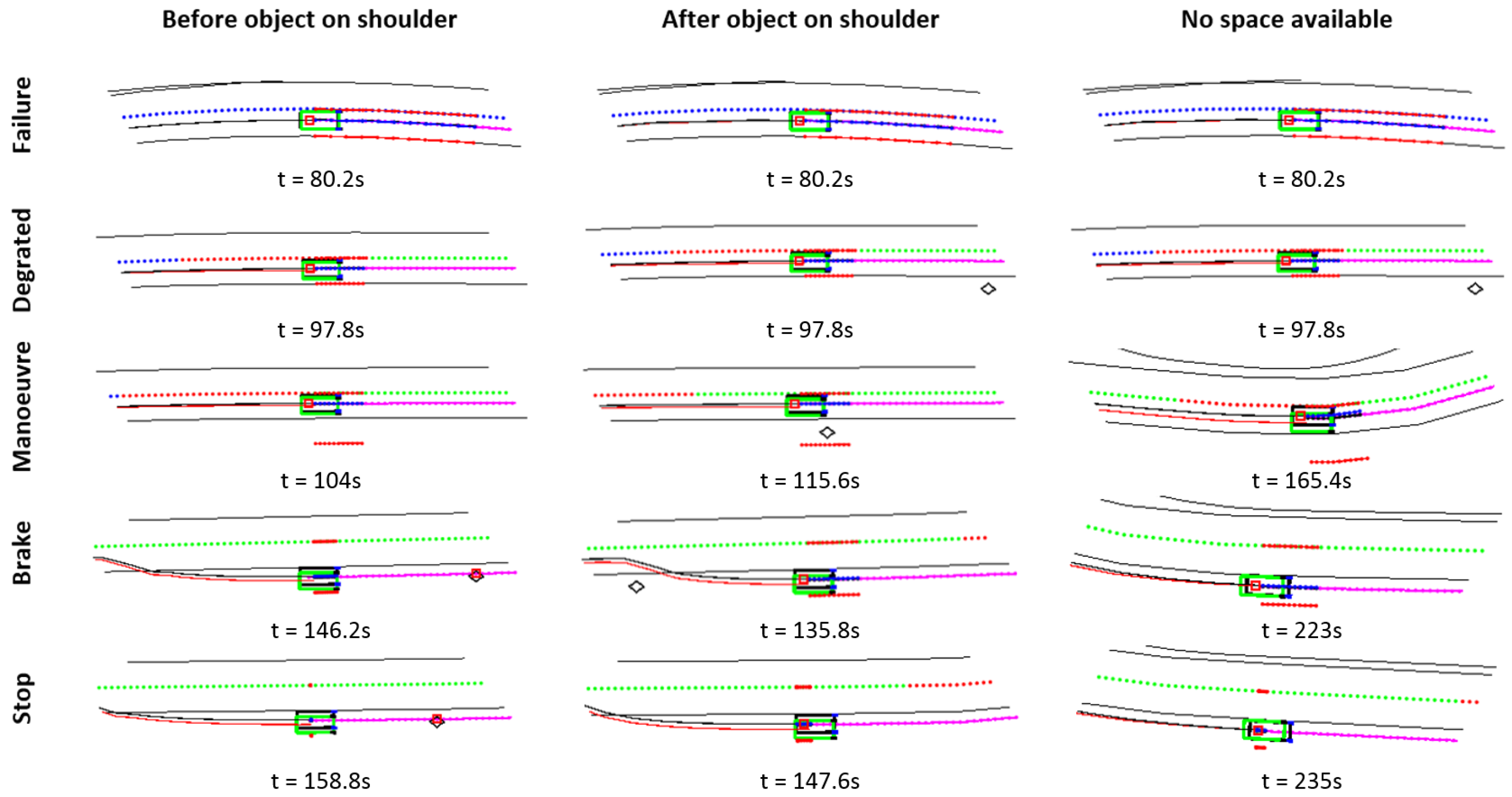
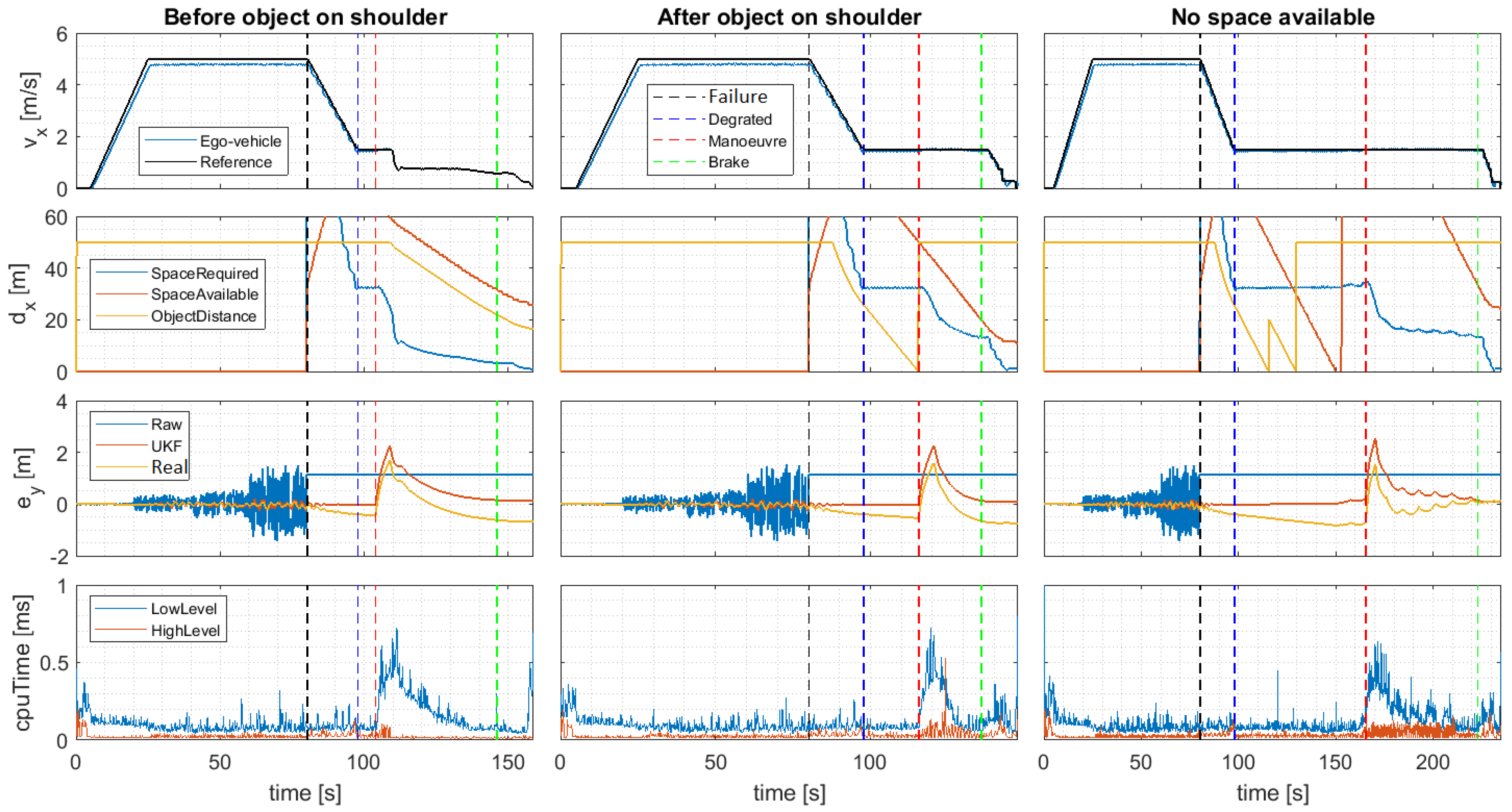
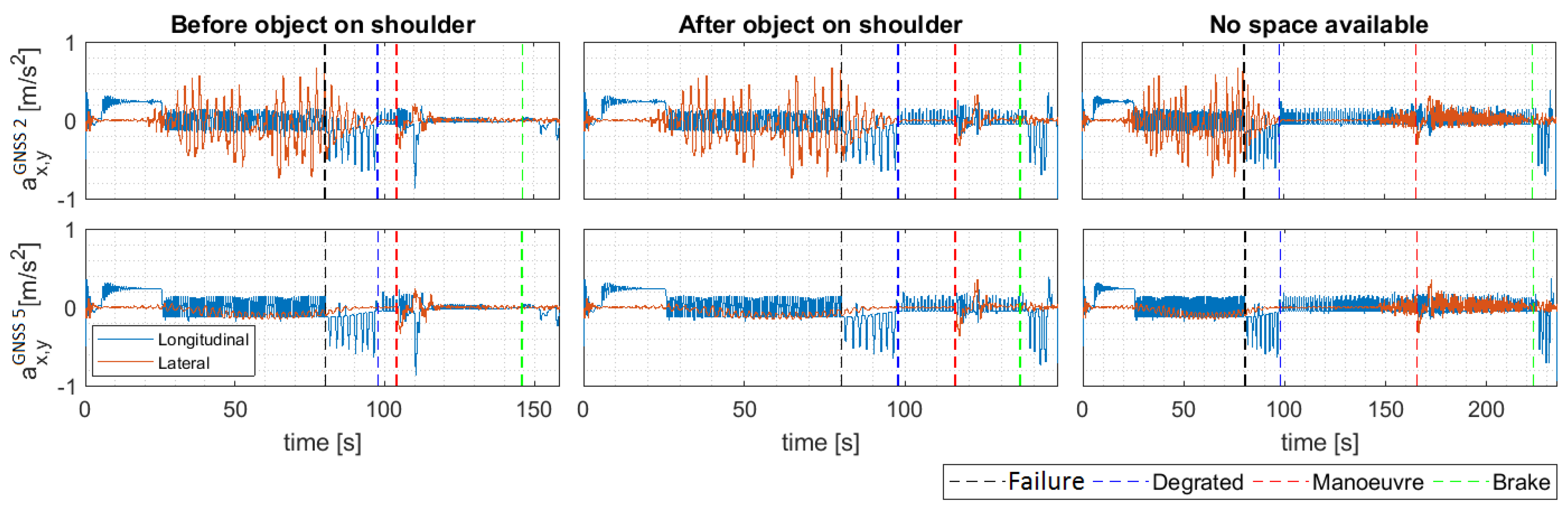
6. Results and Discussions
6.1. Evaluation of the Fail-Operational Positioning System
6.2. Evaluation of the Dynamic Driving Task Fall-back Strategy
Evaluation of Passenger Comfort
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Alonso Raposo, M.; Ciuffo, B.; Ardente, F.; Aurambout, J.; Baldini, G.; Braun, R.; Vandecasteele, I. The Future of Road Transport—Implications of Automated, Connected, Low-Carbon and Shared Mobility; Publications Office of the European Union: Rue Mercier, Luxembourg, 2019. [Google Scholar]
- Marti, E.; de Miguel, M.A.; Garcia, F.; Perez, J. A Review of Sensor Technologies for Perception in Automated Driving. IEEE Intell. Transp. Syst. Mag. 2019, 11, 94–108. [Google Scholar] [CrossRef]
- Llorca, D.F.; Milanés, V.; Alonso, I.P.; Gavilán, M.; Daza, I.G.; Pérez, J.; Sotelo, M.Á. Autonomous pedestrian collision avoidance using a fuzzy steering controller. IEEE Trans. Intell. Transp. Syst. 2011, 12, 390–401. [Google Scholar] [CrossRef]
- Bernini, N.; Bertozzi, M.; Castangia, L.; Patander, M.; Sabbatelli, M. Real-time obstacle detection using stereo vision for autonomous ground vehicles: A survey. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 873–878. [Google Scholar]
- Hillel, A.B.; Lerner, R.; Levi, D.; Raz, G. Recent progress in road and lane detection: a survey. Mach. Vision Appl. 2014, 25, 727–745. [Google Scholar] [CrossRef]
- Milanés, V.; Naranjo, J.E.; González, C.; Alonso, J.; de Pedro, T. Autonomous vehicle based in cooperative GPS and inertial systems. Robotica 2008, 26, 627–633. [Google Scholar] [CrossRef]
- Guan, H.; Yan, W.; Yu, Y.; Zhong, L.; Li, D. Robust traffic-sign detection and classification using mobile LiDAR data with digital images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1715–1724. [Google Scholar] [CrossRef]
- Castanedo, F. A review of data fusion techniques. Sci. World J. 2013, 2013, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Rob. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Balzer, P.; Trautmann, T.; Michler, O. Epe and speed adaptive extended kalman filter for vehicle position and attitude estimation with low cost gnss and imu sensors. In Proceedings of the 2014 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Vienna, Austria, 1–3 September 2014; pp. 649–656. [Google Scholar]
- De Ponte Müller, F. Survey on Ranging Sensors and Cooperative Techniques for Relative Positioning of Vehicles. Sensors 2017, 17, 271. [Google Scholar] [CrossRef] [PubMed]
- Shladover, S.; Bishop, R. Road transport automation as a Public-Private Enterprise. White Pap. 2015, 1, 14–15. [Google Scholar]
- Thorn, E.; Kimmel, S.C.; Chaka, M.; Hamilton, B.A. A Framework for Automated Driving System Testable Cases and Scenarios; Technical Report; United States. Department of Transportation. National Highway Traffic Safety Administration: Washington, DC, USA, 2018.
- Emzivat, Y.; Ibanez-Guzman, J.; Martinet, P.; Roux, O.H. Dynamic driving task fallback for an automated driving system whose ability to monitor the driving environment has been compromised. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1841–1847. [Google Scholar]
- Xue, W.; Yang, B.; Kaizuka, T.; Nakano, K. A Fallback Approach for an Automated Vehicle Encountering Sensor Failure in Monitoring Environment. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1807–1812. [Google Scholar]
- Lee, J.W.; Moshchuk, N.K.; Chen, S.K. Lane Centering Fail-Safe Control Using Differential Braking. U.S. Patent 8,670,903, 11 March 2014. [Google Scholar]
- Magdici, S.; Althoff, M. Fail-safe motion planning of autonomous vehicles. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 452–458. [Google Scholar]
- Ruf, M.; Ziehn, J.R.; Willersinn, D.; Rosenhahny, B.; Beyerer, J.; Gotzig, H. Global trajectory optimization on multilane roads. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 1908–1914. [Google Scholar]
- Mudalige, U.P. Fail-Safe Speed Profiles for Cooperative Autonomous Vehicles. U.S. Patent 8,676,466, 18 March 2014. [Google Scholar]
- An, N.; Mittag, J.; Hartenstein, H. Designing fail-safe and traffic efficient 802.11 p-based rear-end collision avoidance. In Proceedings of the 2014 IEEE Vehicular Networking Conference (VNC), Paderborn, Germany, 3–5 December 2014; pp. 9–16. [Google Scholar]
- Isermann, R.; Schwarz, R.; Stolzl, S. Fault-tolerant drive-by-wire systems. IEEE Ctrl. Syst. Mag. 2002, 22, 64–81. [Google Scholar]
- SAE International. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Detroit, MI, USA, 2018. [Google Scholar]
- ECSEL-JU. AutoDrive. Available online: https://autodrive-project.eu/ (accessed on 28 November 2019).
- Council, E.R.T.R.A. Connected Automated Driving Roadmap; Version 8; ERTRAC Working Group “Connectivity and Automated Driving”: Brussels, Belgium, 2019. [Google Scholar]
- Matute, J.A.; Marcano, M.; Zubizarreta, A.; Perez, J. Longitudinal model predictive control with comfortable speed planner. In Proceedings of the 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Torres Vedras, Portugal, 25–27 April 2018; pp. 60–64. [Google Scholar]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Matute, J.A.; Marcano, M.; Diaz, S.; Perez, J. Experimental Validation of a Kinematic Bicycle Model Predictive Control with Lateral Acceleration Consideration. IFAC-PapersOnLine 2019, 52, 289–294. [Google Scholar] [CrossRef]
- Kabzan, J.; Valls, M.d.l.I.; Reijgwart, V.; Hendrikx, H.F.C.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. AMZ Driverless: The Full Autonomous Racing System. arXiv 2019, arXiv:1905.05150. [Google Scholar]
- Sierra, C.; Tseng, E.; Jain, A.; Peng, H. Cornering stiffness estimation based on vehicle lateral dynamics. Veh. Syst. Dyn. 2006, 44, 24–38. [Google Scholar] [CrossRef]
- ISO. ISO 4138: Passenger Cars–Steady-State Circular Driving Behaviour–Open-Loop Test Methods; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Hsu, L.Y.; Chen, T.L. Vehicle dynamic prediction systems with on-line identification of vehicle parameters and road conditions. Sensors 2012, 12, 15778–15800. [Google Scholar] [CrossRef] [PubMed]
- Lattarulo, R.; González, L.; Martí, E.; Matute, J.; Marcano, M.; Pérez, J. Urban motion planning framework based on n-bézier curves considering comfort and safety. J. Adv. Transp. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Villagra, J.; Milanés, V.; Pérez, J.; Godoy, J. Smooth path and speed planning for an automated public transport vehicle. Rob. Autom. Syst. 2012, 60, 252–265. [Google Scholar] [CrossRef]
- Pena, A.; Iglesias, I.; Valera, J.; Martin, A. Development and validation of Dynacar RT software, a new integrated solution for design of electric and hybrid vehicles. EVS26 Los Angeles 2012, 26, 1–7. [Google Scholar]
- Pacejka, H. Tire and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]

| System | Functionality | Fall-Back Strategy |
|---|---|---|
| Perception | Object detection | Create ghost vehicles to replace the hidden ones due high curvatures in highways [15]. |
| Create ghost objects due sensor failure and perform lane-changing maneuver to emergency shoulder [16]. | ||
| Decision | Lane centering | switch to differential braking control if electrical power steering fails [17]. |
| Trajectory planning | Emergency maneuver bring vehicle to stop if collision free trajectories fails [18]. | |
| Emergency trajectory to stop at the slowest lane [19]. | ||
| Control | Speed profile | Use a future velocity if communication of control messages or the propulsion controller fails [20]. |
| Collision avoidance | Brake if reception of data packets or inter-vehicle distance from lead vehicle fails [21]. | |
| Actuation | Drive-by-wire | Various forms of monitoring and redundancy are considered in failure cases [22]. |
| Position Covariances | Inertial Covariances | |||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Quality | Unit | Parameter | Unit | ||||
| 5 | 0.0141 | m | m | |||||
| 4 | 0.2828 | m | ||||||
| 3 | 0.4243 | m | ||||||
| 2 | 1.1314 | m | ||||||
| Parameter | Lower | Upper | Unit |
|---|---|---|---|
| 1 | 1 | ||
| 1 | 1 | ||
| 0.68 | rad | ||
| 0 | |||
| 0.2 | |||
| m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matute-Peaspan, J.A.; Perez, J.; Zubizarreta, A. A Fail-Operational Control Architecture Approach and Dead-Reckoning Strategy in Case of Positioning Failures. Sensors 2020, 20, 442. https://doi.org/10.3390/s20020442
Matute-Peaspan JA, Perez J, Zubizarreta A. A Fail-Operational Control Architecture Approach and Dead-Reckoning Strategy in Case of Positioning Failures. Sensors. 2020; 20(2):442. https://doi.org/10.3390/s20020442
Chicago/Turabian StyleMatute-Peaspan, Jose Angel, Joshue Perez, and Asier Zubizarreta. 2020. "A Fail-Operational Control Architecture Approach and Dead-Reckoning Strategy in Case of Positioning Failures" Sensors 20, no. 2: 442. https://doi.org/10.3390/s20020442
APA StyleMatute-Peaspan, J. A., Perez, J., & Zubizarreta, A. (2020). A Fail-Operational Control Architecture Approach and Dead-Reckoning Strategy in Case of Positioning Failures. Sensors, 20(2), 442. https://doi.org/10.3390/s20020442





