An Actuator Allocation Method for a Variable-Pitch Propeller System of Quadrotor-Based UAVs
Abstract
1. Introduction
2. VPP Modeling and Control Allocation
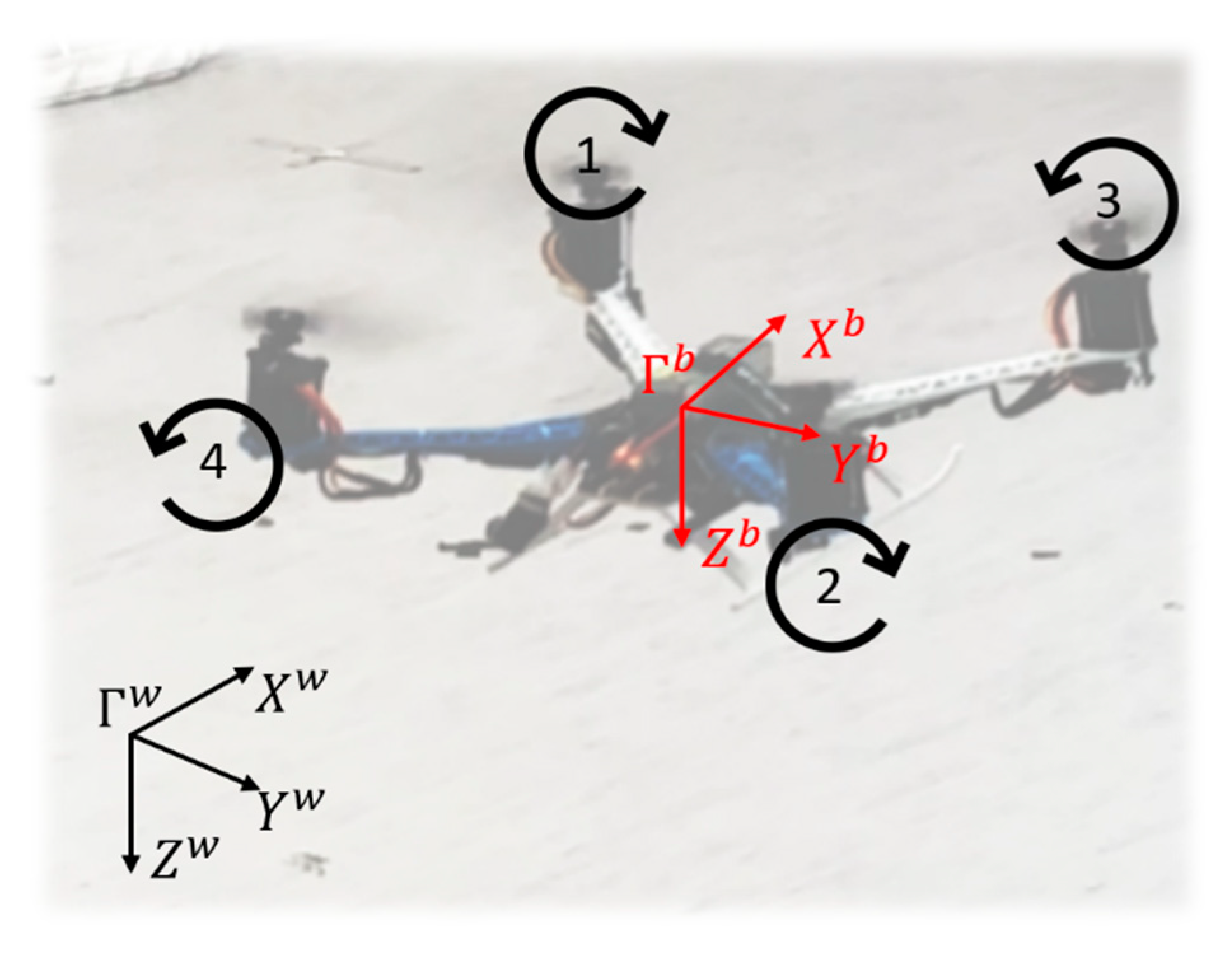
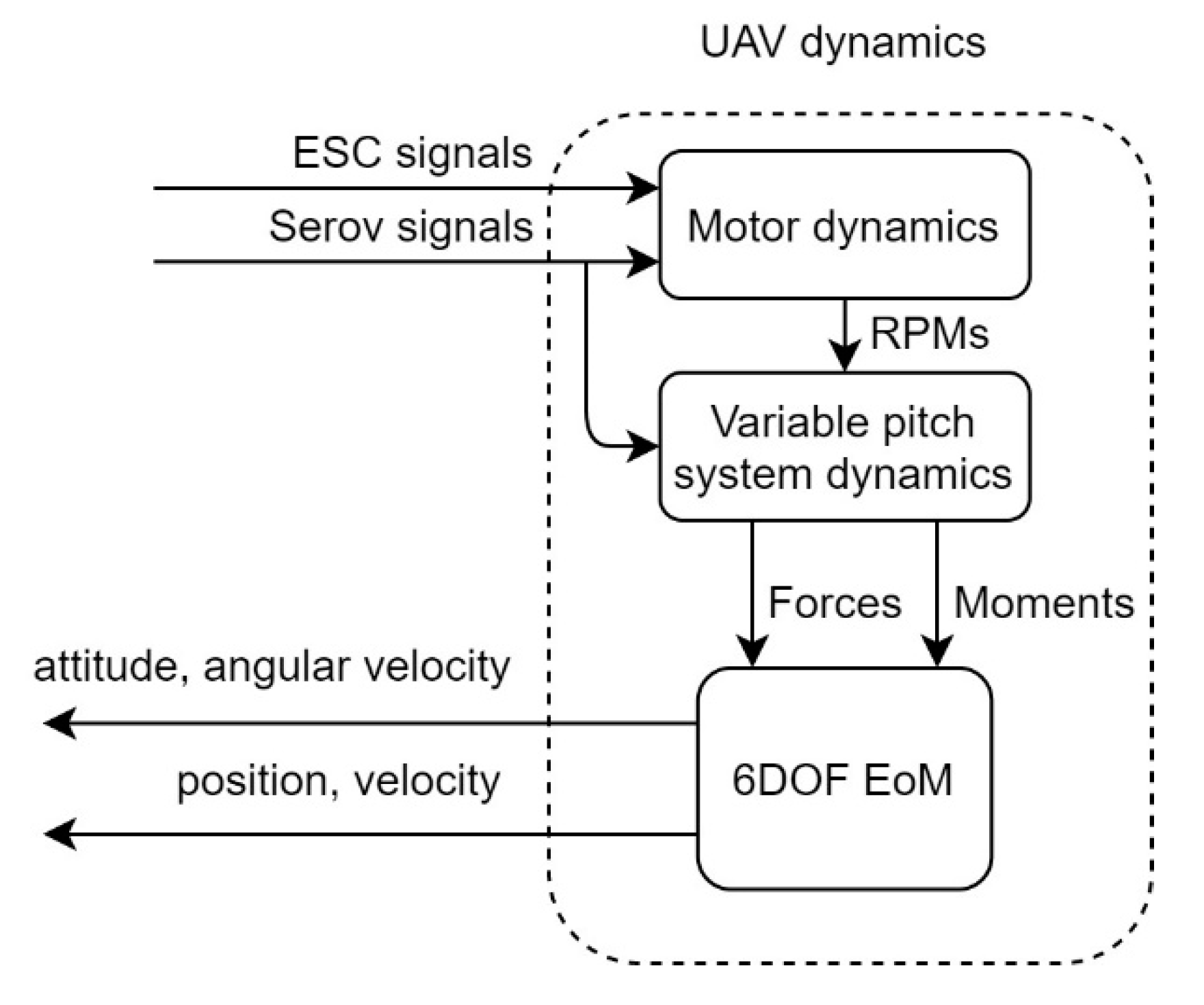
2.1. VPP Modeling
2.2. VPP Control Allocation
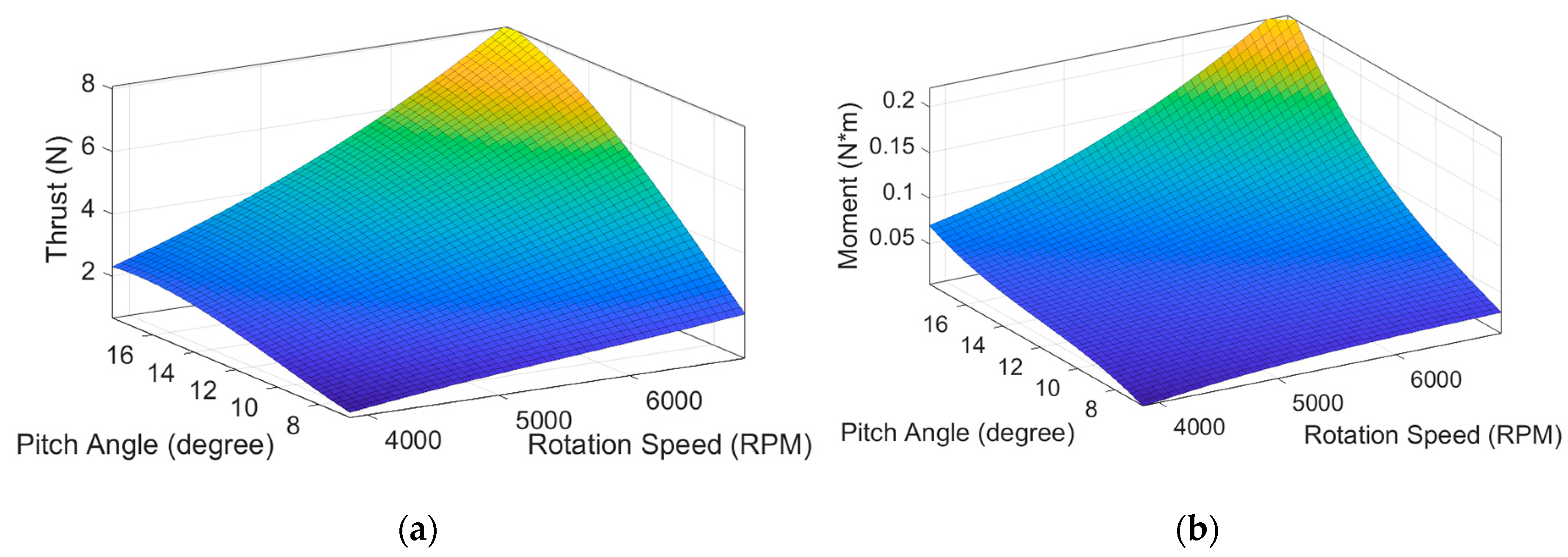
2.3. Static Thrust Experiment
3. Simulation
3.1. Simulation Environment
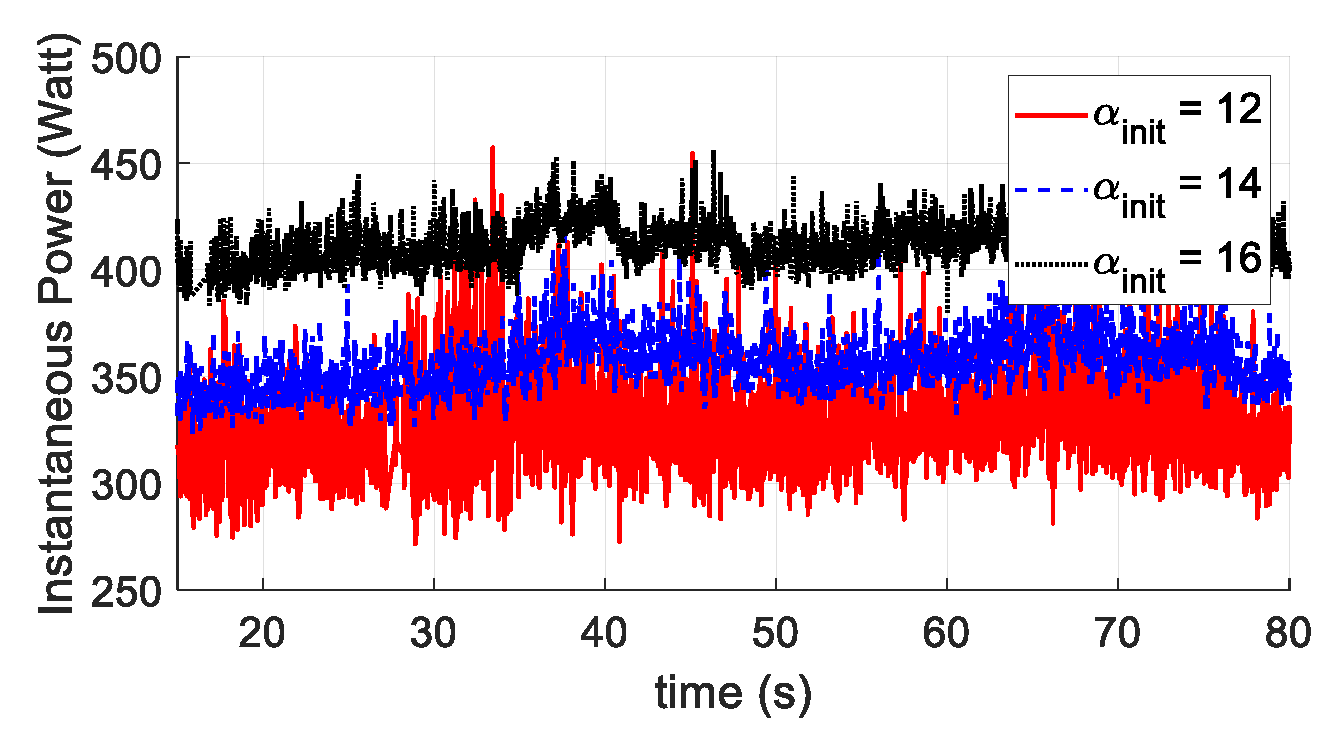
3.2. Simulation Results
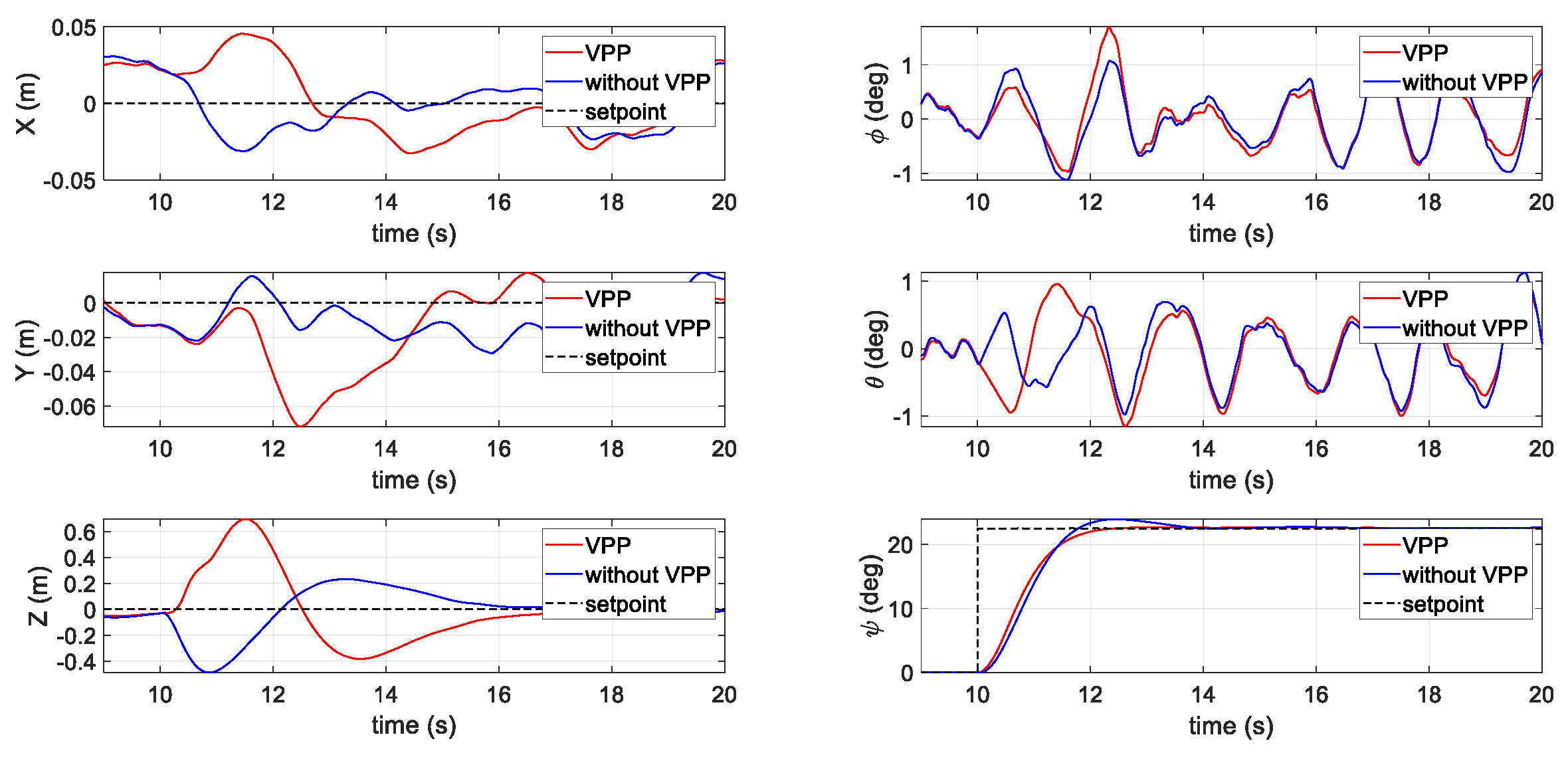
3.2.1. First Scenario: Position Holding with a Yaw Step Command
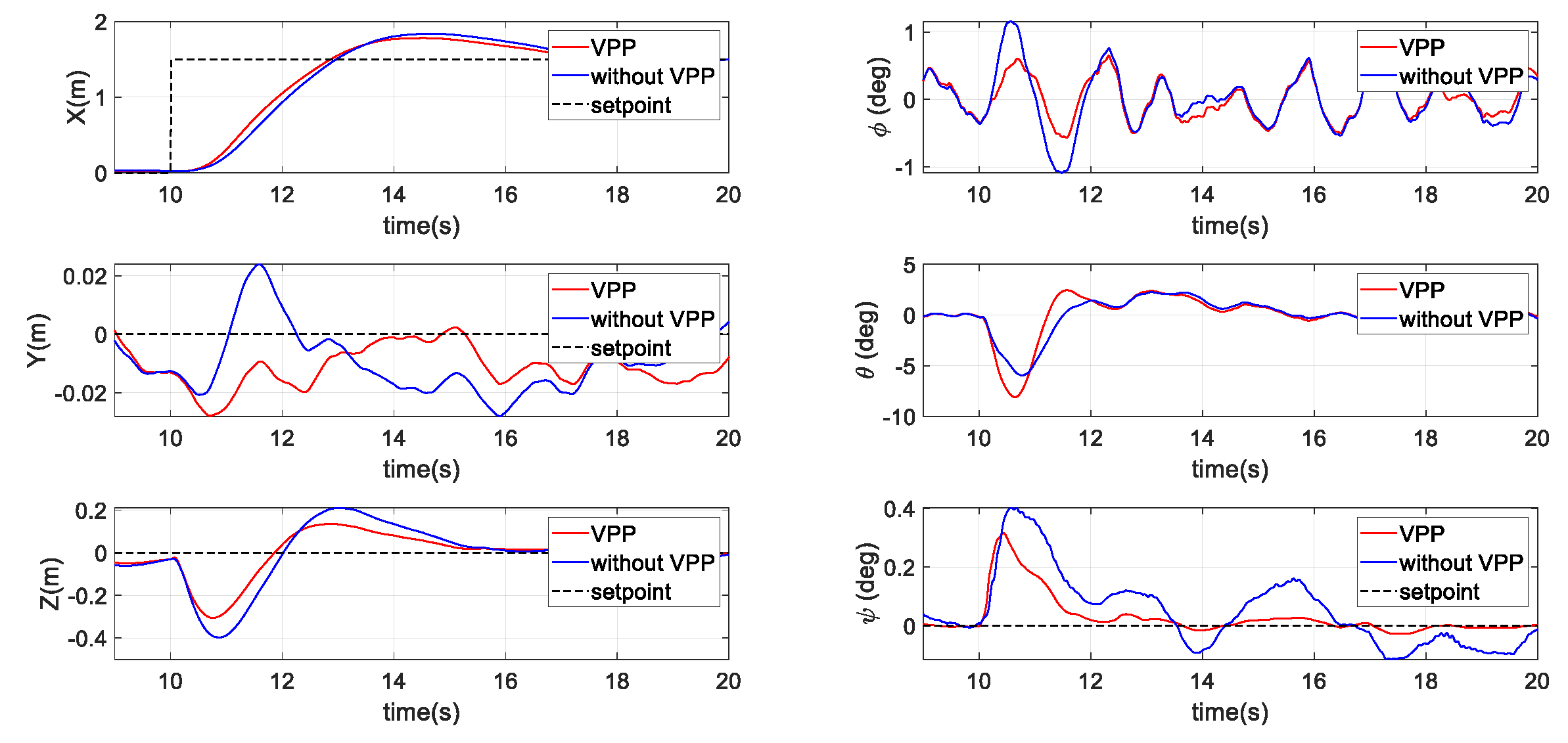
3.2.2. Second Scenario: Position Tracking with a Step Command
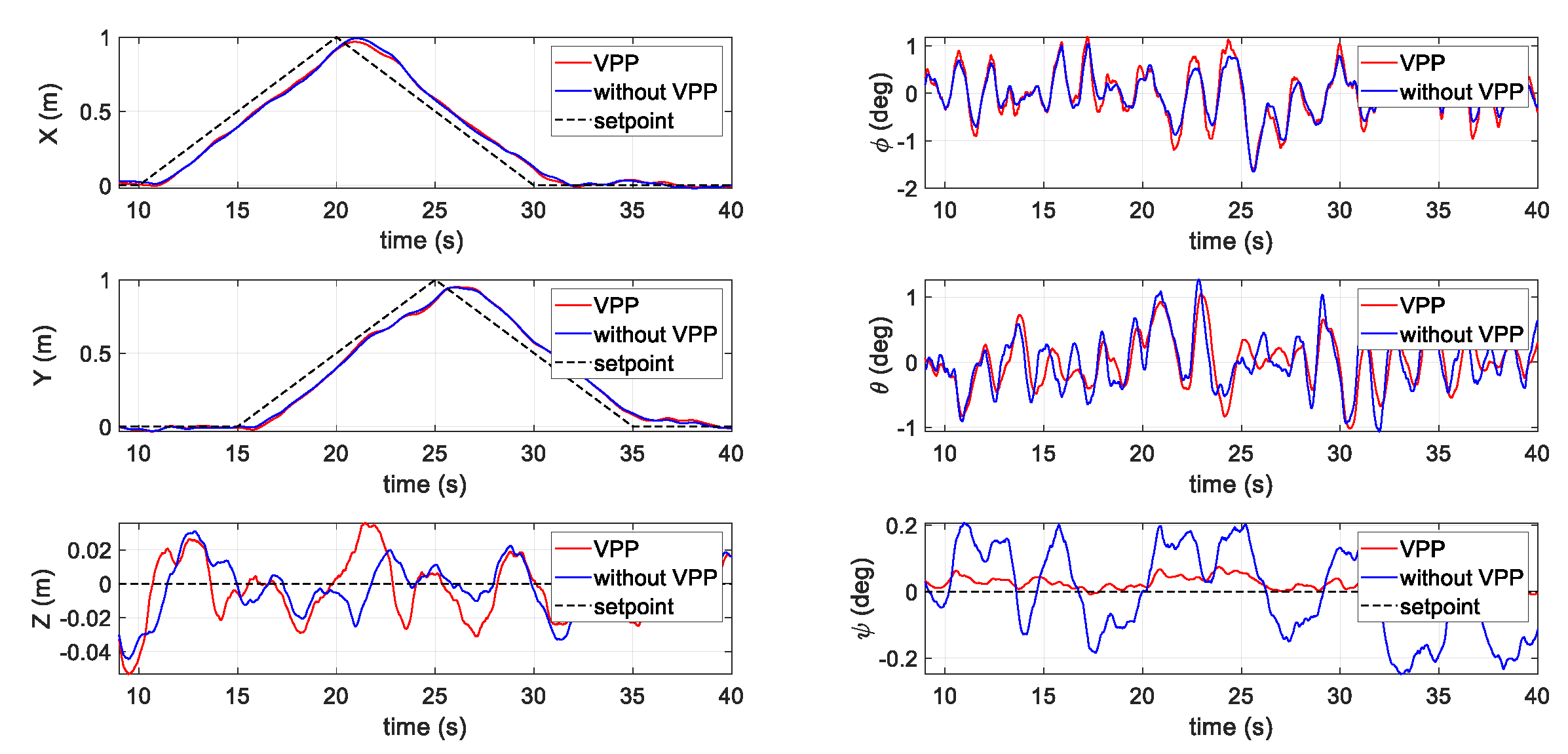
3.2.3. Third Scenario: Waypoint Mission Tracking
3.2.4. Simulation Summary
4. Flight Tests
4.1. Flight Test Equipment
4.1.1. UAV Design
4.1.2. Avionics and Test Environment
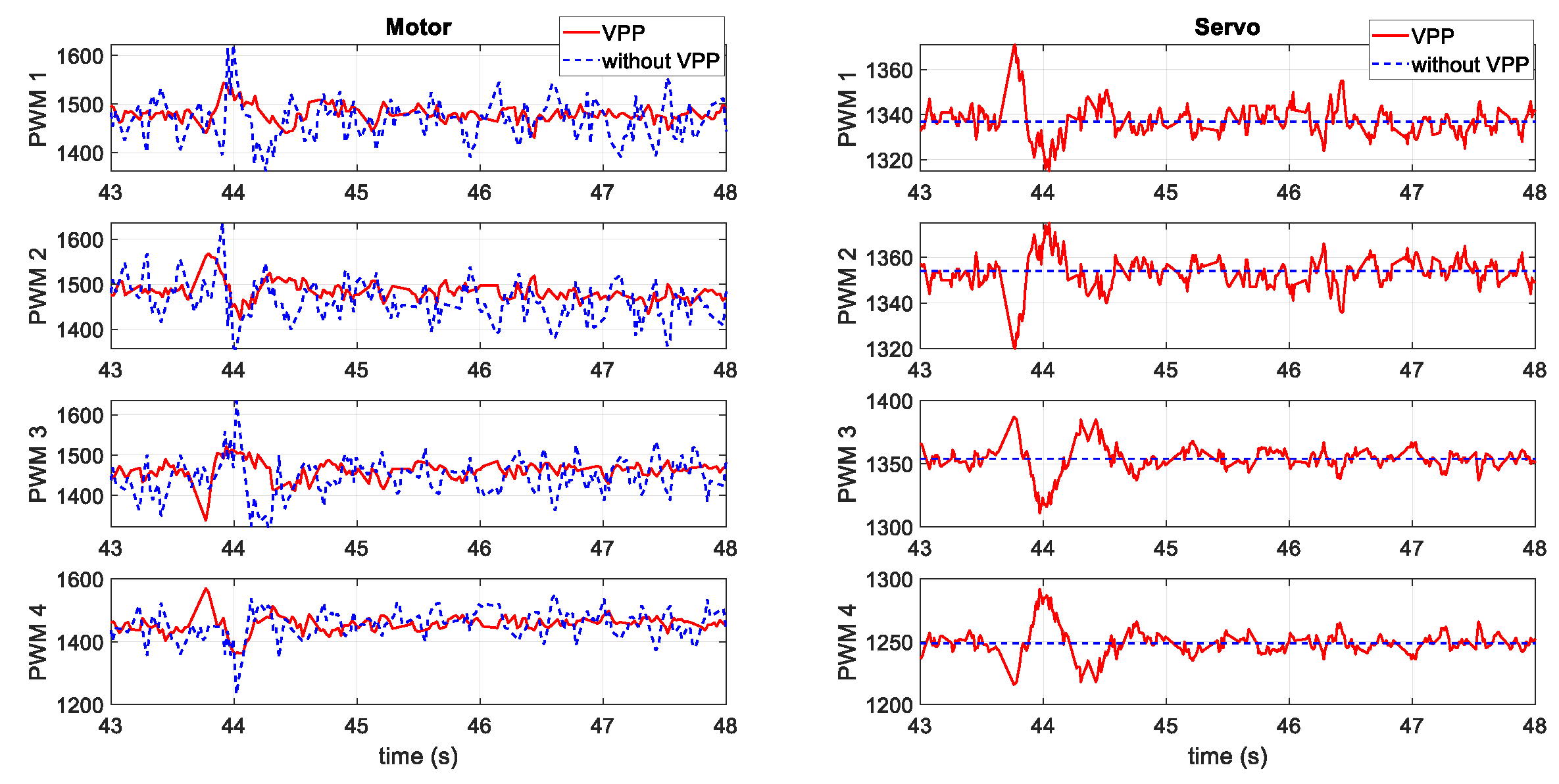
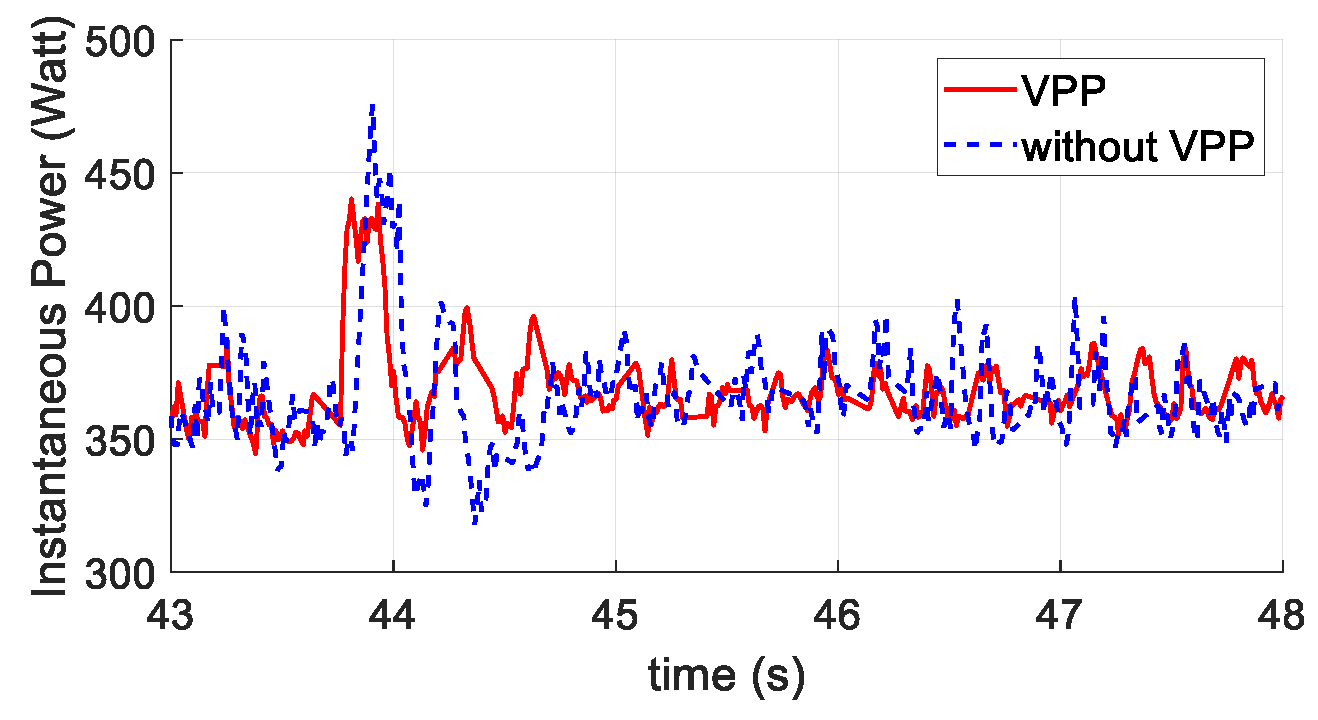
4.2. Flight Test Results
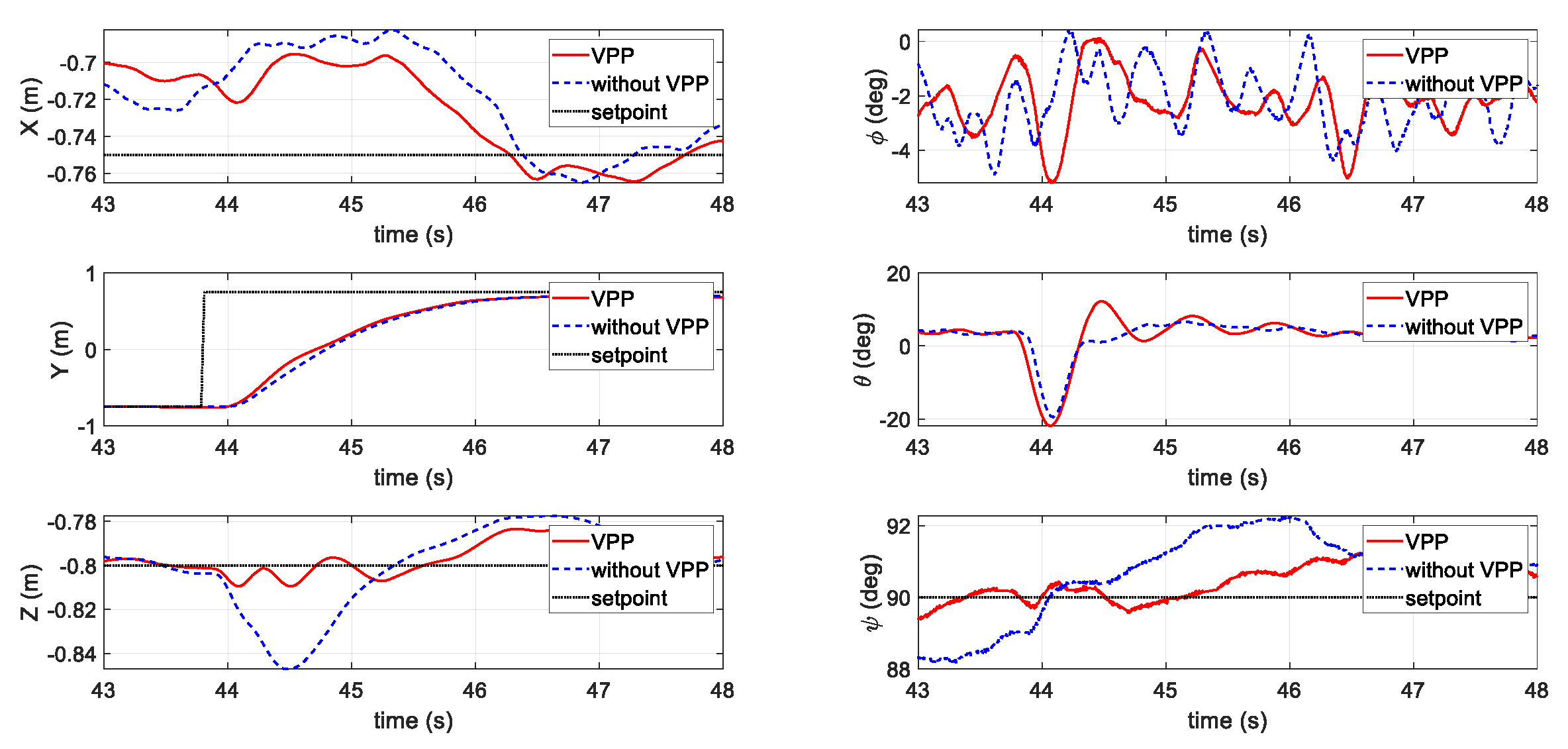
4.2.1. First Flight Test Scenario: Position Holding with a Step Yaw Command
4.2.2. Second Flight Test Scenario: Position Tracking with a Step Command
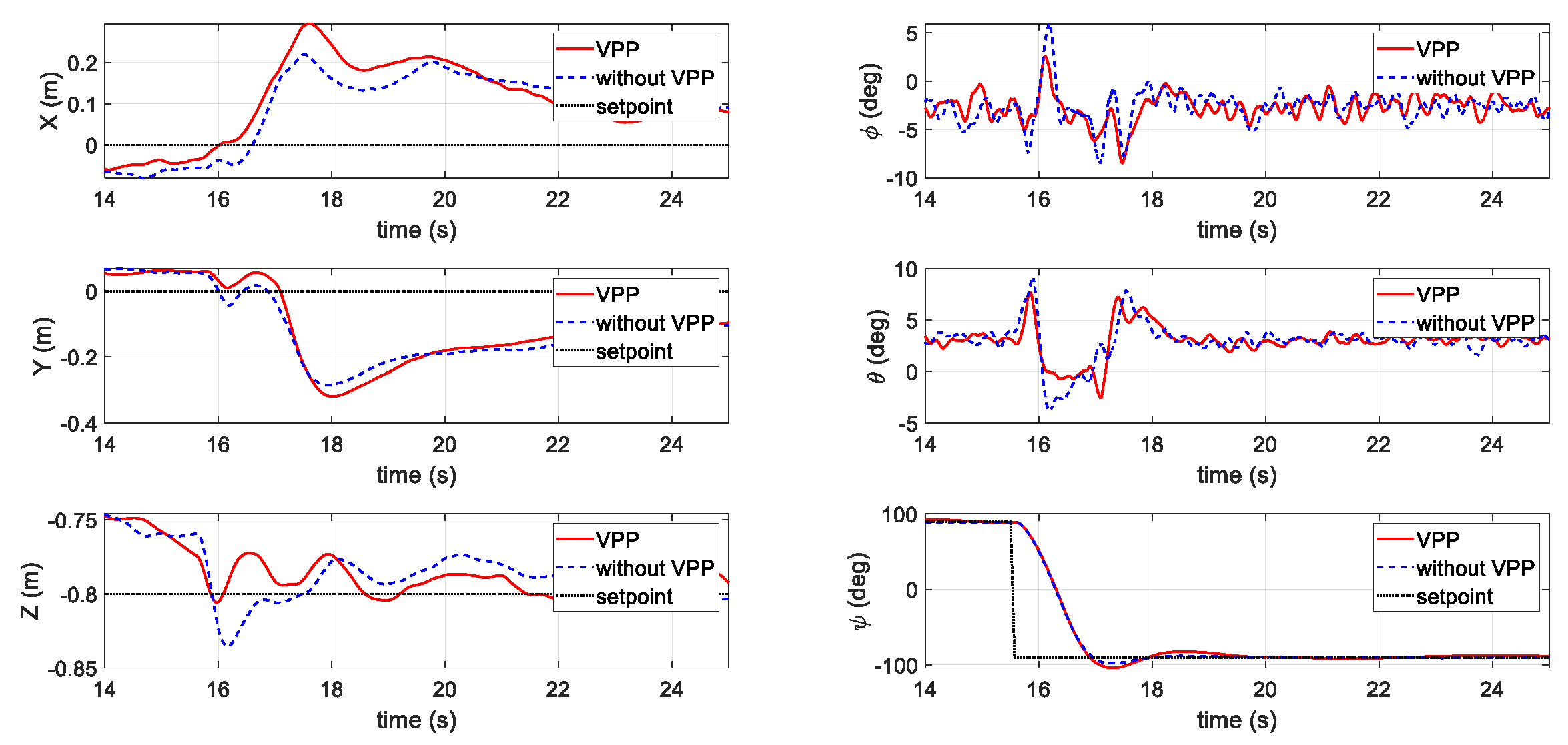
4.2.3. Third Flight Test Scenario: Waypoint Mission Tracking
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Castaño, F.; del Toro, R.M.; Haber, R.E.; Beruvides, G. Conductance sensing for monitoring micromechanical machining of conductive. Sens. Actuators A Phys. 2015, 232, 163–171. [Google Scholar] [CrossRef]
- Nebiker, S.; Annen, A.; Scherrer, M.; Oesch, D. A light-weight multispectral sensor for micro UAV—Opportunities for very high resolution airborne remote sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1193–1199. [Google Scholar]
- Merheb, A.-R.; Noura, H.; Bateman, F. Emergency control of AR drone quadrotor UAV suffering a total loss of one rotor. IEEE/ASME Trans. Mechatron. 2017, 22, 961–971. [Google Scholar] [CrossRef]
- Sun, J.; Li, B.; Jiang, Y.; Wen, C.-Y. A camera-based target detection and positioning UAV system for search and rescue (SAR) purposes. Sensors 2016, 16, 1778. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Jiang, Y.; Sun, J.; Cai, L.; Wen, C.-Y. Development and testing of a two-UAV communication relay system. Sensors 2016, 16, 1696. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Chang, C.-W.; Wen, C.-Y. Perception in the Dark—Development of a ToF Visual Inertial Odometry System. Sensors 2020, 20, 1263. [Google Scholar] [CrossRef] [PubMed]
- Finger, D.F.; Braun, C.; Bil, C. A review of configuration design for distributed propulsion transitioning VTOL aircraft. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology-APISAT, Chengdu, China, 16–18 October 2017. [Google Scholar]
- Li, B.; Zhou, W.; Sun, J.; Wen, C.-Y.; Chen, C.-K. Development of model predictive controller for a Tail-Sitter VTOL UAV in hover flight. Sensors 2018, 18, 2859. [Google Scholar] [CrossRef] [PubMed]
- Lyu, X.; Gu, H.; Zhou, J.; Li, Z.; Shen, S.; Zhang, F. Simulation and flight experiments of a quadrotor tail-sitter vertical take-off and landing unmanned aerial vehicle with wide flight envelope. Int. J. Micro Air Veh. 2018, 10, 303–317. [Google Scholar] [CrossRef]
- Sun, J.; Li, B.; Wen, C.-Y.; Chen, C.-K. Model-aided wind estimation method for a tail-sitter aircraft. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1262–1278. [Google Scholar] [CrossRef]
- Zhou, W.; Li, B.; Sun, J.; Wen, C.-Y.; Chen, C.-K. Position control of a tail-sitter UAV using successive linearization based model predictive control. Control Eng. Pract. 2019, 91, 104125. [Google Scholar] [CrossRef]
- Johnson, W. Helicopter Theory; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- McAndrw, I.R.; Navarro, E.; Witcher, K. Propeller Design Requirements for Quadcopters Utilizing Variable Pitch Propellers. Int. J. Mater. Mech. Manuf. 2018, 6, 51. [Google Scholar] [CrossRef]
- de Wagter, C.; Meulenbeld, J. Modeling the unstable DelftaCopter vertical take-off and landing tailsitter unmanned air vehicle in hover and forward flight from flight test data. Int. J. Micro Air Veh. 2019, 11, 1756829319880302. [Google Scholar] [CrossRef]
- De Wagter, C.; Remes, B.D.W.; Ruijsink, R.; van der Horst, E.; van Tienen, F.; van Wijngaarden, D.; Meulenbeld, J.F.; van Hecke, K. DelftaCopter Propulsion Optimization from Hover to Fast Forward Flight using Windtunnel Measurements. In Proceedings of the 10th International Micro-Air Vehicles Conference, Melbourne, Australia, 22 November 2018. [Google Scholar]
- Forshaw, J.L.; Lappas, V.J. Architecture and systems design of a reusable Martian twin rotor tailsitter. Acta Astronaut. 2012, 80, 166–180. [Google Scholar] [CrossRef]
- Chipade, V.S.; Kothari, M.; Chaudhari, R.R. Systematic design methodology for development and flight testing of a variable pitch quadrotor biplane VTOL UAV for payload delivery. Mechatronics 2018, 55, 94–114. [Google Scholar] [CrossRef]
- Pang, T.; Peng, K.; Lin, F.; Chen, B.M. Towards long-endurance flight: Design and implementation of a variable-pitch gasoline-engine quadrotor. In Proceedings of the 2016 12th IEEE International Conference on Control and Automation (ICCA), Kathmandu, Nepal, 1–3 June 2016. [Google Scholar]
- Abhishek, A.; Duhoon, A.; Kothari, M.; Kadukar, S.; Rane, L.; Suryavanshi, G. Design, Development, and Closed-loop Flight-Testing of a Single Power Plant Variable Pitch Quadrotor Unmanned Air Vehicle. In Proceedings of the 73rd American Helicopter Society Annual Forum, Worth, TX, USA, 8–11 May 2017; pp. 9–11. [Google Scholar]
- Sheng, S.; Sun, C. Control and optimization of a variable-pitch quadrotor with minimum power consumption. Energies 2016, 9, 232. [Google Scholar] [CrossRef]
- Cutler, M.; How, J.P. Analysis and control of a variable-pitch quadrotor for agile flight. J. Dyn. Syst. Meas. Control 2015, 137, 101002. [Google Scholar] [CrossRef]
- Bhargavapuri, M.; Sahoo, S.R.; Kothari, M. Robust nonlinear control of a variable-pitch quadrotor with the flip maneuver. Control Eng. Pract. 2019, 87, 26–42. [Google Scholar] [CrossRef]
- Cutler, M.; Ure, N.-K.; Michini, B.; How, J. Comparison of fixed and variable pitch actuators for agile quadrotors. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, Oregon, 8–11 August 2011; p. 6406. [Google Scholar]
- Gao, L.; Zhao, J.; Zhu, Y.; Jin, H.; Wang, H.; Cai, H. Application of cycle variable pitch propeller to morphing unmanned aerial vehicles. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2493–2498. [Google Scholar]
- Henderson, T.; Papanikolopoulos, N. Power-Minimizing Control of a Variable-Pitch Propulsion System for Versatile Unmanned Aerial Vehicles. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4148–4153. [Google Scholar]
- Manchin, A.; Lafta, W.M.; Dao, D.V. Smart Variable Pitch Propeller System for Unmanned Aerial Vehicles. Int. J. Eng. Technol. 2018, 74, 5238–5242. [Google Scholar]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar]
- Up Board. Available online: https://up-board.org/up/specifications/ (accessed on 13 August 2020).
- ROS Melodic Morenia. Available online: http://wiki.ros.org/melodic (accessed on 13 August 2020).
- MAVROS. Available online: http://wiki.ros.org/mavros (accessed on 13 August 2020).
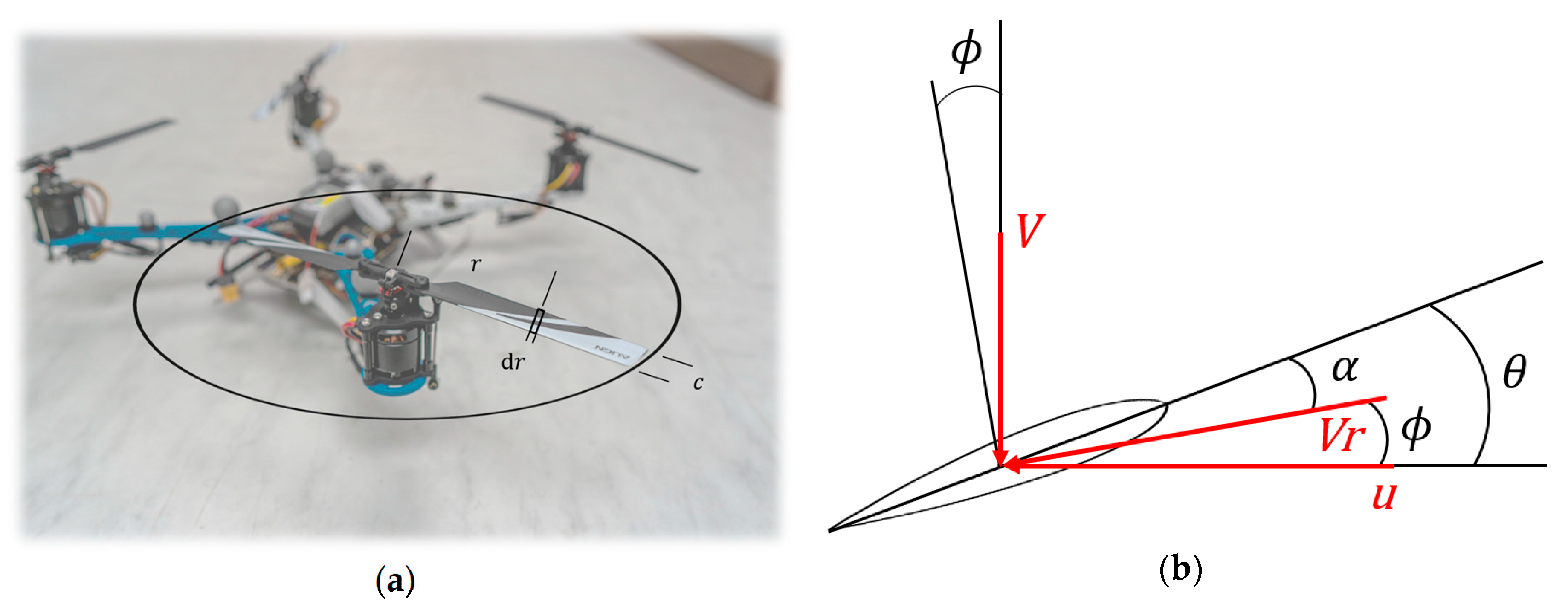







| Abbreviations | |
|---|---|
| Airspeed toward the rotational plane (m/s) | |
| Propeller’s forward speed (m/s) | |
| Resultant airspeed toward airfoil (m/s) | |
| Pitch angle measured from the rotational plane (degrees) | |
| Angle of attack of the airfoil (degrees) | |
| Inflow angle (degrees) |
| RMSE of ψ (deg) | Without VPP | With VPP |
|---|---|---|
| 1st scenario | 3.610 | 3.363 |
| 2nd scenario | 0.128 | 0.053 |
| 3rd scenario | 0.128 | 0.028 |
| Without VPP | With VPP | |
|---|---|---|
| 1st flight test scenario | 12.49 | 11.96 |
| 2nd flight test scenario | 10.08 | 9.98 |
| () | 7.85 | 8.32 | 8.49 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-W.; Chen, S.; Wen, C.-Y.; Li, B. An Actuator Allocation Method for a Variable-Pitch Propeller System of Quadrotor-Based UAVs. Sensors 2020, 20, 5651. https://doi.org/10.3390/s20195651
Chang C-W, Chen S, Wen C-Y, Li B. An Actuator Allocation Method for a Variable-Pitch Propeller System of Quadrotor-Based UAVs. Sensors. 2020; 20(19):5651. https://doi.org/10.3390/s20195651
Chicago/Turabian StyleChang, Ching-Wei, Shengyang Chen, Chih-Yung Wen, and Boyang Li. 2020. "An Actuator Allocation Method for a Variable-Pitch Propeller System of Quadrotor-Based UAVs" Sensors 20, no. 19: 5651. https://doi.org/10.3390/s20195651
APA StyleChang, C.-W., Chen, S., Wen, C.-Y., & Li, B. (2020). An Actuator Allocation Method for a Variable-Pitch Propeller System of Quadrotor-Based UAVs. Sensors, 20(19), 5651. https://doi.org/10.3390/s20195651






