Artificial Intelligence-Based Bolt Loosening Diagnosis Using Deep Learning Algorithms for Laser Ultrasonic Wave Propagation Data
Abstract
1. Introduction
- Introduce a new perspective of bolt looseness quantification which utilizes a DL-based computer vision algorithms with full-field ultrasonic data.
- Determine the applicability of a deep convolutional neural network (DCNN) algorithm and full-field ultrasonic data to estimate the looseness in bolted joints.
- Compare the effects of signal processing techniques for full-field ultrasonic data according to the performance of DL algorithms.
2. Theoretical Background
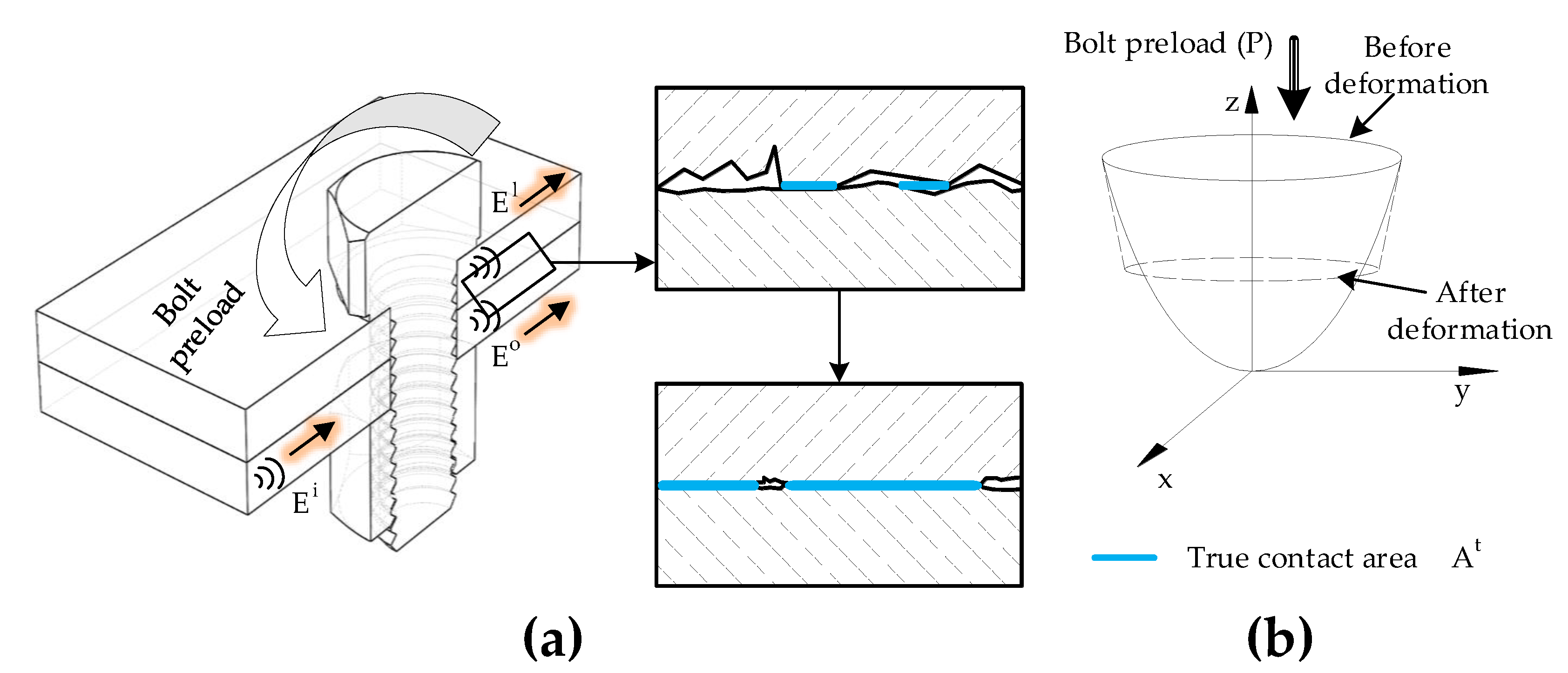
2.1. Micro Contact Theory
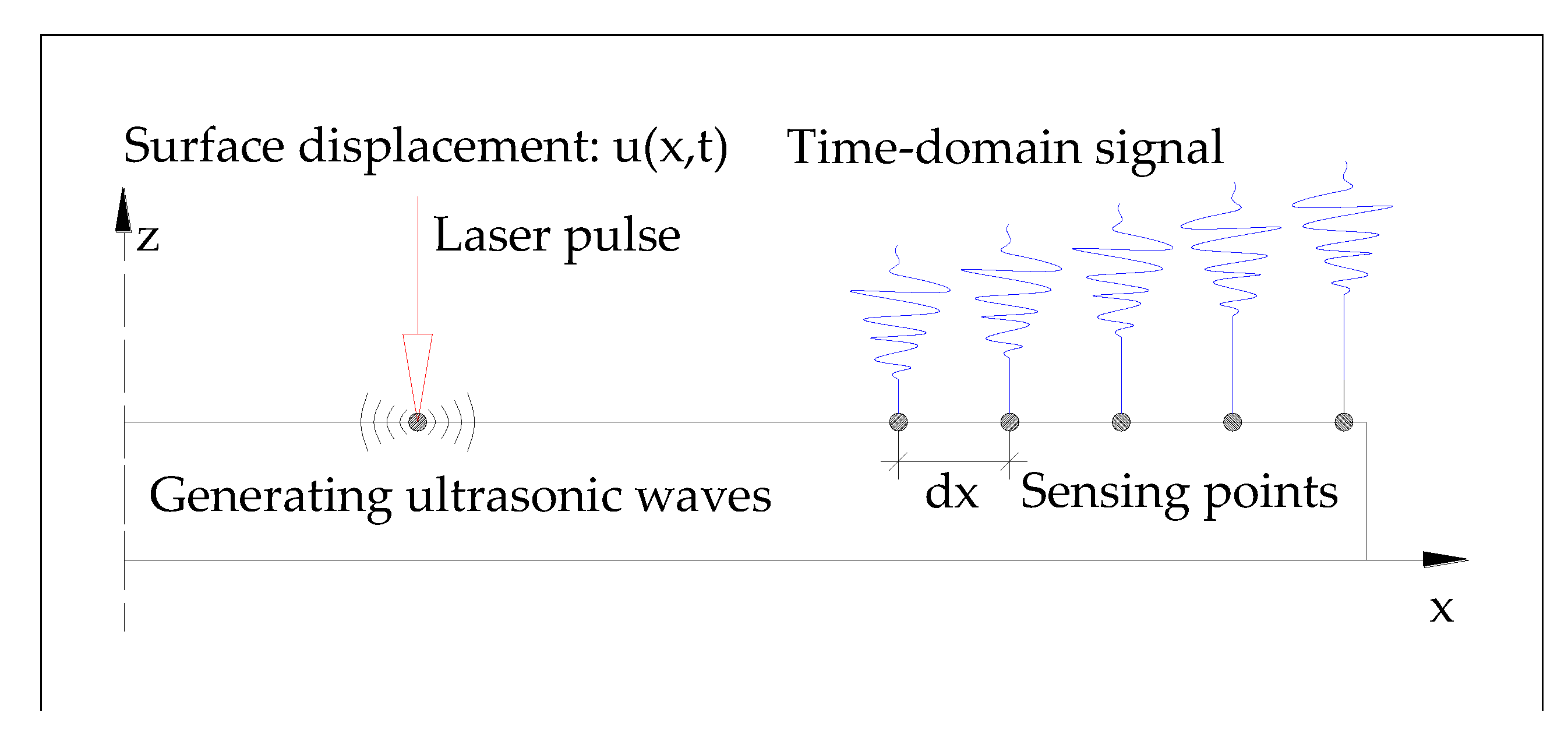
2.2. Ultrasonic Wave Generation Mechanism Using Pulsed Laser: Scheme
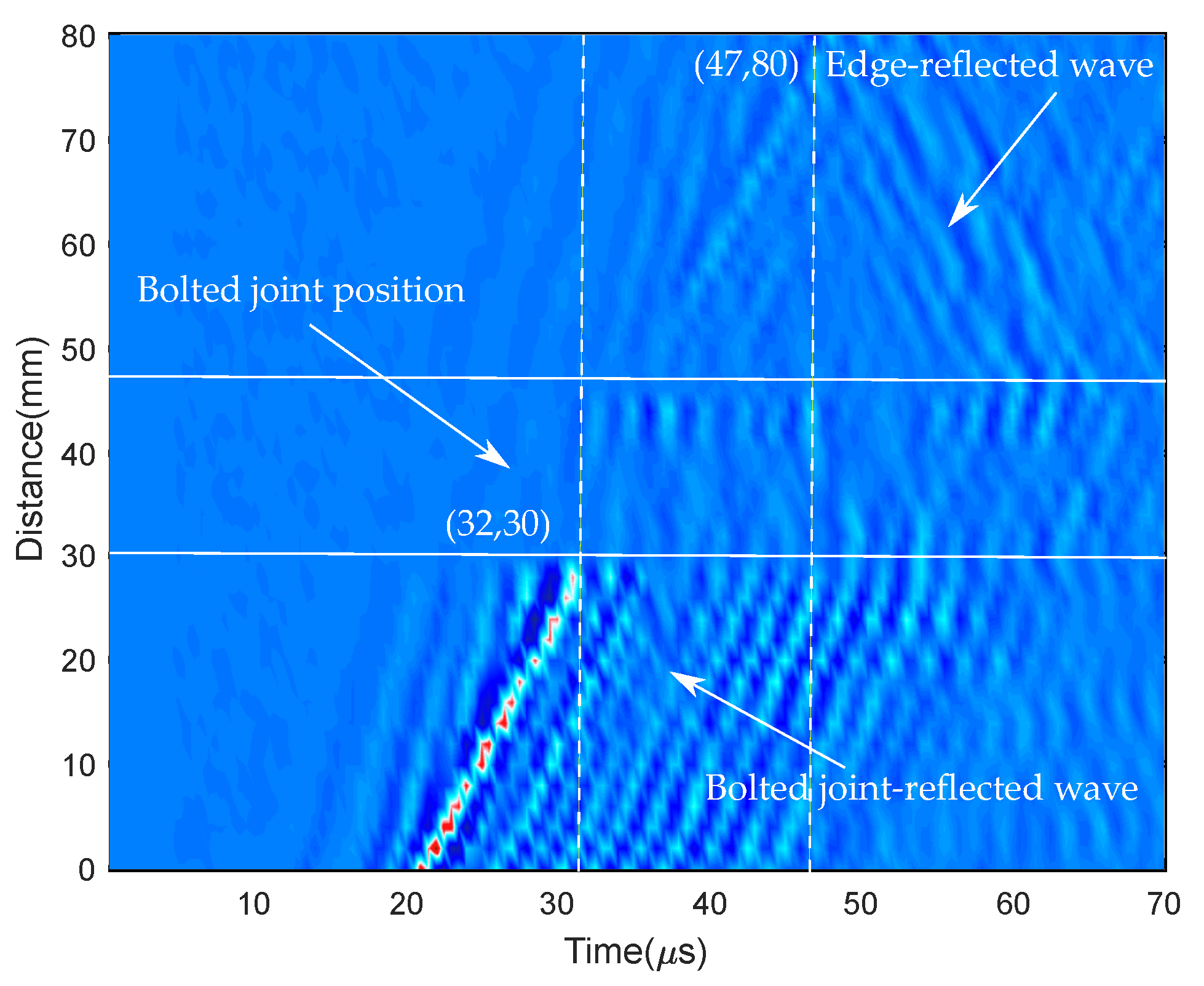
- Measuring the time-domain response at each impinging point.
- Placing the measured signals at their corresponding laser impinging points that are outlined at the image processor (resulting in a vertical plane containing all impinging points and an into-the-page axis representing the time axis).
- Slicing along the time axis of 3D space.
2.3. Full-Wavefield Signal Processing
2.3.1. Reflection Separation
- The filtering process starts with a 3D Fourier transformation that produces the wavenumber frequency domain representation of the wavefield .
- The elimination of waves in a wavenumber-frequency domain having a positive or negative sign at a fixed frequency filters a portion of the wave propagating in a specific direction .
- Eventually, the filtered wavenumber-frequency’s inverse 3D Fourier transformation was used to extract the filtered data .
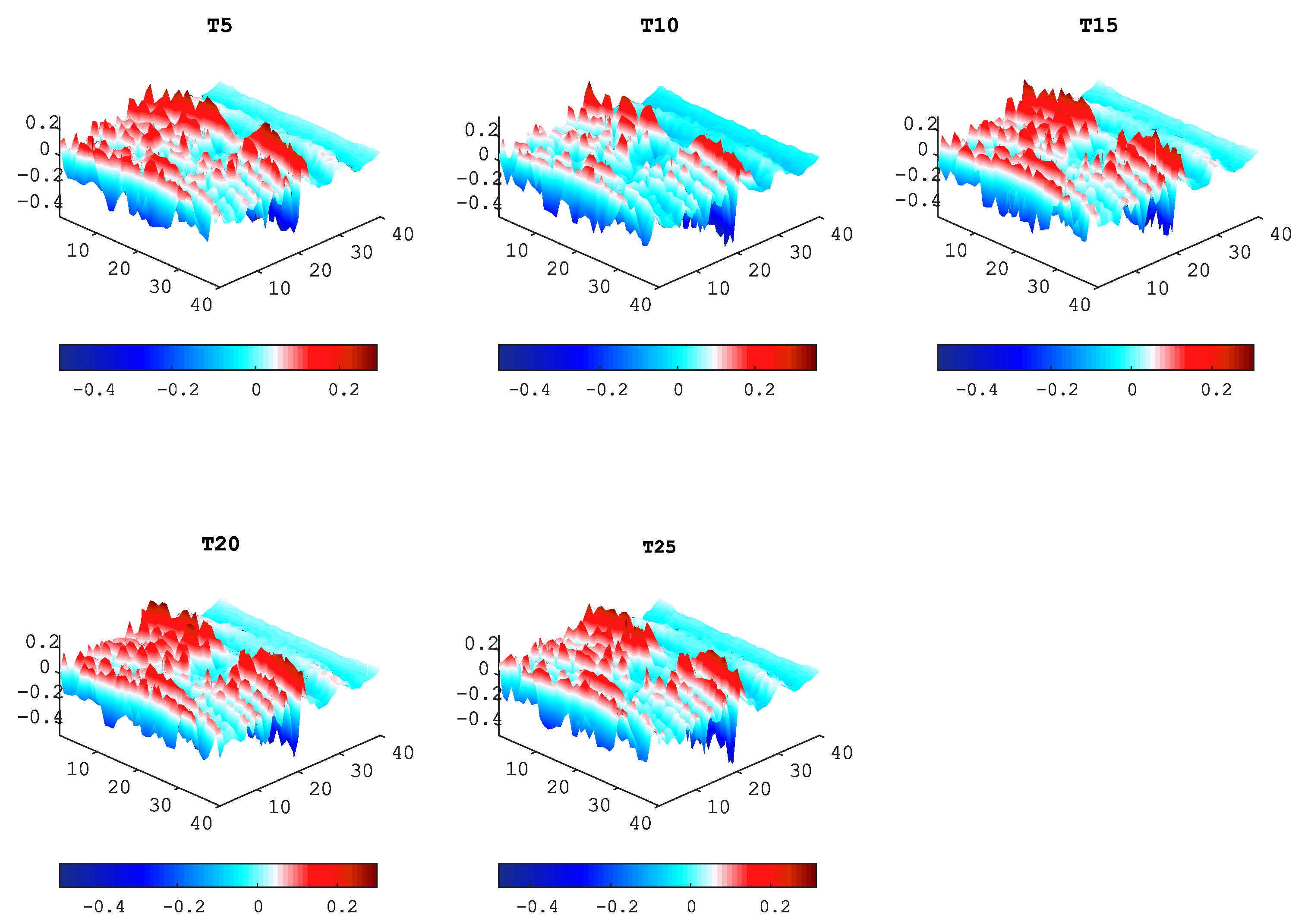
2.3.2. Isolated Cumulative Standing Wave Energy
2.3.3. Wavenumber Adaptive Image Filtering
- D1: Raw full-field ultrasonic data;
- D2: Filtered down-propagation wave data;
- D3: Filtered up-propagation wave data;
- D4: Standing waves data;
- D5: Wavenumber adaptive image-filtered data.
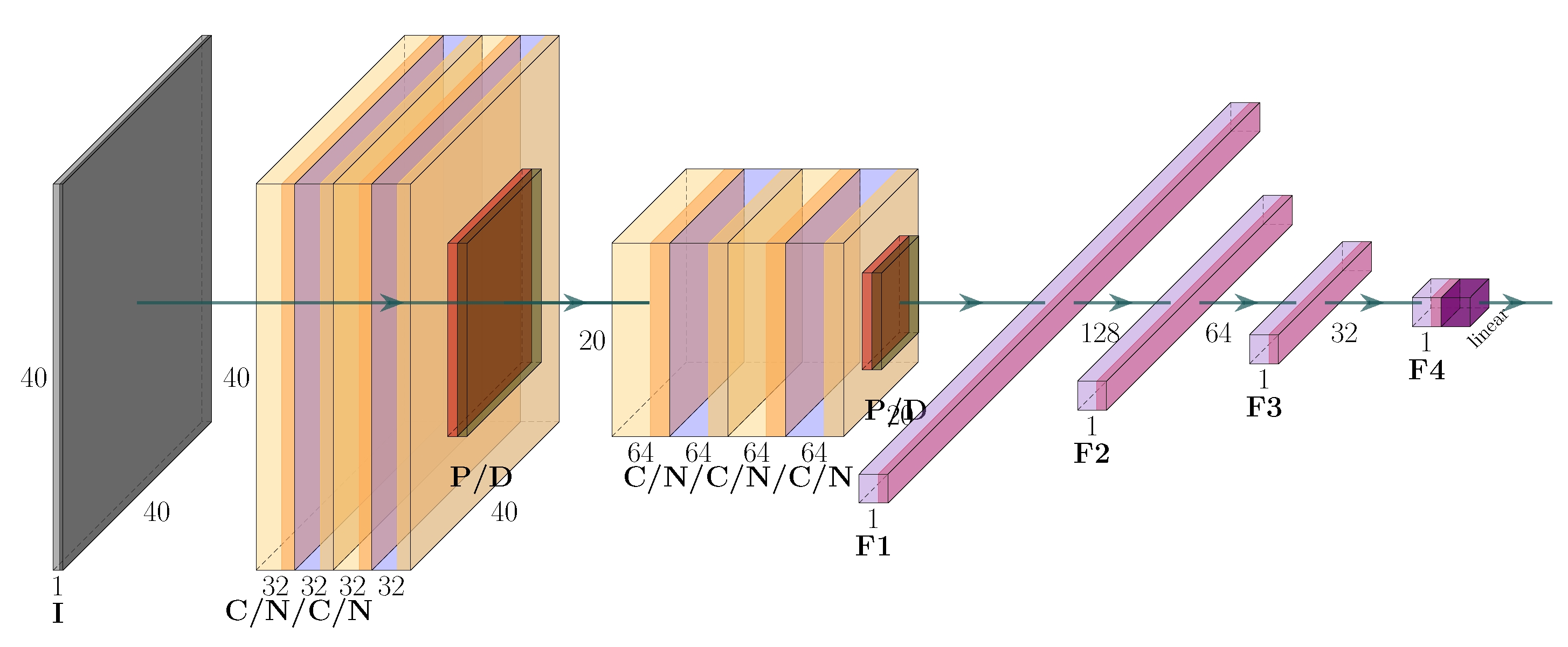
2.4. Deep Regression Convolutional Neural Network
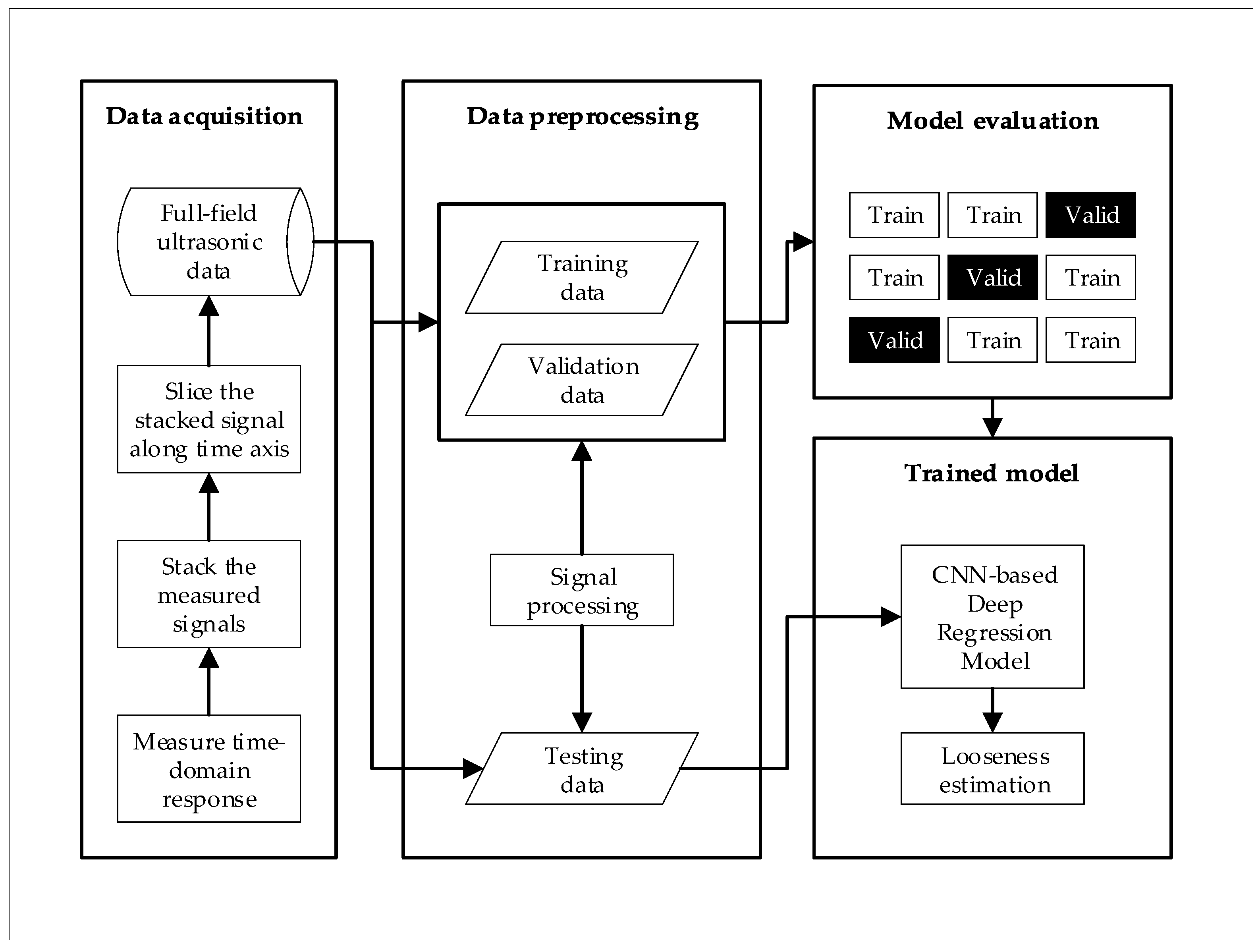
3. Proposed Method
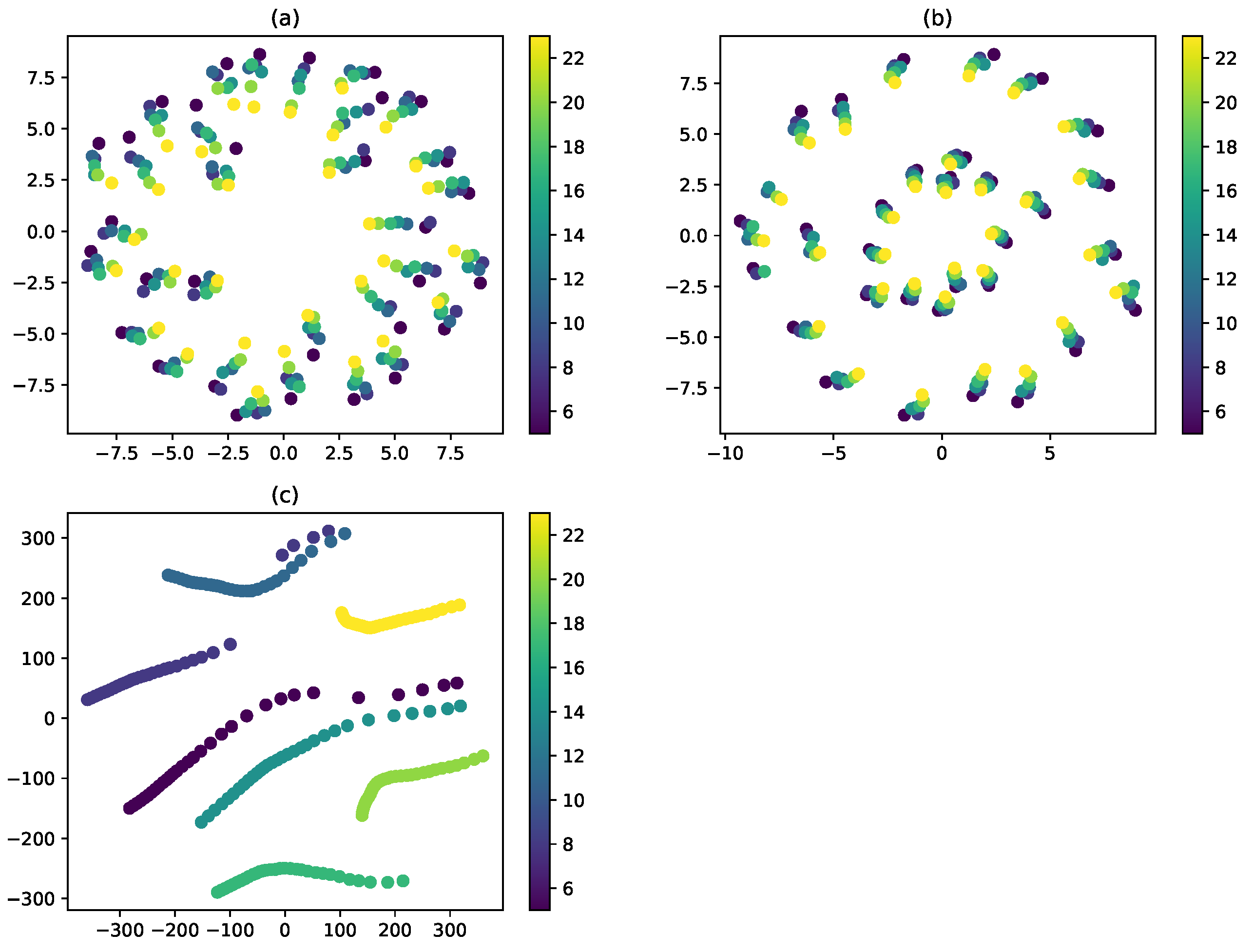
- First, the signals are measured at each impinging point using Nd:YAG pulsed laser scanning and an R-CAST AE sensor. The UWPI process is then performed, after which the full-field ultrasonic data sets are produced.
- The second phase starts with the application of signal processing techniques for full-field ultrasonic raw data.
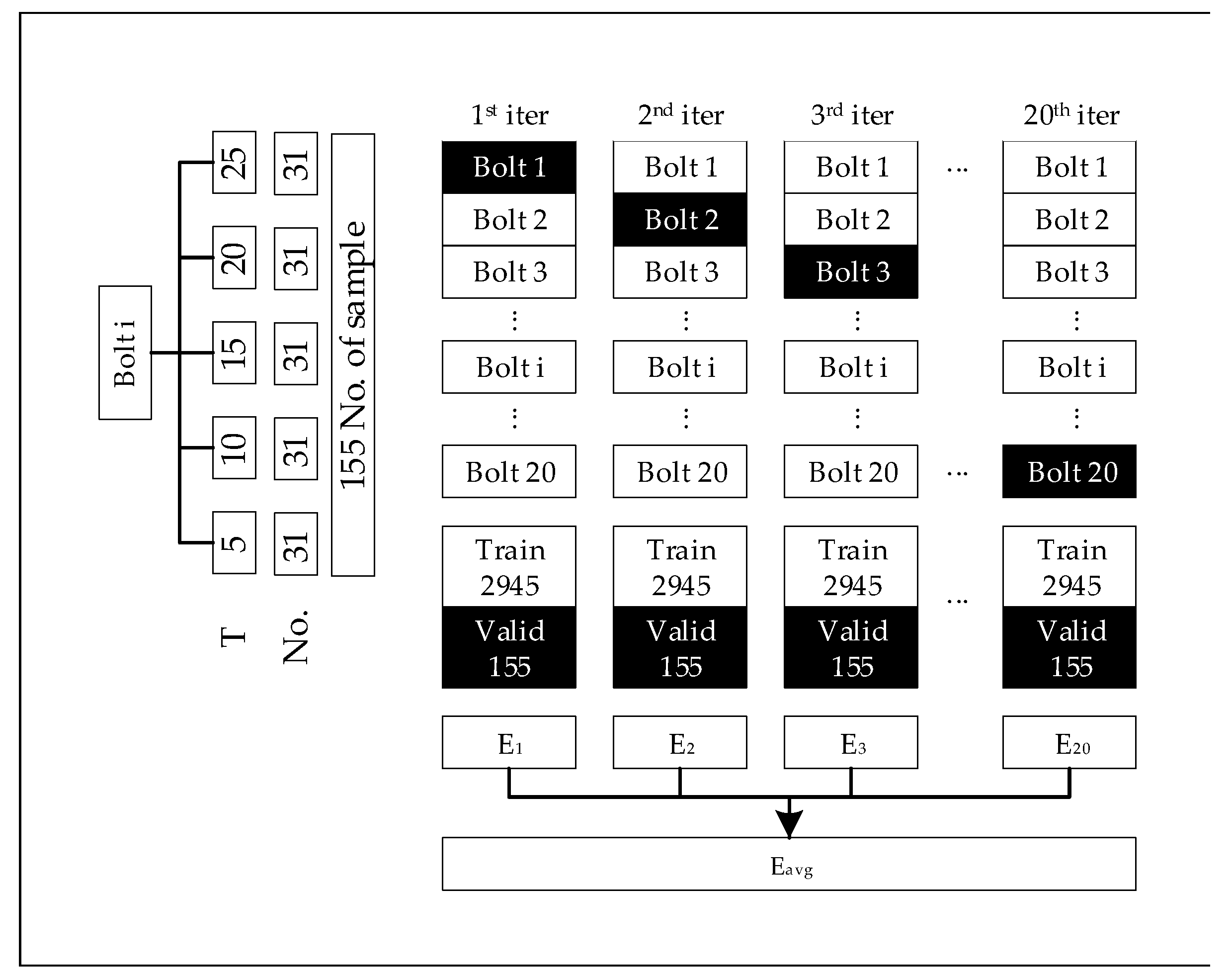
- A model evaluation process is utilized for choosing the best model performance on different data sets.
- Finally, the DCNN model is generated to estimate the looseness value of bolted joints after training and optimization.
4. Performance of Proposed Approach
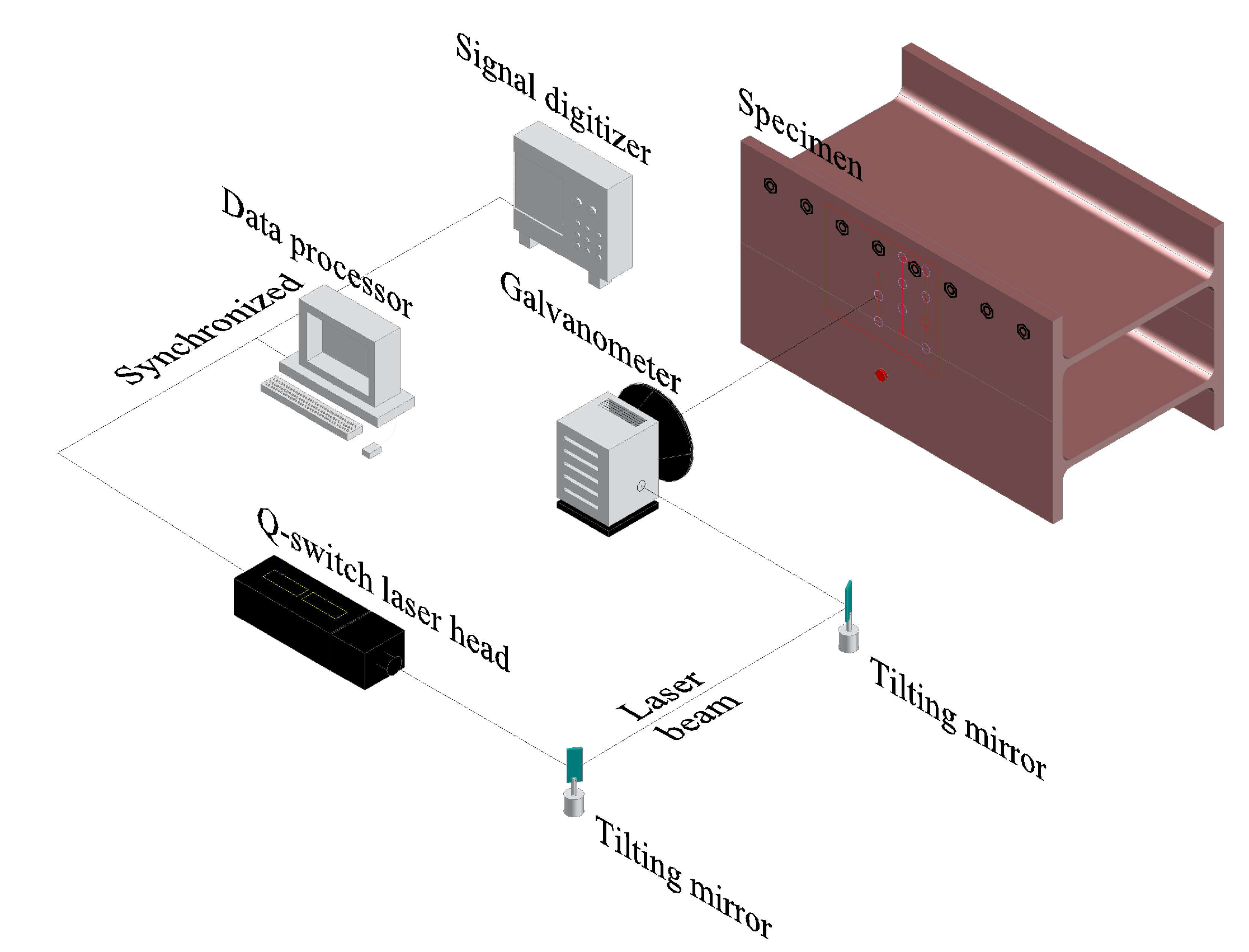
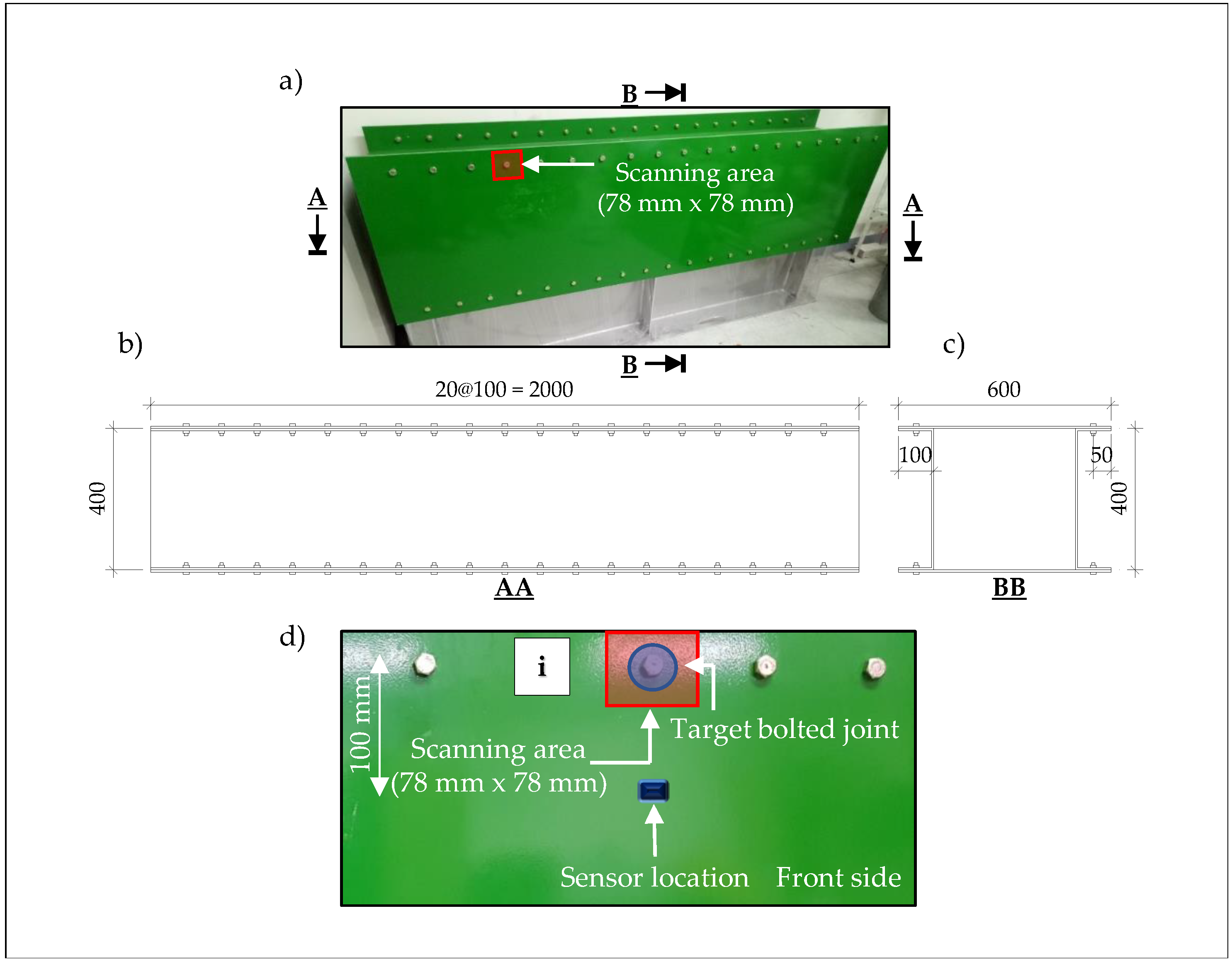
4.1. Experiment Setup
4.2. Deep Regression CNN for Full-Field Ultrasonic Data
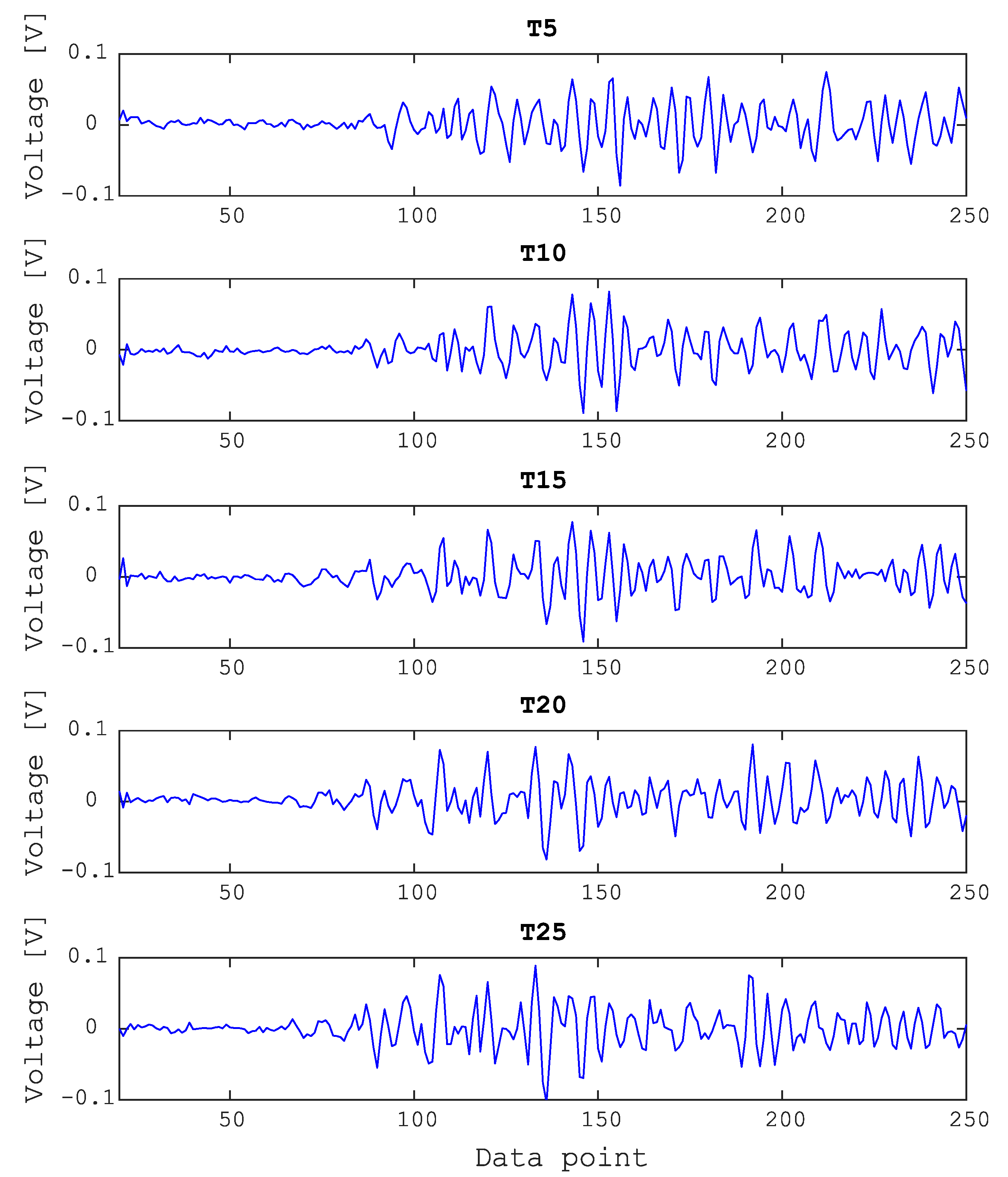
4.2.1. Input Data
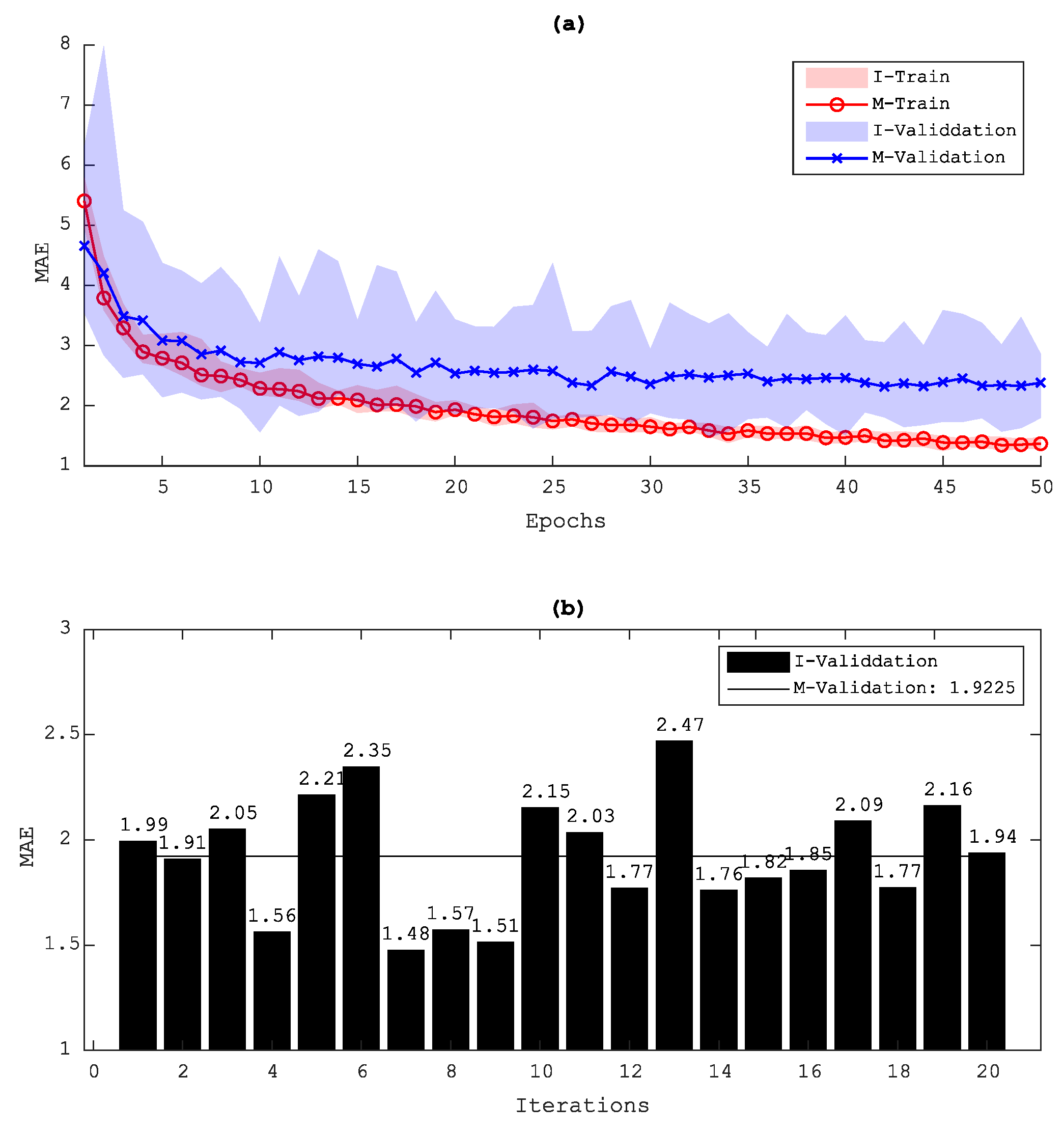
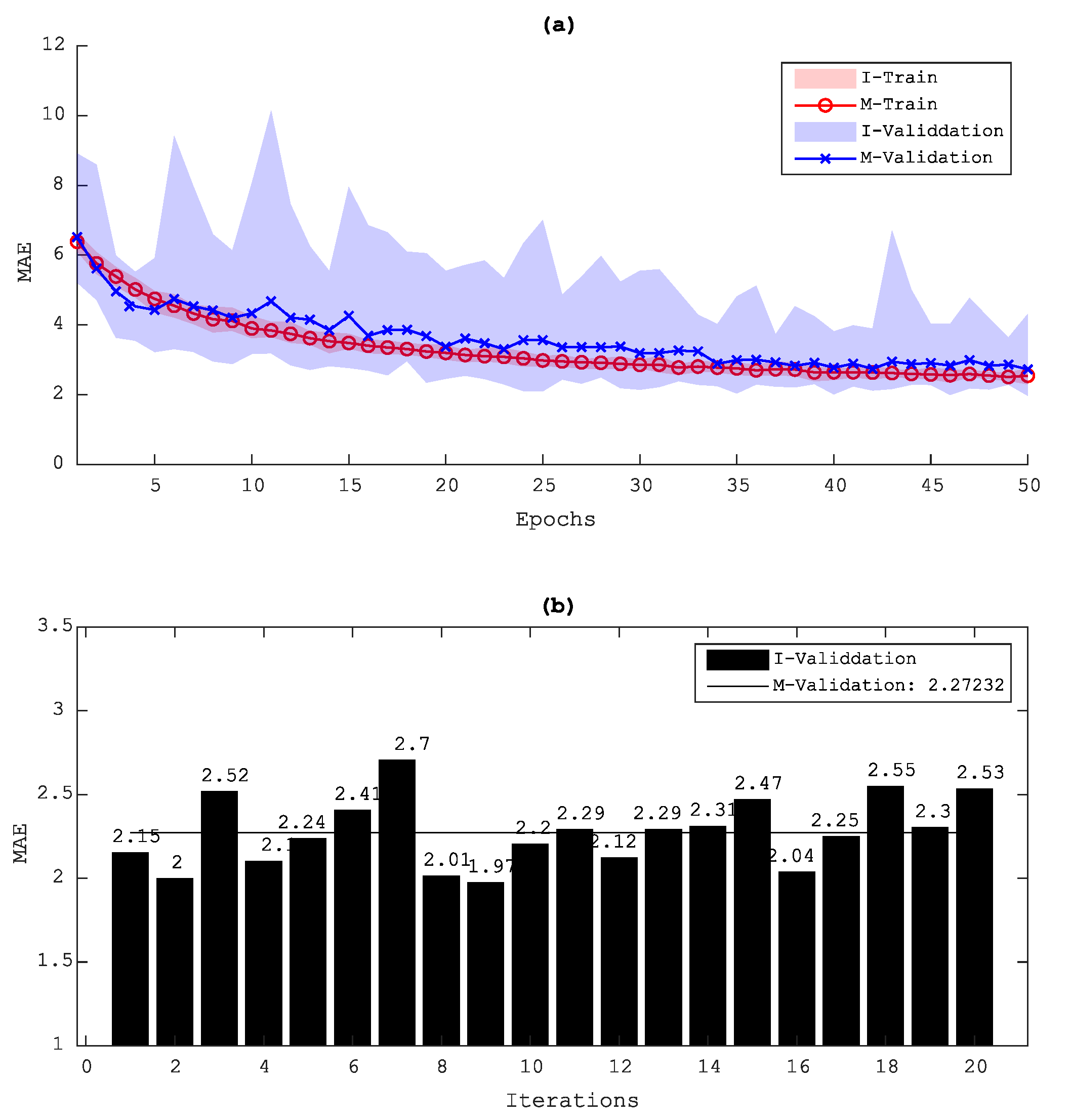
4.2.2. Process of Model Evaluation
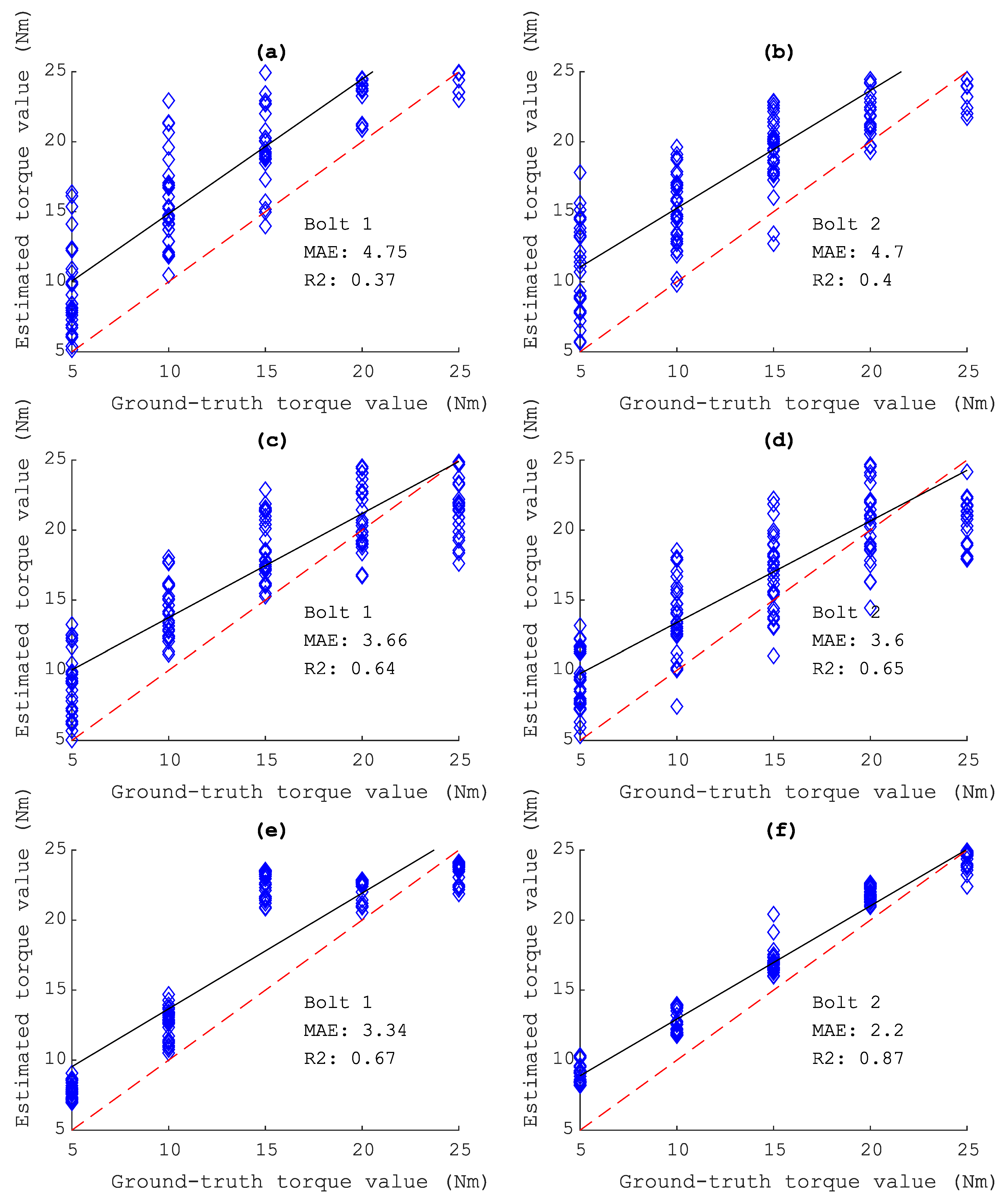
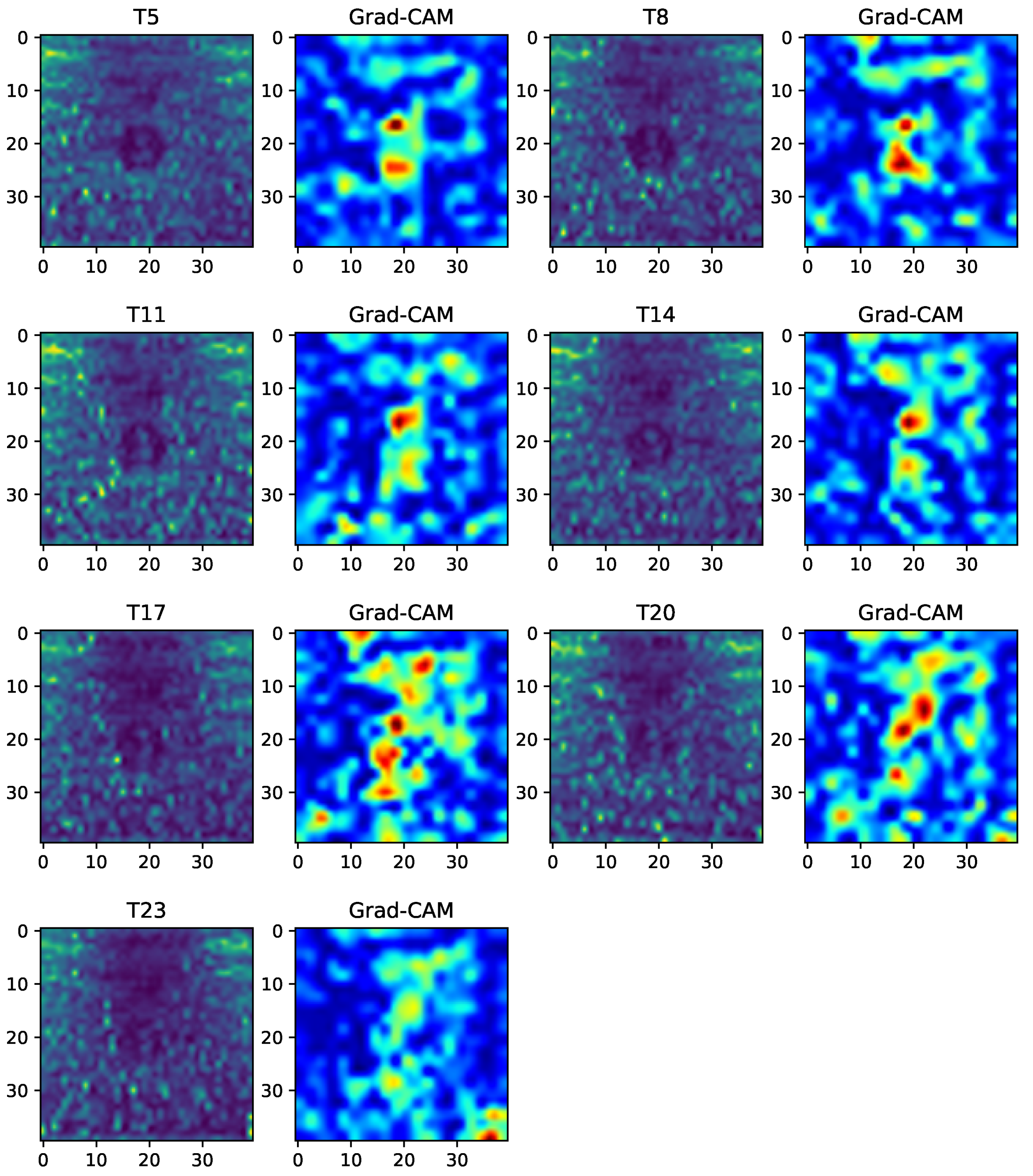
4.2.3. Model Prediction
5. Conclusions
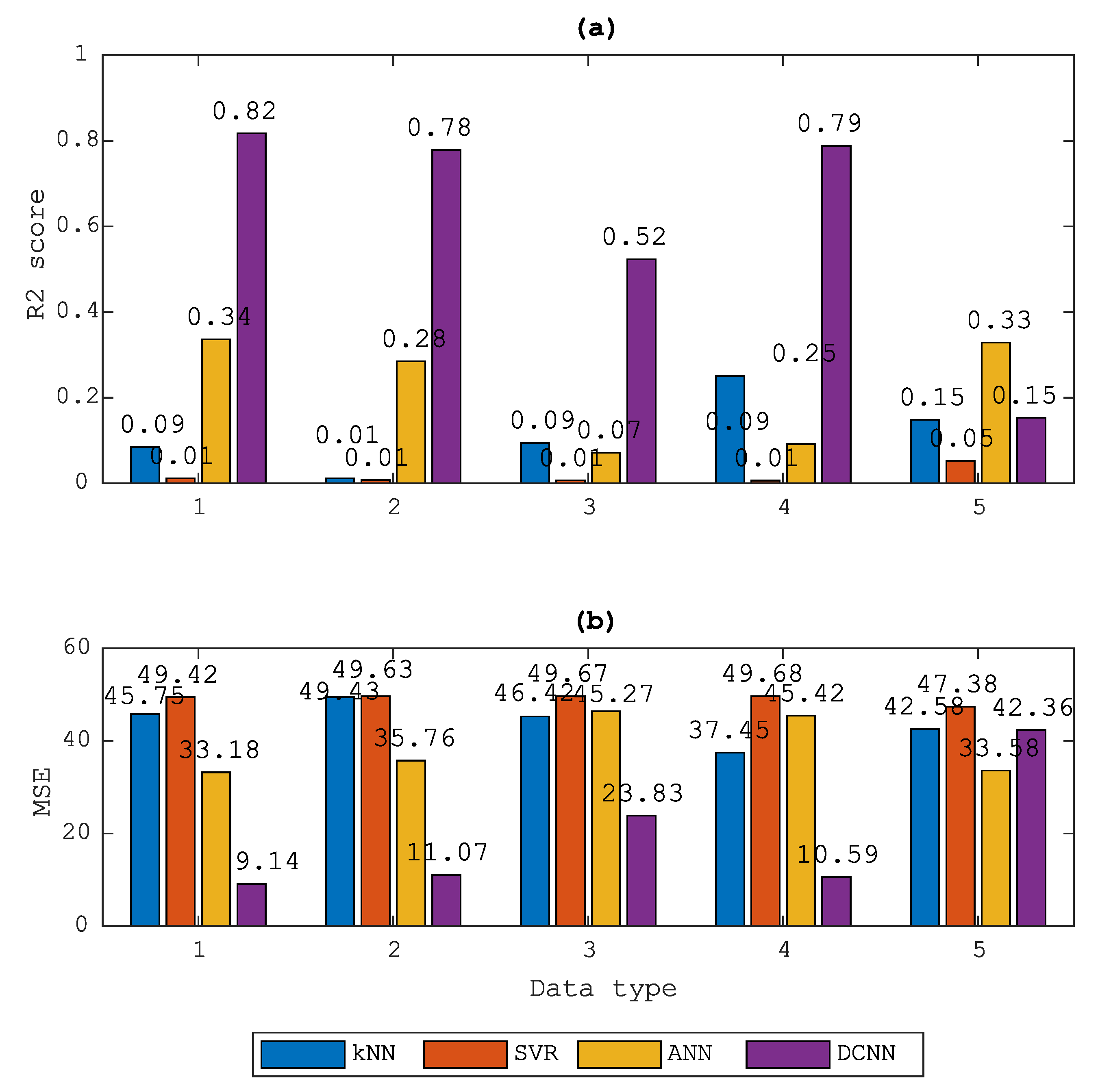
- Application of the data augmentation technique was necessary for the DCNN to produce acceptable results on full-field ultrasonic data.
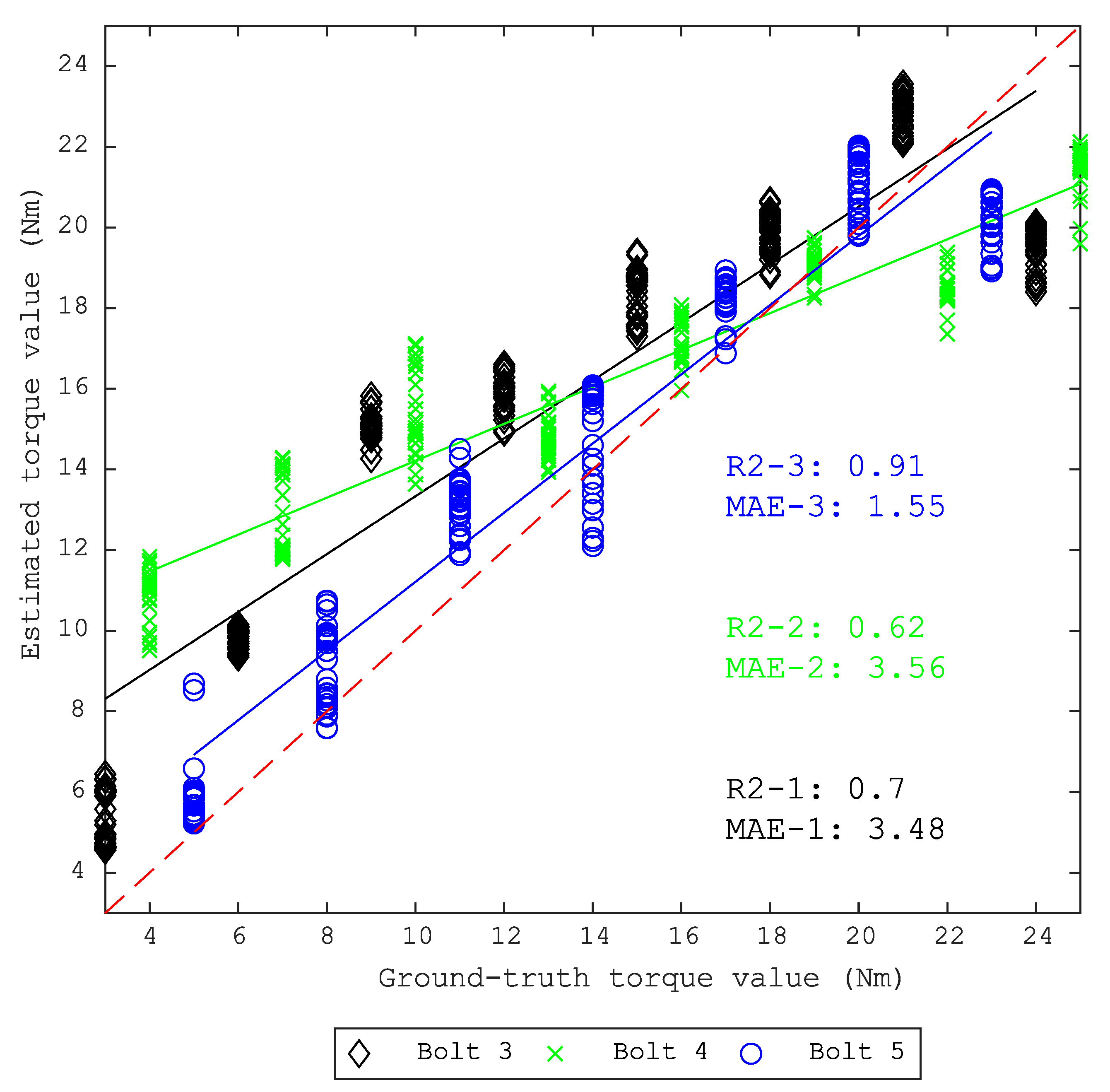
- To obtain better results, an isolated cumulative standing wave energy can be used as a signal processing technique. In this research, the DCNN and this signal processing technique produced the highest R2 score and lowest MSE score, 0.91 and 1.55, respectively.
- The UWPI system is still partially non-contact laser scanning, that is, the AE sensor is used as an ultrasonic receiver in the experiment and needs to be set up manually. To overcome this limitation, the LDV will be developed to replace the AE sensor for acquiring ultrasonic signals. Finally, the system can become fully non contact scanning and work without the need for setting up manually.
- The proposed method can be applied to the bolt in the straight line area only. In the cases of complex areas where the bolt locations are not on a straight line, the system will meet the challenge to excite and receive the ultrasonic signal. Thus, the method needs to improve the hardware of the device used for scanning.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DL | Deep learning |
| ML | Machine learning |
| NDE | Non-destructive evaluation |
| SHM | Structural health monitoring |
| Nd:YAG | Neodymium-doped Yttrium Aluminum Garnet |
| UWPI | Ultrasonic Wave Propagation Imaging |
| DCNN | Deep convolutional neural network |
| AE | Acoustic emission |
| kNN | k-nearest neighbors |
| SVR | Support vector machine |
| DNN | Deep neural network |
| Grad-CAM | Gradient-weight class activation mapping |
References
- Lovell, P.A.; Pines, D.J. Damage Assessment in a Bolted Lap Joint; International Society for Optics and Photonics: Washington, DC, USA, 1998; pp. 112–126. [Google Scholar] [CrossRef]
- Todd, M.D.; Nichols, J.M.; Nichols, C.J.; Virgin, L.N. An assessment of modal property effectiveness in detecting bolted joint degradation: Theory and experiment. J. Sound Vib. 2004, 275, 1113–1126. [Google Scholar] [CrossRef]
- Amerini, F.; Barbieri, E.; Meo, M.; Polimeno, U. Detecting loosening/tightening of clamped structures using nonlinear vibration techniques. Smart Mater. Struct. 2010, 19, 085013. [Google Scholar] [CrossRef]
- Ritdumrongkul, S.; Abe, M.; Fujino, Y.; Miyashita, T. Quantitative health monitoring of bolted joints using a piezoceramic actuator–sensor. Smart Mater. Struct. 2003, 13, 20. [Google Scholar] [CrossRef]
- Peairs, D.M.; Park, G.; Inman, D.J. Practical issues of activating self-repairing bolted joints. Smart Mater. Struct. 2004, 13, 1414. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.J.; Yun, C.B.; Inman, D.J. Electro-mechanical impedance-based wireless structural health monitoring using PCA-data compression and k-means clustering algorithms. J. Intell. Mater. Syst. Struct. 2008, 19, 509–520. [Google Scholar] [CrossRef]
- Wang, F.; Ho, S.C.M.; Huo, L.; Song, G. A novel fractal contact-electromechanical impedance model for quantitative monitoring of bolted joint looseness. IEEE Access 2018, 6, 40212–40220. [Google Scholar] [CrossRef]
- Chen, D.; Huo, L.; Song, G. EMI based multi-bolt looseness detection using series/parallel multi-sensing technique. Smart Struct. Syst. 2020, 25, 423–432. [Google Scholar]
- Argatov, I.; Sevostianov, I. Health monitoring of bolted joints via electrical conductivity measurements. Int. J. Eng. Sci. 2010, 48, 874–887. [Google Scholar] [CrossRef]
- Park, S.; Yun, C.B.; Roh, Y. Active sensing-based real-time nondestructive evaluations for steel bridge members. KSCE J. Civ. Eng. 2006, 10, 33–39. [Google Scholar]
- Park, S.; Yun, C.B.; Roh, Y.; Lee, J.J. PZT-based active damage detection techniques for steel bridge components. Smart Mater. Struct. 2006, 15, 957. [Google Scholar] [CrossRef]
- Amerini, F.; Meo, M. Structural health monitoring of bolted joints using linear and nonlinear acoustic/ultrasound methods. Struct. Health Monit. 2011, 10, 659–672. [Google Scholar] [CrossRef]
- Martinez, J.; Sisman, A.; Onen, O.; Velasquez, D.; Guldiken, R. A synthetic phased array surface acoustic wave sensor for quantifying bolt tension. Sensors 2012, 12, 12265–12278. [Google Scholar] [CrossRef]
- Huda, F.; Kajiwara, I.; Hosoya, N.; Kawamura, S. Bolt loosening analysis and diagnosis by non-contact laser excitation vibration tests. Mech. Syst. Signal Process. 2013, 40, 589–604. [Google Scholar] [CrossRef]
- Tao, W.; Shaopeng, L.; Junhua, S.; Yourong, L. Health monitoring of bolted joints using the time reversal method and piezoelectric transducers. Smart Mater. Struct. 2016, 25, 025010. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2017, 27, 015023. [Google Scholar] [CrossRef]
- Huo, L.; Chen, D.; Kong, Q.; Li, H.; Song, G. Smart washer—A piezoceramic-based transducer to monitor looseness of bolted connection. Smart Mater. Struct. 2017, 26, 025033. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Su, Z.; Pan, Y. Continuous monitoring of tightening condition of single-lap bolted composite joints using intrinsic mode functions of acoustic emission signals: A proof-of-concept study. Struct. Health Monit. 2019, 18, 1219–1234. [Google Scholar] [CrossRef]
- Jung, B.H.; Kim, Y.W.; Lee, J.R. Laser-based structural training algorithm for acoustic emission localization and damage accumulation visualization in a bolt joint structure. Struct. Health Monit. 2019, 18, 1851–1861. [Google Scholar] [CrossRef]
- Zhao, N.; Huo, L.; Song, G. A nonlinear ultrasonic method for real-time bolt looseness monitoring using PZT transducer–enabled vibro-acoustic modulation. J. Intell. Mater. Syst. Struct. 2020, 31, 364–376. [Google Scholar] [CrossRef]
- Cha, Y.J.; You, K.; Choi, W. Vision-based detection of loosened bolts using the Hough transform and support vector machines. Autom. Constr. 2016, 71, 181–188. [Google Scholar] [CrossRef]
- Nguyen, T.C.; Huynh, T.C.; Ryu, J.Y.; Park, J.H.; Kim, J.T. Bolt-loosening identification of bolt connections by vision image-based technique. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure 2016; International Society for Optics and Photonics: Washington, DC, USA, 2016; Volume 9804, p. 980413. [Google Scholar]
- Ramana, L.; Choi, W.; Cha, Y.J. Fully automated vision-based loosened bolt detection using the Viola–Jones algorithm. Struct. Health Monit. 2019, 18, 422–434. [Google Scholar] [CrossRef]
- Huynh, T.C.; Park, J.H.; Jung, H.J.; Kim, J.T. Quasi-autonomous bolt-loosening detection method using vision-based deep learning and image processing. Autom. Constr. 2019, 105, 102844. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Loh, K.J.; Su, W.; Xue, Z.; Zhao, X. Autonomous bolt loosening detection using deep learning. Struct. Health Monit. 2020, 19, 105–122. [Google Scholar] [CrossRef]
- Wang, C.; Wang, N.; Ho, S.C.; Chen, X.; Song, G. Design of a New Vision-Based Method for the Bolts Looseness Detection in Flange Connections. IEEE Trans. Ind. Electron. 2020, 67, 1366–1375. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-Driven Structural Health Monitoring and Damage Detection through Deep Learning: State-of-the-Art Review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Büyüköztürk, O. Deep learning-based crack damage detection using convolutional neural networks. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 731–747. [Google Scholar] [CrossRef]
- Wang, T.; Tan, B.; Lu, G.; Liu, B.; Yang, D. Bolt Pretightening Force Measurement Based on Strain Distribution of Bolt Head Surface. J. Aerosp. Eng. 2020, 33, 04020034. [Google Scholar] [CrossRef]
- Drain, L.E. Laser Ultrasonics Techniques and Applications; Routledge: Abington, UK, 2019. [Google Scholar]
- Lee, J.R.; Chia, C.C.; Shin, H.J.; Park, C.Y.; Yoon, D.J. Laser ultrasonic propagation imaging method in the frequency domain based on wavelet transformation. Opt. Lasers Eng. 2011, 49, 167–175. [Google Scholar] [CrossRef]
- Lee, I.; Zhang, A.; Lee, C.; Park, S. A Visualization Method for Corrosion Damage on Aluminum Plates Using an Nd: YAG Pulsed Laser Scanning System. Sensors 2016, 16, 2150. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zhang, A.; Yu, B.; Park, S. Comparison Study between RMS and Edge Detection Image Processing Algorithms for a Pulsed Laser UWPI (Ultrasonic Wave Propagation Imaging)-Based NDT Technique. Sensors 2017, 17, 1224. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Park, S. Flaw imaging technique for plate-like structures using scanning laser source actuation. Shock Vib. 2014, 2014, 725030. [Google Scholar] [CrossRef]
- Lee, C.; Park, S. Damage visualization of pipeline structures using laser-induced ultrasonic waves. Struct. Health Monit. Int. J. 2015, 14, 475–488. [Google Scholar] [CrossRef]
- Lee, C.; Kang, D.; Park, S. Visualization of fatigue cracks at structural members using a pulsed laser scanning system. Res. Nondestruct. Eval. 2015, 26, 123–132. [Google Scholar] [CrossRef]
- Liu, P.; Nazirah, A.W.; Sohn, H. Numerical simulation of damage detection using laser-generated ultrasound. Ultrasonics 2016, 69, 248–258. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.C.; Lee, J.R. Thickness reconstruction of nuclear power plant pipes with flow-accelerated corrosion damage using laser ultrasonic wavenumber imaging. Struct. Health Monit. 2018, 17, 255–265. [Google Scholar] [CrossRef]
- An, Y.K.; Park, B.; Sohn, H. Complete noncontact laser ultrasonic imaging for automated crack visualization in a plate. Smart Mater. Struct. 2013, 22, 025022. [Google Scholar] [CrossRef]
- Keshmiri Esfandabadi, Y.; Bilodeau, M.; Masson, P.; De Marchi, L. Deep learning for enhancing wavefield image quality in fast non-contact inspections. Struct. Health Monit. 2019. [Google Scholar] [CrossRef]
- Michaels, J.E. Ultrasonic wavefield imaging: Research tool or emerging NDE method? In AIP Conference Proceedings; AIP Publishing: Park City, MD, USA, 2017; Volume 1806, p. 020001. [Google Scholar]
- Haynes, C.; Yeager, M.; Todd, M.; Lee, J.R. Monitoring bolt torque levels through signal processing of full-field ultrasonic data. In Health Monitoring of Structural and Biological Systems 2014; International Society for Optics and Photonics: Washington, DC, USA, 2014; Volume 9064, p. 906428. [Google Scholar]
- Gooda Sahib, M.I.; Leong, S.J.; Chia, C.C.; Mustapha, F. Detection of fastener loosening in simple lap joint based on ultrasonic wavefield imaging. Mater. Sci. Eng. Conf. Ser. 2017, 270, 012035. [Google Scholar] [CrossRef]
- Tola, K.; Lee, C.; Park, J.; Kim, J.W.; Park, S. Bolt Looseness Detection Based on Ultrasonic Wavefield Energy Analysis Using an Nd:YAG Pulsed Laser Scanning System. Struct. Control Health Monit. 2020, 27, e2590. [Google Scholar] [CrossRef]
- An, Y.K.; Song, H.; Sohn, H. Wireless ultrasonic wavefield imaging via laser for hidden damage detection inside a steel box girder bridge. Smart Mater. Struct. 2014, 23, 095019. [Google Scholar] [CrossRef]
- Ye, J.; Ito, S.; Toyama, N. Computerized Ultrasonic Imaging Inspection: From Shallow to Deep Learning. Sensors 2018, 18, 3820. [Google Scholar] [CrossRef]
- Yang, J.; Chang, F.K. Detection of bolt loosening in C–C composite thermal protection panels: I. Diagnostic principle. Smart Mater. Struct. 2006, 15, 581. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]
- Margetan, F.J.; Thompson, R.B.; Rose, J.H.; Gray, T.A. The interaction of ultrasound with imperfect interfaces: Experimental studies of model structures. J. Nondestruct. Eval. 1992, 11, 109–126. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Hefets, M.; Rosen, M. An ultrasonic interface-wave method for predicting the strength of adhesive bonds. J. Appl. Phys. 1981, 52, 2847–2851. [Google Scholar] [CrossRef]
- Nikravesh, S.M.Y.; Goudarzi, M. A Review Paper on Looseness Detection Methods in Bolted Structures. Lat. Am. J. Solids Struct. 2017, 14, 2153–2176. [Google Scholar] [CrossRef]
- Hayward, G.; Hyslop, J. Determination of lamb wave dispersion data in lossy anisotropic plates using time domain finite element analysis. Part I: Theory and experimental verification. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 443–448. [Google Scholar] [CrossRef]
- White, R.M. Generation of elastic waves by transient surface heating. J. Appl. Phys. 1963, 34, 3559–3567. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Technical Report; Los Alamos National Laboratory: Los Alamos, NM, USA, 1996. [Google Scholar]
- Ostachowicz, W.; Radzieński, M.; Kudela, P. 50th anniversary article: Comparison studies of full wavefield signal processing for crack detection. Strain 2014, 50, 275–291. [Google Scholar] [CrossRef]
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W. Damage visualization enhancement by the wave field filtering and processing. In Nondestructive Characterization for Composite Materials, Aerospace Engineering, Civil Infrastructure, and Homeland Security 2012; International Society for Optics and Photonics: Washington, DC, USA, 2012; Volume 8347, p. 83471H. [Google Scholar]
- Kudela, P.; Radzieński, M.; Ostachowicz, W. Identification of cracks in thin-walled structures by means of wavenumber filtering. Mech. Syst. Signal Process. 2015, 50, 456–466. [Google Scholar] [CrossRef]
- Radzieński, M.; Kudela, P.; Ostachowicz, W.; Bolimowski, P.; Kozera, R.; Boczkowska, A. Lamb-Wave-Based Method in the Evaluation of Self-Healing Efficiency. Appl. Sci. 2020, 10, 2585. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io/ (accessed on 14 September 2020).

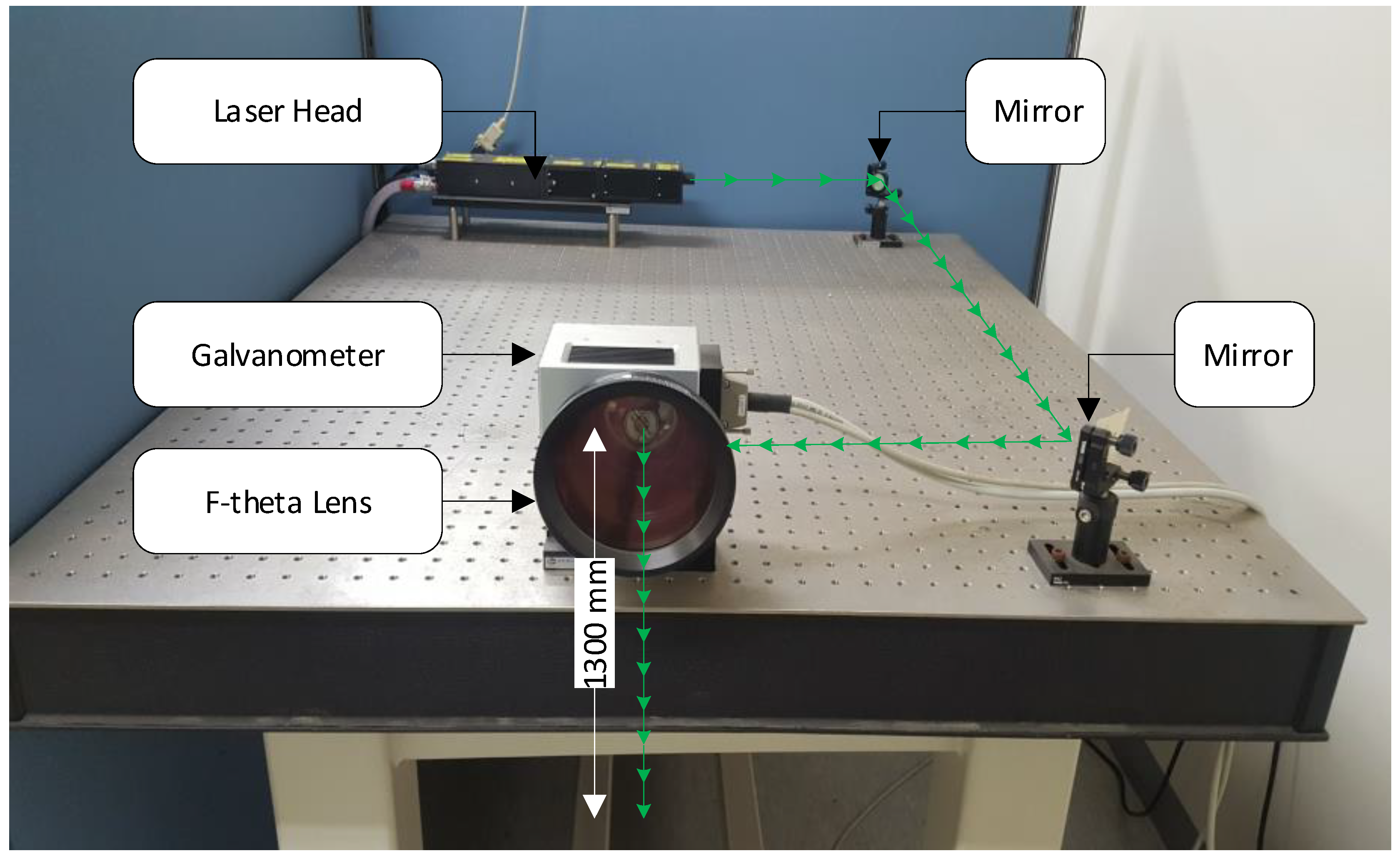


| Laser Head | Galvanometer |
|---|---|
| Wavelength: 532 nm | Wavelength: 532 nm |
| Maximum laser energy per pulse: 55 mJ | Tracking error: 0.16 ms |
| Pulse repetition rate: 20 Hz | Positioning speed: 10 m/s |
| Pulse duration: 6.5 ns | Max. angular velocity: 100 rad/s |
| Beam diameter: 3 mm |
| Tested Bolt | Torque Values (Nm) |
|---|---|
| 1, 2 | 5, 10, 15, 20, 25 |
| 3 | 3, 6, 9, 12, 15, 18, 21, 24 |
| 4 | 4, 7, 10, 13, 16, 19, 22, 25 |
| 5 | 5, 8, 11, 14, 17, 20, 23 |
| D1 | D2 | D4 | ||||
|---|---|---|---|---|---|---|
| MAE | R2 | MAE | R2 | MAE | R2 | |
| Bolt 3 | 3.51 | 0.58 | 3.16 | 0.67 | 3.48 | 0.7 |
| Bolt 4 | 4.23 | 0.42 | 3.23 | 0.63 | 3.56 | 0.62 |
| Bolt 5 | 3.06 | 0.44 | 4.29 | 0.22 | 1.55 | 0.91 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, D.Q.; Kim, J.-W.; Tola, K.D.; Kim, W.; Park, S. Artificial Intelligence-Based Bolt Loosening Diagnosis Using Deep Learning Algorithms for Laser Ultrasonic Wave Propagation Data. Sensors 2020, 20, 5329. https://doi.org/10.3390/s20185329
Tran DQ, Kim J-W, Tola KD, Kim W, Park S. Artificial Intelligence-Based Bolt Loosening Diagnosis Using Deep Learning Algorithms for Laser Ultrasonic Wave Propagation Data. Sensors. 2020; 20(18):5329. https://doi.org/10.3390/s20185329
Chicago/Turabian StyleTran, Dai Quoc, Ju-Won Kim, Kassahun Demissie Tola, Wonkyu Kim, and Seunghee Park. 2020. "Artificial Intelligence-Based Bolt Loosening Diagnosis Using Deep Learning Algorithms for Laser Ultrasonic Wave Propagation Data" Sensors 20, no. 18: 5329. https://doi.org/10.3390/s20185329
APA StyleTran, D. Q., Kim, J.-W., Tola, K. D., Kim, W., & Park, S. (2020). Artificial Intelligence-Based Bolt Loosening Diagnosis Using Deep Learning Algorithms for Laser Ultrasonic Wave Propagation Data. Sensors, 20(18), 5329. https://doi.org/10.3390/s20185329






