Braided Fabrication of a Fiber Bragg Grating Sensor
Abstract
1. Introduction
1.1. Measurement Method of Bragg Grating Sensor
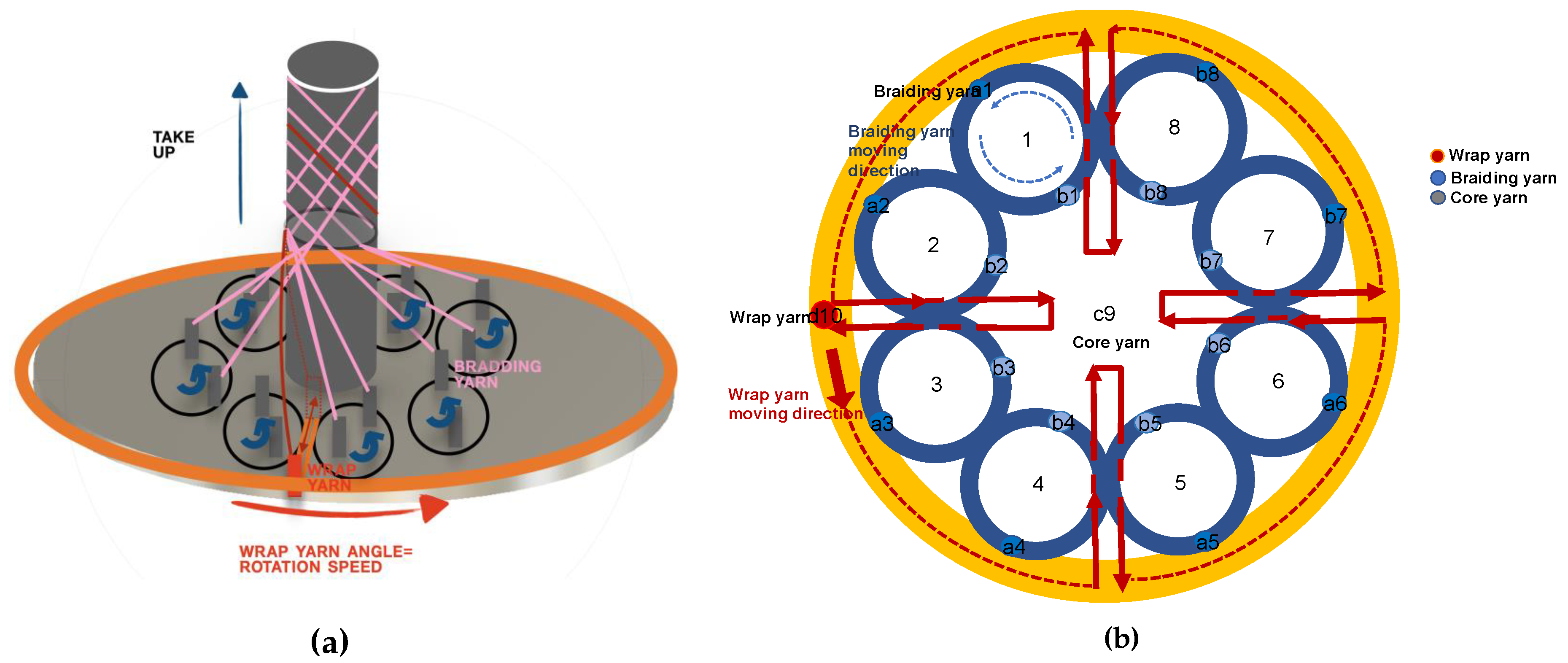
1.2. Braiding Mechanical Structure
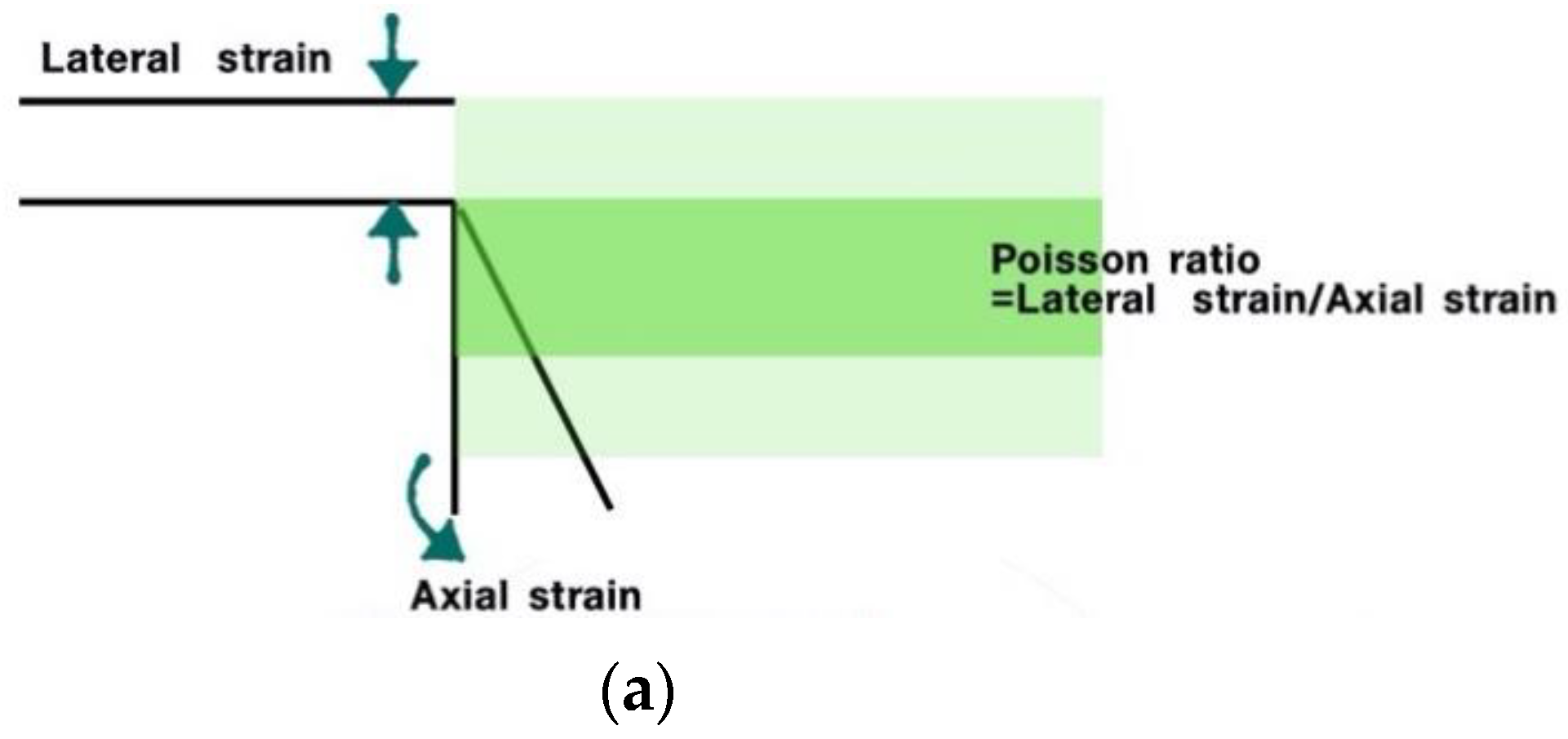
Negative Poisson’s Ratio
2. Materials and Methods
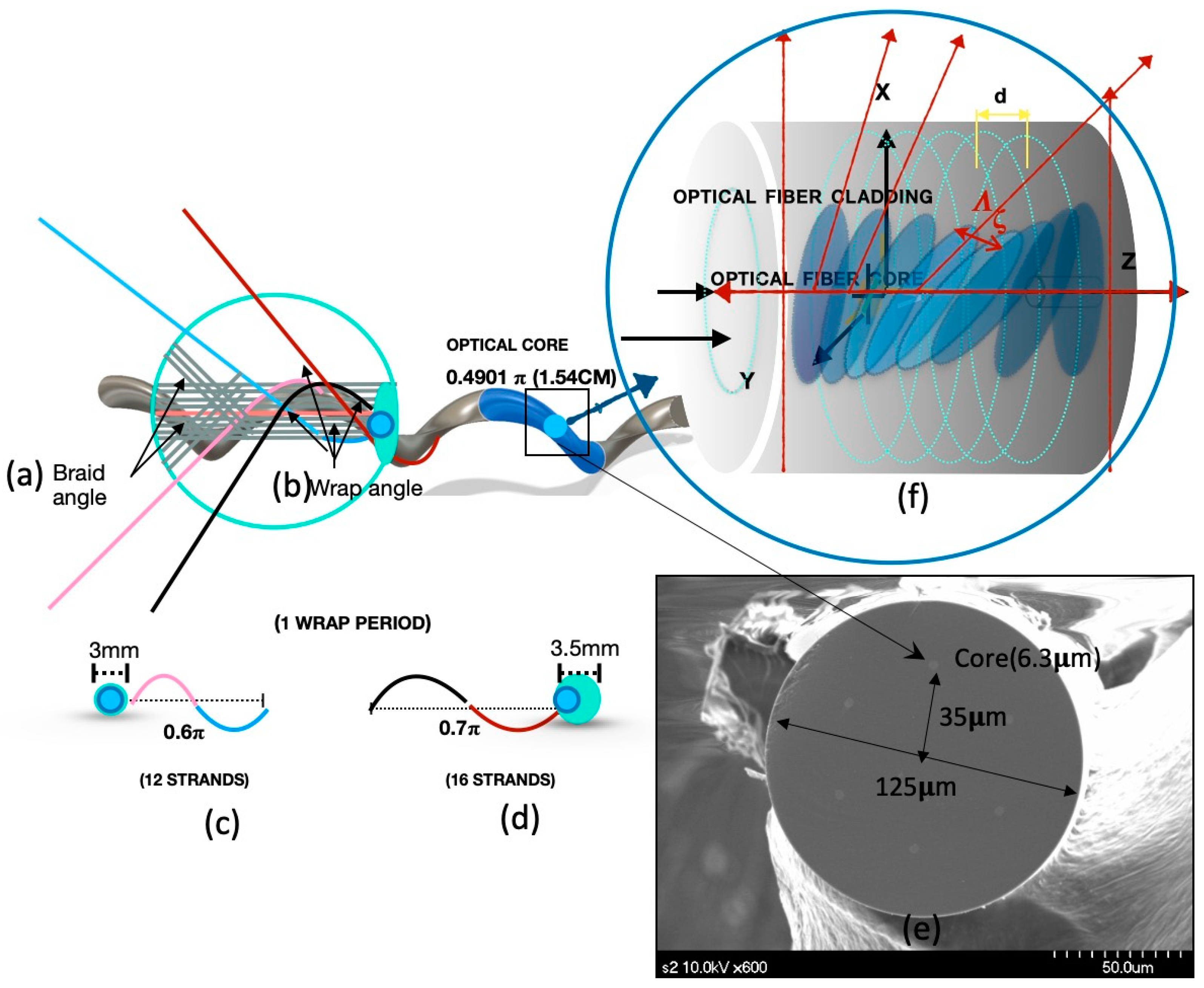
2.1. Design of the Braided Sensor
2.2. Methodology
2.3. Experiment
2.3.1. Prototype
Bragg Grating Sensor Process
Braiding Process
2.3.2. Prototypes A, B, C
2.3.3. Subject
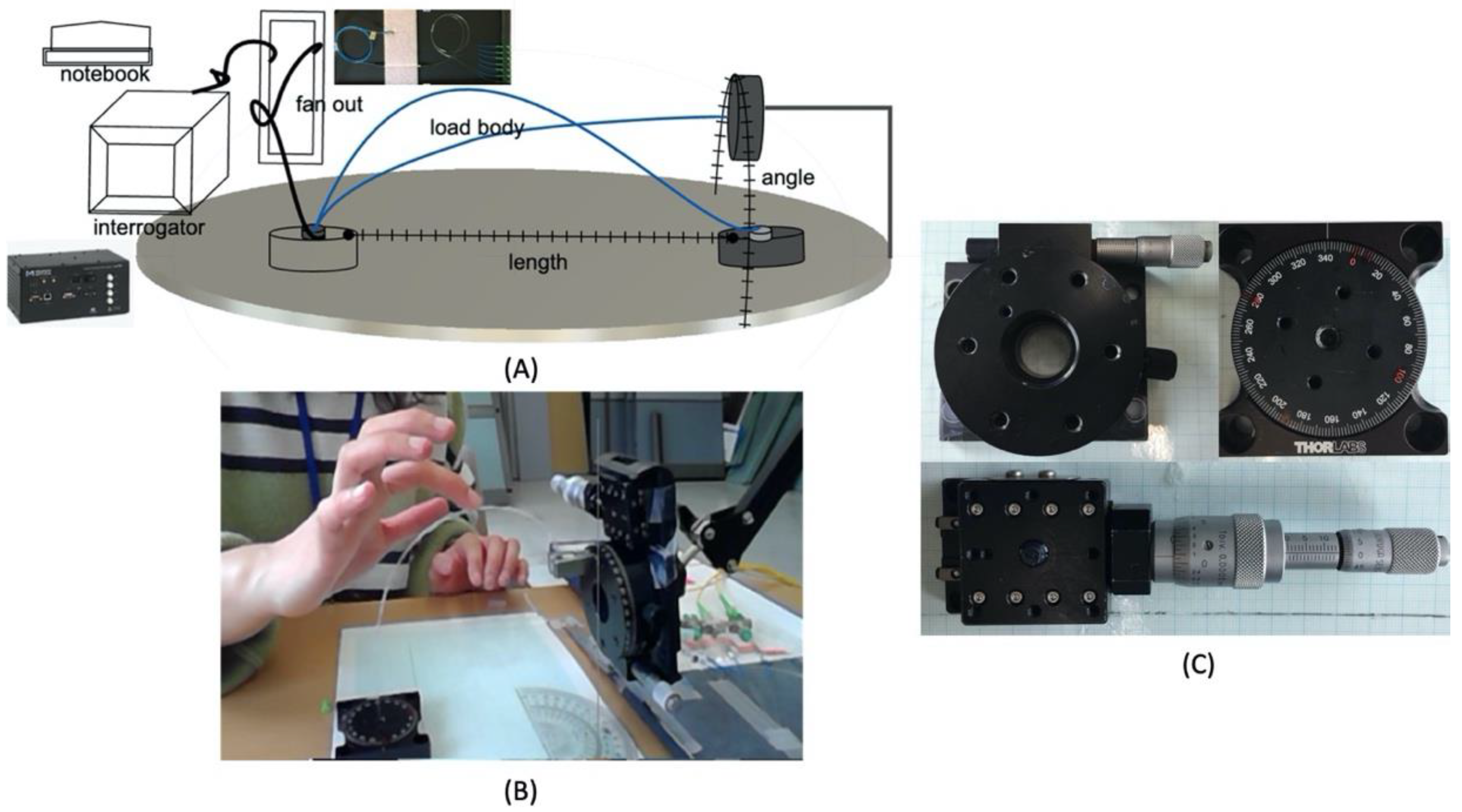
2.3.4. Experimental Device and Tools
2.3.5. Protocol
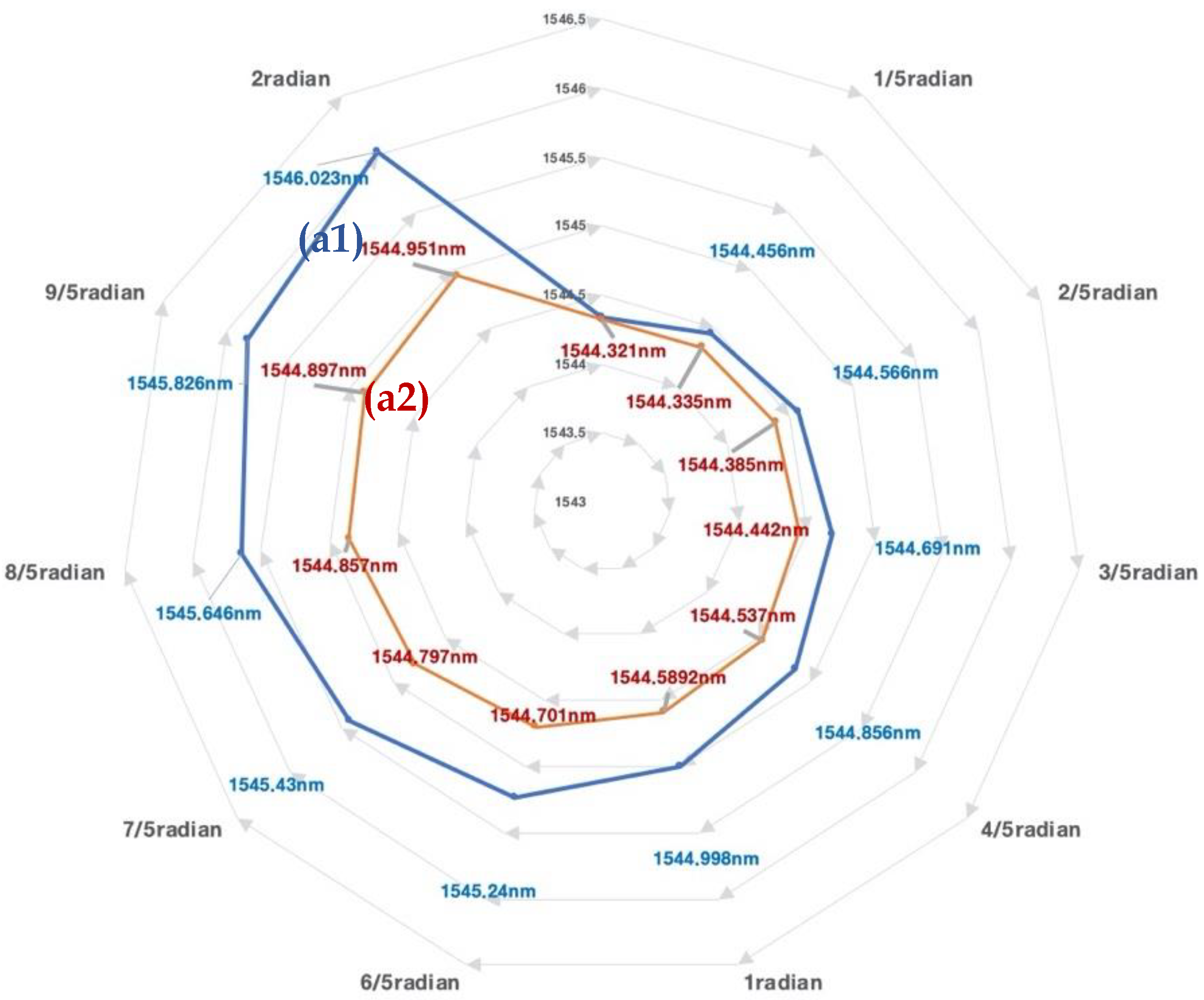
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Correlation | Deleted Variable | Standardized Cronbach’s α | Difference | Correlation with Total |
|---|---|---|---|---|
| Standardized Cronbach’s α | 1546.497 1546.509 1546.496 1546.499 1546.507 1546.505 | 0.847 0.863 0.884 0.904 0.842 0.840 | −0.038 −0.022 −0.001 0.019 −0.043 −0.045 | 0.8023 0.7065 0.5766 0.4457 0.8337 0.8433 |
| 0.885 | ||||
| Correlation | Pair | Kendall’s tau | 95% | CI |
| 1546.497, 1546.509 1546.497, 1546.496 1546.497, 1546.499 1546.497, 1546.507 1546.497, 1546.505 1546.509, 1546.496 1546.509, 1546.499 1546.509, 1546.507 1546.509, 1546.505 1546.496, 1546.499 1546.496, 1546.507 1546.496, 1546.505 1546.499, 1546.507 1546.499, 1546.505 1546.507, 1546.505 | 0.645 0.678 0.381 0.803 0.652 0.435 0.539 0.739 0.622 0.501 0.589 0.492 0.410 0.488 0.711 | 0.481 0.507 0.167 0.699 0.531 0.206 0.368 0.597 0.494 0.325 0.394 0.320 0.205 0.320 0.606 | 0.809 0.849 0.594 0.772 0.665 0.709 0.881 0.750 0.677 0.785 0.665 0.615 0.655 0.817 | |
| Variable | Mean | SD | Minimum | Median |
| 1546.497 1546.509 1546.496 1546.499 1546.507 1546.505 - 1546.497 1546.509 1546.496 1546.499 1546.507 1546.505 | 1546.5837 1546.5791 1546.5804 1546.5744 1546.5693 1546.5838 1546.497 0.001692 8.484 × 10−4 0.001105 4.466 × 10−4 0.001017 9.849 × 10−4 | 1546.522 1546.526 1546.499 1546.524 1546.519 1546.541 1546.496 0.001105 5.603 × 10−4 0.001966 5.545 × 10−4 6.880 × 10−4 6.323 × 10−4 | 1546.522 1546.526 1546.499 1546.524 1546.519 1546.541 1546.496 0.001105 5.603 × 10−4 0.001966 5.545 × 10−4 6.880 × 10−4 6.323 × 10−4 | 1546.5890 1546.5850 1546.5920 1546.5675 1546.5740 1546.5865 1546.499 4.466 × 10−4 4.338 × 10−4 5.545 × 10−4 7.592 × 10−4 2.490 × 10−4 2.638 × 10−4 |
References
- Li, Z.; Liu, S.; Bai, Z.; Fu, C.; Zhang, Y.; Sun, Z.; Liu, X.; Wang, Y. Residual-stress-induced helical long period fiber gratings for sensing applications. Opt. Express 2018, 26, 24114–24123. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Chen, X.; Oladipo, A.O.; Panoiu, N.C.; Ye, F. Generation of Subwavelength Plasmonic Nanovortices via Helically Corrugated Metallic Nanowires. Sci. Rep. 2015, 5, 13089. [Google Scholar] [CrossRef] [PubMed]
- McCoy, C.A.; Gregor, M.C.; Polsin, D.N.; Fratanduono, D.E.; Celliers, P.M.; Boehly, T.R.; Meyerhofer, D.D. Shock-wave equation-of-state measurements in fused silica up to 1600 GPa. J. Appl. Phys. 2016, 119, 215901. [Google Scholar] [CrossRef]
- Durana, G.; Kirchhof, M.; Luber, M.; de Ocariz, I.S.Á.; Poisel, H.; Zubia, J.; Vazquez, C. Use of a Novel Fiber Optical Strain Sensor for Monitoring the Vertical Deflection of an Aircraft Flap. IEEE Sens. J. 2009, 9, 1219–1225. [Google Scholar] [CrossRef]
- Chen, X.; Du, F.; Guo, T.; Lao, J.; Zhang, X.; Zhang, Z.; Liu, F.; Li, J.; Chen, C.; Guan, B.-O. Liquid Crystal-Embedded Tilted Fiber Grating Electric Field Intensity Sensor. J. Lightwave Technol. 2017, 35, 3347–3353. [Google Scholar] [CrossRef]
- Kim, D.-H.; Feng, M.Q. Real-Time Structural Health Monitoring Using a Novel Fiber-Optic Accelerometer System. IEEE Sens. J. 2007, 7, 536–543. [Google Scholar] [CrossRef]
- Choudhury, D.; Macdonald, J.R.; Kar, A.K. Ultrafast laser inscription: Perspectives on future integrated applications. Laser Photonics Rev. 2014, 8, 827–846. [Google Scholar] [CrossRef]
- Alemohammad, H.; Toyserkani, E.; Pinkerton, A.J. Femtosecond laser micromachining of fiber Bragg gratings for simultaneous measurement of temperature and concentration of liquids. J. Phys. D Appl. Phys. 2008, 41, 185101. [Google Scholar] [CrossRef]
- Bilisik, K.; Sahbaz, N. Structure-unit cell-based approach on three-dimensional representative braided preforms from four-step braiding: Experimental determination of effects of structure-process parameters on predetermined yarn path. Text. Res. J. 2012, 82, 220–241. [Google Scholar] [CrossRef]
- Rana, S.; Zdraveva, E.; Pereira, C.; Fangueiro, R.; Correia, A.G. Development of hybrid braided composite rods for reinforcement and health monitoring of structures. Sci. World J. 2014, 2014, 170187. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Z.; Hu, X.; Su, L.; Sun, Y. Modeling and analysis of friction in end-face/inner-face circular braiding processes. J. Text. Inst. 2018, 109, 1400–1408. [Google Scholar] [CrossRef]
- Ahmadi, M.S.; Johari, M.S.; Sadighi, M.; Esfandeh, M. An experimental study on mechanical properties of GFRP braid-pultruded composite rods. Express Polym. Lett. 2009, 3, 560–568. [Google Scholar] [CrossRef]
- Czichos, R.; Bareiro, O.; Pickett, A.K.; Middendorf, P.; Gries, T. Experimental and numerical studies of process variabilities in biaxial carbon fiber braids. Int. J. Mater. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Zou, Q.; Xue, W.; Lin, J.; Fu, Y.; Guan, G.; Wang, F.; Wang, L. Mechanical characteristics of novel polyester/NiTi wires braided composite stent for the medical application. Results Phys. 2016, 6, 440–446. [Google Scholar] [CrossRef]
- Rawal, A.; Saraswat, H.; Sibal, A. Tensile response of braided structures: A review. Text. Res. J. 2015, 85, 2083–2096. [Google Scholar] [CrossRef]
- Fang, G.; Liang, J.; Wang, B.; Wang, Y. Effect of Interface Properties on Mechanical Behavior of 3D Four-Directional Braided Composites with Large Braid Angle Subjected to Uniaxial Tension. Appl. Compos. Mater. 2011, 18, 449–465. [Google Scholar] [CrossRef]
- Rawal, A.; Gupta, S.; Saraswat, H.; Sibal, A. Geometrical modeling of near-net shape braided preforms. Text. Res. J. 2015, 85, 1055–1064. [Google Scholar] [CrossRef]
- Soh, D.B.S.; Nilsson, J.; Sahu, J.K.; Cooper, L.J. Geometrical factor modification of helical-core fiber radiation loss formula. Opt. Commun. 2003, 222, 235–242. [Google Scholar] [CrossRef]
- Tchen, T. The Bragg law modified for X-ray diffraction from a bent crystal in the backscattering mode. Tech. Phys. Lett. 2003, 29, 235–236. [Google Scholar] [CrossRef]
- Tiwari, U.; Mishra, V.; Bhalla, A.; Singh, N.; Jain, S.C.; Garg, H.; Kapur, P. Fiber Bragg grating sensor for measurement of impact absorption capability of mouthguards. Dent. Traumatol. 2011, 27, 263–268. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, Q.; Wang, C.; Sun, Z.; Mou, C.; Zhou, K.; Zhang, L. Refractive index and temperature sensitivity characterization of excessively tilted fiber grating. Opt. Express 2017, 25, 3336–3346. [Google Scholar] [CrossRef] [PubMed]
- Guyader, G.; Gabor, A.; Hamelin, P. Analysis of 2D and 3D circular braiding processes: Modeling the interaction between the process parameters and the pre-form architecture. Mech. Mach. Theory 2013, 69, 90–104. [Google Scholar] [CrossRef]
- Jiang, N.; Hu, H. Auxetic Yarn Made with Circular Braiding Technology. Phys. Status Solidi 2019, 256, 1800168. [Google Scholar] [CrossRef]
- Subramani, P.; Rana, S.; Ghiassi, B.; Fangueiro, R.; Oliveira, D.V.; Lourenco, P.B.; Xavier, J. Development and characterization of novel auxetic structures based on re-entrant hexagon design produced from braided composites. Compos. Part B Eng. 2016, 93, 132–142. [Google Scholar] [CrossRef]
- David, B.P.; David, B.; Royall, B. New Directions in Braiding. J. Eng. Fibers Fabr. 2013, 8, 11–12. [Google Scholar]
- McAfee, J.; Faisal, N.H. Parametric sensitivity analysis to maximise auxetic effect of polymeric fibre based helical yarn. Compos. Struct. 2017, 162, 1–12. [Google Scholar] [CrossRef]
- Sry, V.; Mizutani, Y.; Endo, G.; Suzuki, Y.; Todoroki, A. Estimation of the Longitudinal Elasticity Modulus of Braided Synthetic Fiber Rope Utilizing Classical Laminate Theory with the Unit N/tex. Appl. Sci. 2018, 8, 1096. [Google Scholar] [CrossRef]
- Rawal, A.; Kumar, R.; Saraswat, H. Tensile mechanics of braided sutures. Text. Res. J. 2012, 82, 1703–1710. [Google Scholar] [CrossRef]



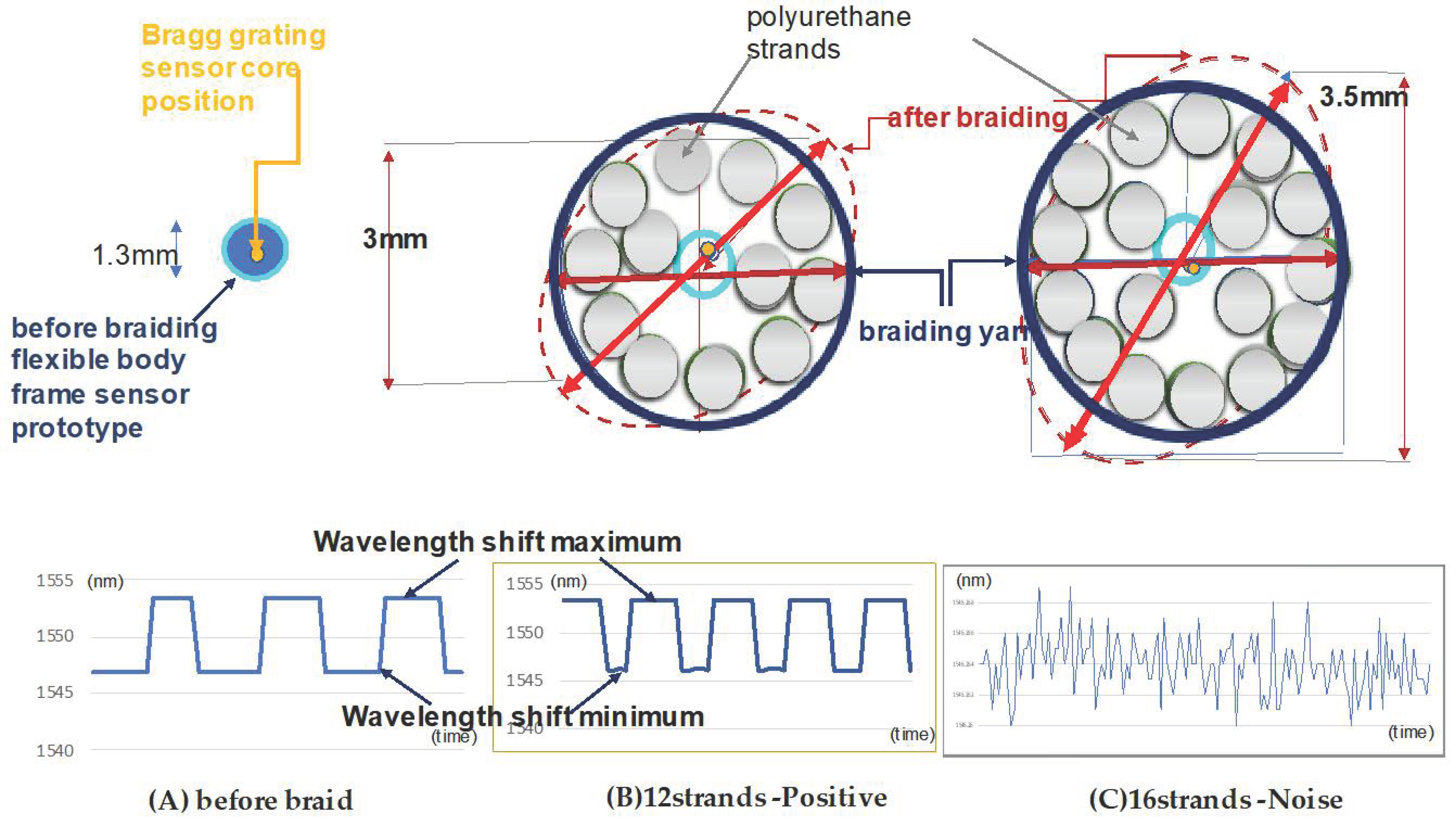

| Types | Prototype A | Prototype B | Prototype C | |
|---|---|---|---|---|
| Parameter | ||||
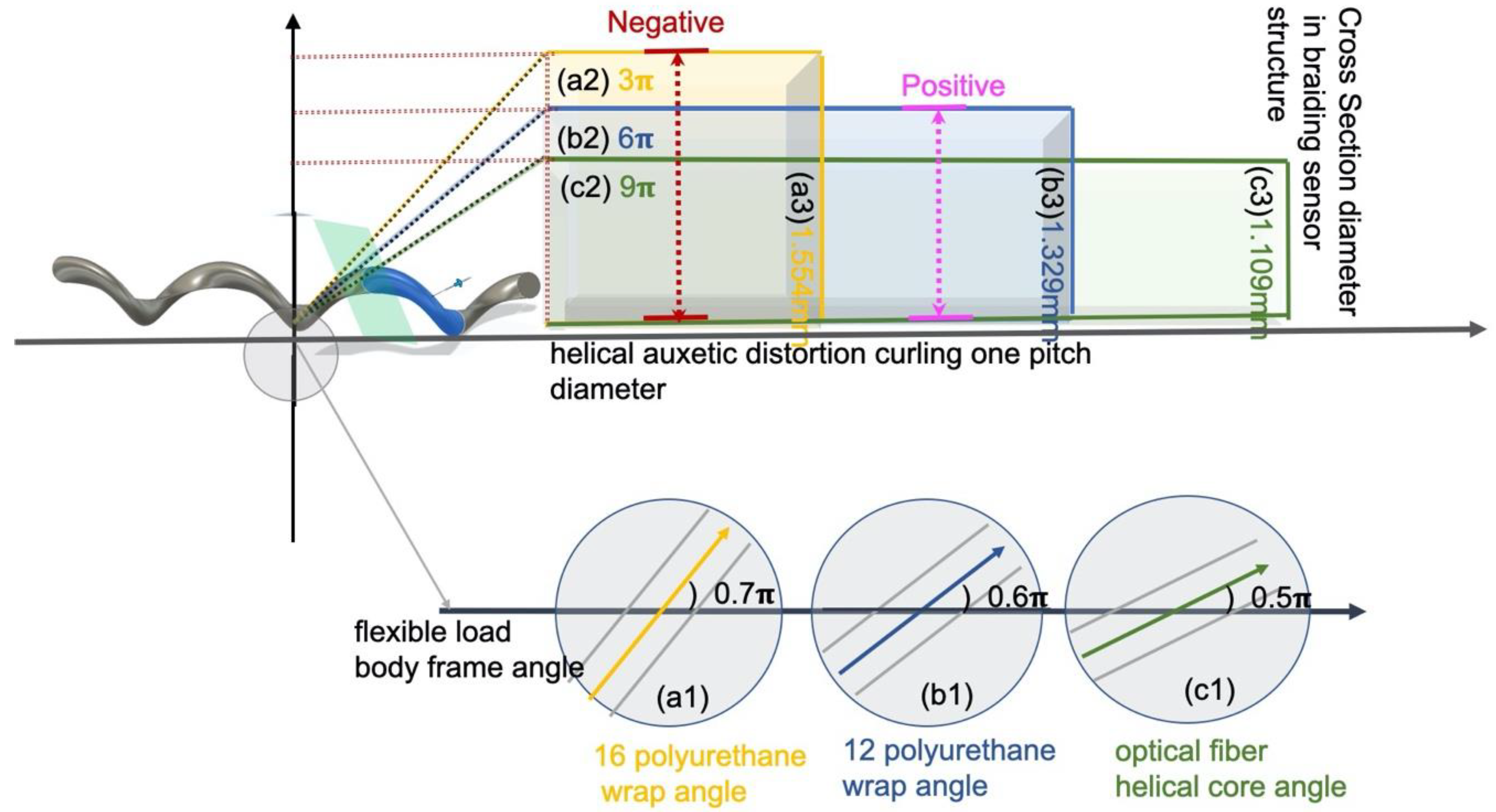
| Sensor fabrication conditions | flexible rod-body frame | 12 strands | 16 strands | |
| Cross-section diameter (cm) | 0.2 | 0.3 | 0.35 | |
| Initial braid angle (degree) | No | 45 | 45 | |
| Number of polyurethane strands (number) | No | 12 | 16 | |
| Braided sensor body curling diameter (cm) | 9 | 6 | 3 | |
| Prototype photos | ||||
 | ||||
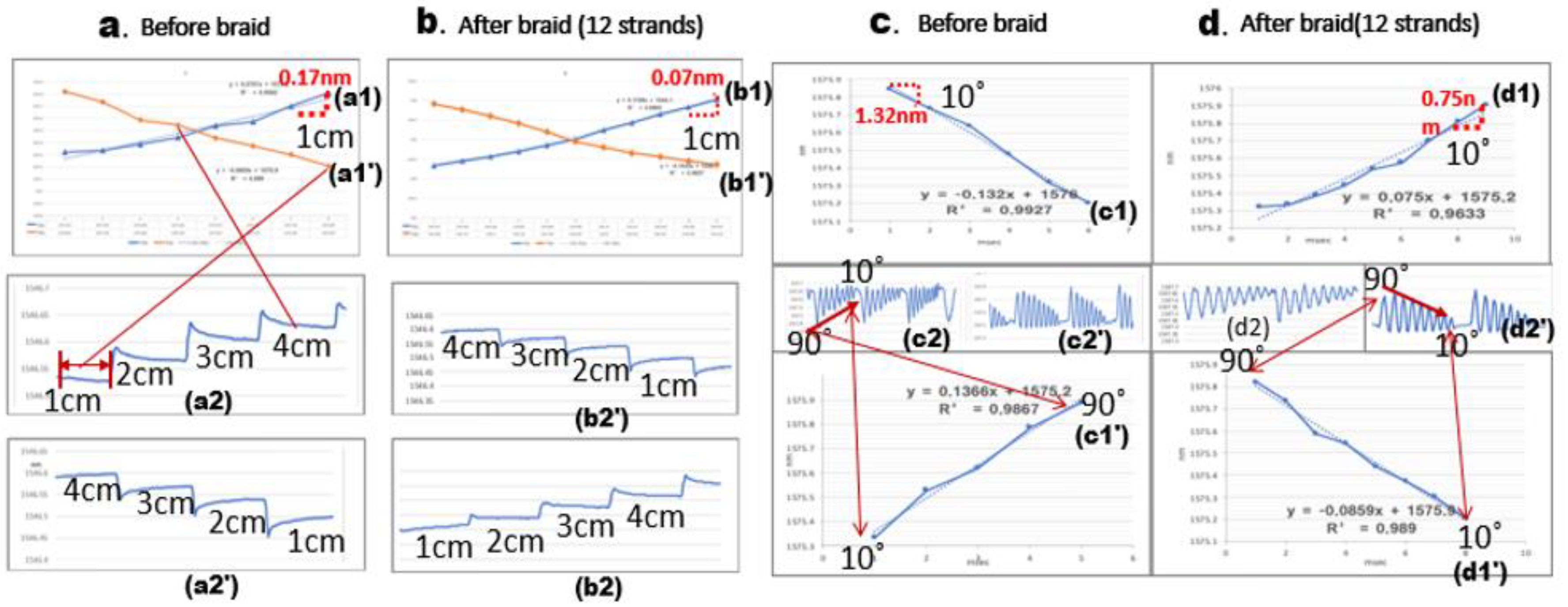
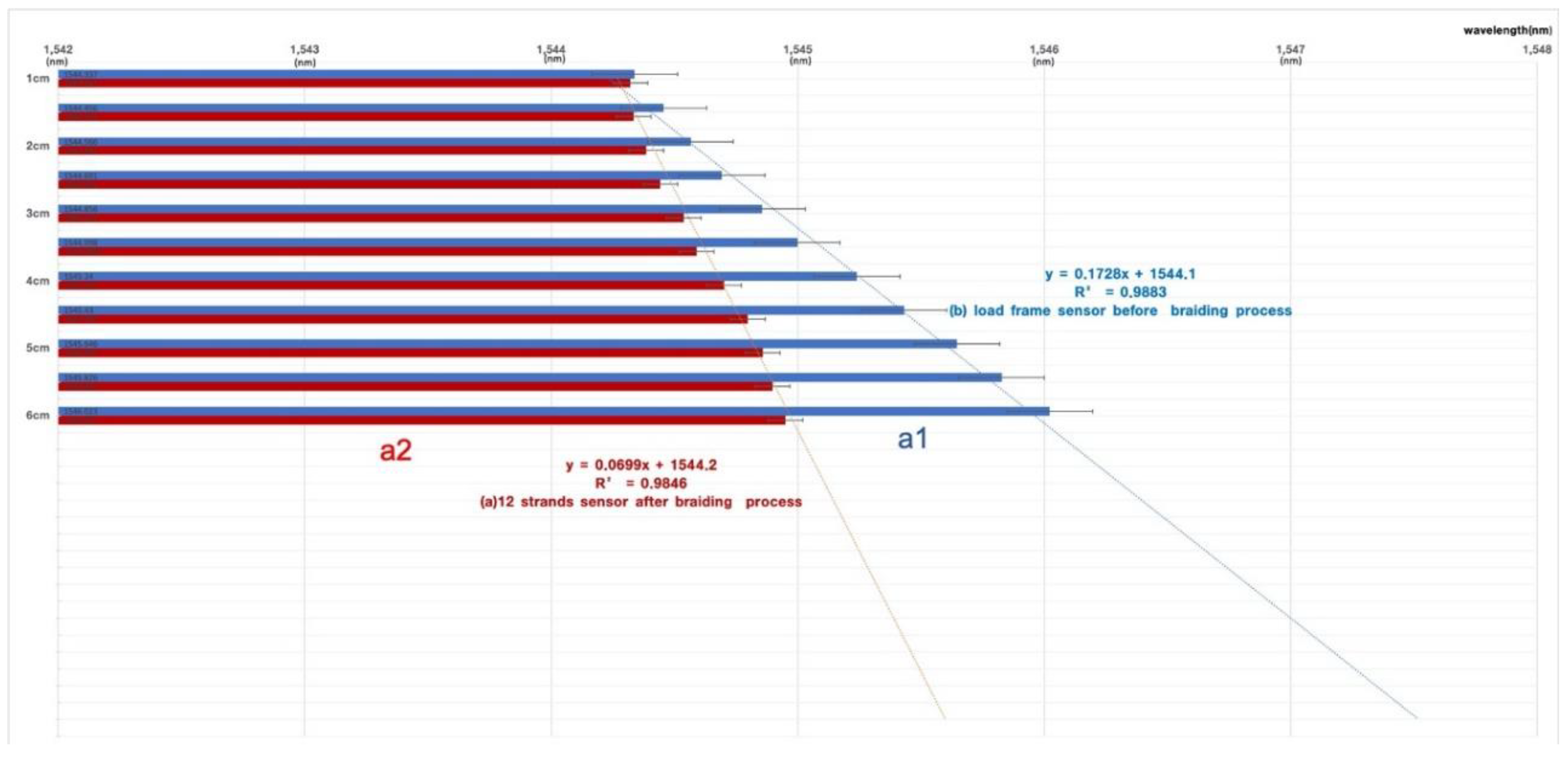
| Subject | Length (Wavelength Shift/1 cm) | |||||
|---|---|---|---|---|---|---|
| Prototype | ||||||
| flexible frame | 1 cm 6 cm | 2 cm 7 cm | 3 cm 8 cm | 4 cm 9 cm | 5 cm 10 cm | |
| 1547.337 nm 1547.563 nm | 1547.409 nm 1547.568 nm | 1547.44 nm 1547.594 nm | 1547.519 nm 1547.619 nm | 1547.53 nm 1547.63 nm | ||
| y = 0.172x + 1575.2 R2 = 0.9562 (1st, 2nd, 3rd mean) | ||||||
| Standardized Cronbach’s α 0.894 (3rd) (α ≧ 0.9 (excellent), 0.8 ≦ α ≦ 0.9 (good), 0.7 ≦ α ≦ 0.8 (acceptable)) | ||||||
| 12-strand braid | 1575.321 nm 1575.63 nm | 1575.392 nm 1575.71 nm | 1575.465 nm 1575.79 nm | 1575.52 nm 1575.86 nm | 1575.355 nm 1575.948 nm | |
| y = 0.0701x + 1575.2 R2 = 0.9562 (1st, 2nd, 3rd mean) | ||||||
| Standardized Cronbach’s α 0.861 (3rd) (α ≧ 0.9 (excellent), 0.8 ≦ α ≦ 0.9 (good), 0.7 ≦ α ≦ 0.8 (acceptable)) | ||||||
| 16-strand braid | NO | |||||
| angle (wavelength shift/1°) | ||||||
| flexible frame | 0° 50° | 10° 60° | 20° 70° | 30° 80° | 40° 90° | |
| 1547.7 nm 1547.561 nm | 1547.671 nm 1547.538 nm | 1547.611 nm 1547.527 nm | 1547.597 nm 1547.496 nm | 1547.571 nm 1547.458 nm | ||
| y = 0.134x + 1547.4 R2 = 0.9827 (1st, 2nd, 3rd mean) | ||||||
| Standardized Cronbach’s α 0.885 (3rd) α ≧ 0.9 (excellent), 0.8 ≦ α ≦ 0.9 (good), 0.7 ≦ α ≦ 0.8 (acceptable), 0.6 ≦ α ≦0.7 (questionable), 0.5 ≦ α ≦ 0.6 (poor), α ≦ 0.5 (unacceptable) | ||||||
| 12-strand braid | 1547.453 nm 1547.568 nm | 1547.467 nm 1547.594 nm | 1547.493 nm 1547.612 nm | 1547.512 nm 1547.63 nm | 1547.563 nm 1547.451 nm | |
| y = 0.0233x + 1547.4 R2 = 0.9827 (1st, 2nd, 3rd mean) | ||||||
| Standardized Cronbach’s alpha. 0.884 (3rd) α ≧ 0.9 (excellent), 0.8 ≦ α ≦ 0.9 (good), 0.7 ≦ α ≦ 0.8 (acceptable), 0.6 ≦ α ≦ 0.7 (questionable), 0.5 ≦ α ≦ 0.6 (poor), α ≦ 0.5 (unacceptable) | ||||||
| 16-strand braid | NO | |||||
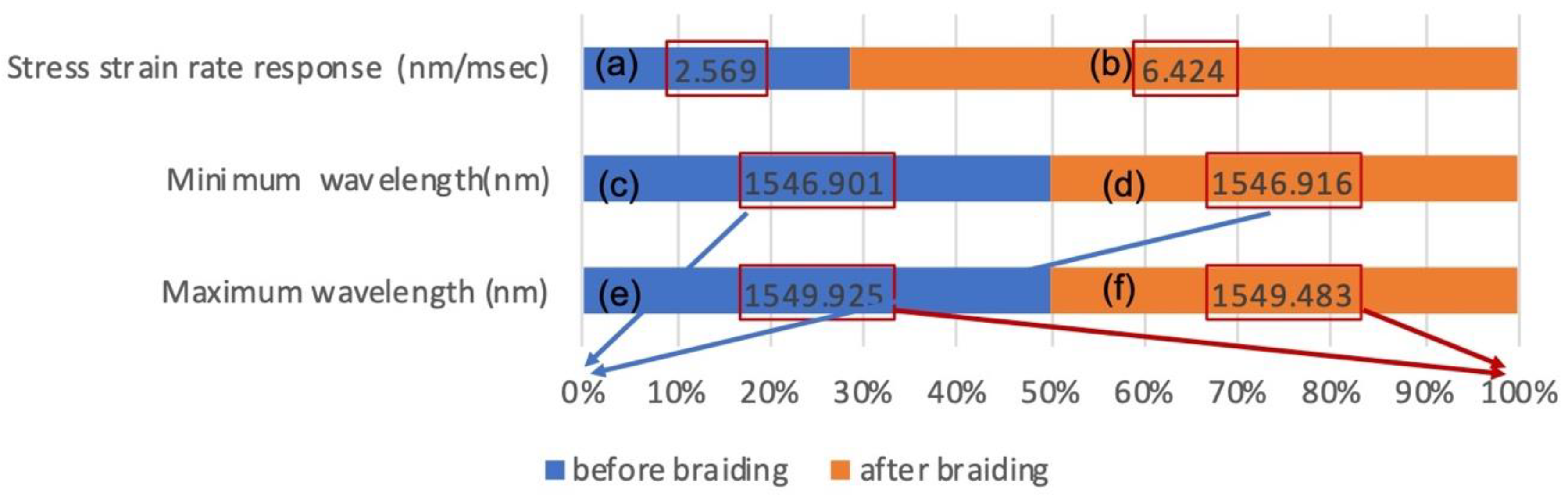
| maximum and minimum values of the stress–strain response | ||||||
| flexible frame | 0° 1546.901 nm | 90° 1549.925 nm | y = −3.567x + 1554.1 R2 = 1 (1st, 2nd, 3rd mean) | |||
| 12-strand braid | 1546.916 nm | 1549.483 nm | y = −6.424x + 1559.7 R2 = 1 (1st, 2nd, 3rd mean) | |||
| 16-strand braid | NO | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Lee, J. Braided Fabrication of a Fiber Bragg Grating Sensor. Sensors 2020, 20, 5246. https://doi.org/10.3390/s20185246
Lee S, Lee J. Braided Fabrication of a Fiber Bragg Grating Sensor. Sensors. 2020; 20(18):5246. https://doi.org/10.3390/s20185246
Chicago/Turabian StyleLee, Songbi, and Joohyeon Lee. 2020. "Braided Fabrication of a Fiber Bragg Grating Sensor" Sensors 20, no. 18: 5246. https://doi.org/10.3390/s20185246
APA StyleLee, S., & Lee, J. (2020). Braided Fabrication of a Fiber Bragg Grating Sensor. Sensors, 20(18), 5246. https://doi.org/10.3390/s20185246





