Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement
Abstract
1. Introduction
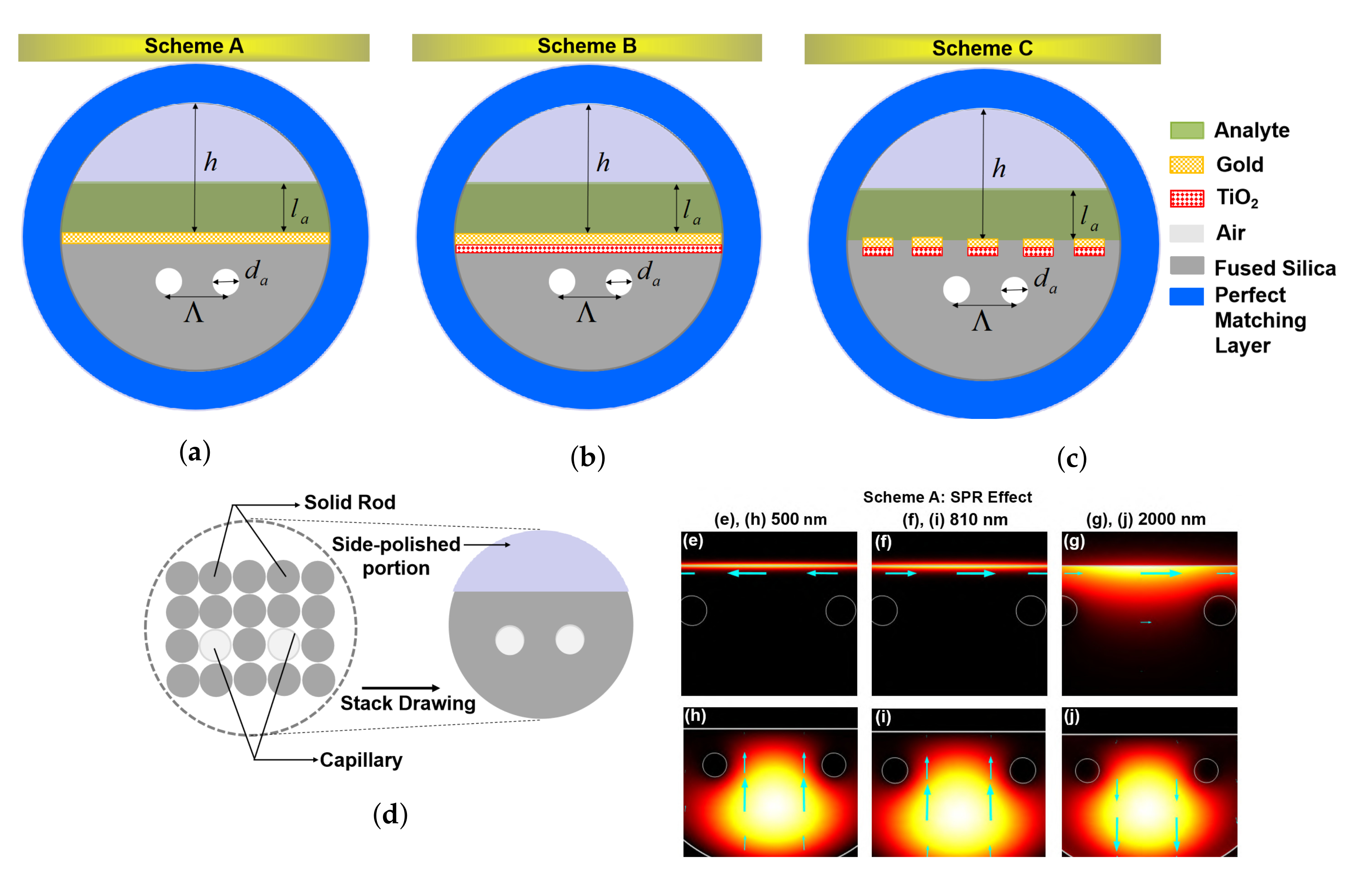
2. Sensor Design and Principles
2.1. D-Type Twin-Hole PCF-RIBS Microbiosensor
2.2. COMSOL 2D Modeling
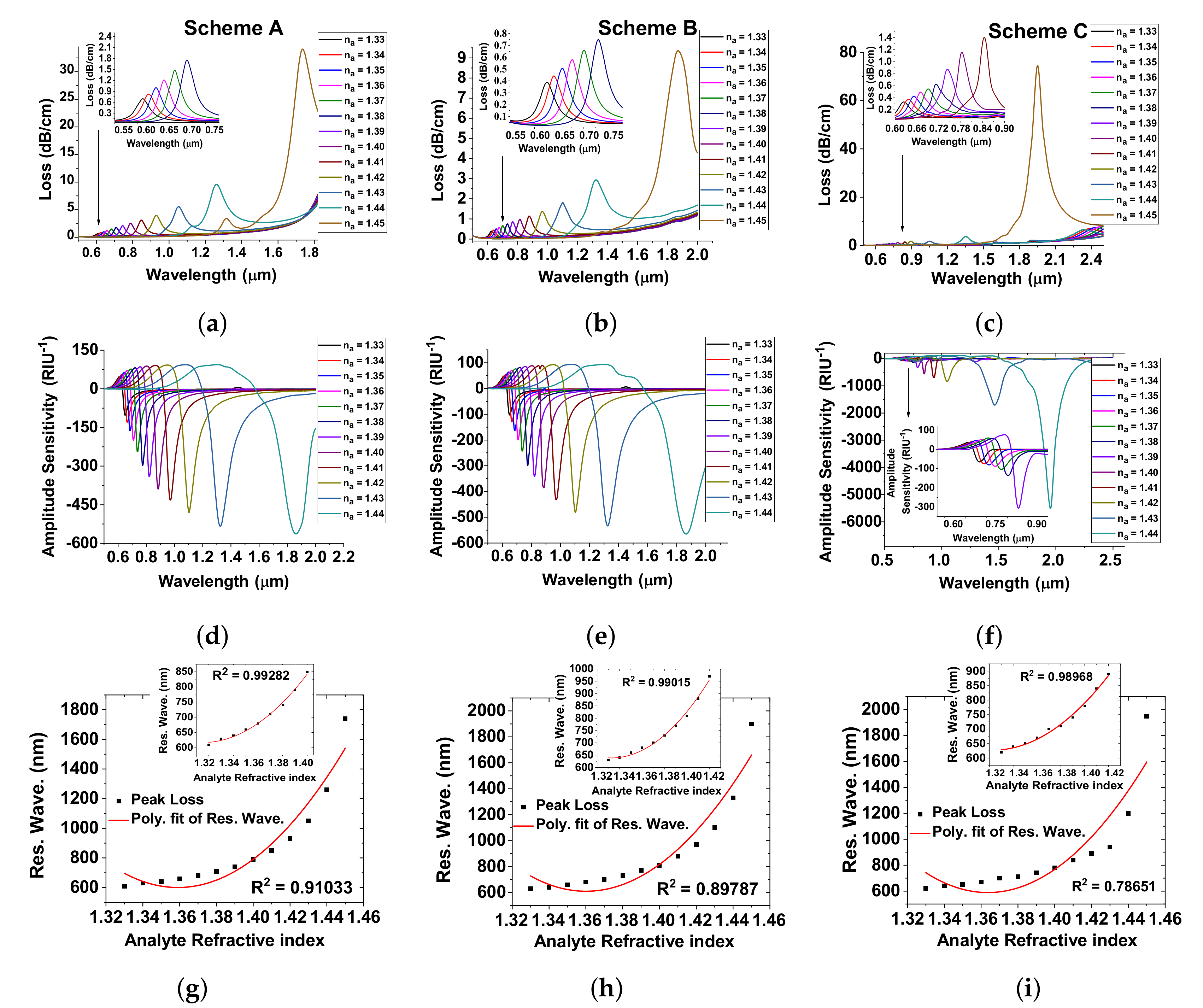
3. Investigation of Modes and Physical Mechanism
4. Influence of Metals and Optimization
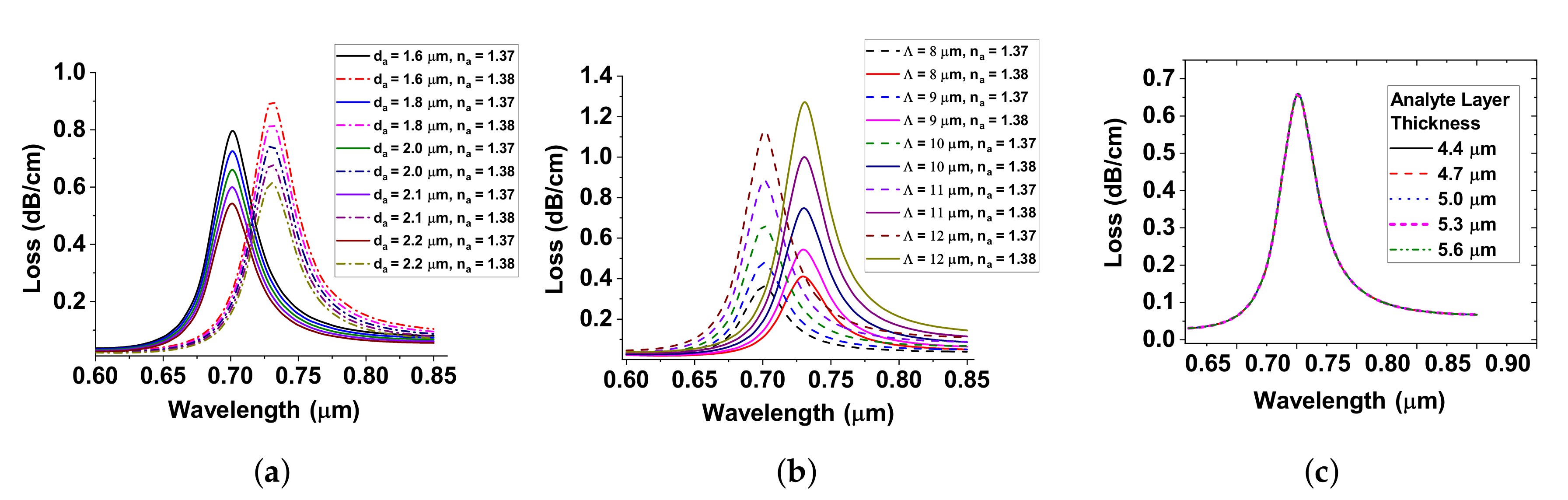
5. Fabrication Tolerance
6. Analysis of Sensitivity and Linearity
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SERS | Stimulated Emission of Raman Scattering |
| PCF | Photonic Crystal Fiber |
| RIBS | Refractive Index Based Sensor |
| Au | Gold |
| TiO | Titanium-di-Oxide |
| SPR | Surface Plasmon Resonance |
| LSPR | Localized Surface Plasmon Resonance |
| SPM | Surface Plasmonic Mode |
| LSPM | Localized Surface Plasmon Mode |
| AUI | Analyte under Investigation |
| n | Analyte-Refractive Index |
| LOD | Limit Of Detection |
| PM | Plasmonic Mode |
| FM | Fundamental Mode |
| CL | Confinement Loss |
| WS | Wavelength Sensitivity |
| AS | Amplitude Sensitivity |
| SNR | Signal to Noise Ratio |
| FWHM | Full-Width at Half Maximum |
| FOM | Figure of Merit |
| Detection Limit |
References
- Maier, S.A.; Kik, P.G.; Atwater, H.A.; Meltzer, S.; Harel, E.; Koel, B.E.; Requicha, A.A. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nature Mater. 2003, 2, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, H.; Dong, J.; Hu, S.; Zhu, W.; Qiu, W.; Lu, H.; Yu, J.; Guan, H.; Gao, S.; et al. Sensitivity-enhanced surface plasmon resonance sensor utilizing a tungsten disulfide (WS2) nanosheets overlayer. Photon. Res. 2018, 6, 485–491. [Google Scholar] [CrossRef]
- Cao, S.; Shao, Y.; Wang, Y.; Wu, T.; Zhang, L.; Huang, Y.; Zhang, F.; Liao, C.; He, J.; Wang, Y. Highly sensitive surface plasmon resonance biosensor based on a low-index polymer optical fiber. Opt. Express 2018, 26, 3988–3994. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Li, Y.; Han, Y.; Liu, Y.; Gao, J. D-shaped photonic crystal fiber plasmonic refractive index sensor based on gold grating. Appl. Opt. 2018, 57, 5268–5272. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.M.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Mishra, Y. Terahertz plasmonics: The rise of toroidal metadevices towards immunobiosensings. Mater. Today 2020, 32, 108–130. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Gerislioglu, B.; Dong, L.; Ahmadivand, A.; Hu, H.; Nordlander, P.; Halas, N.J. Monolithic Metal Dimer-on-Film Structure: New Plasmonic Properties Introduced by the Underlying Metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar] [CrossRef]
- Quero, G.; Zito, G.; Managò, S.; Galeotti, F.; Pisco, M.; De Luca, A.C.; Cusano, A. Nanosphere Lithography on Fiber: Towards Engineered Lab-On-Fiber SERS Optrodes. Sensors 2018, 18, 680. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, Z.-Q.; Li, J. Photonic crystal fiber based surface plasmon resonance chemical sensors. Sens. Actuators B 2014, 202, 557–567. [Google Scholar] [CrossRef]
- Liu, B.-H.; Jiang, Y.-X.; Zhu, X.-S.; Tang, X.-L.; Shi, Y.-W. Hollow fiber surface plasmon resonance sensor for the detection of liquid with high refractive index. Opt. Express 2013, 21, 32349–32357. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.W.; Schmidt, M.A.; Russell, R.F.; Joly, N.Y.; Tyagi, H.K.; Uebel, P.; Russell, P. Pressure-assisted melt-filling and optical characterization of Au nano-wires in microstructured fibers. Opt. Express 2011, 19, 12180–12189. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Zhang, Y.; Pan, S.; Shum, P.; Yan, M.; Leviatan, Y.; Li, C.M. A selectively coated photonic crystal fiber based surface plasmon resonance sensor. J. Opt. 2010, 12, 015005. [Google Scholar] [CrossRef]
- Klantsataya, E.; Francois, A.; Ebendorff-Heidepriem, H.; Hoffmann, P.; Monro, T.M. Surface plasmon scattering in exposed core optical fiber for enhanced resolution refractive index sensing. Sensors 2015, 15, 25090–25102. [Google Scholar] [CrossRef] [PubMed]
- Luan, N.; Wang, R.; Lv, W.; Yao, J. Surface plasmon resonance sensor based on D-shaped microstructured optical fiber with hollow core. Opt. Express 2015, 23, 8576–8582. [Google Scholar] [CrossRef] [PubMed]
- Luan, N.; Zhao, L.; Lian, Y.; Lou, S. A High Refractive Index Plasmonic Sensor Based on D-Shaped Photonic Crystal Fiber with Laterally Accessible Hollow-Core. IEEE Photon. J. 2018, 10, 6803707. [Google Scholar] [CrossRef]
- Bing, P.; Sui, J.; Huang, S.; Guo, X.; Li, Z.; Tan, L.; Yao, J. A Novel Photonic Crystal Fiber Sensor with Three D-shaped Holes Based on Surface Plasmon Resonance. Curr. Opt. Photon. 2019, 3, 541–547. [Google Scholar]
- Islam, S.; Sultana, J.; Aoni, R.A.; Ahmed, R.; Dinovitser, A.; Ng, B.W.-H.; Ebendorff-Heidepriem, H.; Abbott, D. Dual-polarized highly sensitive plasmonic sensor in the visible to near-IR spectrum. Opt. Express 2018, 26, 30347–30361. [Google Scholar] [CrossRef]
- Paul, D.; Biswas, R. Highly sensitive LSPR based photonic crystal fiber sensor with embodiment of nanospheres in different material domain. Opt. Laser Technol. 2018, 101, 379–387. [Google Scholar] [CrossRef]
- Islam, S.; Sultana, J.; Aoni, R.A.; Habib, S.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. Localized surface plasmon resonance biosensor: An improved technique for SERS response intensification. Opt. Lett. 2019, 44, 1134–1137. [Google Scholar] [CrossRef]
- Devore, J.R. Refractive Indices of Rutile and Sphalerite. J. Opt. Soc. Am. 1951, 41, 416–419. [Google Scholar] [CrossRef]
- Tatian, B. Fitting refractive-index data with the Sellmeier dispersion formula. Appl. Opt. 1984, 23, 4477–4485. [Google Scholar] [CrossRef] [PubMed]
- Vial, A.; Grimault, A.-S.; Macías, D.; Barchiesi, D.; De La Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Russell, P. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Ashok, N.; Shin, W. Effective d-shape fiber with air hole assistant design for birefringence analysis. Optik 2018, 162, 27–34. [Google Scholar] [CrossRef]
- Boehm, J.; Francois, A.; Ebendorff-Heidepriem, H.; Monro, T.M. Chemical deposition of silver for the fabrication of surface plasmon microstructured optical fibre sensors. Plasmonics 2011, 6, 133–136. [Google Scholar] [CrossRef]
- Yang, X.; Duan, L.; Liu, B.; Yao, J.; Lu, Y. Temperature sensor based on hollow fiber filled with graphene-ag composite nanowire and liquid. Plasmonics 2017, 12, 1805–1811. [Google Scholar] [CrossRef]
- Popescu, V.A.; Puscas, N.N.; Perrone, G. Simulation of the Sensing Performance of a Plasmonic Biosensor Based on Birefringent Solid-Core Microstructured Optical Fiber. Plasmonics 2017, 12, 905–911. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Ahmed, R.; Shee, Y.G.; Adikan, F.M. Highly sensitive multi-core flat fiber surface plasmon resonance refractive index sensor. Opt. Express 2016, 24, 2485–2495. [Google Scholar] [CrossRef]
- Haider, F.; Aoni, R.A.; Ahmed, R.; Miroshnichenko, A.E. Highly amplitude-sensitive photonic-crystal- fiber-based plasmonic sensor. J. Opt. Soc. Am. B. 2018, 35, 2816–2821. [Google Scholar] [CrossRef]
- An, G.; Li, S.; Cheng, T.; Yan, X.; Zhang, X.; Zhou, X.; Yuan, Z. Ultra-stable D-shaped optical fiber refractive index sensor with graphene-gold deposited platform. Plasmonics 2019, 14, 155–163. [Google Scholar] [CrossRef]
- Pathak, A.K.; Singh, V.K. Theoretical assessment of D-shaped optical fiber chemical sensor associated with nanoscale silver strip operating in near-infrared region. Opt. Quantum Electron. 2020, 52, 1–13. [Google Scholar] [CrossRef]
- Fang, L.-M.; Chen, H.-M. Double-core D-type photonic crystal fiber refractive index sensor based on grid coating. Adv. Sens. Syst. Appl. IX 2019, 11191, 111910H. [Google Scholar]
- An, G.; Li, S.; Wang, H.; Zhang, X.; Yan, X. Quasi-D-shaped optical fiber plasmonic refractive index sensor. J. Opt. 2018, 20, 035403. [Google Scholar] [CrossRef]
- Khanikar, T.; Singh, V.K. Gold grating SPR based D-shaped single mode fiber for detection of liquid refractive index. Optic. Quantum Electron. 2019, 51, 296. [Google Scholar]
- Thenmozhi, H.; Rajan, M.M.; Ahmed, K. D-shaped PCF sensor based on SPR for the detection of carcinogenic agents in food and cosmetics. Optik 2019, 180, 264–270. [Google Scholar] [CrossRef]
- Monfared, Y.E. Refractive index sensor based on surface plasmon resonance excitation in a D-shaped photonic crystal fiber coated by titanium nitride. Plasmonics 2020, 15, 535–542. [Google Scholar] [CrossRef]
- Khan, S.; Ahmed, K.; Hossain, N.; Paul, B.K.; Nguyen, T.K.; Dhasarathan, V. Exploring refractive index sensor using gold coated D-shaped photonic crystal fiber for biosensing applications. Optik 2020, 202, 163949. [Google Scholar] [CrossRef]


| Analyte-RI | Res. Wave. (nm) | Wave. Sensitivity (nm/RIU) | Resolution (RIU) | Amp. Sensitivity (RIU) | SNR | Detection Limit | FWHM (nm) | FOM |
|---|---|---|---|---|---|---|---|---|
| Scheme A-SPR PCF-RIBS | ||||||||
| 1.33 | 610 | 2000 | 5 × 10 | 99 | 0.5 | 31 | 40 | 50 |
| 1.34 | 630 | 1000 | 1 × 10 | 134 | 0.25 | 36 | 39 | 25 |
| 1.35 | 640 | 2000 | 5 × 10 | 170 | 0.55 | 27 | 36 | 55 |
| 1.36 | 660 | 2000 | 5 × 10 | 223 | 0.55 | 27 | 36 | 55 |
| 1.37 | 680 | 3000 | 3.33 × 10 | 274 | 0.83 | 25 | 36 | 83 |
| 1.38 | 710 | 3000 | 3.33 × 10 | 353 | 0.83 | 25 | 37 | 81 |
| 1.39 | 740 | 5000 | 2 × 10 | 407 | 1.38 | 22 | 36 | 138 |
| 1.4 | 790 | 6000 | 1.66 × 10 | 493 | 1.39 | 26 | 43 | 139 |
| 1.41 | 850 | 8000 | 1.25 × 10 | 560 | 1.45 | 33 | 55 | 145 |
| 1.42 | 930 | 12000 | 8.33 × 10 | 644 | 1.90 | 35 | 63 | 190 |
| 1.43 | 1050 | 21000 | 4.76 × 10 | 720 | 2.44 | 45 | 86 | 244 |
| 1.44 | 1260 | 48000 | 2.08 × 10 | 761 | 3.72 | 61 | 129 | 372 |
| 1.45 | 1740 | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| Scheme B-SPR PCF-RIBS | ||||||||
| 1.33 | 630 | 1000 | 1 × 10 | 102 | 0.24 | 38 | 41 | 21 |
| 1.34 | 640 | 2000 | 5 × 10 | 124 | 0.54 | 28 | 37 | 54 |
| 1.35 | 660 | 2000 | 5 × 10 | 153 | 0.52 | 29 | 38 | 52 |
| 1.36 | 680 | 2000 | 5 × 10 | 199 | 0.52 | 29 | 38 | 52 |
| 1.37 | 700 | 3000 | 3.33 × 10 | 242 | 0.76 | 27 | 39 | 76 |
| 1.38 | 730 | 4000 | 2.5 × 10 | 280 | 0.95 | 28 | 42 | 95 |
| 1.39 | 770 | 4000 | 2.5 × 10 | 340 | 0.95 | 28 | 42 | 95 |
| 1.4 | 810 | 7000 | 1.42 × 10 | 380 | 1.32 | 32 | 53 | 132 |
| 1.41 | 880 | 8000 | 1.25 × 10 | 431 | 1.40 | 34 | 57 | 140 |
| 1.42 | 960 | 14000 | 7.14 × 10 | 476 | 1.75 | 46 | 80 | 175 |
| 1.43 | 1100 | 23000 | 4.34 × 10 | 529 | 2.09 | 60 | 110 | 209 |
| 1.44 | 1330 | 52000 | 1.9 × 10 | 560 | 3.04 | 86 | 171 | 304 |
| 1.45 | 1850 | N/A | N/A | N/A | N/A | N/A | 213 | N/A |
| Scheme C-LSPR PCF-RIBS | ||||||||
| 1.33 | 620 | 2000 | 5 × 10 | 69 | 0.43 | 16 | 46 | 43 |
| 1.34 | 640 | 1000 | 1 × 10 | 76 | 0.20 | 10 | 49 | 20 |
| 1.35 | 650 | 2000 | 5 × 10 | 82 | 0.43 | 16 | 46 | 43 |
| 1.36 | 670 | 3000 | 3.33 × 10 | 89 | 0.63 | 22 | 48 | 63 |
| 1.37 | 700 | 1000 | 1 × 10 | 107 | 0.21 | 10 | 48 | 21 |
| 1.38 | 710 | 3000 | 3.33 × 10 | 138 | 0.6 | 23 | 50 | 60 |
| 1.39 | 740 | 4000 | 2.5 × 10 | 330 | 0.83 | 27 | 48 | 83 |
| 1.4 | 780 | 6000 | 1.6 × 10 | 532 | 1.58 | 36 | 38 | 158 |
| 1.41 | 840 | 5000 | 2 × 10 | 702 | 1.47 | 30 | 34 | 147 |
| 1.42 | 890 | 5000 | 2 × 10 | 835 | 1.04 | 33 | 48 | 104 |
| 1.43 | 940 | 26000 | 3.84 × 10 | 1638 | 4.81 | 117 | 54 | 481 |
| 1.44 | 1200 | 75000 | 1.33 × 10 | 5503 | 9.03 | 288 | 83 | 904 |
| 1.45 | 1950 | N/A | N/A | N/A | N/A | N/A | 137 | N/A |
| Ref. | Fiber Structure | RI-Range | Wave. Sensitivity (nm/RIU) | Resolution (Wave. Int.) (RIU) | Amp. Sensitivity (RIU) | Resolution (RIU) |
|---|---|---|---|---|---|---|
| [4] | SPR based D-shaped PCF | 1.36–1.38 | 3340 | 5.98 × 10 | 693 | 2.84 × 10 |
| [15] | SPR based D-shaped MOF with hollow core | 1.33–1.34 | 2900 | N/A | 120 | N/A |
| [16] | SPR based D-shaped PCF with laterally accessible hollow-core | 1.46–1.47 | 7200 | N/A | 91 | N/A |
| [17] | Three D-shaped holes SPR-PCF | 1.33–1.39 | 10,100 | 9.9 × 10 | N/A | N/A |
| [31] | Graphene-Au coated D-shaped optical fiber | 1.33–1.39 | 4391 | 2.28× 10 | 1139 | 8.78× 10 |
| [32] | D-shaped nanoscale silver strip SMF | 1.38–1.42 | 3240 | 3.08× 10 | 192 | N/A |
| [33] | Double-core D-type PCF | 1.30–1.33 | 12,000 | 1.01 × 10 | N/a | N/A |
| [34] | Quasi D-shaped nanoscale silver strip SMF | 1.33–1.42 | 3877 | 2.58 × 10 | 1236 | 8.1 × 10 |
| [35] | Gold grating assisted SPR-D-shaped SMF | 1.34–1.38 | 7500 | 1.31 × 10 | 67,608 | N/A |
| [36] | D-shaped SPR PCF | 14,136–14,154 | 50,000 | 4 × 10 | 1266.67 | N/A |
| [37] | Titanium nitride coated SPR D-shaped PCF | 1.44–1.48 | 16,275 | N/A | 20,625 | N/A |
| [38] | D-shaped SPR PCF | 1.36–1.39 | 66,666.67 | 9.66 × 10 | 1488.82 | N/A |
| Proposed work | Twin-hole D-type PCF-RIBS | 1.33–1.45 | 75,000 | 1.33 × 10 | 5503 | 1.81 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aruna Gandhi, M.S.; Senthilnathan, K.; Ramesh Babu, P.; Li, Q. Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement. Sensors 2020, 20, 5248. https://doi.org/10.3390/s20185248
Aruna Gandhi MS, Senthilnathan K, Ramesh Babu P, Li Q. Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement. Sensors. 2020; 20(18):5248. https://doi.org/10.3390/s20185248
Chicago/Turabian StyleAruna Gandhi, Manthangal Sivanesan, Krishnamoorthy Senthilnathan, Padmanabhan Ramesh Babu, and Qian Li. 2020. "Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement" Sensors 20, no. 18: 5248. https://doi.org/10.3390/s20185248
APA StyleAruna Gandhi, M. S., Senthilnathan, K., Ramesh Babu, P., & Li, Q. (2020). Highly Sensitive Localized Surface Plasmon Polariton Based D-Type Twin-Hole Photonic Crystal Fiber Microbiosensor: Enhanced Scheme for SERS Reinforcement. Sensors, 20(18), 5248. https://doi.org/10.3390/s20185248





