Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task
Abstract
1. Introduction
2. Theoretical Background
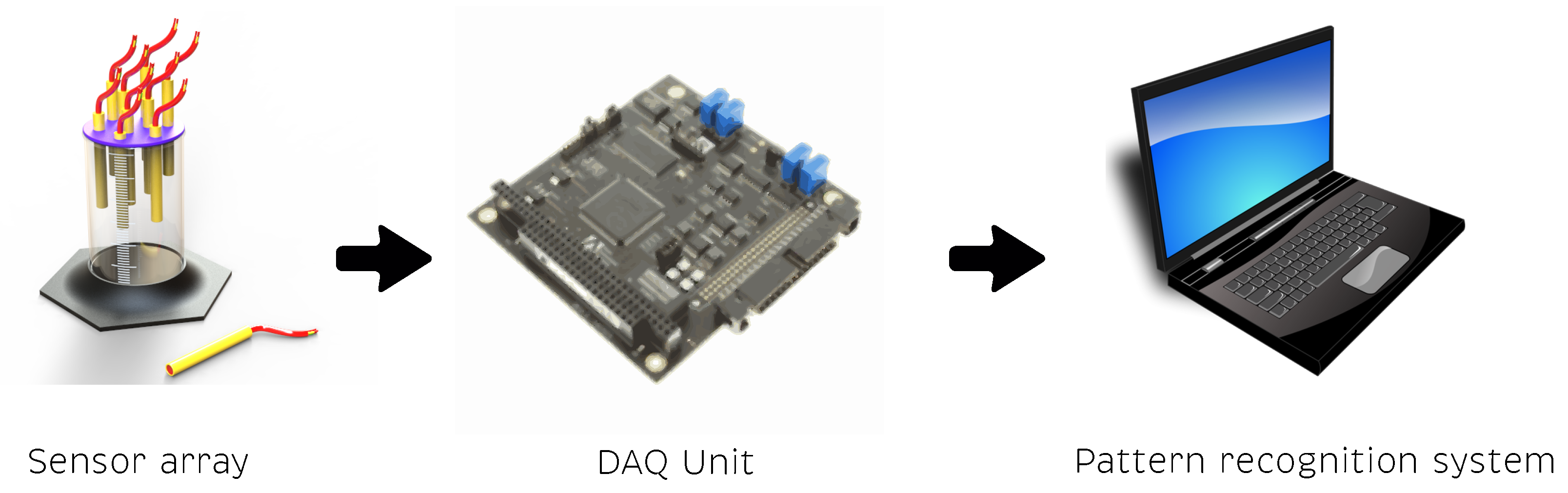
2.1. Electronic Tongue
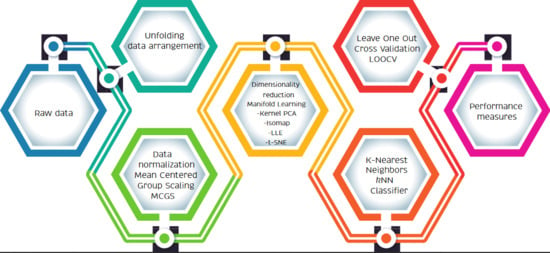
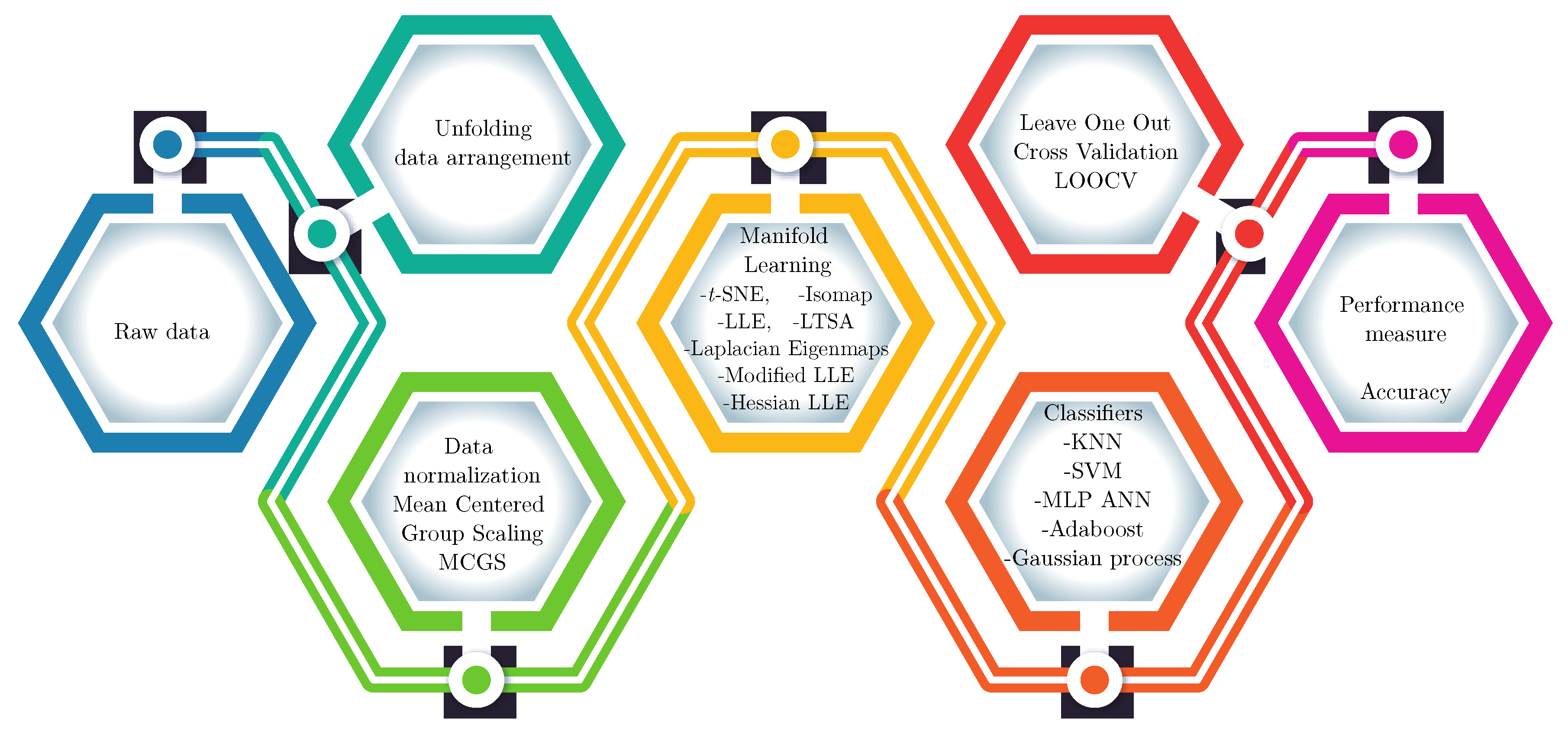
2.2. Data Unfolding
2.3. Mean-Centered Group Scaling
2.4. Dimensionality Reduction
2.5. Manifold Learning
2.5.1. Isomap
2.5.2. Locally Linear Embedding
2.5.3. Laplacian Eigenmaps
2.5.4. Modified LLE
2.5.5. Hessian LLE
2.5.6. Local Tangent Space Alignment (LTSA)
2.5.7. t-Distributed Stochastic Neighbor Embedding (t-SNE)
2.6. Supervised Machine Learning Classifiers
2.7. Leave-One-Out Cross Validation
2.8. Performance Measure
3. Dataset of a MLAPV Electronic Tongue
4. Artificial Taste Recognition Methodology
5. Results and Discussion
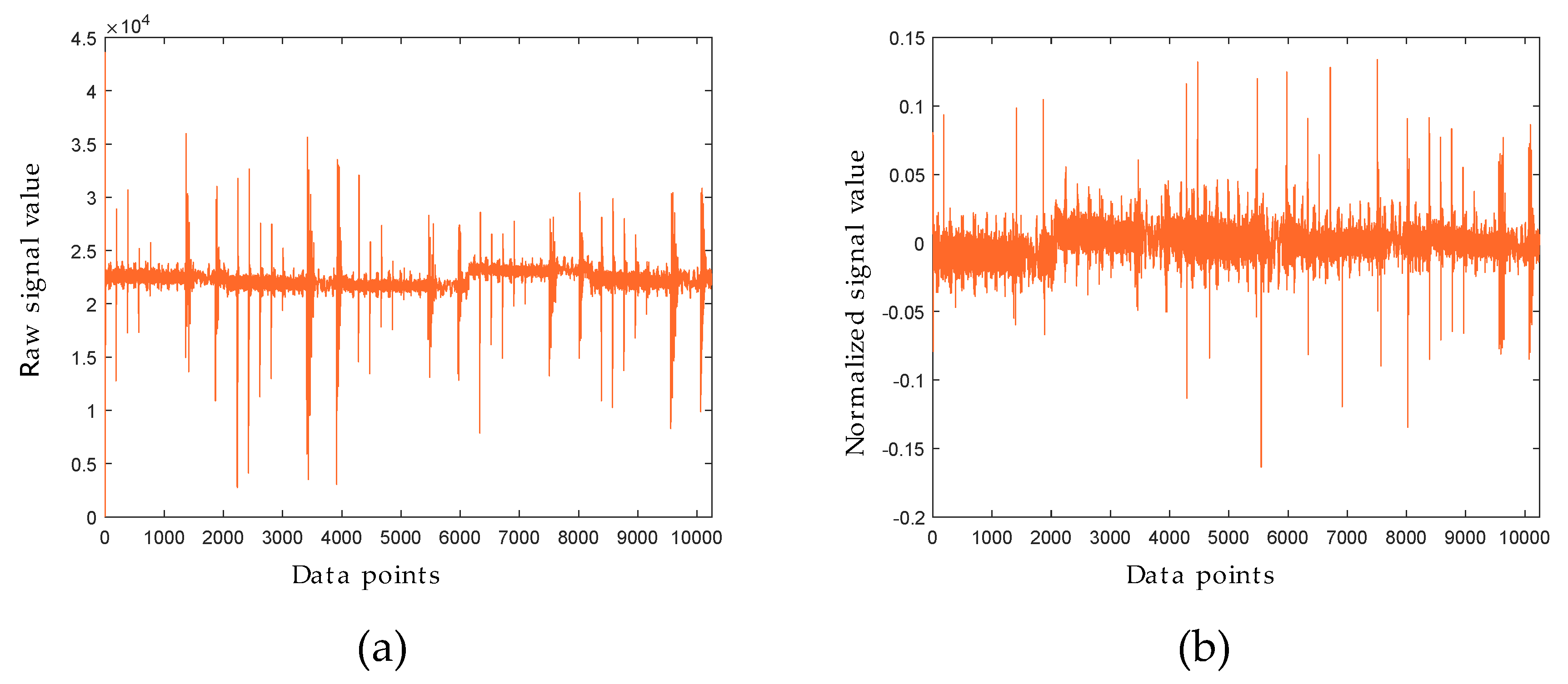
5.1. MCGS Scaling
5.2. Manifold Learning, Dimensionality Reduction and Classification
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ASF | active feature selection |
| DWT | discrete wavelet transform |
| FN | false negative |
| FP | false positive |
| kNN | k nearest neighbors |
| LDA | linear discriminant analysis |
| LDPP | local discriminant preservation projection |
| LLE | locally linear embedding |
| LOOCV | leave-one-out cross validation |
| LTSA | local tangent space alingment |
| MCGS | mean-centered group scaling |
| MLAPV | multifrequency large amplitude pulse signal voltammetry |
| PCA | principal component analysis |
| RBF | radial basis function |
| SHM | structural health monitoring |
| TN | true negative |
| TP | true positive |
| t-SNE | t-distributed stochastic neighbor embedding |
References
- Leon-Medina, J.X.; Cardenas-Flechas, L.J.; Tibaduiza, D.A. A data-driven methodology for the classification of different liquids in artificial taste recognition applications with a pulse voltammetric electronic tongue. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Del Valle, M. Electronic tongues employing electrochemical sensors. Electroanalysis 2010, 22, 1539–1555. [Google Scholar] [CrossRef]
- Leon-Medina, J.X.; Vejar, M.A.; Tibaduiza, D.A. Signal Processing and Pattern Recognition in Electronic Tongues: A Review. In Pattern Recognition Applications in Engineering; IGI Global: Hershey, PA, USA, 2020; pp. 84–108. [Google Scholar]
- Oliveri, P.; Casolino, M.C.; Forina, M. Chemometric Brains for Artificial Tongues, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010; Volume 61, pp. 57–117. [Google Scholar] [CrossRef]
- Tian, S.Y.; Deng, S.P.; Chen, Z.X. Multifrequency large amplitude pulse voltammetry: A novel electrochemical method for electronic tongue. Sens. Actuators B Chem. 2007, 123, 1049–1056. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, J.; Jin, W. Evaluation of varieties of set yogurts and their physical properties using a voltammetric electronic tongue based on various potential waveforms. Sens. Actuators B Chem. 2013, 177, 684–694. [Google Scholar] [CrossRef]
- Ivarsson, P.; Holmin, S.; Höjer, N.E.; Krantz-Rülcker, C.; Winquist, F. Discrimination of tea by means of a voltammetric electronic tongue and different applied waveforms. Sens. Actuators B Chem. 2001, 76, 449–454. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, J.; Ye, L. Classification and prediction of rice wines with different marked ages by using a voltammetric electronic tongue. Biosens. Bioelectron. 2011, 26, 4767–4773. [Google Scholar] [CrossRef]
- Palit, M.; Tudu, B.; Dutta, P.K.; Dutta, A.; Jana, A.; Roy, J.K.; Bhattacharyya, N.; Bandyopadhyay, R.; Chatterjee, A. Classification of black tea taste and correlation with tea taster’s mark using voltammetric electronic tongue. IEEE Trans. Instrum. Meas. 2009, 59, 2230–2239. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, J. Classification of monofloral honeys by voltammetric electronic tongue with chemometrics method. Electrochim. Acta 2011, 56, 4907–4915. [Google Scholar] [CrossRef]
- Gutes, A.; Cespedes, F.; Del Valle, M.; Louthander, D.; Krantz-Rülcker, C.; Winquist, F. A flow injection voltammetric electronic tongue applied to paper mill industrial waters. Sens. Actuators B Chem. 2006, 115, 390–395. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.; Li, D.; Yang, T.; Cao, J. Electronic Tongue Recognition with Feature Specificity Enhancement. Sensors 2020, 20, 772. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.; Li, D.; Wu, M. An Active Feature Selection Strategy for DWT in Artificial Taste. J. Sens. 2018, 2018. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Huang, G.B.; Liu, T.; Tan, X. Taste Recognition in E-Tongue Using Local Discriminant Preservation Projection. IEEE Trans. Cybern. 2018, 1–14. [Google Scholar] [CrossRef]
- Wang, X.; Paliwal, K.K. Feature extraction and dimensionality reduction algorithms and their applications in vowel recognition. Pattern Recognit. 2003, 36, 2429–2439. [Google Scholar] [CrossRef]
- Levner, I. Feature selection and nearest centroid classification for protein mass spectrometry. BMC Bioinform. 2005, 6, 68. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Guo, X.; Duan, S.; Jia, P.; Wang, L.; Peng, C.; Zhang, S. Electronic nose feature extraction methods: A review. Sensors 2015, 15, 27804–27831. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Kou, G.; Peng, Y. Nonlinear manifold learning for early warnings in financial markets. Eur. J. Oper. Res. 2017, 258, 692–702. [Google Scholar] [CrossRef]
- Lunga, D.; Prasad, S.; Crawford, M.M.; Ersoy, O. Manifold-learning-based feature extraction for classification of hyperspectral data: A review of advances in manifold learning. IEEE Signal Process. Mag. 2013, 31, 55–66. [Google Scholar] [CrossRef]
- Yildiz, K.; Çamurcu, A.Y.; Dogan, B. Comparison of dimension reduction techniques on high dimensional datasets. Int. Arab J. Inf. Technol. 2018, 15, 256–262. [Google Scholar]
- Leon, J.X.; Pineda Muñoz, W.A.; Anaya, M.; Vitola, J.; Tibaduiza, D.A. Structural Damage Classification Using Machine Learning Algorithms and Performance Measures. In Proceedings of the 12th International Workshop On Structural Health Monitoring-IWSHM 2019, Stanford, CA. USA, 10–12 September 2019. [Google Scholar]
- Agis, D.; Pozo, F. A frequency-based approach for the detection and classification of structural changes using t-SNE. Sensors 2019, 19, 5097. [Google Scholar] [CrossRef]
- Silva, V.D.; Tenenbaum, J.B. Global versus local methods in nonlinear dimensionality reduction. In Advances in Neural Information Processing Systems (NIPS) 15; The MIT Press: Cambridge, MA, USA, 2003; pp. 721–728. [Google Scholar]
- Plastria, F.; De Bruyne, S.; Carrizosa, E. Dimensionality reduction for classification, comparison of techniques and dimension choice. In Proceedings of the 4th International Conference on Advanced Data Mining and Applications- ADMA 08, Chengdu, China, 8–10 October 2008; pp. 411–418. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, F.C. A new kernel discriminant analysis framework for electronic nose recognition. Anal. Chim. Acta 2014, 816, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Huang, T.; Wang, L.; Duan, S.; Yan, J.; Wang, L. A novel pre-processing technique for original feature matrix of electronic nose based on supervised locality preserving projections. Sensors 2016, 16, 1019. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Du, J.; Xu, B.; Lu, M. Modified unsupervised discriminant projection with an electronic nose for the rapid determination of Chinese mitten crab freshness. Anal. Methods 2017, 9, 1806–1815. [Google Scholar] [CrossRef]
- Ding, L.; Guo, Z.; Pan, S.; Zhu, P. Manifold learning for dimension reduction of electronic nose data. In Proceedings of the 2017 International Conference on Control, Automation and Information Sciences (ICCAIS), Chiang Mai, Thailand, 31 October–1 November 2017; pp. 169–174. [Google Scholar]
- Zhang, L.; Tian, F.; Zhang, D. E-nose algorithms and challenges. In Electronic Nose: Algorithmic Challenges; Springer: Berlin/Heidelberg, Germany, 2018; pp. 11–20. [Google Scholar]
- Zhu, P.; Zhang, Y.; Ding, L. Rapid freshness prediction of crab based on a portable electronic nose system. Int. J. Comput. Appl. Technol. 2019, 61, 241–246. [Google Scholar] [CrossRef]
- Leon-Medina, J.; Anaya, M.; Pozo, F.; Tibaduiza, D. Application of manifold learning algorithms to improve the classification performance of an electronic nose. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar]
- Zhi, R.; Zhao, L.; Shi, B.; Jin, Y. New dimensionality reduction model (manifold learning) coupled with electronic tongue for green tea grade identification. Eur. Food Res. Technol. 2014, 239, 157–167. [Google Scholar] [CrossRef]
- Liu, M.; Wang, M.; Wang, J.; Li, D. Comparison of random forest, support vector machine and back propagation neural network for electronic tongue data classification: Application to the recognition of orange beverage and Chinese vinegar. Sens. Actuators B Chem. 2013, 177, 970–980. [Google Scholar] [CrossRef]
- Gutiérrez, J.M.; Haddi, Z.; Amari, A.; Bouchikhi, B.; Mimendia, A.; Cetó, X.; del Valle, M. Hybrid electronic tongue based on multisensor data fusion for discrimination of beers. Sens. Actuators B Chem. 2013, 177, 989–996. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, S.; He, R.; Zhang, J.; Zhou, Z.; Cheng, X.; Huang, G.; Zhang, J. A Convolutional Neural Network Based Auto Features Extraction Method for Tea Classification with Electronic Tongue. Appl. Sci. 2019, 9, 2518. [Google Scholar] [CrossRef]
- Shi, Q.; Guo, T.; Yin, T.; Wang, Z.; Li, C.; Sun, X.; Guo, Y.; Yuan, W. Classification of Pericarpium Citri Reticulatae of different ages by using a voltammetric electronic tongue system. Int. J. Electrochem. Sci. 2018, 13, 11359–11374. [Google Scholar] [CrossRef]
- Palit, M.; Tudu, B.; Bhattacharyya, N.; Dutta, A.; Dutta, P.K.; Jana, A.; Bandyopadhyay, R.; Chatterjee, A. Comparison of multivariate preprocessing techniques as applied to electronic tongue based pattern classification for black tea. Anal. Chim. Acta 2010, 675, 8–15. [Google Scholar] [CrossRef]
- Pozo, F.; Vidal, Y.; Salgado, Ó. Wind turbine condition monitoring strategy through multiway PCA and multivariate inference. Energies 2018, 11, 749. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Comparing alternative approaches for multivariate statistical analysis of batch process data. J. Chemom. 1999, 13, 397–413. [Google Scholar] [CrossRef]
- Anaya, M.; Tibaduiza, D.A.; Pozo, F. Detection and classification of structural changes using artificial immune systems and fuzzy clustering. Int. J. Bio-Inspired Comput. 2017, 9, 35–52. [Google Scholar] [CrossRef]
- Agis, D.; Tibaduiza, D.A.; Pozo, F. Vibration-based detection and classification of structural changes using principal component analysis and-distributed stochastic neighbor embedding. Struct. Control Health Monit. 2020, 27, e2533. [Google Scholar] [CrossRef]
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58. [Google Scholar] [CrossRef]
- Ma, Y.; Fu, Y. Manifold Learning Theory and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Koutroumbas, K.; Theodoridis, S. Pattern Recognition; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Ni, Y.; Chai, J.; Wang, Y.; Fang, W. A Fast Radio Map Construction Method Merging Self-Adaptive Local Linear Embedding (LLE) and Graph-Based Label Propagation in WLAN Fingerprint Localization Systems. Sensors 2020, 20, 767. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Advances in Neural Information Processing Systems (NIPS) 14; The MIT Press: Cambridge, MA, USA, 2002; pp. 585–591. [Google Scholar]
- Sakthivel, N.; Nair, B.B.; Elangovan, M.; Sugumaran, V.; Saravanmurugan, S. Comparison of dimensionality reduction techniques for the fault diagnosis of mono block centrifugal pump using vibration signals. Eng. Sci. Technol. Int. J. 2014, 17, 30–38. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J. MLLE: Modified locally linear embedding using multiple weights. In Advances in Neural Information Processing Systems (NIPS) 19; The MIT Press: Cambridge, MA, USA, 2007; pp. 1593–1600. [Google Scholar]
- Donoho, D.L.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591–5596. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn. Res. 2009, 10, 13. [Google Scholar]
- Zhang, Z.; Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM J. Sci. Comput. 2004, 26, 313–338. [Google Scholar] [CrossRef]
- Maaten, L.V.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hinton, G.E.; Roweis, S.T. Stochastic neighbor embedding. In Advances in Neural Information Processing Systems (NIPS) 15; The MIT Press: Cambridge, MA, USA, 2003; pp. 857–864. [Google Scholar]
- Husnain, M.; Missen, M.M.S.; Mumtaz, S.; Luqman, M.M.; Coustaty, M.; Ogier, J.M. Visualization of High-Dimensional data by pairwise fusion matrices using t-SNE. Symmetry 2019, 11, 107. [Google Scholar] [CrossRef]
- Agis, D.; Pozo, F. Vibration-Based Structural Health Monitoring Using Piezoelectric Transducers and Parametric t-SNE. Sensors 2020, 20, 1716. [Google Scholar] [CrossRef] [PubMed]
- Vitola, J.; Pozo, F.; Tibaduiza, D.A.; Anaya, M. A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications. Sensors 2017, 17, 417. [Google Scholar] [CrossRef] [PubMed]
- Torres-Arredondo, M.A.; Tibaduiza-Burgos, D.A. An acousto-ultrasonics approach for probabilistic modelling and inference based on Gaussian processes. Struct. Control. Health Monit. 2018, e2178. [Google Scholar] [CrossRef]
- Tibaduiza, D.; Torres-arredondo, M.Á.; Vitola, J.; Anaya, M.; Pozo, F. A Damage Classification Approach for Structural Health Monitoring Using Machine Learning. Complex. Hindawi 2018, 2018. [Google Scholar] [CrossRef]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
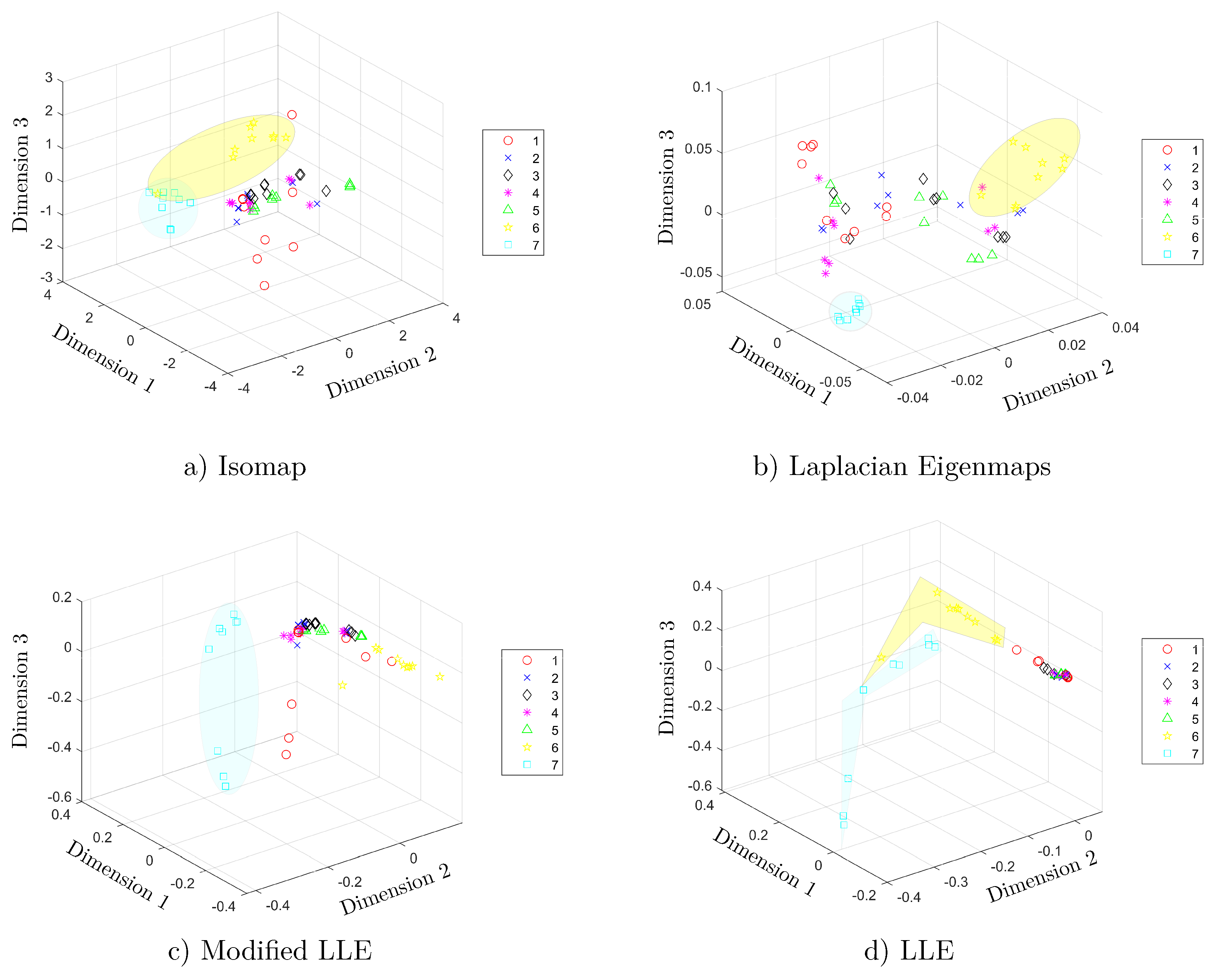
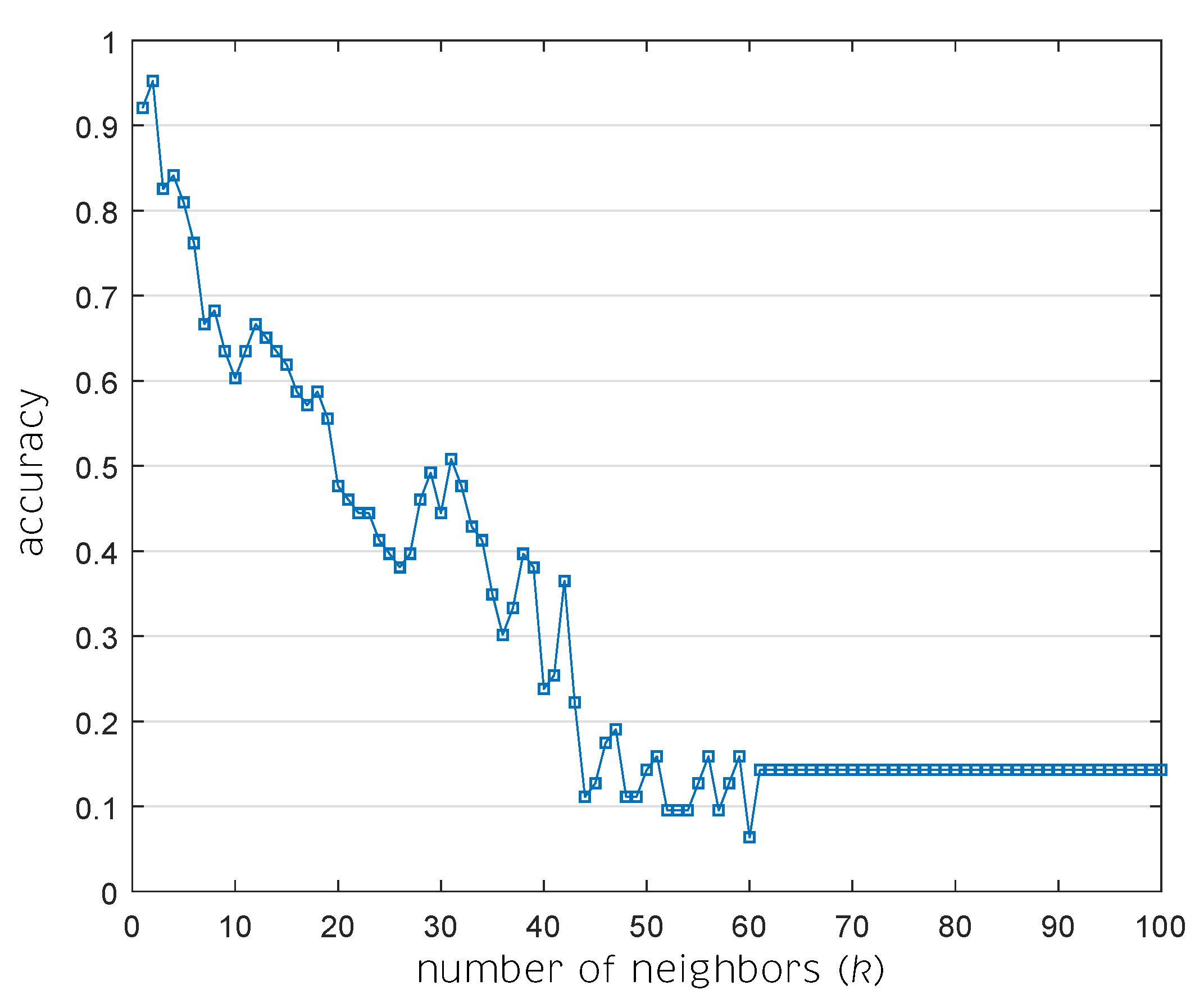
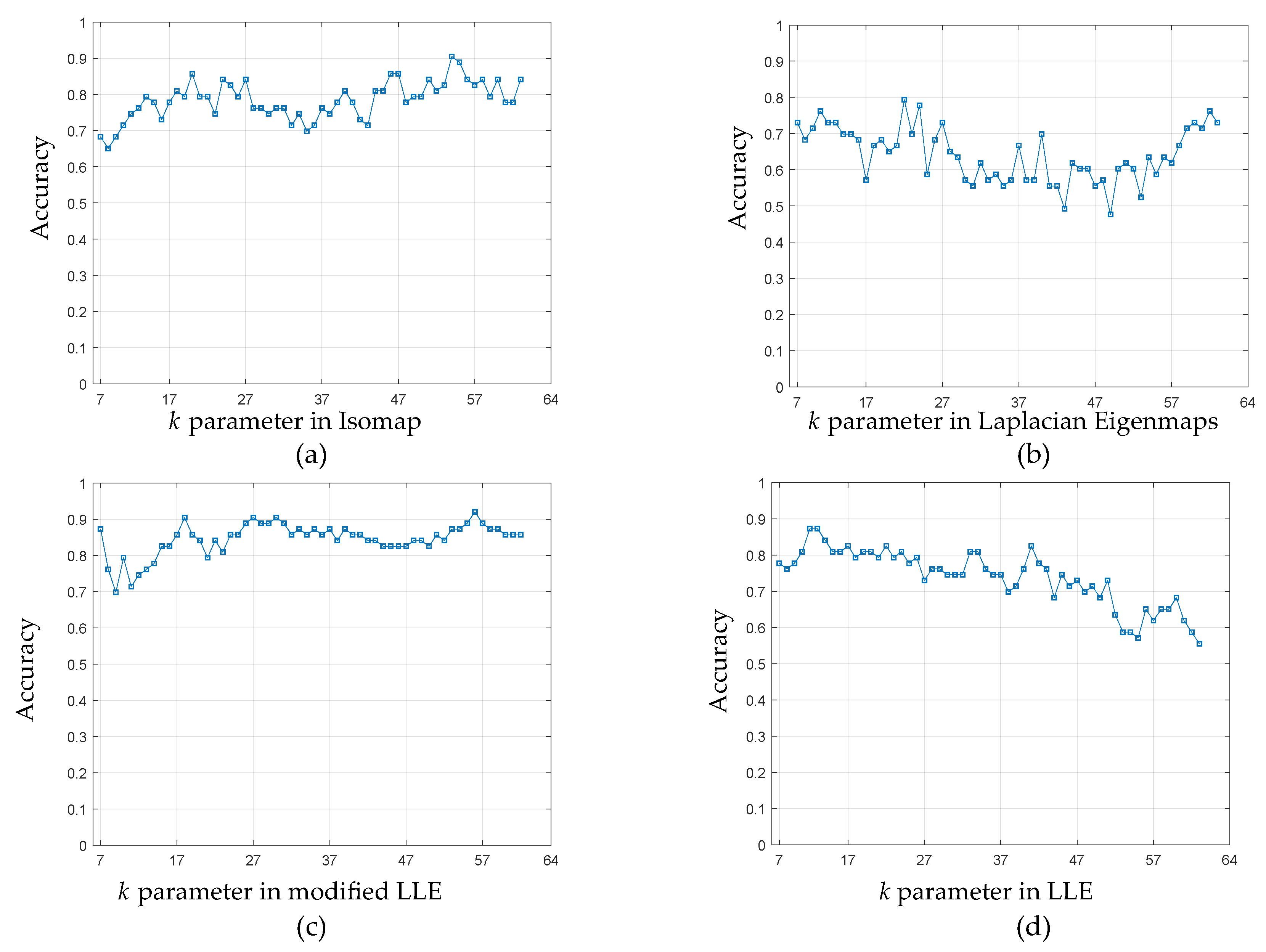
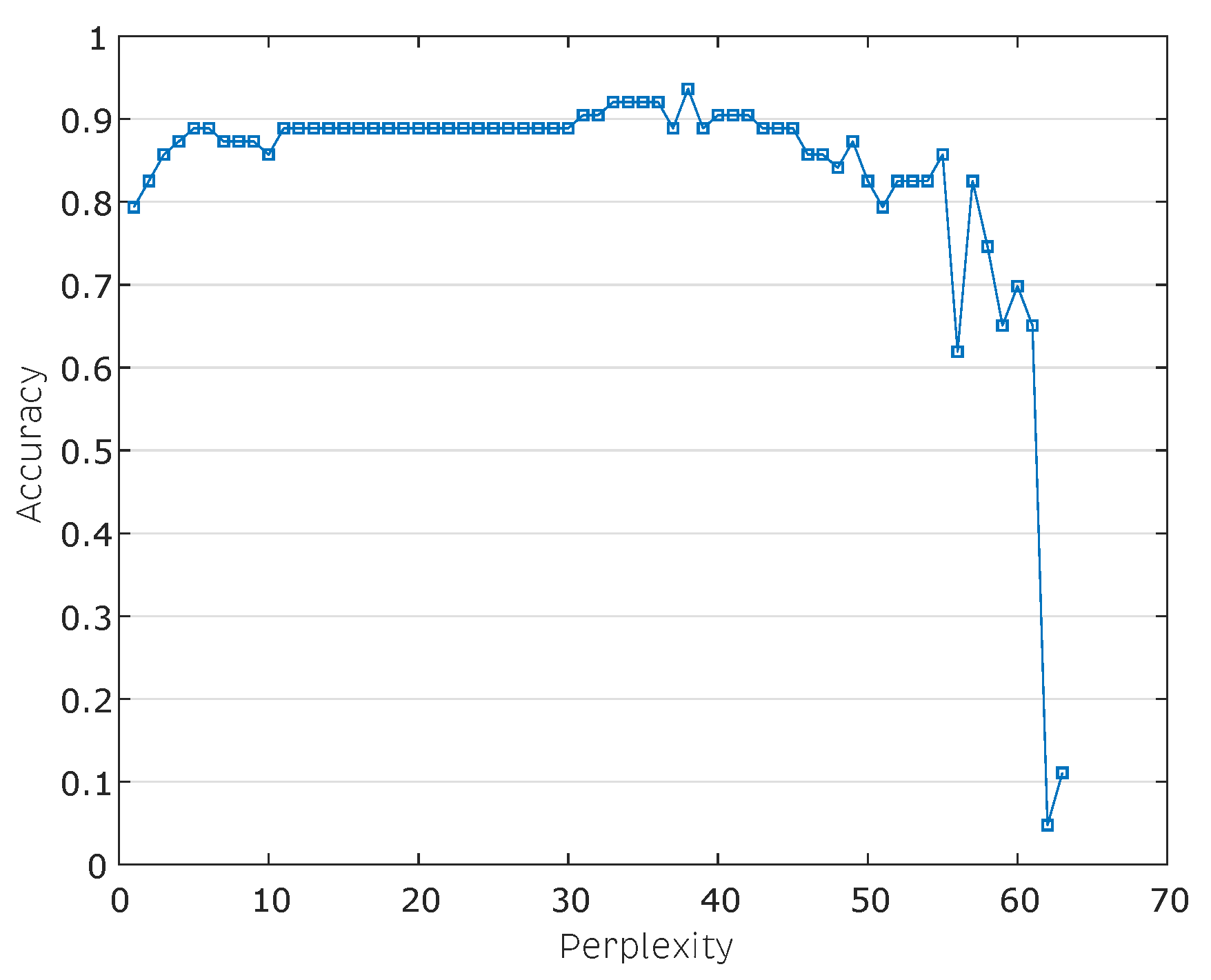
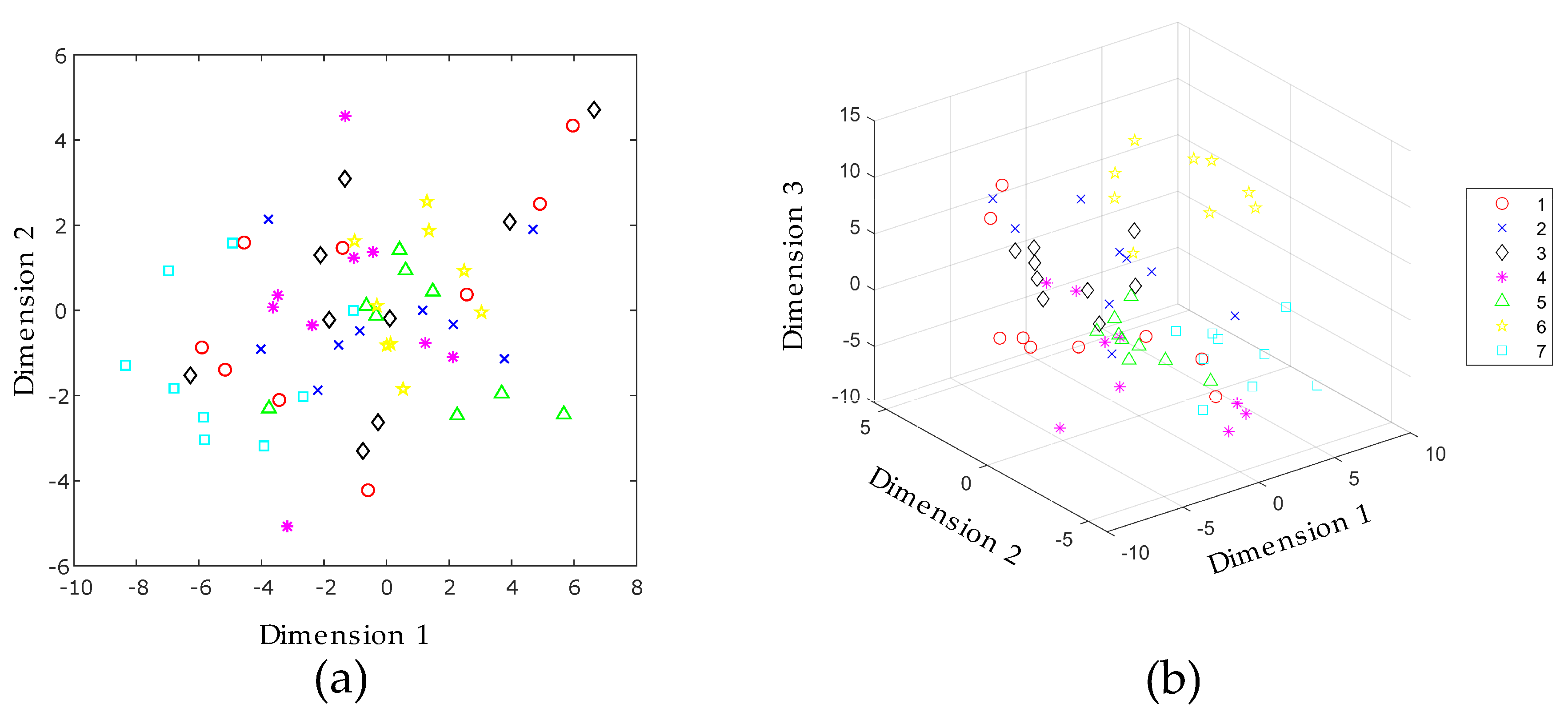
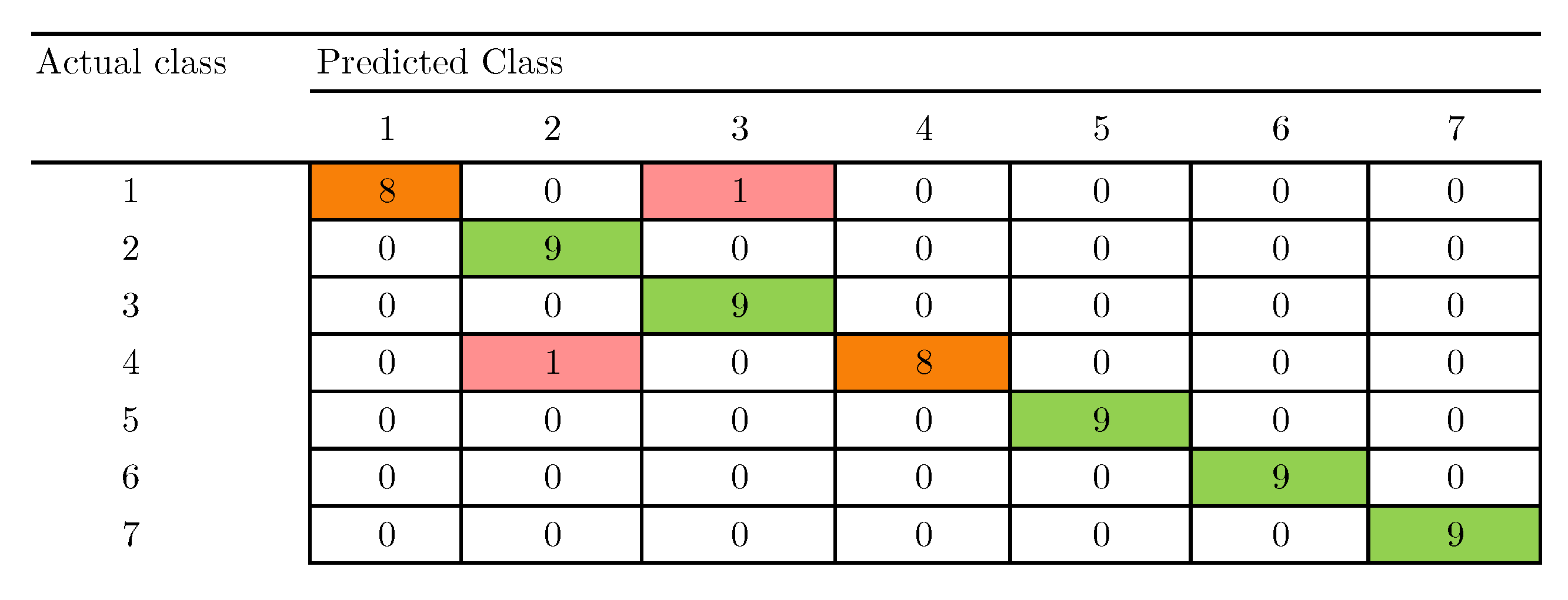
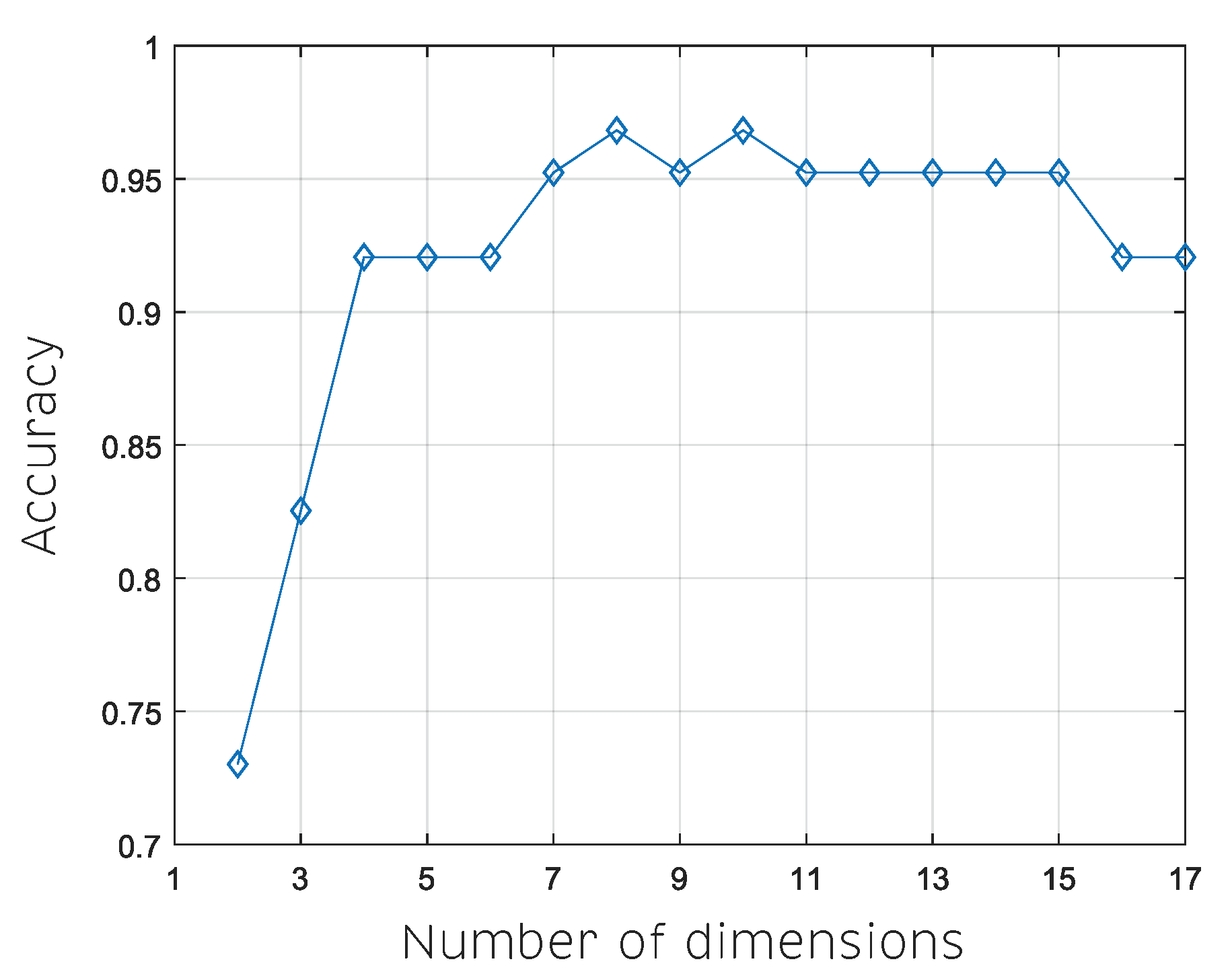
| ID | Reference | Electronic Tongue Type | Balanced/ Unbalanced | Number of Classes | Data Processing Stages | Best Combination of Methods | Cross Validation Method | Best Recognition Accuracy |
|---|---|---|---|---|---|---|---|---|
| 1 | [36] | MLAPV | Balanced | 5 | Normalization Feature Extraction Classifier | Normalization 0–1 STFT CNN-AFE | 5 fold cross validation | 99.9% |
| 2 | [1] | MLAPV | Unbalanced | 13 | Normalization Feature Extraction Classifier | Group Scaling PCA KNN | 5 fold cross validation | 94.74% |
| 3 | [14] | MLAPV | Unbalanced | 13 | Filter Feature Selection Feature Extraction Classifier | sliding window-based smooth filter LDPP KELM | 5 fold cross validation | 98.22% |
| 4 | [13] | MLAPV | Balanced | 7 | Feature Selection Classifier | ASF-DWT KNN | Leave one out cross validation | 84.13% |
| 5 | [37] | LAPV | Balanced | 4 | Feature Selection Classifier | DWT ELM | Hold out cross validation | 95% |
| 6 | [12] | MLAPV | Balanced | 7 | Feature Extraction Classifier | FSE KELM | Leave one out cross validation | 95.24% |
| 7 | [38] | MLAPV | Balanced | 5 | Normalization Feature Selection Classifier | Baseline substraction +autoscale DWT RBF ANN | 10 fold cross validation | 98.33% |
| ID | Aqueous Matrices | Samples |
|---|---|---|
| 1 | red wine | 9 |
| 2 | white spirit | 9 |
| 3 | beer | 9 |
| 4 | black tea | 9 |
| 5 | oolong tea | 9 |
| 6 | maofeng tea | 9 |
| 7 | pu’er tea | 9 |
| Research Articles | Methods | Accuracy |
|---|---|---|
| Liu et al., 2018 [13] | ASF-DWT + KNN | 84.13% |
| Liu et al., 2020 [12] | FSE + KELM | 95.24% |
| In the present article | MCGS + t-SNE + KNN | 96.83% |
| Classifier | t-SNE | Isomap | Laplacian | LLE | Modified LLE | Hessian LLE | LTSA |
|---|---|---|---|---|---|---|---|
| KNN | 0.9683 ± 0.018 | 0.8730 ± 0.028 | 0.8413 ± 0.038 | 0.8730 ± 0.017 | 0.7778 ± 0.022 | 0.7619 ± 0.027 | 0.8254 ± 0.022 |
| SVM | 0.7940 ± 0.034 | 0.7940 ± 0.032 | 0.7780 ± 0.038 | 0.7460 ± 0.035 | 0.7300 ± 0.003 | 0.6670 ± 0.014 | 0.6980 ± 0.024 |
| MLP ANN | 0.7619 ± 0.022 | 0.7777 ± 0.012 | 0.7460 ± 0.029 | 0.3968 ± 0.025 | 0.3968 ± 0.005 | 0.3492 ± 0.019 | 0.3968 ± 0.014 |
| Adaboost | 0.2857 ± 0.016 | 0.2857 ± 0.005 | 0.2698 ± 0.022 | 0.2857 ± 0.019 | 0.1428 ± 0.012 | 0.2698 ± 0.022 | 0.1269 ± 0.003 |
| Gaussian Process | 0.4444 ± 0.005 | 0.4285 ± 0.027 | 0.5396 ± 0.024 | 0.6031 ± 0.015 | 0.5873 ± 0.017 | 0.4920 ± 0.027 | 0.6666 ± 0.005 |
| D | t-SNE | Isomap | Laplacian | LLE | Modified LLE | Hessian LLE | LTSA |
|---|---|---|---|---|---|---|---|
| 2 | 0.7460 ± 0.045 | 0.7143 ± 0.003 | 0.5873 ± 0.005 | 0.7460 ± 0.011 | 0.6825 ± 0.003 | 0.6667 ± 0.023 | 0.7302 ± 0.007 |
| 3 | 0.7937 ± 0.034 | 0.8095 ± 0.026 | 0.7937 ± 0.011 | 0.7619 ± 0.023 | 0.7302 ± 0.023 | 0.7619 ± 0.006 | 0.7778 ± 0.011 |
| 4 | 0.8730 ± 0.017 | 0.9048 ± 0.033 | 0.8413 ± 0.003 | 0.7460 ± 0.010 | 0.8413 ± 0.008 | 0.8571 ± 0.008 | 0.7778 ± 0.017 |
| 5 | 0.8889 ± 0.028 | 0.8571 ± 0.005 | 0.8571 ± 0.034 | 0.7937 ± 0.005 | 0.8413 ± 0.017 | 0.8571 ± 0.003 | 0.8254 ± 0.020 |
| 6 | 0.9365 ± 0.022 | 0.8730 ± 0.011 | 0.8889 ± 0.025 | 0.8413 ± 0.003 | 0.8095 ± 0.003 | 0.8571 ± 0.011 | 0.8095 ± 0.005 |
| 7 | 0.8889 ± 0.013 | 0.8571 ± 0.028 | 0.8413 ± 0.028 | 0.7937 ± 0.033 | 0.8413 ± 0.037 | 0.8095 ± 0.033 | 0.8095 ± 0.016 |
| 8 | 0.9206 ± 0.015 | 0.8413 ± 0.022 | 0.8254 ± 0.017 | 0.8571 ± 0.022 | 0.7619 ± 0.005 | 0.7937 ± 0.024 | 0.6825 ± 0.003 |
| 9 | 0.9206 ± 0.016 | 0.8254 ± 0.027 | 0.7619 ± 0.003 | 0.8730 ± 0.019 | 0.7460 ± 0.011 | 0.7460 ± 0.020 | 0.6667 ± 0.008 |
| 10 | 0.9048 ± 0.003 | 0.8254 ± 0.011 | 0.7143 ± 0.011 | 0.8413 ± 0.004 | 0.6825 ± 0.018 | 0.7460 ± 0.027 | 0.7460 ± 0.005 |
| 11 | 0.9206 ± 0.034 | 0.8254 ± 0.009 | 0.7937 ± 0.019 | 0.8730 ± 0.008 | 0.5873 ± 0.017 | 0.7460 ± 0.029 | 0.6825 ± 0.014 |
| 12 | 0.9206 ± 0.005 | 0.8889 ± 0.003 | 0.7937 ± 0.018 | 0.8571 ± 0.005 | 0.6190 ± 0.009 | 0.6508 ± 0.015 | 0.7460 ± 0.016 |
| 13 | 0.9048 ± 0.018 | 0.8413 ± 0.012 | 0.6825 ± 0.008 | 0.7778 ± 0.015 | 0.6190 ± 0.003 | 0.7460 ± 0.012 | 0.6667 ± 0.023 |
| 14 | 0.9206 ± 0.008 | 0.8095 ± 0.017 | 0.7302 ± 0.004 | 0.8095 ± 0.019 | 0.6825 ± 0.030 | 0.6508 ± 0.016 | 0.6825 ± 0.027 |
| 15 | 0.9048 ± 0.025 | 0.8413 ± 0.013 | 0.6667 ± 0.009 | 0.7937 ± 0.023 | 0.6349 ± 0.032 | 0.6508 ± 0.005 | 0.6825 ± 0.004 |
| 16 | 0.8571 ± 0.003 | 0.8413 ± 0.007 | 0.6825 ± 0.029 | 0.7937 ± 0.027 | 0.6508 ± 0.011 | 0.6825 ± 0.033 | 0.7460 ± 0.026 |
| 17 | 0.8730 ± 0.025 | 0.8413 ± 0.015 | 0.6825 ± 0.005 | 0.7937 ± 0.035 | 0.6508 ± 0.012 | 0.6825 ± 0.026 | 0.6667 ± 0.033 |
| D | t-SNE | Isomap | Laplacian | LLE | Modified LLE | Hessian LLE | LTSA |
|---|---|---|---|---|---|---|---|
| 2 | 0.7302 ± 0.039 | 0.8730 ± 0.025 | 0.8413 ± 0.008 | 0.7937 ± 0.007 | 0.8571 ± 0.011 | 0.9048 ± 0.003 | 0.8889 ± 0.032 |
| 3 | 0.8254 ± 0.013 | 0.9048 ± 0.038 | 0.8254 ± 0.005 | 0.8254 ± 0.005 | 0.8095 ± 0.027 | 0.8730 ± 0.032 | 0.8571 ± 0.011 |
| 4 | 0.9206 ± 0.025 | 0.9524 ± 0.011 | 0.9206 ± 0.012 | 0.8889 ± 0.009 | 0.9048 ± 0.008 | 0.8889 ± 0.022 | 0.8571 ± 0.006 |
| 5 | 0.9206 ± 0.025 | 0.8889 ± 0.007 | 0.9048 ± 0.017 | 0.8571 ± 0.011 | 0.9206 ± 0.009 | 0.8730 ± 0.029 | 0.8730 ± 0.005 |
| 6 | 0.9206 ± 0.047 | 0.8889 ± 0.000 | 0.8889 ± 0.004 | 0.8571 ± 0.005 | 0.8730 ± 0.013 | 0.8730 ± 0.005 | 0.8889 ± 0.016 |
| 7 | 0.9524 ± 0.017 | 0.8889 ± 0.010 | 0.8730 ± 0.027 | 0.8730 ± 0.021 | 0.8254 ± 0.018 | 0.8254 ± 0.008 | 0.8889 ± 0.025 |
| 8 | 0.9683 ± 0.018 | 0.8730 ± 0.028 | 0.8413 ± 0.038 | 0.8730 ± 0.017 | 0.7778 ± 0.022 | 0.7619 ± 0.027 | 0.8254 ± 0.022 |
| 9 | 0.9524 ± 0.015 | 0.8730 ± 0.033 | 0.8730 ± 0.026 | 0.8889 ± 0.005 | 0.7143 ± 0.014 | 0.7937 ± 0.035 | 0.7937 ± 0.034 |
| 10 | 0.9683 ± 0.011 | 0.8730 ± 0.040 | 0.8571 ± 0.029 | 0.8889 ± 0.020 | 0.7619 ± 0.005 | 0.7937 ± 0.012 | 0.7937 ± 0.003 |
| 11 | 0.9524 ± 0.019 | 0.9206 ± 0.032 | 0.7937 ± 0.022 | 0.8889 ± 0.022 | 0.6508 ± 0.027 | 0.7619 ± 0.014 | 0.8413 ± 0.016 |
| 12 | 0.9524 ± 0.011 | 0.9206 ± 0.012 | 0.8095 ± 0.020 | 0.9206 ± 0.029 | 0.6508 ± 0.010 | 0.7619 ± 0.022 | 0.8254 ± 0.018 |
| 13 | 0.9524 ± 0.011 | 0.9206 ± 0.037 | 0.7619 ± 0.014 | 0.8889 ± 0.032 | 0.6349 ± 0.032 | 0.7460 ± 0.029 | 0.7937 ± 0.015 |
| 14 | 0.9524 ± 0.015 | 0.9048 ± 0.022 | 0.7460 ± 0.015 | 0.9048 ± 0.022 | 0.6349 ± 0.027 | 0.7937 ± 0.009 | 0.8413 ± 0.003 |
| 15 | 0.9524 ± 0.015 | 0.8413 ± 0.024 | 0.7619 ± 0.018 | 0.8571 ± 0.008 | 0.6190 ± 0.003 | 0.7460 ± 0.007 | 0.7937 ± 0.005 |
| 16 | 0.9206 ± 0.014 | 0.8413 ± 0.013 | 0.7778 ± 0.014 | 0.8730 ± 0.021 | 0.6508 ± 0.005 | 0.8254 ± 0.011 | 0.7937 ± 0.034 |
| 17 | 0.9206 ± 0.014 | 0.8413 ± 0.015 | 0.6825 ± 0.010 | 0.8889 ± 0.026 | 0.6508 ± 0.018 | 0.8254 ± 0.023 | 0.7937 ± 0.023 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon-Medina, J.X.; Anaya, M.; Pozo, F.; Tibaduiza, D. Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task. Sensors 2020, 20, 4834. https://doi.org/10.3390/s20174834
Leon-Medina JX, Anaya M, Pozo F, Tibaduiza D. Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task. Sensors. 2020; 20(17):4834. https://doi.org/10.3390/s20174834
Chicago/Turabian StyleLeon-Medina, Jersson X., Maribel Anaya, Francesc Pozo, and Diego Tibaduiza. 2020. "Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task" Sensors 20, no. 17: 4834. https://doi.org/10.3390/s20174834
APA StyleLeon-Medina, J. X., Anaya, M., Pozo, F., & Tibaduiza, D. (2020). Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task. Sensors, 20(17), 4834. https://doi.org/10.3390/s20174834