A New Optical Sensor Based on Laser Speckle and Chemometrics for Precision Agriculture: Application to Sunflower Plant-Breeding
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Experiment
2.1.1. Speckle Measurement
2.1.2. Experimental Design
2.2. Data Analysis
2.2.1. Polarized Speckle Parameters
2.2.2. Multivariate Data Analysis
REP-ASCA
3. Results and Discussion
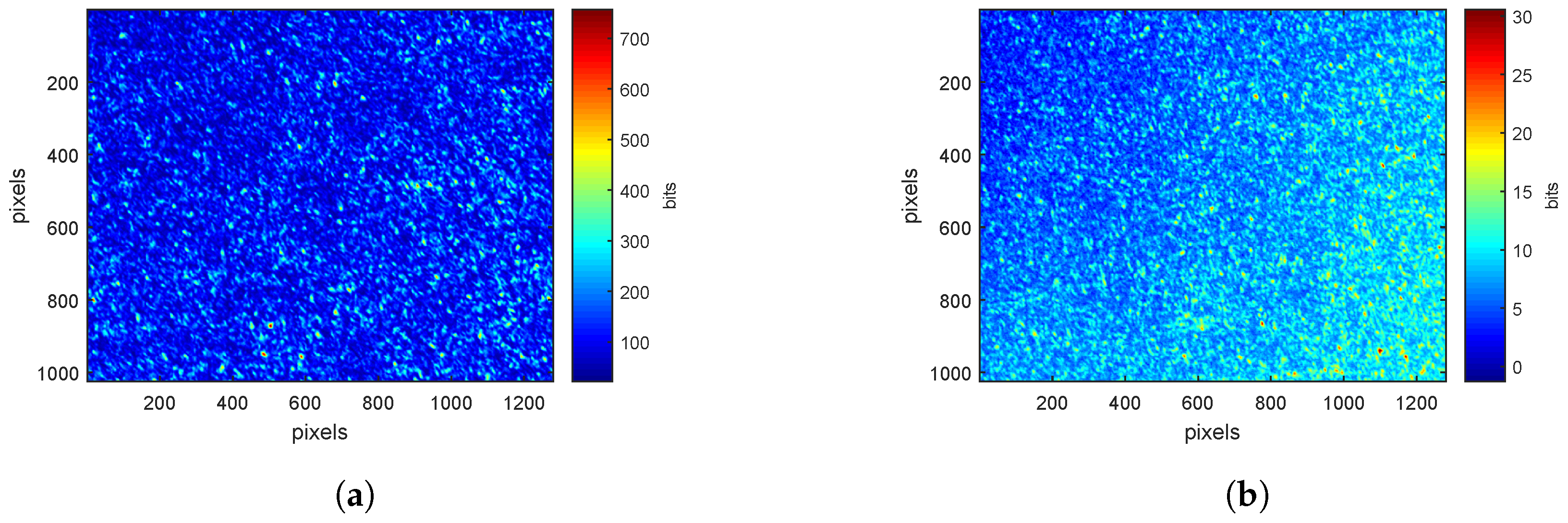
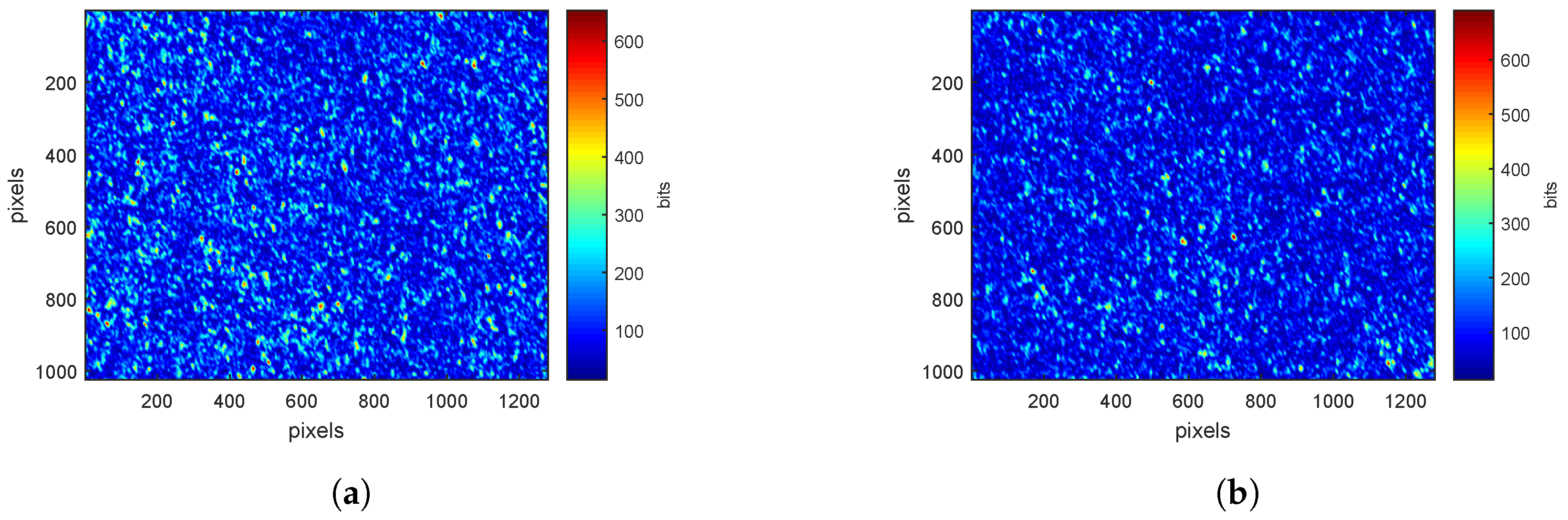
3.1. Speckle Images
3.2. Multivariate Data Analysis
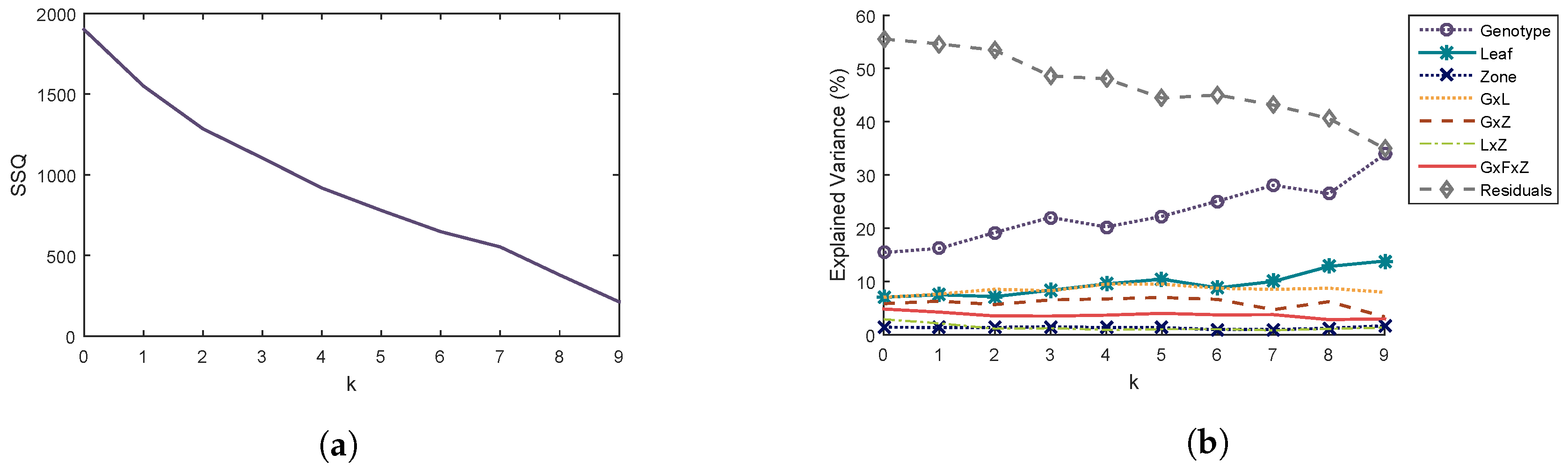
3.2.1. Repeatability Error Reduction
Selection of the k-First Components of the Repeatability Error
Description of the k-First Components of the Repeatability Error
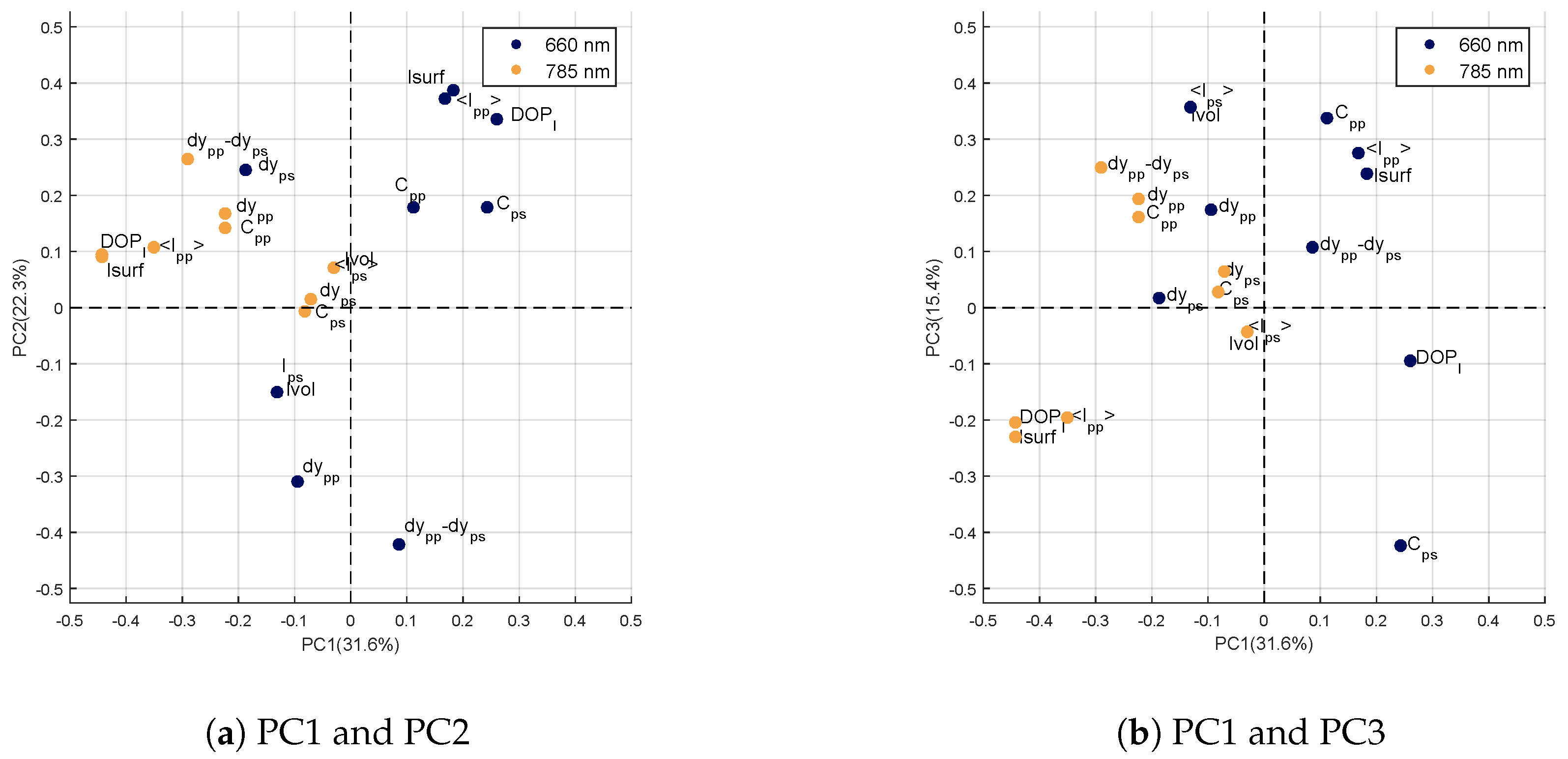
3.2.2. Dataset Orthogonalization and Description of the Genotype Factor
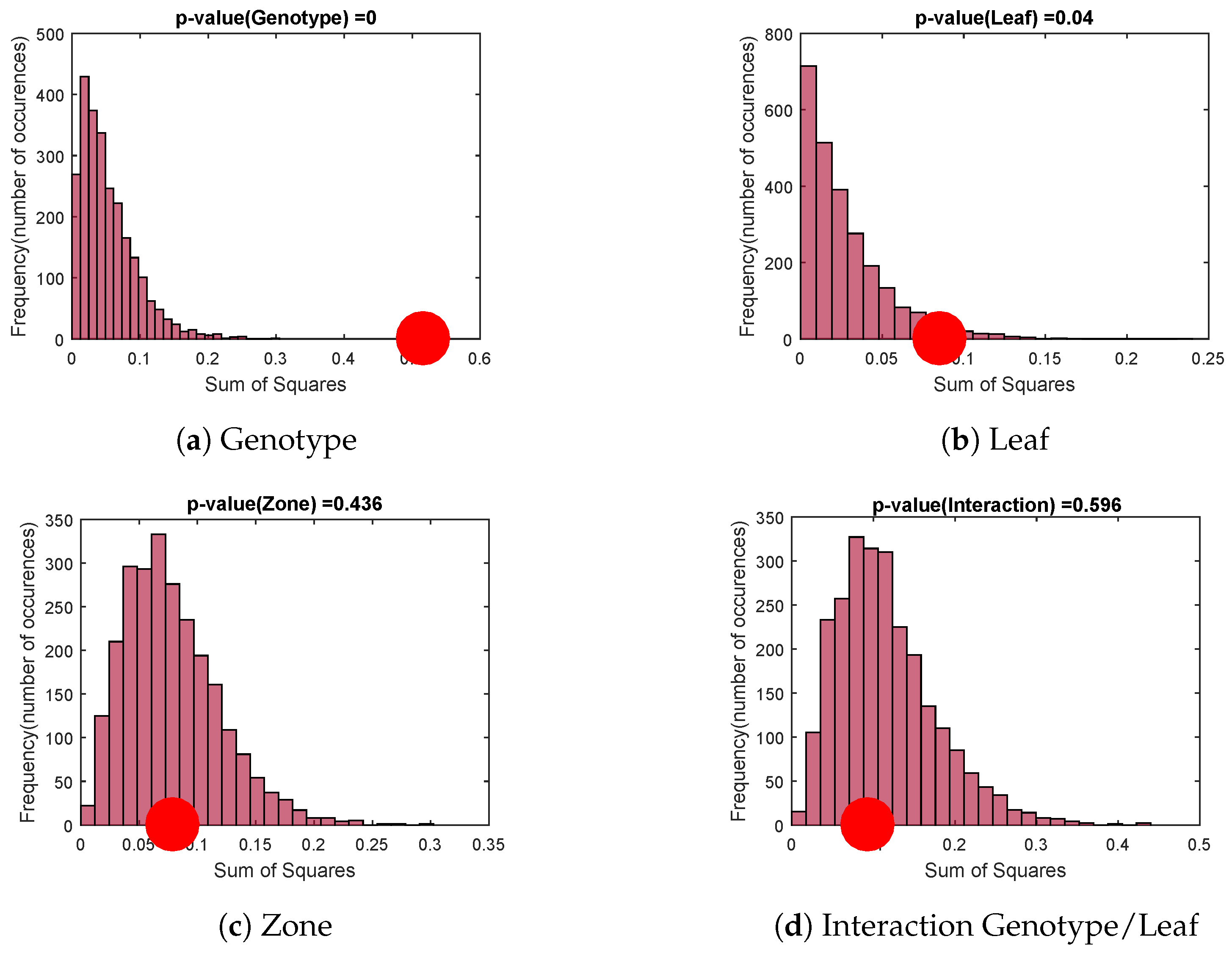
Permutation Test
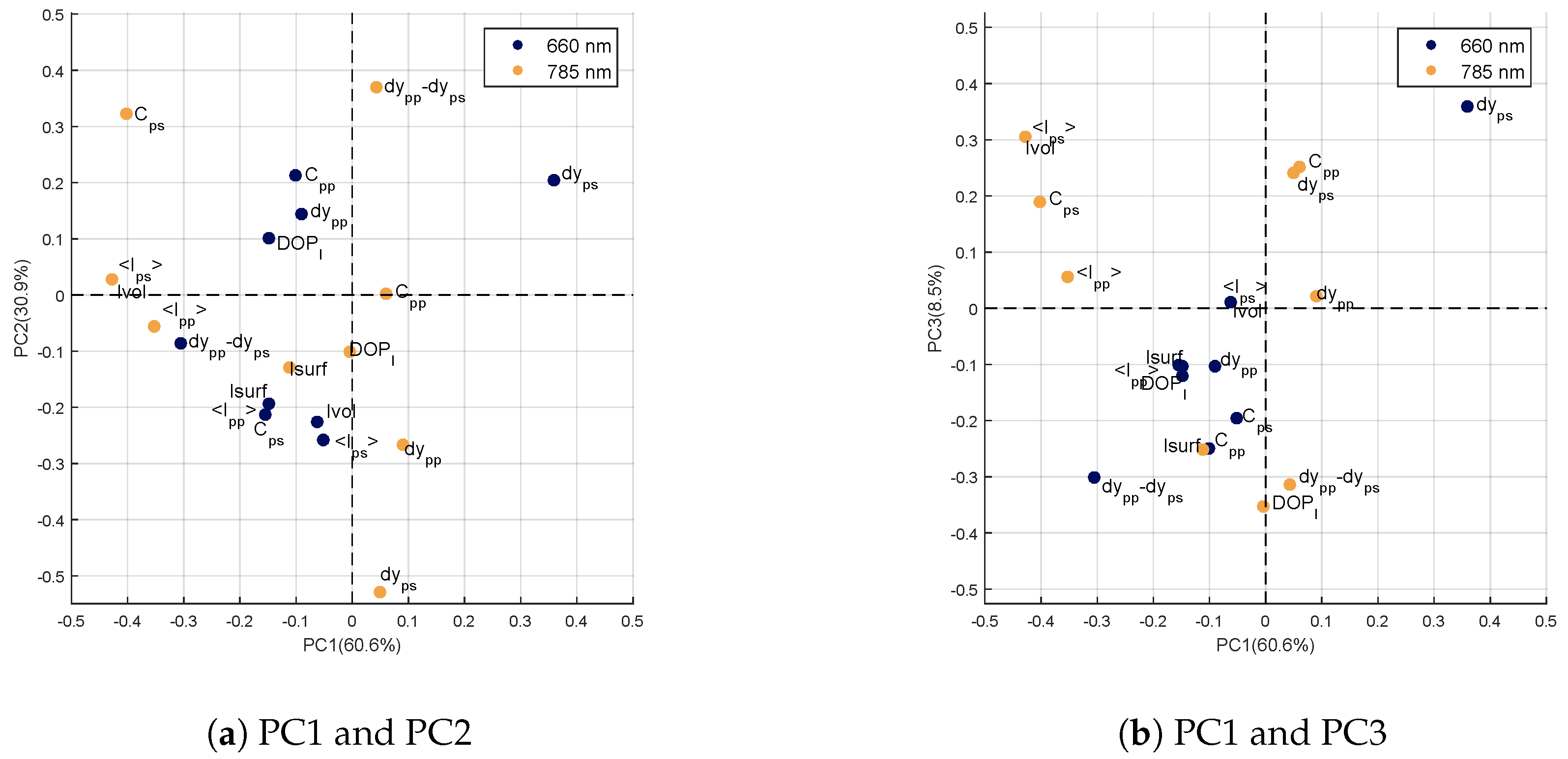
Loadings of the Genotype Factor
Scores for Each Genotype
3.2.3. Example of Application to Discriminant Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blum, A. Plant Breeding for Stress Environments; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Kumar, S.; Gupta, P.; Kumar, J.; Pratap, A. Phenotyping Crop Plants for Drought and Heat-Related Traits. In Phenomics in Crop Plants: Trends, Options and Limitations; Kumar, J., Pratap, A., Kumar, S., Eds.; Springer India: New Delhi, India, 2015; pp. 89–100. [Google Scholar] [CrossRef]
- Blum, A. Drought resistance—Is it really a complex trait? Funct. Plant Biol. 2011, 38, 753. [Google Scholar] [CrossRef] [PubMed]
- Fiorani, F.; Schurr, U. Future Scenarios for Plant Phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Cobb, J.N.; DeClerck, G.; Greenberg, A.; Clark, R.; McCouch, S. Next-generation phenotyping: Requirements and strategies for enhancing our understanding of genotype–phenotype relationships and its relevance to crop improvement. Theor. Appl. Genet. 2013, 126, 867–887. [Google Scholar] [CrossRef] [PubMed]
- Phillips, R.L. Mobilizing Science to Break Yield Barriers. Crop. Sci. 2010, 50, S-99–S-108. [Google Scholar] [CrossRef]
- Reynolds, D.; Baret, F.; Welcker, C.; Bostrom, A.; Ball, J.; Cellini, F.; Lorence, A.; Chawade, A.; Khafif, M.; Noshita, K.; et al. What is cost-efficient phenotyping? Optimizing costs for different scenarios. Plant Sci. 2019, 282, 14–22. [Google Scholar] [CrossRef]
- Araus, J.L.; Cairns, J.E. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef]
- Deery, D.; Jimenez-Berni, J.; Jones, H.; Sirault, X.; Furbank, R. Proximal Remote Sensing Buggies and Potential Applications for Field-Based Phenotyping. Agronomy 2014, 4, 349–379. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D. A Review of Imaging Techniques for Plant Phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef]
- Araus, J.L.; Elazab, A.; Vergara, O.; Cabrera-Bosquet, L.; Serret, M.D.; Zaman-Allah, M.; Cairns, J.E. New Technologies for Phenotyping. In Phenomics; Fritsche-Neto, R., Borém, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–14. [Google Scholar]
- Tuchin, V.V. Light scattering study of tissues. Physics-Uspekhi. 1997, 40, 495–515. [Google Scholar] [CrossRef]
- Briers, J.D. Speckle fluctuations and biomedical optics: Implications and applications. Opt. Eng. 1993, 32, 277–283. [Google Scholar] [CrossRef]
- Pieczywek, P.M.; Cybulska, J.; Szymańska-Chargot, M.; Siedliska, A.; Zdunek, A.; Nosalewicz, A.; Baranowski, P.; Kurenda, A. Early detection of fungal infection of stored apple fruit with optical sensors—Comparison of biospeckle, hyperspectral imaging and chlorophyll fluorescence. Food Control. 2018, 85, 327–338. [Google Scholar] [CrossRef]
- Romero, G.G.; Martinez, C.C.; Alanís, E.E.; Salazar, G.A.; Broglia, V.G.; Álvarez, L. Bio-speckle activity applied to the assessment of tomato fruit ripening. Biosyst. Eng. 2009, 103, 116–119. [Google Scholar] [CrossRef]
- Zerrad, M.; Sorrentini, J.; Soriano, G.; Amra, C. Gradual loss of polarization in light scattered from rough surfaces: Electromagnetic prediction. Opt. Express 2010, 18, 15832–15843. [Google Scholar] [CrossRef] [PubMed]
- Zerrad, M.; Tortel, H.; Soriano, G.; Ghabbach, A.; Amra, C. Spatial depolarization of light from the bulks: Electromagnetic prediction. Opt. Express 2015, 23, 8246–8260. [Google Scholar] [CrossRef] [PubMed]
- Dupont, J.; Orlik, X.; Ghabbach, A.; Zerrad, M.; Soriano, G.; Amra, C. Polarization analysis of speckle field below its transverse correlation width: Application to surface and bulk scattering. Opt. Express 2014, 22, 24133–24141. [Google Scholar] [CrossRef] [PubMed]
- Khaksari, K.; Kirkpatrick, S.J. Combined effects of scattering and absorption on laser speckle contrast imaging. J. Biomed. Opt. 2016, 21, 076002. [Google Scholar] [CrossRef]
- Nader, C.A.; Nassif, R.; Pellen, F.; Le Jeune, B.; Le Brun, G.; Abboud, M. Influence of size, proportion, and absorption coefficient of spherical scatterers on the degree of light polarization and the grain size of speckle pattern. Appl. Opt. 2015, 54, 10369–10375. [Google Scholar] [CrossRef]
- Héran, D.; Ryckewaert, M.; Abautret, Y.; Zerrad, M.; Amra, C.; Bendoula, R. Combining light polarization and speckle measurements with multivariate analysis to predict bulk optical properties of turbid media. Appl. Opt. 2019, 58, 8247. [Google Scholar] [CrossRef]
- Evans, J.R. Leaf anatomy enables more equal access to light and CO2 between chloroplasts. New Phytol. 1999, 143, 93–104. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S. Modelling of Photosynthetic Response to Environmental Conditions. In Physiological Plant Ecology II; Lange, O.L., Nobel, P.S., Osmond, C.B., Ziegler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 549–587. [Google Scholar] [CrossRef]
- Ryckewaert, M.; Gorretta, N.; Henriot, F.; Marini, F.; Roger, J.M. Reduction of repeatability error for analysis of variance-Simultaneous Component Analysis (REP-ASCA): Application to NIR spectroscopy on coffee sample. Anal. Chim. Acta 2020, 1101, 23–31. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote. Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote. Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Bendoula, R.; Gobrecht, A.; Moulin, B.; Roger, J.M.; Bellon-Maurel, V. Improvement of the Chemical Content Prediction of a Model Powder System by Reducing Multiple Scattering Using Polarized Light Spectroscopy. Appl. Spectrosc. 2015, 69, 95–102. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Properties of Laser Speckle Patterns. In Laser Speckle and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 1975; pp. 9–75. [Google Scholar]
- Piederrière, Y.; Cariou, J.; Guern, Y.; Le Jeune, B.; Le Brun, G.; Lotrian, J. Scattering through fluids: Speckle size measurement and Monte Carlo simulations close to and into the multiple scattering. Opt. Express 2004, 12, 176–188. [Google Scholar] [CrossRef] [PubMed]
- Smilde, A.K.; Jansen, J.J.; Hoefsloot, H.C.J.; Lamers, R.J.A.N.; van der Greef, J.; Timmerman, M.E. ANOVA-simultaneous component analysis (ASCA): A new tool for analyzing designed metabolomics data. Bioinformatics 2005, 21, 3043–3048. [Google Scholar] [CrossRef]
- Anderson, M.; Braak, C.T. Permutation tests for multi-factorial analysis of variance. J. Stat. Comput. Simul. 2003, 73, 85–113. [Google Scholar] [CrossRef]
- Gausman, H.W.; Allen, W.A. Optical parameters of leaves of 30 plant species. Plant Physiol. 1973, 52, 57–62. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Grant, L. Diffuse and specular characteristics of leaf reflectance. Remote. Sens. Environ. 1987, 22, 309–322. [Google Scholar] [CrossRef]
- Liland, K.H.; Smilde, A.; Marini, F.; Naes, T. Confidence ellipsoids for ASCA models based on multivariate regression theory: ASCA ellipsoids. J. Chemom. 2018, 32, e2990. [Google Scholar] [CrossRef]
- Monakhova, Y.B.; Godelmann, R.; Kuballa, T.; Mushtakova, S.P.; Rutledge, D.N. Independent components analysis to increase efficiency of discriminant analysis methods (FDA and LDA): Application to NMR fingerprinting of wine. Talanta 2015, 141, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Song, J.J.; Ren, Y.; Yan, F. Classification for high-throughput data with an optimal subset of principal components. Comput. Biol. Chem. 2009, 33, 408–413. [Google Scholar] [CrossRef] [PubMed]

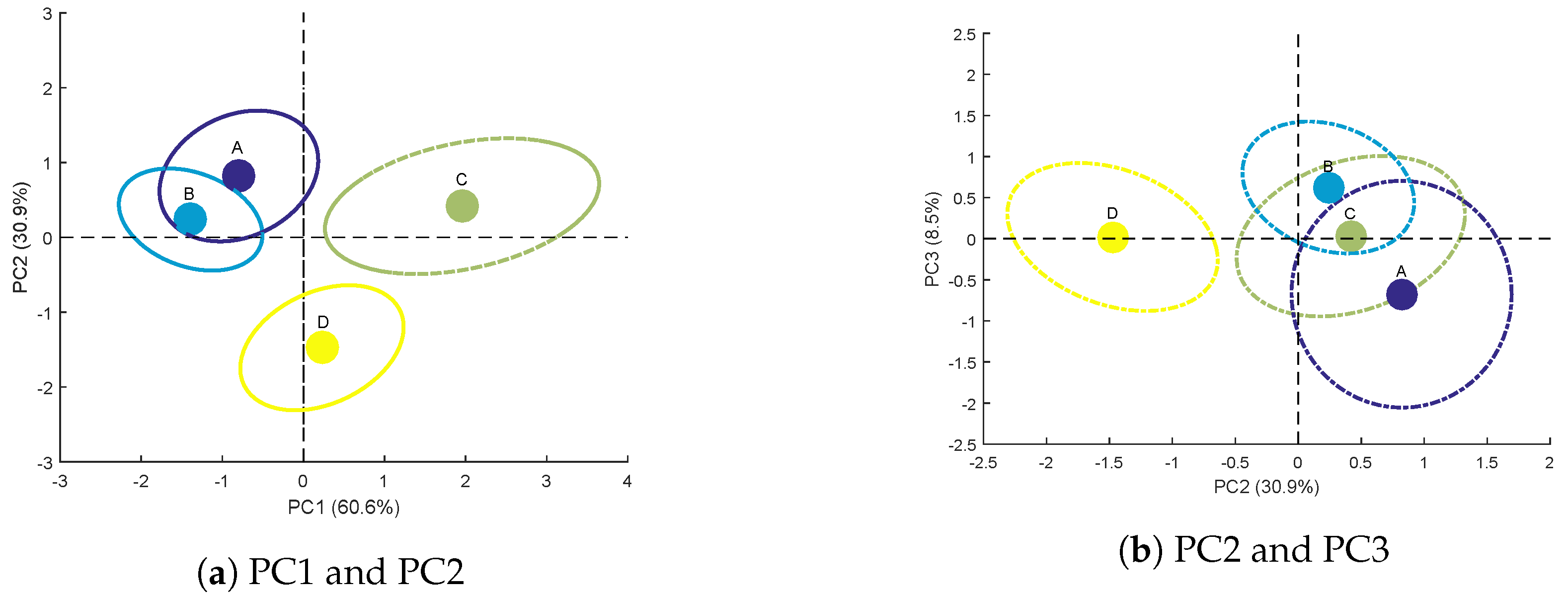
| A | B | C | D | |
| A | 9 | 1 | 2 | 0 |
| B | 1 | 10 | 0 | 0 |
| C | 2 | 1 | 7 | 0 |
| D | 0 | 0 | 3 | 12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryckewaert, M.; Héran, D.; Faur, E.; George, P.; Grèzes-Besset, B.; Chazallet, F.; Abautret, Y.; Zerrad, M.; Amra, C.; Bendoula, R. A New Optical Sensor Based on Laser Speckle and Chemometrics for Precision Agriculture: Application to Sunflower Plant-Breeding. Sensors 2020, 20, 4652. https://doi.org/10.3390/s20164652
Ryckewaert M, Héran D, Faur E, George P, Grèzes-Besset B, Chazallet F, Abautret Y, Zerrad M, Amra C, Bendoula R. A New Optical Sensor Based on Laser Speckle and Chemometrics for Precision Agriculture: Application to Sunflower Plant-Breeding. Sensors. 2020; 20(16):4652. https://doi.org/10.3390/s20164652
Chicago/Turabian StyleRyckewaert, Maxime, Daphné Héran, Emma Faur, Pierre George, Bruno Grèzes-Besset, Frédéric Chazallet, Yannick Abautret, Myriam Zerrad, Claude Amra, and Ryad Bendoula. 2020. "A New Optical Sensor Based on Laser Speckle and Chemometrics for Precision Agriculture: Application to Sunflower Plant-Breeding" Sensors 20, no. 16: 4652. https://doi.org/10.3390/s20164652
APA StyleRyckewaert, M., Héran, D., Faur, E., George, P., Grèzes-Besset, B., Chazallet, F., Abautret, Y., Zerrad, M., Amra, C., & Bendoula, R. (2020). A New Optical Sensor Based on Laser Speckle and Chemometrics for Precision Agriculture: Application to Sunflower Plant-Breeding. Sensors, 20(16), 4652. https://doi.org/10.3390/s20164652





