Wavelength Selection FOR Rapid Identification of Different Particle Size Fractions of Milk Powder Using Hyperspectral Imaging
Abstract
1. Introduction
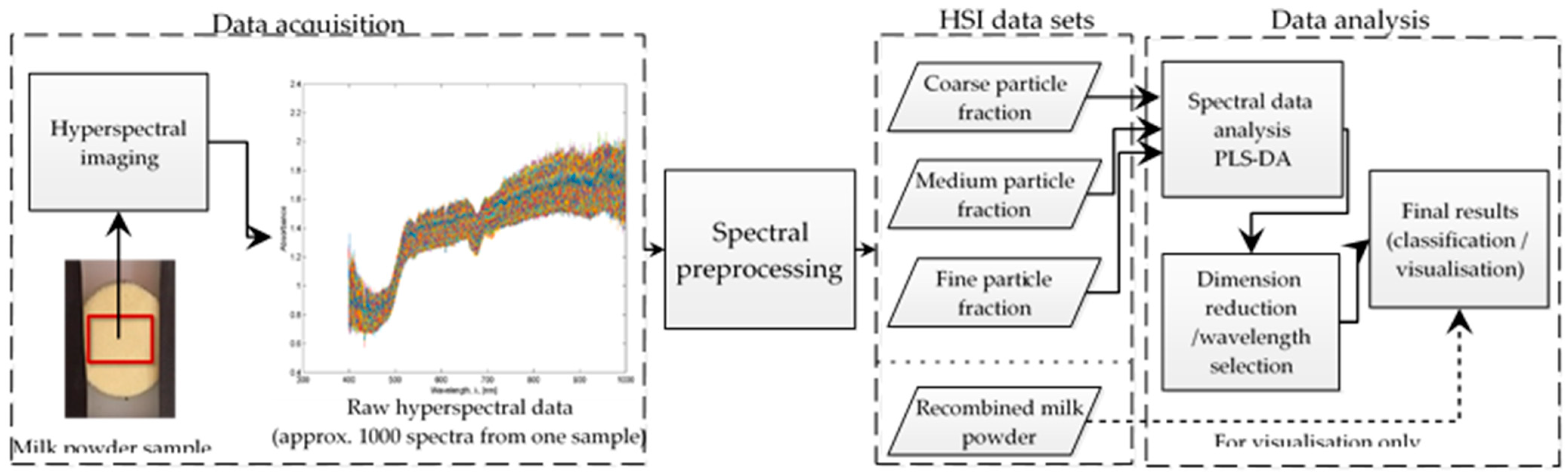
2. Materials and Methods
2.1. Milk Powder Sample Preparation
2.2. Hyperspectral Imaging Setup
2.3. Data Pre-Processing
2.4. Multivariate Data Analysis
Partial Least Square Discriminant Analysis (PLS-DA)
2.5. Wavelength Selection
2.5.1. Principal Component Analysis (PCA)
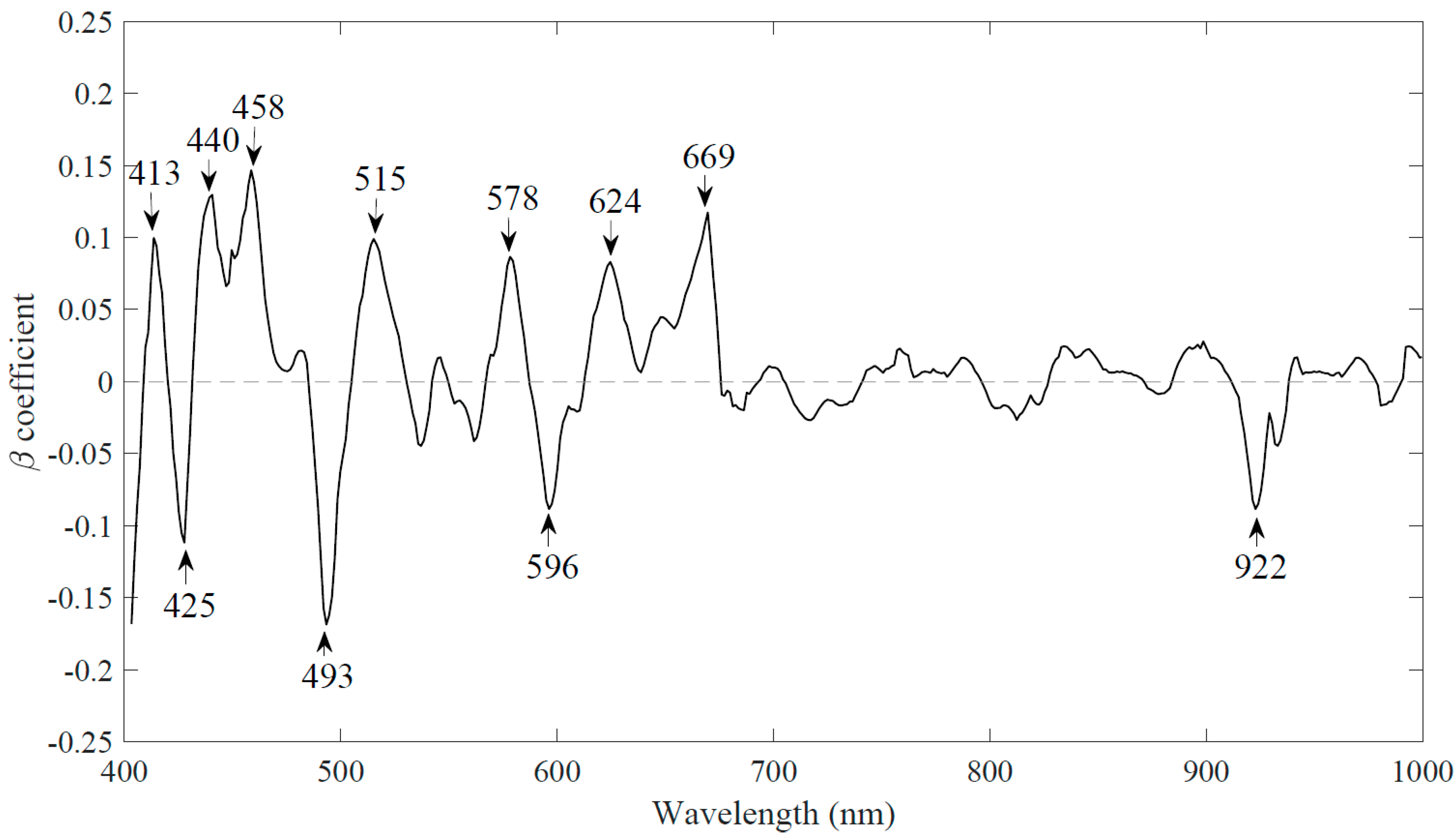
2.5.2. Weighted Regression Coefficient (WRC) Analysis
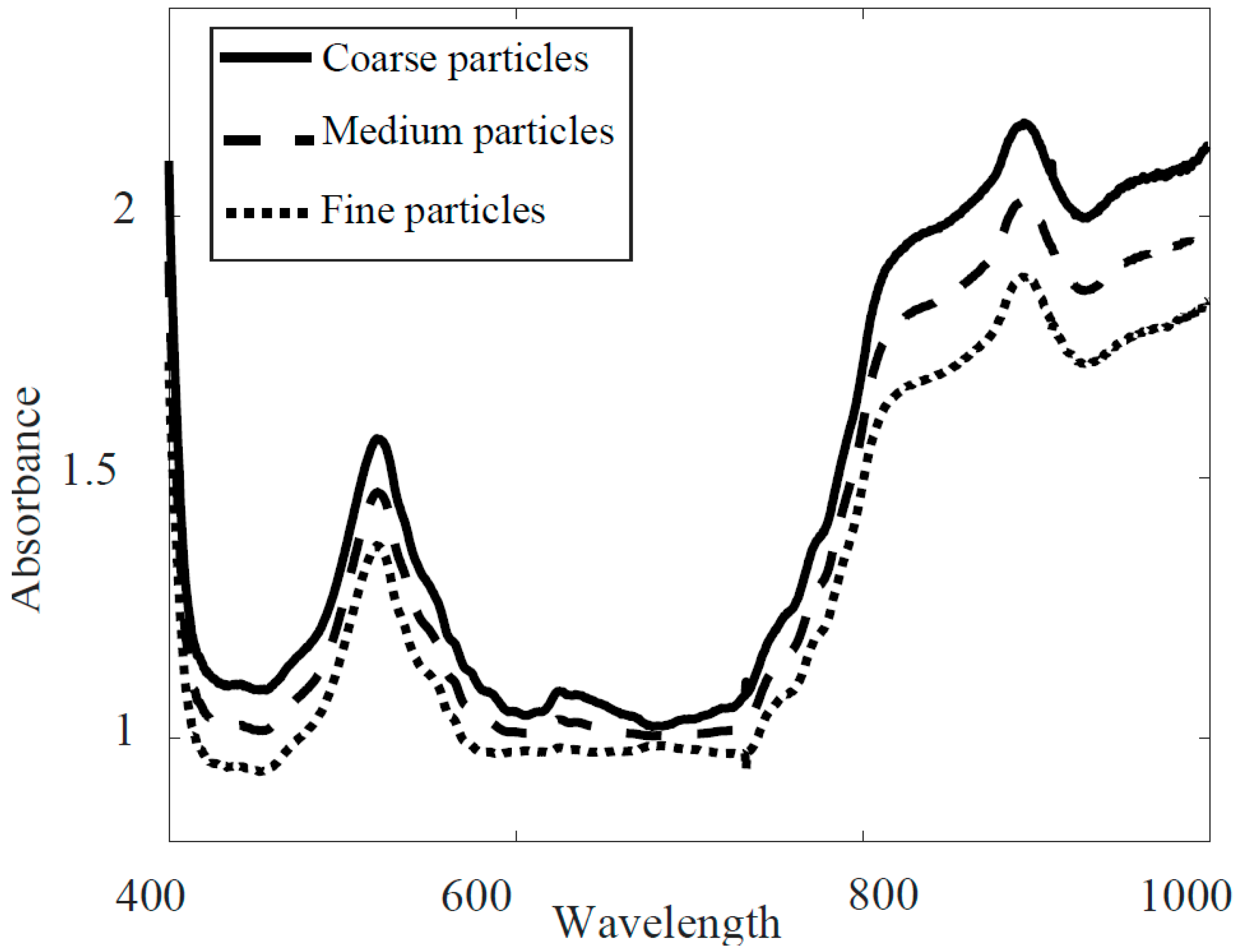
3. Results
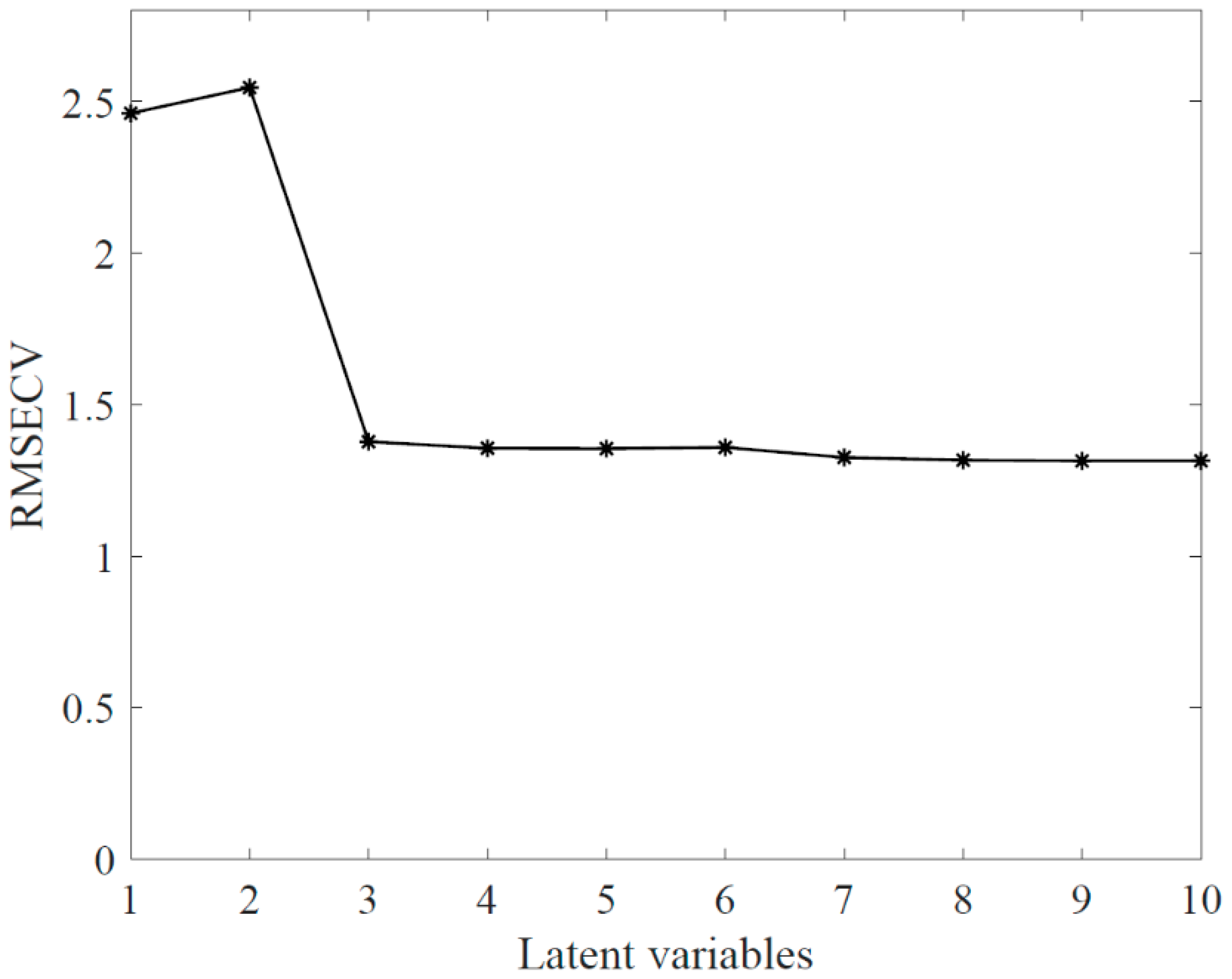
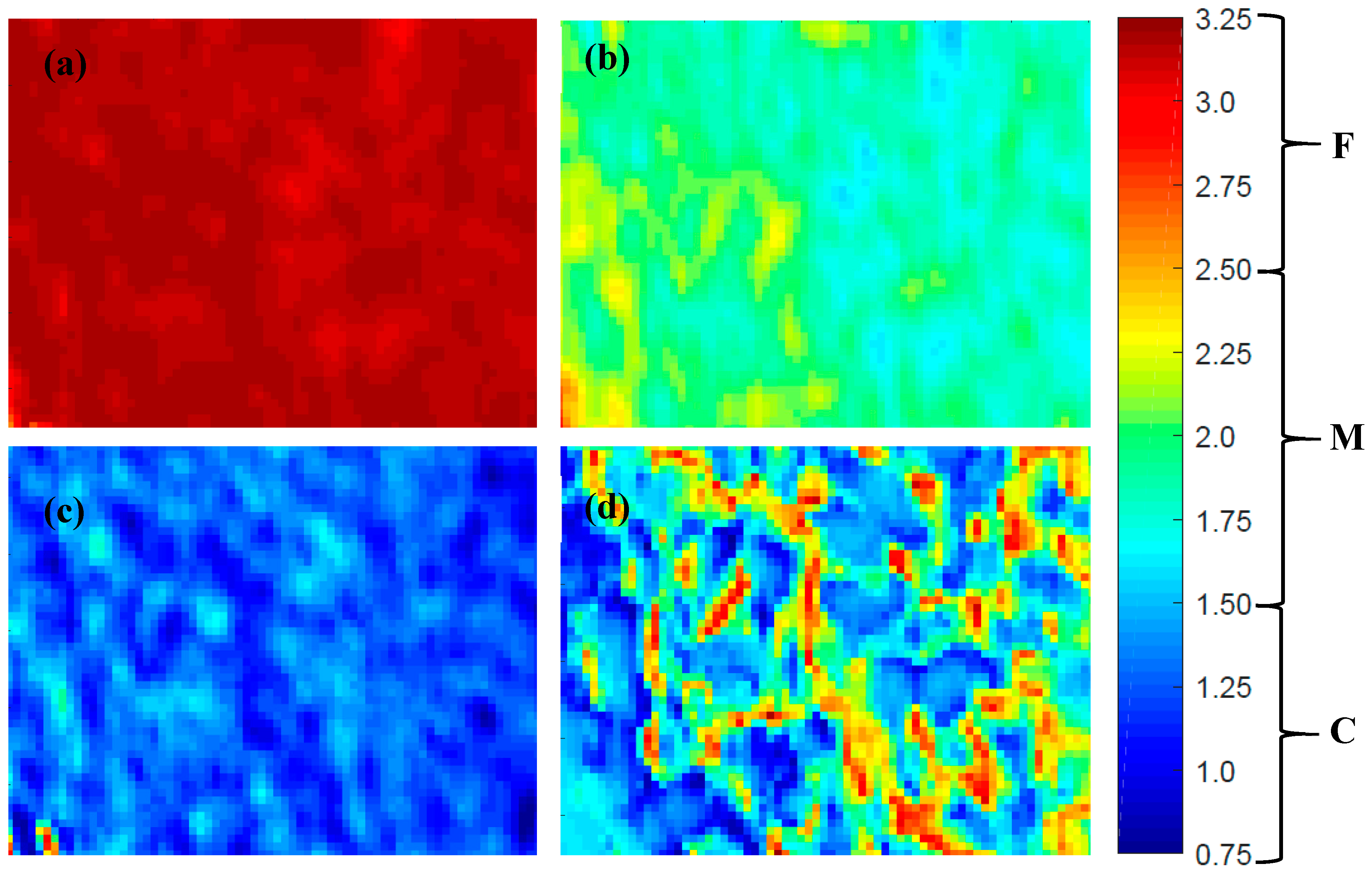
3.1. Full-Range PLS-DA Model
3.2. Selection of Wavelengths
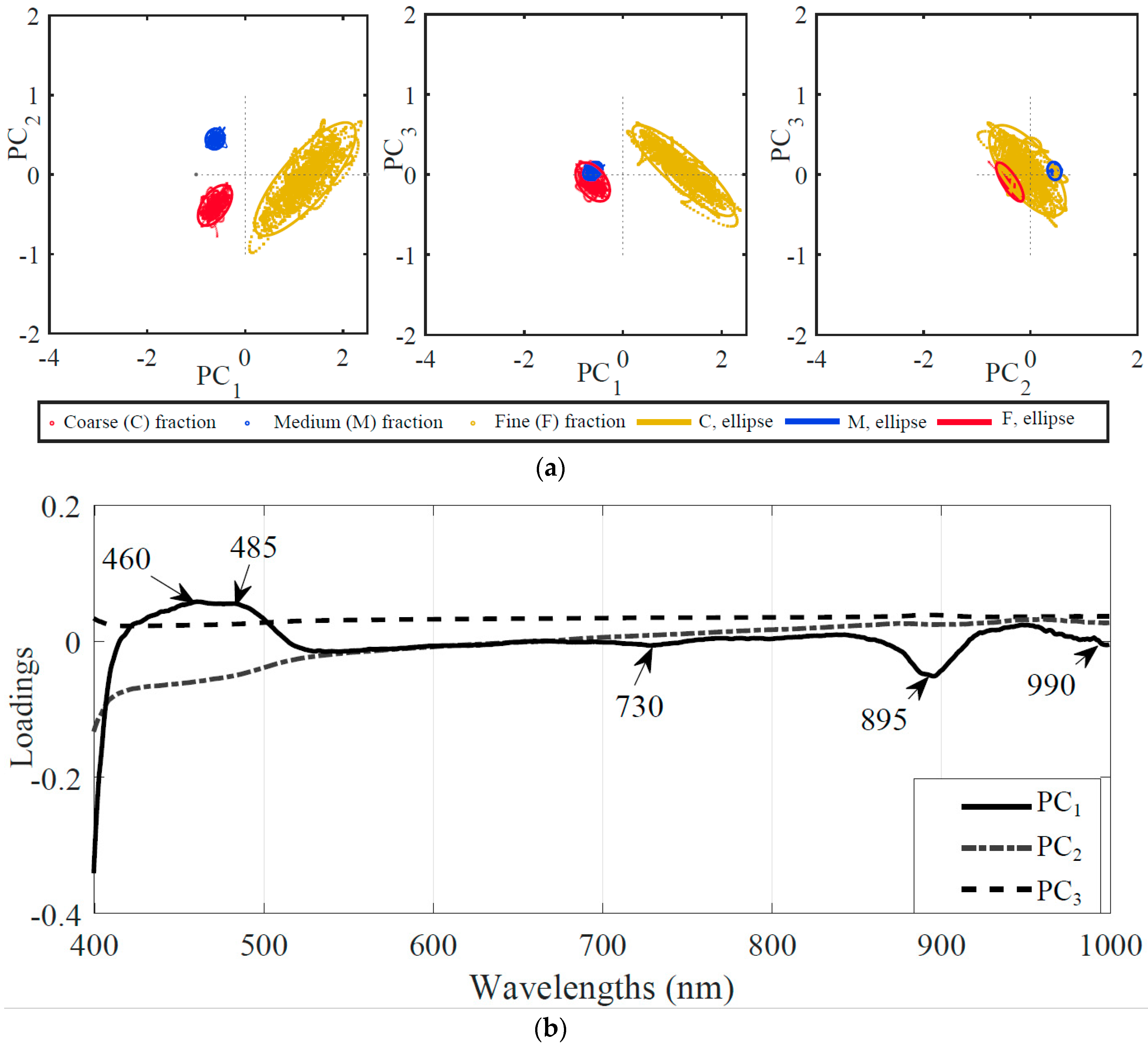
3.2.1. Reduced Number of Wavelengths Based upon Principal Component Analysis (PCA)
3.2.2. Reduced Number of Wavelengths Based upon Weighted Regression Coefficient (WRC)
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FDA. PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance; U.S. Department of Health and Human Services, Food and Drug Administration Center for Biologics Evaluation and Research: Rockville, MD, USA, 2004. [Google Scholar]
- Amigo, J.M. Data Handling in Science and Technology, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Vote, D.; Belk, K.; Tatum, J.; Scanga, J.; Smith, G. Online prediction of beef tenderness using a computer vision system equipped with a BeefCam module. J. Anim. Sci. 2003, 81, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.-W. Infrared Spectroscopy for Food Quality Analysis and Control; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Geladi, P.; Manley, M. Near-Infrared Hyperspectral Imaging in Food Research. In Raman, Infrared, and Near-Infrared Chemical Imaging; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 243–260. [Google Scholar]
- Qiao, T.; Ren, J.; Craigie, C.; Zabalza, J.; Maltin, C.; Marshall, S. Singular spectrum analysis for improving hyperspectral imaging based beef eating quality evaluation. Comput. Electron. Agric. 2015, 115, 21–25. [Google Scholar] [CrossRef]
- Sendin, K.; Williams, P.J.; Manley, M. Near infrared hyperspectral imaging in quality and safety evaluation of cereals. Crit. Rev. Food Sci. Nutr. 2018, 58, 575–590. [Google Scholar] [CrossRef] [PubMed]
- Nanyam, Y.; Choudhary, R.; Gupta, L.; Paliwal, J. A decision-fusion strategy for fruit quality inspection using hyperspectral imaging. Biosyst. Eng. 2012, 111, 118–125. [Google Scholar] [CrossRef]
- Barreto, A.; Cruz-Tirado, J.P.; Siche, R.; Quevedo, R. Determination of starch content in adulterated fresh cheese using hyperspectral imaging. Food Biosci. 2018, 21, 14–19. [Google Scholar] [CrossRef]
- Burger, J.; Geladi, P. Hyperspectral NIR image regression part II: Dataset preprocessing diagnostics. J. Chemom. 2006, 20, 106–119. [Google Scholar] [CrossRef]
- Rajalahti, T.; Kvalheim, O.M. Multivariate data analysis in pharmaceutics: A tutorial review. Int. J. Pharm. 2011, 417, 280–290. [Google Scholar] [CrossRef]
- Liu, D.; Sun, D.-W.; Zeng, X.-A. Recent Advances in Wavelength Selection Techniques for Hyperspectral Image Processing in the Food Industry. Food Bioprocess Technol. 2014, 7, 307–323. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M.L. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Osborne, D.S.; Künnemeyer, R.; Jordan, R.B. Method of Wavelength Selection for Partial Least Squares. R. Soc. Chem. 1997, 122, 1531–1537. [Google Scholar] [CrossRef]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Huang, Y.; Min, S.; Duan, J.; Wu, L.; Li, Q. Identification of additive components in powdered milk by NIR imaging methods. Food Chem. 2014, 145, 278–283. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Kim, M.S.; Chao, K.; Qin, J.; Lim, J.; Lee, H.; Garrido-Varo, A.; Pérez-Marín, D.; Ying, Y. Detection of melamine in milk powders based on NIR hyperspectral imaging and spectral similarity analyses. J. Food Eng. 2014, 124, 97–104. [Google Scholar] [CrossRef]
- Forchetti, D.A.P.; Poppi, R.J. Use of NIR hyperspectral imaging and multivariate curve resolution (MCR) for detection and quantification of adulterants in milk powder. LWT Food Sci. Technol. 2017, 76, 337–343. [Google Scholar] [CrossRef]
- Huang, M.; Kim, M.S.; Delwiche, S.R.; Chao, K.; Qin, J.; Mo, C.; Esquerre, C.; Zhu, Q. Quantitative analysis of melamine in milk powders using near-infrared hyperspectral imaging and band ratio. J. Food Eng. 2016, 181, 10–19. [Google Scholar] [CrossRef]
- Munir, M.T.; Wilson, D.I.; Yu, W.; Young, B.R. An evaluation of hyperspectral imaging for characterising milk powders. J. Food Eng. 2018, 221, 1–10. [Google Scholar] [CrossRef]
- Schuck, P. Milk Powder: Physical and Functional Properties of Milk Powders. In Encyclopedia of Dairy Sciences; Mississippi State University: Mississippi State, MS, USA, 2011. [Google Scholar]
- Silva, J.V.C.; O’Mahony, J.A. Flowability and wetting behaviour of milk protein ingredients as influenced by powder composition, particle size and microstructure. Int. J. Dairy Technol. 2016, 70, 277–286. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard Normal Variate Transformation and De-trending of Near-Infrared Diffuse Reflectance Spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Khan, A.; Munir, M.; Yu, W.; Young, B.R. A review towards hyperspectral imaging for real-time quality control of food products with an illustrative case study of milk powder production. J. Food Bioprocess Technol. 2020. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
- Amigo, J.M.; Ravn, C.; Gallagher, N.B.; Bro, R. A comparison of a common approach to partial least squares-discriminant analysis and classical least squares in hyperspectral imaging. Int. J. Pharm. 2009, 373, 179–182. [Google Scholar] [CrossRef] [PubMed]
- Gad, S.C. Pharmaceutical Manufacturing Handbook: Production and Processes; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 5. [Google Scholar]
- Williams, P.; Norris, K. Near-Infrared Technology in the Agricultural and Food Industries; American Association of Cereal Chemists, Inc.: Saint Paul, MI, USA, 1987. [Google Scholar]
- Sun, D.-W. Modern Techniques for Food Authentication; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Boiarkina, I.; Depree, N.; Yu, W.; Wilson, D.; Young, B. Rapid particle size measurements used as a proxy to control instant whole milk powder dispersibility. Dairy Sci. Technol. 2017, 96, 777–786. [Google Scholar] [CrossRef]
- Wold, H. Estimation of principal components and related models by iterative least squares. In Multivariate Analysis; Krishnaiaah, P.R., Ed.; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Xing, J.; De Baerdemaeker, J. Bruise detection on ‘Jonagold’apples using hyperspectral imaging. Postharvest Biol. Technol. 2005, 37, 152–162. [Google Scholar] [CrossRef]
- Zhang, H.; Qiao, X.; Li, Z.; Li, D. Effective Wavelengths Selection of Hyperspectral Images of Plastic Films in Cotton. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Beijing, China, 27–30 September 2015; pp. 519–527. [Google Scholar]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, H.; Liu, F.; He, Y. Application of Near-Infrared Hyperspectral Imaging with Variable Selection Methods to Determine and Visualize Caffeine Content of Coffee Beans. Food Bioprocess Technol. 2017, 10, 213–221. [Google Scholar] [CrossRef]
- ElMasry, G.; Sun, D.-W.; Allen, P. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef. J. Food Eng. 2012, 110, 127–140. [Google Scholar] [CrossRef]
- ElMasry, G.; Iqbal, A.; Sun, D.-W.; Allen, P.; Ward, P. Quality classification of cooked, sliced turkey hams using NIR hyperspectral imaging system. J. Food Eng. 2011, 103, 333–344. [Google Scholar] [CrossRef]
- Rutlidge, H.T.; Reedy, B.J. Classification of Heterogeneous Solids Using Infrared Hyperspectral Imaging. Appl. Spectrosc. 2009, 63, 172–179. [Google Scholar] [CrossRef] [PubMed]
- Anzanello, M.; Fogliatto, F. A review of recent variable selection methods in industrial and chemometrics applications. Eur. J. Ind. Eng. 2014, 8, 619. [Google Scholar] [CrossRef]
- Ravikanth, L.; Jayas, D.S.; White, N.D.G.; Fields, P.G.; Sun, D.-W. Extraction of Spectral Information from Hyperspectral Data and Application of Hyperspectral Imaging for Food and Agricultural Products. Food Bioprocess Technol. 2017, 10, 1–33. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2018. [Google Scholar] [CrossRef]

| Model | Wavelengths | LVs | Calibration | Prediction | Cross-Validation | RPD | Computation Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Rc2 | RMSEC | Rp2 | RMSEP | Rcv2 | RMSECV | |||||
| PLS-DA | 933 | 3 | 0.975 | 0.128 | 0.943 | 0.147 | 0.954 | 0.129 | 5.835 | 32.2 ± 1.5 |
| WRC-PLS-DA | 11 | 3 | 0.982 | 0.016 | 0.979 | 0.013 | 0.979 | 0.015 | 5.942 | 2.8 ± 0.3 |
| PCA-PLS-DA | 5 | 3 | 0.971 | 0.062 | 0.962 | 0.066 | 0.964 | 0.648 | 5.716 | 2.1 ± 0.2 |
| PLS-DA | Predicted Class | FN | Sensitivity | |||
|---|---|---|---|---|---|---|
| C | M | F | ||||
| Actual class | C | 37,651 | 3964 | 385 | 4349 | 0.897 |
| M | 1236 | 31,295 | 9469 | 10,705 | 0.745 | |
| F | 1061 | 5067 | 35,872 | 6128 | 0.854 | |
| FP | 2297 | 9031 | 9854 | Overall accuracy | 0.832 | |
| Specificity | 0.967 | 0.890 | 0.875 | |||
| WRC-PLS-DA | Predicted class | FN | Sensitivity | |||
| C | M | F | ||||
| Actual class | C | 40,511 | 1086 | 403 | 1489 | 0.964 |
| M | 1909 | 36,854 | 3237 | 5146 | 0.877 | |
| F | 63 | 3112 | 38,825 | 3175 | 0.924 | |
| FP | 1972 | 4198 | 3640 | Overall accuracy | 0.922 | |
| Specificity | 0.975 | 0.949 | 0.955 | |||
| PCA-PLS-DA | Predicted class | FN | Sensitivity | |||
| C | M | F | ||||
| Actual class | C | 38,456 | 2946 | 598 | 3544 | 0.916 |
| M | 1380 | 35,591 | 5029 | 6409 | 0.847 | |
| F | 345 | 3047 | 38,608 | 3392 | 0.919 | |
| FP | 1725 | 5993 | 5627 | Overall accuracy | 0.894 | |
| Specificity | 0.977 | 0.928 | 0.929 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Munir, M.T.; Yu, W.; Young, B. Wavelength Selection FOR Rapid Identification of Different Particle Size Fractions of Milk Powder Using Hyperspectral Imaging. Sensors 2020, 20, 4645. https://doi.org/10.3390/s20164645
Khan A, Munir MT, Yu W, Young B. Wavelength Selection FOR Rapid Identification of Different Particle Size Fractions of Milk Powder Using Hyperspectral Imaging. Sensors. 2020; 20(16):4645. https://doi.org/10.3390/s20164645
Chicago/Turabian StyleKhan, Asma, Muhammad Tajammal Munir, Wei Yu, and Brent Young. 2020. "Wavelength Selection FOR Rapid Identification of Different Particle Size Fractions of Milk Powder Using Hyperspectral Imaging" Sensors 20, no. 16: 4645. https://doi.org/10.3390/s20164645
APA StyleKhan, A., Munir, M. T., Yu, W., & Young, B. (2020). Wavelength Selection FOR Rapid Identification of Different Particle Size Fractions of Milk Powder Using Hyperspectral Imaging. Sensors, 20(16), 4645. https://doi.org/10.3390/s20164645





