A Novel Sensor Prototype with Enhanced and Adaptive Sensitivity Based on Negative Stiffness Mechanism
Abstract
1. Introduction
2. The Mechanism of the Sensitive Sensor Prototype Based on Negative Stiffness
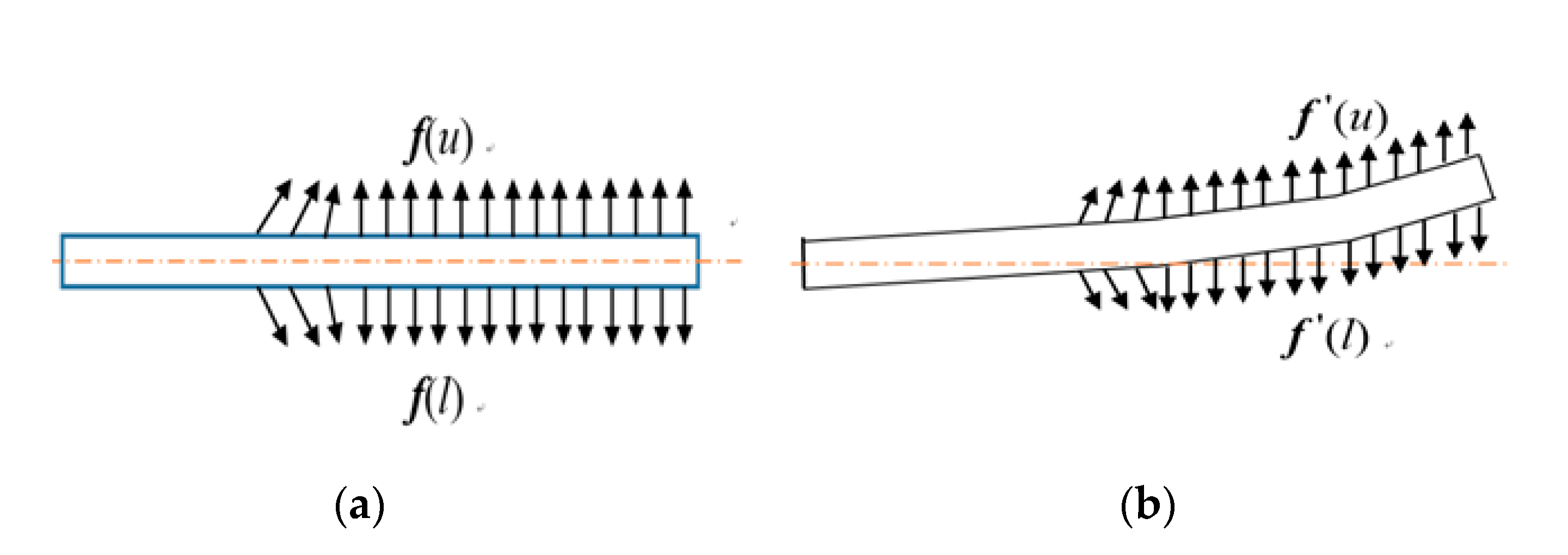
2.1. The Traditional Linear Model with Positive Stiffness Mechanism
2.2. The Proposed Model with Negative Stiffness Mechanisms
3. The Design and Manufacture of the Proposed Sensor Prototype
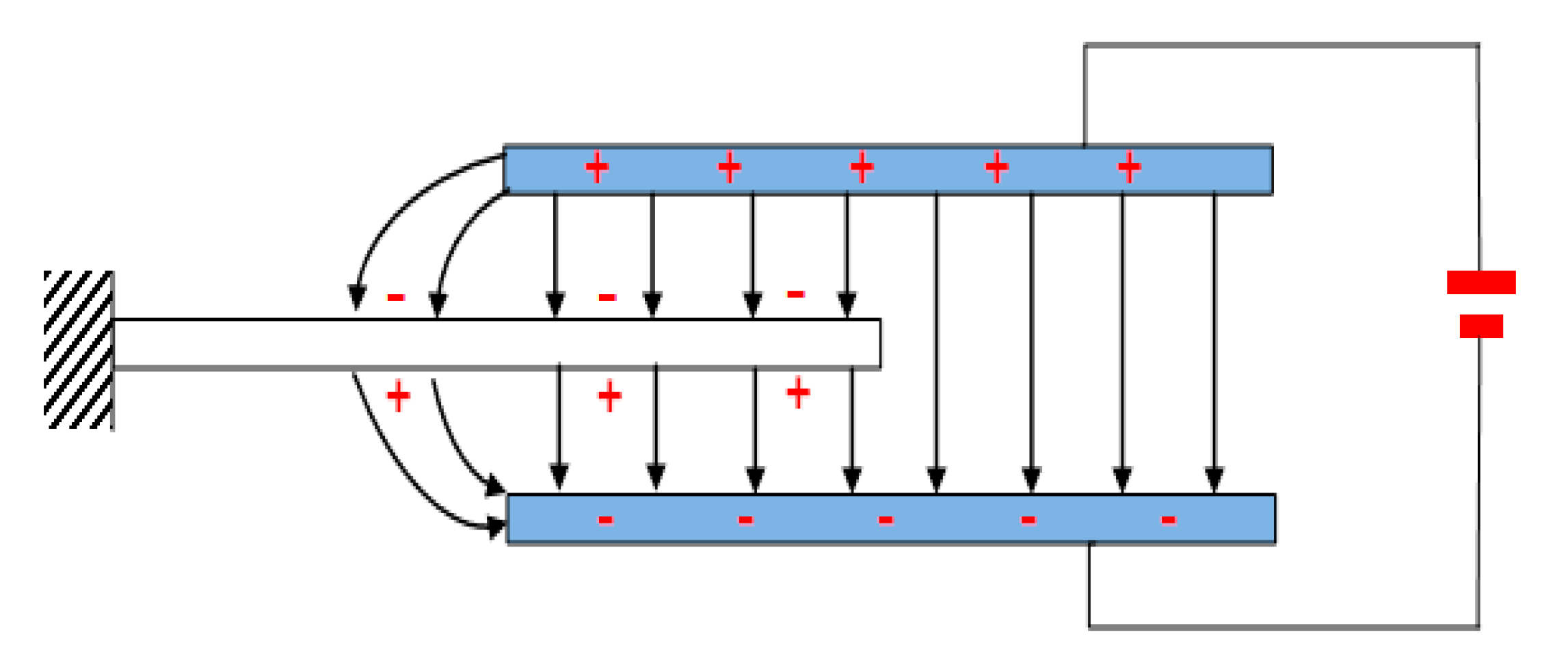
3.1. The Design of the Proposed Sensor Prototype
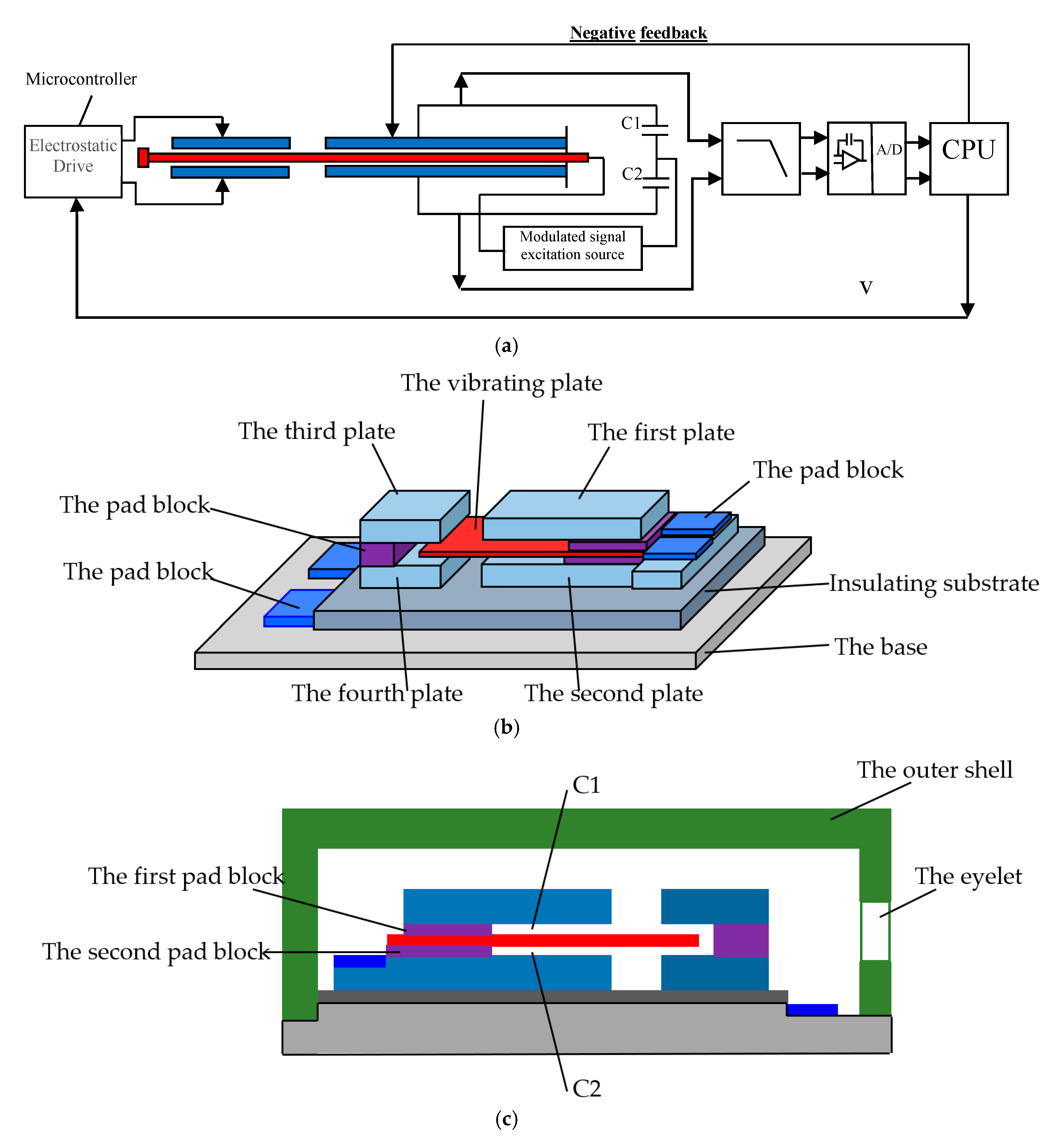
3.2. The Manufacture of the Proposed Sensor Prototype with Packaging
3.3. Post-Signal Processing
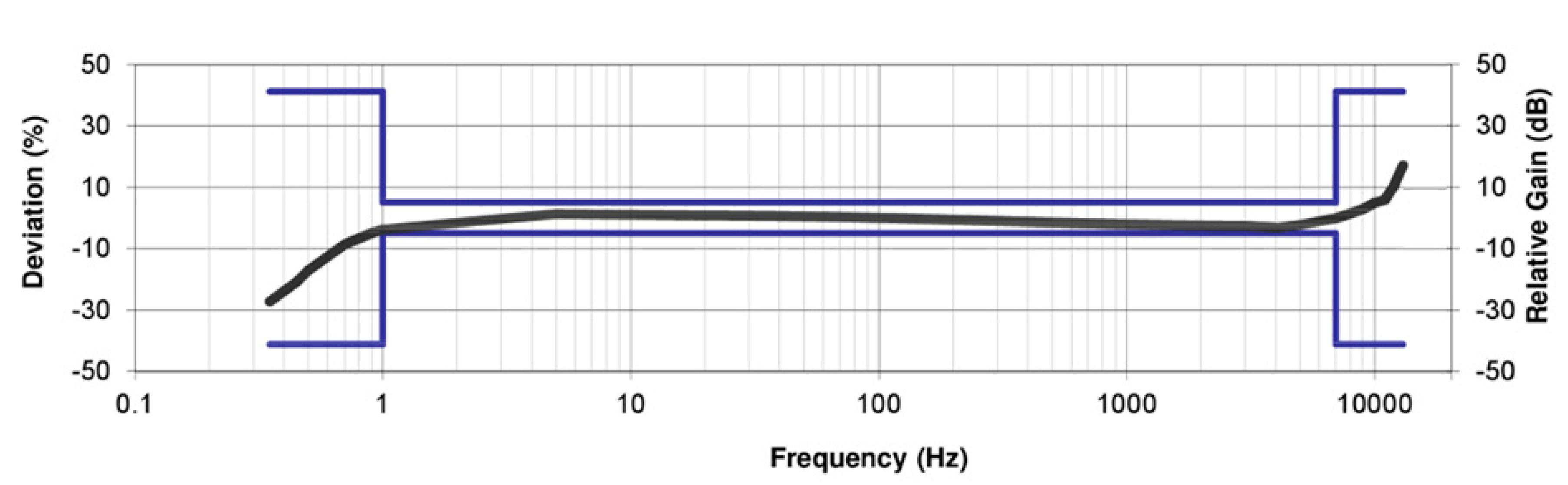
4. Preliminary Testing
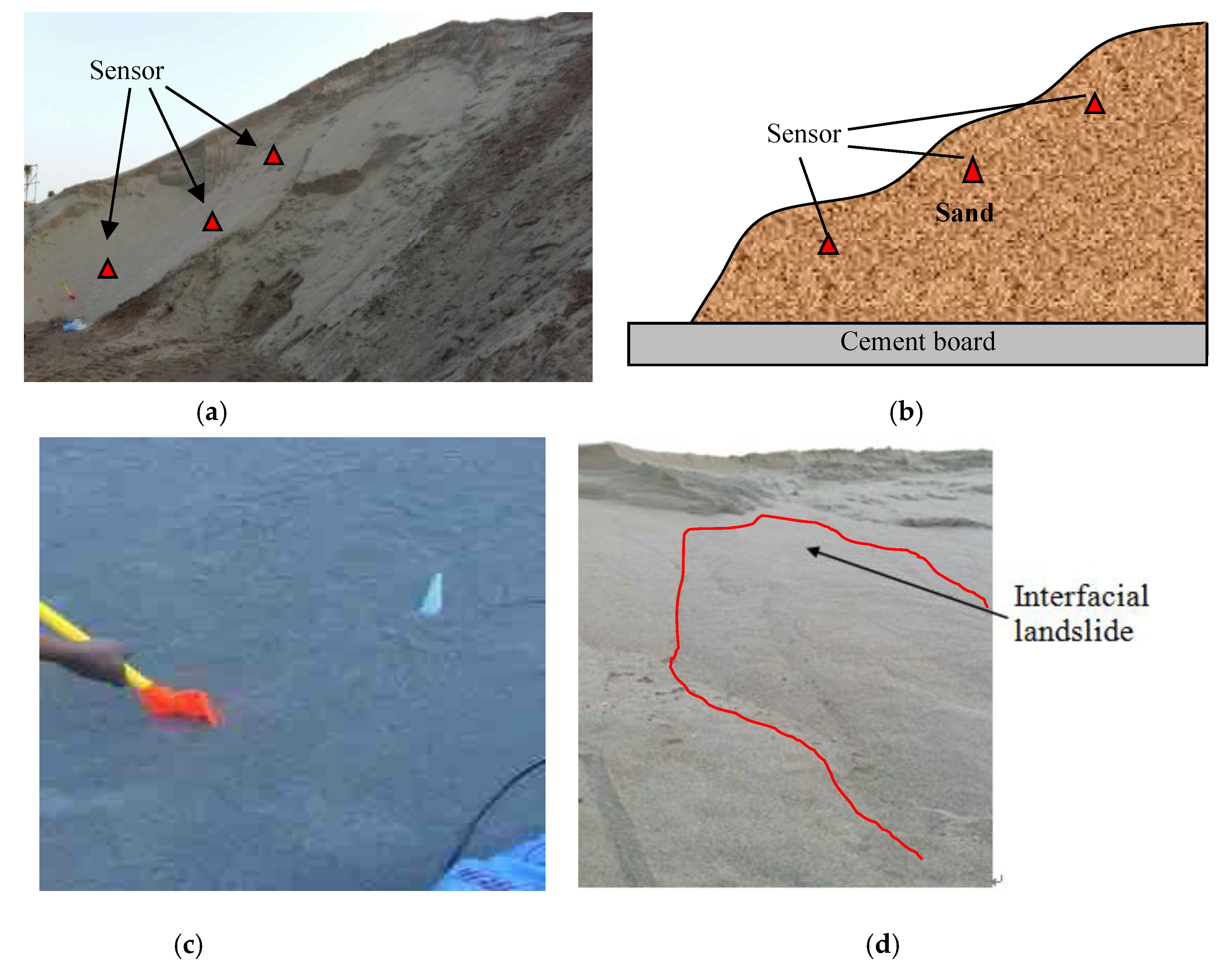
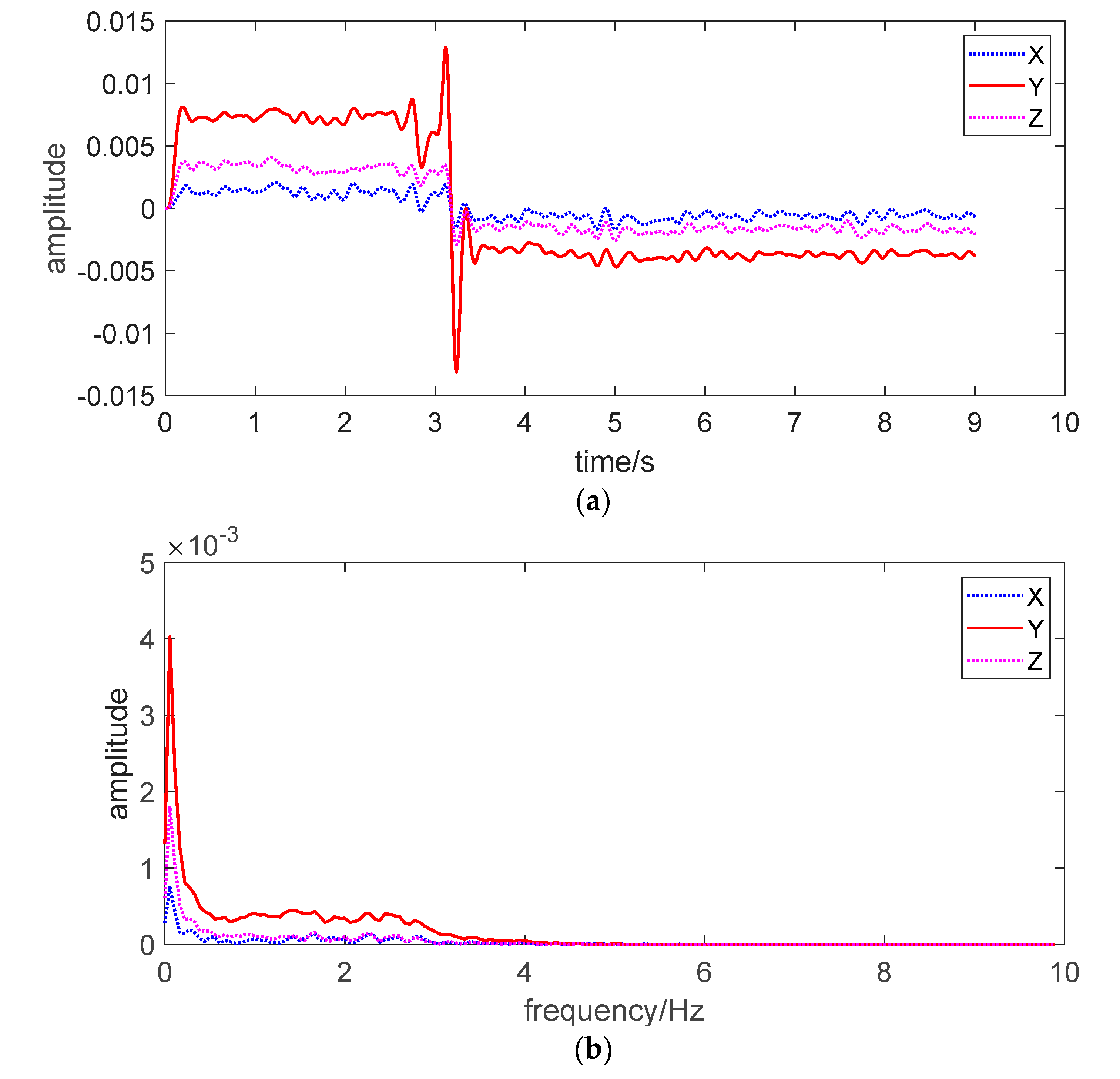
5. Preliminary Experimental Monitoring Sand Interfacial Slide by the Sensor Prototype
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.; Yao, D.; Wang, Z.; Liu, C.; Wuliji, N.; Yang, L.; Li, L.; Amini, F. Model test on rainfall-induced loess–mudstone interfacial landslides in Qingshuihe, China. Environ. Earth Sci. 2016, 75, 835. [Google Scholar] [CrossRef]
- Wang, W.S.; Wan, X. Distribution regularity and forming condition of loess landslide. J. Catastr. 2001, 16, 82–83. [Google Scholar]
- Wu, W.J.; Su, X.; Liu, W. Loess–mudstone interface landslides: Characteristics and causes. J. Glaciol. Geocryo. 2014, 36, 1168–1175. [Google Scholar]
- Tang, Y.M.; Xue, Q.; Li, Z.G.; Feng, W. Three modes of rainfall infiltration inducing loess landslide. Nat. Hazards 2015, 79, 137–150. [Google Scholar] [CrossRef]
- Zheng, C.B. The Numerical Simulation of Sliding about Contact Surface between Loess and Mudstone in Inner Mongolia Autonomous Region. Master’s Dissertation, Inner Mongolia University of Technology, Hohhot, China, 2013. (In Chinese). [Google Scholar]
- Jian, W.X.; Xu, Q.; Yang, H.F.; Wang, F.W. Mechanism and failure process of Qianjiangping landslide in the Three Gorges Reservoir, China. Env. Earth Sci. 2014, 72, 2999–3013. [Google Scholar] [CrossRef]
- Li, C.; Yang, L.; Wuliji, N.; Yao, D.; Wang, X. Model experiment of engineering protection on loess-mudstone interfacial Landslide. Chin. J. Rock Mech. Eng. 2016, 35, 3923–3929. (In Chinese) [Google Scholar]
- Li, S.H.; Li, C.; Yao, D.; Liu, C.C. Interdisciplinary asperity theory to analyze nonlinear motion of loess landslides with weak sliding interface. Landslides 2020. [Google Scholar] [CrossRef]
- Provost, F.; Malet, J.P.; Hibert, C.; Helmstetter, A.; Radiguet, M.; Amitrano, D.; Langet, N.; Larose, E.; Abanco, C.; Hurlimann, M.; et al. Towards a standard typology of endogenous landslide seismic sources. Earth Surf. Dyn. 2018, 6, 1059–1088. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Wang, Y.; Sun, Y.Y.; Gao, L.; Zhang, Z.L.; Zhang, W.Y.; Zhao, P.C.; Yue, Y. Using custom fiber bragg grating-based sensors to monitor artificial landslides. Sensors 2016, 16, 1417. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Chen, J.P.; Xie, R.L.; Li, X.F. A high performance piezoelectric sensor for dynamic force monitoring of landslide. Sensors 2017, 17, 394. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, S.J.; Chen, J.; Teng, P.X.; Wei, F.Q.; Chen, Q. A laboratory experimental study: An FBG-PVC tube integrated device for monitoring the slip surface of landslides. Sensors 2017, 17, 2486. [Google Scholar] [CrossRef] [PubMed]
- Amitrano, D.; Gaffet, S.; Malet, J.-P.; Maquaire, O. Understanding mudslides through micro-seismic monitoring: The Super-Sauze (South-East French Alps) case study. Bull. Lasocietegeologique Fr. 2007, 178, 149–158. [Google Scholar] [CrossRef]
- Zhang, Z.; He, S.M.; Li, Q.F. Analyzing high-frequency seismic signals generated during a landslide using source discrepancies between two landslides. Eng. Geol. 2020, 272, 105640. [Google Scholar] [CrossRef]
- Yamada, M.; Matsushi, Y.; Chigira, M.; Mori, J. Seismic recordings of landslides caused by Typhoon Talas (2011), Japan. Geophys. Res. Lett. 2012, 39, L13301. [Google Scholar] [CrossRef]
- Manconi, A.; Gariano, S.L.; Coviello, V.; Guzzetti, F. How many rainfall-induced landslides are detectable by a regional seismic monitoring network? Adv. Cult. Living Landslides 2017, 3, 161–168. [Google Scholar] [CrossRef]
- Feng, Z. The seismic signatures of the 2009 Shiaolin landslide in Taiwan. J. Nat. Hazards Earth Syst. Sci. 2011, 11, 1559–1569. [Google Scholar] [CrossRef]
- Feng, Z. The seismic signatures of the surge wave from the 2009 Xiaolin landslide-dam breach in Taiwan. Hydrol. Process. 2012, 26, 1342–1351. [Google Scholar] [CrossRef]
- Kao, H.; Kan, C.; Chen, R.; Chang, C.; Rosenberger, A.; Shin, T.; Leu, P.; Kuo, K.; Liang, W. Locating, monitoring, and characterizing typhoon-linduced landslides with real-time seismic signals. Landslides 2012, 9, 557–563. [Google Scholar] [CrossRef]
- Qiu, J.; Chen, H.J.; Wen, Y.M.; Li, P. Magnetoelectric and electromagnetic composite vibration energy harvester for wireless sensor networks. J. Appl. Phys. 2015, 117, 17A331. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, H.; Xu, Y. Low-frequency vibration sensors based on acascaded gapped cantilever. Smart Mater. Struct. 2016, 25, 095007. [Google Scholar] [CrossRef]
- Xu, B.; Li, B.; Song, G.B. Active debonding detection for large rectangular CFSTs based on wavelet packet energy spectrum with piezoceramics. J. Struct. Eng. 2013, 139, 1435–1443. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregate for seismic shear stress monitoring. Smart Mater. Struct. 2013, 22, 065012. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregate for compressive seismic stress monitoring. Smart Mater. Struct. 2012, 21, 105035. [Google Scholar] [CrossRef]
- Fan, X.Y.; Li, J.; Hao, H. Piezoelectric impedance based damage detection in truss bridges based on time frequency ARMA model. Smart Struct. Syst. 2016, 18, 18501–18523. [Google Scholar] [CrossRef]
- Wang, S.; Lu, P.; Liu, L. An infrasound sensor based on extrinsic fiber-optic fabry-perot interferometer structure. IEEE Photonics Technol. Lett. 2016, 28, 1264–1267. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, Y.F.; Hao, H.; Huang, X. An efficient method to derive statistical mechanical properties of concrete reinforced with spiral-shaped steel fibers in dynamic tension. Constr. Build. Mater. 2016, 124, 732–745. [Google Scholar] [CrossRef]
- Myung, H.; Wang, Y.; Kang, S.C. Survey on robotics and automation technologies for civil infrastructure. Smart Struct. Syst. 2014, 13, 891–899. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Ren, L.; Labib, E.; Kapadia, A.; Mo, Y.L.; Li, H.N.; Song, G.B. Inference of bond slip in prestressed tendons in concrete bridge girders. Struct. Control Health Monit. 2015, 22, 289–300. [Google Scholar] [CrossRef]
- Song, T.; Park, H.C.; Ahn, K.H. Proposal for high sensitivity force sensor inspired by auditory hair cells. Appl. Phys. Lett. 2009, 95, 013702. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, Y.; Lei, Y.; Song, J.; Xu, Y. Haircell-inspired capacitive accelerometer with both high sensitivity and broad dynamic range. In Proceedings of the IEEE Sensors, Waikoloa, HI, USA, 1–4 November 2010; pp. 1468–1473. [Google Scholar]
- Lee, C.; Park, S. A mechanical model of stereocilia that demonstrates a shift in the high-sensitivity region due to the interplay of a negative stiffness and an adaptation mechanism. Bioinspir. Biomim. 2012, 7, 046013. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.J.; Lei, Y. A Bioinspired Tilt Sensor Model with Adaptive Gain and Enhanced Sensitivity. Math. Probl. Eng. 2014, 2014, 957850. [Google Scholar] [CrossRef]
- Liu, L.J.; Lei, Y. Mechanism of a hair cell bioinspired sensor with ultra–sensitivity to weak and low frequency vibration signals. Int. J. Distrib. Sens. Netw. 2013, 2013, 278151. [Google Scholar] [CrossRef]
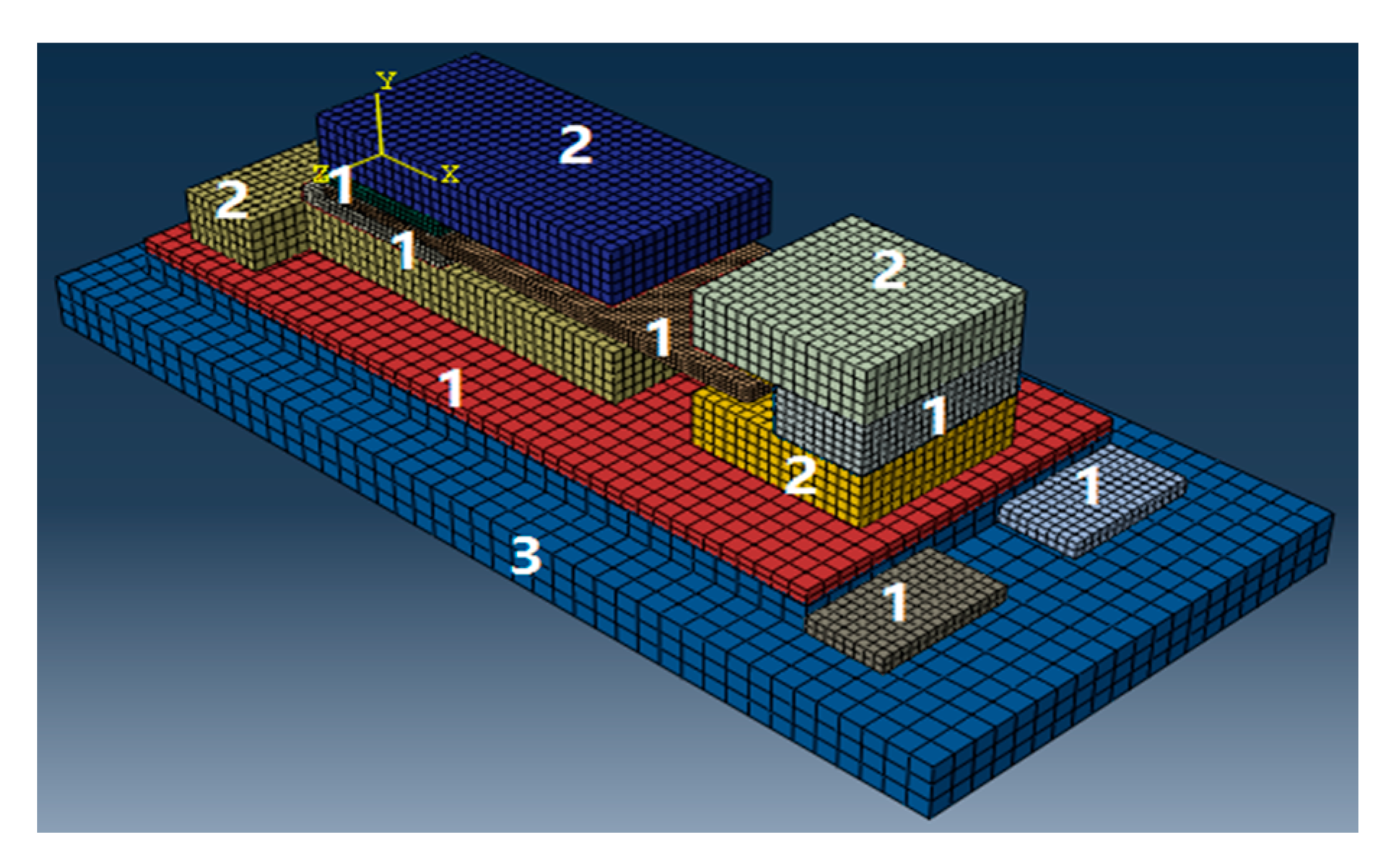




| No. | Material | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 1 | Resin film | 2230 | 71.7 | 0.21 |
| 2 | Beryllium bronze | 8260 | 110 | 0.35 |
| 3 | AL6061 | 2200 | 65 | 0.17 |
| Frequency (Hz) | |||
|---|---|---|---|
| X | Y | Z | |
| 0.2 | 10.07 | 10.38 | 10.05 |
| 0.5 | 10.22 | 10.37 | 10.22 |
| 1 | 10.29 | 10.29 | 10.24 |
| 2 | 10.28 | 10.28 | 10.22 |
| 4 | 10.27 | 10.27 | 10.19 |
| 8 | 10.23 | 10.25 | 10.22 |
| 10 | 10.15 | 10.08 | 10.06 |
| 20 | 10.01 | 9.91 | 10.01 |
| 40 | 9.51 | 9.32 | 9.87 |
| 80 | 8.11 | 7.75 | 9.31 |
| 160 | 5.62 | 5.2 | 7.83 |
| 315 | 3.08 | 2.88 | 5.33 |
| 630 | 1.44 | 1.28 | 2.87 |
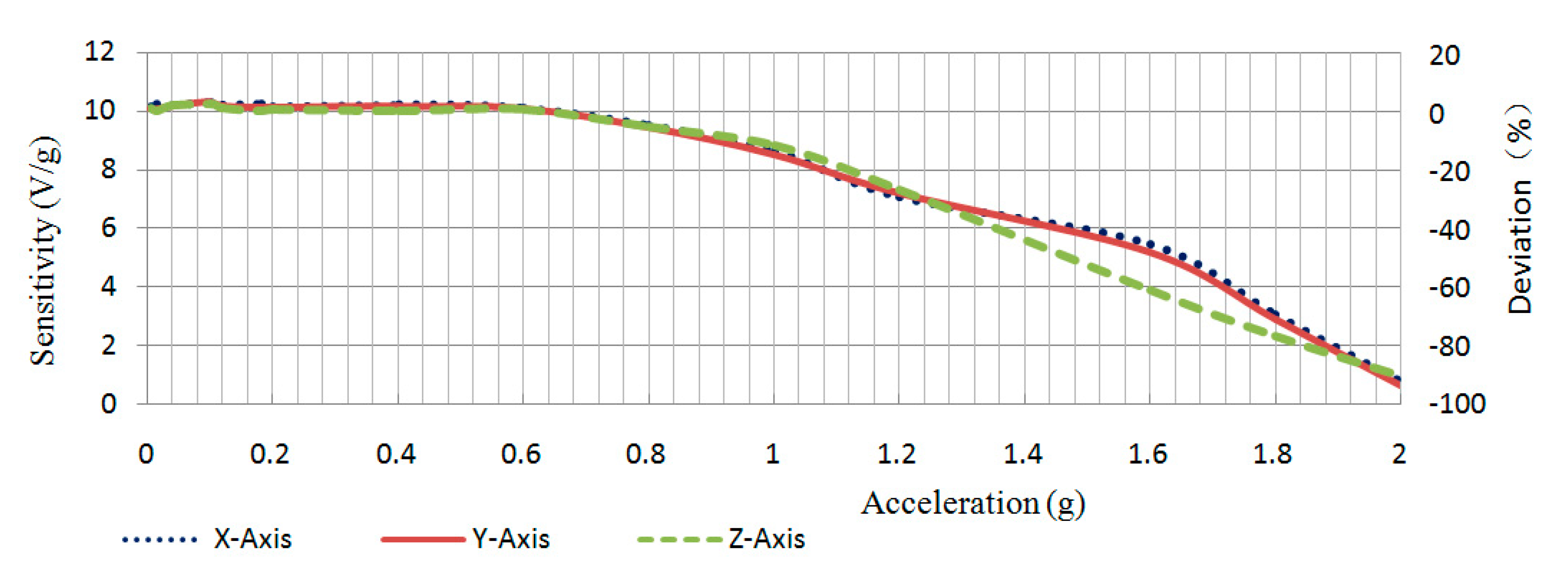
| Acceleration (g) | |||
|---|---|---|---|
| X | Y | Z | |
| 0.004 | 10.15 | 10.08 | 10.10 |
| 0.015 | 10.22 | 10.06 | 10.02 |
| 0.04 | 10.19 | 10.19 | 10.18 |
| 0.1 | 10.29 | 10.29 | 10.24 |
| 0.12 | 10.21 | 10.17 | 10.11 |
| 0.18 | 10.23 | 10.13 | 10.02 |
| 0.2 | 10.15 | 10.12 | 10.06 |
| 0.4 | 10.21 | 10.14 | 10.01 |
| 0.6 | 10.11 | 10.08 | 10.07 |
| 0.8 | 9.51 | 9.42 | 9.46 |
| 1.0 | 8.62 | 8.52 | 8.83 |
| 1.2 | 7.08 | 7.18 | 7.33 |
| 1.6 | 5.44 | 5.18 | 3.87 |
| 1.8 | 3.03 | 2.9 | 2.31 |
| 2.0 | 0.74 | 0.63 | 0.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Nie, Y.; Lei, Y. A Novel Sensor Prototype with Enhanced and Adaptive Sensitivity Based on Negative Stiffness Mechanism. Sensors 2020, 20, 4644. https://doi.org/10.3390/s20164644
Liu L, Nie Y, Lei Y. A Novel Sensor Prototype with Enhanced and Adaptive Sensitivity Based on Negative Stiffness Mechanism. Sensors. 2020; 20(16):4644. https://doi.org/10.3390/s20164644
Chicago/Turabian StyleLiu, Lijun, Yongzhong Nie, and Ying Lei. 2020. "A Novel Sensor Prototype with Enhanced and Adaptive Sensitivity Based on Negative Stiffness Mechanism" Sensors 20, no. 16: 4644. https://doi.org/10.3390/s20164644
APA StyleLiu, L., Nie, Y., & Lei, Y. (2020). A Novel Sensor Prototype with Enhanced and Adaptive Sensitivity Based on Negative Stiffness Mechanism. Sensors, 20(16), 4644. https://doi.org/10.3390/s20164644







