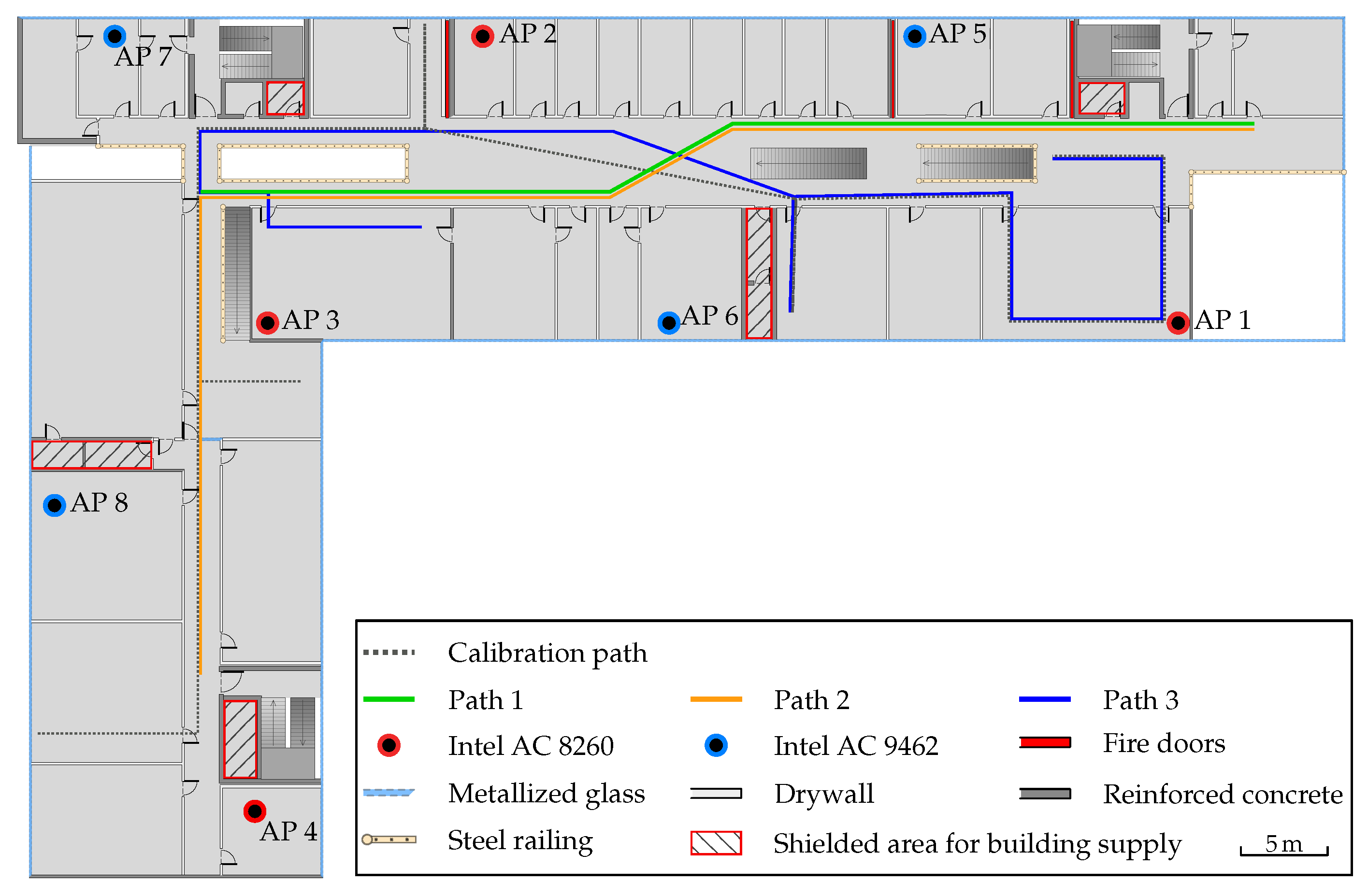
6.1. Hardware Setup
In all our experiments, we used Intel mini PCs running a patched Linux to enable FTM support as access points. Two model generations were used: Intel NUC6CAYS and Intel NUC7CJYSAL. In total, we are using eight APs based on IntelWi-Fi cards. Four of them are based on Intel Dualband-Wireless-AC 8260 cards configured as described by Ibrahim et al. [
14]. The remaining four are based on Intel Wireless-AC 9462 modules and run a recent Linux kernel 5.3.7, where the iwlwifi driver and hostapd are already prepared to support FTM. However, the driver still requires small manual changes, as a global Boolean flag needs to be set to activate the FTM related code. In addition, the firmware of the card returns that the chip is not calibrated for FTM. As a consequence, the driver disables FTM responder functionality. Overriding this check, allows us to use the chip as responder and FTM measurements can be presumably performed reliably. At this point, it is not clear to us what the exact purpose of the flag is. While it indicates that the card is not calibrated, the accuracy of the measurements is reliable as will be shown in our experiments. Due to regulatory limitations, both wireless cards can only be configured as access points in the
GHz frequency band. Furthermore only 20 MHz channel bandwidth is used. Using 802.11n with 40 MHz bandwidth was not possible, due to the coexistence with the university’s existing Wi-Fi infrastructure.
In all our experiments we used a Google Pixel 2 XL and a Google Pixel 3a smartphone, both running Android 9. This is because Google introduced official ranging APIs based on FTM for supported devices with Android 9. Starting with Android 9, Google limited the number of network scans to four every two minutes. This limitation renders the commonly used network scanning API virtually unusable for measuring RSSI values for real-time positioning purposes. However, the new FTM API also provides RSSI values, thus with each measurement, the signal strength and distance to one AP can be simultaneously obtained. More importantly, the new FTM ranging API has no rate limit.
Within the following experiments, FTM measurements to all known access points are queried every 200 ms. This does not guarantee that distance measurements for every access point are available at that frequency. Due to blocked sight or harsh environmental conditions, the measurements can fail. According to our observations, Android issues eight FTM measurements for a single ranging request. The API returns various values, e.g., mean distance, standard deviation, RSSI, number of attempted measurements, as well as the number of successful measurements. It is not documented how Android aggregates the eight measurements, but it is assumed that the arithmetic mean is calculated on the distance values as in (
5).
The list of access points is statically stored in the application and known beforehand. With Android 10 it is possible to transfer the AP position dynamically using the location configuration information protocol. This allows for more flexible applications as access points can be added or modified dynamically without updating the client application.
In some cases, we noticed that Android did not provide FTM measurements for intervals of about three and up to five seconds for unknown reasons, although multiple APs were clearly in reach. Due to the rarity of this problem we decided to repeat these faulty experiment runs.
6.2. Verification of FTM Performance in LOS Scenario
The first experiment evaluates the indoor precision and accuracy of FTM distance measurements given different hardware configurations. While Ibrahim et al. [
14] already verified the precision of the Intel AC 8260 card in great detail, our setup differs from theirs and requires a new evaluation. In contrast to Ibrahim et al. we use smartphones as receivers and an additional card with a newer firmware version as sender. For these reasons we deployed a static distance measurement experimental setup to confirm that the combination of Pixel devices and Intel cards provide reliable values.
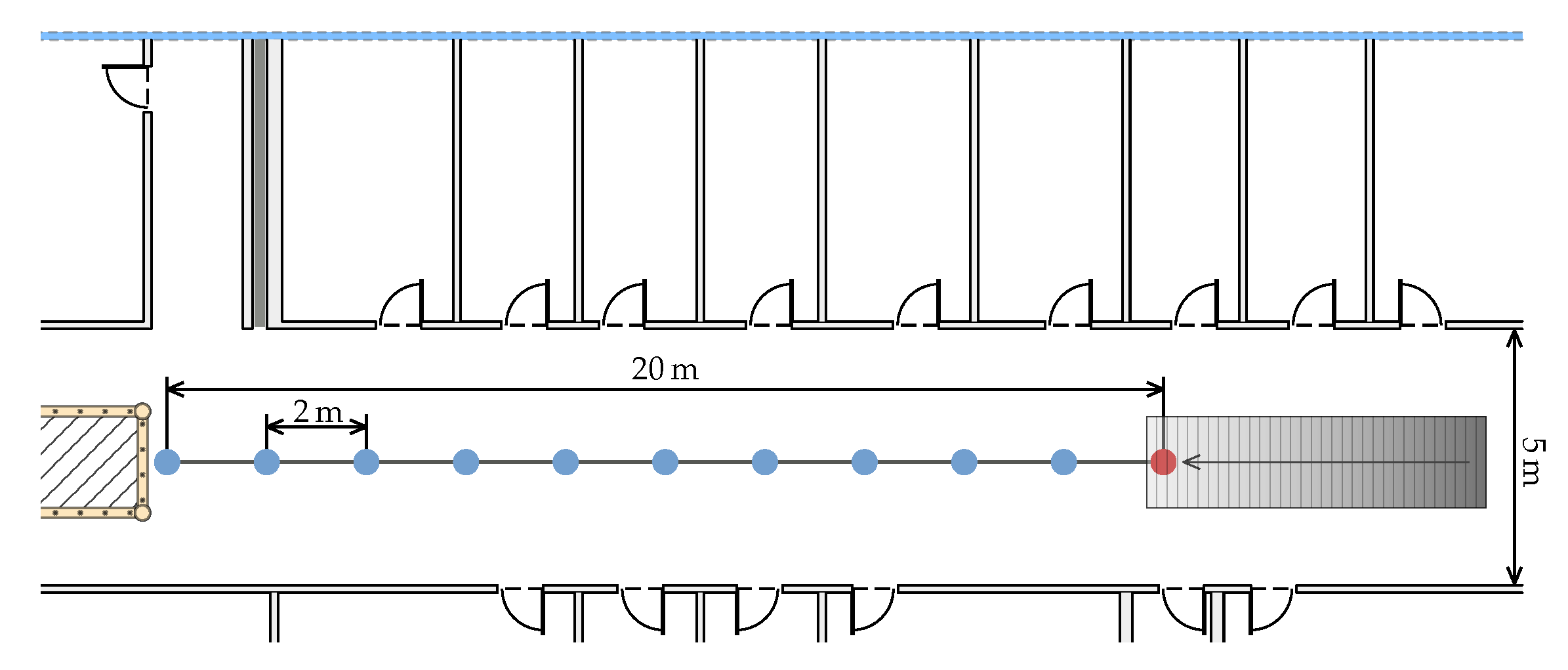
Our test setup consists of 10 measurement points evenly spaced at a distance of 2 m on a straight line. The closest point to the AP is 2 m away and the furthest 20 m. The setup is shown in
Figure 2. At every point, each phone is placed on a stand. Around 140 FTM measurements are recorded, which corresponds to a measure period of 30 s per point. The APs and the phones are placed on an empty cardboard box on a metal stand to allow some distance between the metal and the phone. The box is 12 cm high and the phones laid flat on it. Both the APs and the phones are located at
m above the floor. Even though recording measurements for 30 s at a single point is not realistic in a dynamic positioning system, it allows us to evaluate the statistical properties of the method.
The whole experiment was deployed in the hallway of our university. Each distance measurement is performed with every hardware combination. We used a Google Pixel 2 XL and a Pixel 3a as FTM initiators and the Intel AC 8260 and 9462 as responders. In total, there are four smartphone-AP combinations.
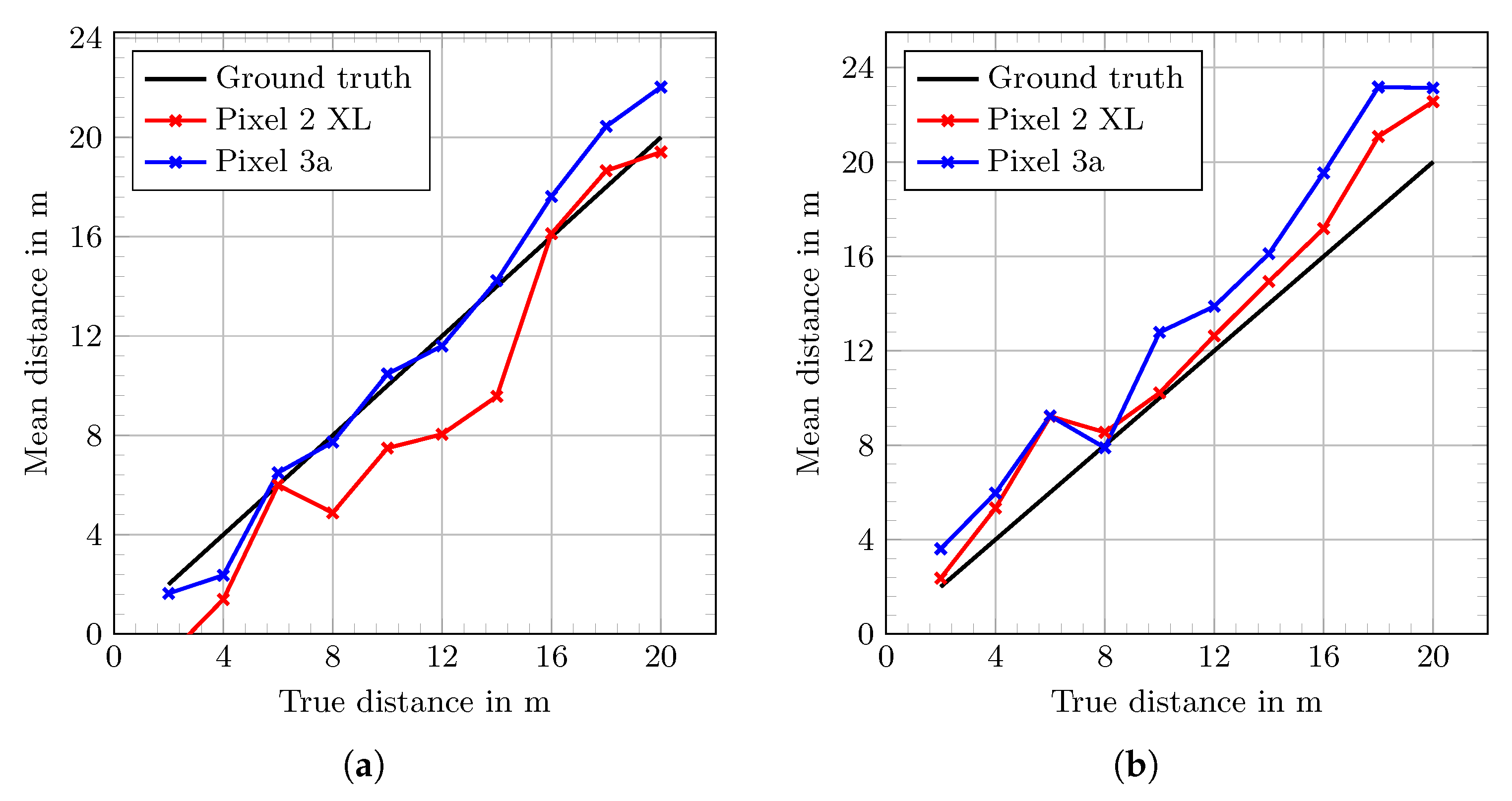
Figure 3a shows the mean measured distance with respect to the ground truth distance, using the Intel AC 8260 with 20 Mhz channel bandwidth as responder.
Likewise,
Figure 3b depicts the mean distances using the Intel AC 9462 with 20 Mhz channel bandwidth as responder. The corresponding values of these figures are shown in
Table 1. We compute the mean over the 140 FTM measurements denoted as
and its standard deviation. Because
can be larger or smaller than the true distance, we used the signed difference between
and the true distance as the error metric. However, when it is necessary to quantify the error regardless of its direction the mean absolute error is used, i.e., the mean of all absolute differences between the measurement and ground truth.
Using the Pixel 2 XL as initiator and Intel AC 8260 as responder, the overall error is mostly negative. Contrarily, the Pixel 3a with Intel AC 8260 provides distance estimates close to the ground truth. In case of the Intel AC 9462 as responder both Pixel devices produce similar good values.
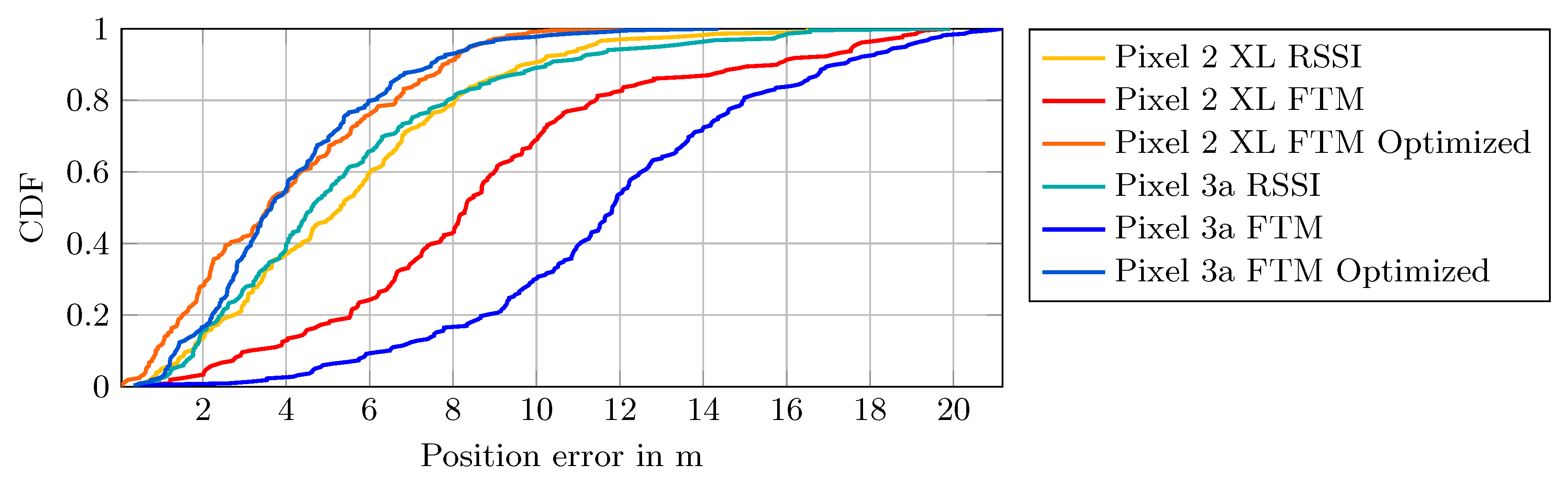
While the mean distance over many measurements is relevant for stationary measure points, in our scenario a pedestrian is moving with the smartphone. Therefore, only one, up to a few measurements, can be observed at a given position. A more expressive visualization for this scenario is given with the cumulative distribution function (CDF) graph in
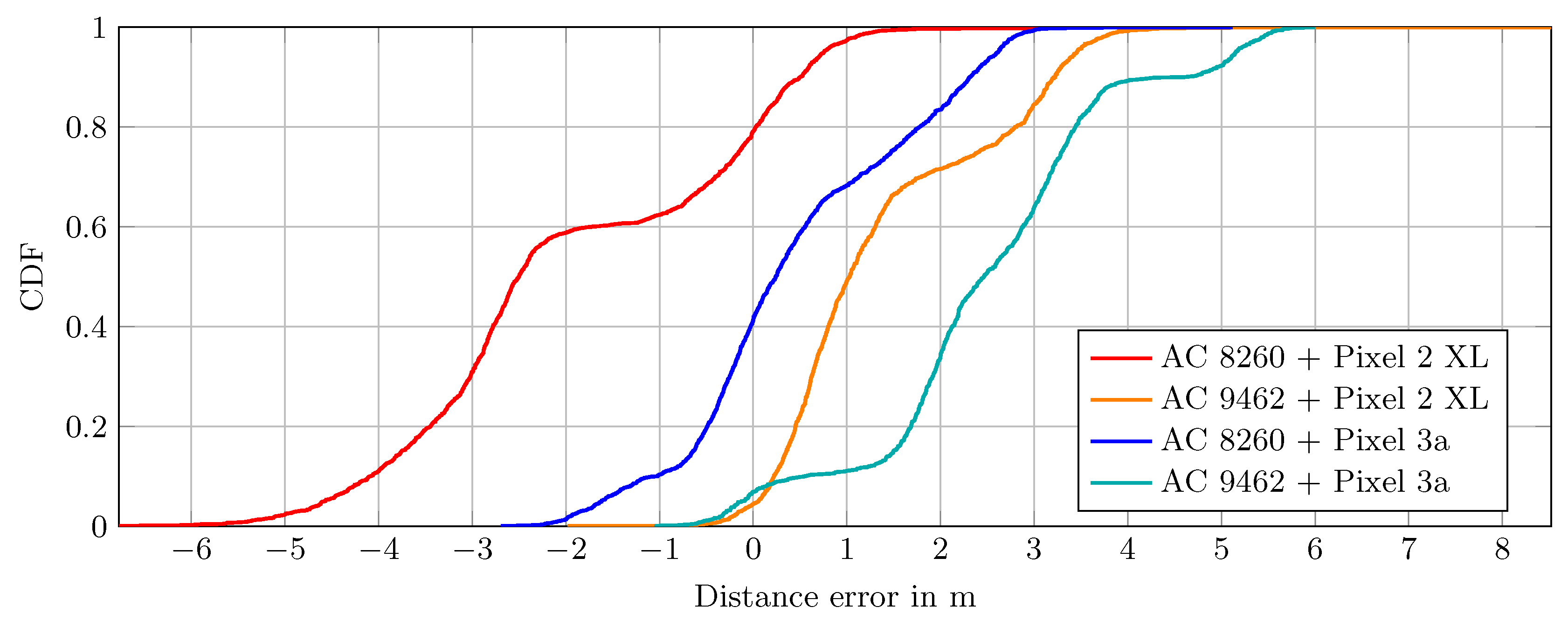
Figure 4, which allows us to reason about the underlying error distribution.
Most striking is the curve of the Intel AC 8260 and Pixel 2 XL combination (red line). Firstly, about 80% of the measurements have a negative error, i.e., underestimate the true distance. Secondly, the curve indicates that the error distribution is a Gaussian mixture distribution with two modes at m and m, whereas the mode at m provides about 60% of the probability mass.
However, using the same card together with the Pixel 3a (blue line), the error is already much smaller and only a small portion is negative. In this case, no constant offset is necessary, as it would not significantly improve the measurements for the Pixel 3a.
In sum, based on the presented results, the Intel AC 9462 seems to provide better results compared to the Intel AC 8260, i.e., most of the errors are positive and up to 5 m.
The results suggest that no single global offset, which accounts for hardware delays, significantly improved the measurements across all device combinations in our tests. However, for each combination of smartphone and access point an individual offset could be used. However, the overall error of the device combinations in a LOS scenario is reasonably small and its distribution is mostly Gaussian-like, which justifies the basic applicability of the technique and the devices for indoor positioning.
6.3. Evaluation of FTM Performance in NLOS Scenario
In our experiments, we noticed that at some locations in the building the FTM distance estimates greatly vary compared to other locations. It is likely that environmental factors of the building affect the distance estimation process. Investigating these locations showed that all of them are near special fire doors. These heavy doors are about 12 cm thick, 5 m long, made of metal and presumably grounded. In the case of a fire outbreak, these doors are automatically closed, but normally, they are open and tucked away between walls. Whenever such a fire door is in the line-of-sight between the access point and the smartphone, the ranging error increases significantly. While it is well-known that the environment will affect measurements, especially indoors, it is nevertheless interesting to analyze the underlying cause.
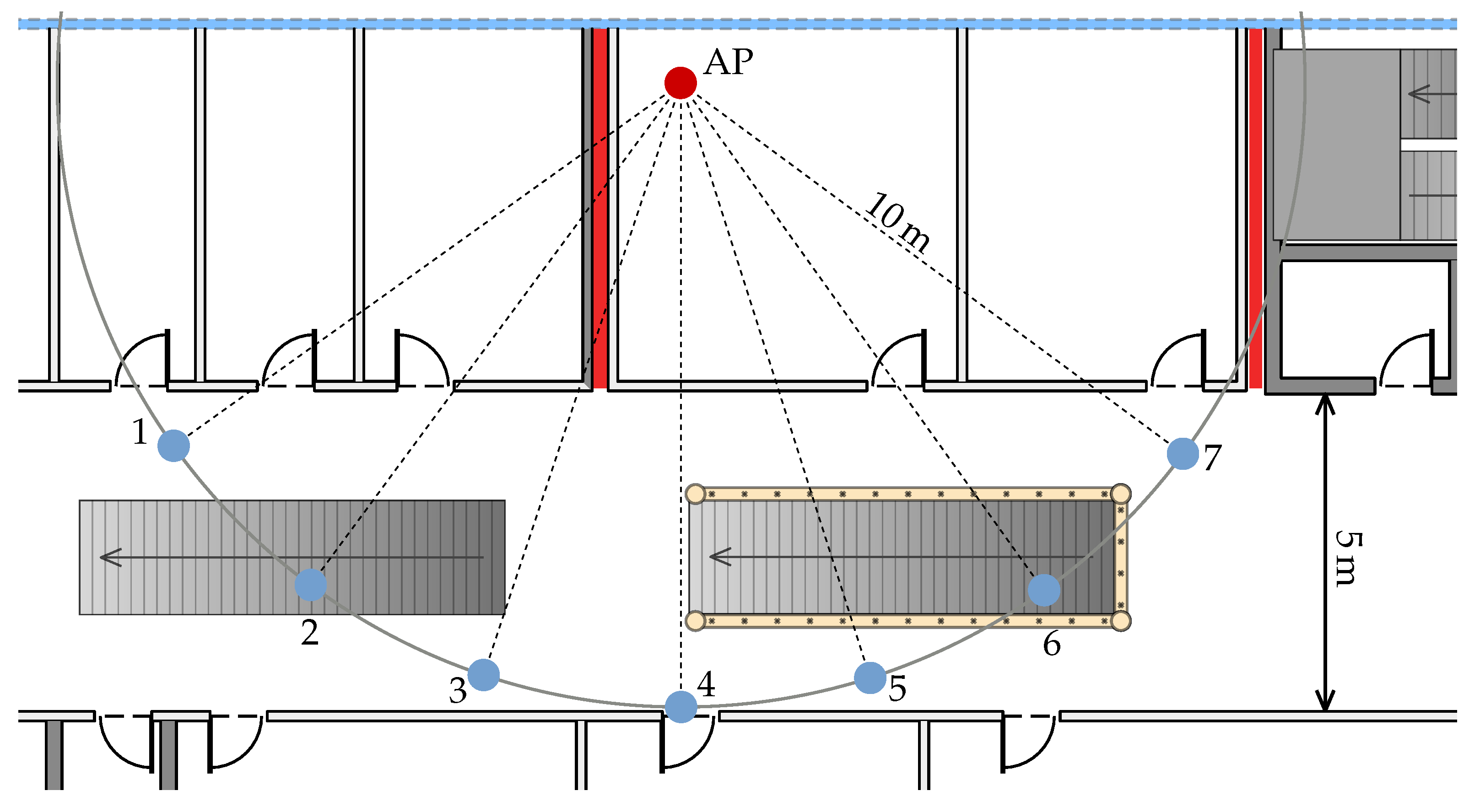
To quantify the impact of these fire doors on the measurements we created two test setups using an Intel AC 9462 AP and the Pixel 2 XL. In the first experiment, as shown in
Figure 5, we placed seven measurement points onto a circle such that most of these points are located in the main hallway. The radius of the circle is 10 m and measure points 1 to 3 are located in the shadow of the fire door while points 4 to 7 are not. At every point we placed the Pixel 2 XL on a card box on a metal stand at
m above the floor, just like in the previous experiment in
Section 6.2. We recorded FTM distance measurements for 60 s with one measurement every 200 ms. On average, around 255 successful distance measurements were obtained at each point. Note that this number differs from the theoretical possible 300 measurements because some FTM measurements failed.
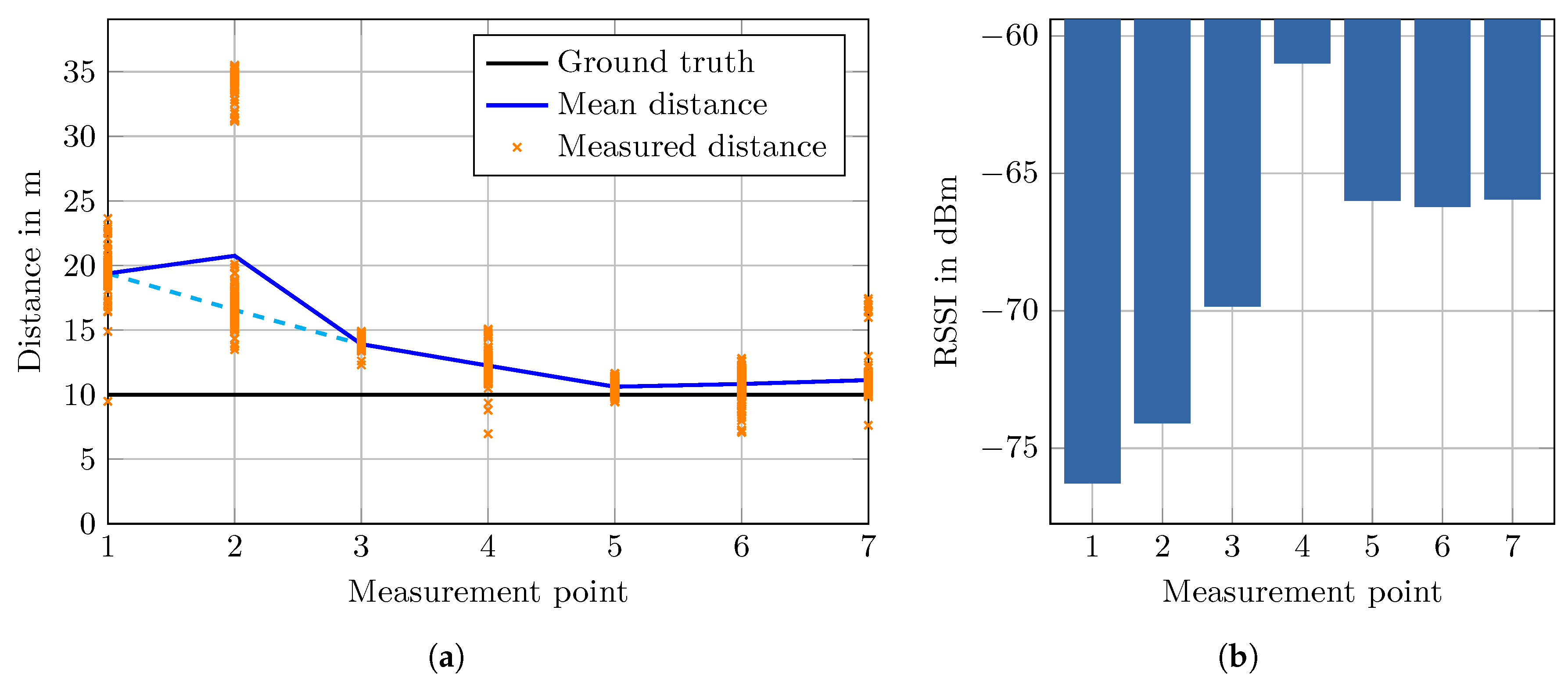
The distance measurement results are depicted in
Figure 6a. The error in the shadow area is larger compared to the points not shadowed by the fire door. While the measured mean distances at point 1 and 2 are off by around 10 m, the error decreases monotonously for the following points. Points 5 to 7 are not affected by the fire door with a mean error of ≈0.8 m. However, the deviation at point 4, with its signal path quite close to the door, is somewhat larger. The distribution of the distances recorded at point 2 has two modes at
m and
m, which are clearly visible in the plot. This bimodal distribution increases the mean distance significantly, if, instead of the mean, the distance at the larger mode (
m) is used, then the overall curve is monotonously decreasing (cyan dashed line).
The mean RSSI, as shown in
Figure 6b, exhibits the same tendency as the mean distance. At points 1, 2 and 3 the RSSI is decreasing with a minimum at point 4 and stable for the remaining points. This suggests that the RSSI correlates somewhat with the measured distances in this scenario, except at point 4, where the RSSI is stronger than every other point. However, this could be caused by measurement inaccuracy of the smartphone chip and might be a nonrecurring outlier. The RSSI values, compared to the FTM measurements, are stable and have insignificantly small variance in this test.
Notice that point 2, 3, 5 and 6 are located near stairways with massive metal railings. It is expected that the stairways also add measurement noise, however, we still included them deliberately in this test setup as they are nonetheless of real interest because they also appear in the test walks.
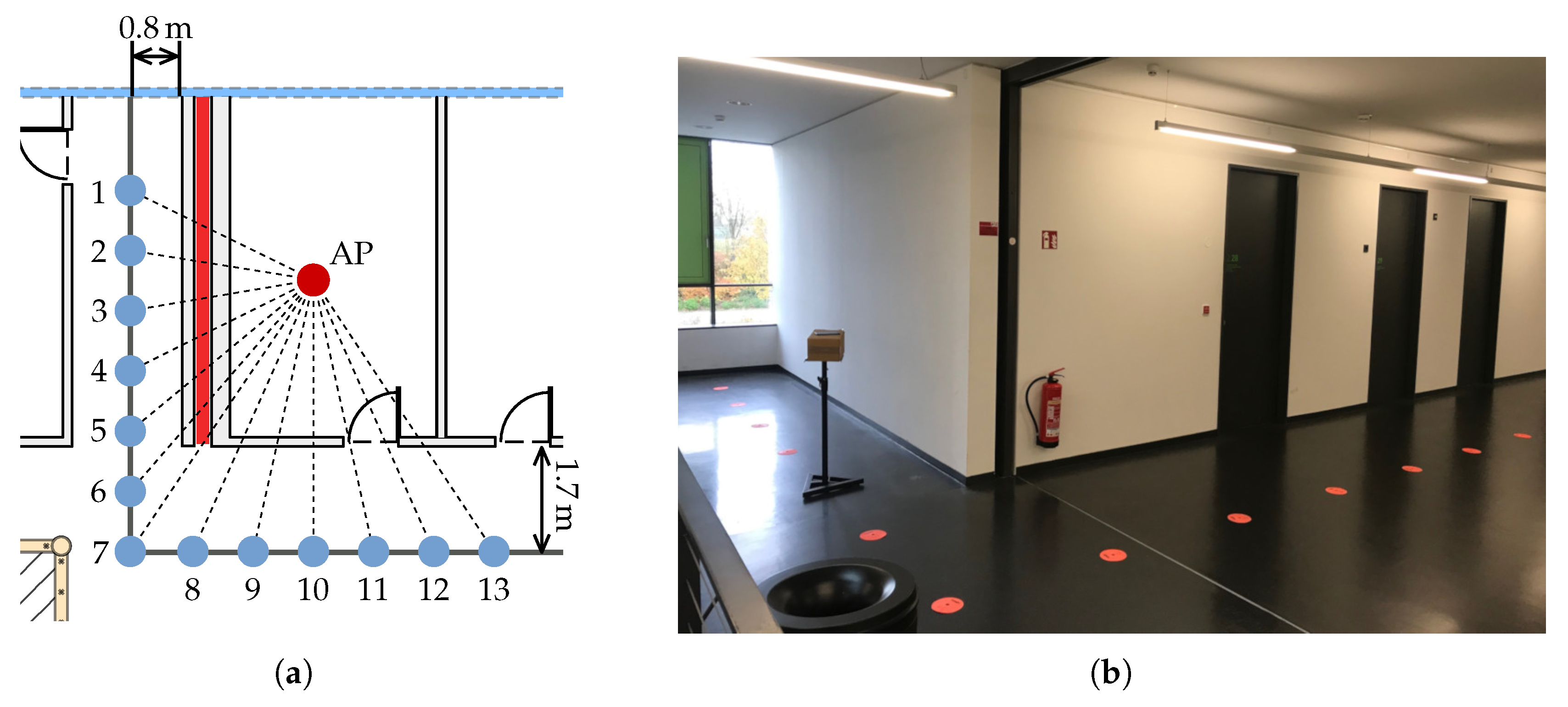
In order to evaluate the effect of the fire door exclusively, we built a second test setup at a corner office located next to a fire door on the same floor. As seen in
Figure 7, the 13 measurement points are placed parallel to the wall. Due to structural limitations, it was not possible to keep the distance to the AP constant, like in the aforementioned experiment. The same hardware and placement of the smartphone are used as in the first experiment. The AP is placed in the center of the room on a table. The ground truth was obtained by carefully measuring the right angle distances to walls and taking the line of sight distance from a true to scale map.
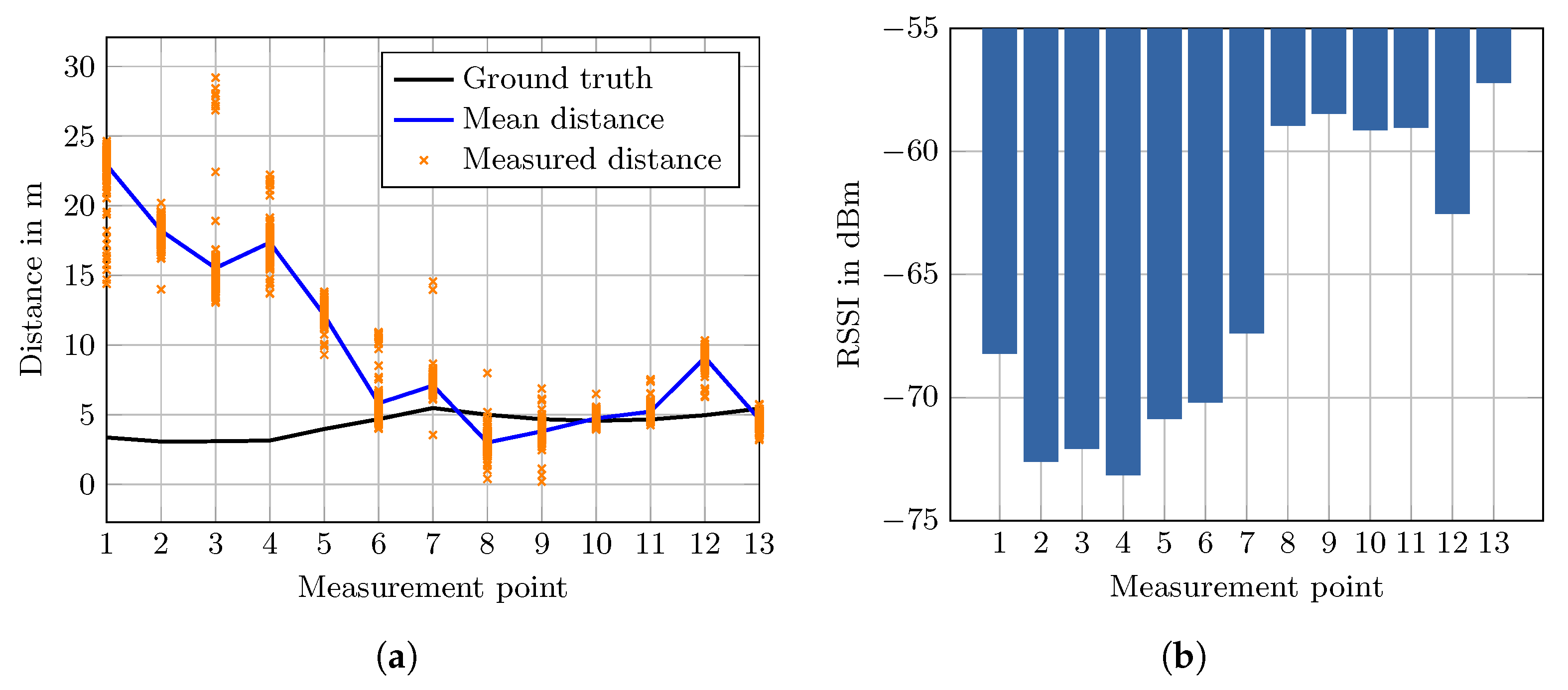
The results are shown in
Figure 8a. Overall, the results shown in
Figure 8a are similar to the first experiment but more significant. Again, the error in the shadow area is larger compared to the points not shadowed by the fire door. Measurement point 1 has the largest error with a distance estimate
m larger than the true distance. Moving towards the end of the shadow area the error decreases nearly monotonously. At point 6, which is still in the shadow area, the error is reasonably small with
m. The mean absolute error for points 6 to 13 is
m with a standard deviation of
m.
Point 12 has a larger error compared to the neighboring points with
m. This correlates with the measured mean RSSI value at that position (see
Figure 8b). As seen in
Figure 8a point 12 is located behind the room door. The regular doors in the building are massive and with higher signal attenuation compared to the surrounding drywalls. This could be a plausible cause of the increased error.
However, signal attenuation cannot explain the overall result of the experiment. In both experiments, the true distances to the smartphone are somewhat equal, but the error varies greatly and is larger than the assumed error for LOS. Assuming that the fire door completely blocks any signal, a hypothesis justified by the results is that the signal is received due to multipath propagation. While the measurement points not located in the shadow of the door receive the signal directly, the points in the shadow receive reflected signals with a longer propagation path, and hence, smaller signal strength. This would also explain why point 1 in the second setup has the largest error and the following points have decreasing errors. Without more sophisticated tests, this remains a hypothesis, but the experiments show that these fire doors definitely have a significant effect on the measurements, FTM and RSSI alike, and therefore, on the positioning estimate.
6.5. Positioning Performance
We compare the positioning performance of the least-squares and probabilistic positioning methods described in
Section 4, as well as a simplistic realization of the particle filter as described in
Section 5. While it is expected that a filter reduces the positioning error, a less complex method like least-squares estimation allows us to see the characteristics of the sensors better. All three methods were individually executed based on FTM and RSSI measurements. While walking, every 200 ms a FTM and RSSI measurement is issued to each AP (see
Section 6.1). Due to the size and environmental factors of the building, it is not possible to obtain a valid measurement for all APs at all times. Therefore, a strategy to deal with missing measurements needs to be considered depending on the used method.
Each distance estimate method has a free parameter: distance offset
for FTM in (
6) and path loss exponent
for RSSI in (
3). Both values account for the environmental effects on the signal caused by the building structure. Hence, their actual values highly affect the performance of the overall system. For each AP we searched for optimized parameters, which reduce the distance error based on the recorded data from the calibration walk. A common set of parameters is used for each path.
Table 2 shows the optimized values obtained from the calibration walk, as well as the values for each test walk in comparison. All four walks per path are used as input for the optimization. When deploying an indoor positioning system, the data required for the optimization could be collected in a pre-deployment calibration step. This is similar to fingerprinting approaches, as an additional calibration step has to be conducted beforehand. However, we believe that optimizing the parameters based on a calibration walk, could reduce the setup time compared to classical fingerprinting.
The results of
Section 6.2 suggest using individual offsets per smartphone and AP combination. However, we decided to only include the individual APs for the parameter search for practical reasons. When an indoor position system is deployed, we assume that the infrastructure can be controlled to some degree, but not the pedestrian’s smartphone. The smartphone is a much more variable factor as the signals are influenced by the pedestrian, other pedestrians, and the actual holding position of the smartphone. Therefore, including the smartphones in the parameter search might further improve the system but at the cost of higher specialization on the deployed hardware and higher calibration overhead.
The optimized values for the path loss exponent are in the interval . The individual values per AP differ about on average between the three paths. Overall, the three paths are quite similar, as the pedestrian is walking in the main hallway most of the time. Hence, the environmental effects on the signal are also similar per AP and walk. As a consequence, a common average path loss exponent value per AP for every path might be sufficient.
The parameter optimization led to large negative values for FTM, which vary significantly between the paths. Overall, the optimized FTM offsets are in the interval
. These offsets compensate for building effects like the fire doors and shielded areas (see
Figure 9). The results of the NLOS distance measurements in
Section 6.3 indicate that the estimated distances differ from the true distance. Hence, the estimated distances are often larger compared to the true distance. This is corrected by a negative FTM offset. Although not separately evaluated, we assume that the shielded areas have the same error characteristics as the fire doors.
The large negative FTM offset values have a significant downside. Every distance measurement, as reported by the device, which is smaller than the offset, will result in a negative distance after the correction. Negative distances cannot be used for the positioning with the here presented models. The straightforward approach to handle such values is to ignore them for the position estimate. Alternatively, the distances could be clamped to an arbitrary positive value or the original distance measurement without the offset correction could be used. Tests have shown that the actual strategy affects the position error negligibly small, thus we chose to ignore negative distances.
For the least-squares method we use the Levenberg–Marquardt algorithm implementation of the Eigen C++ library to solve (
8). The FTM distance values can be directly used in (
8). RSSI values are first converted to distance estimates with (
3). The FTM and converted RSSI values from one AP are smoothed with a moving average window of size 3. This reduces noise and the impact of outliers but causes a delay in the measurements. Every 500 ms a position is estimated. Assuming that every AP was seen at least once, we could use the averaged value for each AP at every update step to estimate a position. However, we refrain from doing so, to avoid using outdated measurements caused by blocked sight to one AP for a longer period. Only averaged values updated in the most recent time interval are used for the estimation. If there are less than three new values, it is not possible to compute the position with least-squares estimation. In these cases, we use the position estimate from the previous update step for the error computation. This is required to ensure that the method is comparable to the others. While this is not optimal, it shows one downside of the least-squares method without any filters.
For the probabilistic positioning method, we use a grid search to find the mode of the densities (
11) and (
15). Analogous to the least-squares estimation, a position estimate is computed every 500 ms. Again, one measurement from at least three APs needs to be available in the current time interval. Otherwise, the last position estimate is used for the error calculation. In theory, the probabilistic positioning method has the advantage over least-squares estimation to produce a result in such scenarios. However, if there are less than three distance measurements it is not possible to obtain a single mode but several equally likely positions. This would render the method incomparable to the others. For FTM the distance measurement is used in (
10), with
for every AP, which was found empirically. In contrast to least-squares estimation, the RSSI obtained by the hardware is used directly in (
13). Again, with an empirically determined
for every AP. The optimized values from
Table 2 are used for both methods. If there are multiple measurements available in an update interval for one AP, the values are not averaged. Instead, an additional density
or
per measurement is added to the joint density.
The particle filter approach is implemented as described in
Section 5. We use 5000 particles and compute a position estimate every 500 ms. In contrast to the other two methods, a new position estimate is always obtained, even when there are no new measurements available. The position is estimated with the weighted average over all particles as in (
25). The primitive transition model is used without map information. We use
and
in (
22). This allows the particles to spread far enough to capture the jumpy nature of the measurements. The weight of a particle is obtained by the probabilistic positioning method as in (
23) and (
24) for FTM and RSSI, respectively. Therefore, the reasoning about the probabilistic positioning apply as well.
Table 3 lists the mean position errors and its standard deviation per path, positioning method, smartphone and distance estimation method. Each path was walked four times for each smartphone. The here shown position errors are the mean position error over the four repetitions.
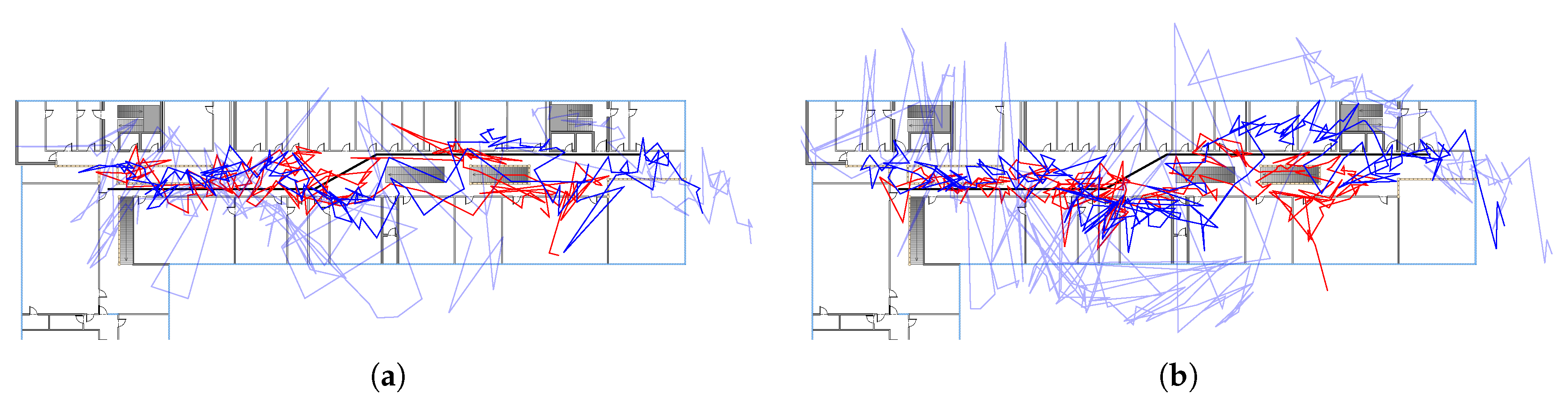
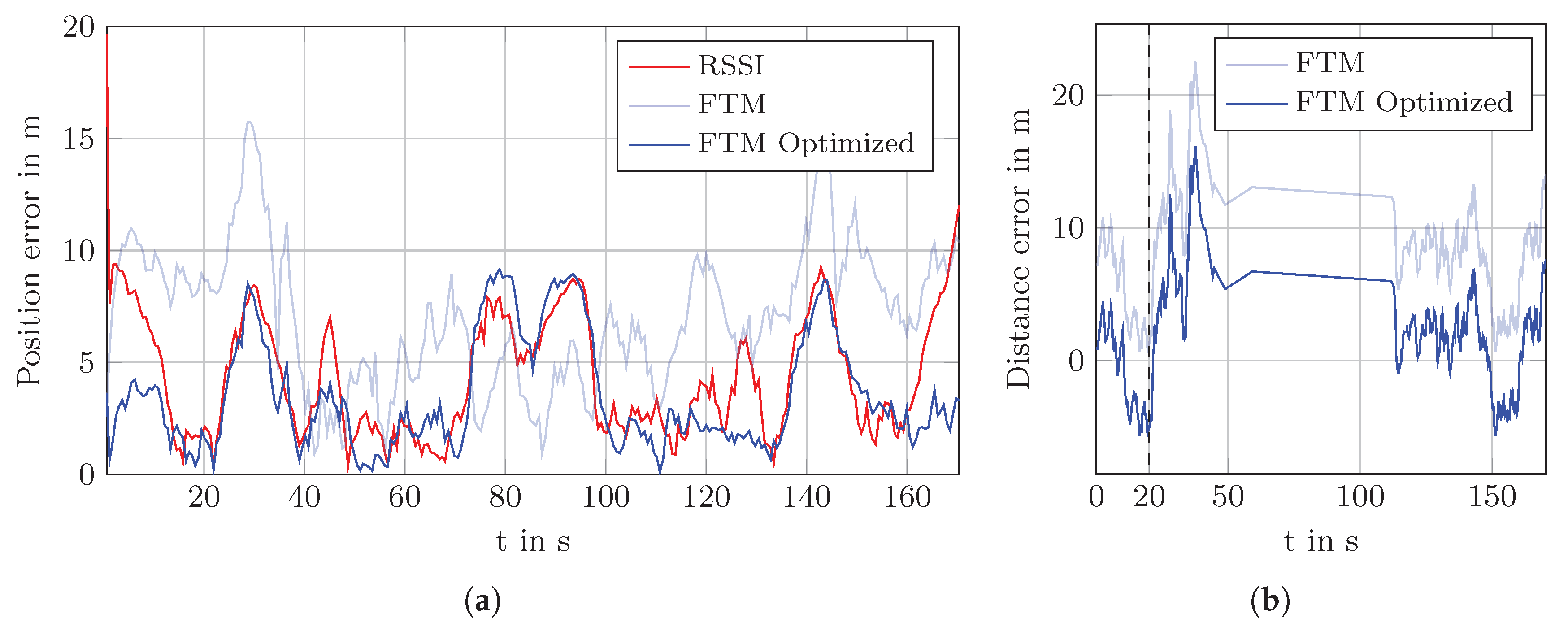
In
Figure 10 the estimated path for path 1 based on least-squares estimation for RSSI (red), FTM (light blue) and optimized FTM (blue) is shown. In case of RSSI, the position error is similar for the Pixel 2 XL and 3a with
and
, respectively. For unoptimized FTM, the position error differs significantly between the Pixel 2 XL and 3a with
and
, respectively. This difference is clearly visible in the estimated path. The Pixel 3a shows much larger jumps and spikes in the position estimate compared to the Pixel 2 XL. The position error is drastically reduced by the optimized values and the estimated path has overall smaller jumps compared to pure FTM. Interestingly, the difference in the position error between the two Pixel devices is also eliminated. Still, the Pixel 3a has visually larger jumps compared to the other device, especially in the middle of the walk.
The effect of distance correction becomes apparent in the CDF of the position error.
Figure 11 shows the CDF of the first path and the least-squares method. The larger position error of the Pixel 3a using the raw FTM measurements is clearly visible in the CDF plot. After the offset correction, both error plots of the Pixel devices are much closer to each other. Additionally, both CDFs are steeper, i.e., the variance in the error is reduced. In contrast, the RSSI position error plots for both devices are already similar without any adjustment.
The performance of the least-squares method for the remaining paths is comparable to path 1. Path 2 is simply an extension to path 1 with an additional detour into the other half of the building. Here, the least-squares method is able to follow the right-angle turn into the additional segment. For path 3, the method is not able to estimate the pedestrian’s position in the rooms. Most estimates are inside the main hallway and not in the rooms, but a tendency towards the rooms is observable. This is visible in the estimated paths, however, the position error does not represent this behavior.
The estimated paths using the probabilistic positioning method are remarkably similar to the least-squares approach. As can be seen in
Table 3, the difference in position error is marginal compared to the least-squares estimation. Furthermore, the characteristics of the estimated paths are the same. Both methods produce jumps in the estimated paths and fail to follow the ground truth closely. The similarity to the least-squares estimation is not surprising as both methods implement the same underlying idea. However, as the densities of the probabilistic method are directly used in the particle filter, it can be interpreted as an in-between method. This allows us to see the effect of the particle filtering compared to plain least-squares estimation.
In case of the particle filter, the estimated paths are smoother, and the position error is reduced in comparison to the other two methods. This is expected as the particle filter includes the temporal context. The transition model avoids sudden large changes in the position estimate and the weighted average over the particle set produces a smooth estimate.
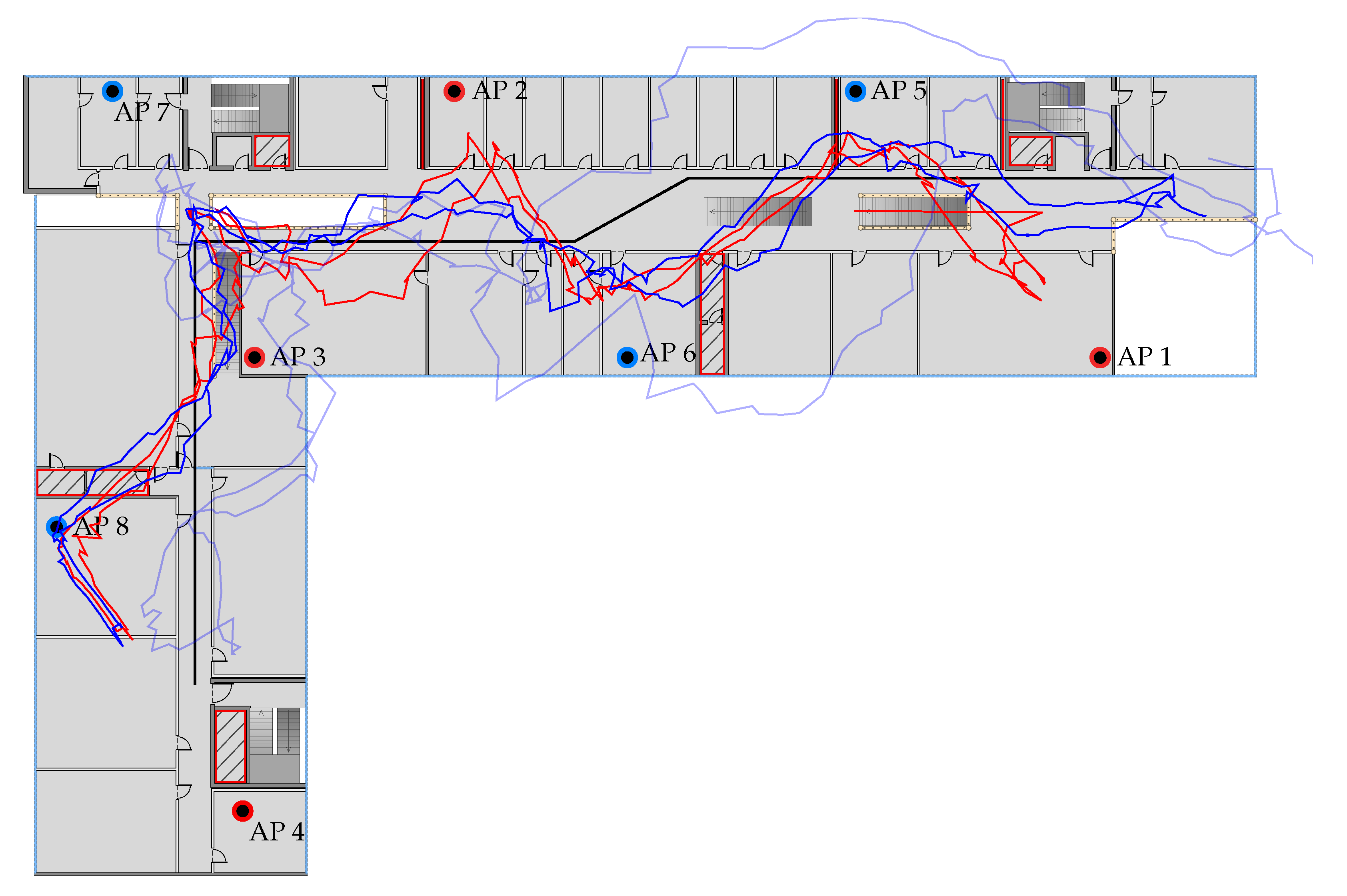
Figure 12 depicts the estimated path for path 2 using the particle filter method and the Pixel 2 XL. The overall courses of the estimated paths based on RSSI and offset corrected FTM after values are somewhat similar. The position estimate based on FTM has the smaller position error with
and
, compared to RSSI with
m and
.
The estimated path based on RSSI shows a sideways S-shaped curve in the main hallway. Especially at the start and end of the walk the RSSI method fails to follow the ground truth to the start/endpoint but drifts away from the actual position. This is also visible in the left half of the main hallway, where the RSSI path noticeably diverges from the ground truth. Overall, the FTM path has a similar course but is closer to the ground truth at the start/endpoint and in the left half of the main hallway.
In the lower-left of the building, both path estimates are getting “pulled” towards AP 8. The reason for this is, that the smartphone receives almost no measurements from AP 4, as it is shielded by reinforced concrete and a building supply room. Hence, AP 3, AP 7 and AP 8 are the only available reference points in that region. AP 7 is rather far away, and AP 3 is also heavily weakened due to the concrete walls and metal staircase. Furthermore, AP 8 gets distorted most of the time due to the shielded building supply room. Consequently, AP 8 has a large negative offset correction of
m (see
Table 2). As soon as the pedestrian passes by the supply room the signal is nearly unaltered which results in accurate distance measurements. However, due to the offset correction, these presumably correct distances are significantly shortened, which is apparent in the estimated path.
This is also visible in the plot of the position error over time in
Figure 13a. Between 70 s and 100 s the error of the uncorrected FTM is actually smaller than the corrected one. Outside of that interval, the corrected values produce a much smaller position error. The before mentioned strategy to use the raw FTM measurement when the distance becomes negative after the correction improves this specific situation. However, the difference is only small and only in that situation.
Generally, the positioning performance in the secondary hallway is poor due to the unfortunate placement of the AP 4 and AP 8. However, this circumstance was only noticed after the data was recorded. Better results are expected, when AP 4 is placed to the room in the farthermost left room and AP 8 to the right room across the hallway. Nevertheless, the results make it clear that RSSI and FTM are equally strong affected by the environment and thoughtful placement of the APs is still crucial for the performance of indoor positioning systems.
The same reasoning also applies to the main hallway. AP 5 is placed in a room which is surrounded by two fire doors. As seen in the NLOS experiment in
Section 6.3 distance estimates to this AP are much larger if the line of sight between the smartphone and the AP crosses the fire door.
Figure 13b shows the distance error for AP 5 with and without offset correction. A positive error indicates that the distance measurement was larger than the true distance and negative value means that the measurement was shorter. The jump in the interval from
to
is due to the absence of measurements to that AP. At 20 s (dashed black line) the error increases abruptly due to the fire door. Likewise, at 150 s the error drops as the pedestrian passes the fire door on his way back. This correlates directly with the drift of the estimated path away from the ground truth path.
The effect of the fire door is also visible in the estimated path based on the unaltered FTM measurements (see
Figure 12, light blue line). Here, the path curves around the room, due to the larger measured distances. Note that the transition model of the particle filter randomly moves the particles. Because of that random nature the estimated path can run above or below the room. Again, this is adjusted by the offset correction but, like with AP 8, too much as the estimated path gets “pulled” into the room.
All in all, there are many situations like this, due to the relatively large number of shielded rooms and fire doors in the university building. This is worsened by the small number of APs. Adding more APs to the setup could improve the result, as overall more measurements are likely to be available during the positioning. Alternatively, a more flexible model which incorporates local distortions in the distance measurement should be beneficial.