Higher-Order Models for Resonant Viscosity and Mass-Density Sensors
Abstract
1. Introduction
2. Materials and Methods
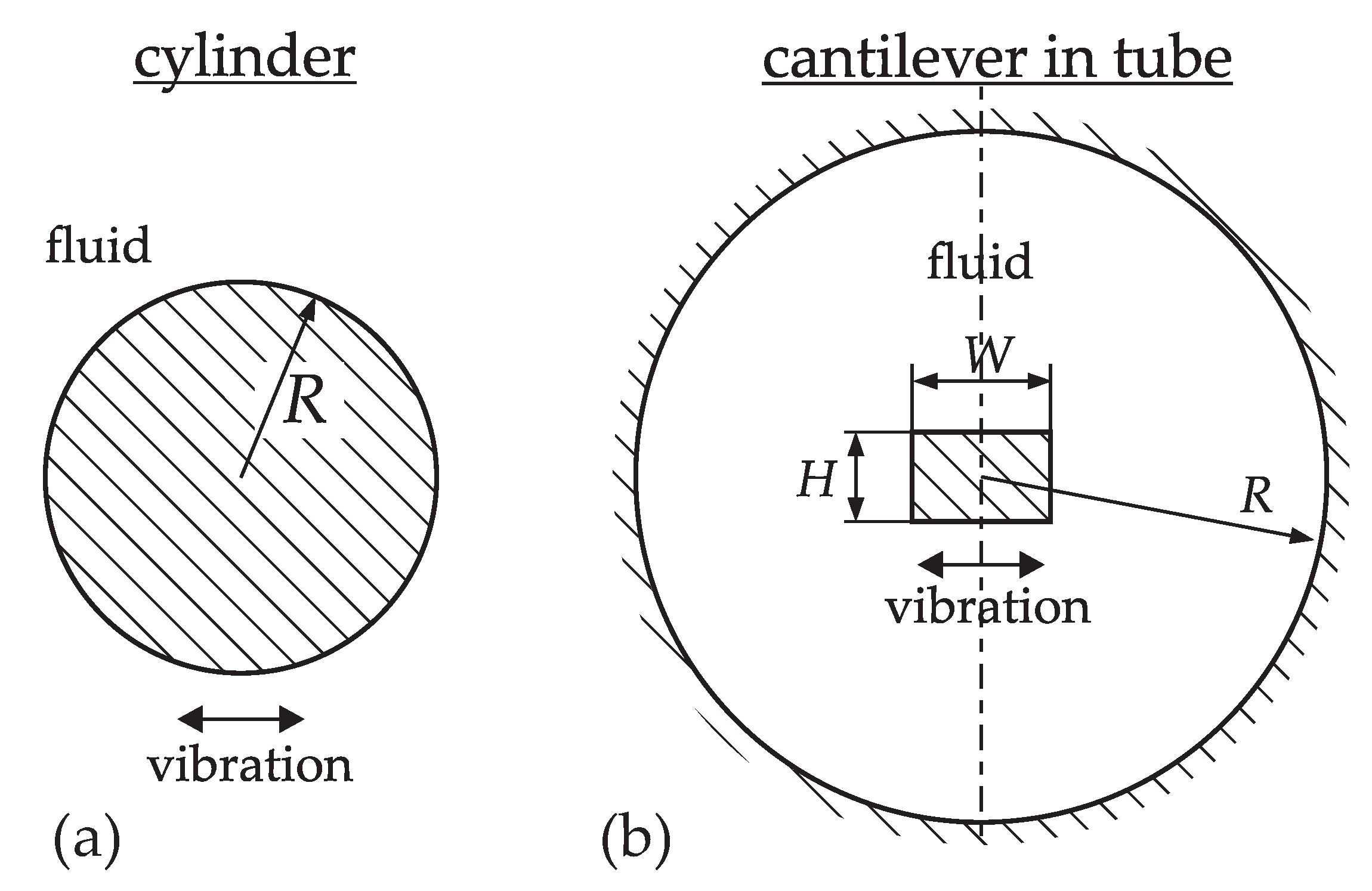
2.1. Vibrating Cylinder Immersed in Viscous Fluid
2.2. Arbitrary Cross-Sections Vibrating in Fluid
2.3. Resonator Model
2.4. Higher-Order Fluid Models
2.4.1. Model Calibration
2.5. Viscosity-Only Model
Model Parameter Calibration
3. Results and Discussion
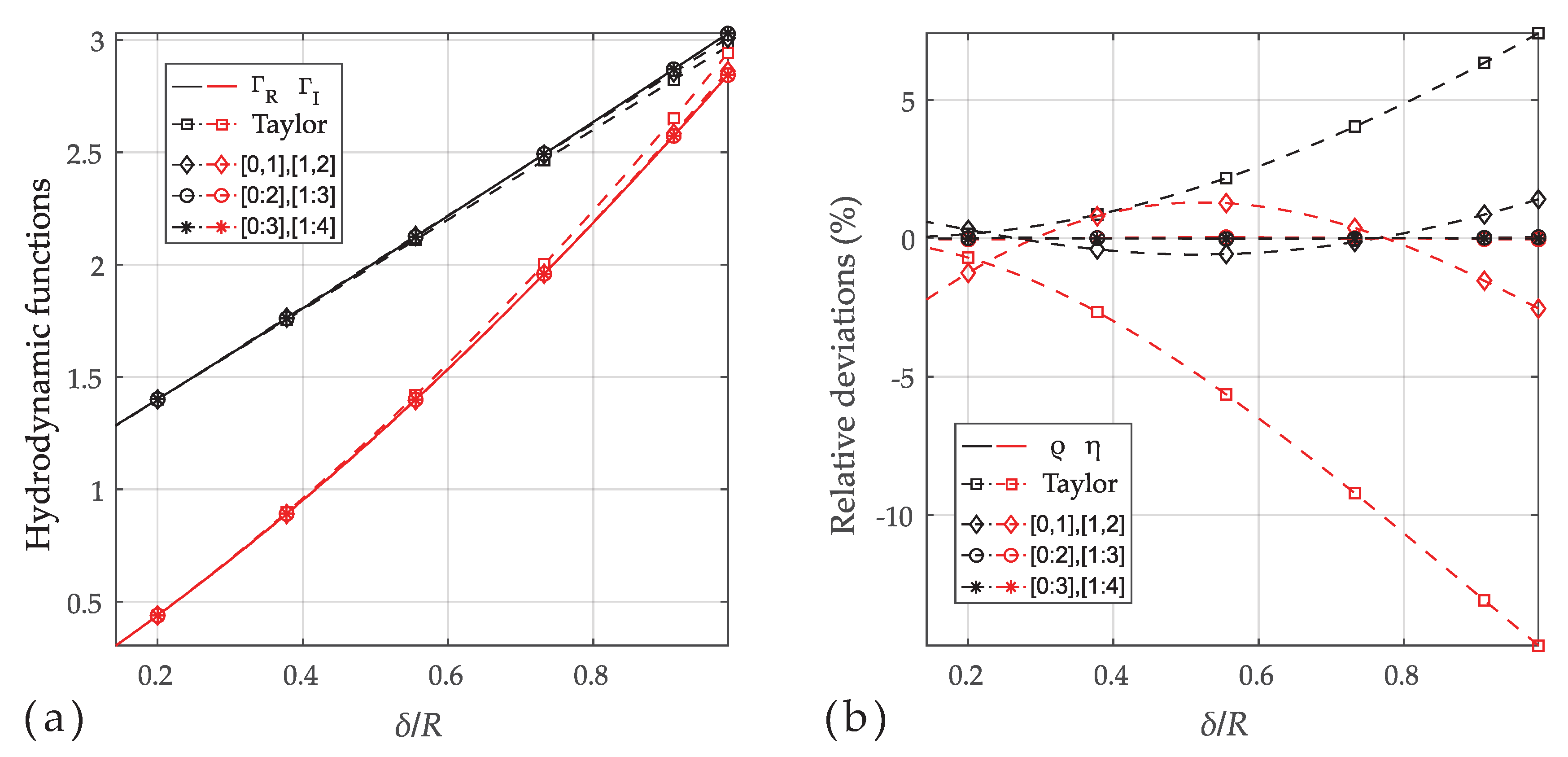
3.1. Numerical Analysis for the Vibrating Cylinder
3.2. Quartz Tuning Fork Measurements
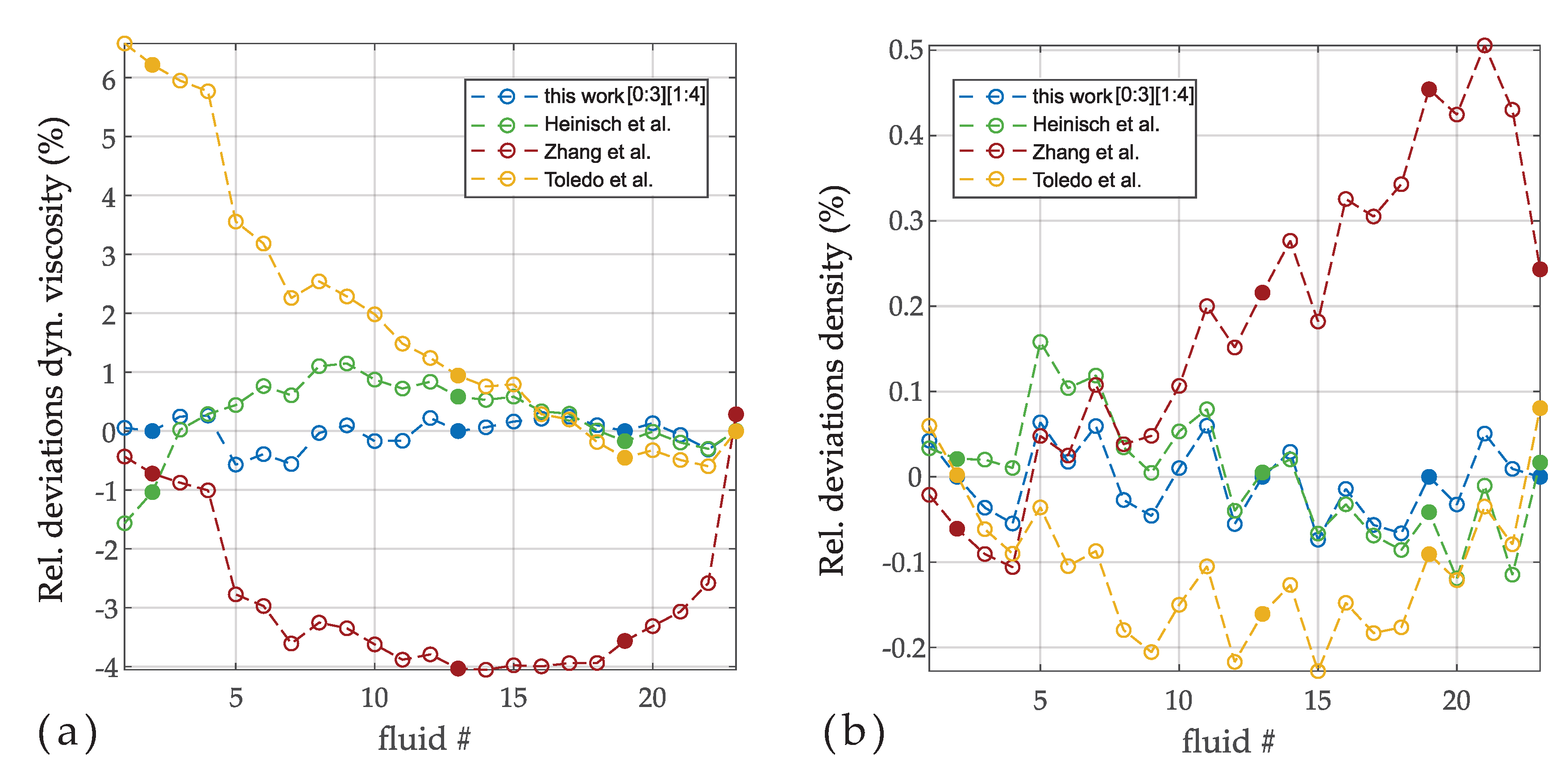
3.2.1. Extended Viscosity and Density Model
3.2.2. Viscosity-Only Model
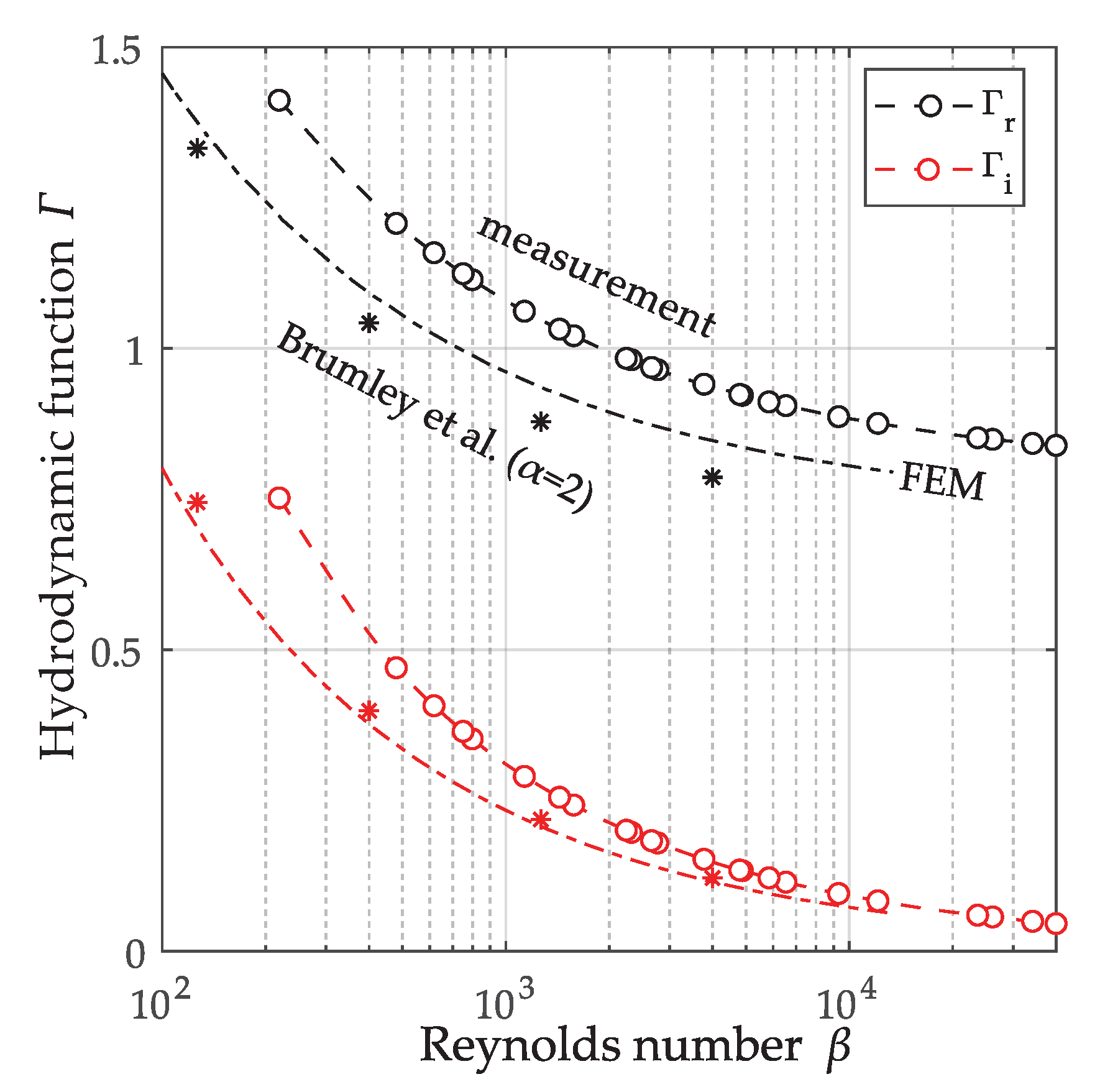
3.2.3. Measurement of the Hydrodynamic Function of the QTF
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Dimensional Analysis
Appendix B. Resonance Parameters
References
- Jakoby, B.; Beigelbeck, R.; Keplinger, F.; Lucklum, F.; Niedermayer, A.; Reichel, E.K.; Riesch, C.; Voglhuber-Brunnmaier, T.; Weiss, B. Miniaturized sensors for the viscosity and density of liquids-performance and issues. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 57, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Z. Für Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon II, J.G. The oscillation frequency of a quartz resonator in contact with liquid. Anal. Chim. Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Jakoby, B.; Vellekoop, M.J. Viscosity sensing using a Love-wave device. Sens. Actuators Phys. 1998, 68, 275–281. [Google Scholar] [CrossRef]
- Abdallah, A.; Reichel, E.K.; Voglhuber-Brunmaier, T.; Heinisch, M.; Clara, S.; Jakoby, B. Symmetric mechanical plate resonators for fluid sensing. Sens. Actuators Phys. 2015, 232, 319–328. [Google Scholar] [CrossRef]
- Martin, S.; Wessendorf, K.; Gebert, C.; Frye, G.; Cernosek, R.; Casaus, L.; Mitchell, M. Measuring liquid properties with smooth-and textured-surface resonators. In Proceedings of the 1993 IEEE International Frequency Control Symposium, Salt Lake City, UT, USA, 2–4 June 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 603–608. [Google Scholar]
- Herrmann, F.; Hahn, D.; Büttgenbach, S. Separate determination of liquid density and viscosity with sagittally corrugated Love-mode sensors. Sens. Actuators Phys. 1999, 78, 99–107. [Google Scholar] [CrossRef]
- Inaba, S.; Akaishi, K.; Mori, T.; Hane, K. Analysis of the resonance characteristics of a cantilever vibrated photothermally in a liquid. J. Appl. Phys. 1993, 73, 2654–2658. [Google Scholar] [CrossRef]
- Oden, P.; Chen, G.; Steele, R.; Warmack, R.; Thundat, T. Viscous drag measurements utilizing microfabricated cantilevers. Appl. Phys. Lett. 1996, 68, 3814–3816. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Shih, W.Y.; Li, X.; Gu, H.; Shih, W.H.; Aksay, I.A. Simultaneous liquid viscosity and density determination with piezoelectric unimorph cantilevers. J. Appl. Phys. 2001, 89, 1497–1505. [Google Scholar] [CrossRef]
- Cakmak, O.; Ermek, E.; Kilinc, N.; Yaralioglu, G.; Urey, H. Precision density and viscosity measurement using two cantilevers with different widths. Sens. Actuators Phys. 2015, 232, 141–147. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, C.; Su, X.; OShea, S.J. Determination of liquid density with a low frequency mechanical sensor based on quartz tuning fork. Sens. Actuators Chem. 2002, 84, 123–128. [Google Scholar] [CrossRef]
- Matsiev, L. Application of flexural mechanical resonators to simultaneous measurements of liquid density and viscosity. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Caesars Tahoe, NV, USA, 17–20 October 1999; pp. 457–460. [Google Scholar]
- Waszczuk, K.; Piasecki, T.; Nitsch, K.; Gotszalk, T. Application of piezoelectric tuning forks in liquid viscosity and density measurements. Sens. Actuators Chem. 2011, 160, 517–523. [Google Scholar] [CrossRef]
- Niedermayer, A.O.; Voglhuber-Brunnmaier, T.; Heinisch, M.; Feichtinger, F.; Jakoby, B. Monitoring of the dilution of motor oil with diesel using an advanced resonant sensor system. Procedia Eng. 2016, 168, 15–18. [Google Scholar] [CrossRef]
- Tuck, E. Calculation of unsteady flows due to small motions of cylinders in a viscous fluid. J. Eng. Math. 1969, 3, 29–44. [Google Scholar] [CrossRef]
- Rosenhead, L. Laminar Boundary Layers: An Account of the Development, Structure, and Stability of Laminar Boundary Layers in Incompressible Fluids, Together With a Description of the Associated Experimental Techniques; Dover Publications: Mineola, NY, USA, 1988. [Google Scholar]
- Cox, R. Theoretical Analysis of Laterally Vibrating Microcantilever Sensors in a Viscous Liquid Medium. Ph.D. Thesis, Marquette University, Milwaukee, WI, USA, 2011. [Google Scholar]
- Brumley, D.R.; Willcox, M.; Sader, J.E. Oscillation of cylinders of rectangular cross section immersed in fluid. Phys. Fluids 2010, 22, 052001. [Google Scholar] [CrossRef]
- Dufour, I.; Lemaire, E.; Caillard, B.; Debéda, H.; Lucat, C.; Heinrich, S.M.; Josse, F.; Brand, O. Effect of hydrodynamic force on microcantilever vibrations: Applications to liquid-phase chemical sensing. Sens. Actuators Chem. 2014, 192, 664–672. [Google Scholar] [CrossRef]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.K.; Dufour, I.; Jakoby, B. Reduced order models for resonant viscosity and mass density sensors. Sens. Actuators Phys. 2014, 220, 76–84. [Google Scholar] [CrossRef]
- Youssry, M.; Belmiloud, N.; Caillard, B.; Ayela, C.; Pellet, C.; Dufour, I. A straightforward determination of fluid viscosity and density using microcantilevers: From experimental data to analytical expressions. Sens. Actuators Phys. 2011, 172, 40–46. [Google Scholar] [CrossRef]
- Toledo, J.; Manzaneque, T.; Ruiz-Díez, V.; Kucera, M.; Pfusterschmied, G.; Wistrela, E.; Schmid, U.; Sánchez-Rojas, J. Piezoelectric resonators and oscillator circuit based on higher-order out-of-plane modes for density-viscosity measurements of liquids. J. Micromech. Microeng. 2016, 26, 084012. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, D.; He, X.; Wang, X. A Hydrodynamic Model for Measuring Fluid Density and Viscosity by Using Quartz Tuning Forks. Sensors 2020, 20, 198. [Google Scholar] [CrossRef] [PubMed]
- Maali, A.; Hurth, C.; Boisgard, R.; Jai, C.; Cohen-Bouhacina, T.; Aimé, J.P. Hydrodynamics of oscillating atomic force microscopy cantilevers in viscous fluids. J. Appl. Phys. 2005, 97, 074907. [Google Scholar] [CrossRef]
- Riesch, C.; Reichel, E.K.; Keplinger, F.; Jakoby, B. Characterizing vibrating cantilevers for liquid viscosity and density sensing. J. Sensors 2008, 2008. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.; Heinisch, M.; Abdallah, A.; Reichel, E.; Jakoby, B.; Putz, V.; Beigelbeck, R. Modeling-free evaluation of resonant liquid sensors for measuring viscosity and density. In Proceedings of the 2015 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 8–10 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 300–305. [Google Scholar]
- Manzaneque, T.; Ruiz-Díez, V.; Hernando-García, J.; Wistrela, E.; Kucera, M.; Schmid, U.; Sánchez-Rojas, J.L. Piezoelectric MEMS resonator-based oscillator for density and viscosity sensing. Sens. Actuators Phys. 2014, 220, 305–315. [Google Scholar] [CrossRef]
- Valente, M.P.; De Paula, I.B. Sensor based on piezo buzzers for simultaneous measurement of fluid viscosity and density. Measurement 2020, 152, 107308. [Google Scholar] [CrossRef]
- Batchelor, C.K.; Batchelor, G. an Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Beigelbeck, R.; Jakoby, B. A two-dimensional analysis of spurious compressional wave excitation by thickness-shear-mode resonators. J. Appl. Phys. 2004, 95, 4989–4995. [Google Scholar] [CrossRef]
- Heinisch, M. Mechanical Resonators for Liquid Viscosity and Mass Density Sensing. Ph.D. Thesis, Johannes Kepler University, Linz, Austria, 2015. [Google Scholar]
- Micro Resonant OG. Homepage. Available online: http://www.micro-resonant.at/cms (accessed on 23 April 2020).
- Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Feichtinger, F.; Jakoby, B. Fluid sensing using quartz tuning forks: Measurement technology and applications. Sens. 2019, 19, 2336. [Google Scholar] [CrossRef]
- Niedermayer, A.O.; Voglhuber-Brunnmaier, T.; Feichtinger, F.; Heinisch, M.; Jakoby, B. Online condition monitoring of lubricating oil based on resonant measurement of fluid properties. In Sensors and Measuring Systems, Proceedings of the 19th ITG/GMA-Symposium, Nuremberg, Germany, 26–27 June 2018; VDE: Frankfurt, Germany, 2018; pp. 1–4. [Google Scholar]
- Voglhuber-Brunnmaier, T.; Heinisch, M.; Reichel, E.K.; Weiss, B.; Jakoby, B. Derivation of reduced order models from complex flow fields determined by semi-numeric spectral domain models. Sens. Actuators Phys. 2013, 202, 44–51. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Reichel, E.K.; Niedermayer, A.O.; Feichtinger, F.; Sell, J.K.; Jakoby, B. Determination of particle distributions from sedimentation measurements using a piezoelectric tuning fork sensor. Sens. Actuators Phys. 2018, 284, 266–275. [Google Scholar] [CrossRef]
- Wilson, T.L.; Campbell, G.A.; Mutharasan, R. Viscosity and density values from excitation level response of piezoelectric-excited cantilever sensors. Sens. Actuators Phys. 2007, 138, 44–51. [Google Scholar] [CrossRef]
- Zohuri, B. Dimensional Analysis and Self-Similarity Methods for Engineers and Scientists; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Beigelbeck, R.; Antlinger, H.; Cerimovic, S.; Clara, S.; Keplinger, F.; Jakoby, B. Resonant pressure wave setup for simultaneous sensing of longitudinal viscosity and sound velocity of liquids. Meas. Sci. Technol. 2013, 24, 125101. [Google Scholar] [CrossRef]

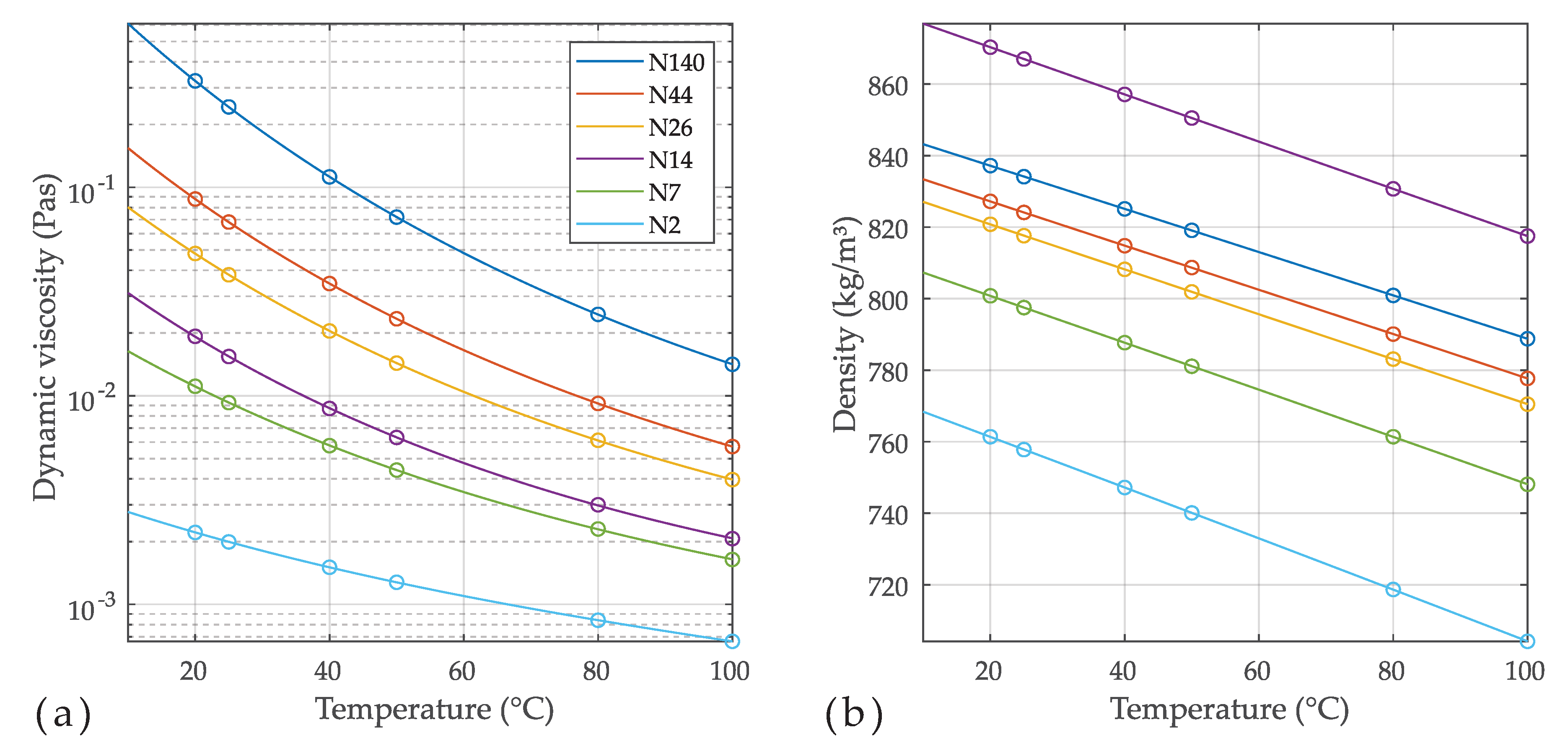

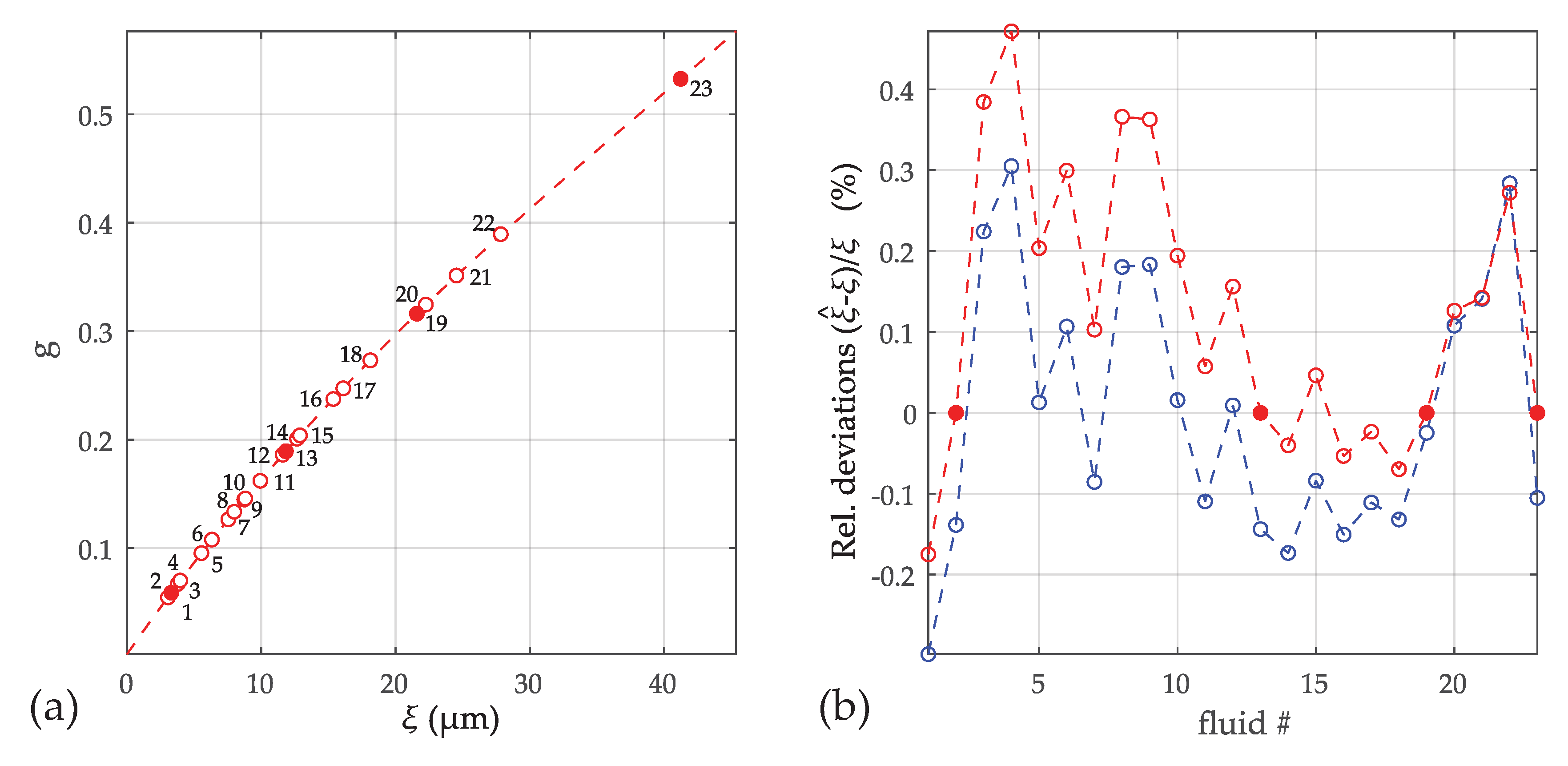

| Fluid | Temp. | Density | Dyn. visc. | Kin. visc. | Res. freq. | Q-Factor | ||
|---|---|---|---|---|---|---|---|---|
| (C) | (m) | (kg/m) | (mPas) | (cSt) | (kHz) | (1) | ||
| 1 | N2 | 50 | ||||||
| 2 | * N2 | 40 | ||||||
| 3 | N2 | 25 | ||||||
| 4 | N2 | 20 | ||||||
| 5 | N7 | 50 | ||||||
| 6 | N7 | 40 | ||||||
| 7 | N14 | 50 | ||||||
| 8 | N7 | 25 | ||||||
| 9 | N7 | 20 | ||||||
| 10 | N14 | 40 | ||||||
| 11 | N26 | 50 | ||||||
| 12 | N14 | 25 | ||||||
| 13 | * N26 | 40 | ||||||
| 14 | N44 | 50 | ||||||
| 15 | N14 | 20 | ||||||
| 16 | N44 | 40 | ||||||
| 17 | N26 | 25 | ||||||
| 18 | N26 | 20 | ||||||
| 19 | * N44 | 25 | ||||||
| 20 | N140 | 50 | ||||||
| 21 | N44 | 20 | ||||||
| 22 | N140 | 40 | ||||||
| 23 | * N140 | 25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voglhuber-Brunnmaier, T.; Jakoby, B. Higher-Order Models for Resonant Viscosity and Mass-Density Sensors. Sensors 2020, 20, 4279. https://doi.org/10.3390/s20154279
Voglhuber-Brunnmaier T, Jakoby B. Higher-Order Models for Resonant Viscosity and Mass-Density Sensors. Sensors. 2020; 20(15):4279. https://doi.org/10.3390/s20154279
Chicago/Turabian StyleVoglhuber-Brunnmaier, Thomas, and Bernhard Jakoby. 2020. "Higher-Order Models for Resonant Viscosity and Mass-Density Sensors" Sensors 20, no. 15: 4279. https://doi.org/10.3390/s20154279
APA StyleVoglhuber-Brunnmaier, T., & Jakoby, B. (2020). Higher-Order Models for Resonant Viscosity and Mass-Density Sensors. Sensors, 20(15), 4279. https://doi.org/10.3390/s20154279





