Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study
Abstract
1. Introduction
2. Materials and Methods
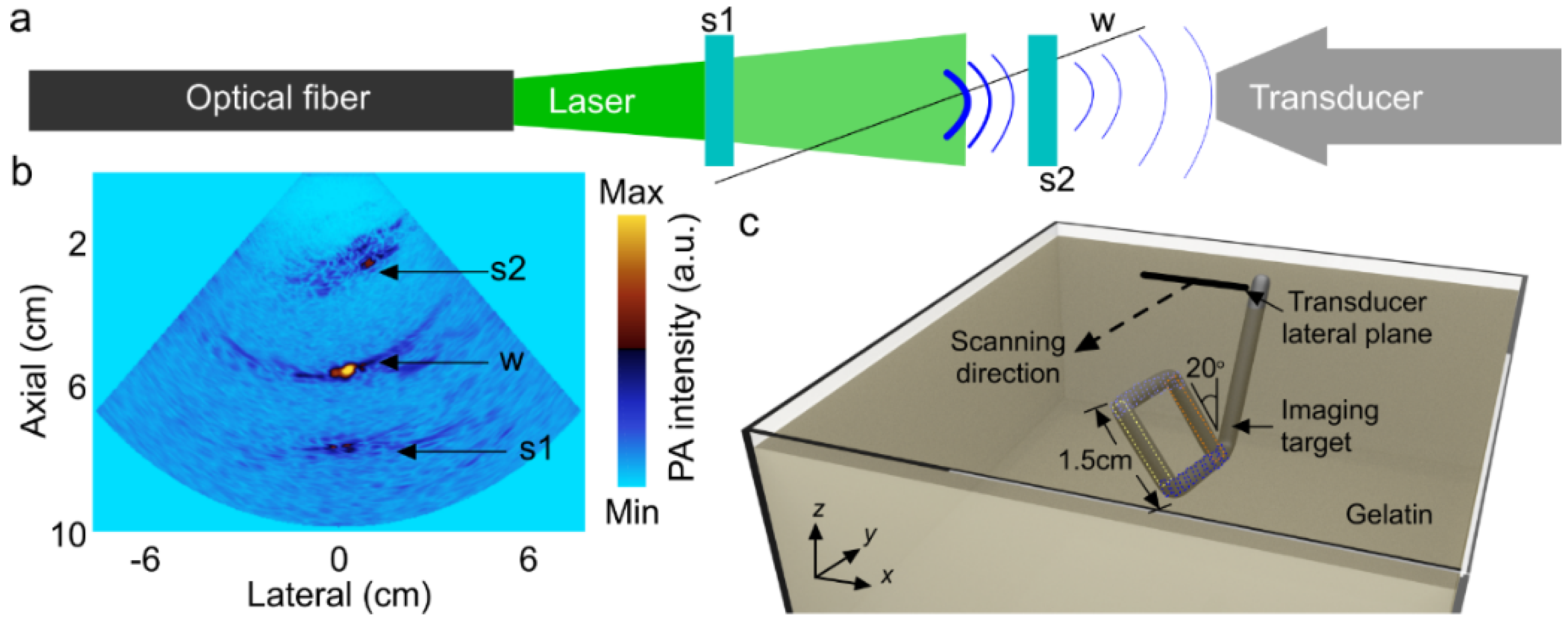
2.1. PAI System
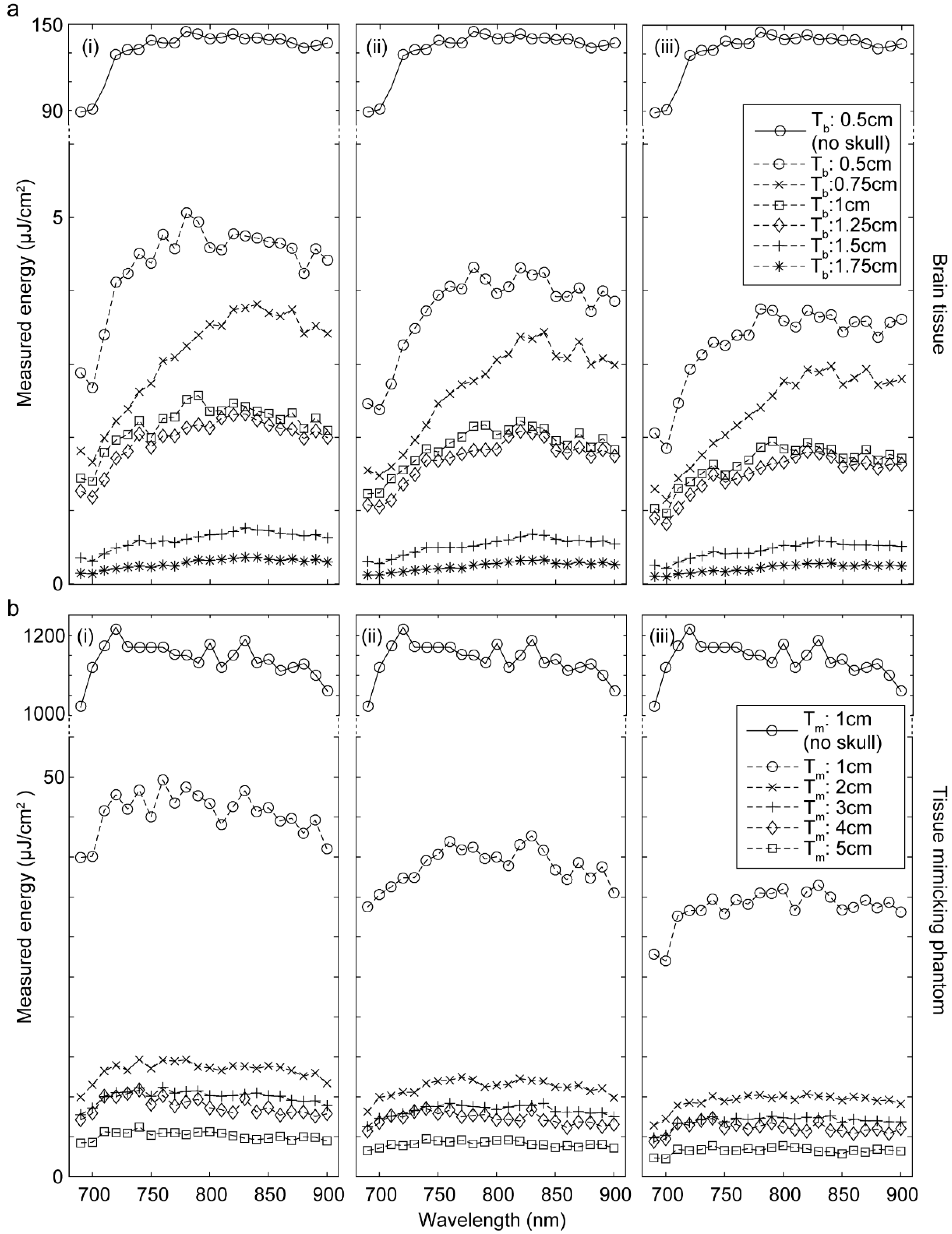
2.2. Skull Tissue Preparation
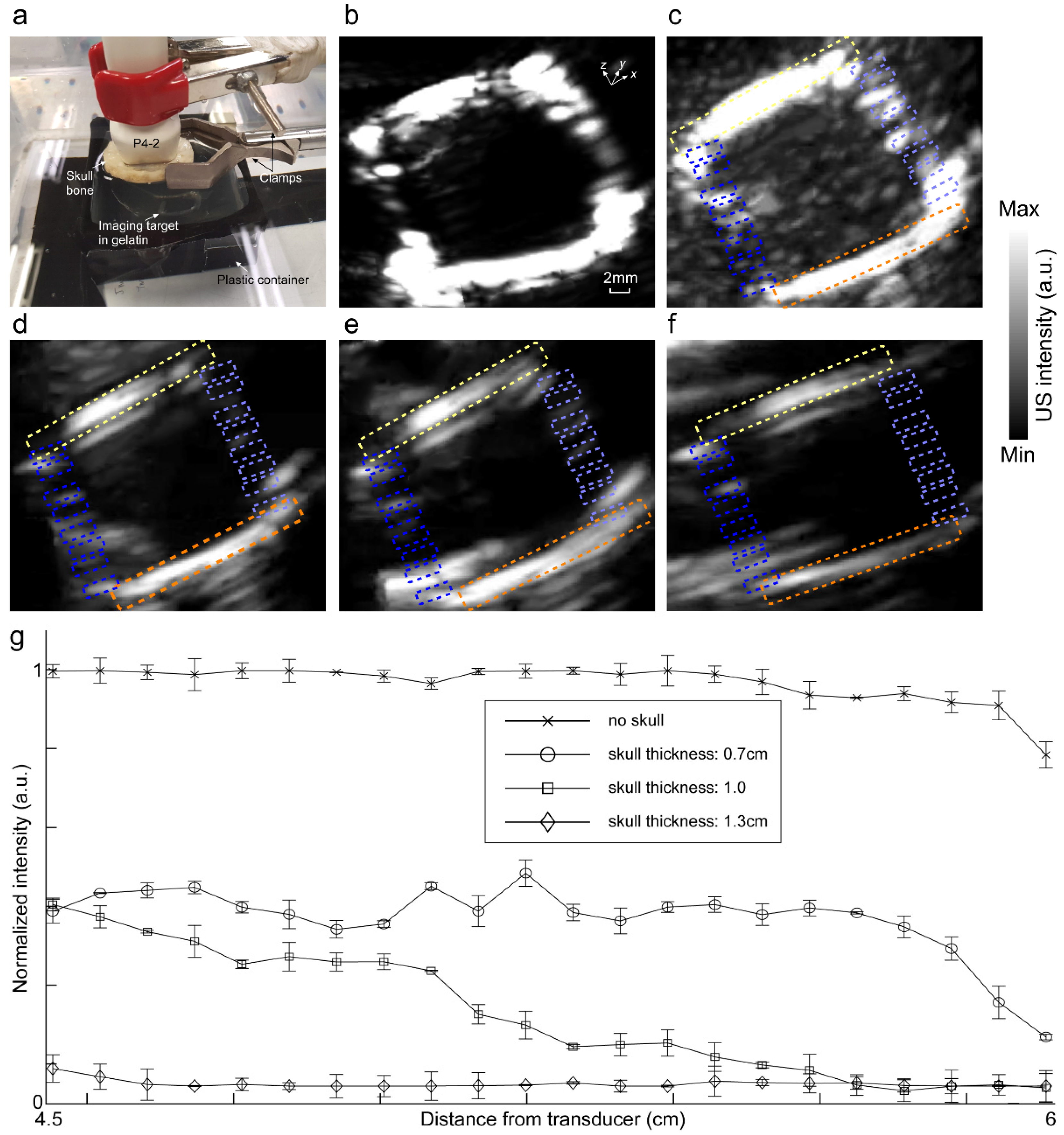
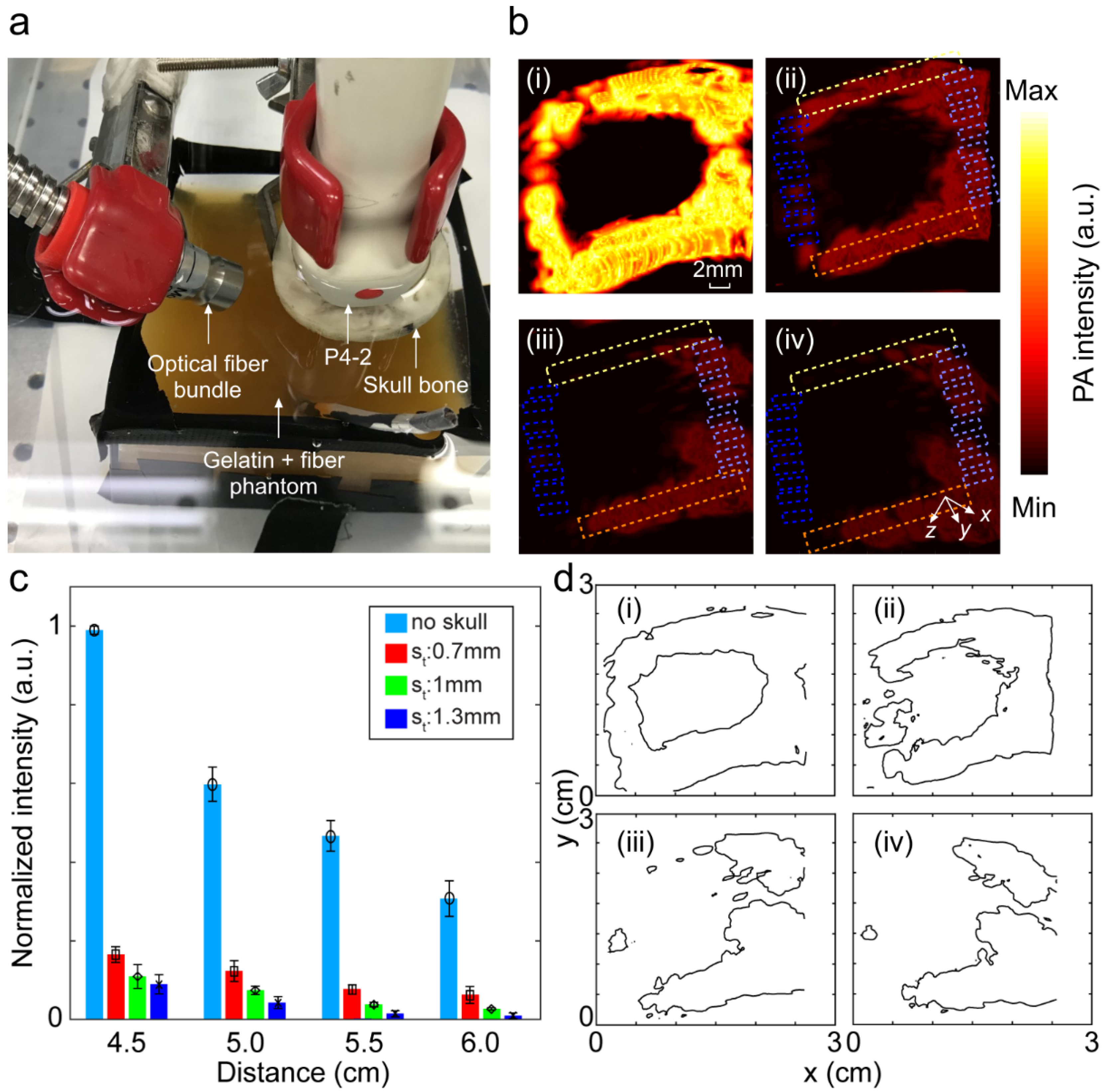
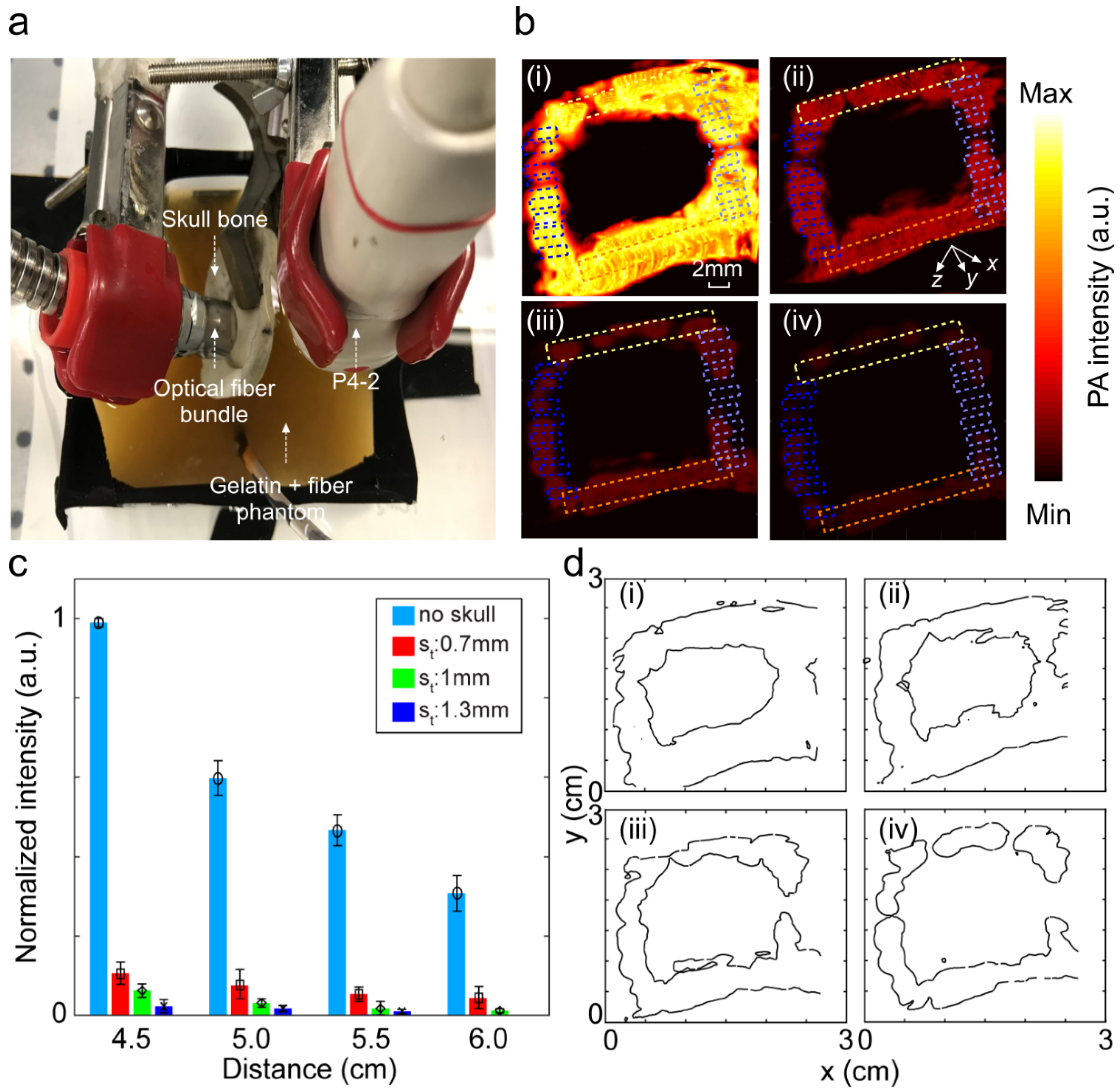
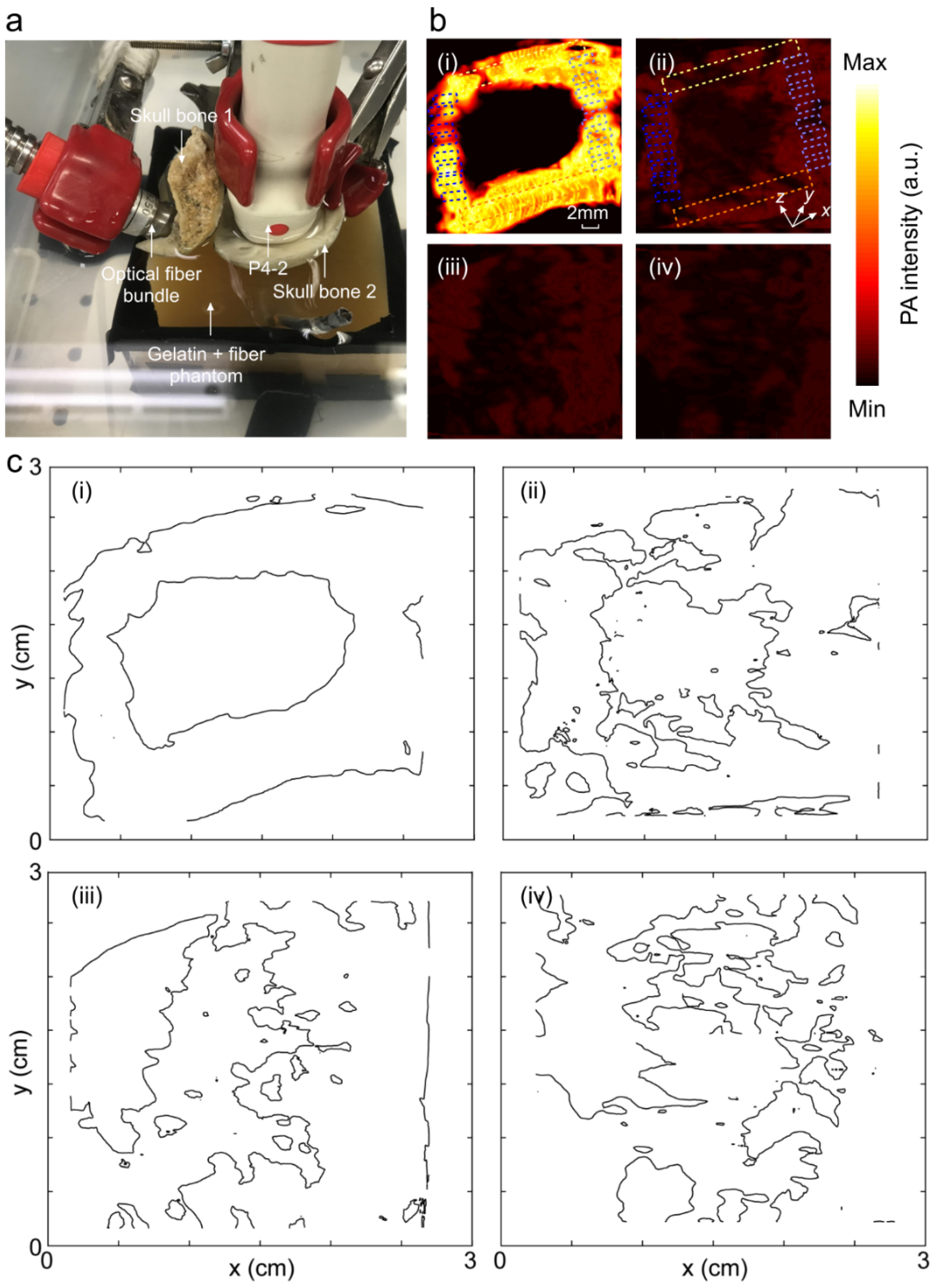
2.3. Phantom Experiments
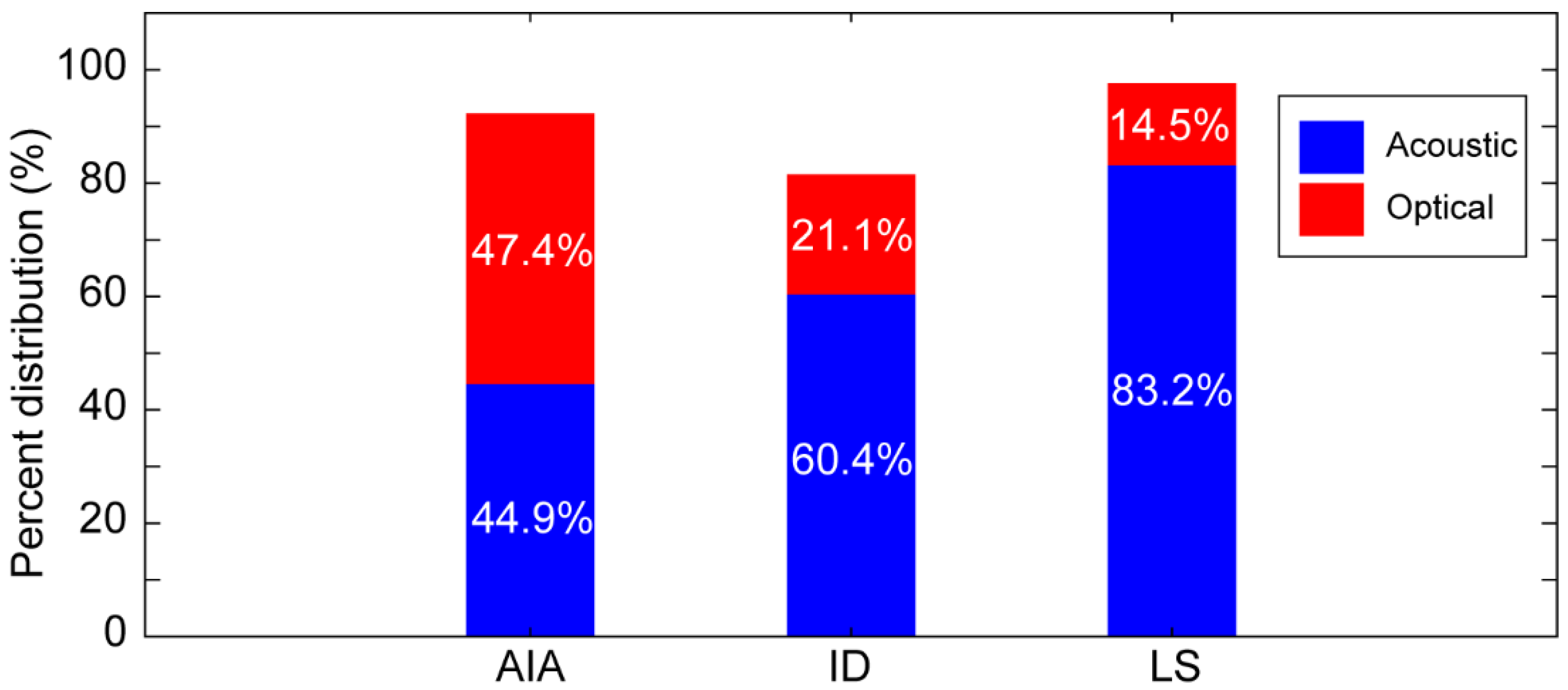
2.4. Quantitative Evaluation Parameters
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kirsch, J.D.; Mathur, M.; Johnson, M.H.; Gowthaman, G.; Scoutt, L.M. Advances in transcranial Doppler US: Imaging ahead. Radiographics 2013, 33, E1–E14. [Google Scholar] [CrossRef]
- Naqvi, J.; Yap, K.H.; Ahmad, G.; Ghosh, J. Transcranial Doppler ultrasound: A review of the physical principles and major applications in critical care. Int. J. Vasc. Med. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Purkayastha, S.; Sorond, F. Transcranial Doppler ultrasound: Technique and application. Semin. Neurol. 2012, 32, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Van Wezel-Meijler, G.; Steggerda, S.J.; Leijser, L.M. Cranial ultrasonography in neonates: Role and limitations. Semin. Neurol. 2010, 34, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Chernyshev, O.Y.; Garami, Z.; Calleja, S.; Song, J.; Campbell, M.S.; Noser, E.A.; Shaltoni, H.; Chen, C.-I.; Iguchi, Y.; Grotta, J.C. Yield and accuracy of urgent combined carotid/transcranial ultrasound testing in acute cerebral ischemia. Stroke 2005, 36, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Bell, M.A.L.; Ostrowski, A.K.; Li, K.; Kazanzides, P.; Boctor, E.M. Localization of transcranial targets for photoacoustic-guided endonasal surgeries. Photoacoustics 2015, 3, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, T.H.; Stieg, P.E.; Anand, V.K. Endoscopic transsphenoidal pituitary surgery with intraoperative magnetic resonance imaging. Op. Neurosurg. 2006, 58, ONS44–ONS51. [Google Scholar] [CrossRef]
- Wang, L.V.; Hu, S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef]
- Hariri, A.; Fatima, A.; Mohammadian, N.; Bely, N.; Nasiriavanaki, M. Low cost photoacoustic spectroscopy system for evaluation of skin health. In Proceedings of the SPIE Optical Engineering+ Applications, San Diego, CA, USA, 28 August–1 September 2016. [Google Scholar]
- Hariri, A.; Bely, N.; Chen, C.; Nasiriavanaki, M. Towards ultrahigh resting-state functional connectivity in the mouse brain using photoacoustic microscopy. In Proceedings of the SPIE BiOS, San Francisco, CA, USA, 13–14 February 2016; p. 97085A. [Google Scholar]
- Manwar, R.; Li, X.; Mahmoodkalayeh, S.; Asano, E.; Zhu, D.; Avanaki, K. Deep Learning Protocol for Improved Photoacoustic Brain Imaging. J. Biophotonics 2020. [Google Scholar] [CrossRef]
- Mahmoodkalayeh, S.; Zarei, M.; Ansari, M.A.; Kratkiewicz, K.; Ranjbaran, M.; Manwar, R.; Avanaki, K. Improving vascular imaging with co-planar mutually guided photoacoustic and diffuse optical tomography: a simulation study. Biomed. Optics Express 2020, 11, 4333–4347. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Yan, H.; Liu, Y.; Zhang, J.; Shan, W.; Lai, P.; Li, H.; Ren, L.; Li, Z. Aggregation-Induced Absorption Enhancement for Deep Near-Infrared II Photoacoustic Imaging of Brain Gliomas In Vivo. Adv. Sci. 2019, 6, 1801615. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, B.D.; Light, E.D.; Nicoletto, H.A.; Bennett, E.R.; Laskowitz, D.T.; Smith, S.W. The ultrasound brain helmet: New transducers and volume registration for in vivo simultaneous multi-transducer 3-D transcranial imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1189–1202. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T.L.; Lewin, P.A. Ultrasound transducer selection in clinical imaging practice. J. Ultrasound Med. 2013, 32, 573–582. [Google Scholar] [CrossRef]
- Wang, L.V. Tutorial on photoacoustic microscopy and computed tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Zhou, Y.; Yao, J.; Wang, L.V. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2016, 21, 61007. [Google Scholar] [CrossRef]
- Mohammadi-Nejad, A.-R.; Mahmoudzadeh, M.; Hassanpour, M.S.; Wallois, F.; Muzik, O.; Papadelis, C.; Hansen, A.; Soltanian-Zadeh, H.; Gelovani, J.; Nasiriavanaki, M. Neonatal brain resting-state functional connectivity imaging modalities. Photoacoustics 2018, 10, 1–19. [Google Scholar] [CrossRef]
- Fatima, A.; Kratkiewicz, K.; Manwar, R.; Zafar, M.; Zhang, R.; Huang, B.; Dadashzadesh, N.; Xia, J.; Avanaki, M. Review of Cost Reduction Methods in Photoacoustic Computed Tomography. Photoacoustics 2019, 15, 100137. [Google Scholar] [CrossRef]
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef]
- Kim, C.; Erpelding, T.N.; Jankovic, L.; Pashley, M.D.; Wang, L.V. Deeply penetrating in vivo photoacoustic imaging using a clinical ultrasound array system. Biomed. Opt. Express 2010, 1, 278–284. [Google Scholar] [CrossRef]
- Mohammadi, L.; Behnam, H.; Tavakkoli, J.; Avanaki, M.R. Skull’s Photoacoustic Attenuation and Dispersion Modeling with Deterministic Ray-Tracing: Towards Real-Time Aberration Correction. Sensors 2019, 19, 345. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, L.; Manwar, R.; Behnam, H.; Tavakkoli, J.; Avanaki, M.R.N. Skull’s aberration modeling: Towards photoacoustic human brain imaging. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 3–6 February 2019; p. 108785W. [Google Scholar]
- Fry, F.J.; Barger, J.E. Acoustical properties of the human skull. J. Acoust. Soc. Am. 1978, 63, 1576–1590. [Google Scholar] [CrossRef]
- White, P.J.; Clement, G.T.; Hynynen, K. Longitudinal and shear mode ultrasound propagation in human skull bone. Ultrasound Med. Biol. 2006, 32, 1085–1096. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E. Acoustic attenuation compensation in photoacoustic tomography using time-variant filtering. J. Biomed. Opt. 2013, 18, 36008. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B.T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J. Acoust. Soc. Am. 2010, 127, 2741–2748. [Google Scholar] [CrossRef]
- Pichardo, S.; Sin, V.W.; Hynynen, K. Multi-frequency characterization of the speed of sound and attenuation coefficient for longitudinal transmission of freshly excised human skulls. Phys. Med. Biol. 2011, 56, 219–250. [Google Scholar] [CrossRef]
- Dean-Ben, X.L.; Razansky, D.; Ntziachristos, V. The effects of acoustic attenuation in optoacoustic signals. Phys. Med. Biol. 2011, 56, 6129–6148. [Google Scholar] [CrossRef]
- Fenster, A.; Lacefield, J.C. Ultrasound Imaging and Therapy; Taylor and Francis: Washington, DC, USA, 2015. [Google Scholar]
- Nam, K.; Rosado-Mendez, I.M.; Rubert, N.C.; Madsen, E.L.; Zagzebski, J.A.; Hall, T.J. Ultrasound attenuation measurements using a reference phantom with sound speed mismatch. Ultrason Imaging 2011, 33, 251–263. [Google Scholar] [CrossRef]
- Mohammadi, L.; Behnam, H.; Nasiriavanaki, M. Modeling skull’s acoustic attenuation and dispersion on photoacoustic signal. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 29 January–1 February 2017; p. 100643U. [Google Scholar]
- Volinski, B.; Hariri, A.; Fatima, A.; Xu, Q.; Nasiriavanaki, M. Photoacoustic investigation of a neonatal skull phantom. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 29 January–1 February 2017; p. 100643T. [Google Scholar]
- Xu, Q.; Volinski, B.; Hariri, A.; Fatima, A.; Nasiriavanaki, M. Effect of small and large animal skull bone on photoacoustic signal. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 29 January–1 February 2017; p. 100643S. [Google Scholar]
- Turani, Z.; Fatemizadeh, E.; Blumetti, T.; Daveluy, S.; Moraes, A.F.; Chen, W.; Mehregan, D.; Andersen, P.E.; Nasiriavanaki, M. Optical Radiomic Signatures Derived from Optical Coherence Tomography Images to Improve Identification of Melanoma. Cancer Res. 2019, 79, 2021–2030. [Google Scholar] [CrossRef]
- Tournat, V.; Pagneux, V.; Lafarge, D.; Jaouen, L. Multiple scattering of acoustic waves and porous absorbing media. Phys. Rev. E 2004, 70, 26609. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.V. Monkey brain cortex imaging by photoacoustic tomography. J. Biomed. Opt. 2008, 13, 44009. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Wang, L.V. Photoacoustic brain imaging: From microscopic to macroscopic scales. Neurophotonics 2014, 1, 11003. [Google Scholar] [CrossRef] [PubMed]
- Zubiaurre-Elorza, L.; Soria-Pastor, S.; Junque, C.; Sala-Llonch, R.; Segarra, D.; Bargallo, N.; Macaya, A. Cortical thickness and behavior abnormalities in children born preterm. PLoS ONE 2012, 7, e42148. [Google Scholar] [CrossRef] [PubMed]
- Ballardini, E.; Tarocco, A.; Baldan, A.; Antoniazzi, E.; Garani, G.; Borgna-Pignatti, C. Universal cranial ultrasound screening in preterm infants with gestational age 33–36 weeks: A retrospective analysis of 724 newborns. Pediatr. Neurol. 2014, 51, 790–794. [Google Scholar] [CrossRef]
- Manwar, R.; Hosseinzadeh, M.; Hariri, A.; Kratkiewicz, K.; Noei, S.; N Avanaki, M. Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging. Sensors 2018, 18, 3498. [Google Scholar] [CrossRef]
- Lynnerup, N.; Astrup, J.G.; Sejrsen, B. Thickness of the human cranial diploe in relation to age, sex and general body build. Head Face Med. 2005, 1, 13. [Google Scholar] [CrossRef]
- Jin, S.-W.; Sim, K.-B.; Kim, S.-D. Development and growth of the normal cranial vault: An embryologic review. J. Korean Neurosurg. Soc. 2016, 59, 192. [Google Scholar] [CrossRef]
- Webster, S.J.; Jee, S. The Skeletal Tissues: Histology; Elsevier Biomedical Press: Amsterdam, The Netherlands, 1983; pp. 200–254. [Google Scholar]
- Abousleiman, Y.N.; Cheung, A.H.-D.; Ulm, F.-J. Poromechanics III-Biot Centennial (1905–2005): Proceedings of the 3rd Biot Conference on Poromechanics, 24–27 May 2005, Norman, Oklahoma, USA; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Braidotti, P.; Branca, F.; Stagni, L. Scanning electron microscopy of human cortical bone failure surfaces. J. Biomech. 1997, 30, 155–162. [Google Scholar] [CrossRef]
- Teoh, S.; Chui, C. Bone material properties and fracture analysis: Needle insertion for spinal surgery. J. Mech. Behav. Biomed. Mater. 2008, 1, 115–139. [Google Scholar] [CrossRef]
- Njeh, C.F. The Dependence of Ultrasound Velocity and Attenuation on the Material Properties of Cancellous Bone; Sheffield Hallam University: Sheffield, UK, 1995. [Google Scholar]
- Osterhoff, G.; Morgan, E.F.; Shefelbine, S.J.; Karim, L.; McNamara, L.M.; Augat, P. Bone mechanical properties and changes with osteoporosis. Injury 2016, 47, S11–S20. [Google Scholar] [CrossRef]
- Wydra, A.; Malyarenko, E.; Shapoori, K.; Maev, R.G. Development of a practical ultrasonic approach for simultaneous measurement of the thickness and the sound speed in human skull bones: A laboratory phantom study. Phys. Med. Biol. 2013, 58, 1083. [Google Scholar] [CrossRef] [PubMed]
- Geerits, T.W.; Kelder, O. Acoustic wave propagation through porous media: Theory and experiments. J. Acoust. Soc. Am. 1997, 102, 2495–2510. [Google Scholar] [CrossRef]
- Manwar, R.; Kratkiewicz, K.; Avanaki, K. Overview of Ultrasound Detection Technologies for Photoacoustic Imaging. Micromachines 2020, 11, 692. [Google Scholar] [CrossRef]
- Noguera, A.G. Propagation of Ultrasound Through Freshly Excised Human Calvarium; University of Nebraska-Lincoln: Lincoln, UK, 2012. [Google Scholar]
- Han, S.; Rho, J.; Medige, J.; Ziv, I. Ultrasound velocity and broadband attenuation over a wide range of bone mineral density. Osteoporos. Int. 1996, 6, 291–296. [Google Scholar] [CrossRef]
- Wang, S.; Chang, C.; Shih, C.; Teng, M. Evaluation of tibial cortical bone by ultrasound velocity in oriental females. Br. J. Radiol. 1997, 70, 1126–1130. [Google Scholar] [CrossRef]
- Strelitzki, R.; Evans, J.; Clarke, A. The influence of porosity and pore size on the ultrasonic properties of bone investigated using a phantom material. Osteoporos. Int. 1997, 7, 370–375. [Google Scholar] [CrossRef]
- Estrada, H.; Rebling, J.; Turner, J.; Razansky, D. Broadband acoustic properties of a murine skull. Phys. Med. Biol. 2016, 61, 1932. [Google Scholar] [CrossRef]
- Bevilacqua, F.; Piguet, D.; Marquet, P.; Gross, J.D.; Tromberg, B.J.; Depeursinge, C. In vivo local determination of tissue optical properties: Applications to human brain. Appl. Opt. 1999, 38, 4939–4950. [Google Scholar] [CrossRef]
- Antonio, A. Quantitative researches on the optical properties of human bone. Nature 1949, 163, 604. [Google Scholar] [CrossRef]
- Firbank, M.; Hiraoka, M.; Essenpreis, M.; Delpy, D.T. Measurement of the optical properties of the skull in the wavelength range 650–950 nm. Phys. Med. Biol. 1993, 38, 503–510. [Google Scholar] [CrossRef]
- Martin, B.; McElhaney, J.H. The acoustic properties of human skull bone. J. Biomed. Mater. Res. 1971, 5, 325–333. [Google Scholar] [CrossRef] [PubMed]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human cranial bone in the spectral range from 800 to 2000 nm. In Proceedings of the Saratov Fall Meeting 2005: Optical Technologies in Biophysics and Medicine VII, Saratov, Russia, 27–30 October 2005; pp. 616310–616311. [Google Scholar]
- Takeuchi, A.; Araki, R.; Proskurin, S.; Takahashi, Y.; Yamada, Y.; Ishii, J.; Katayama, S.; Itabashi, A. A new method of bone tissue measurement based upon light scattering. J. Bone Miner. Res. 1997, 12, 261–266. [Google Scholar] [CrossRef] [PubMed]
- White, D.; Curry, G.; Stevenson, R. The acoustic characteristics of the skull. Ultrasound Med. Biol. 1978, 4, 225241–239252. [Google Scholar] [CrossRef]
- Wang, Q.; Reganti, N.; Yoshioka, Y.; Howell, M.; Clement, G.T. Comparison between diffuse infrared and acoustic transmission over the human skull. In Proceedings of the Meetings on Acoustics, Providence, RI, USA, 6–9 May 2014; p. 20002. [Google Scholar]
- Lindsey, B.D.; Nicoletto, H.A.; Bennett, E.R.; Laskowitz, D.T.; Smith, S.W. Simultaneous bilateral real-time 3-D transcranial ultrasound imaging at 1 MHz through poor acoustic windows. Ultrasound Med. Biol. 2013, 39, 721–734. [Google Scholar] [CrossRef]
- Bude, R.O.; Adler, R.S. An easily made, low-cost, tissue-like ultrasound phantom material. J. Clin. Ultrasound 1995, 23, 271–273. [Google Scholar] [CrossRef]
- Tengsuthiwat, J.; Yorseng, K.; Siengchin, S.; Parameswaranpillai, J. Thermomechanical, water absorption, ultraviolet resistance and laser-assisted electroless plating behavior of Cu2O and melamine–formaldehyde-coated sisal fiber-modified poly (lactic acid) composites. Polym. Compos. 2019, 40, 3264–3274. [Google Scholar] [CrossRef]
- Karpienko, K.; Gnyba, M.; Milewska, D.; Wróbel, M.; Jędrzejewska-Szczerska, M. Blood equivalent phantom vs whole human blood, a comparative study. J. Innov. Opt. Health Sci. 2016, 9, 1650012. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Bell, M.A.L.; Ostrowski, A.K.; Li, K.; Kaanzides, P.; Boctor, E. Quantifying bone thickness, light transmission, and contrast interrelationships in transcranial photoacoustic imaging. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing, San Francisco, CA, USA, 3 March 2015; p. 93230C. [Google Scholar]
- Boruah, S.; Paskoff, G.R.; Shender, B.S.; Subit, D.L.; Salzar, R.S.; Crandall, J.R. Variation of bone layer thicknesses and trabecular volume fraction in the adult male human calvarium. Bone 2015, 77, 120–134. [Google Scholar] [CrossRef]
- Chaffaı, S.; Peyrin, F.; Nuzzo, S.; Porcher, R.; Berger, G.; Laugier, P. Ultrasonic characterization of human cancellous bone using transmission and backscatter measurements: Relationships to density and microstructure. Bone 2002, 30, 229–237. [Google Scholar] [CrossRef]
- Dehghani, H.; Delpy, D.T. Near-infrared spectroscopy of the adult head: Effect of scattering and absorbing obstructions in the cerebrospinal fluid layer on light distribution in the tissue. Appl. Opt. 2000, 39, 4721–4729. [Google Scholar] [CrossRef] [PubMed]
- Hughes, E.R.; Leighton, T.G.; Petley, G.W.; White, P.R. Ultrasonic propagation in cancellous bone: A new stratified model. Ultrasound Med. Biol. 1999, 25, 811–821. [Google Scholar] [CrossRef]
- Lillie, E.M.; Urban, J.E.; Lynch, S.K.; Weaver, A.A.; Stitzel, J.D. Evaluation of skull cortical thickness changes with age and sex from computed tomography scans. J. Bone Miner. Res. 2016, 31, 299–307. [Google Scholar] [CrossRef] [PubMed]
- McKelvie, M.; Palmer, S. The interaction of ultrasound with cancellous bone. Phys. Med. Biol. 1991, 36, 1331. [Google Scholar] [CrossRef]
- Nicholson, P.; Strelitzki, R.; Cleveland, R.; Bouxsein, M. Scattering of ultrasound in cancellous bone: Predictions from a theoretical model. J. Biomech. 2000, 33, 503–506. [Google Scholar] [CrossRef]
- Liu, J.; Lan, L.; Zhou, J.; Yang, Y. Influence of cancellous bone microstructure on ultrasonic attenuation: A theoretical prediction. Biomed. Eng. Online 2019, 18, 103. [Google Scholar] [CrossRef]
- Samsudin, E.M.; Ismail, L.H.; Kadir, A.A.; Nasidi, I.N. Thickness, density and porosity relationship towards sound absorption performance of mixed palm oil fibers. In Proceedings of the 24th International Congress on Sound and Vibration (ICSV 24), London, UK, 23–27 July 2017. [Google Scholar]
- Mahmoodkalayeh, S.; Jooya, H.Z.; Hariri, A.; Zhou, Y.; Xu, Q.; Ansari, M.A.; Avanaki, M.R. Low temperature-mediated enhancement of photoacoustic imaging depth. Sci. Rep. 2018, 8, 4873. [Google Scholar] [CrossRef]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Adabi, S.; Nasiriavanaki, M. Double-Stage Delay Multiply and Sum Beamforming Algorithm: Application to Linear-Array Photoacoustic Imaging. IEEE Trans. Biomed. Eng. 2018, 65, 31–42. [Google Scholar] [CrossRef]
- Estrada, H.C.; Huang, X.; Rebling, J.; Zwack, M.; Gottschalk, S.; Razansky, D. Virtual craniotomy for high-resolution optoacoustic brain microscopy. Sci. Rep. 2018, 8, 1459. [Google Scholar] [CrossRef]
- Omidi, P.; Zafar, M.; Mozaffarzadeh, M.; Hariri, A.; Haung, X.; Orooji, M.; Nasiriavanaki, M. A novel dictionary-based image reconstruction for photoacoustic computed tomography. Appl. Sci. 2018, 8, 1570. [Google Scholar] [CrossRef]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Kratkiewicz, K.; Adabi, S.; Nasiriavanaki, M. Linear-array photoacoustic imaging using minimum variance-based delay multiply and sum adaptive beamforming algorithm. J. Biomed. Opt. 2018, 23, 26002. [Google Scholar] [CrossRef] [PubMed]



| Skull Thickness (mm) | Image Average Intensity Attenuation (%) | Image Distortion (%) | Smoothness (%) |
|---|---|---|---|
| 0.7 | 46.5 ± 1.30 | 32.5 | 50 ± 1.47 |
| 1.0 | 48.23 ± 3.74 | 35.6 | 10.7 ± 1.26 |
| 1.3 | 78.4 ± 4.23 | 56.28 | 1.8 ± 0.89 |
| Skull Thickness (mm) | Image Average Intensity Attenuation (%) | Image Distortion (%) | Smoothness (%) |
|---|---|---|---|
| 0.7 | 88.42 ± 1.12 | 32.12 | 5.74 ± 2.71 |
| 1 | 92.59 ± 0.27 | 72.45 | 4.41 ± 2.05 |
| 1.3 | 95.17 ± 0.21 | 79.73 | 2.46 ± 1.87 |
| Skull Thickness (mm) | Image Average Intensity Attenuation (%) | Image Distortion (%) | Smoothness (%) |
|---|---|---|---|
| 0.7 | 91.10 ± 2.98 | 11.26 | 32.5 ± 1.56 |
| 1 | 95.07 ± 2.24 | 18.67 | 6.18 ± 1.06 |
| 1.3 | 97.03 ± 1.89 | 23.91 | 2.46 ± 0.74 |
| Skull Thickness (mm) | Image Average Intensity Attenuation (%) | Image Distortion (%) | Smoothness (%) |
|---|---|---|---|
| 0.7 | 92.3 ± 2.83 | 81.6 | 1.76 ± 1.38 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manwar, R.; Kratkiewicz, K.; Avanaki, K. Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study. Sensors 2020, 20, 4189. https://doi.org/10.3390/s20154189
Manwar R, Kratkiewicz K, Avanaki K. Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study. Sensors. 2020; 20(15):4189. https://doi.org/10.3390/s20154189
Chicago/Turabian StyleManwar, Rayyan, Karl Kratkiewicz, and Kamran Avanaki. 2020. "Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study" Sensors 20, no. 15: 4189. https://doi.org/10.3390/s20154189
APA StyleManwar, R., Kratkiewicz, K., & Avanaki, K. (2020). Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study. Sensors, 20(15), 4189. https://doi.org/10.3390/s20154189





