Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry
Abstract
1. Introduction
2. Principles of Measuring Methods
2.1. Strain Measurements
2.1.1. Fiber Optic Sensors
2.1.2. Digital Image Correlation
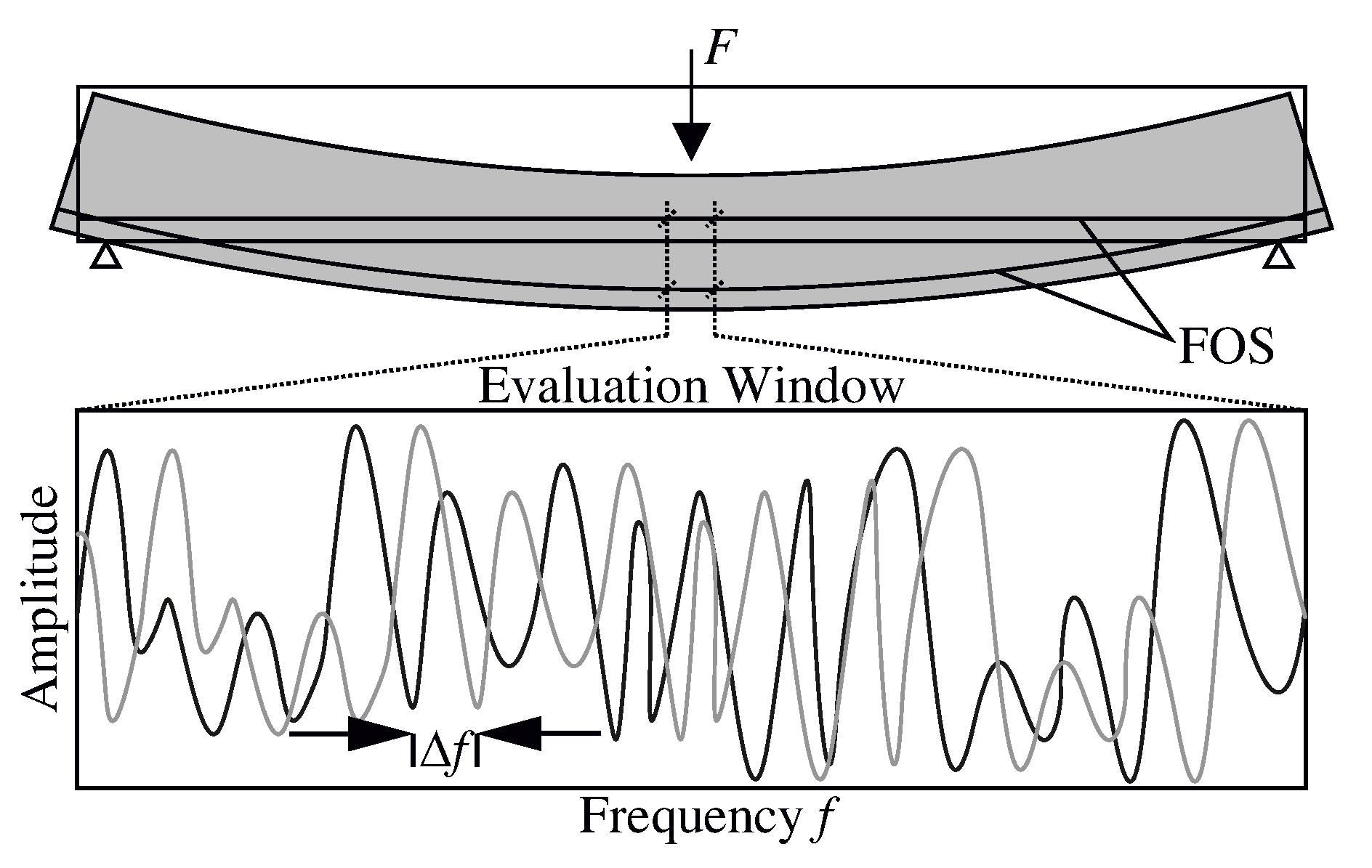
2.2. Ultrasound
3. Experiments
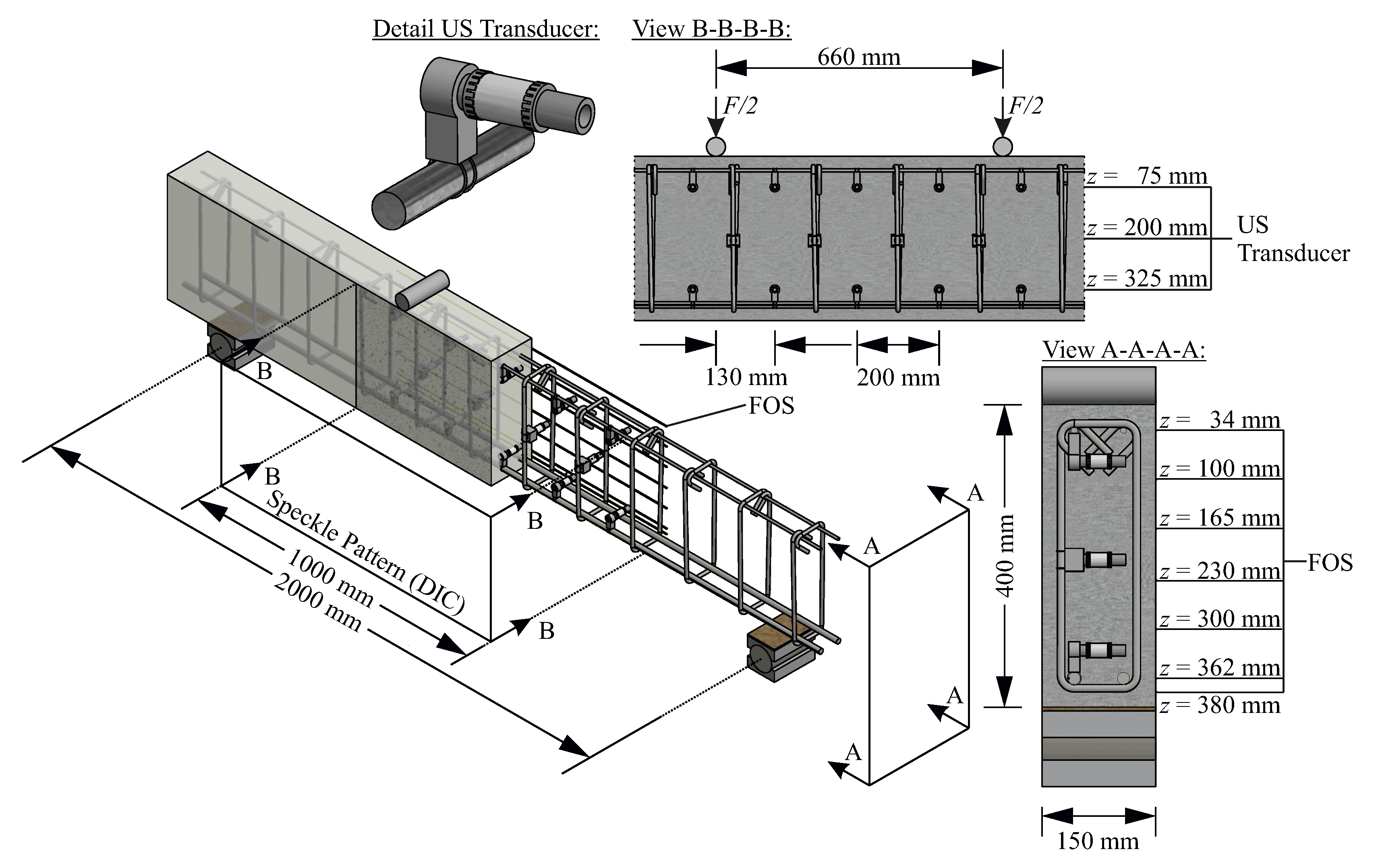
3.1. Method of Investigation
3.2. Test Set-Up
3.3. Results
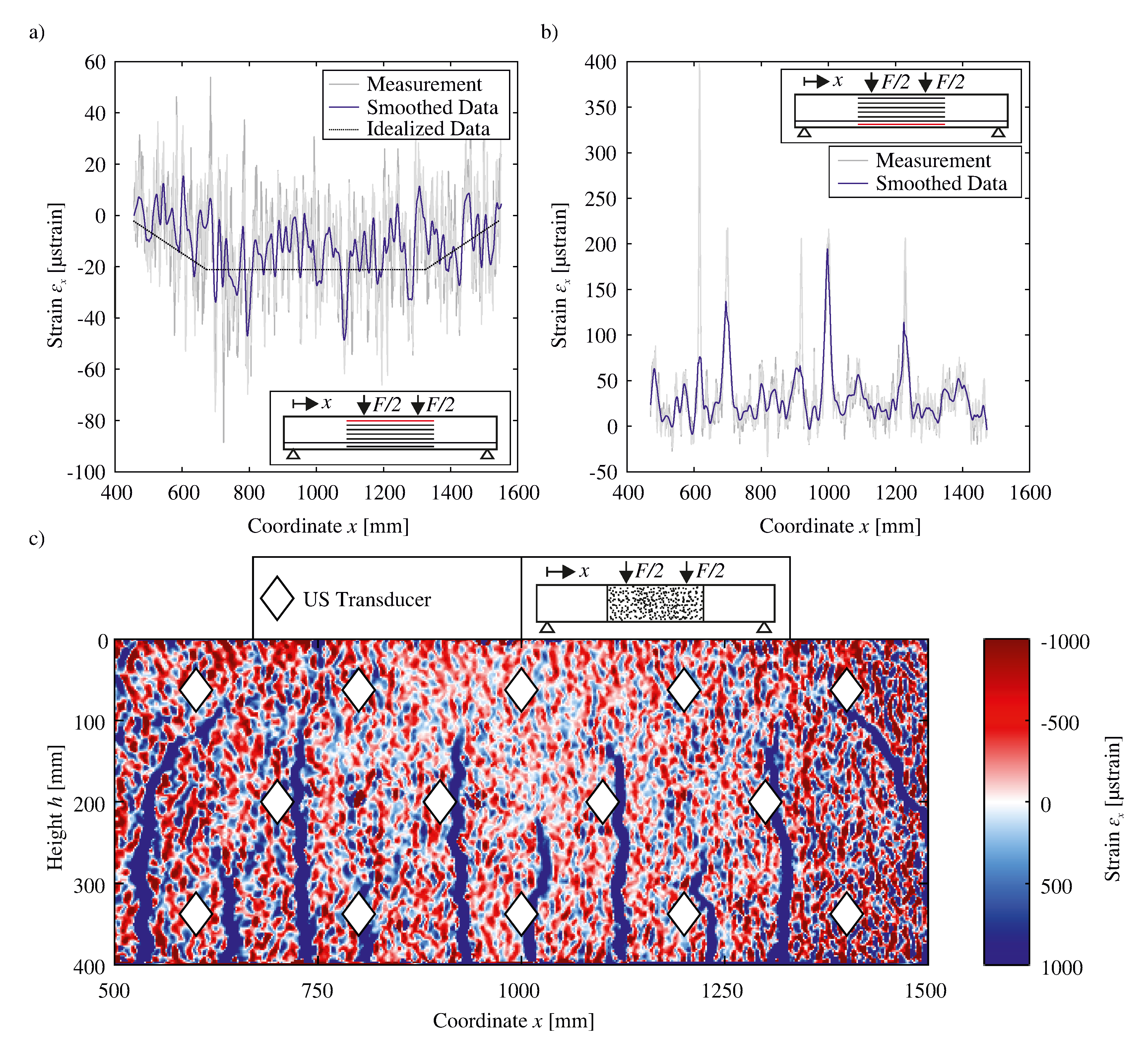
3.3.1. Strain
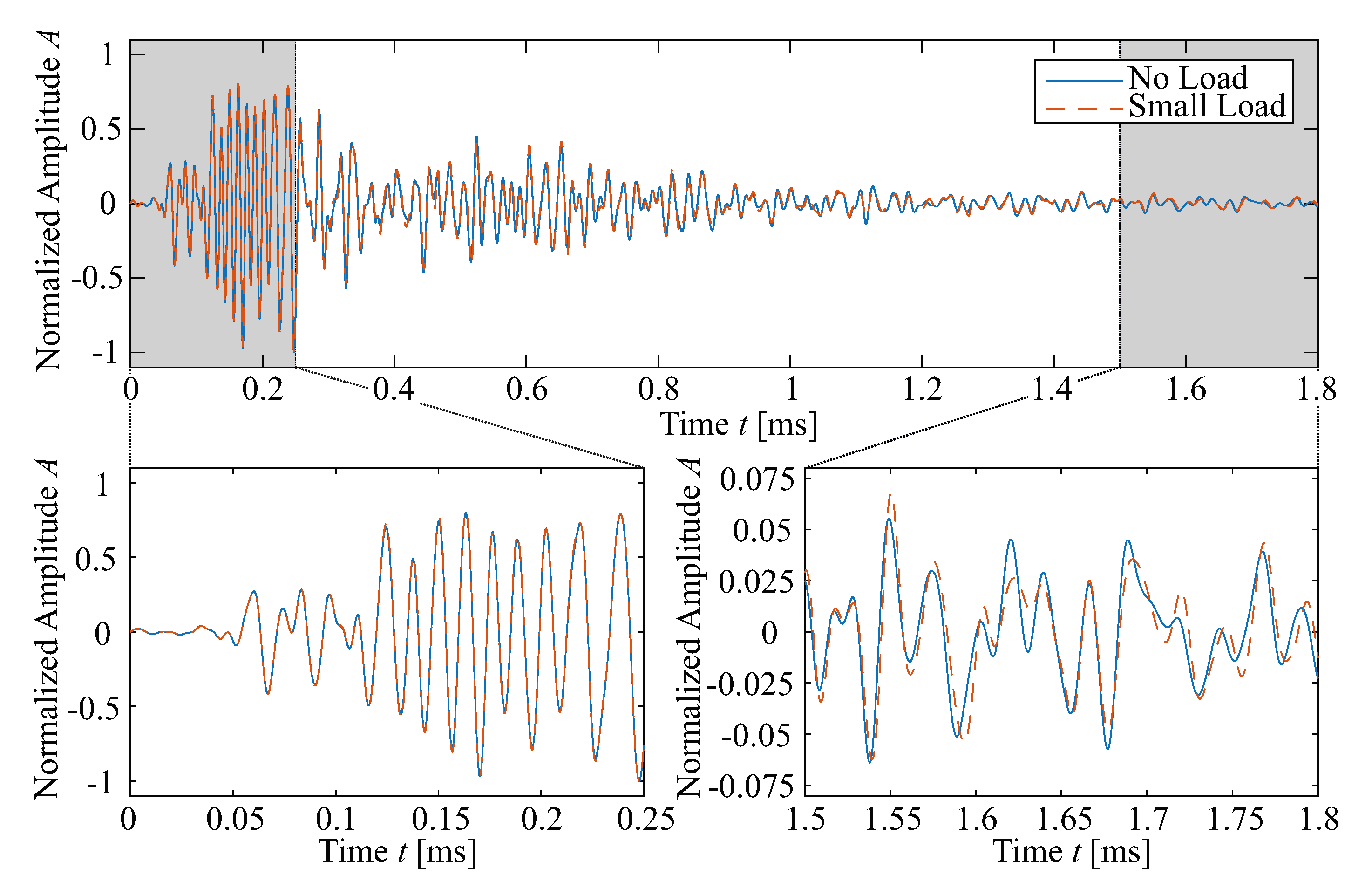
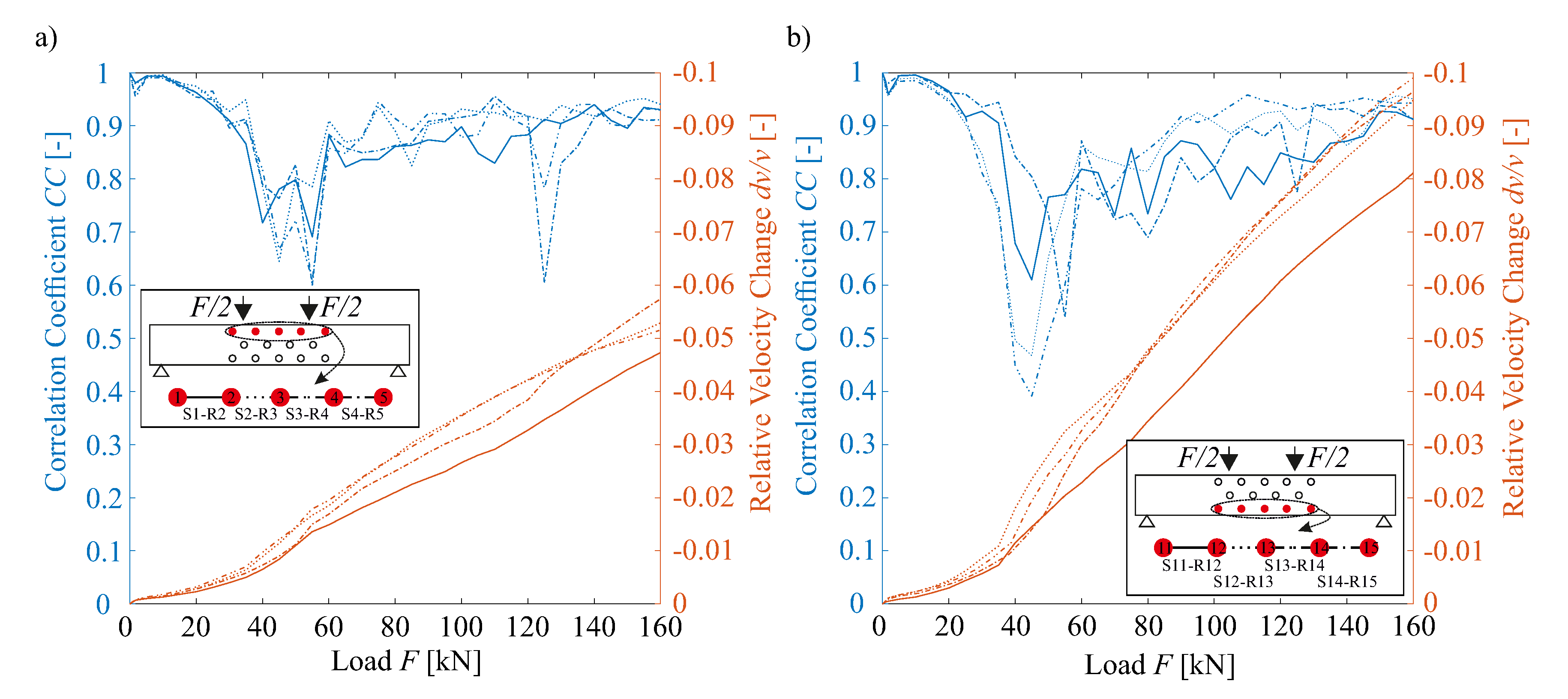
3.3.2. Ultrasound
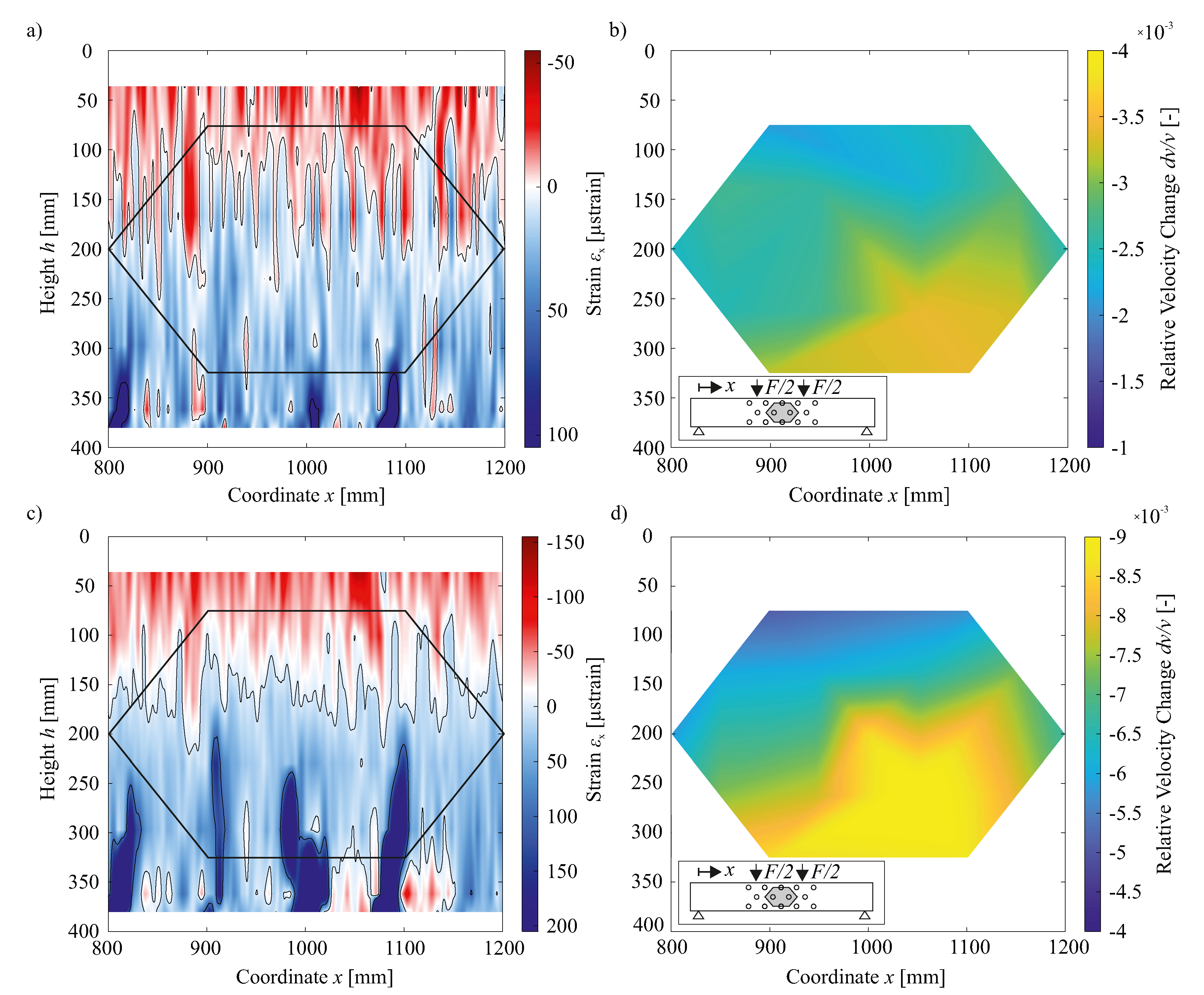
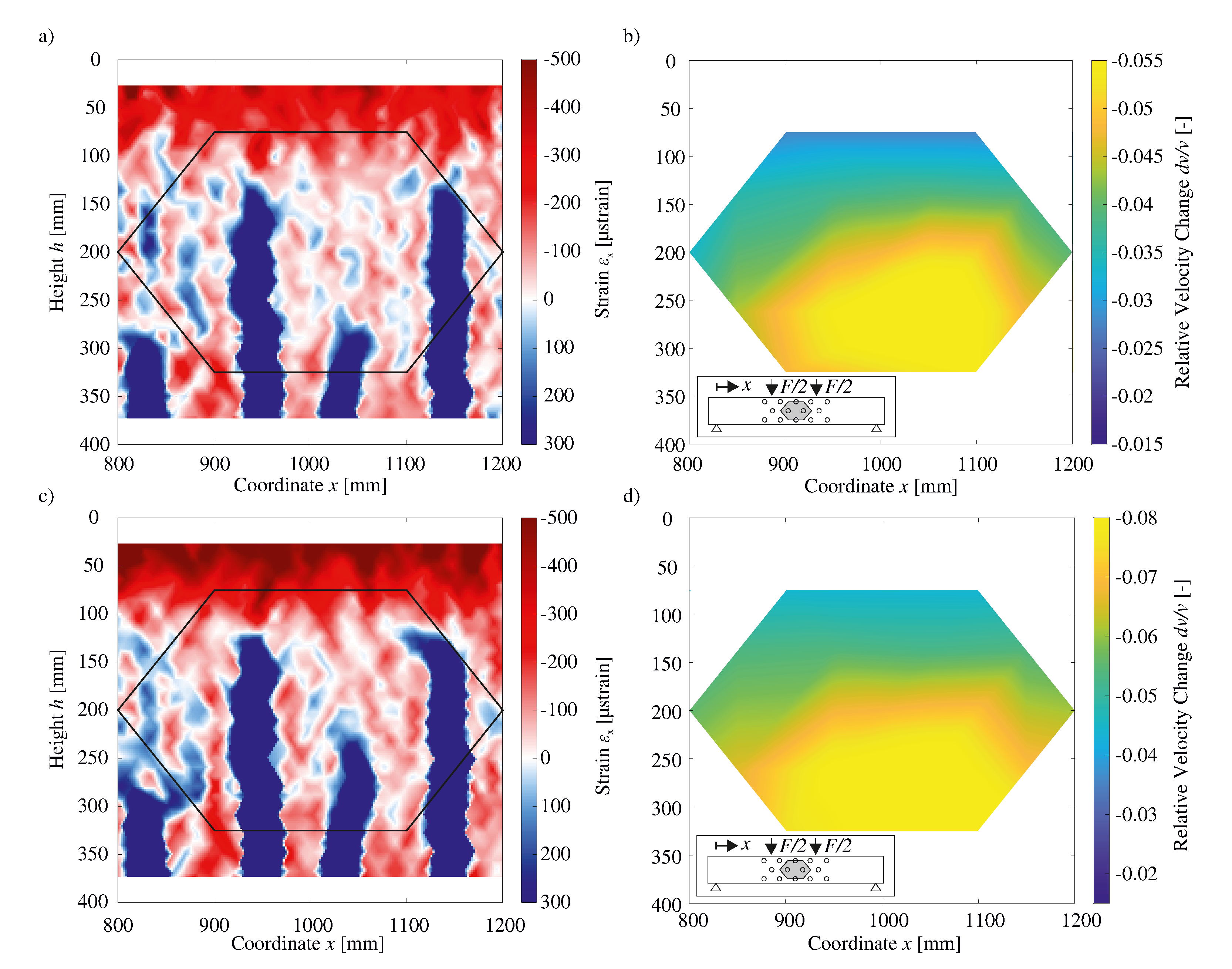
4. Comparison of US Results and Strain Fields
4.1. Non-Cracked to Slightly Cracked State
4.2. Completed Crack Pattern and Increasing Crack Widening
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| US | Ultrasonic |
| CWI | Code Wave Interferometry |
| DIC | Digital Image Correlation |
| FOS | Fiber Optic Sensor |
| RC | Reinforced Concrete |
| NDT | Non-Destructive Testing |
References
- Löschmann, J.; Ahrens, M.A.; Dankmeyer, U.; Ziem, E.; Mark, P. Methods to reduce the partial safety factor concerning dead loads of existing bridges (Methoden zur Reduktion des Teilsicherheitsbeiwerts für Eigenlasten bei Bestandsbrücken). Beton- und Stahlbetonbau 2017, 112, 506–516. [Google Scholar] [CrossRef]
- Löschmann, J.; Stötzel, A.; Dankmeyer, U.; Mark, P. Gekoppelte Vermessungsstrategien für intelligente, digitale 3D-Stadtmodelle. Messtechnik Bauwesen 2018, 2018, 6–11. [Google Scholar]
- Heek, P.; Ahrens, M.A.; Mark, P. Incremental-iterative model for time-variant analysis of SFRC subjected to flexural fatigue. Mater. Struct. 2017, 50. [Google Scholar] [CrossRef]
- Obel, M.; Marwan, A.; Alsahly, A.; Freitag, S.; Mark, P.; Meschke, G. Damage assessment concepts for urban structures during mechanized tunneling (Schadensbewertungskonzepte für innerstädtische Bauwerke bei maschinellen Tunnelvortrieben). Bauingenieur 2018, 93, 482–491. [Google Scholar]
- Niederleithinger, E.; Wang, X.; Herbrand, M.; Müller, M. Processing Ultrasonic Data by Coda Wave Interferometry to Monitor Load Tests of Concrete Beams. Sensors 2018, 18, 1971. [Google Scholar] [CrossRef]
- Sanio, D.; Mark, P.; Ahrens, M.A. Computation of temperature fields on bridges—Implementation by means of spread-sheets (Temperaturfeldberechnung für Brücken). Beton- und Stahlbetonbau 2017, 112, 85–95. [Google Scholar] [CrossRef]
- Heek, P.; Tkocz, J.; Mark, P. A thermo-mechanical model for SFRC beams or slabs at elevated temperatures. Mater. Struct. 2018, 51, 87-1–87-16. [Google Scholar] [CrossRef]
- Sanio, D.; Ahrens, M.A.; Mark, P. Tackling uncertainty in structural lifetime evaluations—Assessment of the impact of monitoring data and correlated input parameters on a prognosis. Beton- und Stahlbetonbau 2018, 113, 48–54. [Google Scholar] [CrossRef]
- Sanio, D.; Löschmann, J.; Mark, P.; Ahrens, M.A. Measurements vs. analytical methods to evaluate fatigue of tendons in concrete bridges (Bauwerksmessungen versus Rechenkonzepte zur Beurteilung von Spannstahlermüdung in Betonbrücken). Bautechnik 2018, 95, 99–110. [Google Scholar] [CrossRef]
- Snieder, R. The Theory of Coda Wave Interferometry. Pure Appl. Geophys. 2006, 163, 455–473. [Google Scholar] [CrossRef]
- Fischer, O.; Thoma, S.; Crepaz, S. Distributed fiber optic sensing for crack detection in concrete structures (Quasikontinuierliche faseroptische Dehnungsmessung zur Rissdetektion in Betonkonstruktionen). Beton-und Stahlbetonbau 2019, 114, 150–159. [Google Scholar] [CrossRef]
- Fischer, O.; Thoma, S.; Crepaz, S. Distributed fiber optic sensing for crack detection in concrete structures. Civ. Eng. Des. 2019, 1, 97–105. [Google Scholar] [CrossRef]
- Speck, K.; Vogdt, F.; Curbach, M.; Petryna, Y. Fiber optic sensors for continuous strain measurement in concrete (Faseroptische Sensoren zur kontinuierlichen Dehnungsmessung im Beton). Beton- und Stahlbetonbau 2019, 114, 160–167. [Google Scholar] [CrossRef]
- Hugenschmidt, M. Lasermesstechnik: Diagnostik der Kurzzeitphysik; Springer-Lehrbuch; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Luna Innovations. Optical Distributed Sensor Interrogator Model ODiSI-B: User’s Guide; Version 5.2.1; ODiSI-B Software 5.2.0; Luna Innovations: Blacksburg, VA, USA, 2017. [Google Scholar]
- Luna Innovations. Distributed Fiber Optic Sensing: Temperature Coefficient for Polyimide Coated Low Bend Loss Fiber, in the −40 °C to 200 °C Range; Luna Innovations: Roanoke, VA, USA, 2014. [Google Scholar]
- Konertz, D.; Löschmann, J.; Clauß, F.; Mark, P. Fiber optic sensors for continuous strain measurement in concrete (Faseroptische Messung von Dehnungs- und Temperaturfeldern). Bauingenieur 2019, 94, 60–167. [Google Scholar]
- GOM. GOM Testing Technical Documentation since V8 SR1: Basics of Digital Image Correlation and Strain Calculation; (GOM Testing Technische Dokumentation ab V8 SR1: Grundlagen der digitalen Bildkorrelation und Dehnungsberechnung.); GOM GmbH: Braunschweig, Germany, 2016. [Google Scholar]
- Winter, D. Optische Verschiebungsmessung nach dem Objektrasterprinzip mit Hilfe eines flächenorientierten Ansatzes. Ph.D. Thesis, Technische Universität Carola-Wilhelmina zu Braunschweig, Braunschweig, Germany, 1993. [Google Scholar]
- Pacheco, C.; Snieder, R. Time-lapse travel time change of multiply scattered acoustic waves. J. Acoust. Soc. Am. 2005, 118, 1300–1310. [Google Scholar] [CrossRef]
- Poupinet, G.; Ellsworth, W.L.; Frechet, J. Monitoring velocity variations in the crust using earthquake doublets: An application to the Calaveras Fault, California. J. Geophys. Res. Solid Earth 1984, 89, 5719–5731. [Google Scholar] [CrossRef]
- Roberts, P. Development of the active doublet method for monitoring small changes in crustal properties. Seismol. Res. Lett 1991, 62, 36–37. [Google Scholar]
- Snieder, R.; Grêt, A.; Douma, H.; Scales, J. Coda wave interferometry for estimating nonlinear behavior in seismic velocity. Science 2002, 295, 2253–2255. [Google Scholar] [CrossRef]
- Lobkis, O.I.; Weaver, R.L. Coda-Wave Interferometry in Finite Solids: Recovery of p-to-s Conversion Rates in an Elastodynamic Billiard. Phys. Rev. Lett. 2003, 90, 4. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry and seasonal variations of seismic velocities at Merapi Volcano, Indonesia. Geophys. Res. Lett. 2006, 33, L21302. [Google Scholar] [CrossRef]
- Larose, E.; Hall, S. Monitoring stress related velocity variation in concrete with a 2 × 10−5 relative resolution using diffuse ultrasound. J. Acoust. Soc. Am. 2009, 125, 1853–1856. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chakraborty, J.; Bassil, A.; Niederleithinger, E. Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method. Sensors 2020, 20, 1986. [Google Scholar] [CrossRef] [PubMed]
- Wolf, J.; Niederleithinger, E.; Mielentz, F.; Grothe, S.; Wiggenhauser, H. Monitoring of concrete constructions by embedded ultrasonic sensors (Überwachung von Betonkonstruktionen mit eingebetteten Ultraschallsensoren). Bautechnik 2014, 91, 783–796. [Google Scholar] [CrossRef]
- Zilch, K.; Zehetmaier, G. Bemessung im konstruktiven Betonbau: Nach DIN 1045-1 (Fassung 2008) und EN 1992-1-1 (Eurocode 2), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- JCSS Joint Committee on Structural Safety. JCSS Probabilistic Model Code Part 3: Resistance Models; JCSS, 2001; Available online: https://www.jcss-lc.org/publications/jcsspmc/concrete.pdf (accessed on 20 July 2020).
- Niederleithinger, E.; Herbrand, M.; Müller, M. Monitoring of shear tests on prestressed concrete continuous beams using ultrasound and coda wave interferometry (Monitoring von Querkraftversuchen an Spannbetondurchlaufträgern mit Ultraschall und Codawelleninterferometrie). Bauingenieur 2014, 11, 474–481. [Google Scholar]



| 35.0 | 2.5 | 28,618 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clauß, F.; Epple, N.; Ahrens, M.A.; Niederleithinger, E.; Mark, P. Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry. Sensors 2020, 20, 4023. https://doi.org/10.3390/s20144023
Clauß F, Epple N, Ahrens MA, Niederleithinger E, Mark P. Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry. Sensors. 2020; 20(14):4023. https://doi.org/10.3390/s20144023
Chicago/Turabian StyleClauß, Felix, Niklas Epple, Mark Alexander Ahrens, Ernst Niederleithinger, and Peter Mark. 2020. "Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry" Sensors 20, no. 14: 4023. https://doi.org/10.3390/s20144023
APA StyleClauß, F., Epple, N., Ahrens, M. A., Niederleithinger, E., & Mark, P. (2020). Comparison of Experimentally Determined Two-Dimensional Strain Fields and Mapped Ultrasonic Data Processed by Coda Wave Interferometry. Sensors, 20(14), 4023. https://doi.org/10.3390/s20144023





