Estimation for Runway Friction Coefficient Based on Multi-Sensor Information Fusion and Model Correlation
Abstract
:1. Introduction
1.1. Problem Statement
1.2. Objectives of Research
1.3. Summary of Contributions
2. Related Work
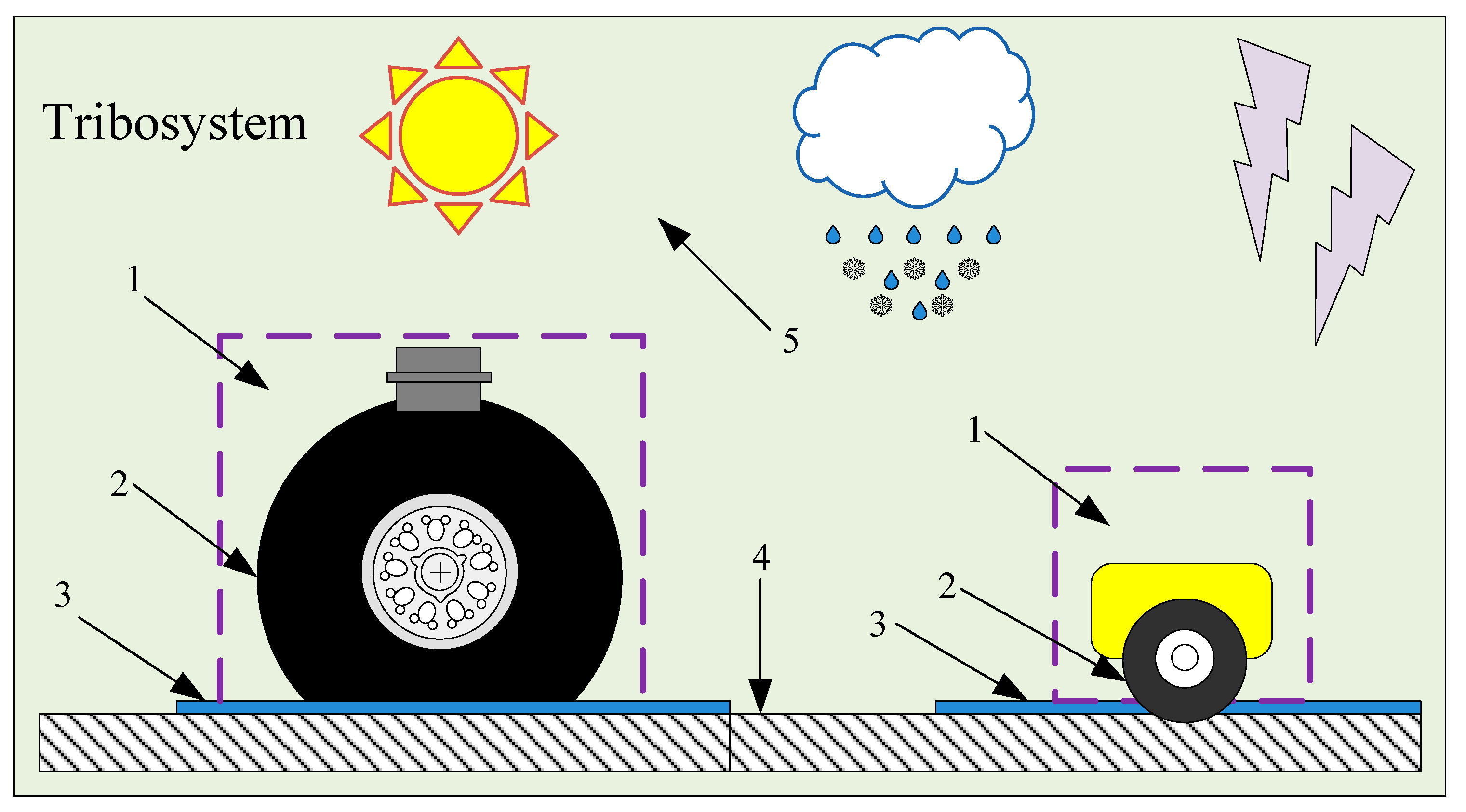
3. Tribo-System and Influencing Factors
- Tires;
- Runway;
- Deposit;
- Atmosphere.
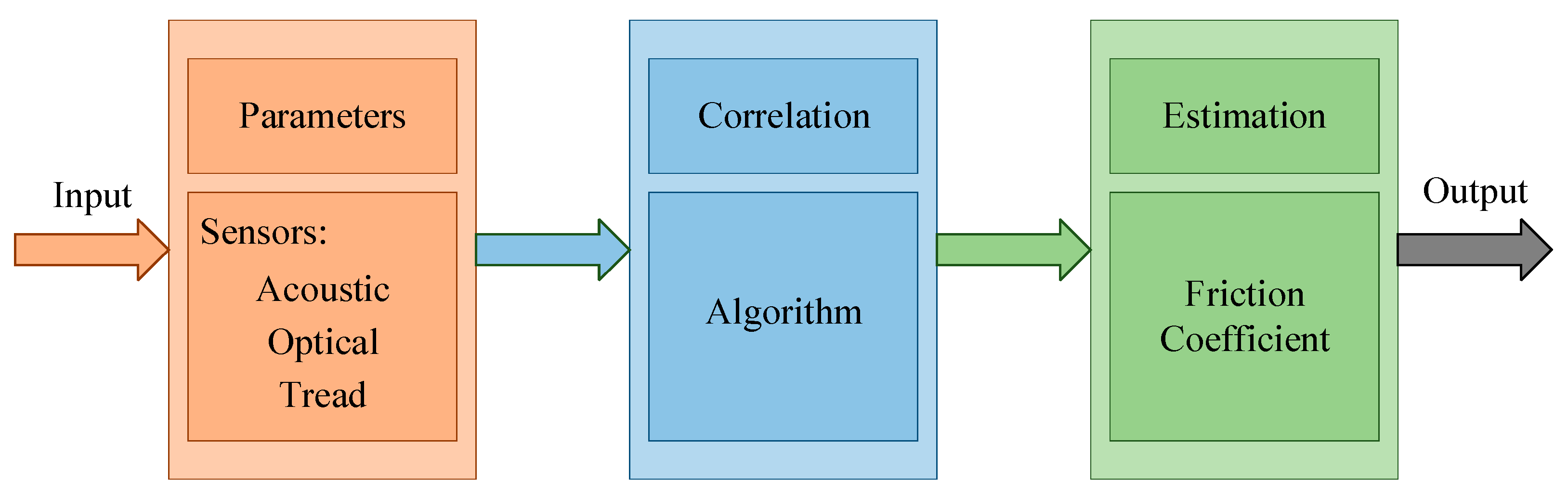
4. Measurement for Friction Coefficient
4.1. The Cause-Based Method
4.1.1. Acoustic Sensor
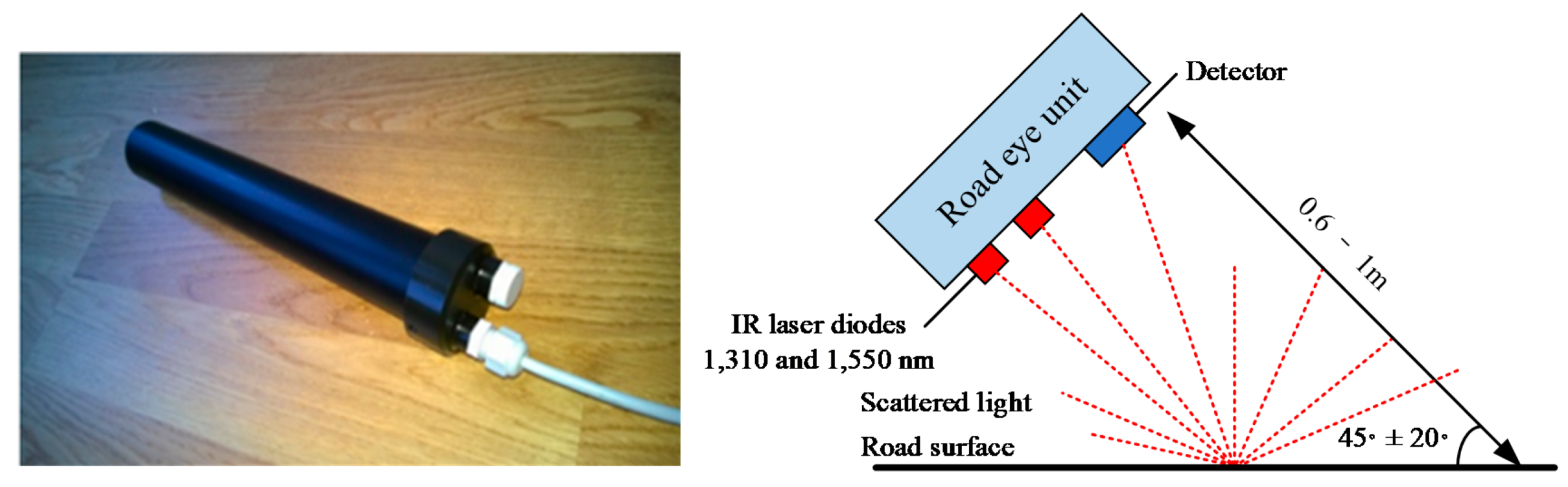
4.1.2. Optical Sensor
4.1.3. Tire Tread Sensor
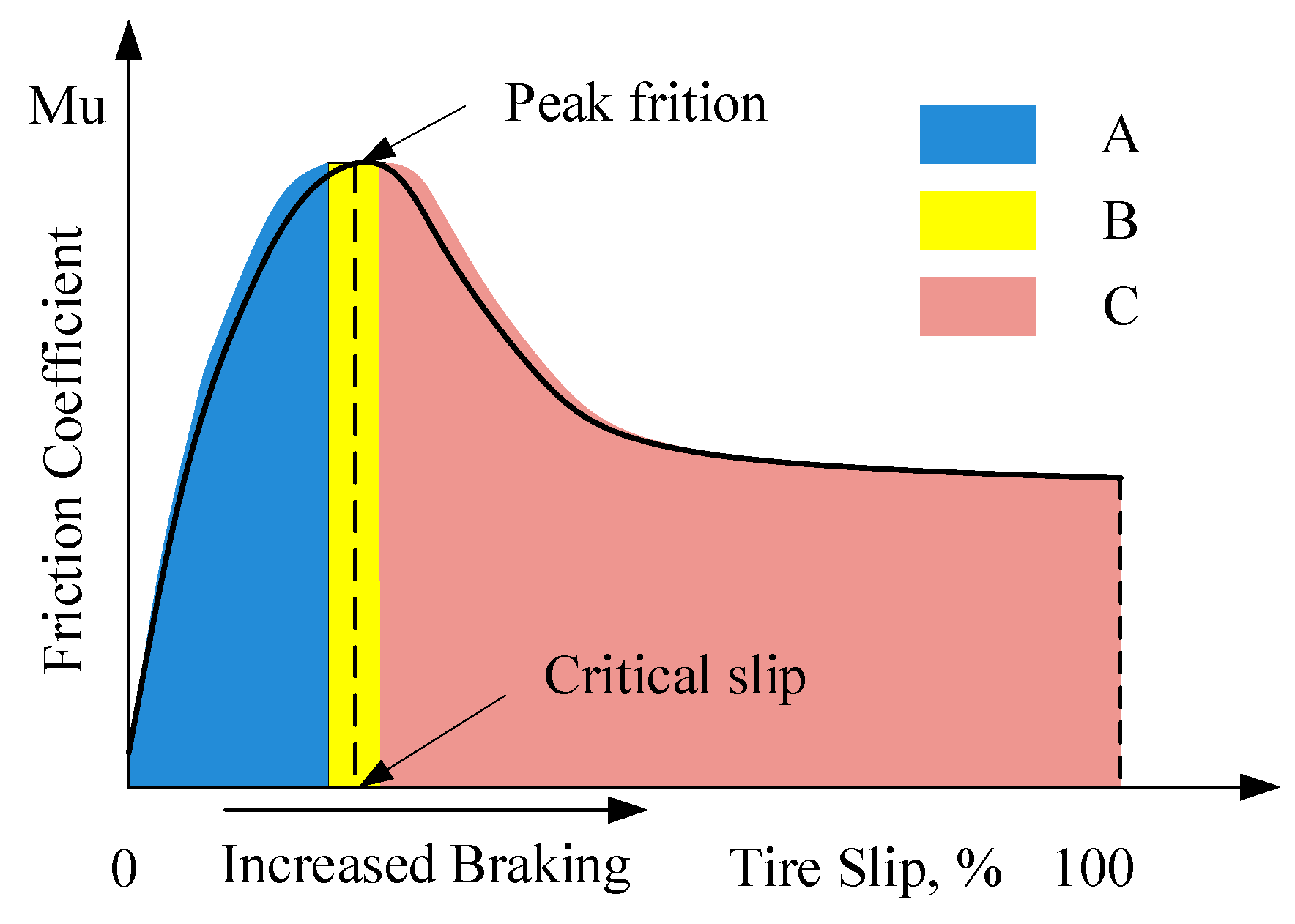
4.2. The Effect-Based Method
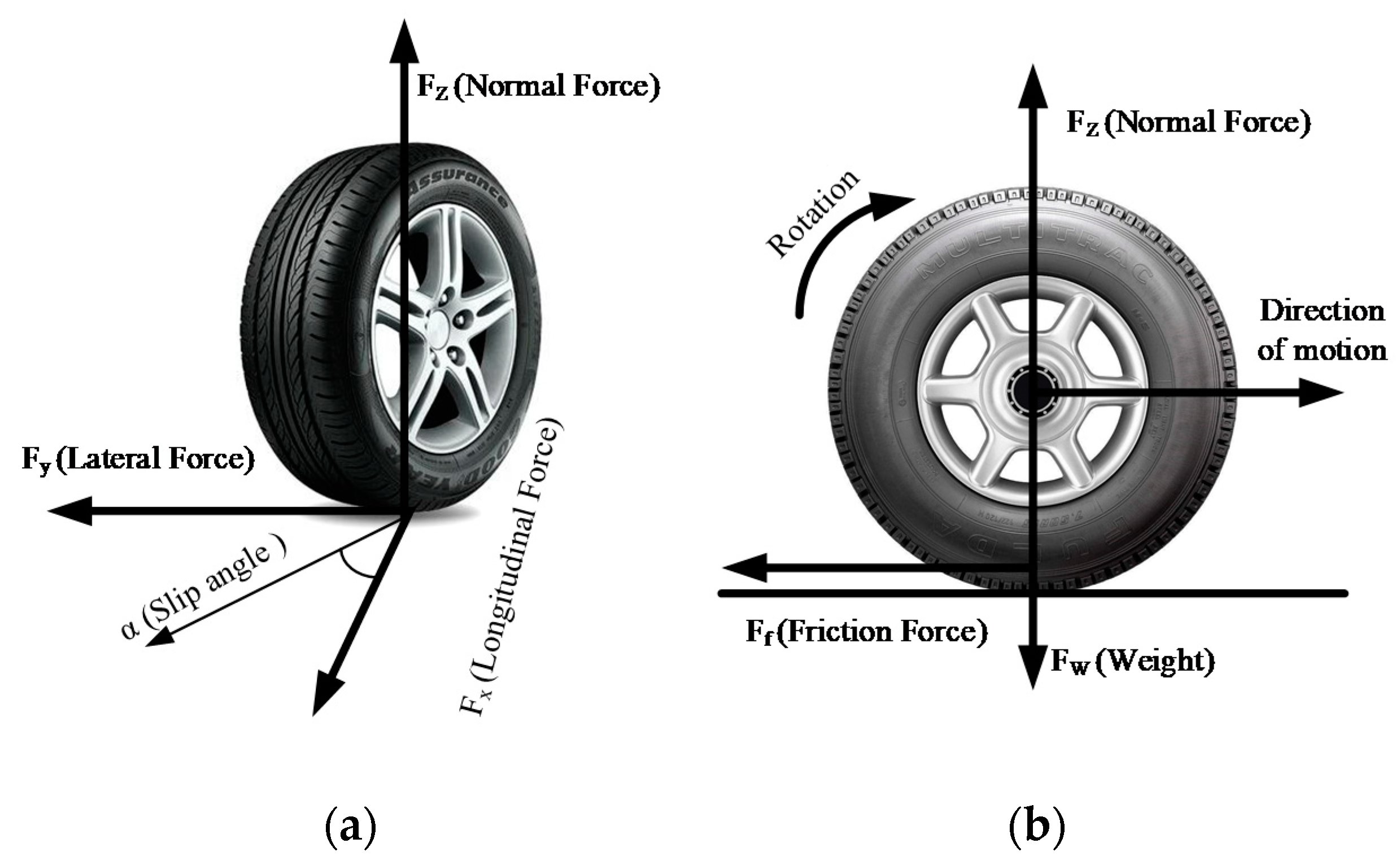
4.2.1. Tire Model
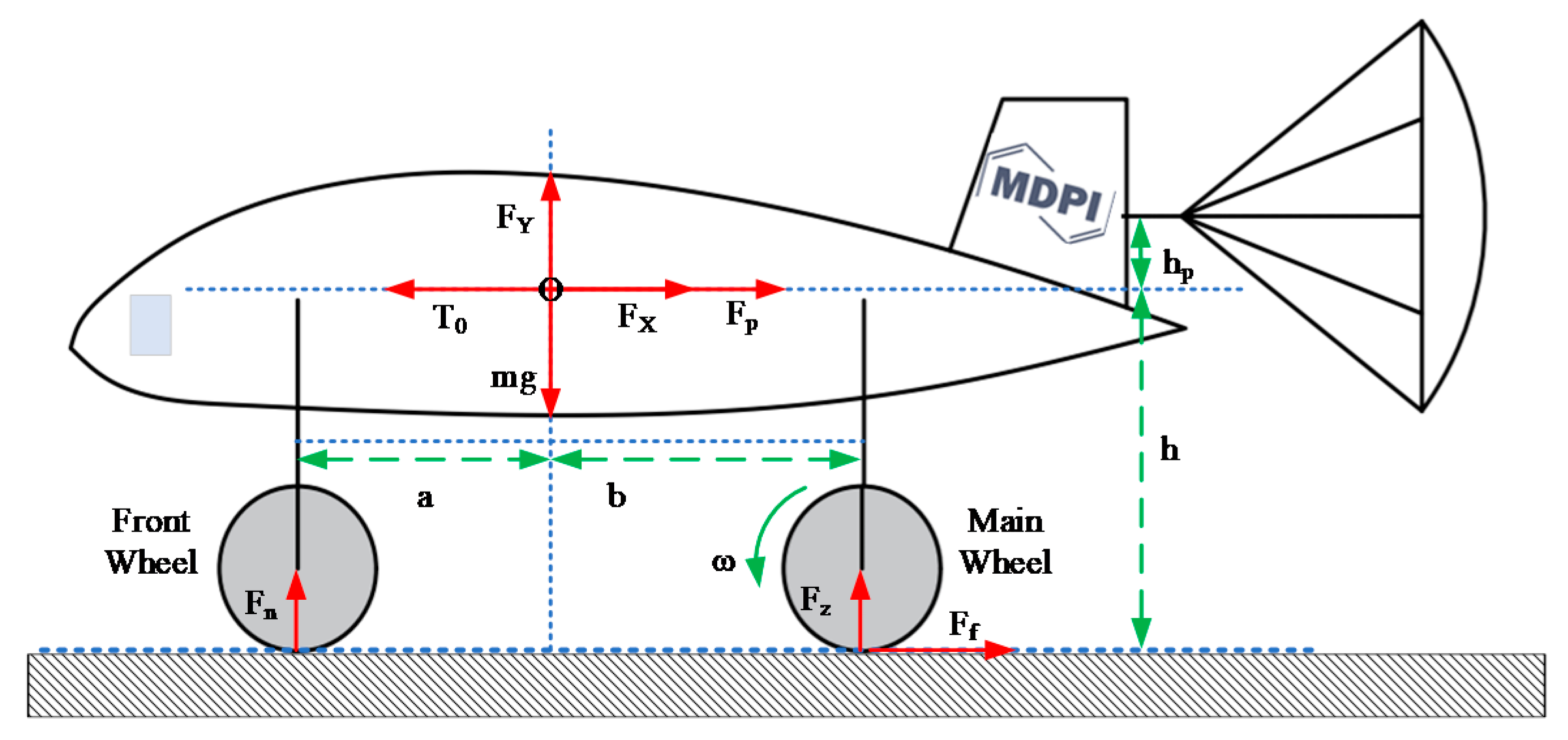
4.2.2. Aircraft Model
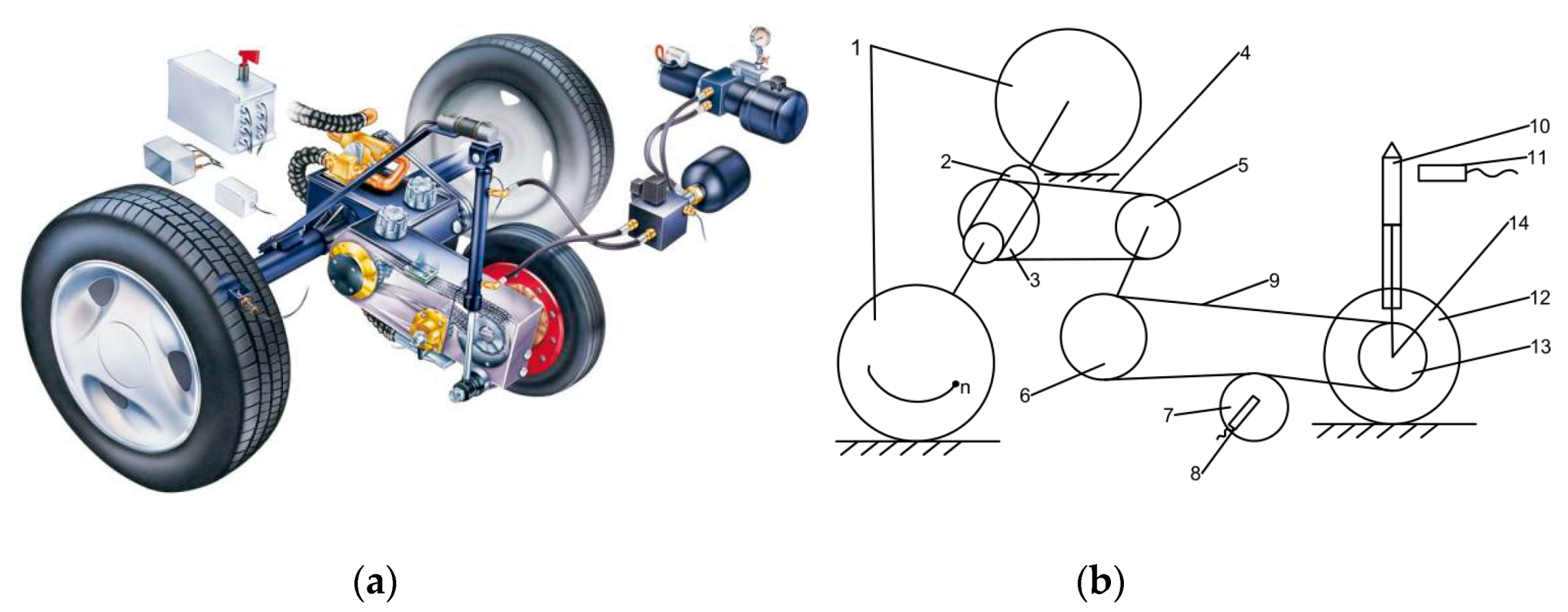
4.3. Airport Runway Friction Coefficient Test Car
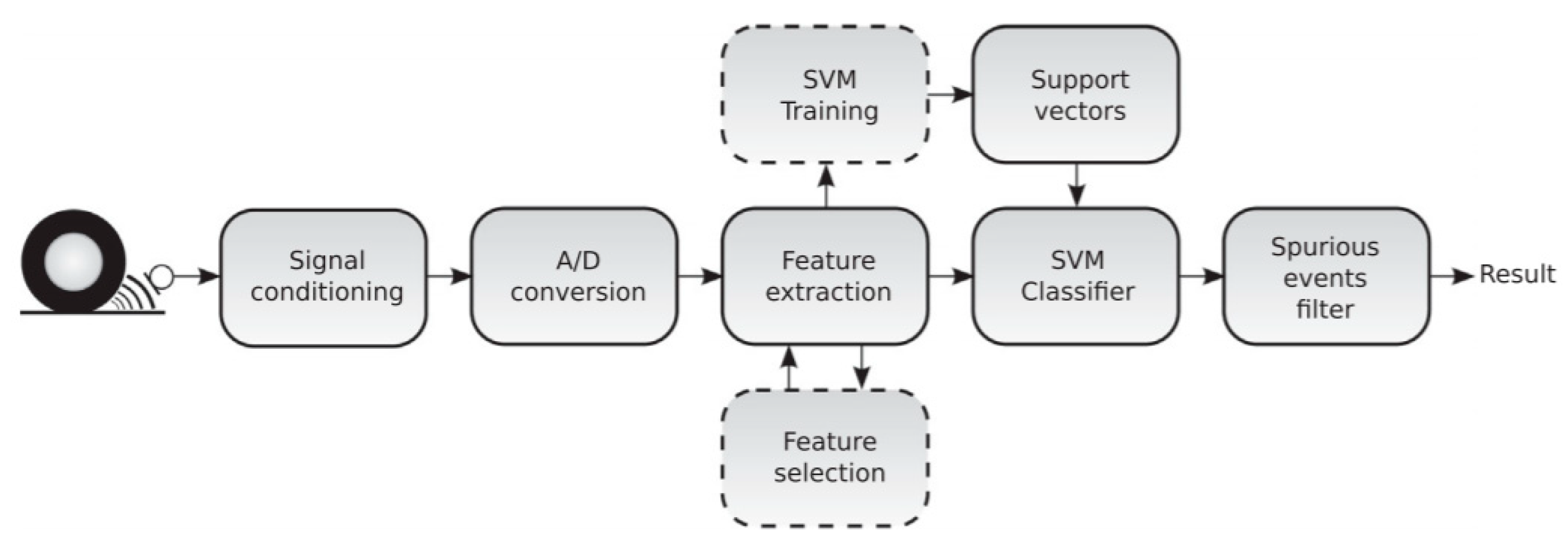
5. Friction Coefficient Estimation Based on Multi-Sensor Information Fusion
5.1. Feasibility Analysis Based on Multi-Sensor Information Fusion
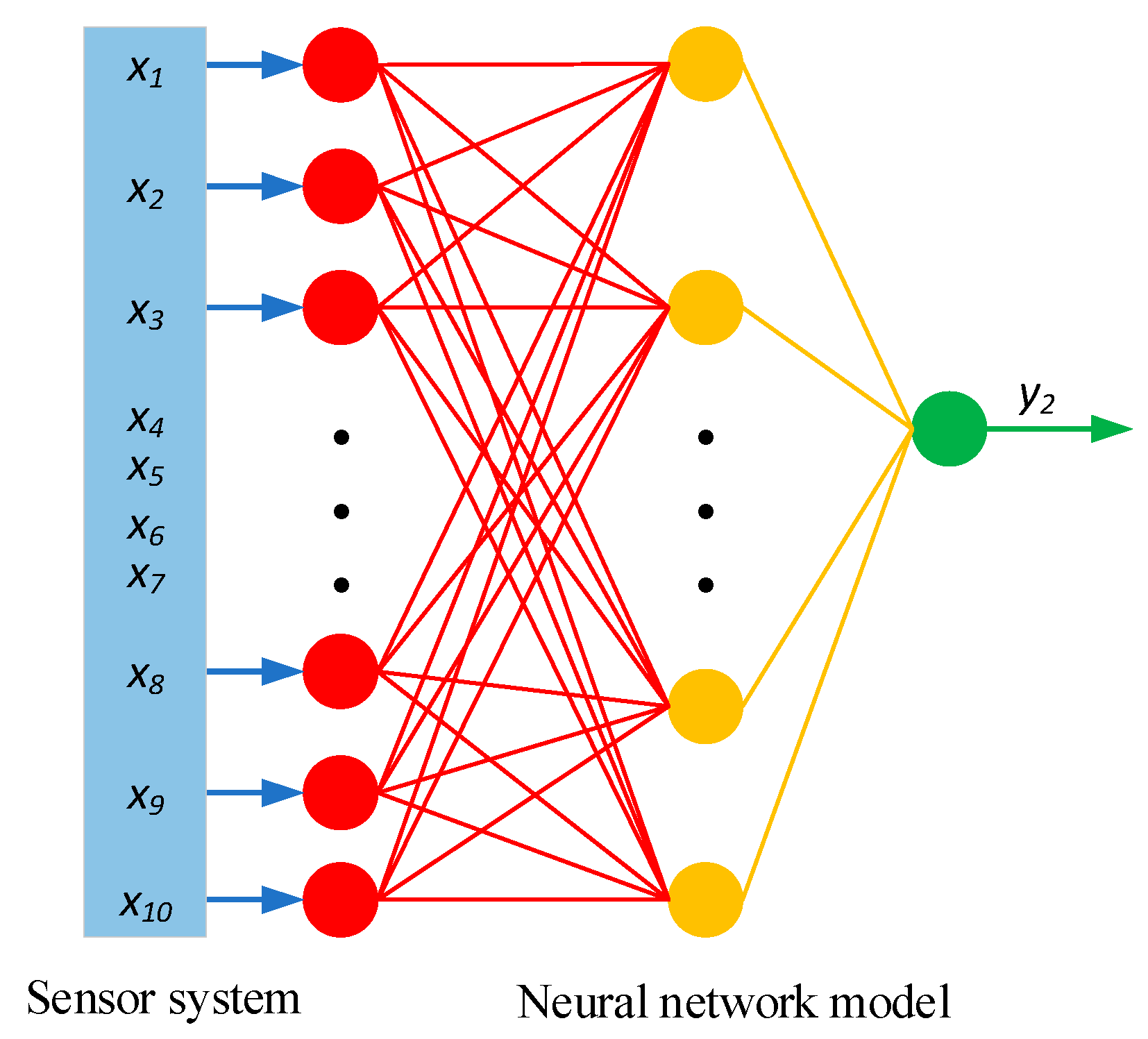
5.2. Variable Analysis and Sensor System
5.3. Fusion Algorithm, Data Acquisition, and Real-Time Calculation
6. Correlation of Ground Friction Measurements to Aircraft Braking Friction
6.1. Kollerud Theory
6.2. IRFI and CRFI model
6.3. NASA Model
7. Discussion
- ASTM standard methods;
- Friction coefficient car;
- The cause-based;
- The effect-based;
- Multi-sensor information fusion and model correlation.
- In the first stage, the sensor system is built, and it is installed on a friction coefficient car to collect data;
- In the second stage, the network is trained, and the friction-related parameters and the friction coefficient are obtained through the neural network;
- The third is a real-time estimation, the sensor system collects data in real-time, and automatically obtains the real-time friction coefficient through the neural network model.
- Compared with ASTM standard methods;
- The sensor system is installed on the car, and can measure the friction coefficient of any position in the entire runway without traffic control, and can repeat the measurement;
- Compared with the friction coefficient car;
- Under winter conditions, the friction coefficient car changes tires on average every 10 days. Once the original is replaced, its core sensors need to be re-calibrated. The sensor system proposed in this paper can replace the core sensors without re-calibration and greatly reduce costs;
- Compared with the cause-based and the effect-based method;
- Friction is the result of the joint action of the tire and the runway. The cause-based method uses sensors to measure the parameters related to the runway surface, while the tire-based method pays more attention to the characteristics of the tire itself. In the sensor system, the optical sensor is used to measure the surface characteristics of the runway, and the tread sensor is used to measure the characteristics of the tire. The combined effect of the two is considered to make the prediction more accurate.
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Nomenclature | |||
| Dimensionless friction coefficient | Tangential friction force | ||
| Vertical force | Slip speed | ||
| Tire peripheral velocity | Velocity | ||
| Slip | Tire radius | ||
| Tire angular velocity | Engine thrust | ||
| Aerodynamic drag | Drag parachute resistance | ||
| Aerodynamic lift | Front-wheel load | ||
| Main wheel load | Bonding force between wheel and runway | ||
| Number of the brake wheels | Moment of inertia of the wheel | ||
| Friction coefficient of an axle | Braking torque | ||
| Radius of the brake disc (rotor/ stator assembly) | Friction coefficient of the brake disc | ||
| Number of friction surfaces | Pressure applied to the brake disc | ||
| Torque-pressure conversion coefficient | m | Aircraft weight | |
| Force caused by thrust | Force contribution from wheels | ||
| Aerodynamic drag | Aerodynamic lift | ||
| Effective aircraft braking coefficient | Runway slope | ||
| Gravitational constant | Correlation coefficient | ||
| Aircraft braking coefficient | Ground friction coefficient | ||
| Aircraft braking coefficient under different models | |||
| Vertical height between aircraft center of gravity and runway | |||
| Vertical distance between drag parachute and aircraft center of gravity | |||
| Horizontal distance between aircraft center of gravity and front wheel | |||
| Horizontal distance between aircraft center of gravity and rear wheel | |||
References
- Aviation Safety Office of Civil Aviation Administration of China; Accident Investigation Center of Civil Aviation Administration of China. Cases of Runway Excursion/Overrun in Civil Aviation of China; China Civil Aviation Press: Beijing, China, 2015.
- Tingle, J.S.; Norwood, G.J.; Cotter, B. Use of Continuous friction measurement equipment to predict runway condition rating on unpaved runways. Transp. Res. Rec. J. Transp. Res. Board 2017, 2626, 58–65. [Google Scholar] [CrossRef]
- Shi, X.D.; Shi, S.W.; Zhang, L.; Li, J.L. Research on modeling method of runway frictional coefficient measuring vehicle based on impedance diagrams. Adv. Mater. Res. 2011, 214, 133–137. [Google Scholar] [CrossRef]
- Shi, X.D.; Shi, S.W.; Zhang, L.; Li, J.L. Modeling and simulation of airport runway frictional coefficient measuring vehicle based on bond-graph method. Appl. Mech. Mater. 2011, 52, 49–53. [Google Scholar] [CrossRef]
- Han, J. Research on the key technology of airport runway surface friction tester based on high speed on-off valve. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2012. [Google Scholar]
- Zhou, W.; Zhang, S.X.; Guo, J.Z.; Dai, S.D.; Zhou, C.H.; Shen, H.L. Design of software for airstrip friction coefficient measuring vehicle. Meas. Control Technol. 2010, 29, 78–81. [Google Scholar]
- Shan, J. Research on the Calibration Method and Experimental Study of Friction Coefficient Tester. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2010. [Google Scholar]
- Gao, L.T.; Xiong, L.; Lin, X.F.; Xia, X.; Liu, W.; Lu, Y.S.; Yu, Z.P. Multi-sensor fusion road friction coefficient estimation during steering with lyapunov method. Sensors 2019, 19, 3816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alonso, J.; López, J.M.; Pavón, I.; Recuero, M.; Asensio, C.; Arcas, G.; Bravo, A. On-board wet road surface identification using tyre/road noise and Support Vector Machines. Appl. Acoust. 2014, 76, 407–415. [Google Scholar] [CrossRef]
- Kongrattanaprasert, W.; Nomura, H.; Kamakura, T.; Ueda, K. Wavelet-based neural networks applied to automatic detection of road surface conditions using tire noise from vehicles. J. Acoust. Soc. Am. 2009, 125, 2731. [Google Scholar] [CrossRef]
- Kongrattanaprasert, W.; Nomura, H.; Kamakura, T.; Ueda, K. Detection of road surface states from tire noise using neural network analysis. IEEJ Trans. Ind. Appl. 2010, 130, 920–925. [Google Scholar] [CrossRef]
- Andersson, M.; Bruzelius, F.; Casselgren, J.; Hjort, M.; Lofving, S.; Olsson, G.; Ronnberg, J.; Sjodahl, M.; Solyom, S.; Svendenius, J.; et al. Road Friction Estimation, part II: IVSS Project Report. Sweden. 2010. Available online: https://www.semanticscholar.org/paper/Road-Friction-Estimation-%2C-part-II-IVSS-Project-Andersson-Bruzelius/4a087c3fd6cf98318fb36932d4c9ef82cd64e2ef (accessed on 10 July 2020).
- Vikki, E.; John, W.; Micheal, L.; Malal, K.; James, M.; Islam, S. Improved non-contact 3D field and processing techniques to achieve macrotexture characterisation of pavements. Constr. Build. Mater. 2019, 227, 116693. [Google Scholar]
- Holzmann, F.; Bellino, M.; Siegwart, R.; Bubb, H. Predictive estimation of the road-tire friction coefficient. In Proceedings of the 2006 IEEE International Conference on Control Applications, Munich, Germany, 4–6 October 2006. [Google Scholar]
- Sohini, R.; Zhao, M.M.; Andreas, W.; Niklas, O.; Mats, J. Machine learning models for road surface and friction estimation using front-camera images. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Matthew, E.P.; Clark, C.B.; Jim, M.; Scott, M. Wireless smart -tires for road friction measurement and self state determination. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002. [Google Scholar]
- Arto, N.; Ari, J.T. Three three-axis iepe accelerometers on the inner liner of a tire for finding the tire-road friction potential indicators. Sensors 2015, 15, 19251–19263. [Google Scholar]
- Zhang, X.W.; Wang, F.Y.; Wang, Z.; Wei, L.; He, D.Z. Intelligent tires based on wireless passive surface acoustic wave sensors. In Proceedings of the 2004 IEEE Intelligent Transportation Systems International Conference, Washington, DC, USA, 3–6 October 2004; pp. 960–964. [Google Scholar]
- Pohl, A.; Steindl, R. The “intelligent tire” utilizing passive SAW sensors measurement of tire friction. IEEE Trans. Instrum. Meas. 1999, 48, 1041–1046. [Google Scholar] [CrossRef]
- Tuononen, A.J. Optical position detection to measure tyre carcass deflections. Veh. Syst. Dyn. 2008, 46, 471–481. [Google Scholar] [CrossRef]
- Yi, J. A piezo-sensor-based “smart tire” system for mobile robots and vehicles. IEEE/ASME Trans. Mechatron. 2008, 13, 95–103. [Google Scholar] [CrossRef]
- Erdogan, G.; Alexander, L.; Rajamani, R. Estimation of tire-road friction coefficient using a novel wireless piezoelectric tire sensor. IEEE Sens. J. 2011, 11, 267–279. [Google Scholar] [CrossRef]
- Seyedmeysam, K.; Anahita, E.; Saied, T. A technical survey on tire-road friction estimation. Friction 2017, 5, 123–146. [Google Scholar]
- Manuel, A.; Stratis, K.; Mike, B. Road Friction Virtual Sensing: A Review of Estimation Techniques with Emphasis on Low Excitation Approaches. Appl. Sci. 2017, 7, 1230. [Google Scholar]
- Pacejka, H.B.; Bakker, E. The Magic Formula Tyre Model. Veh. Syst. Dynamics Int. J. Veh. Mech. Mobil. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Kyongsu, Y.; Karl, H.; Lee, S.C. Estimation of Tire-Road Friction Using Observer Based Identifiers. Veh. Syst. Dyn. 1999, 31, 233–261. [Google Scholar]
- Germann, S.; Wurtenberger; Daiss, A. Monitoring of the friction coefficient between tyre and road surface. In Proceedings of the IEEE International Conference on Control and Applications, Glasgow, UK, 24–26 August 1994; pp. 613–618. [Google Scholar]
- López, A.; Olazagoitia, J.L.; Francisco, M.; Maria, R.R. Optimal parameter estimation in semi-empirical tire models. Proc. IMechE. Part D J. Automob. Eng. 2019, 233, 73–87. [Google Scholar] [CrossRef]
- Rui, H.; Corina, S.; Javier, E.O. Systematic tests for study of tire tractive performance on soft soil: Part II—Parameterization of terramechanics model and tire model. J. Terramechanics 2019, 85, 77–88. [Google Scholar]
- Zhun, C.; Lu, Z.X. Nonlinear research and efficient parameter identification of magic formula tire model. Math. Probl. Eng. 2017, 2017, 6924506. [Google Scholar]
- Deepak, P.; Efstathios, V.; Francois, H.; Cao, D.P.; Tamas, D.; Simon, H. Tyre–road friction μ-estimation based on braking force distribution. Proc. IMechE. Part D J. Automob. Eng. 2018, 2018, 1–18. [Google Scholar]
- Sun, D.; Jiao, Z.X.; Shang, Y.X.; Wu, S.; Liu, X.C. High-efficiency aircraft antiskid brake control algorithm via runway condition identification based on an on-off valve array. Chin. J. Aeronaut. 2019, 32, 2538–2556. [Google Scholar] [CrossRef]
- Jiao, Z.X.; Sun, D.; Shang, Y.X.; Liu, X.C.; Wu, S. A high efficiency aircraft anti-skid brake control with runway identification. Aerosp. Sci. Technol. 2019, 91, 82–95. [Google Scholar] [CrossRef]
- Fu, L.F. Research on the application of nonlinear control technology for aircraft anti-skid braking system. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2017. [Google Scholar]
- Shang, Y.M.; Liu, X.C.; Jiao, Z.X.; Wu, S. A novel integrated self-powered brake system for more electric aircraft. Chin. J. Aeronaut. 2018, 31, 976–989. [Google Scholar] [CrossRef]
- Klein-Paste, A.; Huseby, A.B.; Anderson, J.D.; Giesman, P.; Bugge, H.G.; Langedahl, T.B. Braking performance of commercial airplanes during operation on winter contaminated runways. Cold Reg. Sci. Technol. 2012, 79–80, 29–37. [Google Scholar] [CrossRef]
- AIRBUS. Using Aircraft as a Sensor on Contaminated Runways. Available online: https://safetyfirst.airbus.com/using-aircraft-as-a-sensor-on-contaminated-runways/ (accessed on 10 July 2020).
- Bin, H.; Xiang, F.; Xiang, F.; Song, H. Calculation algorithm of tire-road friction coefficient based on limited-memory adaptive extended kalman filter. Math. Probl. Eng. 2019, 1, 1–14. [Google Scholar]
- Liu, Y.H.; Li, T.; Yang, Y.Y.; Ji, X.W.; Wu, J. Estimation of tire-road friction coefficient based on combined APF-IEKF and iteration algorithm. Mech. Syst. Signal Process. 2017, 88, 25–35. [Google Scholar] [CrossRef]
- Chen, L.; Luo, Y.G.; Bian, M.Y.; Qin, Z.B.; Luo, J.; Li, K.Q. Estimation of tire-road friction coefficient based on frequency domain data fusion. Mech. Syst. Signal Process. 2017, 85, 177–192. [Google Scholar] [CrossRef]
- Rado, Z.; Wambold, J.C. Correlation of ground friction measurements to aircraft braking friction calculated from flight data recorders. In Proceedings of the 4th International Safer Roads Conference, Cheltenham, UK, 18–21 May 2014. [Google Scholar]
- Véronique, C.; Gerthoffert, J.; Bouteldja, M.; Do, M.T. A modelling-based approach to relate ground friction measurements to aircraft braking performance. J. Aircr. 2015, 53, 1–11. [Google Scholar]
- Yager, T.J.; William, A.V.; Baldasare, P. Summary report on aircraft and ground vehicle friction correlation test results obtained under winter runway conditions during joint FAA/NASA runway friction program. NASA, TM-100506. 1988. Available online: https://www.researchgate.net/publication/24326686_Aircraft_and_ground_vehicle_friction_correlation_test_results_obtained_under_winter_runway_conditions_during_joint_FAANASA_Runway_Friction_Program (accessed on 10 July 2020).
- Jonathan, G.; Cyrielle, G.; Véronique, C.; Do, M.T. Modelling of aircraft braking coefficient from IMAG friction measurements. In Proceedings of the Airports in Urban Networks, Paris, France, 15–16 April 2014. [Google Scholar]
- Norheim, A.; Sinha, N.S.; Yager, T.J. Effects of the structure and properties of ice and snow on the friction of aircraft tyres on movement area surfaces. Tribol. Int. 2001, 34, 617–623. [Google Scholar] [CrossRef]
- Mahinder, K.W. A tire runway interface friction prediction model concept. J. Aircr. 1979, 16, 407–416. [Google Scholar]
- Rosu, I.; Elias-Birembaux, H.L.; Lebon, F.; Hagen, L.; Wangenheim, M. Experimental and numerical simulation of the dynamic frictional contact between an aircraft tire rubber and a rough surface. Lubricants 2016, 4, 29. [Google Scholar] [CrossRef] [Green Version]

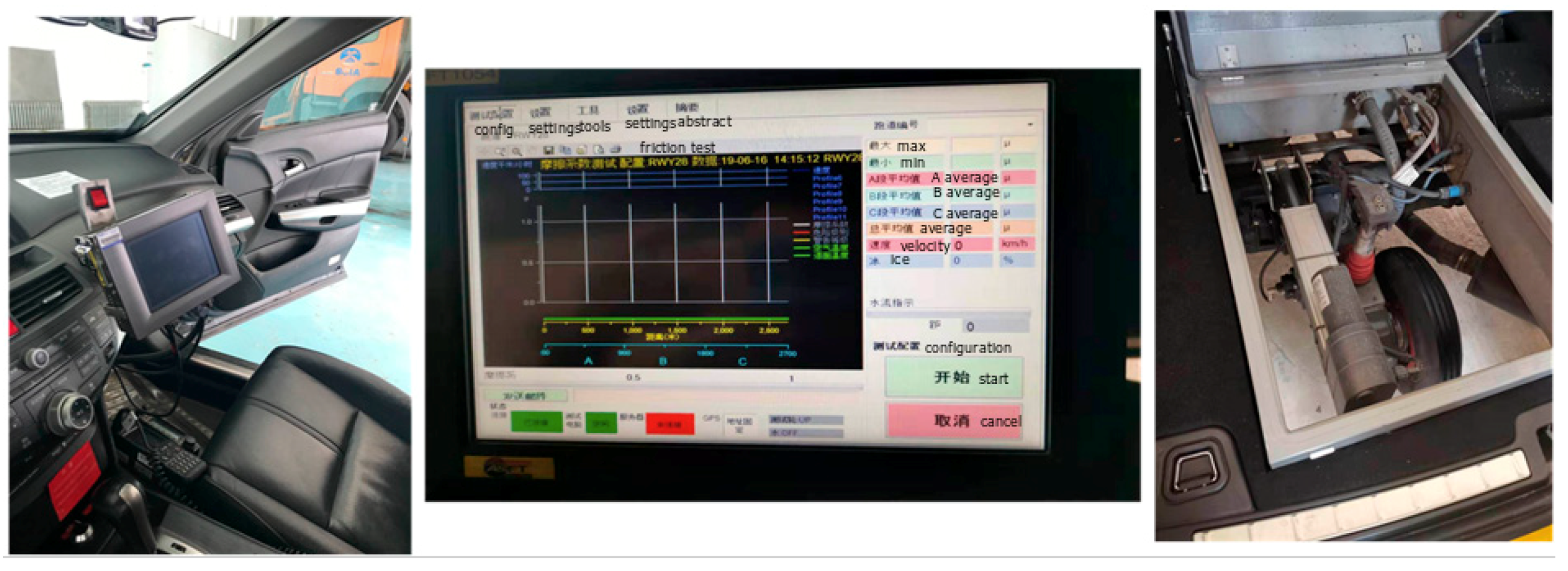



| Category | Detailed | Category | Detailed |
|---|---|---|---|
| Tire | 1. Tire load | Pavement | 1. Type |
| 2. Tire inflation | 2. Surface texture | ||
| 3. Tire size | 3. Microtexture | ||
| 4. Tire construction and design | 4. Macrotexture | ||
| 5. Tire tread pattern design | 5. Resistance to polishing by traffic | ||
| 6.Chemical formulation | 6. Resistance to abrasion and crushing strength | ||
| 7. Polymer type | 7. Weathering characteristics | ||
| 8. Carbon black type | 8. Temperature | ||
| 9. Curing system | 9. Thermal properties | ||
| 10. Other ingredients of tread compound | 10. Matrix properties | ||
| 11. Physical properties | 11. Contamination | ||
| 12.Tread surface conditions | 12. Grooving | ||
| 13. Surface degradation | Operating Conditions | 1. Traffic density | |
| 14. Chemical/physical absorption | 2. Velocity | ||
| 15. Thermal properties | 3. Tire slip, peak or locked-wheel conditions | ||
| 16. Dynamic properties | 4. Site design | ||
| 17. Surface temperature | 5. Prevailing climatic conditions | ||
| Lubricant | 1. Type | 6. Testing vehicle design | |
| 2. Viscosity | 7. Method of measurement | ||
| 3. Surface tension | 8. Stopping distance | ||
| 4. Film depth | 9. Decelerometer | ||
| 5. Film strength | 10. Cornering force coefficient | ||
| 6. Temperature | 11. Braking force coefficient | ||
| 7. Impurities | 12. Towed vehicle (impending slide) |
| Nation/Company | Product | Feature |
|---|---|---|
| Finland | RCM411 RTS411 | It is a vehicle-mounted road surface condition rapid detection device, which can detect the road surface status in real-time, and is mainly used to provide a decision-making basis for road maintenance in winter. The device is also suitable for testing airport runways. RCM411 can detect all road conditions, including dry (green light), wet (light blue), accumulated water (dark blue), muddy (purple), snow (white), and icy (red). In addition to the surface condition, the output information includes friction coefficient, water film thickness, and optional surface temperature sensor RTS411. |
| Germany/ LUFFT | MARVIS | The mobile road weather sensor MARVIS turns vehicles into driving weather stations by detecting several critical road and runway weather parameters. Further, it can deliver information about temperatures, water film thickness, dew points, road conditions (dry, moist, wet, snow, ice), ice percentages, real humidity, and friction. |
| Sweden/ Met Sense | MetRoad Mobile | MetRoad Mobile is a mobile laser sensor for road conditions and road friction detection. Based on near-infrared spectroscopy, it can identify other unknown road conditions except for dry, moist, wet, ice, slush, and snow. It can measure the dimensionless friction coefficient from 0 to 1. |
| Finland/Vaisala | DRS511 | It not only provides the temperature of the surface, but it also detects the presence of moisture on the surface, and thus provides a road state such as dry, wet, ice, and snow. |
| DSC111 | Several measurements combined compactly in one sensor. It can individually identify the presence of water, ice, slush, snow, or frost, and accurate and stable measurement results even with intense traffic. |
| Code | Braking Coefficient | Friction Coefficient |
|---|---|---|
| 5.Good | 0.40 and above | |
| 4.Medium-Good | 0.39 to 0.36 | |
| 3.Medium | 0.35 to 0.30 | |
| 2.Poor-Medium | 0.29 to 0.26 | |
| 1.Poor | 0.25 and below | |
| 0. NIL | / |
| Type | Category | Symbol | Variable |
|---|---|---|---|
| Input | Optical sensor | Runway condition | |
| Runway contaminant density | |||
| Runway contaminant depth | |||
| Runway surface temperature | |||
| Runway surface texture | |||
| Tread Sensor | Tire pressure | ||
| Tire load | |||
| Deceleration | |||
| Others | SFT forward speed | ||
| Input/Output | Tire model | Friction coefficient based on magic formula | |
| Output | Force sensor | Friction coefficient measured by SFT | |
| Estimator* | Friction coefficient estimated by estimator |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Zhang, S.; Tian, G.; Zhu, H.; Zhou, W. Estimation for Runway Friction Coefficient Based on Multi-Sensor Information Fusion and Model Correlation. Sensors 2020, 20, 3886. https://doi.org/10.3390/s20143886
Niu Y, Zhang S, Tian G, Zhu H, Zhou W. Estimation for Runway Friction Coefficient Based on Multi-Sensor Information Fusion and Model Correlation. Sensors. 2020; 20(14):3886. https://doi.org/10.3390/s20143886
Chicago/Turabian StyleNiu, Yadong, Sixiang Zhang, Guangjun Tian, Huabo Zhu, and Wei Zhou. 2020. "Estimation for Runway Friction Coefficient Based on Multi-Sensor Information Fusion and Model Correlation" Sensors 20, no. 14: 3886. https://doi.org/10.3390/s20143886
APA StyleNiu, Y., Zhang, S., Tian, G., Zhu, H., & Zhou, W. (2020). Estimation for Runway Friction Coefficient Based on Multi-Sensor Information Fusion and Model Correlation. Sensors, 20(14), 3886. https://doi.org/10.3390/s20143886






