Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source and Preprocessing
2.1.1. Additional Aggregation
2.1.2. Data Splitting
2.2. Feature Selection
2.3. Sampling Methods
2.4. Classification Models
Ensemble Methods
2.5. Evaluation
3. Results
3.1. Feature Importance
3.1.1. Mastitis Treatments
3.1.2. Lameness Treatments
3.2. Classification Results
3.2.1. Results for Training Data
3.2.2. Results for Testing Data
4. Discussion
4.1. Feature Importance
4.2. Sampling Methods
4.3. Interpretation of the Final Classification Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barkema, H.W.; Von Keyserlingk, M.; Kastelic, J.; Lam, T.; Luby, C.; Roy, J.-P.; Leblanc, S.J.; Keefe, G.; Kelton, D. Invited review: Changes in the dairy industry affecting dairy cattle health and welfare. J. Dairy Sci. 2015, 98, 7426–7445. [Google Scholar] [CrossRef] [PubMed]
- Pintado, D.C. Automated Mastitis Detection in Dairy Cows Using Different Statistical Methods. Ph.D. Thesis, Christian-Albrechts-Universität zu Kiel, Kiel, Germany, 2006. [Google Scholar]
- Steeneveld, W.; Van Der Gaag, L.C.; Ouweltjes, W.; Mollenhorst, H.; Hogeveen, H. Discriminating between true-positive and false-positive clinical mastitis alerts from automatic milking systems. J. Dairy Sci. 2010, 93, 2559–2568. [Google Scholar] [CrossRef] [PubMed]
- Jensen, D.; Hogeveen, H.; De Vries, A. Bayesian integration of sensor information and a multivariate dynamic linear model for prediction of dairy cow mastitis. J. Dairy Sci. 2016, 99, 7344–7361. [Google Scholar] [CrossRef] [PubMed]
- Stangaferro, M.; Wijma, R.; Caixeta, L.; Al Abri, M.; Giordano, J. Use of rumination and activity monitoring for the identification of dairy cows with health disorders: Part II. Mastitis. J. Dairy Sci. 2016, 99, 7411–7421. [Google Scholar] [CrossRef]
- Alsaaod, M.; Römer, C.; Kleinmanns, J.; Hendriksen, K.; Rose-Meierhöfer, S.; Plümer, L.; Buscher, W. Electronic detection of lameness in dairy cows through measuring pedometric activity and lying behavior. Appl. Anim. Behav. Sci. 2012, 142, 134–141. [Google Scholar] [CrossRef]
- Miekley, B.; Traulsen, I.; Krieter, J. Principal component analysis for the early detection of mastitis and lameness in dairy cows. J. Dairy Res. 2013, 80, 335–343. [Google Scholar] [CrossRef]
- Van Hertem, T.; Maltz, E.; Antler, A.; Romanini, C.E.B.; Viazzi, S.; Bähr, C.; Schlageter-Tello, A.; Lokhorst, C.; Berckmans, D.; Halachmi, I. Lameness detection based on multivariate continuous sensing of milk yield, rumination, and neck activity. J. Dairy Sci. 2013, 96, 4286–4298. [Google Scholar] [CrossRef]
- Van Nuffel, A.; Zwertvaegher, I.; Pluym, L.; Van Weyenberg, S.; Thorup, V.M.; Pastell, M.; Sonck, B.; Saeys, W. Lameness Detection in Dairy Cows: Part 1. How to Distinguish between Non-Lame and Lame Cows Based on Differences in Locomotion or Behavior. Animals 2015, 5, 838–860. [Google Scholar] [CrossRef]
- Kamphuis, C.; Frank, E.; Burke, J.; Verkerk, G.; Jago, J. Applying additive logistic regression to data derived from sensors monitoring behavioral and physiological characteristics of dairy cows to detect lameness. J. Dairy Sci. 2013, 96, 7043–7053. [Google Scholar] [CrossRef]
- Pastell, M.; Kujala, M. A Probabilistic Neural Network Model for Lameness Detection. J. Dairy Sci. 2007, 90, 2283–2292. [Google Scholar] [CrossRef]
- Lehmann, C.; Koenig, T.; Jelic, V.; Prichep, L.; John, R.E.; Wahlund, L.-O.; Dodge, Y.; Dierks, T. Application and comparison of classification algorithms for recognition of Alzheimer’s disease in electrical brain activity (EEG). J. Neurosci. Methods 2007, 161, 342–350. [Google Scholar] [CrossRef]
- Nechanitzky, K.; Starke, A.; Vidondo, B.; Müller, H.; Reckardt, M.; Friedli, K.; Steiner, A. Analysis of behavioral changes in dairy cows associated with claw horn lesions. J. Dairy Sci. 2016, 99, 2904–2914. [Google Scholar] [CrossRef] [PubMed]
- Mollenhorst, H.; Van Der Tol, P.; Hogeveen, H. Somatic cell count assessment at the quarter or cow milking level. J. Dairy Sci. 2010, 93, 3358–3364. [Google Scholar] [CrossRef] [PubMed]
- Dominiak, K.; Kristensen, A. Prioritizing alarms from sensor-based detection models in livestock production—A review on model performance and alarm reducing methods. Comput. Electron. Agric. 2017, 133, 46–67. [Google Scholar] [CrossRef]
- Garcia, E.; Klaas, I.; Amigó, J.; Bro, R.; Enevoldsen, C. Lameness detection challenges in automated milking systems addressed with partial least squares discriminant analysis. J. Dairy Sci. 2014, 97, 7476–7486. [Google Scholar] [CrossRef] [PubMed]
- Cavero, D.; Tölle, K.-H.; Rave, G.; Buxadé, C.; Krieter, J. Analysing serial data for mastitis detection by means of local regression. Livest. Sci. 2007, 110, 101–110. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Schenk, J.; Kaiser, M.S.; Rigoll, G. Selecting Features in On-Line Handwritten Whiteboard Note Recognition: SFS or SFFS? In Proceedings of the 2009 10th International Conference on Document Analysis and Recognition, Barcelona, Spain, 26–29 July 2009; pp. 1251–1254. [Google Scholar]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. J. Mach. Learn. Res. 2017, 1, 559–563. [Google Scholar]
- Chawla, N.V. C4. 5 and imbalanced data sets: Investigating the effect of sampling method, probabilistic estimate, and decision tree structure. In Proceedings of the ICML; CIBC: Toronto, ON, Canada, 2003; pp. 66–73. [Google Scholar]
- Varoquaux, G.; Buitinck, L.; Louppe, G.; Grisel, O.; Pedregosa, F.; Mueller, A. Scikit-learn. GetMob. Mob. Comput. Commun. 2015, 19, 29–33. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 3, 273–297. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Domingos, P.; Pazzani, M. On the Optimality of the Simple Bayesian Classifier under Zero-One Loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kelleher, J.D.; MacNamee, B.; D’Arcy, A. Fundamentals of Machine Learning for Predictive Data Analytics; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 1, 5–32. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Kamphuis, C.; Sherlock, R.; Jago, J.; Mein, G.; Hogeveen, H. Automatic Detection of Clinical Mastitis Is Improved by In-Line Monitoring of Somatic Cell Count. J. Dairy Sci. 2008, 91, 4560–4570. [Google Scholar] [CrossRef]
- Fernando, R.; Rindsig, R.; Spahr, S. Electrical Conductivity of Milk for Detection of Mastitis. J. Dairy Sci. 1982, 65, 659–664. [Google Scholar] [CrossRef]
- Oltenacu, P.A.; Ekesbo, I. Epidemiological study of clinical mastitis in dairy cattle. Veter Res. 1994, 25, 208–212. [Google Scholar]
- De Mol, R.; Andre, G.; Bleumer, E.; Van Der Werf, J.; De Haas, Y.; Van Reenen, C. Applicability of day-to-day variation in behavior for the automated detection of lameness in dairy cows. J. Dairy Sci. 2013, 96, 3703–3712. [Google Scholar] [CrossRef]
- Flower, F.; Weary, D. Effect of Hoof Pathologies on Subjective Assessments of Dairy Cow Gait. J. Dairy Sci. 2006, 89, 139–146. [Google Scholar] [CrossRef]
- Pastell, M.; Hänninen, L.; De Passillé, A.; Rushen, J. Measures of weight distribution of dairy cows to detect lameness and the presence of hoof lesions. J. Dairy Sci. 2010, 93, 954–960. [Google Scholar] [CrossRef] [PubMed]
- Borchers, M.; Chang, Y.; Tsai, I.; Wadsworth, B.; Bewley, J. A validation of technologies monitoring dairy cow feeding, ruminating, and lying behaviors. J. Dairy Sci. 2016, 99, 7458–7466. [Google Scholar] [CrossRef] [PubMed]
- Wolfger, B.; Timsit, E.; Pajor, E.; Cook, N.; Barkema, H.W.; Orsel, K. Technical note: Accuracy of an ear tag-attached accelerometer to monitor rumination and feeding behavior in feedlot cattle1. J. Anim. Sci. 2015, 93, 3164–3168. [Google Scholar] [CrossRef]
- Schindhelm, K.; Haidn, B.; Trembalay, M.; Döpfer, D. Automatisch erfasste Leistungs- und Verhaltensparameter als Risikofaktoren in einem Vorhersagemodell für Lahmheit bei Milchkühen der Rasse Fleckvieh. In Proceedings of the 13. Tagung: Bau, Technik und Umwelt, Stuttgart-Hohenheim, Germany, 18 September 2017; pp. 228–233. [Google Scholar]
- Brown, I.; Mues, C. An experimental comparison of classification algorithms for imbalanced credit scoring data sets. Expert Syst. Appl. 2012, 39, 3446–3453. [Google Scholar] [CrossRef]
- Hogeveen, H.; Kamphuis, C.; Steeneveld, W.; Mollenhorst, H. Sensors and Clinical Mastitis—The Quest for the Perfect Alert. Sensors 2010, 10, 7991–8009. [Google Scholar] [CrossRef] [PubMed]
- González, L.A.; Tolkamp, B.; Coffey, M.; Ferret, A.; Kyriazakis, I. Changes in Feeding Behavior as Possible Indicators for the Automatic Monitoring of Health Disorders in Dairy Cows. J. Dairy Sci. 2008, 91, 1017–1028. [Google Scholar] [CrossRef]
- Lukas, J.; Reneau, J.; Wallace, R.; Hawkins, D.; Munoz-Zanzi, C. A novel method of analyzing daily milk production and electrical conductivity to predict disease onset. J. Dairy Sci. 2009, 92, 5964–5976. [Google Scholar] [CrossRef]
- Cavero, D.; Tölle, K.-H.; Henze, C.; Buxadé, C.; Krieter, J. Mastitis detection in dairy cows by application of neural networks. Livest. Sci. 2008, 114, 280–286. [Google Scholar] [CrossRef]
- Rutten, C.J.; Velthuis, A.G.J.; Steeneveld, W.; Hogeveen, H. Invited review. J. Dairy Sci. 2013, 4, 1928–1952. [Google Scholar] [CrossRef]
- Mansbridge, N.; Mitsch, J.; Bollard, N.; Ellis, K.; Miguel-Pacheco, G.G.; Dottorini, T.; Kaler, J. Feature Selection and Comparison of Machine Learning Algorithms in Classification of Grazing and Rumination Behaviour in Sheep. Sensors 2018, 18, 3532. [Google Scholar] [CrossRef]
- Shahinfar, S.; Page, D.; Guenther, J.; Cabrera, V.; Fricke, P.; Weigel, K. Prediction of insemination outcomes in Holstein dairy cattle using alternative machine learning algorithms. J. Dairy Sci. 2014, 97, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Huzzey, J.; Veira, D.; Weary, D.; Von Keyserlingk, M. Prepartum Behavior and Dry Matter Intake Identify Dairy Cows at Risk for Metritis. J. Dairy Sci. 2007, 90, 3220–3233. [Google Scholar] [CrossRef] [PubMed]
- Zehner, N.; Niederhauser, J.J.; Schick, M.; Umstätter, C. Development and validation of a predictive model for calving time based on sensor measurements of ingestive behavior in dairy cows. Comput. Electron. Agric. 2019, 161, 62–71. [Google Scholar] [CrossRef]
| Aggregation | Description |
|---|---|
| Daily | |
| Mean | Arithmetic mean |
| SD | Standard deviation |
| Median | Median |
| Sum | Sum of values |
| Max | Highest single value |
| Min | Lowest single value |
| Range | Max-Min |
| 3 highest (Sum) | Sum of the 3 highest values |
| 6 highest (Sum) | Sum of the 6 highest values |
| 3 lowest (Sum) | Sum of the 3 lowest values |
| 6 lowest (Sum) | Sum of the 6 lowest values |
| Sum Day | Sum of values from 04:01 to 20:00 |
| Sum Night | Sum of values from 20:01 to 04:00 |
| Day/Night ratio | Sum Day/Sum Night |
| Multiple days | |
| d-1 | Value of previous day |
| d-2 | Value 2 days before |
| d-3 | Value 3 days before |
| RM | Rolling Mean of previous 7 days |
| RMdiff | Difference of current day’s value to RM |
| RMprev | Rolling mean of previous week (d-8 to d-14) |
| slope | Slope of a linear regression from the recent 7 values |
| Category | Number of Features |
|---|---|
| Animal dependent variables | |
| Feed and water intake and visits | 189 |
| Activity | 127 |
| Milking | 77 |
| Concentrate intake | 25 |
| Body weight | 8 |
| Other 1 | 3 |
| Animal independent variables | |
| Climate | 4 |
| Mastitis Treatments Classification | Lameness Treatments Classification | |||||
|---|---|---|---|---|---|---|
| Rank | Feature | RF-I 1 | r | Feature | RF-I | r |
| 1 | Last Milk recording SCC 2 | 0.039 ± 0.009 | +0.176 ± 0.016 | Feeding time with intake | 0.013 ± 0.005 | −0.105 ± 0.014 |
| 2 | Concentrate intake, slope | 0.014 ± 0.005 | −0.076 ± 0.016 | Feed intake Sum day, RMprev 3 | 0.012 ± 0.006 | +0.079 ± 0.010 |
| 3 | Milk conductivity p.m., slope | 0.013 ± 0.006 | +0.082 ± 0.024 | Activity, SD, RMprev | 0.012 ± 0.006 | −0.072 ± 0.012 |
| 4 | Feed intake (Median), RMprev | 0.011 ± 0.004 | +0.067 ± 0.010 | Feeding visits with intake | 0.011 ± 0.005 | −0.080 ± 0.013 |
| 5 | Feed intake (S.D.), RMprev | 0.011 ± 0.004 | +0.064 ± 0.008 | Activity (Range), RMprev | 0.010 ± 0.006 | −0.067 ± 0.011 |
| 6 | Feeding visit duration (mean), RM 4 | 0.011 ± 0.004 | +0.009 ± 0.006 | Activity (Max), RMprev | 0.010 ± 0.004 | −0.066 ± 0.011 |
| 7 | Feed intake 6 highest (Sum), RMprev | 0.011 ± 0.006 | +0.068 ± 0.009 | Air temperature | 0.010 ± 0.004 | −0.061 ± 0.015 |
| 8 | Feed intake 3 highest (Sum), RMprev | 0.010 ± 0.005 | +0.068 ± 0.009 | THI 5 | 0.009 ± 0.003 | −0.061 ± 0.015 |
| 9 | Feeding visit duration (mean), d−3 | 0.010 ± 0.004 | −0.002 ± 0.006 | Feed intake (SD), RM | 0.009 ± 0.004 | +0.098 ± 0.011 |
| 10 | Conc. intake abs. deviation, RM | 0.010 ± 0.004 | −0.047 ± 0.014 | Feeding time with intake, RM | 0.009 ± 0.006 | −0.062 ± 0.008 |
| 11 | Milk conductivity p.m., RMdiff 6 | 0.010 ± 0.005 | +0.080 ± 0.017 | Feeding time with intake, RMdiff | 0.009 ± 0.003 | −0.095 ± 0.018 |
| 12 | Feed intake (Max), RMprev | 0.009 ± 0.006 | +0.065 ± 0.01 | Drinking time with intake | 0.009 ± 0.005 | −0.065 ± 0.009 |
| 13 | Feed intake (Mean), RMprev | 0.009 ± 0.005 | +0.067 ± 0.01 | Feeding time with intake, slope | 0.008 ± 0.003 | −0.090 ± 0.019 |
| 14 | Feeding visits with intake, RMprev | 0.009 ± 0.006 | −0.060 ± 0.005 | Feed intake (Median) | 0.007 ± 0.001 | +0.107 ± 0.010 |
| 15 | Feed intake (S.D.), RM | 0.008 ± 0.003 | +0.052 ± 0.007 | Feed intake, 6 highest (Sum), RM | 0.006 ± 0.003 | +0.101 ± 0.009 |
| 16 | Conc. intake rel. deviation, RM | 0.008 ± 0.004 | −0.036 ± 0.011 | Feed intake per visit | 0.006 ± 0.003 | +0.106 ± 0.011 |
| 17 | Feeding visit duration (Mean), RMprev | 0.008 ± 0.005 | +0.034 ± 0.008 | Activity, 3 highest (Sum), RMprev | 0.006 ± 0.003 | −0.067 ± 0.011 |
| 18 | Feed intake 6 highest (Sum), RM | 0.008 ± 0.003 | +0.062 ± 0.008 | Feeding visits with intake, d-1 | 0.006 ± 0.003 | −0.068 ± 0.011 |
| 19 | Feed intake (Range), RMprev | 0.008 ± 0.005 | +0.065 ± 0.010 | Feed intake, RMprev | 0.006 ± 0.004 | +0.063 ± 0.015 |
| 20 | Feeding visits with intake, RM | 0.008 ± 0.005 | −0.057 ± 0.005 | Drinking visits, RM | 0.006 ± 0.003 | −0.059 ± 0.014 |
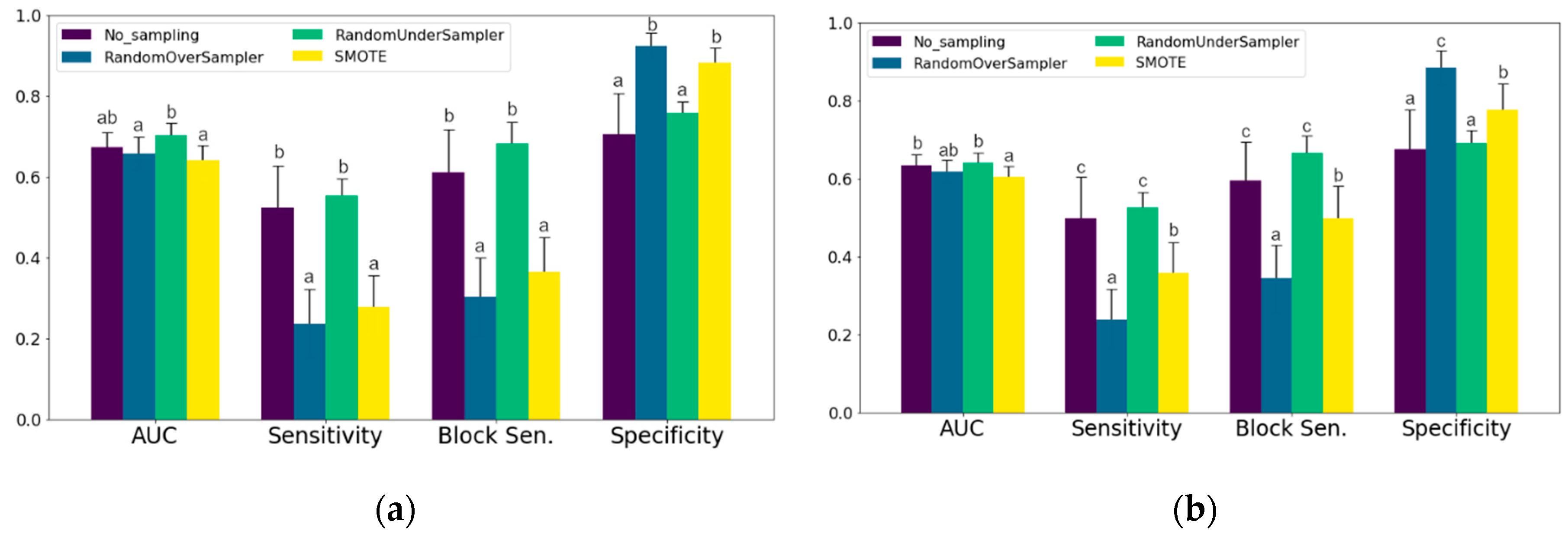
| Sampling of Training Data | AUC 1 | Sen. 2 | Spe. 3 |
|---|---|---|---|
| Mastitis treatments | |||
| No sampling | 0.80 ± 0.02 b | 0.72 ± 0.04 c | 0.72 ± 0.05 b |
| Random Undersampling | 0.76 ± 0.01 c | 0.81 ± 0.02 b | 0.59 ± 0.04 c |
| Random Oversampling | 0.95 ± 0.01 a | 0.89 ± 0.02 a | 0.91 ± 0.02 a |
| SMOTE 4 | 0.95 ± 0.01 a | 0.88 ± 0.01 a | 0.91 ± 0.02 a |
| Lameness treatments | |||
| No sampling | 0.76 ± 0.02 b | 0.70 ± 0.04 b | 0.68 ± 0.05 b |
| Random Undersampling | 0.71 ± 0.01 c | 0.80 ± 0.02 b | 0.53 ± 0.03 c |
| Random Oversampling | 0.91 ± 0.02 a | 0.89 ± 0.02 a | 0.84 ± 0.04 a |
| SMOTE | 0.91 ± 0.02 a | 0.87 ± 0.01 a | 0.83 ± 0.04 a |
| Feed and Water Data Included | AUC 1 | Sen. 2 | Block Sen. | Spe. 3 |
|---|---|---|---|---|
| Mastitis treatments | ||||
| Yes | 0.67 ± 0.01 | 0.40 ± 0.02 | 0.49 ± 0.03 | 0.82 ± 0.02 |
| No | 0.66 ± 0.01 | 0.39 ± 0.02 | 0.51 ± 0.02 | 0.82 ± 0.01 |
| Lameness treatments | ||||
| Yes | 0.62 ± 0.01 a | 0.41 ± 0.02 | 0.53 ± 0.02 a | 0.76 ± 0.02 a |
| No | 0.55 ± 0.01 b | 0.38 ± 0.02 | 0.50 ± 0.02 b | 0.69 ± 0.02 b |
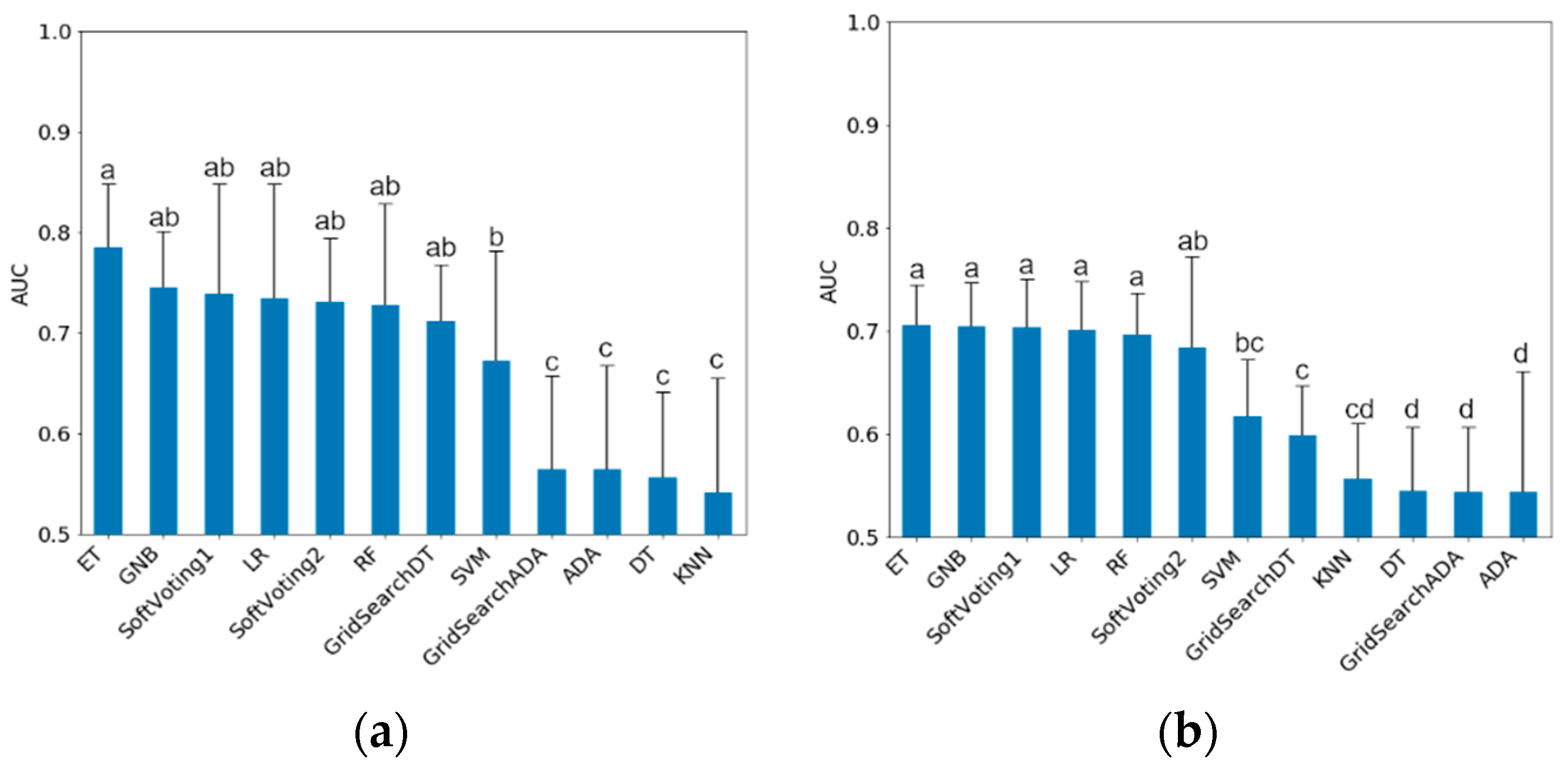
| Mastitis Treatments | Lameness Treatments | ||
|---|---|---|---|
| Classification Method | AUC 1 | Classification Method | AUC 1 |
| LR 2 | 0.75 ± 0.02 a | GNB | 0.70 ± 0.01 a |
| ET 3 | 0.75 ± 0.02 a | Soft Voting 1 | 0.69 ± 0.01 a |
| GNB 4 | 0.75 ± 0.02 a | ET | 0.68 ± 0.01 ab |
| Soft Voting 1 | 0.74 ± 0.02 a | LR | 0.68 ± 0.01 ab |
| Soft Voting 2 | 0.73 ± 0.02 a | RF | 0.67 ± 0.02 ab |
| RF 5 | 0.72 ± 0.02 ab | Soft Voting 2 | 0.66 ± 0.02 abc |
| Grid Search DT 6 | 0.69 ± 0.03 bc | SVM | 0.62 ± 0.03 bc |
| SVM 7 | 0.65 ± 0.03 c | Grid Search DT | 0.60 ± 0.02 cd |
| KNN 8 | 0.58 ± 0.02 d | KNN | 0.57 ± 0.02 de |
| Grid Search ADA 9 | 0.56 ± 0.01 d | Grid Search ADA | 0.54 ± 0.01 e |
| ADA | 0.56 ± 0.01 d | ADA | 0.54 ± 0.01 e |
| DT | 0.55 ± 0.02 d | DT | 0.54 ± 0.01 e |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Post, C.; Rietz, C.; Büscher, W.; Müller, U. Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models. Sensors 2020, 20, 3863. https://doi.org/10.3390/s20143863
Post C, Rietz C, Büscher W, Müller U. Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models. Sensors. 2020; 20(14):3863. https://doi.org/10.3390/s20143863
Chicago/Turabian StylePost, Christian, Christian Rietz, Wolfgang Büscher, and Ute Müller. 2020. "Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models" Sensors 20, no. 14: 3863. https://doi.org/10.3390/s20143863
APA StylePost, C., Rietz, C., Büscher, W., & Müller, U. (2020). Using Sensor Data to Detect Lameness and Mastitis Treatment Events in Dairy Cows: A Comparison of Classification Models. Sensors, 20(14), 3863. https://doi.org/10.3390/s20143863







