Optimizing Irradiation Geometry in LED-Based Photoacoustic Imaging with 3D Printed Flexible and Modular Light Delivery System
Abstract
1. Introduction
2. Materials and Methods
2.1. Photoacoustic System and Modular Arrangement for Varying Illumination Direction
2.1.1. AcousticX
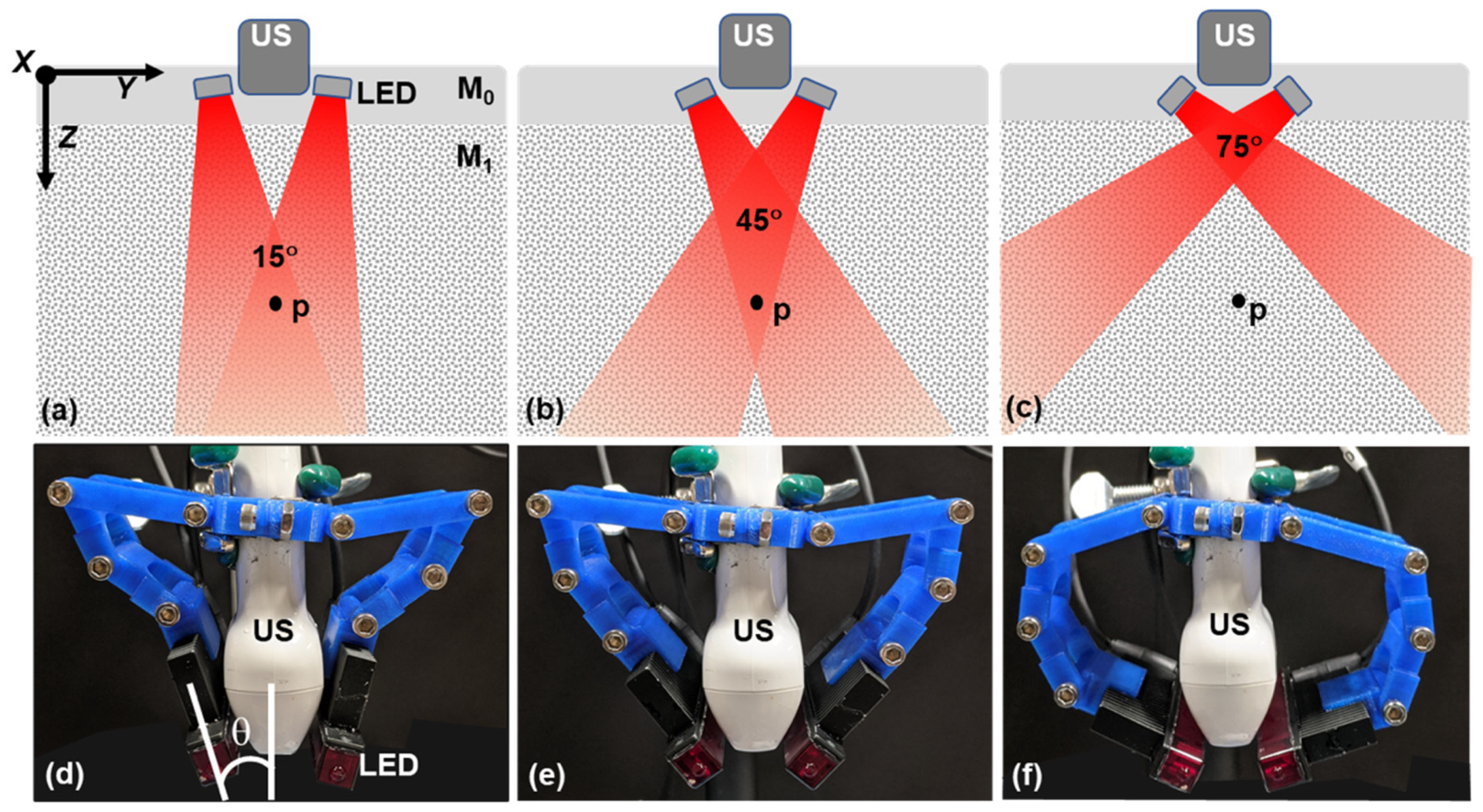
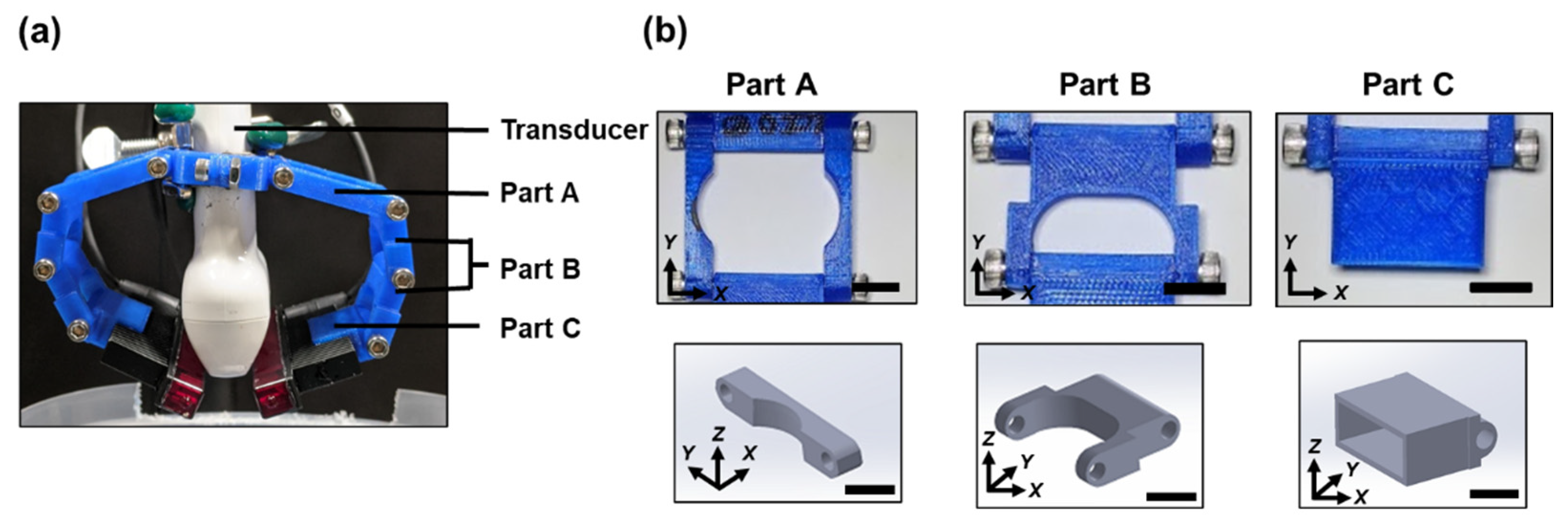
2.1.2. Flexible LED Holder: Modular Design for Adjusting Irradiation Direction
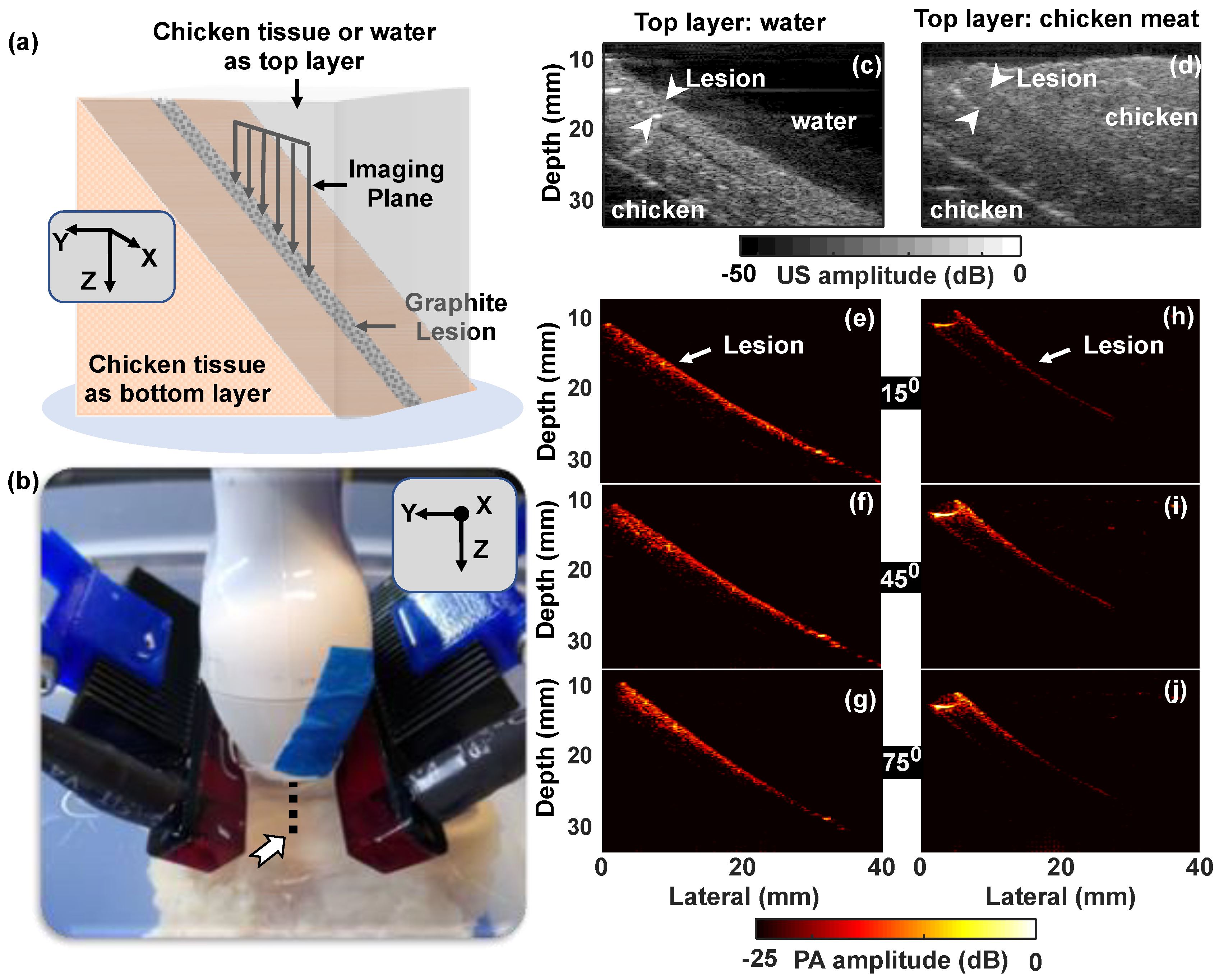
2.2. Phantoms
2.2.1. Graphite Pencil Lead Phantoms
2.2.2. Tissue Mimicking Phantom Containing Lesion with High Optical Absorbance
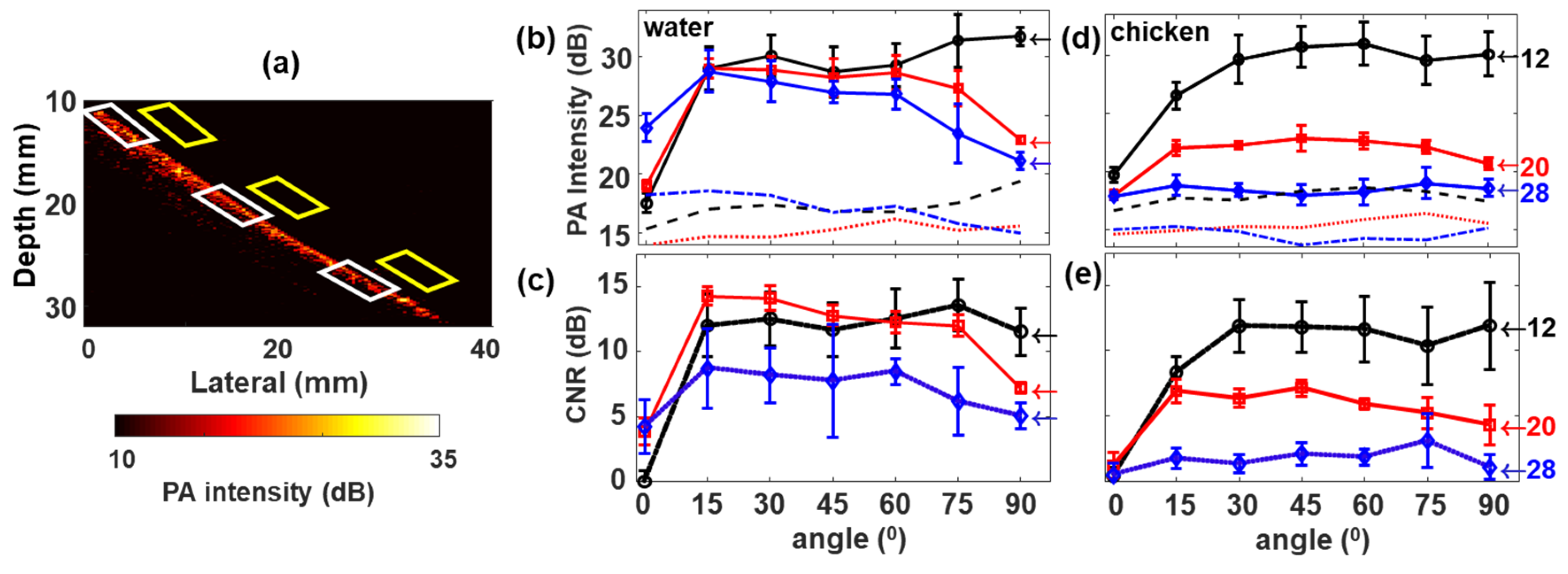
2.3. Signal Analysis
2.3.1. PA Intensity & Contrast to Noise Ratio (CNR) Calculation
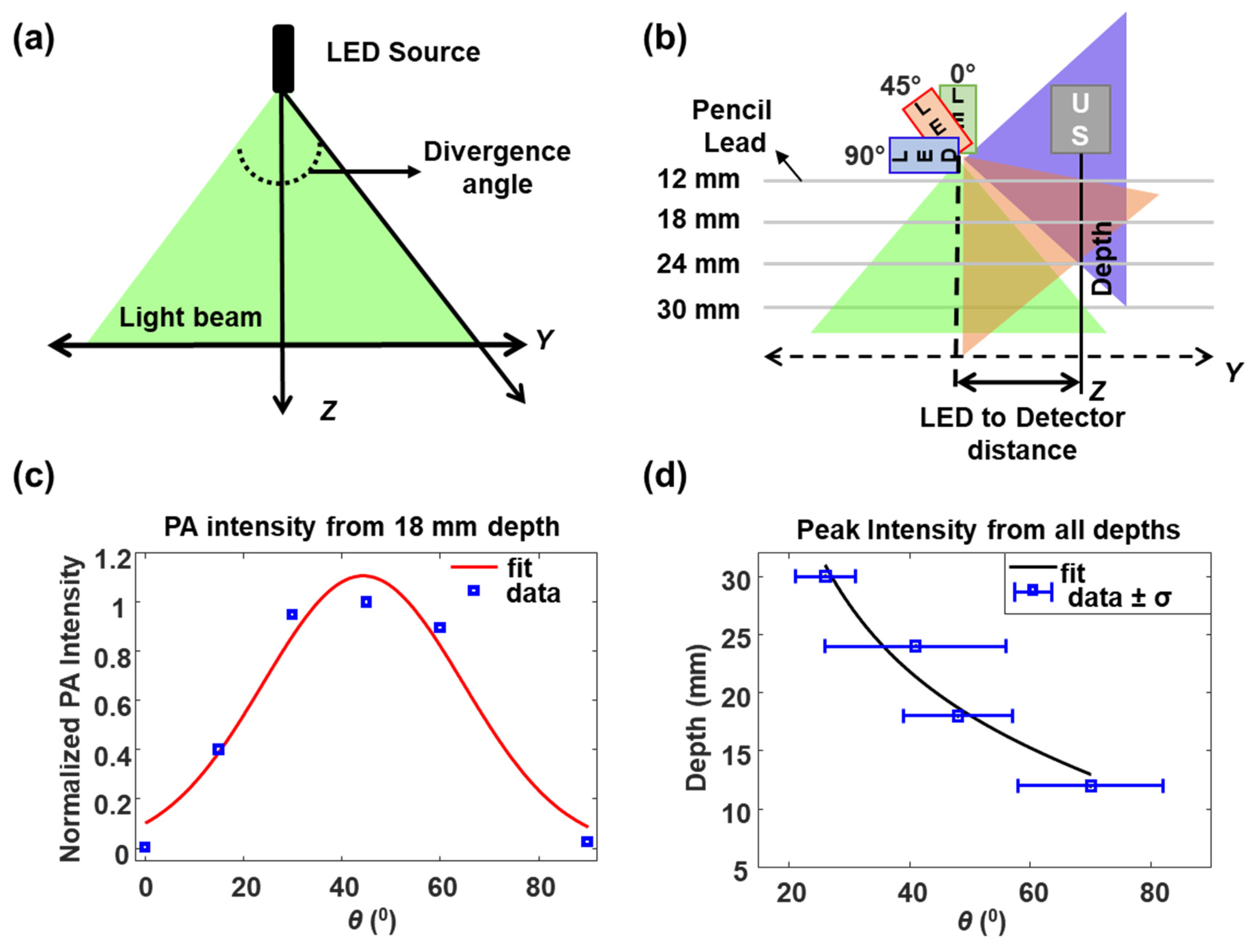
2.3.2. Divergence of the LED Source
3. Results
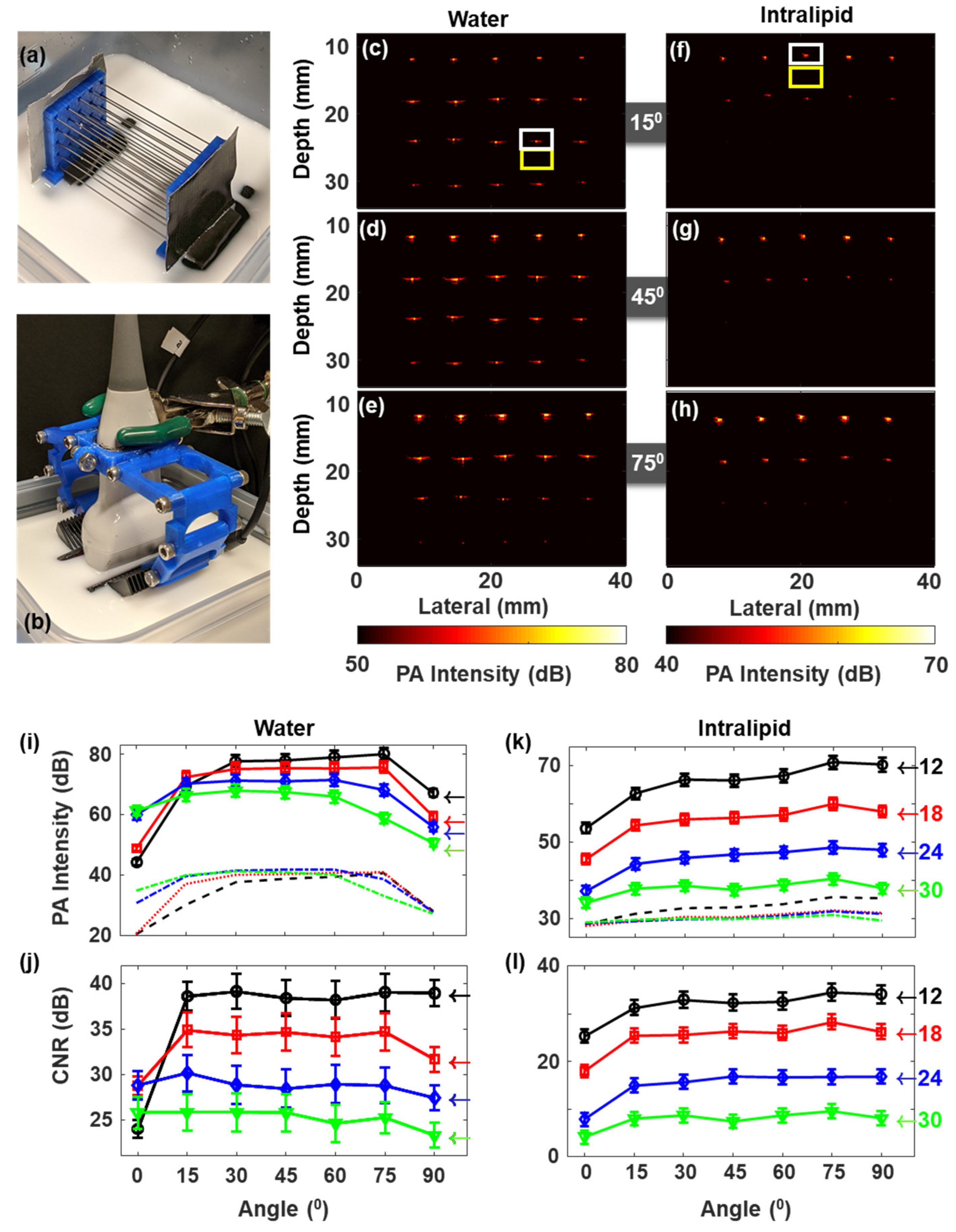
3.1. Pencil Lead Phantom Experiments
3.1.1. Pencil Lead in Scattering and Non-Scattering Media Shows Weak Dependency on the LED Illumination Angle
3.1.2. LED Source Divergence and Optimum Illumination Angle from Pencil Lead Targets in Water
3.2. Effect of Surrounding Media and Illumination Direction on PA Signal from Tumor Mimicking Lesion
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hester, S.C.; Kuriakose, M.; Nguyen, C.D.; Mallidi, S. Role of Ultrasound and Photoacoustic Imaging in Photodynamic Therapy for Cancer. Photochem. Photobiol. 2020, 96, 260–279. [Google Scholar] [CrossRef]
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef]
- Brown, E.; Brunker, J.; Bohndiek, S.E. Photoacoustic imaging as a tool to probe the tumour microenvironment. Dis. Model Mech. 2019, 12, dmm039636. [Google Scholar] [CrossRef]
- Steinberg, I.; Huland, D.M.; Vermesh, O.; Frostig, H.E.; Tummers, W.S.; Gambhir, S.S. Photoacoustic clinical imaging. Photoacoustics 2019, 14, 77–98. [Google Scholar] [CrossRef]
- Zackrisson, S.; van de Ven, S.; Gambhir, S.S. Light in and sound out: Emerging translational strategies for photoacoustic imaging. Cancer Res. 2014, 74, 979–1004. [Google Scholar] [CrossRef]
- Liu, G. Theory of the photoacoustic effect in condensed matter. Appl. Opt. 1982, 21, 955–960. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V. Tutorial on Photoacoustic Microscopy and Computed Tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Craig, B.; Sussman, C.R.; Zhang, Q.; Jiang, H.; Zheng, T.; Steindler, D.; Young, L.; Weiss, M.D. Photoacoustic tomography can detect cerebral hemodynamic alterations in a neonatal rodent model of hypoxia-ischemia. Acta Neurobiol. Exp. 2012, 72, 253–263. [Google Scholar]
- Wang, X.; Chamberland, D.L.; Xi, G. Noninvasive reflection mode photoacoustic imaging through infant skull toward imaging of neonatal brains. J. Neurosci. Methods 2008, 168, 412–421. [Google Scholar] [CrossRef]
- Lin, L.; Hu, P.; Shi, J.; Appleton, C.M.; Maslov, K.; Li, L.; Zhang, R.; Wang, L.V. Single-breath-hold photoacoustic computed tomography of the breast. Nat. Commun. 2018, 9, 2352. [Google Scholar] [CrossRef]
- Dogra, V.S.; Chinni, B.K.; Valluru, K.S.; Moalem, J.; Giampoli, E.J.; Evans, K.; Rao, N.A. Preliminary results of ex vivo multispectral photoacoustic imaging in the management of thyroid cancer. AJR Am. J. Roentgenol. 2014, 202, W552–W558. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhao, L.; He, X.; Su, N.; Zhao, C.; Tang, H.; Hong, T.; Li, W.; Yang, F.; Lin, L.; et al. Photoacoustic/ultrasound dual imaging of human thyroid cancers: An initial clinical study. Biomed. Opt. Express 2017, 8, 3449–3457. [Google Scholar] [CrossRef] [PubMed]
- Mallidi, S.; Luke, G.P.; Emelianov, S. Photoacoustic imaging in cancer detection, diagnosis, and treatment guidance. Trends Biotechnol. 2011, 29, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Valluru, K.S.; Wilson, K.E.; Willmann, J.K. Photoacoustic Imaging in Oncology: Translational Preclinical and Early Clinical Experience. Radiology 2016, 280, 332–349. [Google Scholar] [CrossRef]
- Mallidi, S.; Watanabe, K.; Timerman, D.; Schoenfeld, D.; Hasan, T. Prediction of tumor recurrence and therapy monitoring using ultrasound-guided photoacoustic imaging. Theranostics 2015, 5, 289–301. [Google Scholar] [CrossRef]
- Moore, C.; Jokerst, J.V. Strategies for Image-Guided Therapy, Surgery, and Drug Delivery Using Photoacoustic Imaging. Theranostics 2019, 9, 1550–1571. [Google Scholar] [CrossRef]
- Kim, J.; Park, S.; Jung, Y.; Chang, S.; Park, J.; Zhang, Y.; Lovell, J.F.; Kim, C. Programmable Real-time Clinical Photoacoustic and Ultrasound Imaging System. Sci. Rep. 2016, 6, 35137. [Google Scholar] [CrossRef] [PubMed]
- Schellenberg, M.W.; Hunt, H.K. Hand-held optoacoustic imaging: A review. Photoacoustics 2018, 11, 14–27. [Google Scholar] [CrossRef]
- Upputuri, P.K.; Pramanik, M. Photoacoustic imaging in the second near-infrared window: A review. J. Biomed. Opt. 2019, 24, 1–20. [Google Scholar] [CrossRef]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Oraevsky, A.A.; Karabutov, A.A. Optoacoustic Tomography. In Biomedical Photonics Handbook; Vo-Dinh, T., Ed.; CRC: Boca Raton, FL, USA, 2003; Chapter 34. [Google Scholar]
- Sivasubramanian, K.; Pramanik, M. High frame rate photoacoustic imaging at 7000 frames per second using clinical ultrasound system. Biomed. Opt. Express 2016, 7, 312–323. [Google Scholar] [CrossRef]
- Sowers, T.; Yoon, H.; Emelianov, S. Investigation of light delivery geometries for photoacoustic applications using Monte Carlo simulations with multiple wavelengths, tissue types, and species characteristics. J. Biomed. Opt. 2020, 25, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Lim, R.S.A.; Zhang, H.; Nyayapathi, N.; Oh, K.W.; Xia, J. Optimizing the light delivery of linear-array-based photoacoustic systems by double acoustic reflectors. Sci. Rep. 2018, 8, 13004. [Google Scholar] [CrossRef]
- Wang, Z.; Ha, S.; Kim, K. A new design of light illumination scheme for deep tissue photoacoustic imaging. Opt. Express 2012, 20, 22649–22659. [Google Scholar] [CrossRef]
- Yang, G.; Amidi, E.; Nandy, S.; Mostafa, A.; Zhu, Q. Optimized light delivery probe using ball lenses for co-registered photoacoustic and ultrasound endo-cavity subsurface imaging. Photoacoustics 2019, 13, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Carles, G.; Zammit, P.; Harvey, A.R. Holistic Monte-Carlo optical modelling of biological imaging. Sci. Rep. 2019, 9, 15832. [Google Scholar] [CrossRef] [PubMed]
- Flock, S.T.; Patterson, M.S.; Wilson, B.C.; Wyman, D.R. Monte Carlo modeling of light propagation in highly scattering tissue--I: Model predictions and comparison with diffusion theory. IEEE Trans. Biomed. Eng. 1989, 36, 1162–1168. [Google Scholar] [CrossRef]
- Held, K.G.; Jaeger, M.; Ricka, J.; Frenz, M.; Akarcay, H.G. Multiple irradiation sensing of the optical effective attenuation coefficient for spectral correction in handheld OA imaging. Photoacoustics 2016, 4, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Watte, R.; Aernouts, B.; Van Beers, R.; Herremans, E.; Ho, Q.T.; Verboven, P.; Nicolai, B.; Saeys, W. Modeling the propagation of light in realistic tissue structures with MMC-fpf: A meshed Monte Carlo method with free phase function. Opt. Express 2015, 23, 17467–17486. [Google Scholar] [CrossRef] [PubMed]
- Held, G.; Preisser, S.; Akarcay, H.G.; Peeters, S.; Frenz, M.; Jaeger, M. Effect of irradiation distance on image contrast in epi-optoacoustic imaging of human volunteers. Biomed. Opt. Express 2014, 5, 3765–3780. [Google Scholar] [CrossRef][Green Version]
- Haisch, C.; Eilert-Zell, K.; Vogel, M.M.; Menzenbach, P.; Niessner, R. Combined optoacoustic/ultrasound system for tomographic absorption measurements: Possibilities and limitations. Anal. Bioanal. Chem. 2010, 397, 1503–1510. [Google Scholar] [CrossRef]
- Sivasubramanian, K.; Periyasamy, V.; Wen, K.K.; Pramanik, M. Optimizing light delivery through fiber bundle in photoacoustic imaging with clinical ultrasound system: Monte Carlo simulation and experimental validation. J. Biomed. Opt. 2017, 22, 41008. [Google Scholar] [CrossRef]
- Sangha, G.S.; Hale, N.J.; Goergen, C.J. Adjustable photoacoustic tomography probe improves light delivery and image quality. Photoacoustics 2018, 12, 6–13. [Google Scholar] [CrossRef]
- Jo, J.; Xu, G.; Zhu, Y.; Burton, M.; Sarazin, J.; Schiopu, E.; Gandikota, G.; Wang, X. Detecting joint inflammation by an LED-based photoacoustic imaging system: A feasibility study. J. Biomed. Opt. 2018, 23, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Leskinen, J.; Pulkkinen, A.; Tick, J.; Tarvainen, T.; Ntziachristos, V.; Zemp, R. Photoacoustic tomography setup using LED illumination. In Proceedings of the Opto-Acoustic Methods and Applications in Biophotonics IV, Munich, Germany, 24–25 June 2019. [Google Scholar]
- Zhu, Y.; Feng, T.; Cheng, Q.; Wang, X.; Du, S.; Sato, N.; Kuniyil Ajith Singh, M.; Yuan, J. Towards Clinical Translation of LED-Based Photoacoustic Imaging: A Review. Sensors 2020, 20, 2484. [Google Scholar] [CrossRef]
- Agrawal, S.; Fadden, C.; Dangi, A.; Yang, X.; Albahrani, H.; Frings, N.; Heidari Zadi, S.; Kothapalli, S.R. Light-Emitting-Diode-Based Multispectral Photoacoustic Computed Tomography System. Sensors 2019, 19, 4861. [Google Scholar] [CrossRef]
- Xia, W.; Kuniyil Ajith Singh, M.; Maneas, E.; Sato, N.; Shigeta, Y.; Agano, T.; Ourselin, S.; J West, S.; E Desjardins, A. Handheld real-time LED-based photoacoustic and ultrasound imaging system for accurate visualization of clinical metal needles and superficial vasculature to guide minimally invasive procedures. Sensors 2018, 18, 1394. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, G.; Yuan, J.; Jo, J.; Gandikota, G.; Demirci, H.; Agano, T.; Sato, N.; Shigeta, Y.; Wang, X. Light Emitting Diodes based Photoacoustic Imaging and Potential Clinical Applications. Sci. Rep. 2018, 8, 9885. [Google Scholar] [CrossRef]
- Jo, J.; Xu, G.; Cao, M.; Marquardt, A.; Francis, S.; Gandikota, G.; Wang, X. A Functional Study of Human Inflammatory Arthritis Using Photoacoustic Imaging. Sci. Rep. 2017, 7, 15026. [Google Scholar] [CrossRef]
- Hariri, A.; Lemaster, J.; Wang, J.; Jeevarathinam, A.S.; Chao, D.L.; Jokerst, J.V. The characterization of an economic and portable LED-based photoacoustic imaging system to facilitate molecular imaging. Photoacoustics 2018, 9, 10–20. [Google Scholar] [CrossRef]
- Joseph Francis, K.; Boink, Y.E.; Dantuma, M.; Ajith Singh, M.K.; Manohar, S.; Steenbergen, W. Tomographic imaging with an ultrasound and LED-based photoacoustic system. Biomed. Opt. Express 2020, 11, 2152–2165. [Google Scholar] [CrossRef]
- Toshitaka Agano, M.K.A.S.; Nagaoka, R.; Awazu, K. Effect of light pulse width on frequency characteristics of photoacoustic signal—An experimental study using a pulse-width tunable LED-based photoacoustic imaging system. Int. J. Eng. Technol. 2018, 7, 4300–4303. [Google Scholar]
- Jaeger, M.; Schüpbach, S.; Gertsch, A.; Kitz, M.; Frenz, M. Fourier reconstruction in optoacoustic imaging using truncated regularized inversek-space interpolation. Inverse Probl. 2007, 23, S51–S63. [Google Scholar] [CrossRef]
- Driver, I.; Feather, J.W.; King, P.R.; Dawson, J.B. The optical properties of aqueous suspensions of Intralipid, a fat emulsion. Phys. Med. Biol. 1989, 34, 1927. [Google Scholar] [CrossRef]
- Pogue, B.W.; Patterson, M.S. Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry. J. Biomed. Opt. 2006, 11, 041102. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen-van Zaane, F.; Gamm, U.A.; van Driel, P.B.A.A.; Snoeks, T.J.A.; de Bruijn, H.S.; van der Ploeg-van den Heuvel, A.; Mol, I.M.; Löwik, C.W.G.M.; Sterenborg, H.J.C.M.; Amelink, A.; et al. In vivo quantification of the scattering properties of tissue using multi-diameter single fiber reflectance spectroscopy. Biomed. Opt. Express 2013, 4, 696–708. [Google Scholar] [CrossRef] [PubMed]
- Elena Vladimirovna, S.; Brian, J.; John, N.; Anna, N.Y. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 1–9. [Google Scholar]
- Vogt, W.C.; Jia, C.; Wear, K.A.; Garra, B.S.; Joshua Pfefer, T. Biologically relevant photoacoustic imaging phantoms with tunable optical and acoustic properties. J. Biomed. Opt. 2016, 21, 101405. [Google Scholar] [CrossRef]
- Bohndiek, S.E.; Bodapati, S.; Van De Sompel, D.; Kothapalli, S.R.; Gambhir, S.S. Development and Application of Stable Phantoms for the Evaluation of Photoacoustic Imaging Instruments. PLoS ONE 2013, 8, e75533. [Google Scholar] [CrossRef]
- Nguyen, H.N.Y.; Steenbergen, W. Three-dimensional view of out-of-plane artifacts in photoacoustic imaging using a laser-integrated linear-transducer-array probe. Photoacoustics 2020, 19, 100176. [Google Scholar] [CrossRef]
- Sumit, A.; Mithun Kuniyil Ajith, S.; Xinyi, Y.; Hussain, A.; Ajay, D.; Sri-Rajasekhar, K. Photoacoustic imaging capabilities of light emitting diodes (LED) and laser sources: A comparison study. In Proceedings of the SPIE 11240, Photons Plus Ultrasound: Imaging and Sensing 2020, San Francisco, CA, USA, 17 February 2020. [Google Scholar]
- Kuniyil Ajith Singh, M.; Sato, N.; Ichihashi, F.; Sankai, Y. Clinical Translation of Photoacoustic Imaging—Opportunities and Challenges from an Industry Perspective. In LED-Based Photoacoustic Imaging: From Bench to Bedside; Kuniyil Ajith Singh, M., Ed.; Springer: Singapore, 2020; pp. 379–393. [Google Scholar] [CrossRef]
- Miri Rostami, S.R.; Mozaffarzadeh, M.; Ghaffari-Miab, M.; Hariri, A.; Jokerst, J. GPU-accelerated Double-stage Delay-multiply-and-sum Algorithm for Fast Photoacoustic Tomography Using LED Excitation and Linear Arrays. Ultrason. Imaging 2019, 41, 301–316. [Google Scholar] [CrossRef] [PubMed]
- Farnia, P.; Najafzadeh, E.; Hariri, A.; Lavasani, S.N.; Makkiabadi, B.; Ahmadian, A.; Jokerst, J.V. Dictionary learning technique enhances signal in LED-based photoacoustic imaging. Biomed. Opt. Express 2020, 11, 2533–2547. [Google Scholar] [CrossRef]
- Alijabbari, N.; Alshahrani, S.S.; Pattyn, A.; Mehrmohammadi, M. Photoacoustic Tomography with a Ring Ultrasound Transducer: A Comparison of Different Illumination Strategies. Appl. Sci. 2019, 9, 94. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Yang, G.; Zhu, Q. Fiber endface illumination diffuser for endo-cavity photoacoustic imaging. Opt. Lett. 2020, 45, 632–635. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuriakose, M.; Nguyen, C.D.; Kuniyil Ajith Singh, M.; Mallidi, S. Optimizing Irradiation Geometry in LED-Based Photoacoustic Imaging with 3D Printed Flexible and Modular Light Delivery System. Sensors 2020, 20, 3789. https://doi.org/10.3390/s20133789
Kuriakose M, Nguyen CD, Kuniyil Ajith Singh M, Mallidi S. Optimizing Irradiation Geometry in LED-Based Photoacoustic Imaging with 3D Printed Flexible and Modular Light Delivery System. Sensors. 2020; 20(13):3789. https://doi.org/10.3390/s20133789
Chicago/Turabian StyleKuriakose, Maju, Christopher D. Nguyen, Mithun Kuniyil Ajith Singh, and Srivalleesha Mallidi. 2020. "Optimizing Irradiation Geometry in LED-Based Photoacoustic Imaging with 3D Printed Flexible and Modular Light Delivery System" Sensors 20, no. 13: 3789. https://doi.org/10.3390/s20133789
APA StyleKuriakose, M., Nguyen, C. D., Kuniyil Ajith Singh, M., & Mallidi, S. (2020). Optimizing Irradiation Geometry in LED-Based Photoacoustic Imaging with 3D Printed Flexible and Modular Light Delivery System. Sensors, 20(13), 3789. https://doi.org/10.3390/s20133789






