RNN-Aided Human Velocity Estimation from a Single IMU †
Abstract
1. Introduction
2. Related Work
3. Method
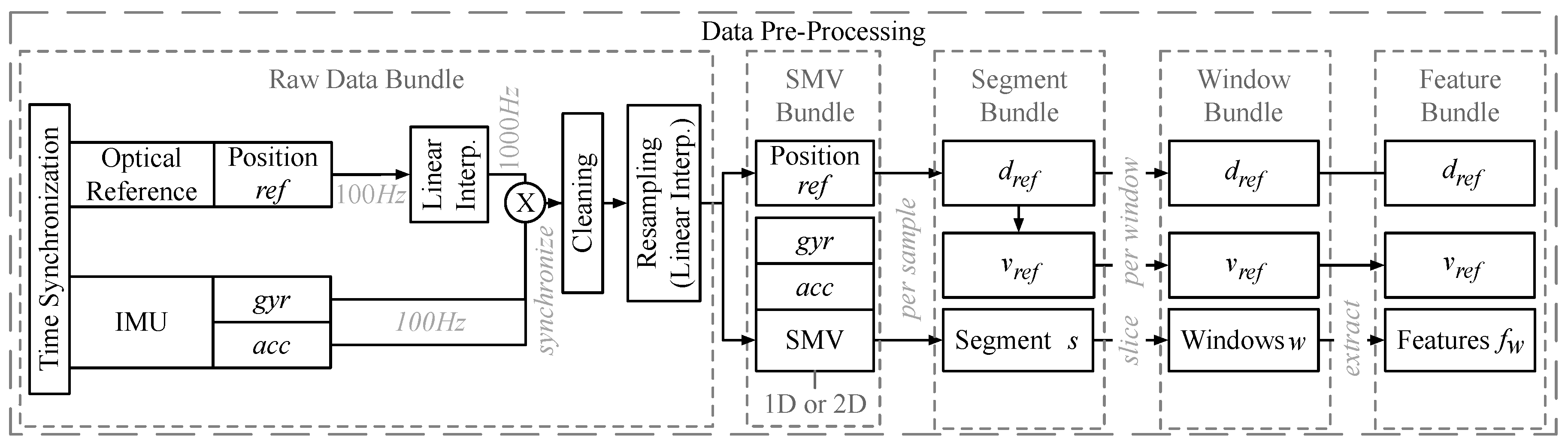
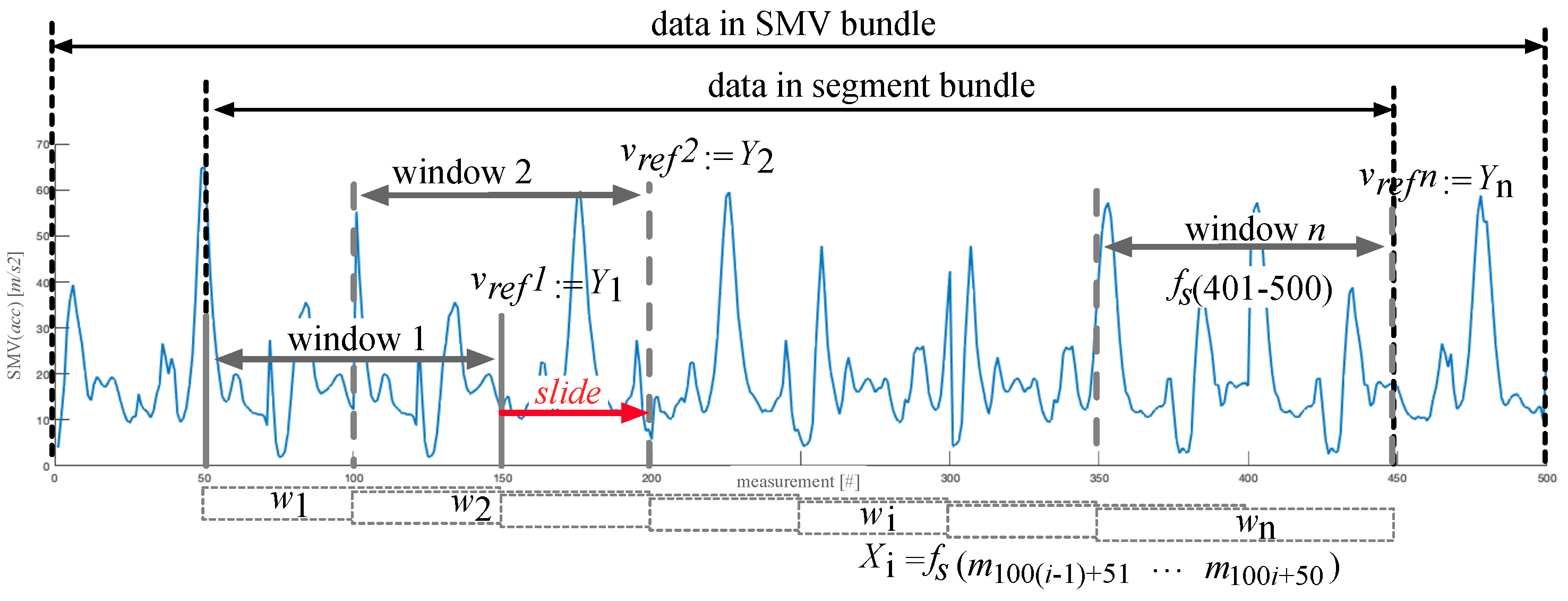
3.1. Data Pre-Processing
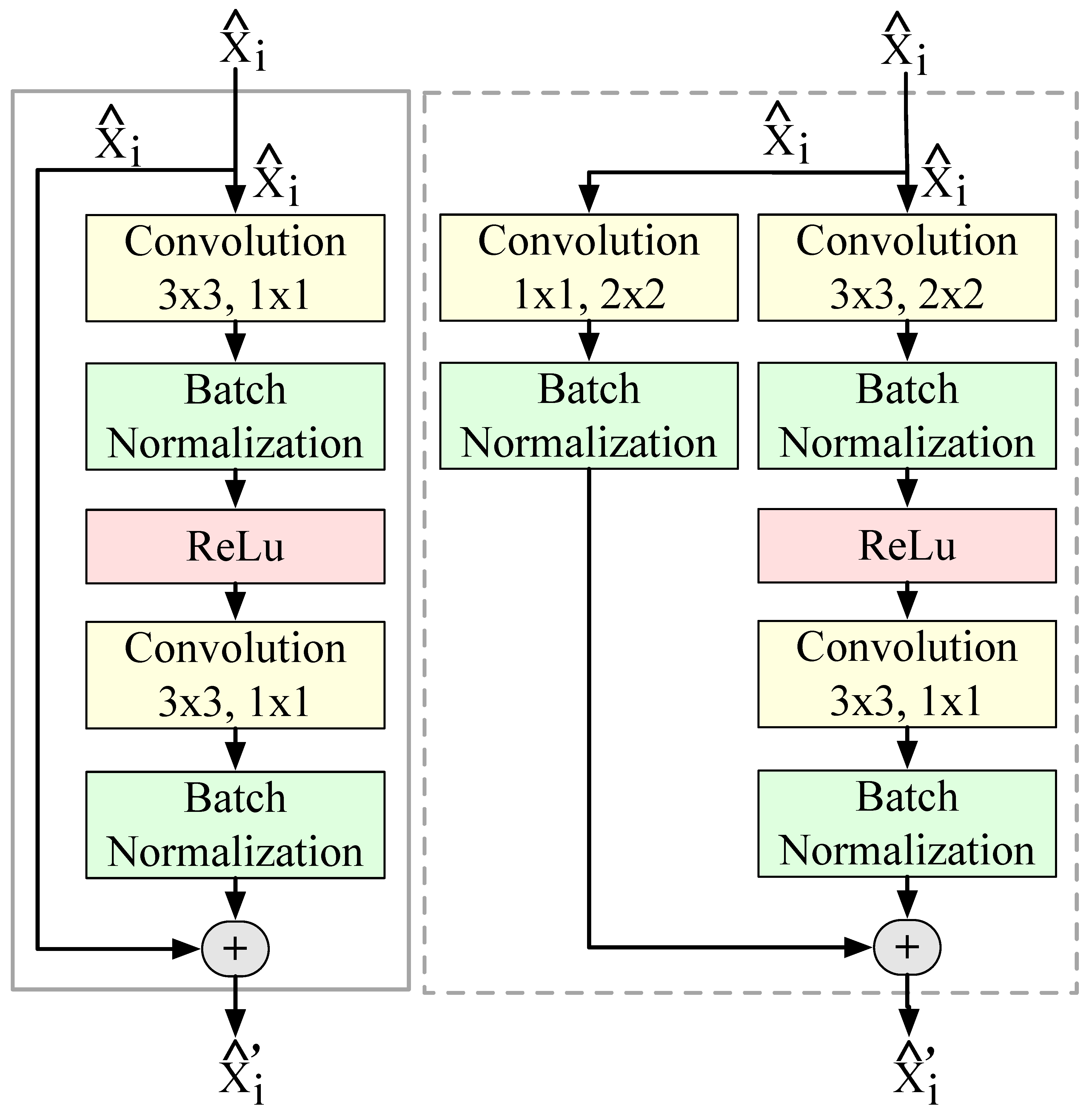
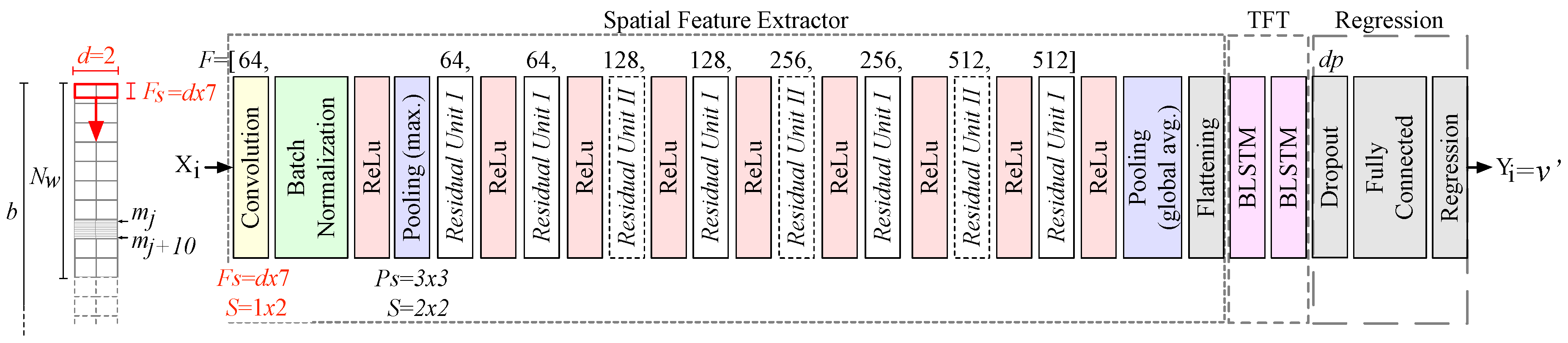
3.2. Main Processing
3.3. Post-Processing
4. Experimental Setup
4.1. Hard- and Software Components
4.2. Data Acquisition and Datasets
4.3. Parameterization of Velocity Estimators
5. Benchmark Results
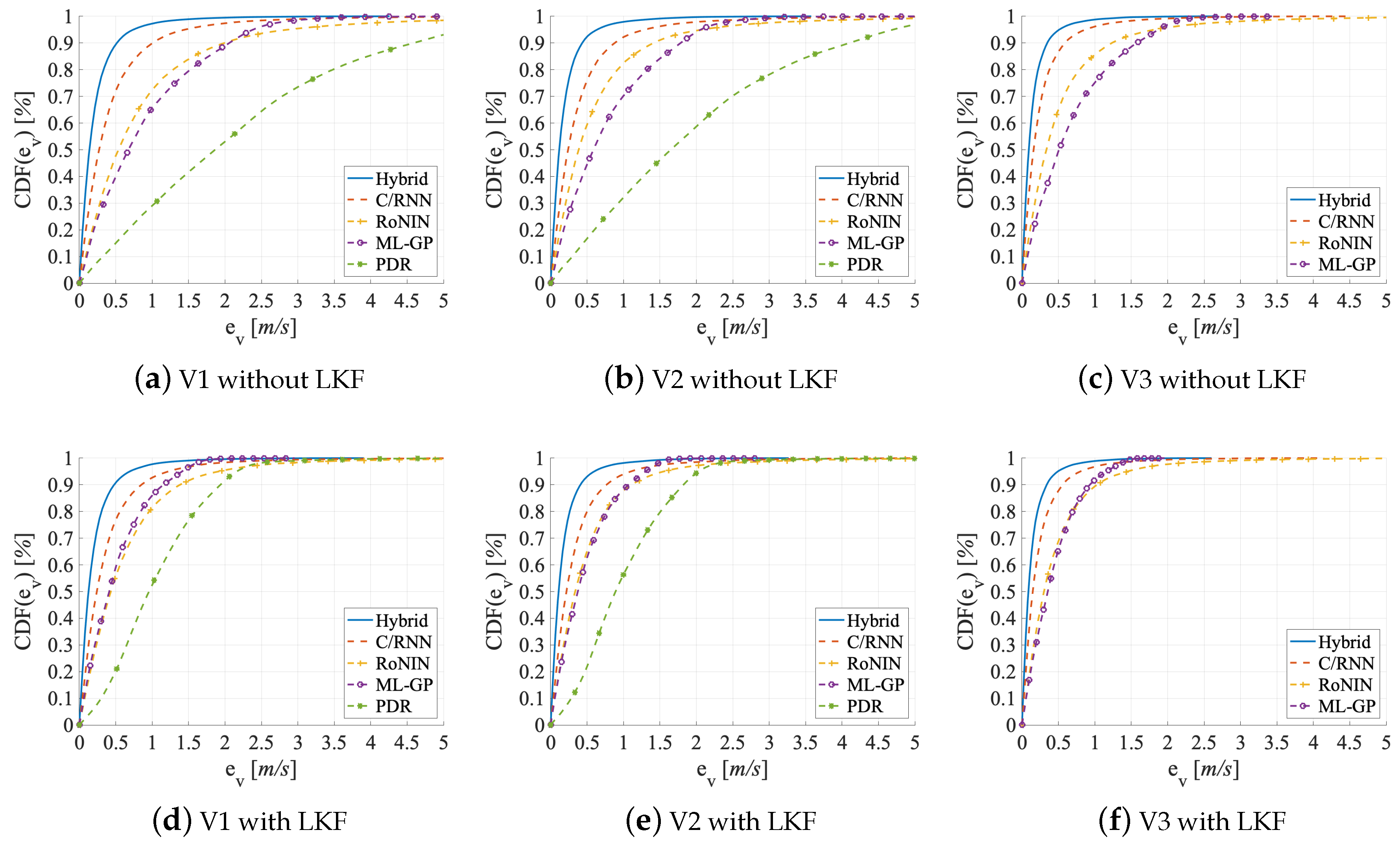
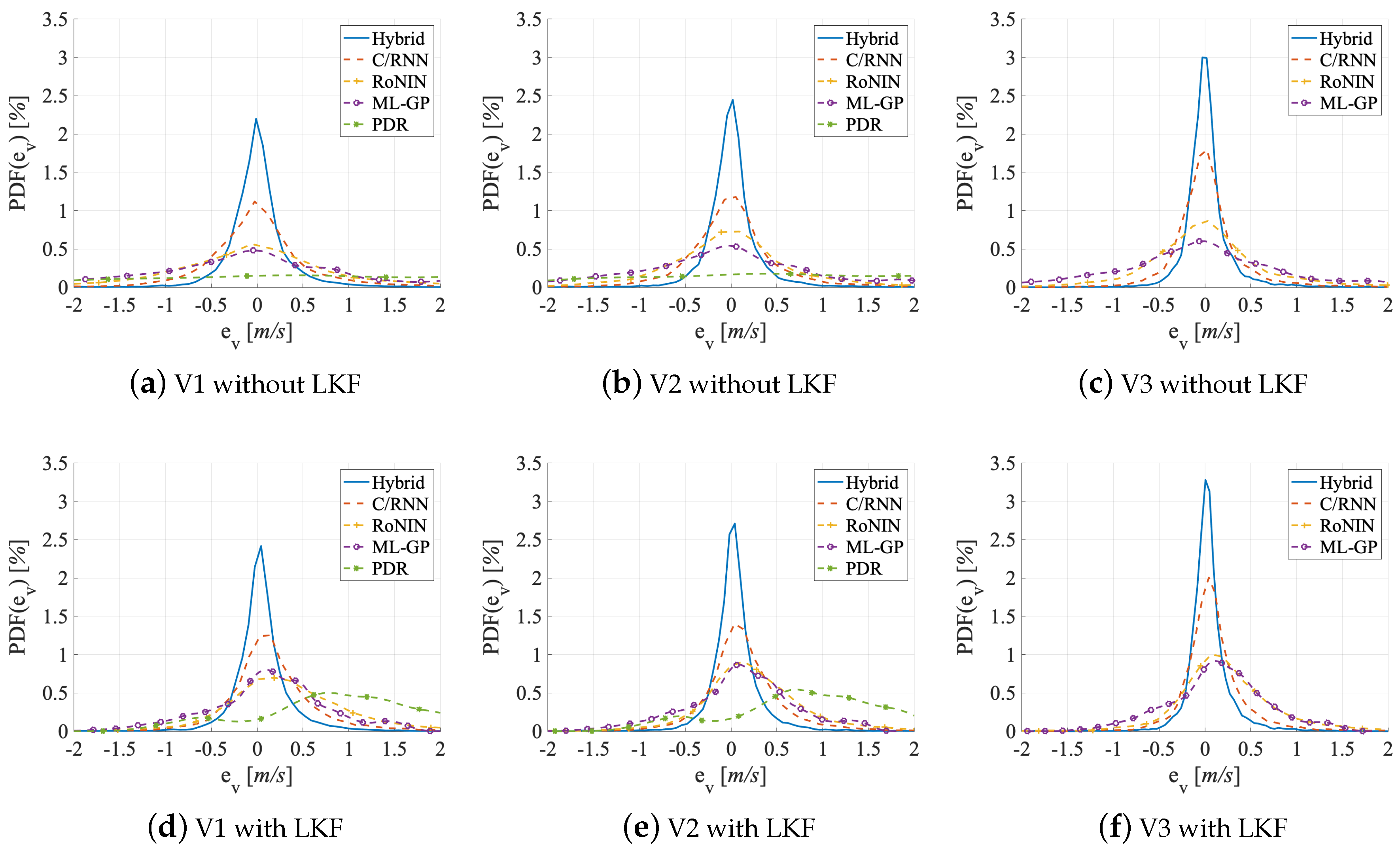
5.1. Accuracy
5.2. Computational Effort
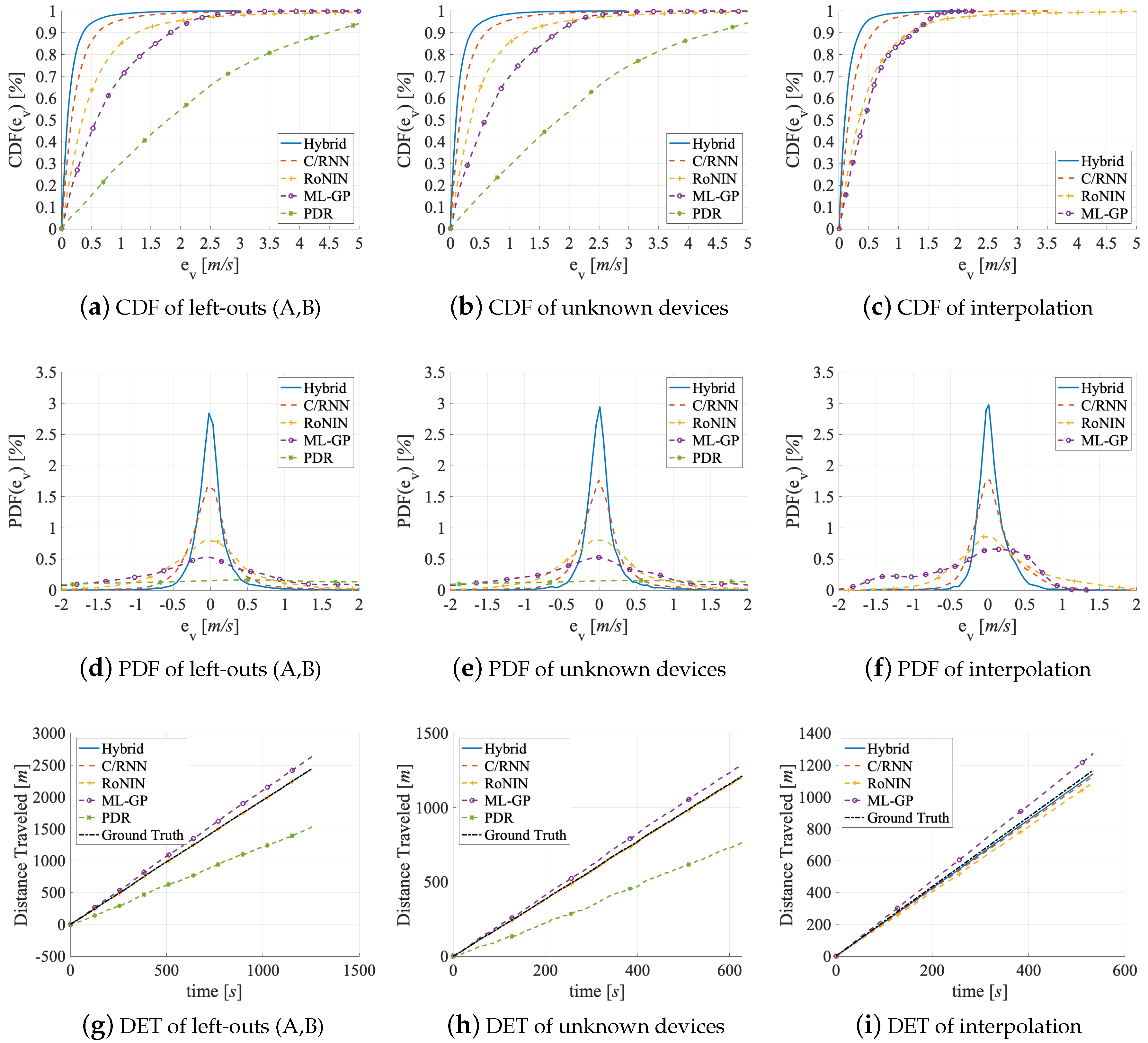
5.3. Generalizability
5.4. Effects of Windows Size
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Parameterization of Velocity Estimators
Appendix A.1. Feature Set of Baseline II, ML with Gaussian Processes ML-GP
Appendix A.2. Grid search results of Baseline II, ML with Gaussian Processes ML-GP
Appendix A.3. Grid search results of Baseline III, DL I, RoNIN
Appendix A.4. Grid search results of Baseline IV, DL II, C/RNN
Appendix A.5. Grid search results of our novel approach, DL III, Hybrid
References
- Edel, M.; Köppe, E. An advanced method for pedestrian dead reckoning using BLSTM-RNNs. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 293–304. [Google Scholar]
- Windau, J.; Itti, L. Walking compass with head-mounted IMU sensor. In Proceedings of the Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 542–549. [Google Scholar]
- Feigl, T.; Mutschler, C.; Philippsen, M. Supervised Learning for Yaw Orientation Estimation. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 87–95. [Google Scholar]
- Zhao, H.; Cheng, W.; Yang, N.; Qiu, S.; Wang, Z.; Wang, J. Smartphone-based 3D indoor pedestrian positioning through multi-modal data fusion. Sens. J. 2019, 19, 4554. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J.L.; Weston, J. Strapdown Inertial Navigation Technology; Institution of Engineering and Technology (IET): London, UK, 2004. [Google Scholar]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. Guid. Control. Dyn. J. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Díez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step Length Estimation Methods Based on Inertial Sensors: A Review. Sens. J. 2018, 18, 908–926. [Google Scholar] [CrossRef]
- Wagstaff, B.; Kelly, J. LSTM-Based Zero-Velocity Detection for Robust Inertial Navigation. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 22–30. [Google Scholar]
- Lymberopoulos, D.; Liu, J.; Yang, X.; Choudhury, R.R.; Handziski, V.; Sen, S. A Realistic Evaluation and Comparison of Indoor Location Technologies: Experiences and Lessons Learned. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 178–189. [Google Scholar]
- Bravo, J.; Herrera, E.P.; Sierra, D.A. Comparison of step length and heading estimation methods for indoor environments. In Proceedings of the IEEE XXIV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Bern, Switzerland, 17–19 November 2017; pp. 12–19. [Google Scholar]
- Wang, Y.; Chernyshoff, A.; Shkel, A.M. Error Analysis of ZUPT-Aided Pedestrian Inertial Navigation. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 206–212. [Google Scholar]
- Lee, J.H.; Ju, H.; Park, C.G. Error Analysis of PDR System Using Dual Foot-mounted IMU. Sens. J. 2019, 94, 41–56. [Google Scholar] [CrossRef]
- Combettes, C.; Renaudin, V. Comparison of misalignment estimation techniques between handheld device and walking directions. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 293–304. [Google Scholar]
- Deng, Z.A.; Wang, G.; Hu, Y.; Wu, D. Heading estimation for indoor pedestrian navigation using a smartphone in the pocket. Sens. J. 2015, 15, 21518–21536. [Google Scholar] [CrossRef]
- Jahn, J.; Batzer, U.; Seitz, J.; Patino-Studencka, L.; Boronat, J.G. Comparison and evaluation of acceleration based step length estimators for handheld devices. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Zurich, Switzerland, 15–17 September 2010; pp. 11–16. [Google Scholar]
- Ho, N.H.; Truong, P.H.; Jeong, G.M. Step-detection and adaptive step-length estimation for pedestrian dead-reckoning at various walking speeds using a smartphone. Sens. J. 2016, 16, 1423. [Google Scholar] [CrossRef]
- Pepa, L.; Marangoni, G.; Di Nicola, M.; Ciabattoni, L.; Verdini, F.; Spalazzi, L.; Longhi, S. Real time step length estimation on smartphone. In Proceedings of the Consumer Electronics (ICCE), Bombay, India, 17–20 November 2016; pp. 315–316. [Google Scholar]
- Jiang, Y.; Li, Z.; Wang, J. Ptrack: Enhancing the applicability of pedestrian tracking with wearables. Trans. Mobile Comput. 2018, 18, 431–443. [Google Scholar] [CrossRef]
- Ladetto, Q. On foot navigation: Continuous step calibration using both complementary recursive prediction and adaptive Kalman filtering. In Proceedings of the Institute of Navigation GPS (ION), Salt Lake City, UT, USA, 19–22 September 2000; pp. 1735–1740. [Google Scholar]
- Weinberg, H. Using the ADXL202 in pedometer and personal navigation applications. In Analog Devices AN-602 Application Note; Analog Devices, Inc.: Norwood, MA, USA, 2002. [Google Scholar]
- Kim, J.W.; Jang, H.J.; Hwang, D.H.; Park, C. A step, stride and heading determination for the pedestrian navigation system. Glob. Position. Syst. J. 2004, 3, 273–279. [Google Scholar] [CrossRef]
- Allseits, E.; Agrawal, V.; Lučarević, J.; Gailey, R.; Gaunaurd, I.; Bennett, C. A practical step length algorithm using lower limb angular velocities. Biomech. J. 2018, 66, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.H.; Park, C.G. Adaptive step length estimation algorithm using optimal parameters and movement status awareness. Med. Eng. Phys. 2011, 33, 1064–1071. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Barth, J.; Schülein, S.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Mobile stride length estimation with deep convolutional neural networks. Biomed. Health Inf. J. 2017, 22, 354–362. [Google Scholar] [CrossRef]
- Xing, H.; Li, J.; Hou, B.; Zhang, Y.; Guo, M. Pedestrian stride length estimation from IMU measurements and ANN based algorithm. Sens. J. 2017, 2017, 6091261. [Google Scholar] [CrossRef]
- Wang, Q.; Ye, L.; Luo, H.; Men, A.; Zhao, F.; Huang, Y. Pedestrian Stride-Length Estimation Based on LSTM and Denoising Autoencoders. Sens. J. 2019, 19, 840. [Google Scholar] [CrossRef]
- Do, T.N.; Liu, R.; Yuen, C.; Tan, U. Personal dead reckoning using IMU device at upper torso for walking and running. In Proceedings of the IEEE Sensors, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. arXiv 2019, arXiv:eess.SP/1905.03554v1. [Google Scholar]
- Yan, H.; Herath, S.; Furukawa, Y. RoNIN: Robust Neural Inertial Navigation in the Wild: Benchmark, Evaluations, and New Methods. arXiv 2019, arXiv:cs.CV/1905.12853. [Google Scholar]
- Chen, C.; Lu, X.; Markham, A.; Trigoni, A. IONet: Learning to Cure the Curse of Drift in Inertial Odometry. In Proceedings of the Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018; pp. 12–17. [Google Scholar]
- Hang, Y.; Qi, S.; Yasutaka, F. RIDI: Robust IMU Double Integration. In Proceedings of the Computer Vision, Munich, Germany, 8–14 September 2018; pp. 111–119. [Google Scholar]
- Feigl, T.; Kram, S.; Woller, P.; Siddiqui, R.H.; Philippsen, M.; Mutschler, C. A Bidirectional LSTM for Estimating Dynamic Human Velocities from a Single IMU. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar]
- Seitz, J.; Patino-Studencki, L.; Schindler, B.; Haimerl, S.; Gutierrez, J.; Meyer, S.; Thielecke, J. Sensor Data Fusion for Pedestrian Navigation Using WLAN and INS. Available online: https://www.iis.fraunhofer.de/content/dam/iis/en/doc/lv/los/lokalisierung/SensorDataFusionforPedestrian.pdf (accessed on 25 June 2020).
- Gentner, C.; Ulmschneider, M. Simultaneous localization and mapping for pedestrians using low-cost ultra-wideband system and gyroscope. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 293–304. [Google Scholar]
- Wu, Y.; Zhu, H.B.; Du, Q.X.; Tang, S.M. A Survey of the Research Status of Pedestrian Dead Reckoning Systems Based on Inertial Sensors. Autom. Comput. J. 2018, 16, 1–19. [Google Scholar] [CrossRef]
- Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; De Vroey, H.; Claeys, K. Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sens. J. 2020, 20, 673. [Google Scholar] [CrossRef]
- Wang, J.S.; Lin, C.W.; Yang, Y.T.C.; Ho, Y.J. Walking pattern classification and walking distance estimation algorithms using gait phase information. Trans. Biomed. Eng. 2012, 59, 2884–2892. [Google Scholar] [CrossRef] [PubMed]
- Parate, A.; Chiu, M.C.; Chadowitz, C.; Ganesan, D.; Kalogerakis, E. Risq: Recognizing smoking gestures with inertial sensors on a wristband. In Proceedings of the Mobile Systems, Applications, and Services (MobiSys), Bretton Woods, NH, USA, 16–19 June 2014; pp. 149–161. [Google Scholar]
- Mannini, A.; Sabatini, A.M. Walking speed estimation using foot-mounted inertial sensors: Comparing machine learning and strap-down integration methods. Med Eng. Phys. J. 2014, 36, 1312–1321. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sens. J. 2010, 10, 1154–1175. [Google Scholar] [CrossRef] [PubMed]
- Valtazanos, A.; Arvind, D.; Ramamoorthy, S. Using wearable inertial sensors for posture and position tracking in unconstrained environments through learned translation manifolds. In Proceedings of the Information Processing in Sensor Networks (IPSN), Philadelphia, PA, USA, 8–11 April 2013; pp. 241–252. [Google Scholar]
- Yuwono, M.; Su, S.W.; Guo, Y.; Moulton, B.D.; Nguyen, H.T. Unsupervised nonparametric method for gait analysis using a waist-worn inertial sensor. Appl. Soft Comput. J. 2014, 14, 72–80. [Google Scholar] [CrossRef]
- Xiao, X.; Zarar, S. Machine learning for placement-insensitive inertial motion capture. In Proceedings of the Robotics and Automation (ICRA), Brisbane, Australia, 20–25 May 2018; pp. 716–721. [Google Scholar]
- Chang, M.B.; Ullman, T.; Torralba, A.; Tenenbaum, J.B. A compositional object-based approach to learning physical dynamics. arXiv 2016, arXiv:cs.AI/1612.00341v2. [Google Scholar]
- Karl, M.; Soelch, M.; Bayer, J.; Van der Smagt, P. Deep variational bayes filters: Unsupervised learning of state space models from raw data. arXiv 2016, arXiv:cs.AI/1612.00341v2. [Google Scholar]
- Stewart, R.; Ermon, S. Label-free supervision of neural networks with physics and domain knowledge. In Proceedings of the Artificial Intelligence (AAAI), San Francisco, CA, USA, 4–9 February 2017; pp. 187–196. [Google Scholar]
- Norrdine, A.; Kasmi, Z.; Blankenbach, J. Step detection for ZUPT-aided inertial pedestrian navigation system using foot-mounted permanent magnet. Sens. J. 2016, 16, 766–773. [Google Scholar] [CrossRef]
- Nilsson, J.O.; Skog, I.; Händel, P.; Hari, K.V.S. Foot-mounted INS for everybody-an open-source embedded implementation. In Proceedings of the Position, Location and Navigation Symposium (ION), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 140–145. [Google Scholar]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Rantanen, J.; Mäkelä, M.; Ruotsalainen, L.; Kirkko-Jaakkola, M. Motion Context Adaptive Fusion of Inertial and Visual Pedestrian Navigation. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 206–212. [Google Scholar]
- Konda, K.R.; Memisevic, R. Learning visual odometry with a convolutional network. In Proceedings of the Computer Vision Theory and Applications (VISAPP), Berlin, Germany, 11–14 March 2015; pp. 486–490. [Google Scholar]
- Carrera, J.L.; Zhao, Z.; Braun, T.; Li, Z. A real-time indoor tracking system by fusing inertial sensor, radio signal and floor plan. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Barcelona, Spain, 4–7 October 2016; pp. 1–9. [Google Scholar]
- Hooman, J.; Roever, W.; Pandya, P.; Xu, Q.; Zhou, P.; Schepers, H. A Compositional Object-Based Approah to Learning Physical Dynamics. In Proceedings of the Learning Representations (ICLR), Toulon, France, 24–26 April 2017; pp. 155–173. [Google Scholar]
- Sabatini, A.M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef]
- Renaudin, V.; Ortiz, M.; Le Scornec, J. Foot-mounted pedestrian navigation reference with tightly coupled GNSS carrier phases, inertial and magnetic data. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 14–19. [Google Scholar]
- Hellmers, H.; Eichhorn, A.; Norrdine, A.; Blankenbach, J. IMU/magnetometer based 3D indoor positioning for wheeled platforms in NLoS scenarios. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Barcelona, Spain, 4–7 October 2016; pp. 1–7. [Google Scholar]
- Nguyen-Huu, K.; Lee, K.; Lee, S. An indoor positioning system using pedestrian dead reckoning with WiFi and map-matching aided. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 623–631. [Google Scholar]
- Gu, F.; Khoshelham, K.; Yu, C.; Shang, J. Accurate Step Length Estimation for Pedestrian Dead Reckoning Localization Using Stacked Autoencoders. Trans. Instrum. Meas. 2018, 2, 1–9. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, P.; Lu, X.; Wang, W.; Markham, A.; Trigoni, N. OxIOD: The Dataset for Deep Inertial Odometry. Comput. Res. Repos. 2018, 13, 1281–1293. [Google Scholar]
- Wahlström, J.; Skog, I.; Gustafsson, F.; Markham, A.; Trigoni, N. Zero-Velocity Detection—A Bayesian Approach to Adaptive Thresholding. Sens. J. 2019, 27, 206–212. [Google Scholar] [CrossRef]
- Cho, S.Y.; Park, C.G. MEMS based pedestrian navigation system. Navig. J. 2006, 59, 135–153. [Google Scholar] [CrossRef]
- Martinelli, A.; Gao, H.; Groves, P.D.; Morosi, S. Probabilistic context-aware step length estimation for pedestrian dead reckoning. Sens. J. 2017, 18, 1600–1611. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, S.; Chen, Y.; Zhang, B.; Feng, Z.; Zhou, H.; Bo, Y. A MEMS IMU De-Noising Method Using Long Short Term Memory Recurrent Neural Networks (LSTM-RNN). Sens. J. 2018, 1, 3470. [Google Scholar] [CrossRef]
- Feigl, T.; Nowak, T.; Philippsen, M.; Edelhäußer, T.; Mutschler, C. Recurrent Neural Networks on Drifting Time-of-Flight Measurements. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 112–120. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Chen, C.; Lu, X.; Wahlstrom, J.; Markham, A.; Trigoni, N. Deep Neural Network Based Inertial Odometry Using Low-cost Inertial Measurement Units. Trans. Mob. Comput. (TMC) 2019, 57, 140–149. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A novel deeper one-dimensional CNN with residual learning for fault diagnosis of wheelset bearings in high-speed trains. Access J. 2018, 7, 1022–1029. [Google Scholar] [CrossRef]
- Shao, W.; Luo, H.; Zhao, F.; Wang, C.; Crivello, A.; Tunio, M.Z. DePedo: Anti Periodic Negative-Step Movement Pedometer with Deep Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 395–401. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:cs.CV/1605.07146v4. [Google Scholar]
- Bianco, S.; Cadene, R.; Celona, L.; Napoletano, P. Benchmark analysis of representative deep neural network architectures. Access J. 2018, 6, 64270–64277. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A Convolutional Neural Network for Modelling Sentences. In Proceedings of the Association for Computational Linguistics, Baltimore, MD, USA, 22–27 June 2014; pp. 655–664. [Google Scholar]
- Li, L.; Wu, Z.; Xu, M.; Meng, H.; Cai, L. Combining CNN and BLSTM to Extract Textual and Acoustic Features for Recognizing Stances in Mandarin Ideological Debate Competition. In Proceedings of the Speech Communication Association (INTERSPEECH), San Francisco, CA, USA, 8–12 September 2016; pp. 1392–1396. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Basic Eng. J. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Ivanov, P.; Raitoharju, M.; Piché, R. Kalman-type filters and smoothers for pedestrian dead reckoning. In Proceedings of the Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 206–212. [Google Scholar]
- Niitsoo, A.; Edelhäußer, T.; Eberlein, E.; Hadaschik, N.; Mutschler, C. A Deep Learning Approach to Position Estimation from Channel Impulse Responses. Sens. J. 2019, 19, 1064. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. Artif. Intell. Res. J. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Weiss, G.; Provost, F. The Effect of Class Distribution on Classifier Learning: An Empirical Study; Technical Report 1; AT&T Labs: New York, NY, USA, 2001. [Google Scholar]
- Tian, Q.; Salcic, Z.; Kevin, I.; Wang, K.; Pan, Y. A multi-mode dead reckoning system for pedestrian tracking using smartphones. Sens. J. 2015, 16, 2079–2093. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin, Germany, 2006. [Google Scholar]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the Science and Information Conference (SAI), London, UK, 27–29 August 2014; pp. 372–378. [Google Scholar]
- Vathsangam, H.; Emken, A.; Spruijt-Metz, D.; Sukhatme, G.S. Toward free-living walking speed estimation using Gaussian Process-based Regression with on-body accelerometers and gyroscopes. In Proceedings of the 2010 4th International Conference on Pervasive Computing Technologies for Healthcare, Munich, Germany, 22–25 March 2010; pp. 22–31. [Google Scholar]
- Rasmussen, C.E.; Williams, E.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Liu, H.; Ong, Y.S.; Shen, X.; Cai, J. When Gaussian process meets big data: A review of scalable GPs. Trans. Neural Netw. Learn. Syst. 2020, 53, 1346–1356. [Google Scholar] [CrossRef]
- Hippe, P. Windup in Control: Its Effects and Their Prevention; Springer Science+Business Media: London, UK, 2006; pp. 1–314. [Google Scholar]
- Brownlee, J. Long Short-Term Memory Networks with Python: Develop Sequence Prediction Models with Deep Learning; Jason Brownlee: Vermont Victoria, Autrilia, 2017. [Google Scholar]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. Comput. Graph. Stat. J. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Startsev, M.; Agtzidis, I.; Dorr, M. 1D CNN with BLSTM for automated classification of fixations, saccades, and smooth pursuits. Behav. Res. Meth. J. 2019, 51, 556–572. [Google Scholar] [CrossRef] [PubMed]


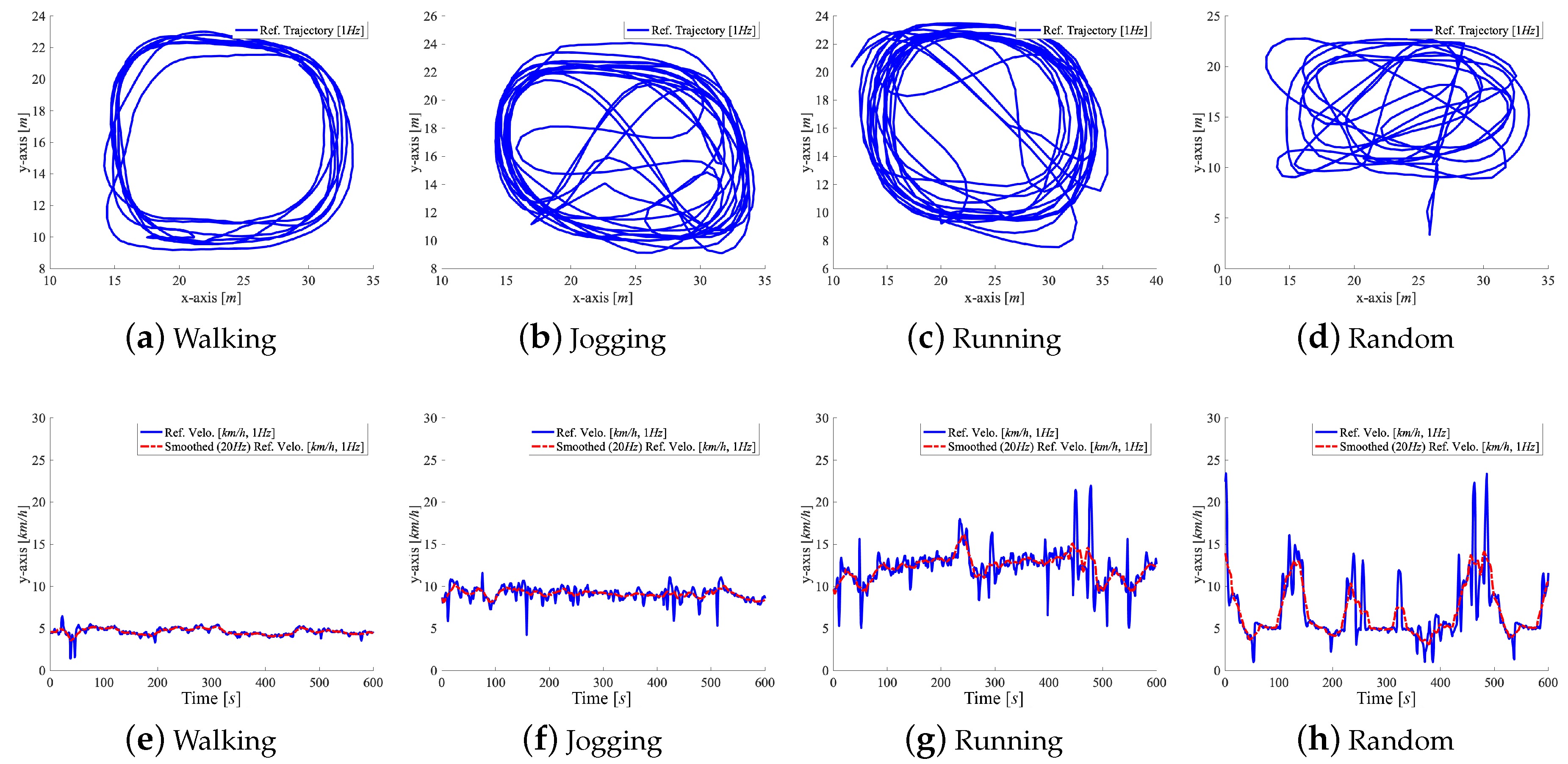


| Name | Num. of Users [#] | Total [#] | Training [#] | Validation [#] | Testing [#] | Duration | Distance | [m/s] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Segm. | Wind./Feat. | Segm. | Wind./Feat. | Segm. | Wind./Feat. | Segm. | Wind./Feat. | [min] | [km] | avg. | min | max | ||
| Accuracy | ||||||||||||||
| V1 | 20 | 160 | 112.500 | 112 | 78.750 | 16 | 11.250 | 32 | 22.500 | 1.203 | 185.40 | 2.5 | 0.8 | 7.9 |
| V2 | 20 | 160 | 97.950 | 112 | 68.565 | 16 | 9.795 | 32 | 19.590 | 1.045 | 161.42 | 2.6 | 0.8 | 7.8 |
| V3 | 20 | - | 31.200 | - | 21.840 | - | 3.120 | - | 6.240 | 666 | 71.9 | 1.8 | 0.8 | 3.6 |
| Comp. Effort | ||||||||||||||
| V1 | 20 | 160 | 112.500 | 112 | 78.750 | 16 | 11.250 | 32 | 22.500 | 1.203 | 185.40 | 2.5 | 0.8 | 7.9 |
| Generalizability | ||||||||||||||
| Left-outs | 2 | 16 | 9.795 | - | - | - | - | 16 | 9.795 | 105 | 16.14 | 2.5 | 0.7 | 3.7 |
| Unknown Device | 1 | 8 | 4.898 | - | - | - | - | 8 | 4.898 | 52 | 8.07 | 2.6 | 1.3 | 3.5 |
| Interpolation (V3) | 20 | - | 31.200 | - | 24.960 | - | 2.059 | - | 4.181 | 666 | 71.9 | 1.8 | 0.8 | 3.6 |
| Extrapolation (V3) | 20 | - | 31.200 | - | 24.960 | - | 2.059 | - | 4.181 | 666 | 71.9 | 1.8 | 0.8 | 3.6 |
| Dataset | PDR | ML-GP | RoNIN | C/RNN | Hybrid | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| of 20 Subjects | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | |||||
| V1 valid. | 2.01 | 6.31 | 2.51 | 4.88 | 0.348 | 977.00 | 0.82 | 1.17 | 1.08 | 2.16 | 0.077 | 21.05 | 0.84 | 1.94 | 1.39 | 2.76 | 0.011 | 37.21 | 0.44 | 0.52 | 0.72 | 1.44 | 0.018 | 18.71 | 0.23 | 0.14 | 0.37 | 0.72 | 0.022 | 9.46 |
| V1 test | 2.16 | 7.37 | 2.71 | 5.25 | 0.374 | 2103.89 | 0.89 | 1.38 | 1.17 | 2.37 | 0.088 | 136.95 | 0.88 | 2.15 | 1.46 | 2.86 | 0.013 | 460.47 | 0.47 | 0.59 | 0.77 | 1.49 | 0.019 | 130.59 | 0.25 | 0.16 | 0.40 | 0.77 | 0.022 | 15.65 |
| V1 test w. LKF | 1.06 | 1.55 | 1.25 | 2.15 | 0.435 | 1451.61 | 0.51 | 0.44 | 0.66 | 1.41 | 0.065 | 363.80 | 0.64 | 0.93 | 0.97 | 1.91 | 0.178 | 101.70 | 0.38 | 0.39 | 0.62 | 1.22 | 0.055 | 38.53 | 0.22 | 0.13 | 0.36 | 0.70 | 0.001 | 5.32 |
| V2 valid. | 1.84 | 5.38 | 2.32 | 4.51 | 0.337 | 817.31 | 0.71 | 0.90 | 0.95 | 1.91 | 0.064 | 14.89 | 0.61 | 1.04 | 1.02 | 1.98 | 0.004 | 10.90 | 0.40 | 0.43 | 0.66 | 1.27 | 0.022 | 10.69 | 0.20 | 0.11 | 0.33 | 0.63 | 0.024 | 3.19 |
| V2 test | 1.93 | 5.82 | 2.41 | 4.69 | 0.328 | 1806.20 | 0.77 | 1.04 | 1.02 | 2.05 | 0.074 | 76.96 | 0.64 | 1.15 | 1.07 | 2.07 | 0.005 | 206.69 | 0.42 | 0.48 | 0.69 | 1.33 | 0.022 | 66.70 | 0.22 | 0.12 | 0.35 | 0.67 | 0.023 | 8.38 |
| V2 test w. LKF | 0.99 | 1.35 | 1.16 | 2.01 | 0.410 | 1010.47 | 0.47 | 0.37 | 0.61 | 1.30 | 0.054 | 267.01 | 0.51 | 0.64 | 0.80 | 1.56 | 0.127 | 62.35 | 0.34 | 0.33 | 0.57 | 1.11 | 0.043 | 36.98 | 0.19 | 0.10 | 0.32 | 0.61 | 0.004 | 4.93 |
| V3 valid. | - | - | - | - | - | - | 0.63 | 0.70 | 0.83 | 1.76 | 0.036 | 26.77 | 0.50 | 0.71 | 0.84 | 1.65 | 0.030 | 31.81 | 0.25 | 0.17 | 0.41 | 0.77 | 0.005 | 14.95 | 0.15 | 0.06 | 0.24 | 0.44 | 0.013 | 8.62 |
| V3 test | - | - | - | - | - | - | 0.67 | 0.78 | 0.88 | 1.87 | 0.047 | 39.84 | 0.55 | 0.85 | 0.92 | 1.80 | 0.042 | 145.08 | 0.28 | 0.21 | 0.46 | 0.89 | 0.010 | 21.50 | 0.17 | 0.07 | 0.27 | 0.53 | 0.016 | 12.66 |
| V3 test w. LKF | - | - | - | - | - | - | 0.43 | 0.30 | 0.55 | 1.16 | 0.076 | 113.82 | 0.47 | 0.52 | 0.72 | 1.45 | 0.135 | 22.52 | 0.24 | 0.17 | 0.41 | 0.80 | 0.026 | 14.80 | 0.16 | 0.07 | 0.26 | 0.50 | 0.003 | 3.75 |
| Method | [h] | [s] | [Hz] | |||
|---|---|---|---|---|---|---|
| CPU | GPU | CPU | GPU | CPU | GPU | |
| PDR | 0.2 | - | 0.00073 | - | 1370 | - |
| ML-GP | 23.6 | - | 0.00203 | - | 493 | - |
| RoNIN | 11.2 | 8.1 | 0.01041 | 0.0147 | 96 | 68 |
| C/RNN | 6.9 | 4.9 | 0.00610 | 0.0069 | 164 | 145 |
| Hybrid | 15.6 | 10.5 | 0.01785 | 0.0277 | 56 | 36 |
| Dataset | PDR | ML-GP | RoNIN | C/RNN | Hybrid | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | ||||||
| Left-out A | 2.10 | 6.94 | 2.63 | 5.09 | 0.376 | 460.19 | 0.76 | 1.03 | 1.01 | 2.09 | 0.082 | 99.75 | 0.57 | 0.90 | 0.95 | 1.82 | 0.035 | 3.97 | 0.29 | 0.23 | 0.48 | 0.91 | 0.027 | 2.00 | 0.18 | 0.08 | 0.29 | 0.55 | 0.026 | 1.26 |
| Left-out B | 2.06 | 6.64 | 2.58 | 5.03 | 0.362 | 442.94 | 0.78 | 1.07 | 1.03 | 2.10 | 0.071 | 86.58 | 0.57 | 0.90 | 0.95 | 1.85 | 0.061 | 6.87 | 0.30 | 0.23 | 0.48 | 0.91 | 0.022 | 3.38 | 0.18 | 0.08 | 0.29 | 0.54 | 0.023 | 2.07 |
| Left-outs A+B | 2.10 | 6.95 | 2.64 | 5.08 | 0.374 | 914.55 | 0.78 | 1.08 | 1.04 | 2.14 | 0.077 | 188.13 | 0.58 | 0.92 | 0.96 | 1.85 | 0.029 | 4.43 | 0.30 | 0.23 | 0.48 | 0.93 | 0.024 | 2.33 | 0.19 | 0.09 | 0.29 | 0.56 | 0.024 | 1.54 |
| Unknown devices | 2.32 | 7.21 | 2.89 | 5.43 | 0.516 | 506.44 | 0.83 | 1.21 | 1.16 | 2.38 | 0.077 | 101.42 | 0.73 | 0.98 | 1.06 | 2.12 | 0.093 | 12.44 | 0.32 | 0.35 | 0.52 | 1.02 | 0.032 | 5.21 | 0.21 | 0.12 | 0.32 | 0.67 | 0.028 | 3.44 |
| Interpolation valid. | - | - | - | - | - | - | 0.54 | 0.49 | 0.70 | 1.47 | 0.105 | 61.31 | 0.49 | 0.61 | 0.78 | 1.49 | 0.060 | 34.84 | 0.24 | 0.15 | 0.38 | 0.70 | 0.005 | 16.86 | 0.15 | 0.05 | 0.23 | 0.42 | 0.007 | 10.12 |
| Interpolation test | - | - | - | - | - | - | 0.53 | 0.47 | 0.68 | 1.46 | 0.089 | 104.44 | 0.52 | 0.66 | 0.82 | 1.58 | 0.064 | 75.19 | 0.26 | 0.16 | 0.40 | 0.76 | 0.007 | 36.41 | 0.16 | 0.06 | 0.24 | 0.44 | 0.006 | 21.872 |
| Dataset of Left-Outs | PDR | ML-GP | RoNIN | C/RNN | Hybrid | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | MAE | MSE | RMSE | DEPM | DET | ||||||
| Walking | 1.15 | 1.82 | 1.35 | 2.17 | 0.054 | 81.51 | 0.70 | 0.68 | 0.83 | 1.36 | 0.093 | 138.81 | 0.67 | 0.62 | 0.78 | 1.33 | 0.004 | 5.67 | 0.32 | 0.15 | 0.38 | 0.66 | 0.015 | 2.56 | 0.17 | 0.04 | 0.20 | 0.32 | 0.003 | 2.26 |
| Jogging | 1.27 | 2.18 | 1.48 | 2.38 | 0.049 | 141.02 | 0.76 | 0.80 | 0.90 | 1.48 | 0.048 | 138.59 | 0.73 | 0.73 | 0.86 | 1.46 | 0.003 | 9.73 | 0.35 | 0.17 | 0.42 | 0.72 | 0.009 | 2.60 | 0.19 | 0.05 | 0.21 | 0.35 | 0.000 | 1.08 |
| Running | 1.35 | 2.50 | 1.58 | 2.54 | 0.023 | 87.74 | 0.83 | 0.95 | 0.97 | 1.62 | 0.037 | 140.97 | 0.80 | 0.87 | 0.94 | 1.56 | 0.001 | 4.49 | 0.39 | 0.21 | 0.46 | 0.77 | 0.006 | 3.52 | 0.21 | 0.05 | 0.23 | 0.38 | 0.002 | 2.33 |
| Random | 1.38 | 2.56 | 1.60 | 2.56 | 0.037 | 105.69 | 0.97 | 0.93 | 0.96 | 1.60 | 0.054 | 153.55 | 0.83 | 0.92 | 0.93 | 1.58 | 0.026 | 75.11 | 0.41 | 0.23 | 0.48 | 0.79 | 0.009 | 21.46 | 0.21 | 0.06 | 0.25 | 0.43 | 0.004 | 11.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feigl, T.; Kram, S.; Woller, P.; Siddiqui, R.H.; Philippsen, M.; Mutschler, C. RNN-Aided Human Velocity Estimation from a Single IMU. Sensors 2020, 20, 3656. https://doi.org/10.3390/s20133656
Feigl T, Kram S, Woller P, Siddiqui RH, Philippsen M, Mutschler C. RNN-Aided Human Velocity Estimation from a Single IMU. Sensors. 2020; 20(13):3656. https://doi.org/10.3390/s20133656
Chicago/Turabian StyleFeigl, Tobias, Sebastian Kram, Philipp Woller, Ramiz H. Siddiqui, Michael Philippsen, and Christopher Mutschler. 2020. "RNN-Aided Human Velocity Estimation from a Single IMU" Sensors 20, no. 13: 3656. https://doi.org/10.3390/s20133656
APA StyleFeigl, T., Kram, S., Woller, P., Siddiqui, R. H., Philippsen, M., & Mutschler, C. (2020). RNN-Aided Human Velocity Estimation from a Single IMU. Sensors, 20(13), 3656. https://doi.org/10.3390/s20133656







