Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection
Abstract
1. Introduction
- Intrinsic variation: Although the gait pattern is highly internalised in the brain, it is impossible to repeat the gait or any other movement in precisely the same way each time; there are always minimal individual variations, which are called intrinsic variations [21]. Intrinsic variation can be exacerbated if the experiment does not take place in a suitable environment that allows the subject to walk using his or her habitual gait pattern [22] or if the subject does not feel comfortable with the devices placed on the body. These situations can cause alterations in the movements [10] and can make the subject feel physically different, or uncoordinated [23].
- Soft tissue movements: The movements of the skin, muscles, and other tissues around the bones are an artefact that occurs persistently in surface-marker MoCap systems [19]. The soft tissue effect is particularly notable on the thighs since the femur is covered by a considerable amount of tissue [24,25]. To avoid these effects, the optical systems based on individual markers often place the markers on bony structures, or “landmarks” [24]. However, it should be assumed that surface-marker MoCap systems do not represent the real movement of the bones [26].
- Positioning: It is difficult to position the devices in the same manner each time. The data obtained from acceleration and angular velocity differ from one location to another for the same body segment [27,29,30]. Differences in acceleration and angular velocity can be minimised by calibrating before the measurements are taken (see factor 7).
- Instrument accuracy: The optical system’s accuracy is in the order of 1% [31] or 1 mm [19] for the measurement. IMUs use a sensor fusion algorithm to provide rotations from the signal of the built-in sensors [18,32]. IMUs are highly sensitive to disturbances in the Earth’s magnetic field, which disorients magnetometers, especially in indoor environments. In addition, a drift artefact is caused by cumulative gyro integration errors [33]. Thus, these types of sensors have accuracy ranges of 0.2°–1° (roll/pitch), 0.4°–2° (yaw) and a dynamic root mean square (RMS) of 1°–2° RMS, depending on the manufacturer [12].
- Gait event detection: Gait events are relevant moments throughout the gait cycle, such as the initial or the final contact of each stride, which allow for the normalisation, superimposition, and analysis of the strides captured [15]. Events can be estimated using additional instrumentation (e.g., pressure platforms or instrumented templates), or using the movement data itself. In either case, there may be inaccuracies of a few milliseconds in the detection. In IMU-based systems, these errors in parameters such as the step length may be cumulative and translated as a few centimetres [34,35,36].
- Anatomical calibration: When the devices are placed on the body, their coordinate systems always differ according to the anatomical segment on which they are fixed [18,37]. The anatomical calibration, also called sensor-to-segment alignment [38,39], is used to calculate the relative rotation between the device and the bone, which is assumed to be time-invariant once the sensor is mounted on the body [18,40]. The calibration allows for the calculation of the joints’ angles and the establishment of the participant’s neutral position, which corresponds to the zero rotation of all the body segments. Two main approaches [18,37] are used to accomplish the calibration: (1) Anatomical approaches, in which the user is asked to stay still in one or more body positions while the sensors are oriented to those expected in the static pose [41,42], and (2) functional approaches, in which the subject is asked to perform mono-dimensional or arbitrary motions to estimate the anatomical axes [39,43,44,45]. As it is not possible to adopt precisely the same position or to execute exactly the same movements in each measurement session, there is always intrinsic variation [21]. Similarly, anthropometric measurements of the participant are usually introduced during the anatomical calibration, which adds errors to those mentioned previously [40,41,44].
2. Materials and Methods
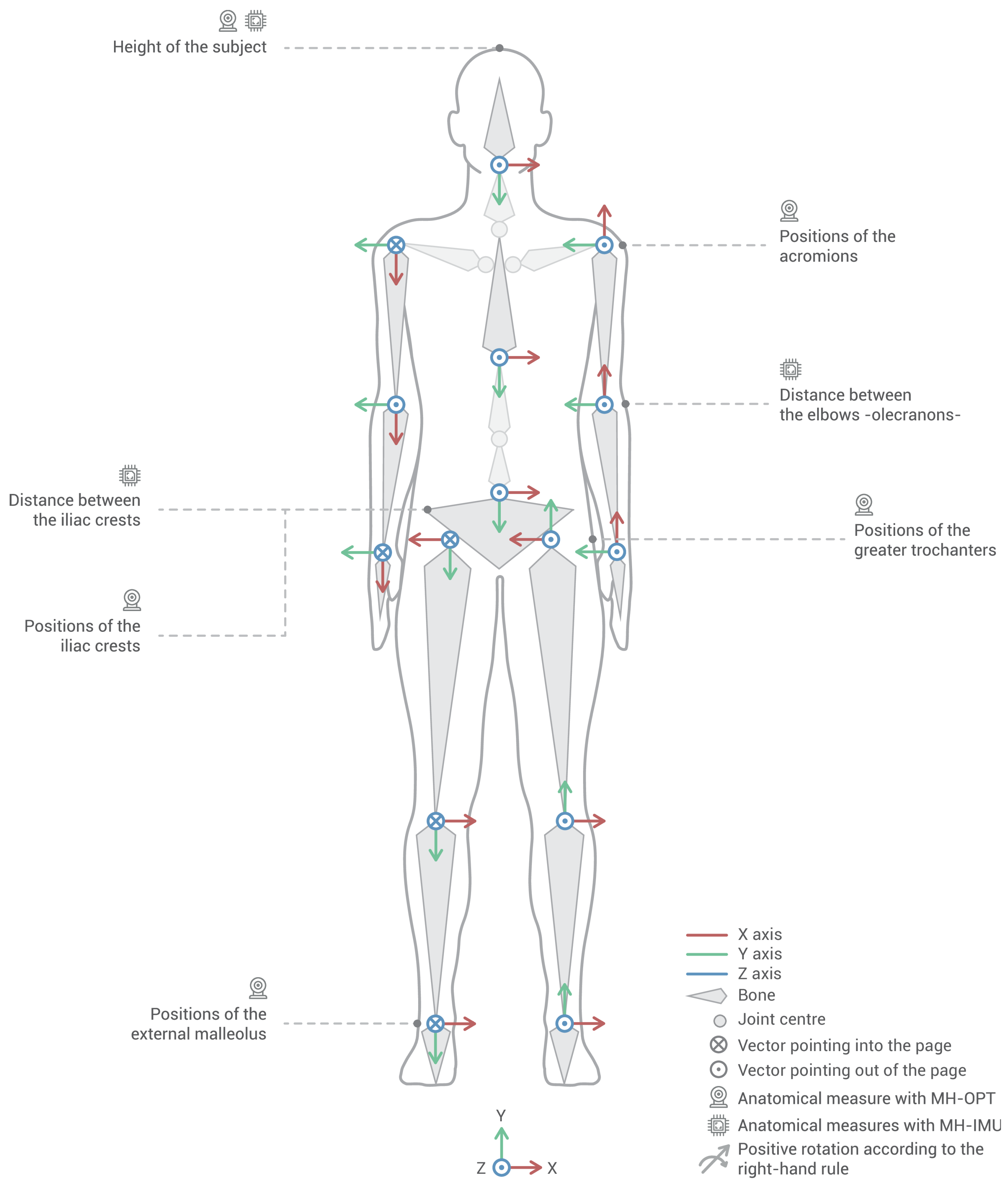
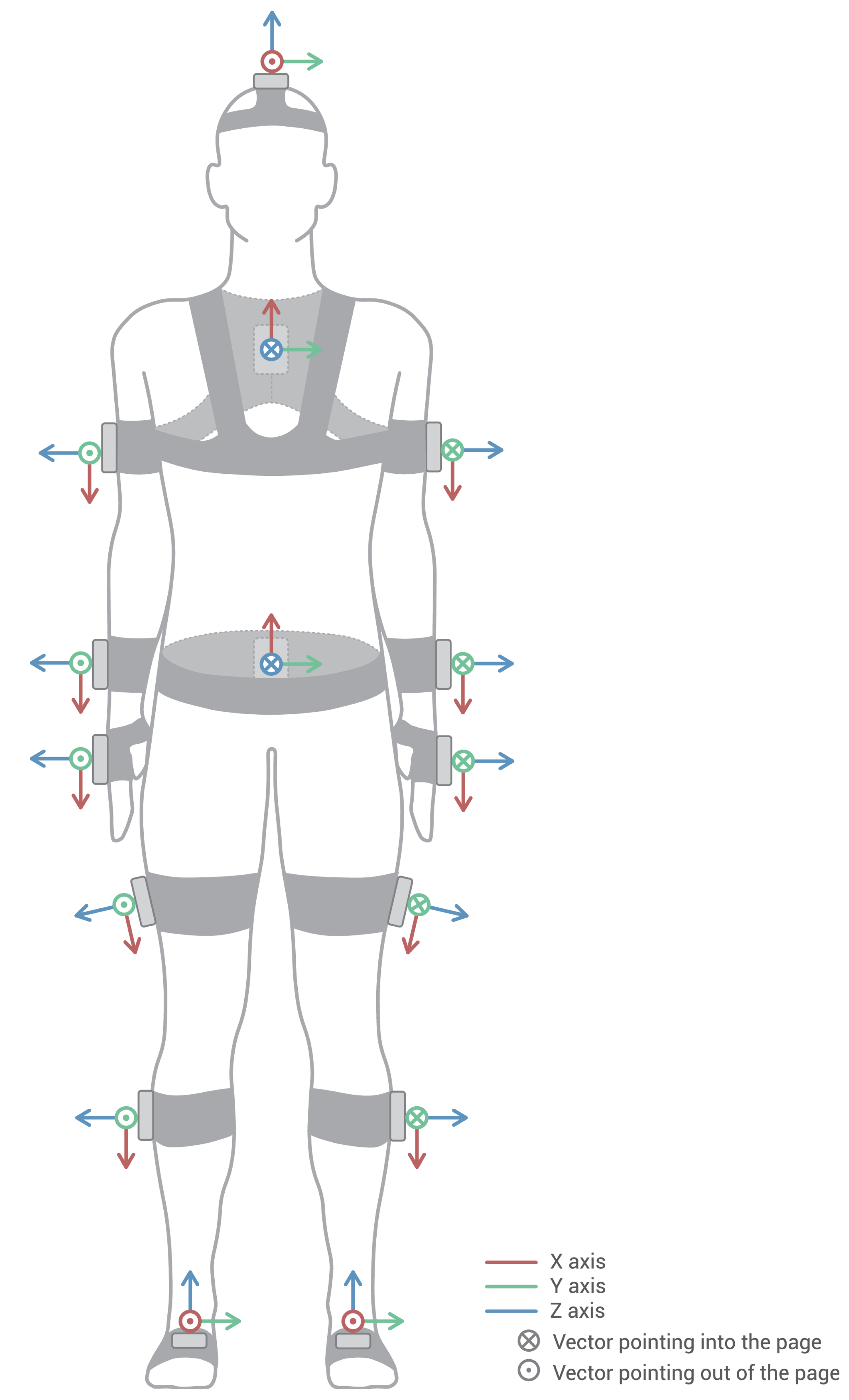
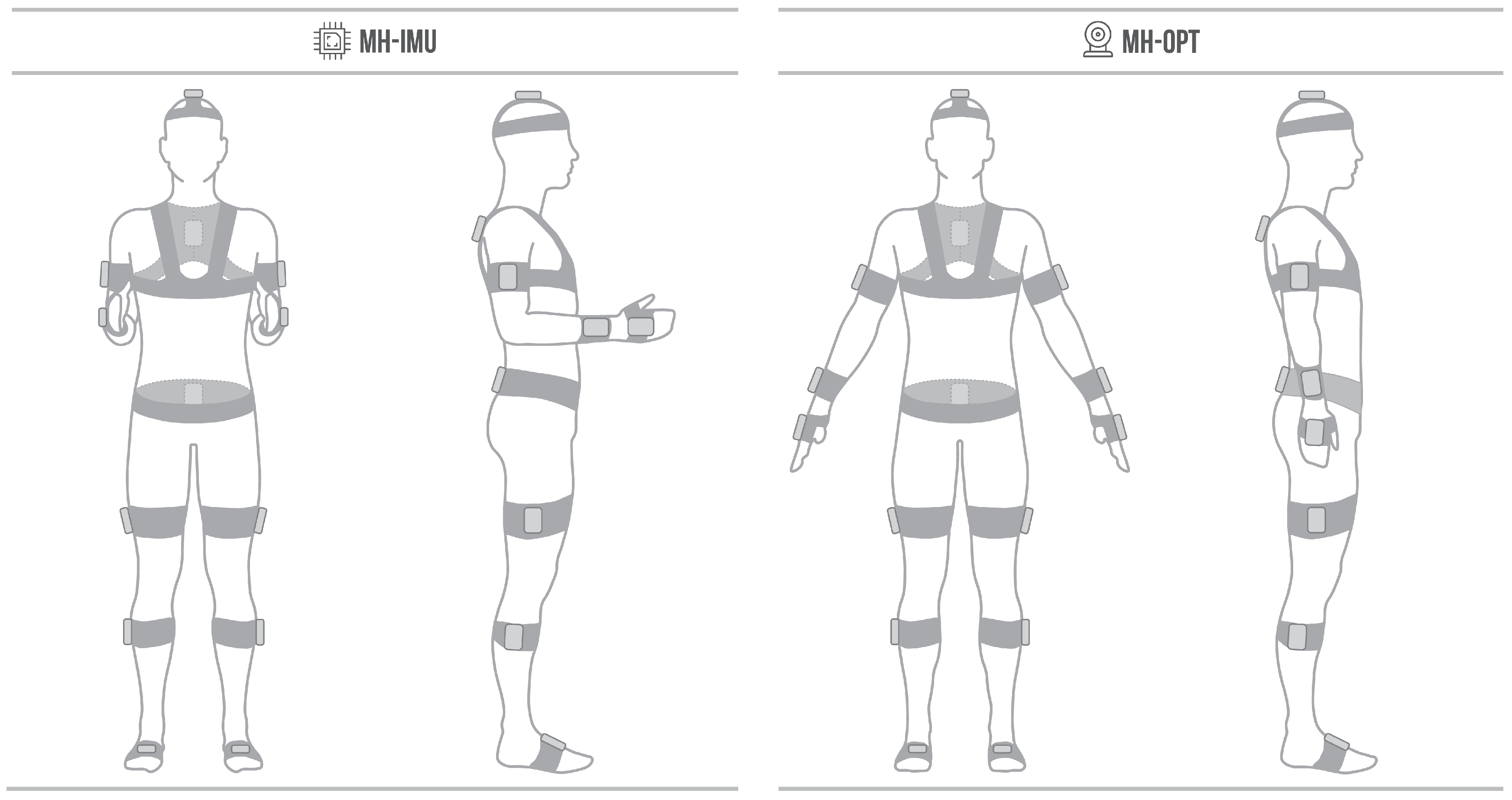
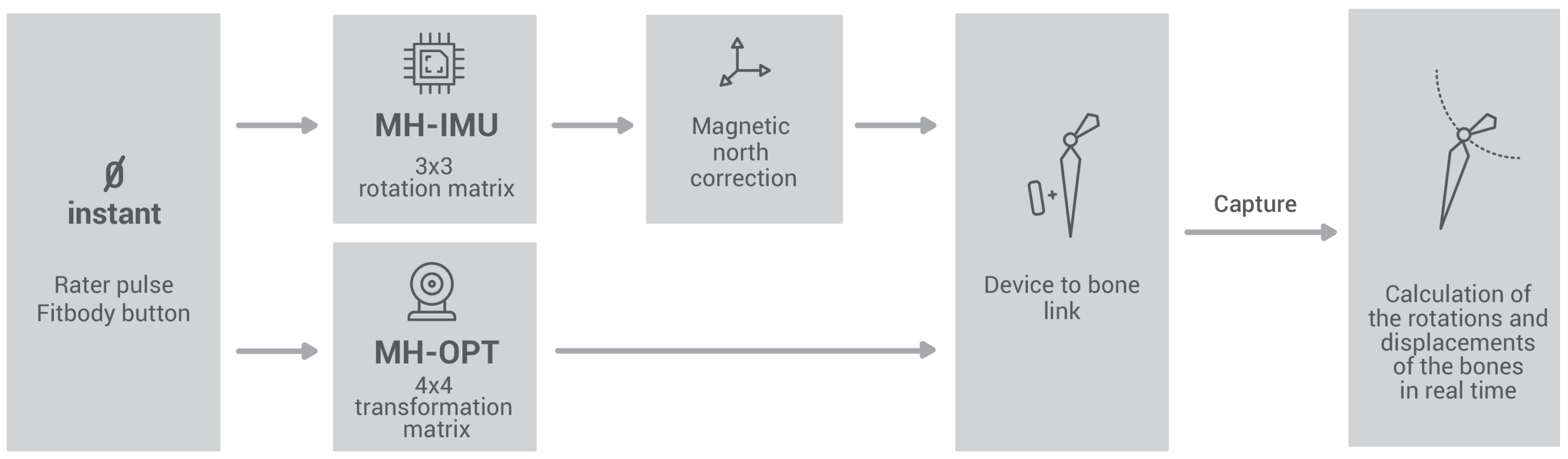
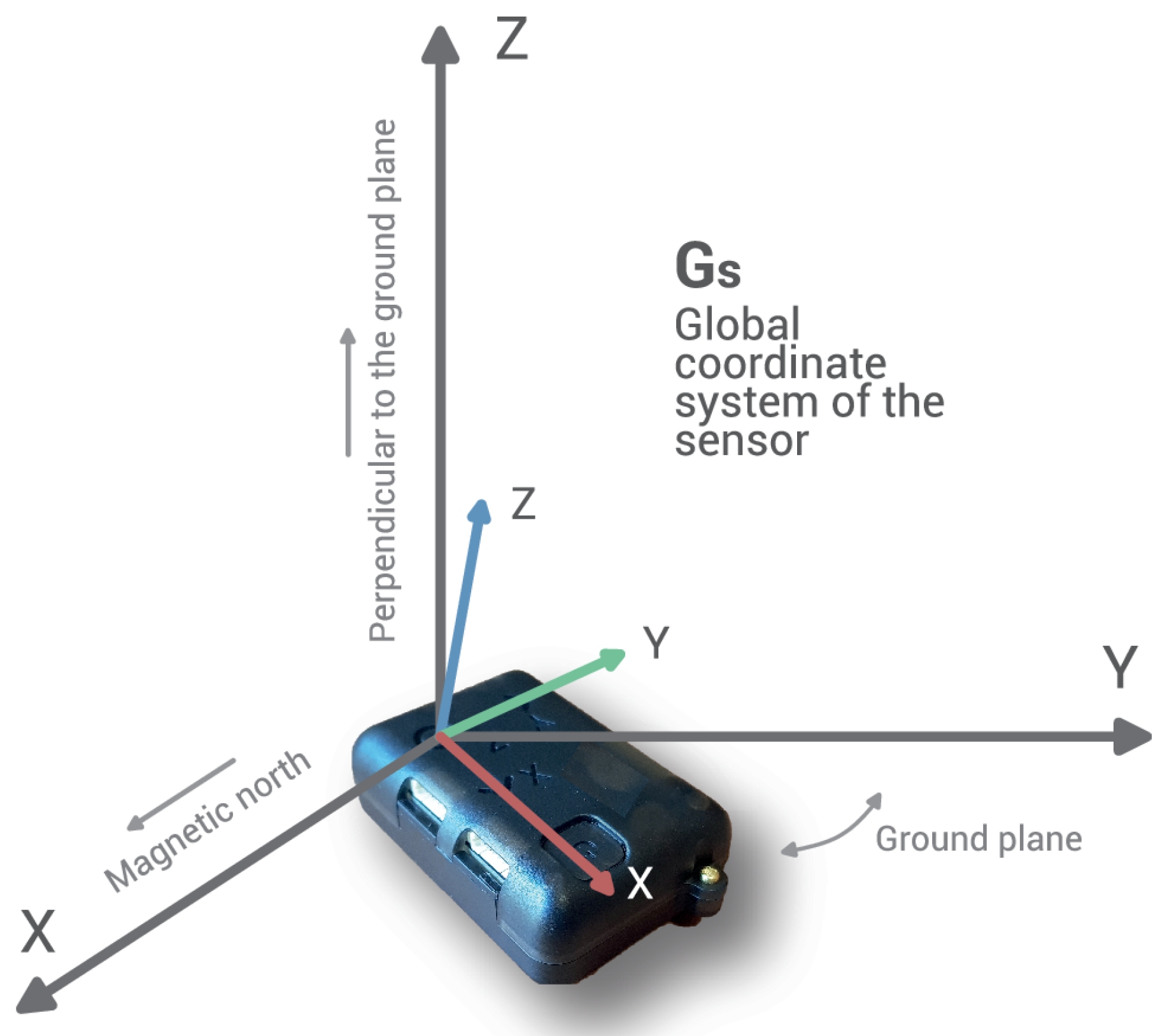
2.1. The Move Human Sensors (MH) System
2.1.1. Human Model
2.1.2. Fitbody Calibration Process
2.1.3. Gait Event Detection Algorithm
2.2. Test–Retest Study Design
3. Results
4. Discussion
4.1. Discussion of the Test–Retest Results
4.2. Usage Considerations and Limitations of the MH System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prakash, C.; Kumar, R.; Mittal, N. Recent Developments in Human Gait Research: Parameters, Approaches, Applications, Machine Learning Techniques, Datasets and Challenges. Artif. Intell. Rev. 2018, 49, 1–40. [Google Scholar] [CrossRef]
- Chambers, H.G.; Sutherland, D.H. A Practical Guide to Gait Analysis. Jaaos J. Am. Acad. Orthop. Surg. 2002, 10, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Hu, H. Human Motion Tracking for rehabilitation—A Survey. Biomed. Signal Process. Control 2008, 3, 1–18. [Google Scholar] [CrossRef]
- Simon, S.R. Quantification of Human Motion: Gait Analysis—Benefits and Limitations to its Application to Clinical Problems. J. Biomech. 2004, 37, 1869–1880. [Google Scholar] [CrossRef] [PubMed]
- Cook, R.E.; Schneider, I.; Hazlewood, M.E.; Hillman, S.J.; Robb, J.E. Gait Analysis Alters Decision-Making in Cerebral Palsy. J. Pediatric Orthop. 2003, 23, 292–295. [Google Scholar] [CrossRef]
- Skogstad, S.A.; Nymoen, K.; Høvin, M. Comparing Inertial and Optical Mocap Technologies for Synthesis Control. In Proceedings of the International Sound and Music Computing Conference, Malaga, Spain, 28–31 May 2019; pp. 421–426. [Google Scholar]
- Mayagoitia, R.E.; Nene, A.V.; Veltink, P.H. Accelerometer and Rate Gyroscope Measurement of Kinematics: An Inexpensive Altern ative to Optical Motion Analysis Systems. J. Biomech. 2002, 35, 537–542. [Google Scholar] [CrossRef]
- Carse, B.; Meadows, B.; Bowers, R.; Rowe, P. Affordable Clinical Gait Analysis: An Assessment of the Marker Tracking Accuracy of a New Low-Cost Optical 3D Motion Analysis System. Physiotherapy 2013, 99, 347–351. [Google Scholar] [CrossRef]
- Cloete, T.; Scheffer, C. Benchmarking of a Full-Body Inertial Motion Capture System for Clinical Gait Analysis. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 21–24 August 2008; pp. 4579–4582. [Google Scholar]
- Mooney, R.; Corley, G.; Godfrey, A.; Quinlan, L.R.; ÓLaighin, G. Inertial Sensor Technology for Elite Swimming Performance Analysis: A Systematic Review. Sensors 2015, 16, 18. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial Sensor-Based Knee Flexion/Extension Angle Estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Marin, J.; Blanco, T.; Marin, J.J. Octopus: A Design Methodology for Motion Capture Wearables. Sensors 2017, 17, 1875. [Google Scholar] [CrossRef]
- Rahul, M. Review on Motion Capture Technology. Glob. J. Comput. Sci. Technol. 2018, 18, 23–26. [Google Scholar]
- Morris, R.G.; Lawson, S.E.M. A Review and Evaluation of Available Gait Analysis Technologies, and their Potential for the Measurement of Impact Transmission. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.508.8196&rep=rep1&type=pdf (accessed on 11 June 2020).
- Tao, W.; Liu, T.; Zheng, R.; Feng, H. Gait Analysis using Wearable Sensors. Sensors 2012, 12, 2255–2283. [Google Scholar] [CrossRef] [PubMed]
- Muro-De-La-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef]
- Chen, S.; Lach, J.; Lo, B.; Yang, G. Toward Pervasive Gait Analysis with Wearable Sensors: A Systematic Review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef]
- Picerno, P. 25 Years of Lower Limb Joint Kinematics by using Inertial and Magnetic Sensors: A Review of Methodological Approaches. Gait Posture 2017, 51, 239–246. [Google Scholar] [CrossRef]
- Baker, R. Gait Analysis Methods in Rehabilitation. J. Neuroeng. Rehabil. 2006, 3, 1. [Google Scholar] [CrossRef]
- Marin, J.; Blanco, T.; Marin, J.J.; Moreno, A.; Martitegui, E.; Aragues, J.C. Integrating a Gait Analysis Test in Hospital Rehabilitation: A Service Design Approach. PLoS ONE 2019, 14, e0224409. [Google Scholar] [CrossRef]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The Reliability of Three-Dimensional Kinematic Gait Measurements: A Systematic Review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef]
- Kribus-Shmiel, L.; Zeilig, G.; Sokolovski, B.; Plotnik, M. How Many Strides are Required for a Reliable Estimation of Temporal Gait Parameters? Implementation of a New Algorithm on the Phase Coordination Index. PLoS ONE 2018, 13, e0192049. [Google Scholar] [CrossRef]
- Gemperle, F.; Kasabach, C.; Stivoric, J.; Bauer, M.; Martin, R. Design for Wearability. In Proceedings of the Digest of Papers. Second International Symposium on Wearable Computers (Cat. No.98EX215), Pittsburgh, PA, USA, 19–20 October 1998; pp. 116–122. [Google Scholar]
- Capozzo, A.; Catani, F.; Leardini, A.; Benedetti, M.; Della Croce, U. Position and Orientation in Space of Bones during Movement: Experimental Artefacts. Clin. Biomech. 1996, 11, 90–100. [Google Scholar] [CrossRef]
- Dejnabadi, H.; Jolles, B.M.; Casanova, E.; Fua, P.; Aminian, K. Estimation and Visualization of Sagittal Kinematics of Lower Limbs Orientation using Body-Fixed Sensors. IEEE Trans. Biomed. Eng. 2006, 53, 1385–1393. [Google Scholar] [CrossRef] [PubMed]
- Benoit, D.L.; Ramsey, D.K.; Lamontagne, M.; Xu, L.; Wretenberg, P.; Renström, P. Effect of Skin Movement Artifact on Knee Kinematics during Gait and Cutting Motions Measured in Vivo. Gait Posture 2006, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Li, Q. Inertial Sensor-Based Methods in Walking Speed Estimation: A Systematic Review. Sensors 2012, 12, 6102–6116. [Google Scholar] [CrossRef] [PubMed]
- Haratian, R.; Twycross-Lewis, R.; Timotijevic, T.; Phillips, C. Toward Flexibility in Sensor Placement for Motion Capture Systems: A Signal Processing Approach. IEEE Sens. J. 2014, 14, 701–709. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of Walking Features from Foot Inertial Sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef]
- Yu, B.; Bao, T.; Zhang, D.; Carender, W.; Sienko, K.H.; Shull, P.B. Determining Inertial Measurement Unit Placement for Estimating Human Trunk Sway while Standing, Walking and Running. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4651–4654. [Google Scholar]
- Thewlis, D.; Bishop, C.; Daniell, N.; Paul, G. Next Generation Low-Cost Motion Capture Systems can Provide Comparable Spatial Accuracy to High-End Systems. J. Appl. Biomech. 2013, 29, 112–117. [Google Scholar] [CrossRef]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef]
- Cloete, T.; Scheffer, C. Repeatability of an Off-the-Shelf, Full Body Inertial Motion Capture System during Clinical Gait Analysis. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 5125–5128. [Google Scholar]
- O’Connor, C.M.; Thorpe, S.K.; O’Malley, M.J.; Vaughan, C.L. Automatic Detection of Gait Events using Kinematic Data. Gait Posture 2007, 25, 469–474. [Google Scholar] [CrossRef]
- Trojaniello, D.; Cereatti, A.; Pelosin, E.; Avanzino, L.; Mirelman, A.; Hausdorff, J.M.; Della Croce, U. Estimation of Step-by-Step Spatio-Temporal Parameters of Normal and Impaired Gait using Shank-Mounted Magneto-Inertial Sensors: Application to Elderly, Hemiparetic, Parkinsonian and Choreic Gait. J. Neuroeng. Rehabil. 2014, 11, 152. [Google Scholar] [CrossRef]
- Bejarano, N.C.; Ambrosini, E.; Pedrocchi, A.; Ferrigno, G.; Monticone, M.; Ferrante, S. A Novel Adaptive, Real-Time Algorithm to Detect Gait Events from Wearable Sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Bergamini, E.; Truppa, L.; Guaitolini, M.; Raggi, M.; Mannini, A.; Sabatini, A.M.; Vannozzi, G.; Garofalo, P. A Wearable Magnetometer-Free Motion Capture System: Innovative Solutions for Real-World Applications. IEEE Sens. J. 2020. [Google Scholar] [CrossRef]
- Lebleu, J.; Gosseye, T.; Detrembleur, C.; Mahaudens, P.; Cartiaux, O.; Penta, M. Lower Limb Kinematics using Inertial Sensors during Locomotion: Accuracy and Reproducibility of Joint Angle Calculations with Different Sensor-to-Segment Calibrations. Sensors 2020, 20, 715. [Google Scholar] [CrossRef] [PubMed]
- Laidig, D.; Müller, P.; Seel, T. Automatic Anatomical Calibration for IMU-Based Elbow Angle Measurement in Disturbed Magnetic Fields. Curr. Dir. Biomed. Eng. 2017, 3, 167–170. [Google Scholar] [CrossRef]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental Evaluation of Accuracy and Repeatability of a Novel Body-to-Sensor Calibration Procedure for Inertial Sensor-Based Gait Analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Vargas-Valencia, L.S.; Elias, A.; Rocon, E.; Bastos-Filho, T.; Frizera, A. An IMU-to-Body Alignment Method Applied to Human Gait Analysis. Sensors 2016, 16, 2090. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wu, J. A Novel Hierarchical Information Fusion Method for Three-Dimensional Upper Limb Motion Estimation. IEEE Trans. Instrum. Meas. 2011, 60, 3709–3719. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Bonnet, S.; Bassompierre, C.; Godin, C.; Lesecq, S.; Barraud, A. Calibration Methods for Inertial and Magnetic Sensors. Sens. Actuators A Phys. 2009, 156, 302–311. [Google Scholar] [CrossRef]
- Eckhoff, K.; Kok, M.; Lucia, S.; Seel, T. Sparse Magnetometer-Free Inertial Motion Tracking—A Condition for Observability in Double Hinge Joint Systems. arXiv 2020, arXiv:2002.00902. Available online: https://arxiv.org/abs/2002.00902 (accessed on 11 June 2020).
- El-Gohary, M.; McNames, J. Human Joint Angle Estimation with Inertial Sensors and Validation with a Robot Arm. IEEE Trans. Biomed. Eng. 2015, 62, 1759–1767. [Google Scholar] [CrossRef] [PubMed]
- Favre, J.; Aissaoui, R.; Jolles, B.; de Guise, J.; Aminian, K. Functional Calibration Procedure for 3D Knee Joint Angle Description using Inertial Sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Sabatini, A.M. Dealing with Magnetic Disturbances in Human Motion Capture: A Survey of Techniques. Micromachines 2016, 7, 43. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, D.; Laidig, D.; Deimel, R.; Seel, T. Magnetometer-Free Inertial Motion Tracking of Arbitrary Joints with Range of Motion Constraints. arXiv 2020, arXiv:2002.00639. Available online: https://arxiv.org/abs/2002.00639 (accessed on 11 June 2020).
- Lee, J.K.; Jeon, T.H. IMU-Based but Magnetometer-Free Joint Angle Estimation of Constrained Links. In Proceedings of the 2018 IEEE Sensors, New Delhi, India, 30 October 2018; pp. 1–4. [Google Scholar]
- Laidig, D.; Lehmann, D.; Bégin, M.; Seel, T. Magnetometer-Free Realtime Inertial Motion Tracking by Exploitation of Kinematic Constraints in 2-DoF Joints. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 1233–1238. [Google Scholar]
- Laidig, D.; Schauer, T.; Seel, T. Exploiting Kinematic Constraints to Compensate Magnetic Disturbances when Calculating Joint Angles of Approximate Hinge Joints from Orientation Estimates of Inertial Sensors. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 971–976. [Google Scholar]
- Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; De Vroey, H.; Claeys, K. Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sensors 2020, 20, 673. [Google Scholar] [CrossRef] [PubMed]
- Cardarelli, S.; di Florio, P.; Mengarelli, A.; Tigrini, A.; Fioretti, S.; Verdini, F. Magnetometer-Free Sensor Fusion Applied to Pedestrian Tracking: A Feasibility Study. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 238–242. [Google Scholar]
- Visi, F.; Georgiou, T.; Holland, S.; Pinzone, O.; Donaldson, G.; Tetley, J. Assessing the Accuracy of an Algorithm for the Estimation of Spatial Gait Parameters using Inertial Measurement Units: Application to Healthy Subject and Hemiparetic Stroke Survivor. In Proceedings of the 4th International Conference on Movement Computing, London, UK, 28–30 June 2017; pp. 1–7. [Google Scholar]
- Mariani, B.; Rochat, S.; Büla, C.J.; Aminian, K. Heel and Toe Clearance Estimation for Gait Analysis using Wireless Inertial Sensors. IEEE Trans. Biomed. Eng. 2012, 59, 3162–3168. [Google Scholar] [CrossRef] [PubMed]
- Mariani, B.; Rouhani, H.; Crevoisier, X.; Aminian, K. Quantitative Estimation of Foot-Flat and Stance Phase of Gait using Foot-Worn Inertial Sensors. Gait Posture 2013, 37, 229–234. [Google Scholar] [CrossRef]
- Teufl, W.; Lorenz, M.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters. Sensors 2019, 19, 38. [Google Scholar] [CrossRef]
- Zeni, J., Jr.; Richards, J.; Higginson, J. Two Simple Methods for Determining Gait Events during Treadmill and Overground Walking using Kinematic Data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef]
- Olsen, E.; Haubro Andersen, P.; Pfau, T. Accuracy and Precision of Equine Gait Event Detection during Walking with Limb and Trunk Mounted Inertial Sensors. Sensors 2012, 12, 8145–8156. [Google Scholar] [CrossRef]
- Taborri, J.; Rossi, S.; Palermo, E.; Patanè, F.; Cappa, P. A Novel HMM Distributed Classifier for the Detection of Gait Phases by Means of a Wearable Inertial Sensor Network. Sensors 2014, 14, 16212–16234. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Furlan, L.; Sterr, A. The Applicability of Standard Error of Measurement and Minimal Detectable Change to Motor Learning Research—A Behavioral Study. Front. Hum. Neurosci. 2018, 12, 95. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, F.M.; Abraira, V.; Royuela, A.; Corcoll, J.; Alegre, L.; Tomás, M.; Mir, M.A.; Cano, A.; Muriel, A.; Zamora, J. Minimum Detectable and Minimal Clinically Important Changes for Pain in Patients with Nonspecific Neck Pain. BMC Musculoskelet. Disord. 2008, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Steffen, T.; Seney, M. Test-Retest Reliability and Minimal Detectable Change on Balance and Ambulation Tests, the 36-Item Short-Form Health Survey, and the Unified Parkinson Disease Rating Scale in People with Parkinsonism. Phys. Ther. 2008, 88, 733–746. [Google Scholar] [CrossRef]
- Marchetti, G.F.; Lin, C.C.; Alghadir, A.; Whitney, S.L. Responsiveness and Minimal Detectable Change of the Dynamic Gait Index and Functional Gait Index in Persons with Balance and Vestibular Disorders. J. Neurol. Phys. Ther. 2014, 38, 119–124. [Google Scholar] [CrossRef]
- Schuck, P.; Zwingmann, C. The ‘smallest Real Difference’ as a Measure of Sensitivity to Change: A Critical Analysis. Int. J. Rehabil. Res. 2003, 26, 85–91. [Google Scholar]
- Lee, P.; Liu, C.; Fan, C.; Lu, C.; Lu, W.; Hsieh, C. The Test–retest Reliability and the Minimal Detectable Change of the Purdue Pegboard Test in Schizophrenia. J. Formos. Med. Assoc. 2013, 112, 332–337. [Google Scholar] [CrossRef]
- Najafi, B.; Khan, T.; Wrobel, J. Laboratory in a Box: Wearable Sensors and its Advantages for Gait Analysis. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6507–6510. [Google Scholar]
- Next Generation IMU (NGIMU). Available online: http://x-io.co.uk/ngimu/ (accessed on 21 January 2020).
- Natural point. OptiTrack. Available online: http://www.naturalpoint.com/ (accessed on 21 January 2020).
- Van de Putte, M.; Hagemeister, N.; St-Onge, N.; Parent, G.; de Guise, J.A. Habituation to Treadmill Walking. Biomed. Mater. Eng. 2006, 16, 43–52. [Google Scholar]
- Faude, O.; Donath, L.; Roth, R.; Fricker, L.; Zahner, L. Reliability of Gait Parameters during Treadmill Walking in Community-Dwelling Healthy Seniors. Gait Posture 2012, 36, 444–448. [Google Scholar] [CrossRef]
- Papegaaij, S.; Steenbrink, F.; Clinical Gait Analysis: Treadmill-Based vs. Overground. Available online: https://knowledge.motekmedical.com/wp-content/uploads/2019/04/Motek-White-Paper-Clinical-Gait-Analysis.pdf (accessed on 11 June 2020).
- Strongman, C.; Morrison, A. A Scoping Review of Non-Linear Analysis Approaches Measuring Variability in Gait due to Lower Body Injury Or Dysfunction. Hum. Mov. Sci. 2020, 69, 102562. [Google Scholar] [CrossRef]
- Animation 3D software. Available online: https://www.daz3d.com/ (accessed on 21 January 2020).
- Bell, A.L.; Brand, R.A.; Pedersen, D.R. Prediction of Hip Joint Centre Location from External Landmarks. Hum. Mov. Sci. 1989, 8, 3–16. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and Orientation in Space of Bones during Movement: Anatomical Frame Definition and Determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Tawy, G.F.; Rowe, P. Is the Instrumented-Pointer Method of Calibrating Anatomical Landmarks in 3D Motion Analysis Reliable? J. Biomech. 2017, 53, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Flat icon. Available online: https://www.flaticon.com/ (accessed on 11 June 2020).
- Zhu, R.; Wang, Y.; Yu, B.; Gan, X.; Jia, H.; Wang, B. Enhanced Heuristic Drift Elimination with Adaptive Zero-Velocity Detection and Heading Correction Algorithms for Pedestrian Navigation. Sensors 2020, 20, 951. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, D.; Wesseling, M.; Xue, B.; Li, F. Comparison of Modelling and Tracking Methods for Analysing Elbow and Forearm Kinematics. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 1113–1121. [Google Scholar] [CrossRef] [PubMed]
- Matrix Transformations. Available online: https://pypi.org/project/transformations/ (accessed on 11 June 2020).
- Petrescu, F.I.; Petrescu, R.V. Direct and Inverse Kinematics to the Anthropomorphic Robots. Engevista 2016, 18, 109–124. [Google Scholar] [CrossRef][Green Version]
- Nielsen, J.; Roth, B. On the Kinematic Analysis of Robotic Mechanisms. Int. J. Robot. Res. 1999, 18, 1147–1160. [Google Scholar] [CrossRef]
- ScyPy, Smoothing of a 1D Signal. Available online: https://scipy-cookbook.readthedocs.io/items/SignalSmooth.html (accessed on 21 January 2020).
- England, S.A.; Granata, K.P. The Influence of Gait Speed on Local Dynamic Stability of Walking. Gait Posture 2007, 25, 172–178. [Google Scholar] [CrossRef]
- Batterham, A.M.; Hopkins, W.G. Making Meaningful Inferences about Magnitudes. Int. J. Sports Physiol. Perform. 2006, 1, 50–57. [Google Scholar] [CrossRef]
- Viteckova, S.; Kutilek, P.; Svoboda, Z.; Krupicka, R.; Kauler, J.; Szabo, Z. Gait Symmetry Measures: A Review of Current and Prospective Methods. Biomed. Signal Process. Control 2018, 42, 89–100. [Google Scholar] [CrossRef]
- Hopkins, W.; Marshall, S.; Batterham, A.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3. [Google Scholar] [CrossRef] [PubMed]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Washabaugh, E.P.; Kalyanaraman, T.; Adamczyk, P.G.; Claflin, E.S.; Krishnan, C. Validity and Repeatability of Inertial Measurement Units for Measuring Gait Parameters. Gait Posture 2017, 55, 87–93. [Google Scholar] [CrossRef] [PubMed]
- Meldrum, D.; Shouldice, C.; Conroy, R.; Jones, K.; Forward, M. Test–retest Reliability of Three Dimensional Gait Analysis: Including a Novel Approach to Visualising Agreement of Gait Cycle Waveforms with Bland and Altman Plots. Gait Posture 2014, 39, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, R.; Armada-da-Silva, P.; Pool-Goudaazward, A.; Moniz-Pereira, V.; Veloso, A.P. Three Dimensional Multi-Segmental Trunk Kinematics and Kinetics during Gait: Test-Retest Reliability and Minimal Detectable Change. Gait Posture 2016, 46, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Wilken, J.M.; Rodriguez, K.M.; Brawner, M.; Darter, B.J. Reliability and Minimal Detectible Change Values for Gait Kinematics and Kinetics in Healthy Adults. Gait Posture 2012, 35, 301–307. [Google Scholar] [CrossRef]
- Rutherford, D.J.; Moyer, R.; Baker, M.; Saleh, S. High Day-to-Day Repeatability of Lower Extremity Muscle Activation Patterns and Joint Biomechanics of Dual-Belt Treadmill Gait: A Reliability Study in Healthy Young Adults. J. Electromyogr. Kinesiol. 2020, 51, 102401. [Google Scholar] [CrossRef]
- Al-Amri, M.; Al Balushi, H.; Mashabi, A. Intra-Rater Repeatability of Gait Parameters in Healthy Adults during Self-Paced Treadmill-Based Virtual Reality Walking. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1669–1677. [Google Scholar] [CrossRef]
- Senden, R.; Grimm, B.; Heyligers, I.; Savelberg, H.; Meijer, K. Acceleration-Based Gait Test for Healthy Subjects: Reliability and Reference Data. Gait Posture 2009, 30, 192–196. [Google Scholar] [CrossRef]
- Georgiou, T. Rhythmic Haptic Cueing for Gait Rehabilitation of Hemiparetic Stroke and Brain Injury Survivors. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2018. [Google Scholar]
- Braga Rodrigues, T.; Catháin, C.O.; O’Connor, N.E.; Murray, N. A Quality of Experience Assessment of Haptic and Augmented Reality Feedback Modalities in a Gait Analysis System. PLoS ONE 2020, 15, e0230570. [Google Scholar] [CrossRef] [PubMed]





| Body Part | Side | |||||
|---|---|---|---|---|---|---|
| Head | - | 132.2 | 116.0 | 151.4 | 0.34 | 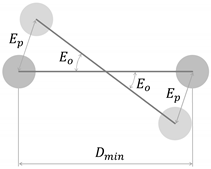 |
| Arm | R | 99.0 | 92.1 | 134.0 | 0.42 | |
| Arm | L | 113.7 | 91.6 | 117.1 | 0.43 | |
| Forearm | R | 104.4 | 81.3 | 95.6 | 0.48 | |
| Forearm | L | 116.3 | 75.3 | 85.7 | 0.52 | |
| Hand | R | 128.2 | 69.4 | 146.3 | 0.56 | |
| Hand | L | 70.3 | 120.3 | 135.6 | 0.55 | |
| Chest | - | 140.1 | 108.7 | 169.9 | 0.36 | |
| Pelvic | - | 180.6 | 105.3 | 163.0 | 0.37 | |
| Thigh | R | 126.2 | 114.8 | 99.6 | 0.39 | |
| Thigh | L | 95.4 | 105.2 | 122.3 | 0.41 | |
| Calf | R | 95.5 | 109.7 | 75.7 | 0.51 | |
| Calf | L | 126.3 | 70.1 | 82.4 | 0.56 | |
| Foot | R | 63.9 | 107.0 | 83.1 | 0.61 | |
| Foot | L | 114.0 | 64.1 | 94.1 | 0.61 | |
| Mean (SD) | - | - | - | - | 0.47 (0.09) |
| IMU Sensor | Axis Projected on the Ground | Angle with the Y-Axis of the Pelvis Projected on the Ground [°] |
|---|---|---|
| Head | X | 90 |
| Arm | Y | 90 |
| Forearm | X | 90 |
| Hand | X | 90 |
| Chest | Y | 0 |
| Thigh | Y | 90 |
| Calf | Y | 90 |
| Foot | Y | 0 |
| Name | Description | |
|---|---|---|
| Spatio-temporal Variables Dimensions that are based on whole-body movement | Step length [cm] | Distance between the centres of both ankle joints in the sagittal plane at T1. |
| Step width [cm] | Distance between the centres of both ankle joints in the frontal plane at T1. | |
| Single support [%] | Percentage of mono-pedal support during the stride time. Percentage of T2 to T4 time with respect to the entire stride time. | |
| Double support [%] | Percentage of bipedal support during the stride time. Percentage of T1 to T2 time and T4 to T5 with respect to the entire stride time. | |
| Gait speed [cm/s] | Mean of the gait speed during the stride. Stride length divided by stride time. | |
| Kinematic Variables [°] Dimensions that are based on the movement of each body segment | Range of the trunk tilt. T2 to T5 | Chest rotation around the Z-axis with regard to the pelvic bone. Range from T2 to T5. |
| Range of the pelvic tilt. T1 to T4 | Pelvic bone rotation around the Z-axis. Range from T1 to T4. | |
| Range of the hip flexion/extension. T1 to T4 | Hip joint rotation around the X-axis. Range from T1 to T4. | |
| Range of the hip adduction/abduction. T4 to T5 | Hip joint rotation around the Z-axis. Range from T4 to T5. | |
| Range of the knee flexion/extension. T4 to T5 | Knee joint rotation around the X-axis. Range from T4 to T5. | |
| Range of the ankle dorsi/plantar flexion. T4 to T5 | Ankle joint rotation around the X-axis. Range from T4 to T5. | |
| Range of the ankle inversion/eversion. T1 to T3 | Ankle joint rotation around the Z-axis. Range from T1 to T3. |
| MH-IMU | MH-OPT | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test µ (SD) | Retest µ (SD) | Dif. µ (SD) | ICC | MCD es95 | MCD 95 | Test µ (SD) | Retest µ (SD) | Dif. µ (SD) | ICC | MCD es95 | MCD 95 | ||
| Step length [cm] | R | 58.8 (4.6) | 58.7 (4.8) | −0.1 (2.4) | 0.93 | 0.8 | 3.5 | 59.5 (4.2) | 59.5 (3.9) | 0.0 (1.6) | 0.96 | 0.5 | 2.3 |
| L | 58.0 (5.0) | 58.6 (5.0) | 0.7 (2.1) | 0.95 | 0.6 | 3.0 | 58.2 (4.0) | 58.4 (4.3) | 0.2 (1.4) | 0.97 | 0.5 | 2.0 | |
| Step width [cm] | R | 8.9 (3.5) | 8.1 (4.0) | −0.8 (3.5) | 0.72 | 1.6 | 5.5 | 12.8 (2.3) | 12.6 (2.6) | −0.3 (1.2) | 0.94 | 0.7 | 1.7 |
| L | 10.1 (4.4) | 9.9 (3.6) | −0.1 (4.1) | 0.64 | 1.5 | 6.6 | 12.0 (2.1) | 11.8 (2.5) | −0.2 (1.1) | 0.94 | 0.8 | 1.6 | |
| Single support [%] | R | 35.2 (2.3) | 35.6 (2.2) | 0.4 (1.1) | 0.93 | 0.7 | 1.6 | 39.9 (0.9) | 39.8 (0.9) | 0.0 (0.5) | 0.89 | 0.9 | 0.8 |
| L | 36.0 (2.1) | 36.4 (2.6) | 0.4 (1.3) | 0.91 | 0.9 | 1.9 | 39.8 (0.8) | 39.7 (0.7) | 0.0 (0.3) | 0.95 | 0.6 | 0.5 | |
| Double support [%] | R | 29.0 (3.9) | 28.2 (4.2) | −0.8 (1.9) | 0.94 | 0.7 | 2.7 | 20.4 (1.5) | 20.4 (1.5) | 0.1 (0.7) | 0.95 | 0.6 | 1.0 |
| L | 29.0 (4.0) | 28.1 (4.4) | −0.8 (2.0) | 0.94 | 0.7 | 2.8 | 20.4 (1.5) | 20.4 (1.5) | 0.0 (0.7) | 0.95 | 0.6 | 0.9 | |
| Gait speed [cm/s] | 121.8 (12.4) | 123.3 (12.9) | 0.1 (0.2) | 0.97 | 0.5 | 6.5 | 114.2 (3.7) | 114.3 (3.8) | 0.0 (0.0) | 1.00 | 0.2 | 0.7 | |
| Range of trunk tilt T2 to T5 [°] | R | 10.0 (2.4) | 9.8 (2.8) | −0.2 (1.2) | 0.94 | 0.7 | 1.7 | 3.3 (2.1) | 3.5 (1.9) | 0.2 (1.4) | 0.87 | 1.0 | 2.0 |
| L | 10.0 (2.4) | 9.8 (2.7) | −0.2 (1.2) | 0.94 | 0.7 | 1.7 | 3.3 (2.1) | 3.5 (1.9) | 0.2 (1.3) | 0.88 | 0.9 | 1.9 | |
| Range of pelvic tilt T1 to T4 [°] | R | 4.8 (2.6) | 4.6 (2.3) | −0.2 (1.1) | 0.95 | 0.6 | 1.5 | 5.2 (2.1) | 5.1 (2.0) | −0.1 (1.0) | 0.94 | 0.7 | 1.4 |
| L | 4.7 (2.5) | 4.5 (2.3) | −0.2 (1.1) | 0.95 | 0.6 | 1.5 | 5.2 (2.1) | 5.1 (2.0) | −0.1 (1.0) | 0.94 | 0.7 | 1.4 | |
| Range of hip flexion-extension T1 to T4 [°] | R | 35.0 (3.5) | 35.3 (4) | 0.4 (1.9) | 0.93 | 0.8 | 2.8 | 32.9 (3.3) | 33.2 (3.6) | 0.3 (1.6) | 0.95 | 0.7 | 2.3 |
| L | 35.3 (4.0) | 35.6 (3.8) | 0.3 (2.5) | 0.89 | 0.9 | 3.6 | 33.4 (3.6) | 33.1 (3.6) | −0.3 (1.8) | 0.93 | 0.7 | 2.6 | |
| Range of hip adduction-abduction T4 to T5 [°] | R | 7.7 (2.3) | 7.7 (2.4) | 0.0 (1.8) | 0.83 | 1.2 | 2.7 | 5.1 (1.0) | 5.2 (1.1) | 0.2 (0.5) | 0.93 | 0.8 | 0.8 |
| L | 8.6 (2.4) | 8.9 (2.8) | 0.3 (1.9) | 0.85 | 1.2 | 2.8 | 4.9 (1.0) | 4.9 (1.1) | 0.0 (0.6) | 0.92 | 0.8 | 0.8 | |
| Range of knee flexion-extension T4 to T5 [°] | R | 34.9 (6.2) | 34.2 (7.1) | −0.8 (3.0) | 0.95 | 0.7 | 4.2 | 22.4 (2.6) | 22.9 (2.6) | 0.5 (1.2) | 0.94 | 0.7 | 1.7 |
| L | 37.3 (6.4) | 36.2 (6.5) | −1.0 (2.6) | 0.96 | 0.6 | 3.7 | 22.0 (2.6) | 22.2 (3.1) | 0.1 (1.6) | 0.91 | 0.9 | 2.4 | |
| Range of ankle dorsi flexion. T4 to T5 [°] | R | 23.2 (4.0) | 22.6 (4.0) | −0.6 (2.1) | 0.92 | 0.8 | 3.1 | 15.6 (1.6) | 15.4 (2.0) | −0.2 (1.6) | 0.77 | 1.5 | 2.4 |
| L | 22.6 (3.5) | 23.2 (3.3) | 0.5 (2.1) | 0.89 | 0.9 | 3.1 | 14.9 (1.6) | 15.1 (1.9) | 0.2 (1.2) | 0.87 | 1.1 | 1.7 | |
| Range of ankle inv.-ev. T1 to T3 [°] | R | 8.1 (4.2) | 9.5 (5.2) | 1.4 (3.3) | 0.86 | 1.1 | 4.8 | 9.1 (3.7) | 9.3 (3.9) | 0.2 (1.6) | 0.95 | 0.6 | 2.3 |
| L | 8.5 (3.9) | 9.2 (4.3) | 0.7 (3.0) | 0.84 | 1.2 | 4.5 | 8.8 (3.8) | 8.8 (4.2) | 0.0 (1.3) | 0.97 | 0.5 | 1.8 | |
| MDCs in the Literature | MDCs in This Study | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [93] | [94] | [95] | [96] | [97] | [92] | MH-IMU | MH OPT | ||
| Spatio-temporal variables | |||||||||
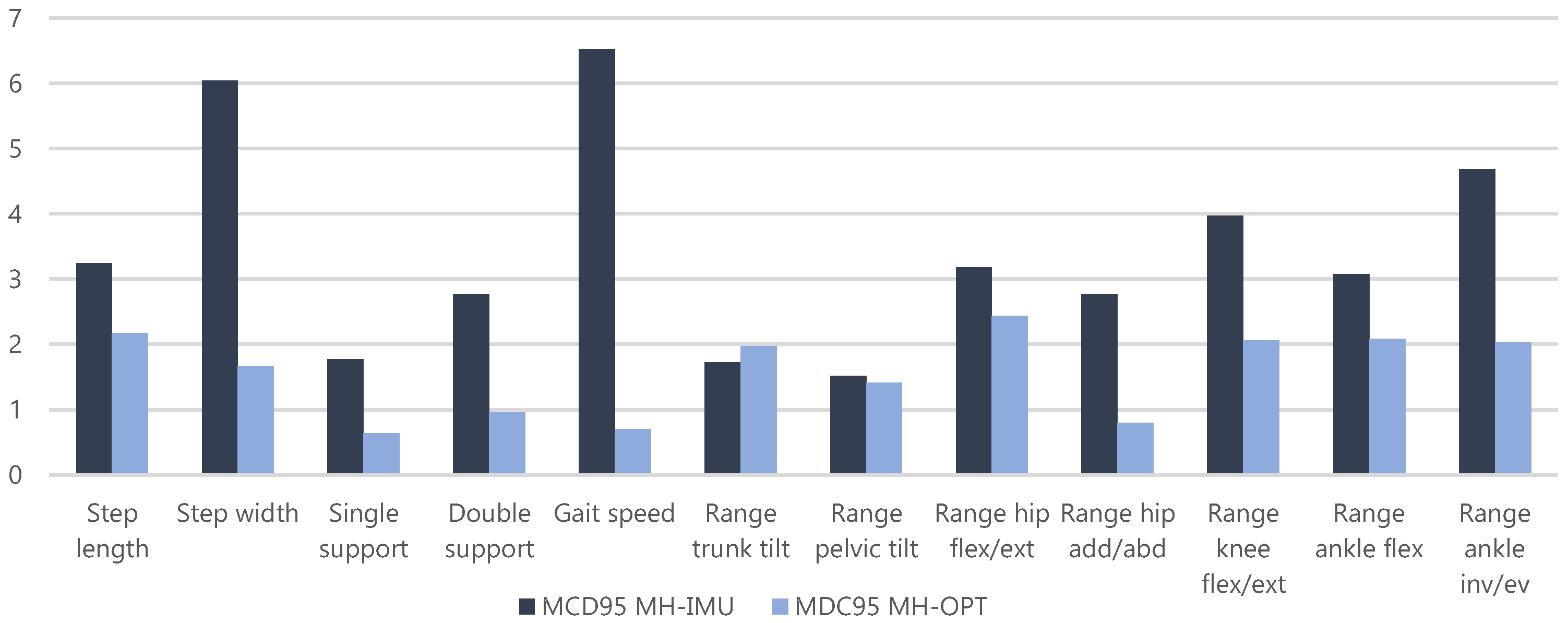
| Step/Stride length [cm] | 8.0 | 8.0 | - | 4.0 | 5.4 | 11.0 | 10.0 | 3.2 | 2.2 |
| Step width [cm] | 3.0 | 2.0 | - | 2.0 | 2.3 | - | - | 6.0* | 1.7 |
| Average of gait phases [%] | 1.9 | - | - | - | - | 1.5 | 1.7 | 2.3* | 0.8 |
| Gait speed [cm/s] | 17.0 | 12.0 | - | 9.0 | 15.0 | 12.0 | 7.0 | 6.5 | 0.7 |
| Kinematic variables [°] | |||||||||
| Range of trunk tilt | - | 2.5 | 1.1 | - | - | - | - | 1.7 | 2.0* |
| Range of pelvic tilt | 1.9 | 4.4 | 2.5 | - | - | - | - | 1.5 | 1.4 |
| Range of hip flexion/extension | 4.4 | 8.3 | 2.7 | 3.0 | 3.3 | - | - | 3.2 | 2.4 |
| Range of hip adduction/abduction | 3.0 | 5.1 | 2.6 | 2.0 | 5.5 | - | - | 2.8 | 0.8 |
| Range of knee flexion/extension | 4.0 | 4.5 | 5.1 | 3.0 | 3.5 | - | - | 4.0 | 2.1 |
| Range of ankle dorsi/plantar flexion | 8.7 | 4.1 | 3.5 | - | 8.5 | - | - | 3. 1 | 2.1 |
| Range of ankle inversion eversion | - | 9.6 | - | - | - | - | - | 4.7 | 2.0 |
| Study details | |||||||||
| Experimental conditions | Floor | Floor | Floor | Treadmill | Treadmill | Floor | Treadmill | Floor | Treadmill |
| MoCap technology | Full body optical | Full body optical | Full body optical | Full body optical | Lower body optical | Feet placement IMU | Full body IMU | Full body optical | |
| Sample | 30 (18F, 12M) | 23 (12F, 11M) | 29 (15F, 14M) | 20 (10F, 10M) | 23 (23M) | 39 (14F, 25M) | 33 (13F, 20M) | ||
| Age | 30 ± 6.8 | 35 ± 7.3 | 24 ± 5.7 | 25 ± 4.0 | 35 ± 5.1 | 23 ± 6.2 | 22 ± 2.9 | ||
| Rater | Same | Same | Same | Same | Same (except for anatomical measures) | Not found | Same | ||
| Time | 1 to 14 days | One week | 5.6 ± 2.2 days | One week | 5 ± 3.0 days | More than one day | Three hours | ||
| Notes | Gait phases averaged: Foot off, Opposite foot contact, and Opposite foot off. MDC from stride length. | They do not provide ranges of movement. We have averaged the MDC of the peaks. MDC from stride length. | Data from ‘intrarater intersession’ at ‘FR3’ speed. | Some ranges are from max. to min. and others from one gait event to another. MDC from step length. | Right and left sides averaged. MDC from step length. | Gait phases averaged: Stance and Swing. Feet IMU placement selected; this was preferred by the authors. MDC from stride length. | Gait phases averaged: Single and double support. Right and left sides averaged. The ranges are from one gait event to another. MDC from step length. | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marín, J.; Blanco, T.; de la Torre, J.; Marín, J.J. Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection. Sensors 2020, 20, 3338. https://doi.org/10.3390/s20123338
Marín J, Blanco T, de la Torre J, Marín JJ. Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection. Sensors. 2020; 20(12):3338. https://doi.org/10.3390/s20123338
Chicago/Turabian StyleMarín, Javier, Teresa Blanco, Juan de la Torre, and José J. Marín. 2020. "Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection" Sensors 20, no. 12: 3338. https://doi.org/10.3390/s20123338
APA StyleMarín, J., Blanco, T., de la Torre, J., & Marín, J. J. (2020). Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection. Sensors, 20(12), 3338. https://doi.org/10.3390/s20123338





