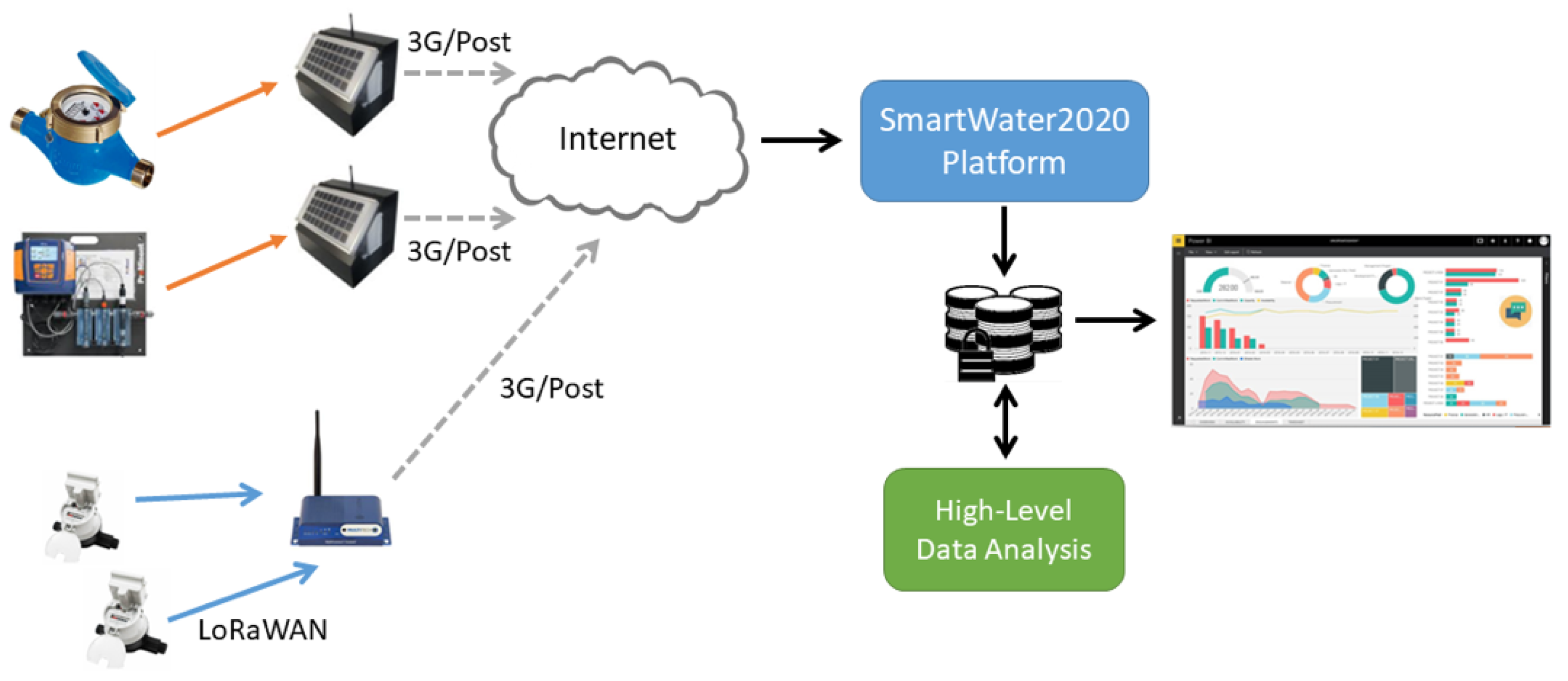
1. Introduction
Drinking water supplies face pressing issues, particularly in island regions, where climate change, water scarcity, pollution, and the high cost of desalination are putting pressure on water distribution organisations. At the same time, 15–25% of the drinking water produced is lost via invisible leakages, which represent a main contributor to non-revenue water. From an economic perspective, the cost of lost water worldwide, due to leakages, metering errors and non-billed consumption, is about US
billion annually [
1]. In addition, the volume and indicators of non-revenue water vary with variations in the system input volume, which is even more critical for monitoring non-revenue water for systems alternating between intermittent and continuous supply [
2]. The challenge for water utility companies is to save resources, thus improving water sustainability. To this end, innovative monitoring and control technologies to reduce water loss are increasingly gaining the interest of the water management communities.
Specifically, water utility companies progressively transform their obsolete water distribution networks (WDNs) to smart infrastructures by exploiting modern Information Communication Technologies (ICT) [
3]. A smart water network infrastructure aims at reducing telemetry costs, detecting leakages in a timely fashion, monitoring the non-revenue water, and visualizing the available data in a user-friendly way. A typical architecture of such an infrastructure consists of two main entities, depending on the functionalities they offer and their spatial location in the space, namely, at the edges of the network (i.e., the hydraulic network of pipes, the consumers’ buildings, etc.) and in the control center [
4]. Our subsequent analysis focuses on the edges of the water network, since the need to satisfy any energy and computational constraints mainly refers to this specific part of the architecture.
In the literature, we often find an additional partition at the edges of the network, namely between a physical infrastructure and the smart sensors [
5,
6,
7]. Specifically, the physical infrastructure includes the tanks where the water is stored, the pipes through which the water is distributed to the network, joints for pipes connection, and water meters to record consumption. Systematic recording of the technical characteristics of the physical infrastructure is imperative, since they affect the hydraulic models and processing of the observed data. Such parameters include, among others, the pipes’ length, diameter and roughness; pump curves and settings; and the number of tanks and their dimensions [
8]. On the other hand, the smart sensors are the part of the architecture associated with the collection, processing, and transmission of the relevant data. These sensors are utilized to control water quality, pressure, and flow, while modern smart meters also provide leakage detection and notification capabilities. In addition, the smart sensing infrastructure also includes all the appropriate network components, such as transmitters and gateways, to send the observed data to a control center for further analysis.
Smart sensing technologies are based on the development of smart metering and sensing devices [
9,
10], in conjunction with advanced numerical methods for high-level data analysis [
11,
12,
13]. Compared to traditional metering devices, smart metering deployments are a key component for the realization of smart environments, since they enable multiple capabilities to water utility companies and consumers, such as accurate data collection, backflow measurements, which is widely used problem indicator in water systems, while they are less susceptible to corrosion. The data collected from a smart infrastructure enables to better comprehend water demands, which further influences the efficient design of urban water supply networks.
Recording and analyzing data in real time allows water utilities to perform various critical tasks, such as identifying leakages, fixing system’s malfunctions, timely scheduling infrastructure maintenance, and essentially enabling them to achieve sustainable water use [
14]. To this end, existing water management systems primarily rely on energy consuming above-ground deployments to monitor and transmit water network states, such as water flow and pressure, to a server periodically, typically via the mobile cellular networks, in order to detect abnormal events such as water leakages and bursts [
15,
16,
17]. Nevertheless, more than
of water network assets are placed at a considerable distance from power resources and often in geographically remote areas. Such constraints put big challenges on current approaches making them unsuitable for next generation smart water networks.
To overcome these limitations, traditional water metering devices of mechanical type, are gradually replaced by sophisticated battery-driven wireless sensor networks, which are emerging as an effective alternative solution for large-scale smart water management systems [
18]. However, the main challenge of these infrastructures is that sensor nodes typically consume a lot of energy to record and transmit high-precision data [
19]. This constraint limits the amounts of data that can be sensed and relayed for analysis, which is necessary for timely and reliable anomaly detection (e.g., leakages and bursts) and alerting. To address this problem, reducing the volume of data that are transmitted to a control center for further processing is a critical task. To this end, data compression mechanisms are integrated on the sensor network’s side. The role of data compression in WDN management is twofold: (i) increase the system’s autonomy by reducing the energy consumption; and (ii) reduce telemetry costs for the water utility companies. To this end, reduction of data volumes is achieved by algorithms roughly classified into: (a) lossless compression methods, when perfect data reproduction is required; and (b) lossy compression methods, when perfect reproduction is either impossible or requires too many bits [
20].
Each compression method has its own advantages and limitations. Specifically, in lossless compression [
21,
22], the recorded data stream can be reconstructed completely without losing information, while lossy compression [
23,
24,
25] introduces a reconstruction error. Nevertheless, in contrast to lossless compression, which places an upper bound on the compression performance, lossy compression can significantly reduce the amount of data, and consequently the communication cost without sacrificing the meaningful information content.
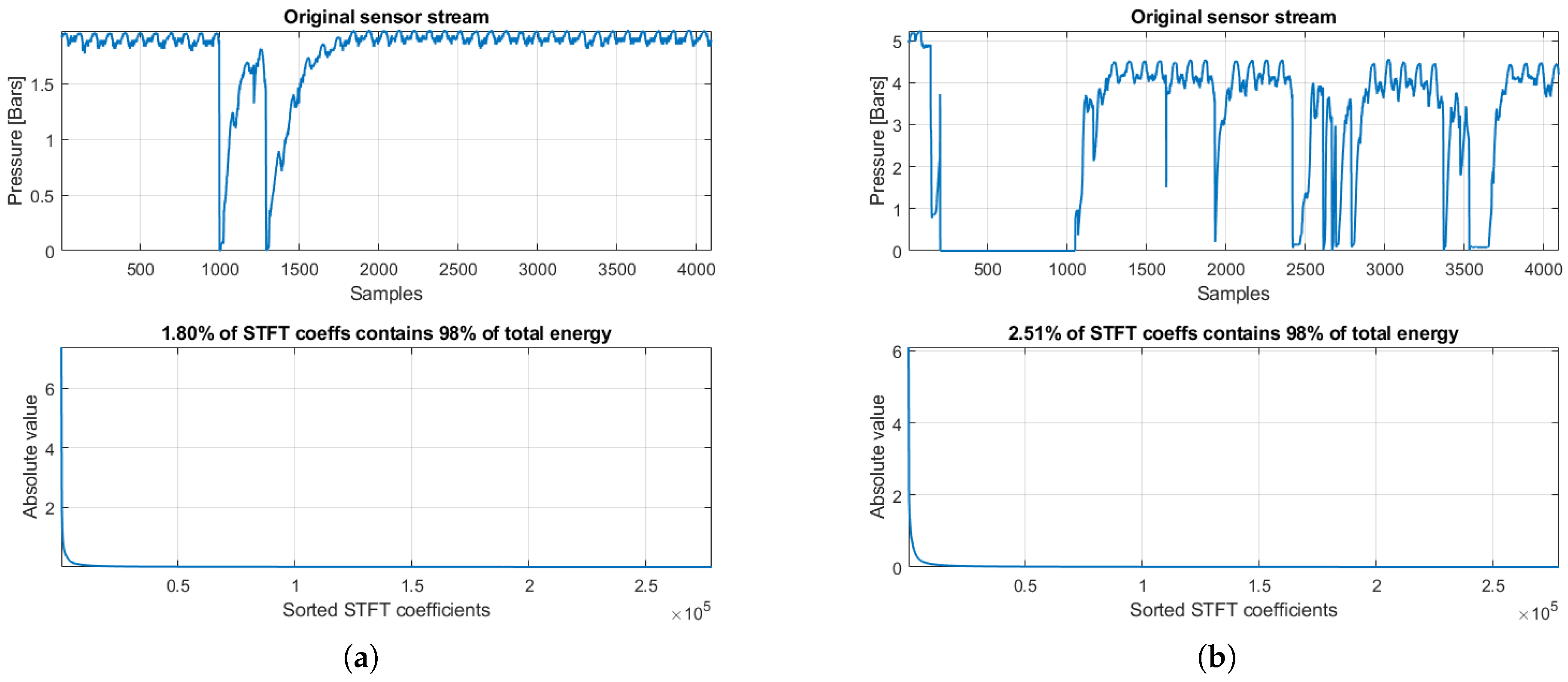
Focusing on time series data, existing lossless and lossy compression methods are applied primarily on temporal samples, with the sampling process being largely dominated by the traditional Nyquist–Shannon theory. According to this theory, the exact recovery of a discrete signal requires a sampling rate twice the signal’s bandwidth. Moreover, the sampling scheme characteristics can have dramatic consequences on the quality of the recorded signals, the hardware necessary to achieve the required quality and therefore the cost, time, and effort that accompany the process. Nevertheless, several studies have shown that many natural signals are amenable to highly sparse representations in appropriate transform domains (e.g., wavelets and sinusoids) [
26,
27]. This means that the resulting vector of transform coefficients has a small number of significant (i.e., large-amplitude) elements, while the great majority of them have an amplitude equal to or near zero.
Compressive sensing (CS) provides a powerful framework for simultaneous sensing and compression [
28,
29], enabling a significant reduction in the sampling, computation, and transmission costs on a sensor node with limited memory and power resources. According to the theory of CS, a signal having a sparse representation in a suitable transform basis can be reconstructed from a small set of projections onto a second, measurement basis that is incoherent with the first one. Intuitively, this means that the vectors of the measurement basis are not statistically correlated with the vectors of the sparsity basis. In the framework of smart water networks, the advantages of CS have recently been exploited for reducing the amount of transmitted pressure data, thus extending the battery life of sensor nodes deployed in a WDN demonstrator [
30], while still maximizing the received information to data centers. Nevertheless, this study was performed in a rather ex post fashion, in the sense that the principles of CS were applied on the recorded full-resolution time series under simulated sensing and water network conditions. Despite the well-established and mathematically rigorous foundations of CS, most of the focus is given on the algorithmic perspective, while the real benefits of CS in practical scenarios are still underexplored.
To address this problem, this work investigates the advantages of implementing a CS mechanism for lossy data compression on real sensing devices utilized in a real urban WDN, in terms of execution speedup and reduced energy consumption, when compared against a lossless compression alternative that is widely used in commercial hardware solutions. It is also important to emphasize that a water management system is required to manage confidential data, such as household consumption. Traditional systems employ a separate software- or hardware-based component to encrypt sensitive data, which increases the deployment cost of the overall infrastructure. In this work, we also demonstrate the efficiency of CS as an effective mechanism for simultaneous data compression and weak encryption, ensuring data confidentiality with high probability, in real smart water network scenarios.
The rest of the paper is organized as follows.
Section 2 overviews the basic concepts of CS for data compression, and describes our CS-based system architecture enabling weak data encryption.
Section 3 analyzes the complete hardware and software platform, which is utilized to quantify the efficiency of CS in a real setting. In
Section 4, the performance of CS is evaluated and compared against lossless compression on real pressure data.
Section 5 summarizes the main results and proposes directions for further research.
3. Hardware Benchmark
To prolong the network’s lifetime, end devices of smart water networks are typically equipped with hardware that achieves low-power operation, both by minimizing the on-board components only to the bare minimum required by the application and by providing features that enable components to operate in low-power mode (e.g., MCU deep sleep and radio deactivation). It is common practice for embedded operating systems running on the devices to provide these features as energy-saving options to upper layers (i.e., applications) as well as inherently make extensive use of them [
43].
Among all the operations performed on the devices, which in our case perform monitoring of a low-frequency phenomenon (water pressure), the communication task is known to be the most power-hungry, due to the high energy consumption of the radio circuitry. Thus, compression techniques employed at the application layer can offer substantial energy savings by minimizing data transmission, at the cost of additional data processing. Lossy CS-based compression, used in this work, can be tuned at a high compression rate, without compromising the decompression fidelity. Most importantly, its processing overhead is significantly smaller than the one imposed by a lossless compression alternative that is widely used in commercial hardware solutions.
A common strategy for assessing the degree to which low-power operation satisfies an application’s requirements, is to employ the so-called software-based energy profiling, performed through enabling appropriate software modules of the embedded operating system. In this section, we describe the hardware platform, software components (along with implementation details) and energy profiling tools used for assessing the energy efficiency of the proposed CS-based scheme.
3.1. Hardware Platform
In the following benchmarking, we use the Zolertia RE-Mote platform, an ultra-low power hardware development platform designed jointly by universities and industrial partners, in the framework of the European research project RERUM [
44]. RE-Mote is a flexible platform that can support several wireless sensor networks and Internet-of-Things (IoT) applications, such as smart building automation, environmental monitoring, and Smart Cities applications. It is based on the Texas Instruments CC2538 ARM Cortex-M3 32MHz System on Chip (SoC) (
https://www.ti.com/product/CC2538), with an on-board 2.4 GHz IEEE 802.15.4 Radio Frequency (RF) interface, 512KB flash memory, and 32KB RAM, as well as an 868 MHz IEEE 802.15.4 compliant RF interface (CC1200). Dual-radio support makes it suitable both for short-range/indoor and long-range/outdoor applications. Additionally, RE-Mote platform offers different interfaces (e.g., Inter-integrated Circuit (I2C), Serial Peripheral Interface (SPI), and Universal Asynchronous Receiver Transmitter (UART)) for connecting a multitude of analog and digital sensors. The platform can be battery-operated and hosts a built-in battery charger for LiPo batteries.
3.2. Software Description
3.2.1. Contiki OS
Contiki OS is a popular open source operating system for wireless sensor networks, originally proposed in [
45], which targets resource-constrained embedded devices. Recognizable for its high portability, it has been ported to several small microcontroller architectures, such as AVR, MSP430, and TI CC2538. The operating system is implemented in C programming language and uses a make/build environment for cross-compilation on most platforms. It follows an event-driven programming model along with a cooperative scheduling approach based on proto-threads [
46], essentially a lightweight mechanism for pseudo-threading that helps minimizing the memory footprint of the OS. This way, it provides a thread-like programming style, which is attractive from a developer’s perspective, although different from conventional multi-threading, in the sense that proto-threads do not have any dedicated memory allocation and all processes share a common stack.
A useful characteristic of Contiki OS, which is of high relevance for evaluating the CS-based scheme proposed herein, is a software-based mechanism for profiling communication and computation power consumption of embedded devices. It is further noted that, in this work, we use the latest version of the OS, namely Contiki-NG. In this major upgrade of the OS, the overall code structure was revised and optimized with new configurations and a thorough cleanup of the code base, thus minimizing the final binary size.
3.2.2. Network Stack
The protocol stack architecture used in this work is in accordance with the Internet Engineering Task Force (IETF) recommended stack, as illustrated in
Figure 7. The protocol layers are briefly described in the next subsections.
IEEE 802.15.4
IEEE 802.15.4 is a standard, which defines both the physical and MAC layer for Low Power Wide Area Networks (LPWANs). The standard operates in both 2.4 GHz and sub-GHz frequency ranges. It was designed by bearing the following requirements in mind: very low complexity, Carrier Sense Multiple Access-Collision Avoidance (CSMA-CA) support, channel hopping, multi-node networks, ultra-low power consumption, low cost, and low data rate. It defines a maximum data rate of 250 kbits/s, depending on the modulation scheme and frequency band selected.
As of Contiki-NG, the implementation offers essentially two different choices for the MAC layer (plus one experimental for BLE radio), namely CSMA (non-beacon-enabled mode, which uses CSMA on always-on radios) and TSCH (Time Slotted Channel Hopping).
6LoWPAN
IPv6 over Low Power Wireless Personal Area Networks (6LoWPAN) defines the standard for IPv6 communication over the physical and MAC layers provided by IEEE 802.15.4. 6LoWPAN acts as an adaptation layer that handles the constraints of the physical layer for providing end-to-end native IPv6 connectivity between a low-power device and any other IPv6 network, including direct connectivity to the Internet. The most profound characteristics of 6LoWPAN are: (i) fragmentation and reassembly of IPv6 packets for supporting the IPv6 minimum Maximum Transmission Unit (MTU) of 1280 bytes; (ii) header compression; (iii) address auto-configuration; and (iv) multicast support (not natively supported by IEEE 802.15.4). In addition, mesh routing is optimized through the RPL (Routing Protocol for Low-power and lossy networks) that provides a mechanism for disseminating information over the dynamic network topology by forming a Destination Oriented Directed Acyclic Graph (DODAG) between the nodes, with the border router (sink node) being the graph’s root.
Contiki-NG achieves full IPv6 compliance through uIP6 implementation [
47]. The uIP stack has minimal memory requirements that are satisfied by adopting several strict design choices (e.g., a single packet buffer).
CoAP
The Constrained Application Protocol (CoAP) [
48] is a RESTful transfer protocol tailored to resource-constrained Internet devices. CoAP follows a request/response interaction model between application endpoints, supports built-in service and resource discovery and can be easily interfaced with HTTP, since it includes key concepts of the Web, such as URIs and Internet media types. It meets specialized requirements, such as multicast support and very low overhead. Since it was originally designed to run on unreliable UDP transport, it integrates a reliability mechanism for managing lost packets at the application layer. Apart from the synchronous request/response mechanism, CoAP supports an asynchronous notifications’ mechanism, named as OBSERVE, that is commonly used for sensor data collection. Finally, it integrates a mechanism, enabled by the Block option, that provides a minimal way to transfer larger representations in a block-wise fashion, for avoiding fragmentation in lower layers. Contiki-NG natively supports CoAP through a refactored implementation of the Erbium library.
3.2.3. Energy Profiling
Energy consumption of a hardware platform running Contiki can be estimated by utilizing the software-based online energy profiling module Energest [
49]. Energest employs power state tracking by recording the amount of time (as provided by the platform’s real-time clock) the device spends in different states. It is implemented as a collection of macros and functions; the macros inform the module on component state change and the functions are used for initializing the module and reporting elapsed time in different states. There are four basic Energest types that track four states, respectively: (a) CPU active mode (CPU); (b) CPU low-power mode (LPM); (c) radio transmission (TRANSMIT); and (d) radio listening (LISTEN). Note that there is no separate type for receiving a packet, thus reception is included in LISTEN type.
The consumed power for each mode is calculated by,
where
is the value returned by Energest (provided in CPU ticks),
denotes the average current consumption for the mode under consideration (it is hardware-specific and can be retrieved from each hardware component’s datasheet),
is the operating voltage,
is the number of CPU ticks per second for the Contiki RTIMER, and
is the time interval between two Energest tracking points. In
Table 1, we report the above values for TI CC2538 SoC.
3.3. Implementation Details
To evaluate the energy efficiency of the CS-based system, as well as to provide a comparison against the LZ77 [
21] lossless compression alternative, we utilize a simple experimental setup, which consists of a RE-Mote that performs data collection, encoding and transmission, and a gateway that receives and decodes the collected data. The gateway is built by attaching a RE-Mote, which plays the role of the 6LoWPAN border-router, to a PC, which acts as the host. IPv6 traffic between the host and the border router is bridged using Serial Line Internet Protocol (SLIP), provided by tunslip6 utility.
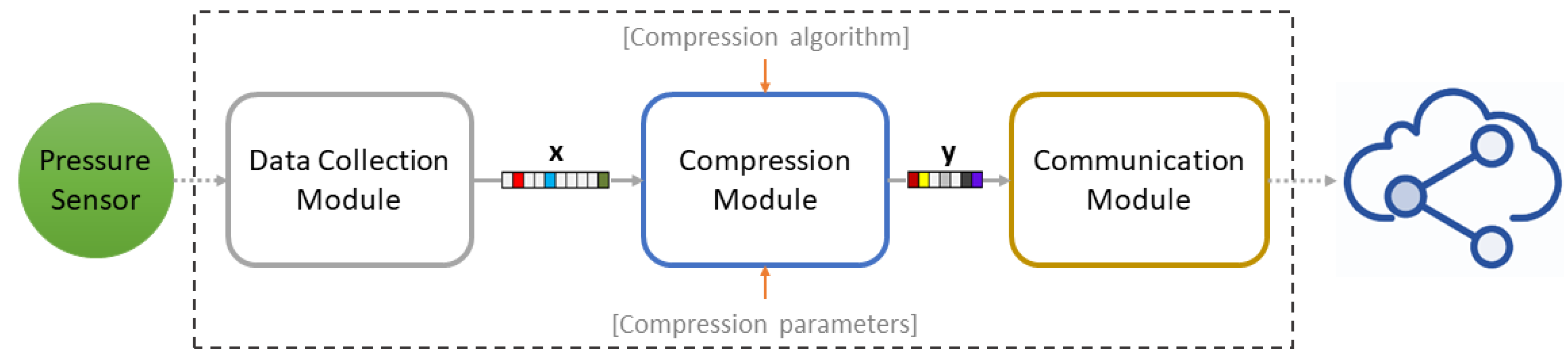
Figure 8 illustrates the software running on the data collection and compression node, which has been implemented in Contiki-NG and consists of the following three distinct modules:
The Data Collection Module is responsible for the sensor data collection. It periodically polls the sensor for value and buffers them, until a pre-defined block of values is collected.
The Compression Module, which applies the selected compression algorithm on the collected sensor data. It receives as input: (i) the buffered sensor values provided by the Data Collection Module; (ii) the compression algorithm (CS or LZ77); and (iii) the compression parameters (i.e., the measurement matrix and compression ratio for CS, and dictionary hash table size for LZ77) and outputs a block of compressed data stored in a buffer.
The Communication Module (built on the network stack described in
Section 3.2.2) receives the output of the Compression Module and sends it to the gateway. More specifically, a CoAP server exposes two CoAP resources for managing the compression and collection of compressed data, one for each alternative, namely CS and LZ77. CoAP asynchronous notifications mechanism, OBSERVE, is used for data collection, while appropriate CoAP POST requests permit compression parameters control, such as dynamic compression ratio for CS.
All data are represented as 4-bytes integers. For interfacing the output of the Data Collection Module with the input of the Compression Module, we adopt a double buffering approach, so that sensor data collection does not block while a buffered block of sensor values is being processed by the Compression Module. Additionally, we enable the Energest module for tracking power states during different phases, namely: (i) compression; and (ii) transmission of compressed data. We stress the fact that we focus on these phases, instead of performing a full energy profiling of the device, since we aim at isolating the effect of the CS methodology related to the device consumption.
On the gateway, we run a CoAP client utilizing the Eclipse Californium library (
https://www.eclipse.org/californium/), for controlling the compression ratio and observing the resources exposed by the CoAP server, running on the RE-Mote. After the per-block compressed data have been collected, the original sensor values are reconstructed and stored in a local time series database, remaining available for further processing.
Special consideration is taken for improving the efficiency of both lossy and lossless compression process. To decrease the CS compression execution time, we avoid performing a direct matrix multiplication for calculating CS measurements. Instead, considering the fact that a (partial) Hadamard measurement matrix is used, we first apply the Fast Walsh–Hadamard Transform (FWHT) to the block of sensor values, followed by the appropriate sub-sampling for attaining the selected CR. As a result, the computational complexity of CS compression reduces to
. Accordingly, since lossless compression algorithms can be in general extremely resource intensive, thus inappropriate for devices with low capabilities, we choose FastLZ (
https://github.com/ariya/FastLZ), a small, portable, and efficient byte-aligned LZ77 implementation. After some code modifications, necessary for eliminating memory allocation and usage problems, we successfully satisfied the constraints imposed by the RE-Mote platform.
4. Performance Evaluation
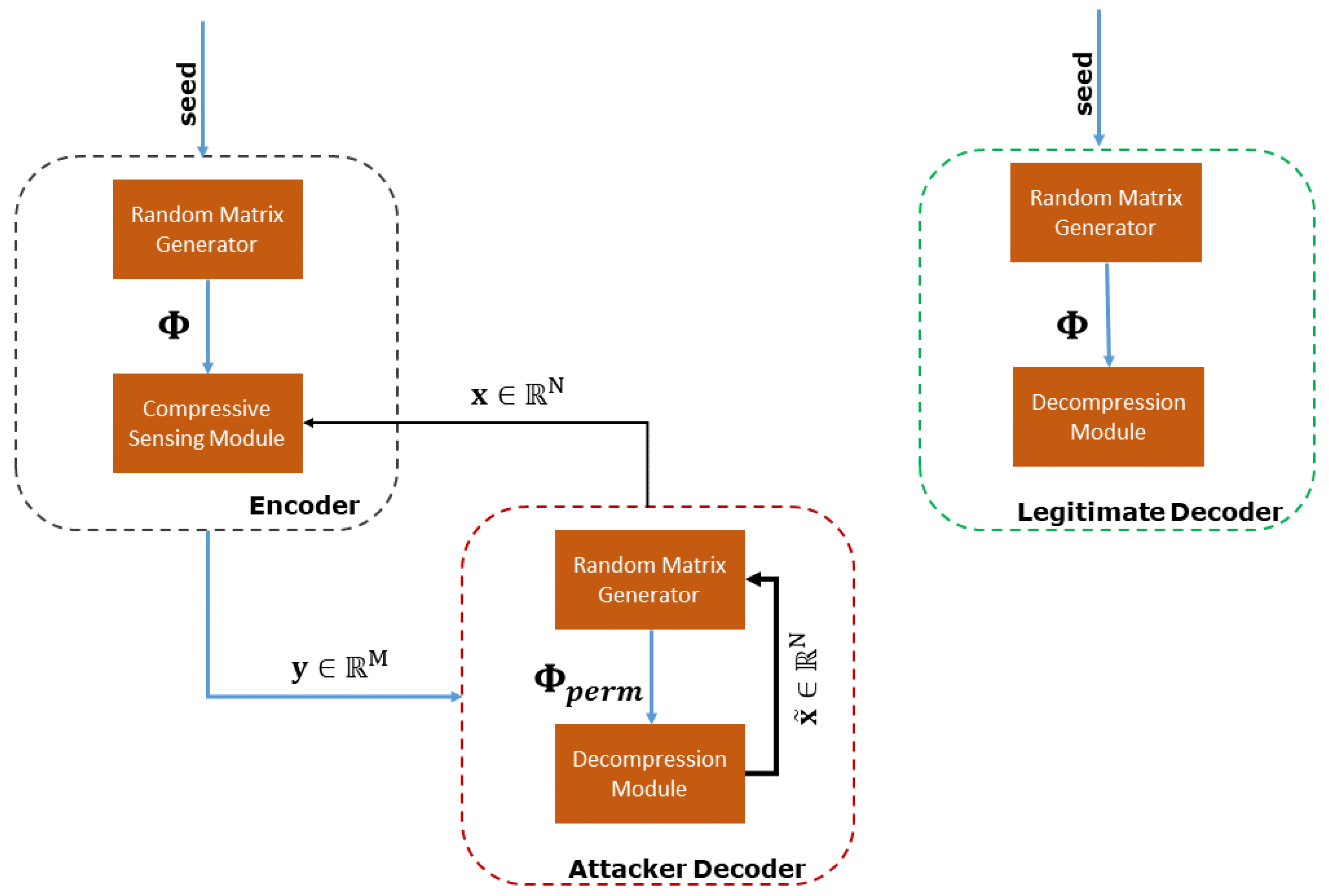
In this section, we evaluate the efficiency of the CS-based mechanism for data compression and transmission in a real smart water network test case and illustrate the execution speedup and energy consumption reduction it offers when compared against a well-established lossless compression method that is widely used in commercial solutions, namely, the LZ77 algorithm. We also quantify the energy savings achieved over the scenario of raw (uncompressed) sensor value transmission. Our experiments reveal that the CS-based mechanism can be tuned to operate at a high compression rate (), that offers almost savings in terms of transmission energy compared to LZ77 and almost savings compared to raw sensor value transmission, without compromising the decompression fidelity. In addition, we show that the CS lightweight compression mechanism imposes a substantially lower processing overhead compared to that of LZ77, which is almost constant irrespective of the compression rate selected and translates to reduced computational energy consumption. The statistical significance of our results is validated by means of the Kruskal–Wallis test. Finally, we demonstrate the encryption property that is inherent to CS under the assumption that an adversary has full knowledge of the compressed random measurements, as well as a partial knowledge of the measurement matrix up to a permutation of its rows.
4.1. Performance Metrics
We define three performance metrics for evaluating our CS-based system: compression execution time (CET), compression energy consumption (CEC), and transmission energy consumption (TEC). The CET is defined as the time the Compression Module needs for calculating the buffered compressed output after receiving a block of sensor values as input and expresses the computational overhead imposed by the compression algorithm. The CEC is the energy spent for the compression of a block of sensor values, as reported by the Energest CPU type. Finally, TEC is the energy spent by the device’s radio for transmitting the block of compressed measurements, as reported by the Energest TRANSMIT type.
We compared the performance of CS against two well-established alternatives, namely: (i) Lempel–Ziv (LZ77) lossless compression and transmission of sensor value blocks; and (ii) transmission of the raw sensor values, without any compression. In our experiments, each pressure sensor was sampled every 15 min, yielding a total of 9984 pressure values for the testing period. Three different block sizes,
N, were tested with
, in conjunction with three distinct CS compression ratios (
), with
. In terms of LZ77 implementation, we fixed the size of the dictionary hash table to be 1 KB, which we empirically found to be a good compromise between memory efficiency and the compression ratio (
). The experimental setup parameters are summarized in
Table 2.
To evaluate the effect of different compression types to the performance metrics defined here, we followed a statistical-based approach. Due to lack of normality in our dataset (as reported by Shapiro–Wilk test), we applied the non-parametric Kruskal–Wallis test, followed by Dunn post-hoc test for pairwise comparisons of compression types, in the case a significant difference in the means exists. It is noted that compression type takes values in the set {LZ77, CS-, CS-, CS-}, when considering CET and CEC. In the case of TEC, the compression type belongs to the set {Raw, LZ77, CS-, CS-, CS-}, where the value ”Raw” corresponds to the scenario of raw sensor value transmission, without applying any compression beforehand. The level of significance for all tests was set at .
4.2. Results
In this section, we present the results in terms of the performance metrics defined in
Section 4.1. As a first illustration,
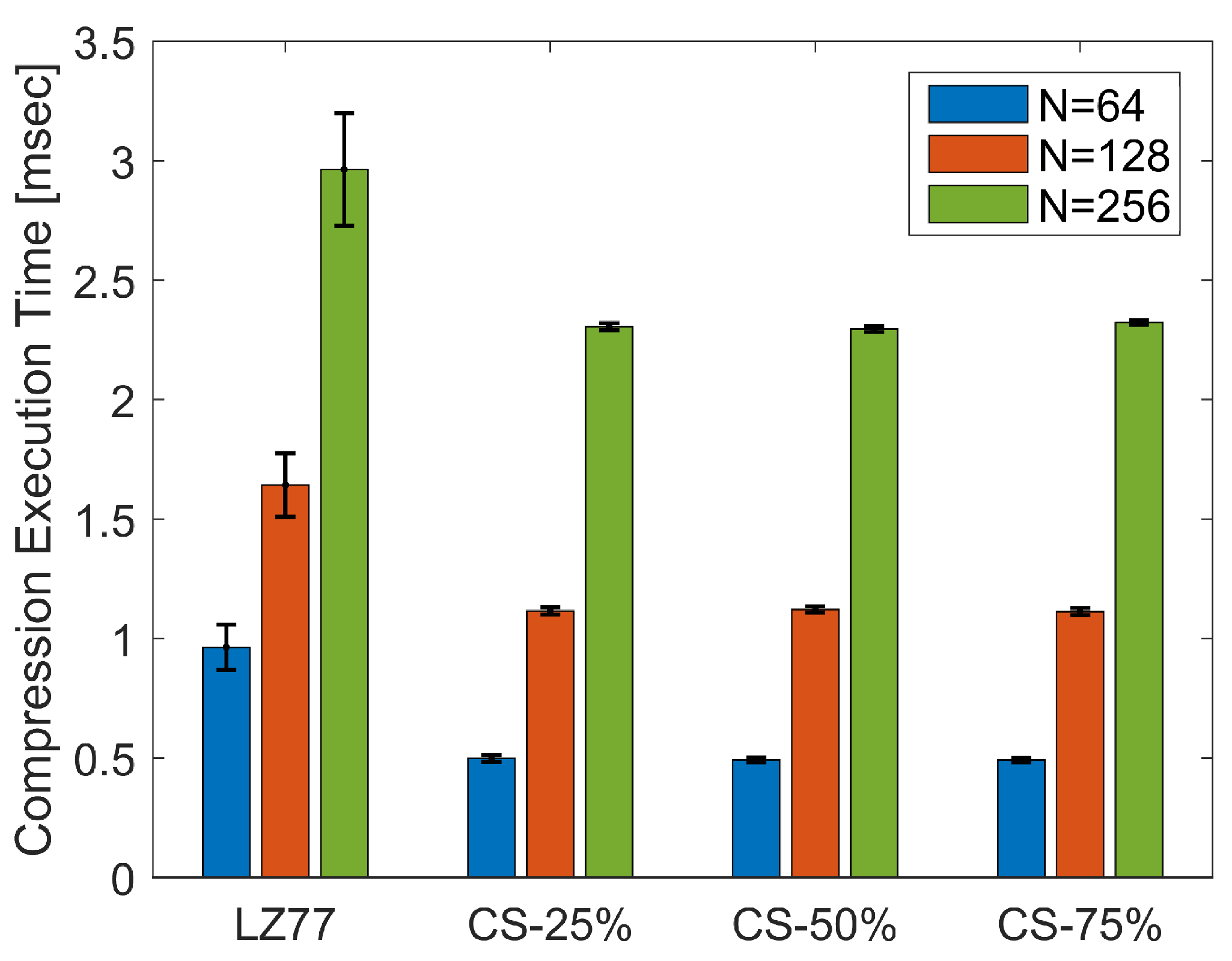
Figure 9 shows the CET average and standard deviation (displayed as error bars), over the total number of blocks of pressure values, for the three block sizes
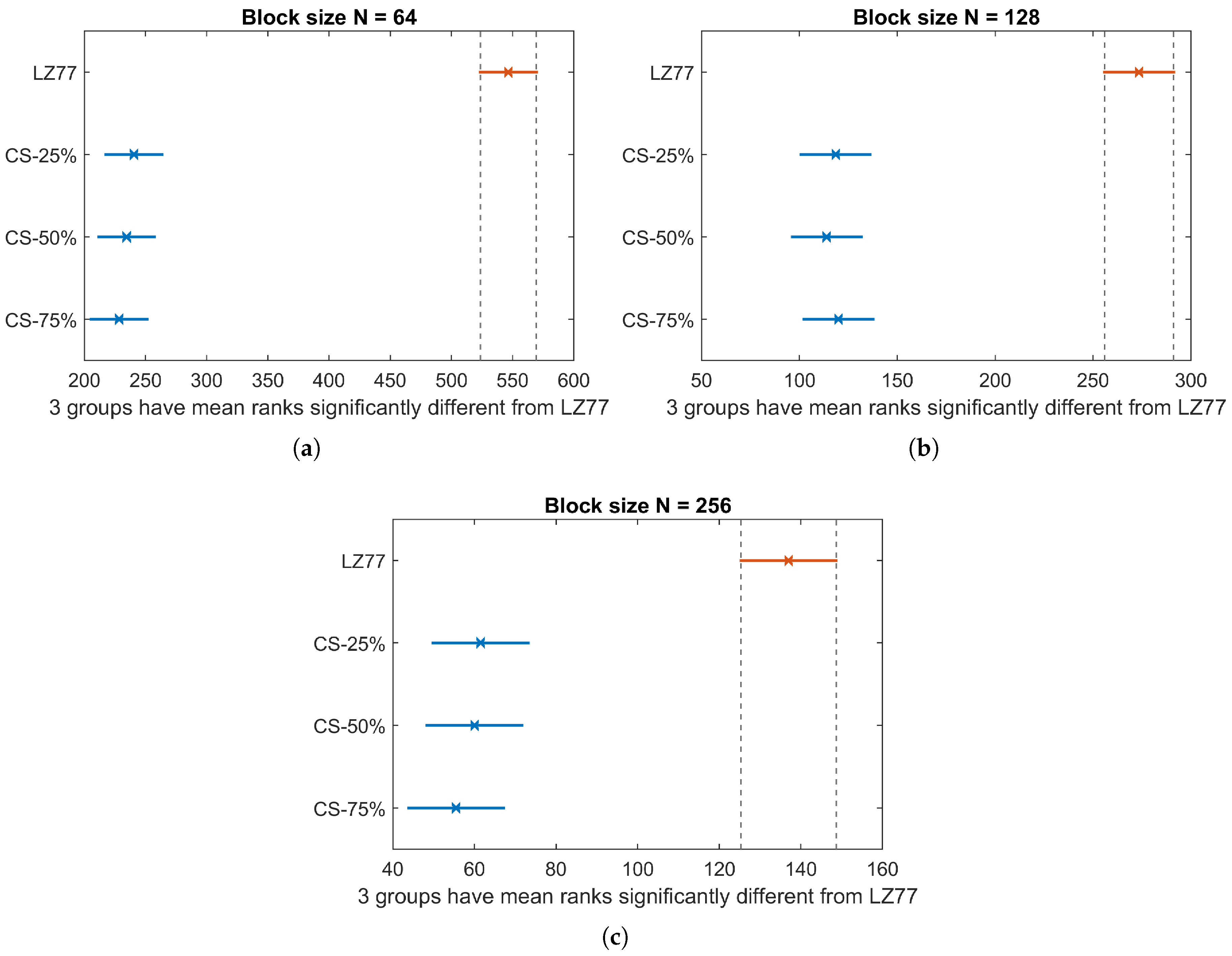
N, both for lossless (CS) and lossy (LZ77) compression. Kruskal–Wallis test revealed a significant effect of compression type on CET, for all block sizes (
,
for
,
;
for
; and
,
for
). The pairwise multiple-comparison between compression types in
Figure 10 shows a significant difference between LZ77 and CS compression for any rate
. However, CET does not differ significantly among CS with different compression rates. This is expected, since, irrespective of
, the CS calculations are dominated by the FWHT applied to the raw sensor values that, as stated before, bears a computational complexity of
.
In
Table 3, we report the average compression rate
achieved by LZ77, for the three block sizes. In any case, CS provides a compression speedup of at least
over LZ77, even for larger compression rates (
) than the ones achieved by the lossless algorithm.
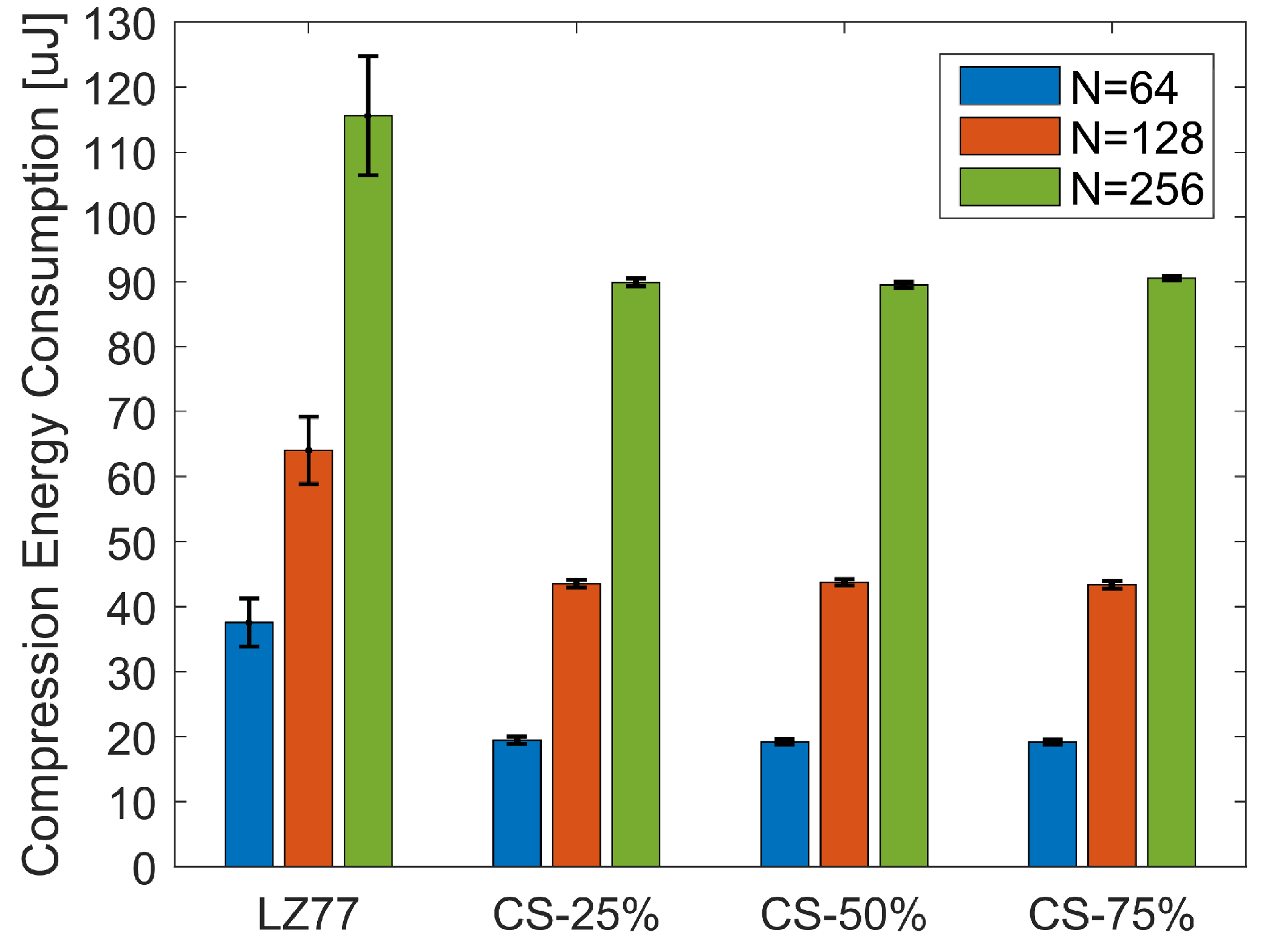
Figure 11 illustrates the CEC average and standard deviation, over the total number of blocks of pressure values, for the three block sizes
N. Similar to CET, Kruskal–Wallis analysis (
Figure 12) showed that, in terms of CEC, there is a significant difference between lossy and lossless compression (
,
for
;
,
for
; and
,
for
). No significant difference exists in CEC among different compression rates of CS, for a given block size. The average CEC and the savings of CS compression over LZ77 compression are summarized in
Table 4. Observe that, even for the smallest block size
, we achieve a compression energy saving at the order of 50%.
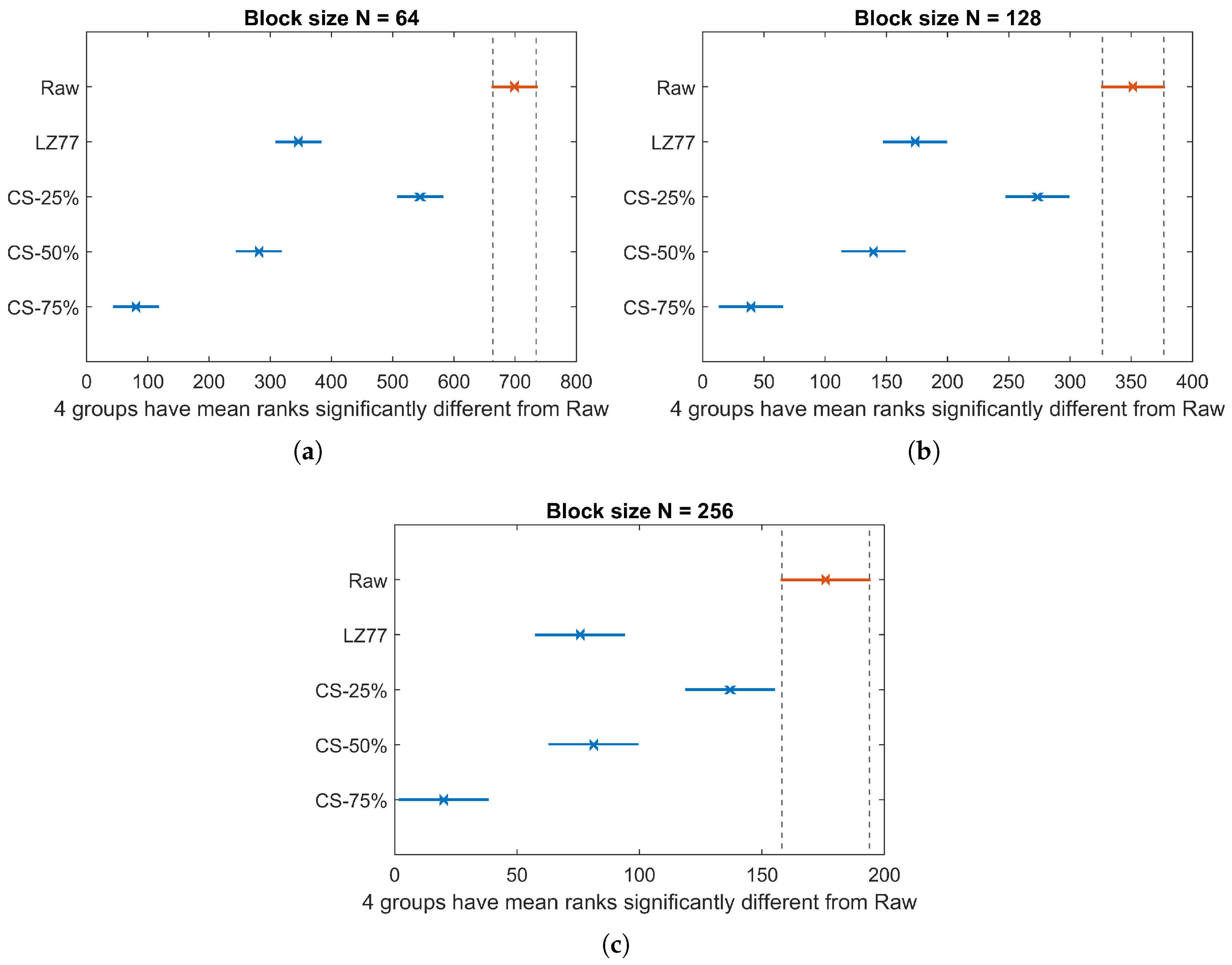
Figure 13 depicts the TEC average and standard deviation, over the total number of blocks of pressure values, for all three block sizes. Here, the energy consumption for raw sensor value transmission is labeled as “Raw” and corresponds to the worst case in terms of transmission energy cost. According to Kruskal–Wallis test, a significant effect of compression type on TEC exists for all block sizes (
,
for
;
,
for
; and
,
for
). The multiple-comparison between compression types (
Figure 14), shows a significant difference between any compression type pair, apart from the pair {LZ77, CS-50%}, whose elements share an almost equal compression rate (see to
Table 3). For all values of
N, TEC decreases as the CR increases, since less packets need to be transmitted. Finally, in
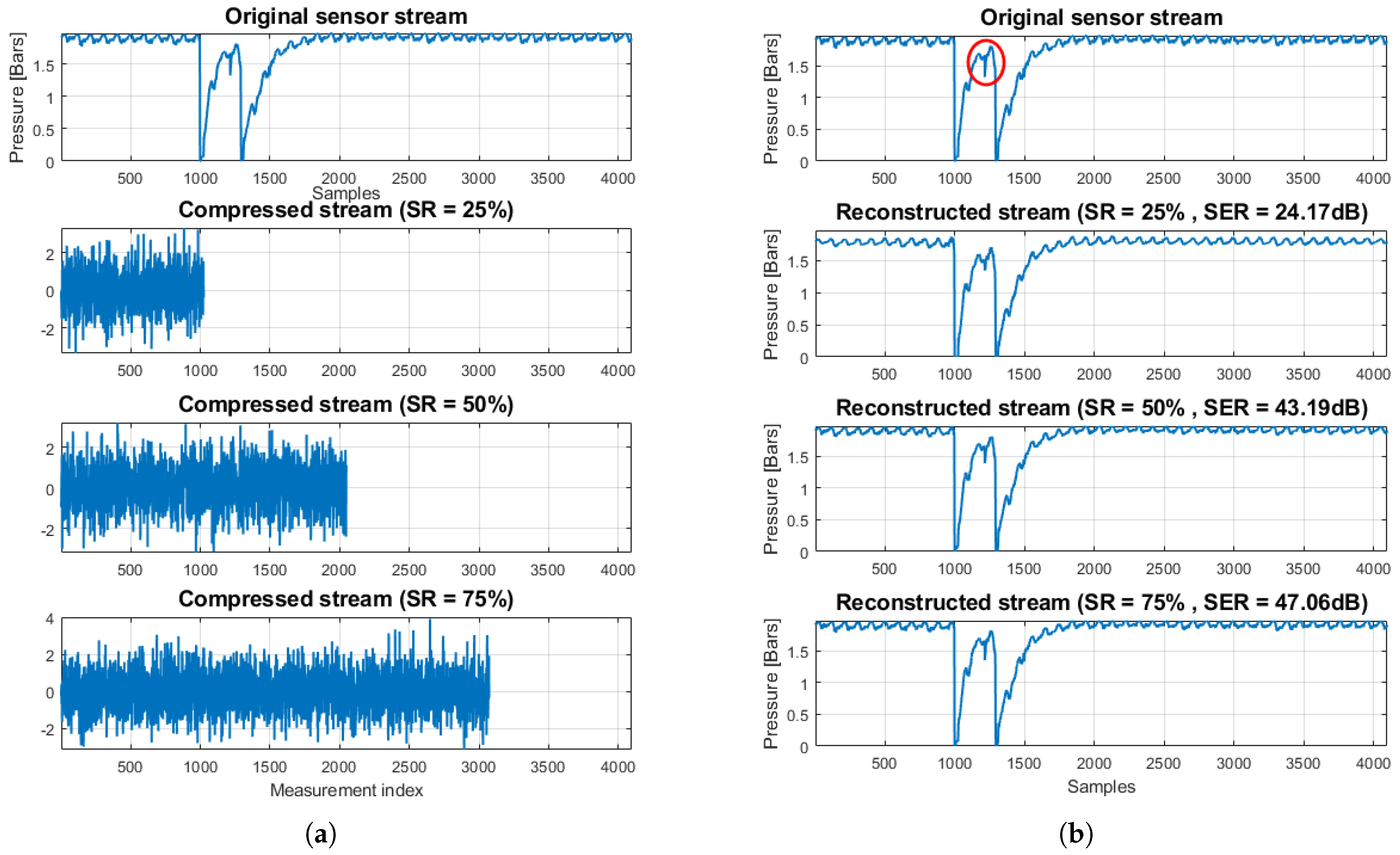
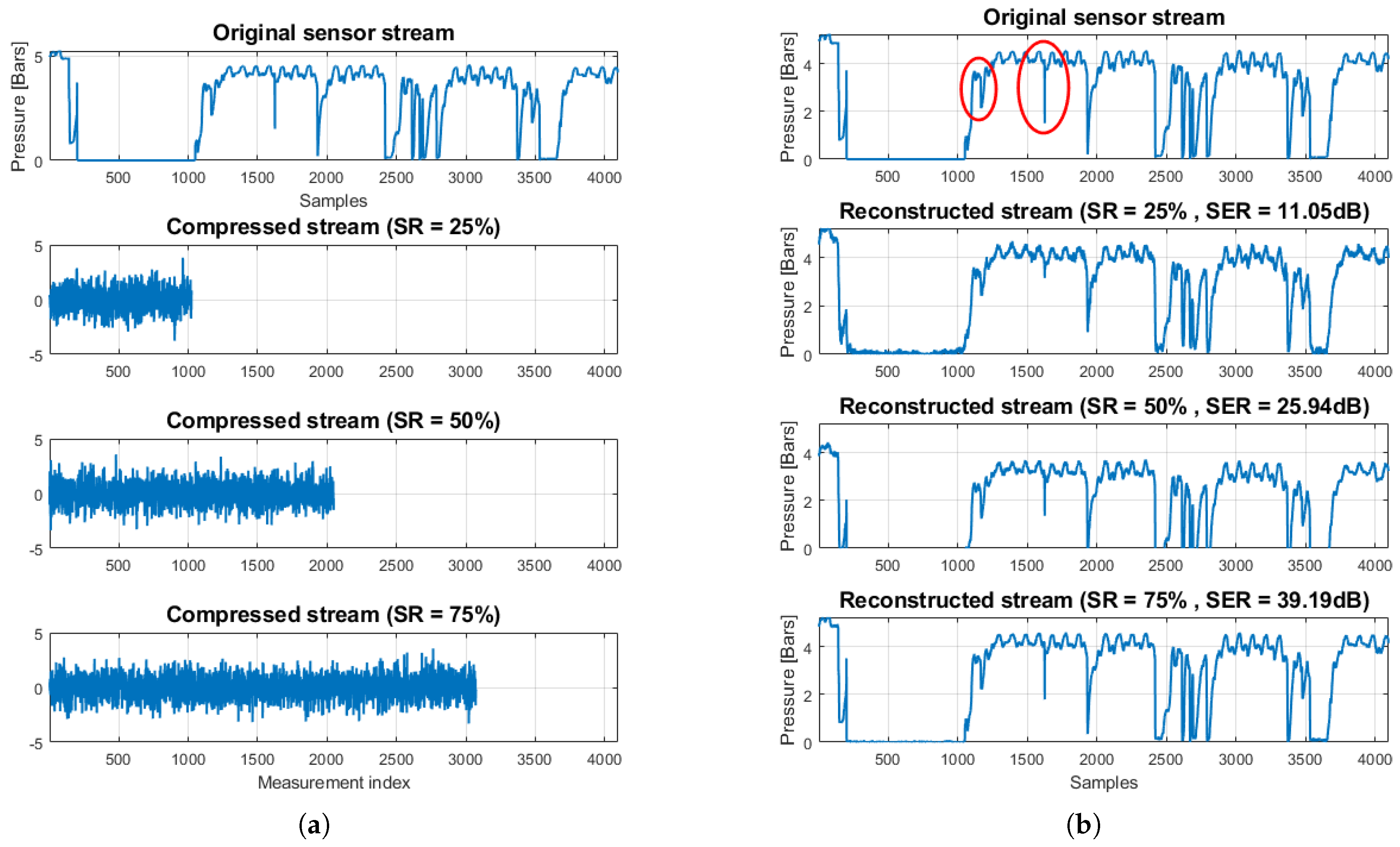
Table 5, we present the total energy consumption savings (by summing CEC and TEC averages) achieved by different compression types, against the energy spent for the transmission of raw sensor values. Observe that in all cases, a larger block size translates to better energy efficiency. This is more profound in the case of LZ77, since the algorithm’s compression efficiency improves as the number of long, repetitive words in the input data increases. Additionally, the overhead imposed by the compression algorithm (and consequently the CEC) is substantially small, so the reported total energy savings primarily result from the gain due to transmitting less data. Thus, CS can achieve significant savings compared to LZ77, if a high CR is selected. Although someone could argue that this could in general compromise the fidelity of CS decompression, we showed that the data used in this application can be accurately reconstructed, even for
as high as 75% (see
Figure 4 and
Figure 5).
As a last experiment, we demonstrated the weak encryption capability of CS. Specifically, as described in
Section 2.3, an adversary has access to the true measurement vector
, whereas the measurement matrix
is decrypted up to a permutation of a percentage
p of its rows, with
.
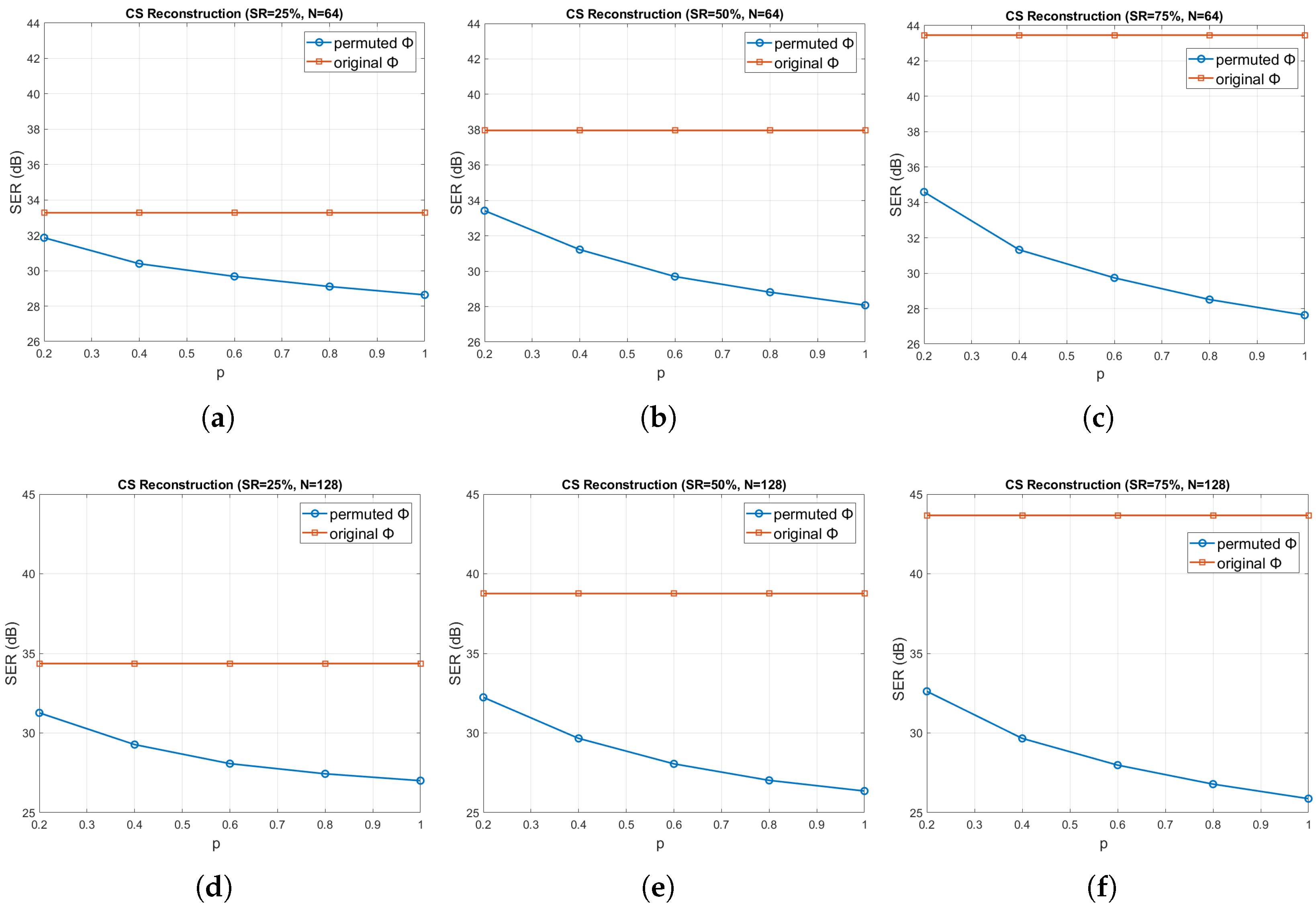
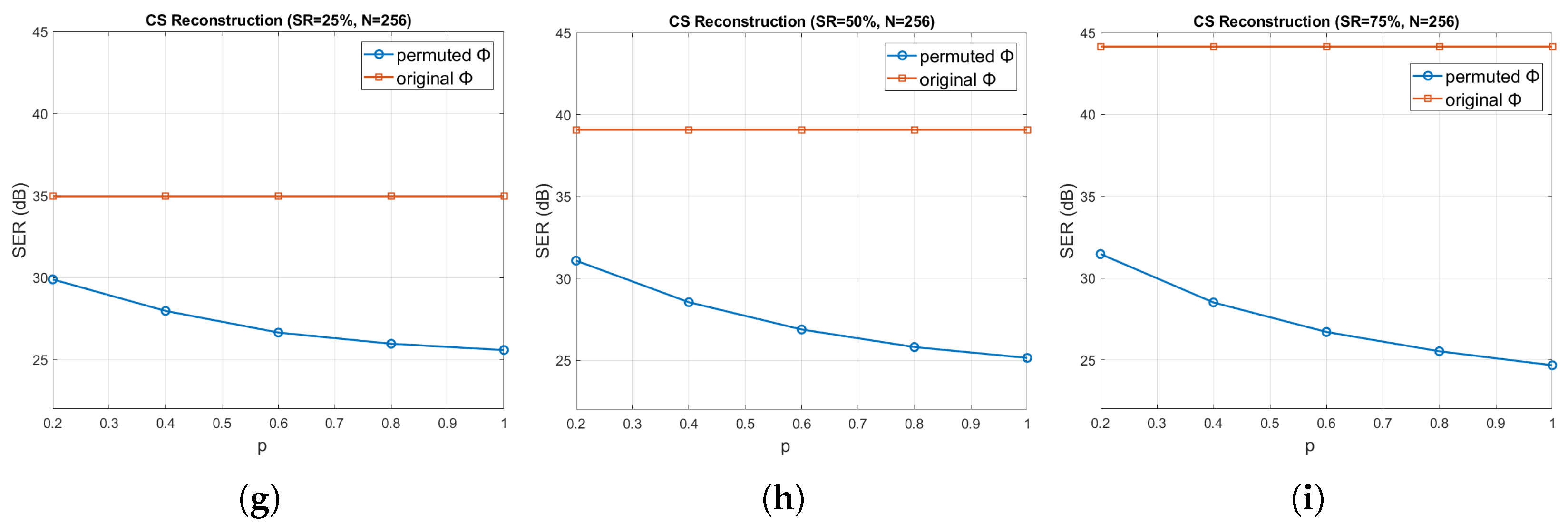
Figure 15 shows the reconstruction error, in terms of the achieved SER (in dB) averaged over all the pressure sensors, for sliding windows of length
, as a function of
p, for the three sampling ratios
(or, equivalently, compression ratios
). Clearly, the reconstruction accuracy deteriorates dramatically, as
p increases, for all the window lengths and sampling ratios, which verifies the weak encryption capability of CS. The difference in performance between the original and permuted
especially increases as the sampling ratio and window length increase. Furthermore, the larger is the window length
N and the smaller is the CR (i.e., the higher is the SR), the better is the reconstruction performance (i.e., higher SER), as expected.
5. Conclusions and Future Work
This study demonstrated the execution and energy efficiency of a CS-based system for smart water network infrastructures equipped with sensing devices with possibly limited power and computational resources. More specifically, our implementation on real hardware revealed a significant reduction of the average execution time up to approximately , when compared against a well-established lossless compression method that is also used in commercial solutions, namely the fast Lempel–Ziv (LZ77) algorithm. Furthermore, our performance evaluation, by varying the sampling ratio and the sliding window length, showed that a CS-based design enables savings of the data compression energy consumption as high as compared with LZ77. Regarding the energy consumed for data transmission, CS can achieve significant savings compared to LZ77 by selecting a high compression ratio, without compromising reconstruction fidelity.
In addition, we successfully demonstrated the weak encryption property of CS, in the case when an adversary has full access to the generated random measurements, but the knowledge of the random measurement matrix is up to a permutation of its rows. Specifically, the experimental results show that, by permuting even of the rows of the measurement matrix, an adversary is not capable of recovering accurately the original sensor stream samples. This is especially important for the design of low-cost smart water monitoring platforms, since no additional software or hardware encryption modules are required.
In the current work, our study primarily focused on the sensing side of smart water network. Nevertheless, in real-time applications, we are also interested in achieving accurate and fast decision making at the side of the control center. For this, we will investigate the effects of the measurement matrix type, as well as of the CS reconstruction algorithm, in the overall system performance, in terms of fast reconstruction while aiming at accurately detecting abnormal events. Furthermore, the weak encryption enabled by CS may not suffice in cases when higher privacy and security standards are required. To this end, we will investigate the combination of a CS scheme with quantum encryption mechanisms towards increasing our system’s security while maintaining the computation cost for edge encryption low enough for smart water networks with limited resources.