Adaptive and Efficient Mixture-Based Representation for Range Data
Abstract
1. Introduction
2. Gaussian Mixture Model Representation
2.1. Gaussian Mixture Model
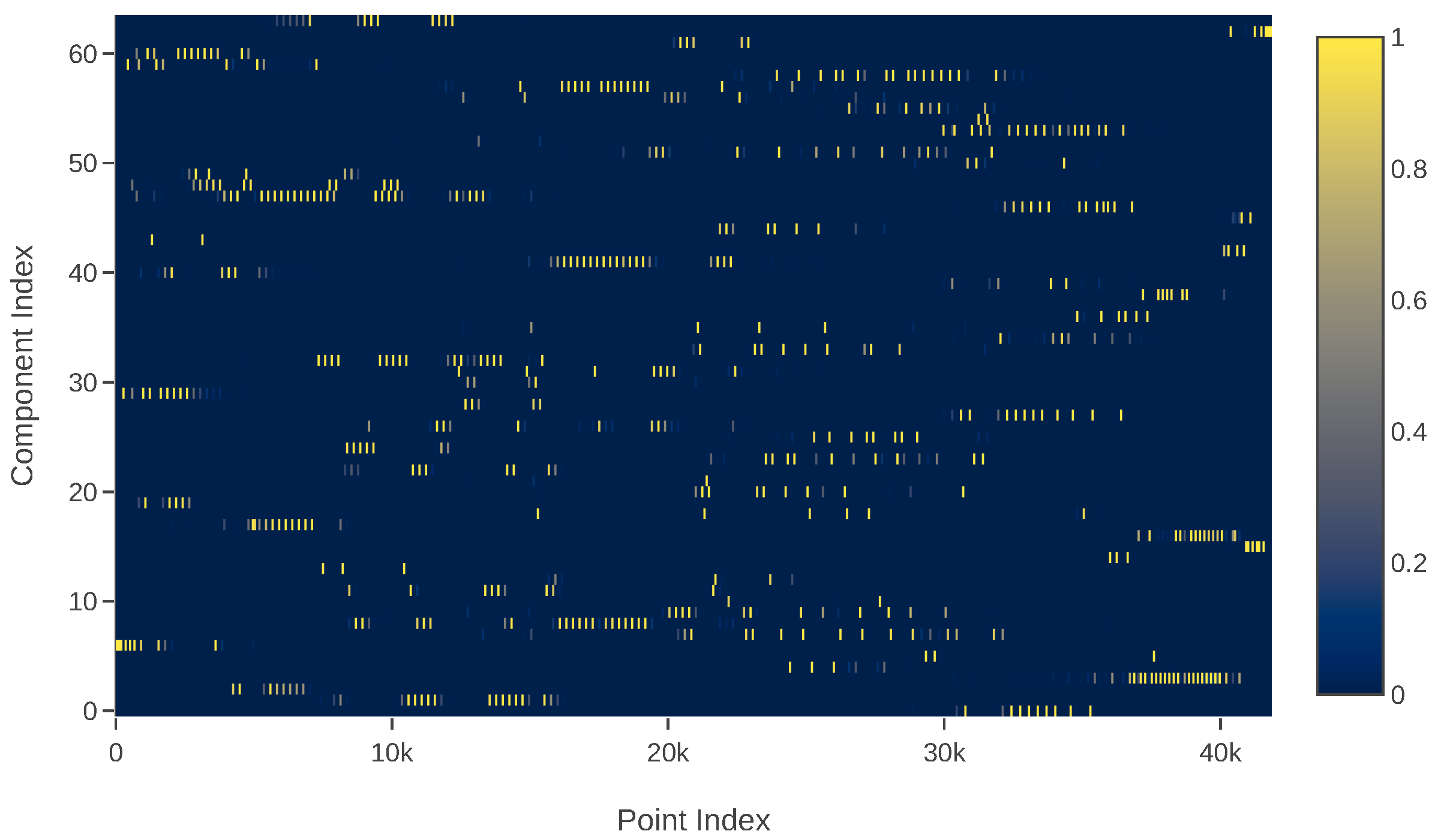
2.2. Sparsity of Responsibility Matrix
3. Method
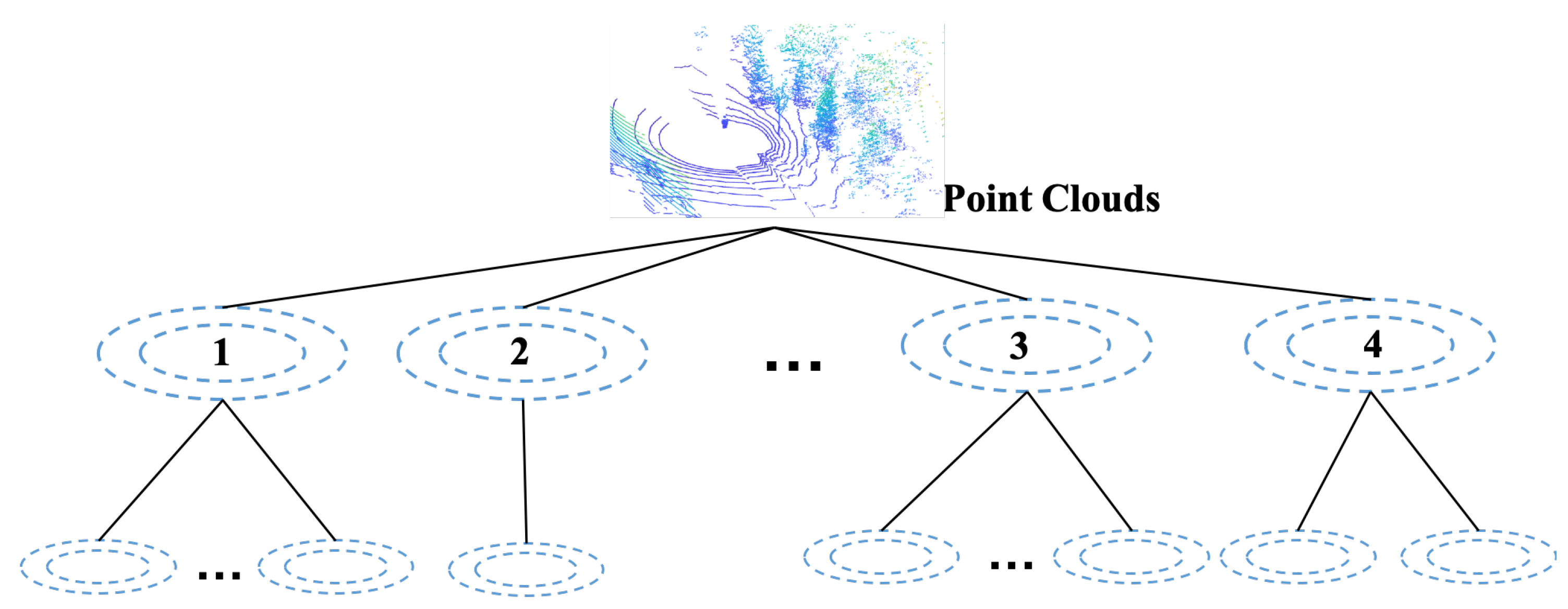
3.1. Hierarchy
3.2. Partition
| Algorithm 1 Partition |
|
3.3. Stop Conditions
3.3.1. Distribution Shape
3.3.2. Information Metric
4. Implementation
4.1. M-Step Vectorization
| Algorithm 2 M Step Rewrite |
|
4.2. Implementation
| Algorithm 3 Hierarchical Training |
|
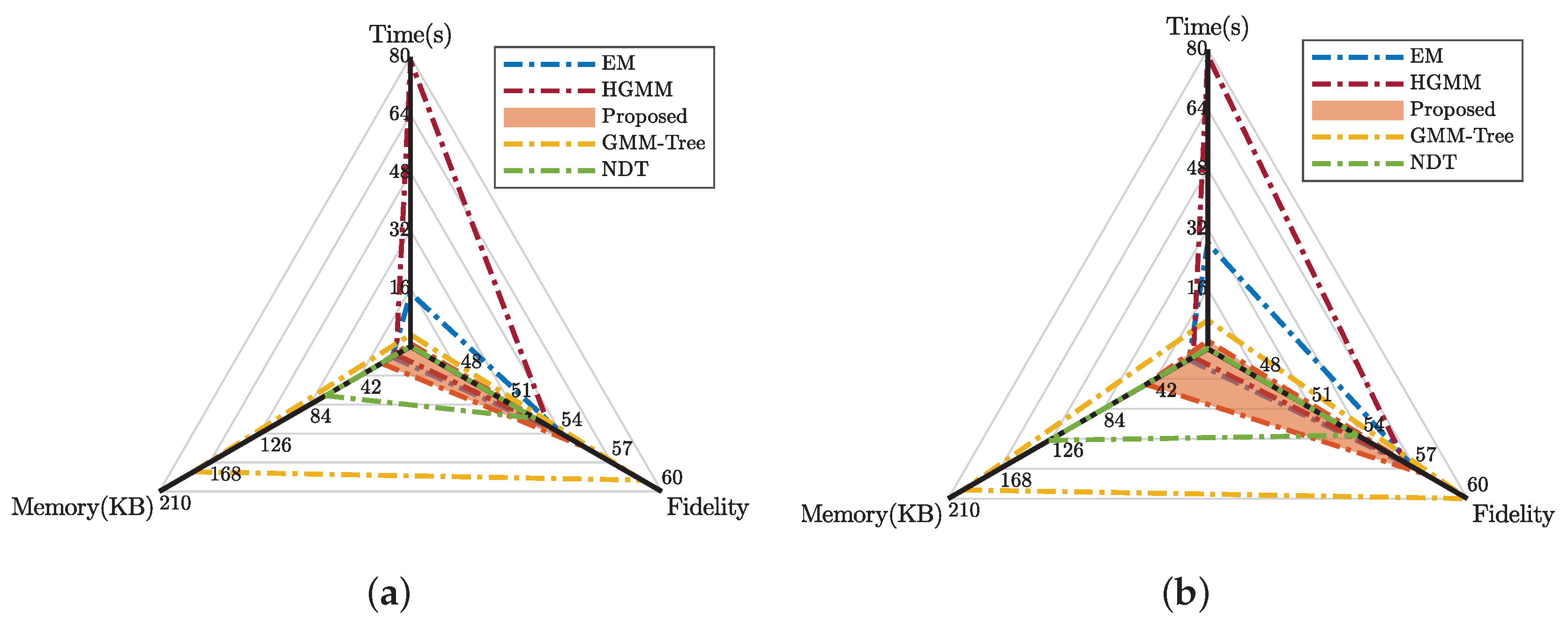
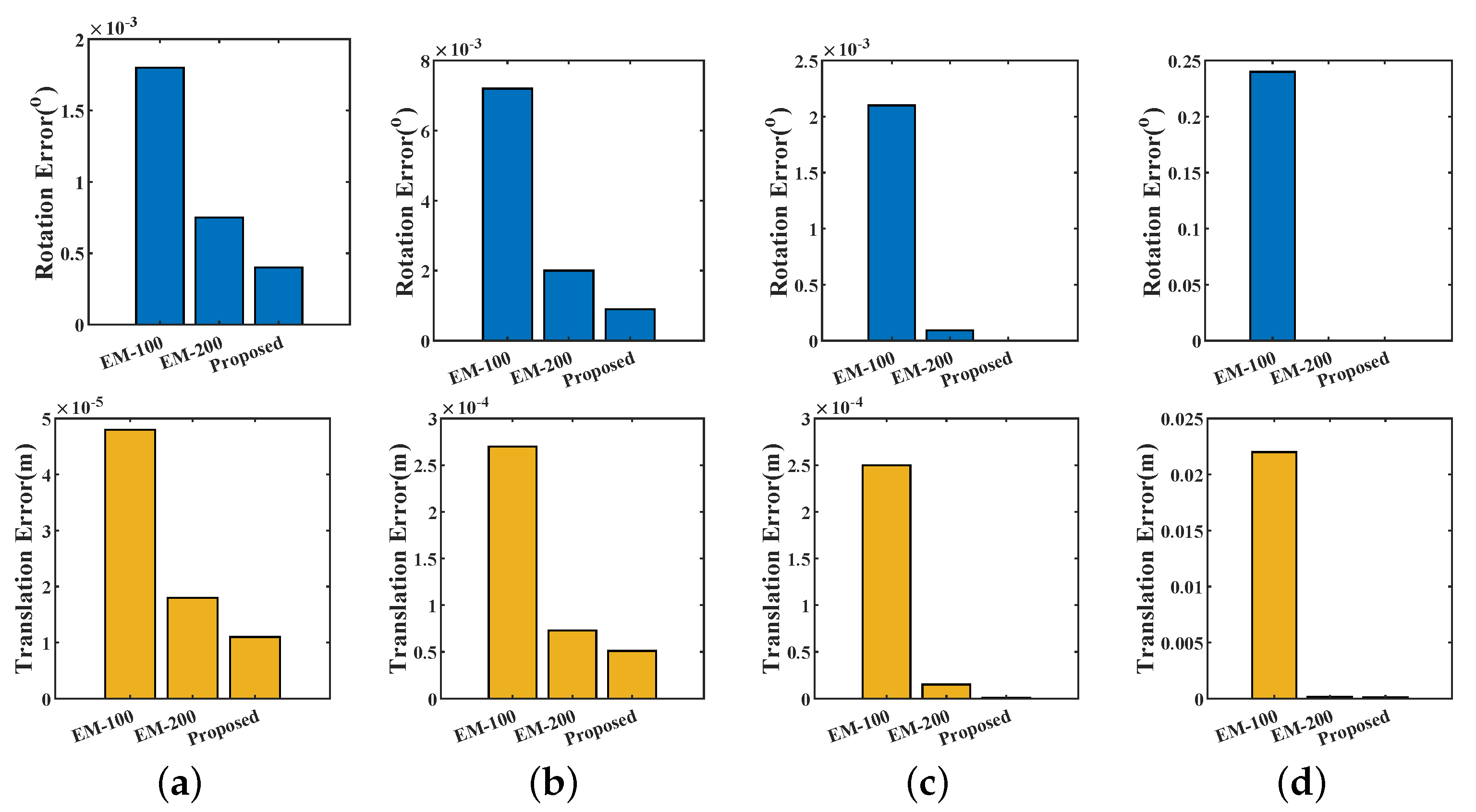
5. Evaluation
5.1. RGB-D Dataset
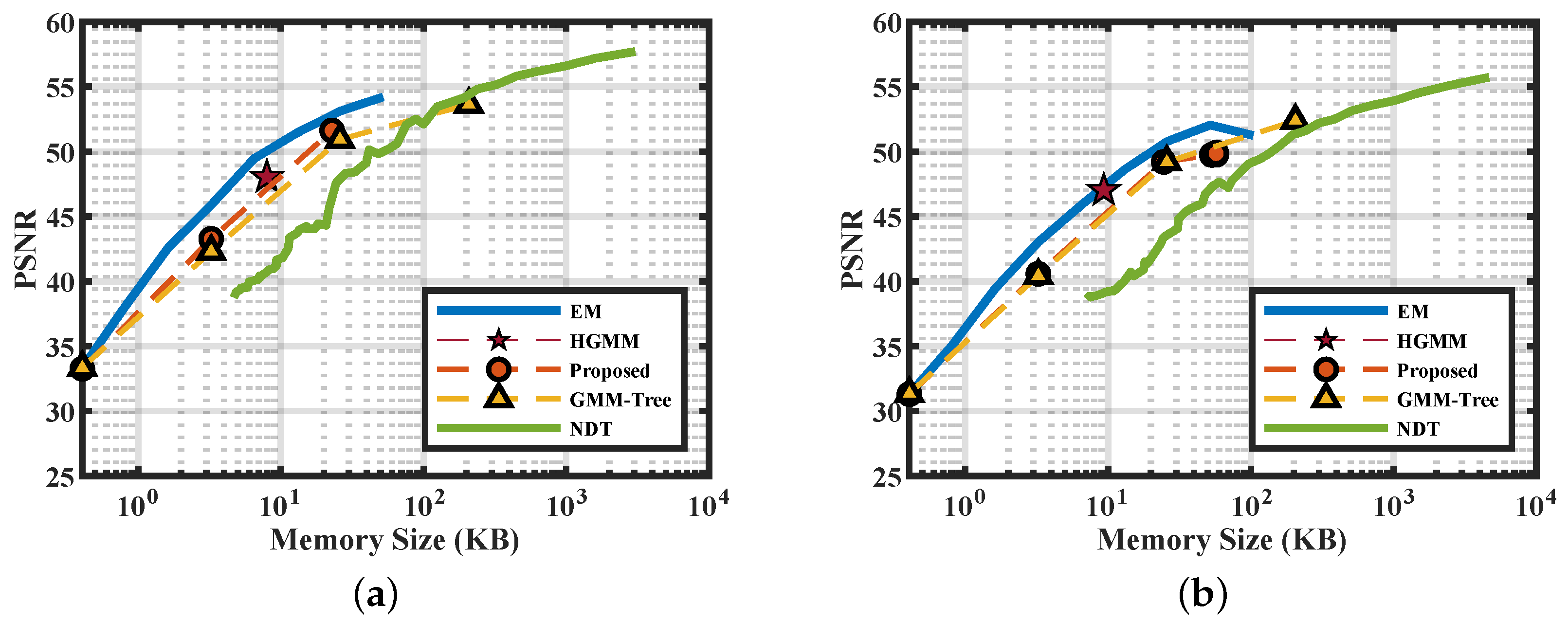
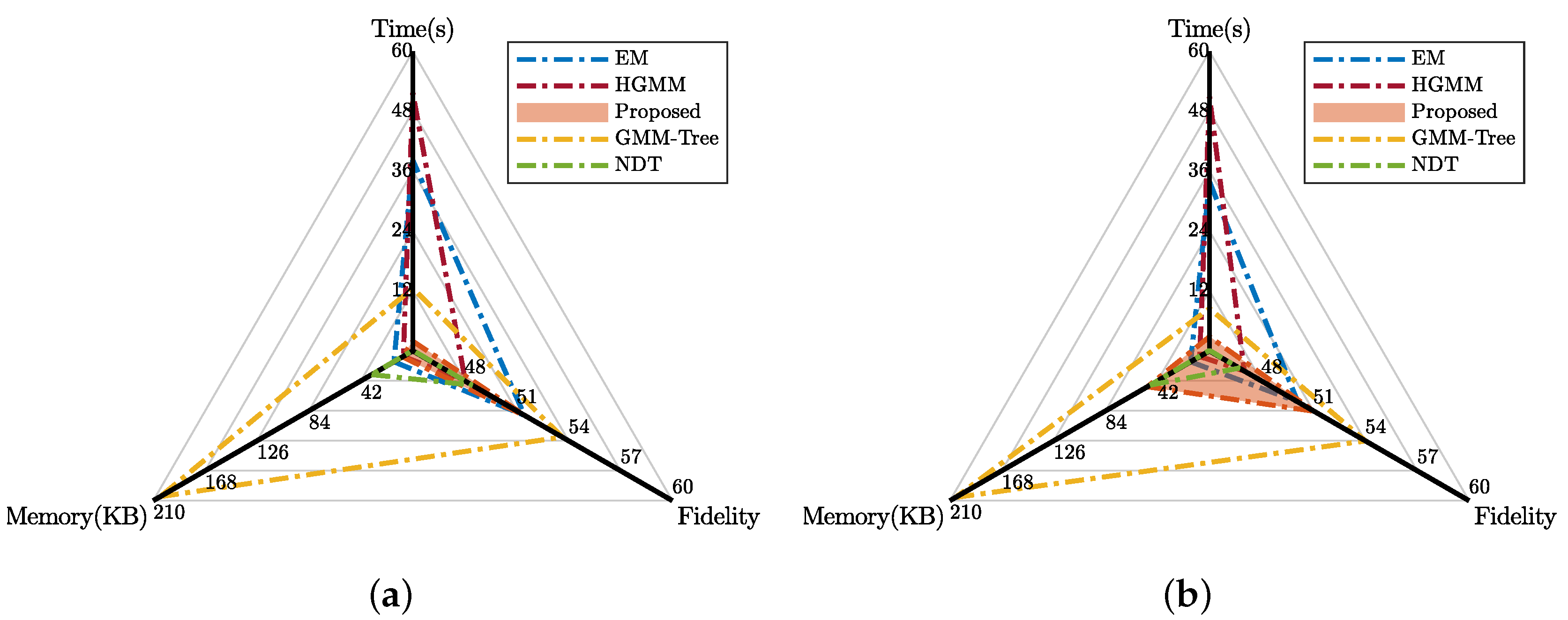
5.1.1. Fidelity
5.1.2. Efficiency
5.2. Lidar Dataset
5.2.1. Fidelity
5.2.2. Efficiency
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Elfes, A. Using Occupancy Grids for Mobile Robot Perception and Navigation. Computer 1989. [Google Scholar] [CrossRef]
- Ryde, J.; Hu, H. 3D mapping with multi-resolution occupied voxel lists. Auton. Robot. 2010. [Google Scholar] [CrossRef]
- Li, Y.; Ruichek, Y. Occupancy grid mapping in urban environments from a moving on-board stereo-vision system. Sensors 2014, 14, 10454–10478. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013. [Google Scholar] [CrossRef]
- Biber, P.; Strasser, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar] [CrossRef]
- Magnusson, M. The Three-Dimensional Normal-Distributions Transform: An Efficient Representation for Registration, Surface Analysis, and Loop Detection. Ph.D. Thesis, Örebro Universitet, Örebro, Sweden, December 2009. [Google Scholar]
- Maltezos, E.; Doulamis, A.; Doulamis, N.; Ioannidis, C. Building extraction from LiDAR data applying deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 16, 155–159. [Google Scholar] [CrossRef]
- Kehl, W.; Milletari, F.; Tombari, F.; Ilic, S.; Navab, N. Deep learning of local RGB-D patches for 3D object detection and 6D pose estimation. In European Conference on Computer Vision; Springer: Amsterdam, The Netherlands, 2016; pp. 205–220. [Google Scholar]
- Eitel, A.; Springenberg, J.T.; Spinello, L.; Riedmiller, M.; Burgard, W. Multimodal deep learning for robust RGB-D object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 681–687. [Google Scholar]
- Wang, C.; Wang, T.; Wang, E.; Sun, E.; Luo, Z. Flying Small Target Detection for Anti-UAV Based on a Gaussian Mixture Model in a Compressive Sensing Domain. Sensors 2019, 19, 2168. [Google Scholar] [CrossRef]
- Merisaari, H.; Parkkola, R.; Alhoniemi, E.; Teräs, M.; Lehtonen, L.; Haataja, L.; Lapinleimu, H.; Nevalainen, O.S. Gaussian mixture model-based segmentation of MR images taken from premature infant brains. J. Neurosci. Methods 2009, 182, 110–122. [Google Scholar] [CrossRef]
- Ban, Z.; Chen, Z.; Liu, J. Supervoxel segmentation with voxel-related Gaussian mixture model. Sensors 2018, 18, 128. [Google Scholar] [CrossRef]
- Yang, C.H.; Chang, C.C.; Liang, D. A novel GMM-based behavioral modeling approach for smartwatch-based driver authentication. Sensors 2018, 18, 1007. [Google Scholar] [CrossRef]
- Kim, N.K.; Jeon, K.M.; Kim, H.K. Convolutional Recurrent Neural Network-Based Event Detection in Tunnels Using Multiple Microphones. Sensors 2019, 19, 2695. [Google Scholar] [CrossRef]
- Srivastava, S.; Michael, N. Approximate continuous belief distributions for precise autonomous inspection. In Proceedings of the SSRR 2016—International Symposium on Safety, Security and Rescue Robotics, Lausanne, Switzerland, 23–27 October 2016; pp. 74–80. [Google Scholar] [CrossRef]
- Eckart, B.; Kim, K.; Troccoli, A.; Kelly, A.; Kautz, J. Accelerated Generative Models for 3D Point Cloud Data. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5497–5505. [Google Scholar] [CrossRef]
- Zhu, H.; Zou, K.; Li, Y.; Cen, M.; Mihaylova, L. Robust Non-Rigid Feature Matching for Image Registration Using Geometry Preserving. Sensors 2019, 19, 2729. [Google Scholar] [CrossRef] [PubMed]
- Jian, B.; Vemuri, B.C. Robust Point Set Registration Using Gaussian Mixture Models. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1633–1645. [Google Scholar] [CrossRef] [PubMed]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. Robot. Sci. Syst. 2009, 2, 435. [Google Scholar] [CrossRef]
- Tabib, W.; Omeadhra, C.; Michael, N. On-Manifold GMM Registration. IEEE Robot. Autom. Lett. 2018, 3, 3805–3812. [Google Scholar] [CrossRef]
- Eckart, B.; Kim, K.; Kautz, J. HGMR: Hierarchical Gaussian Mixtures for Adaptive 3D Registration. Eur. Conf. Comput.Vis. (ECCV) 2018, 705–721. [Google Scholar] [CrossRef]
- Eckart, B.; Kim, K.; Troccoli, A.; Kelly, A.; Kautz, J. MLMD: Maximum Likelihood Mixture Decoupling for Fast and Accurate Point Cloud Registration. In Proceedings of the 2015 International Conference on 3D Vision, Lyon, France, 19–22 October 2015; pp. 241–249. [Google Scholar] [CrossRef]
- Omeadhra, C. Generative Point Cloud Modeling with Gaussian Mixture Models for Multi-Robot Exploration. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, August 2018. [Google Scholar]
- O’Meadhra, C.; Tabib, W.; Michael, N. Variable Resolution Occupancy Mapping using Gaussian Mixture Models. Handb. Mach. Learn. 2018, 245–261. [Google Scholar] [CrossRef]
- Corah, M.; O’Meadhra, C.; Goel, K.; Michael, N. Communication-efficient planning and mapping for multi-robot exploration in large environments. IEEE Robot. Autom. Lett. 2019, 4, 1715–1721. [Google Scholar] [CrossRef]
- Dhawale, A.; Shankar, K.S.; Michael, N. Fast Monte-Carlo Localization on Aerial Vehicles using Approximate Continuous Belief Representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5851–5859. [Google Scholar] [CrossRef]
- Goldberger, J.; Roweis, S. Hierarchical clustering of a mixture model. In Proceedings of the NIPS 2005—Advances in Neural Information Processing Systems 18, Vancouver, BC, Canada, 5–8 December 2005. [Google Scholar]
- Garcia, V.; Nielsen, F.; Nock, R. Levels of details for Gaussian mixture models. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2010; pp. 514–525. [Google Scholar] [CrossRef]
- Goldberger, J.; Gordon, S.; Greenspan, H. An efficient image similarity measure based on approximations of KL-divergence between two gaussian mixtures. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 487–493. [Google Scholar] [CrossRef]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007. [Google Scholar] [CrossRef]
- Durrieu, J.L.; Thiran, J.P.; Kelly, F. Lower and upper bounds for approximation of the Kullback-Leibler divergence between Gaussian mixture models. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 25–30 March 2012. [Google Scholar] [CrossRef]
- Jenssen, R.; Erdogmus, D.; Hild, K.E.; Principe, J.C.; Eltoft, T. Optimizing the Cauchy-Schwarz PDF distance for information theoretic, non-parametric clustering. In Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2005; pp. 34–45. [Google Scholar] [CrossRef]
- Kampa, K.; Hasanbelliu, E.; Principe, J.C. Closed-form cauchy-schwarz PDF divergence for mixture of Gaussians. In Proceedings of the Proceedings of the International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; Volume 2, pp. 2578–2585. [Google Scholar] [CrossRef]
- Wang, F.; Syeda-Mahmood, T.; Vemuri, B.C.; Beymer, D.; Rangarajan, A. Closed-Form Jensen-Renyi Divergence for Mixture of Gaussians and Applications to Group-Wise Shape Registration. Med. Image Comput. Comput. Assist. Interv. 2009, 12, 648–655. [Google Scholar]
- Ben Hamza, A.; Krim, H. Jensen-renyi divergence measure: Theoretical and computational perspectives. In Proceedings of the IEEE International Symposium on Information Theory, Yokohama, Japan, 29 June–4 July 2003. [Google Scholar] [CrossRef]
- Ma, J.; Qiu, W.; Zhao, J.; Ma, Y.; Yuille, A.L.; Tu, Z. Robust L2E estimation of transformation for non-rigid registration. IEEE Trans. Signal Process. 2015, 63, 1115–1129. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Beard, M.; Vo, B.T.; Vo, B.N.; Arulampalam, S. Void Probabilities and Cauchy-Schwarz Divergence for Generalized Labeled Multi-Bernoulli Models. IEEE Trans. Signal Process. 2017. [Google Scholar] [CrossRef]
- Chirikjian, G.S. Information theory on lie groups and mobile robotics applications. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar] [CrossRef]
- Charrow, B.; Kahn, G.; Patil, S.; Liu, S.; Goldberg, K.; Abbeel, P.; Michael, N.; Kumar, V. Information-Theoretic Planning with Trajectory Optimization for Dense 3D Mapping. Robot. Sci. Syst. 2015, 11. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012. [Google Scholar] [CrossRef]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2016, 35, 1023–1035. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. (IJRR) 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2007; pp. 325–358. [Google Scholar] [CrossRef]
- Srivastava, S. Efficient, Multi-Fidelity Perceptual Representations via Hierarchical Gaussian Mixture Models. IEEE Trans. Rob. 2019, 35, 248–260. [Google Scholar] [CrossRef]
- Tian, D.; Ochimizu, H.; Feng, C.; Cohen, R.; Vetro, A. Geometric distortion metrics for point cloud compression. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3460–3464. [Google Scholar]



| Corner | Office | Street | Campus | |
|---|---|---|---|---|
| Sensor | RGB-D Camera | RGB-D Camera | LiDAR | LiDAR |
| Model | Microsoft Kinect | Microsoft Kinect | Velodyne HDL-32E | Velodyne HDL-64E |
| Source | TUM | TUM | NCLT | KITTI |
| Scene | Indoor | Indoor | Outdoor | Outdoor |
| Structure | Simple | Complex | Medium | Complex |
| Valid Size | ∼2.91 MB | ∼2.54 MB | ∼0.61 MB | ∼1.22 MB |
| Grid Size | 0.3 m | 0.2 m | 0.1 m | |||
|---|---|---|---|---|---|---|
| TNR | FPR | TNR | FPR | TNR | FPR | |
| Corner | 0.44% | 1.33% | 0.27% | 1.37% | 0.24% | 0.99% |
| Office | 0.29% | 0.86% | 0.15% | 1.44% | 0.24% | 1.19% |
| Street | 0.70% | 1.34% | 0.46% | 0.78% | 0.13% | 0.19% |
| Campus | 1.20% | 3.79% | 1.01% | 2.50% | 0.52% | 0.84% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Wang, J.; Ming, L. Adaptive and Efficient Mixture-Based Representation for Range Data. Sensors 2020, 20, 3272. https://doi.org/10.3390/s20113272
Cao M, Wang J, Ming L. Adaptive and Efficient Mixture-Based Representation for Range Data. Sensors. 2020; 20(11):3272. https://doi.org/10.3390/s20113272
Chicago/Turabian StyleCao, Minghe, Jianzhong Wang, and Li Ming. 2020. "Adaptive and Efficient Mixture-Based Representation for Range Data" Sensors 20, no. 11: 3272. https://doi.org/10.3390/s20113272
APA StyleCao, M., Wang, J., & Ming, L. (2020). Adaptive and Efficient Mixture-Based Representation for Range Data. Sensors, 20(11), 3272. https://doi.org/10.3390/s20113272





