Ambiguity of Residual Constraint-Based Precise Point Positioning with Partial Ambiguity Resolution under No Real-Time Network Corrections Using Real Global Positioning System (GPS) Data
Abstract
1. Introduction
- An improved FCB update strategy is presented to satisfy requirements of real-time PPP without the assistance of real-time network corrections.
- An ambiguity residual constraint-based precise point positioning with partial ambiguity resolution (PPP-PARC) is proposed to fix partial ambiguities successfully so that convergence time can be reduced under no real-time network corrections.
- A PPP experiment is operated to analyze the performance of the new algorithm in post-processing and real-time PPP.
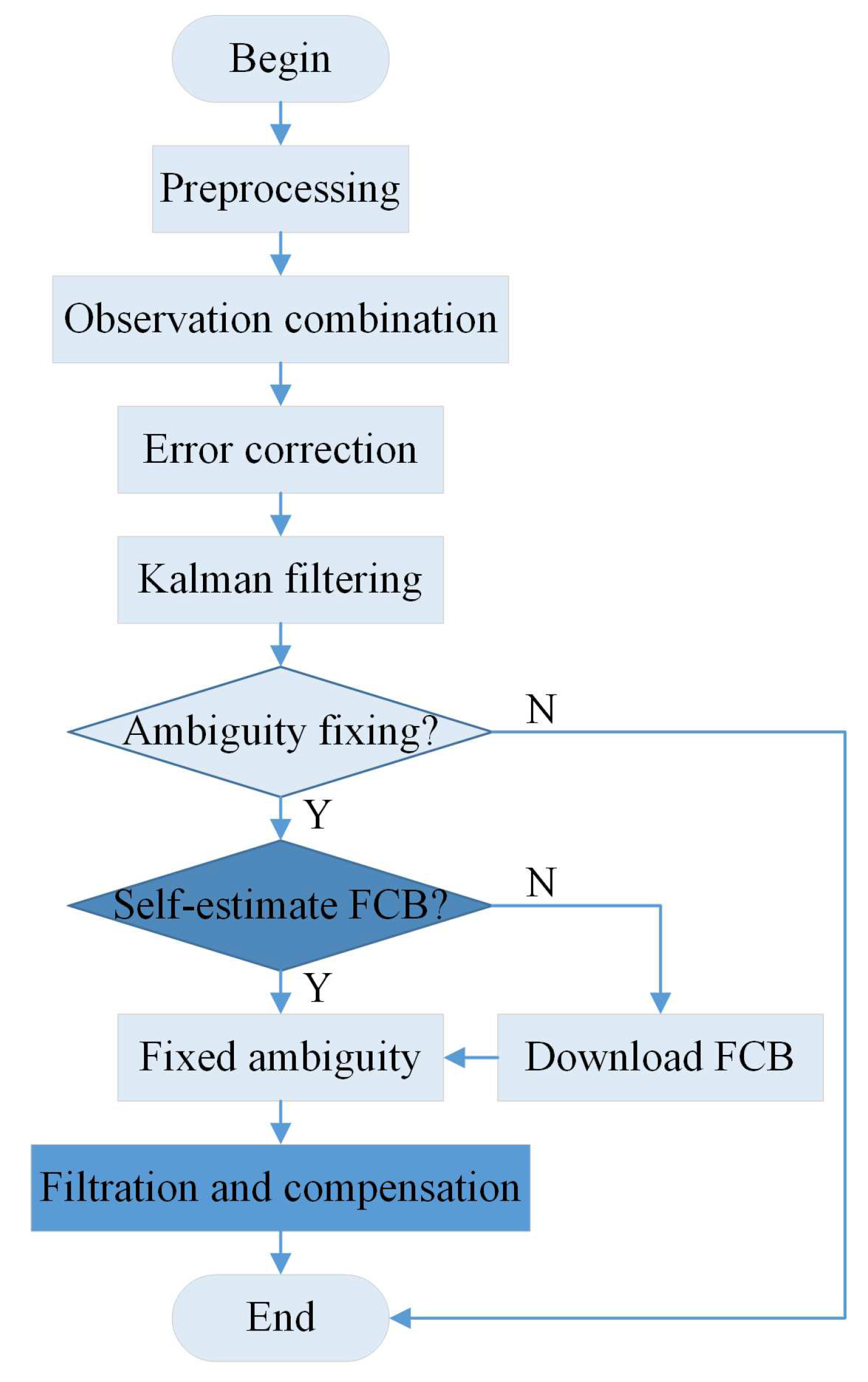
2. Partial Ambiguity Fixing
2.1. Non-Integer Ambiguity
2.2. Ambiguity Residual Constraint-Based PPP-PAR
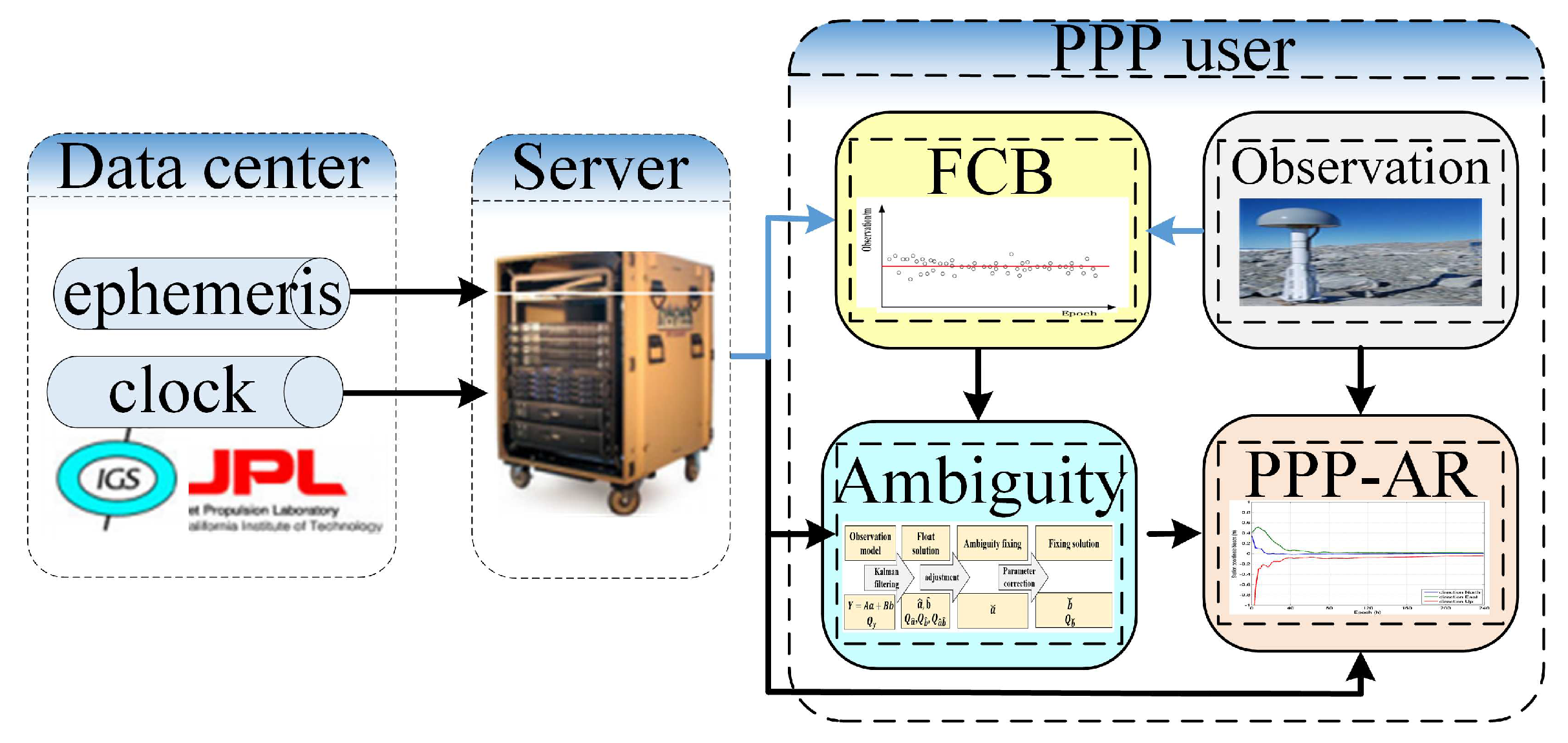
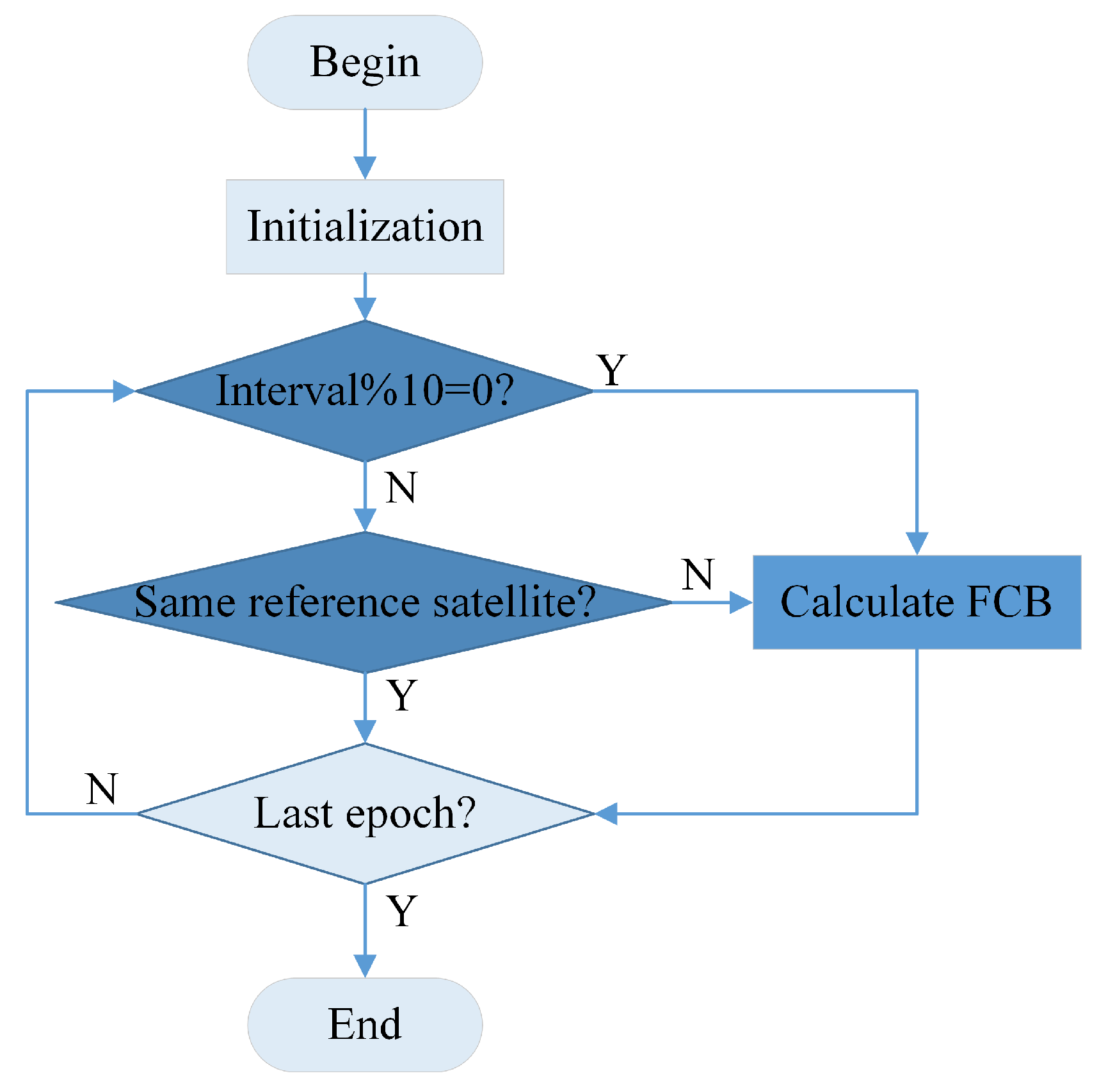
3. FCB Estimation
3.1. System Architecture
3.2. FCB Estimation Algorithm
3.3. The Improved FCB Update Strategy
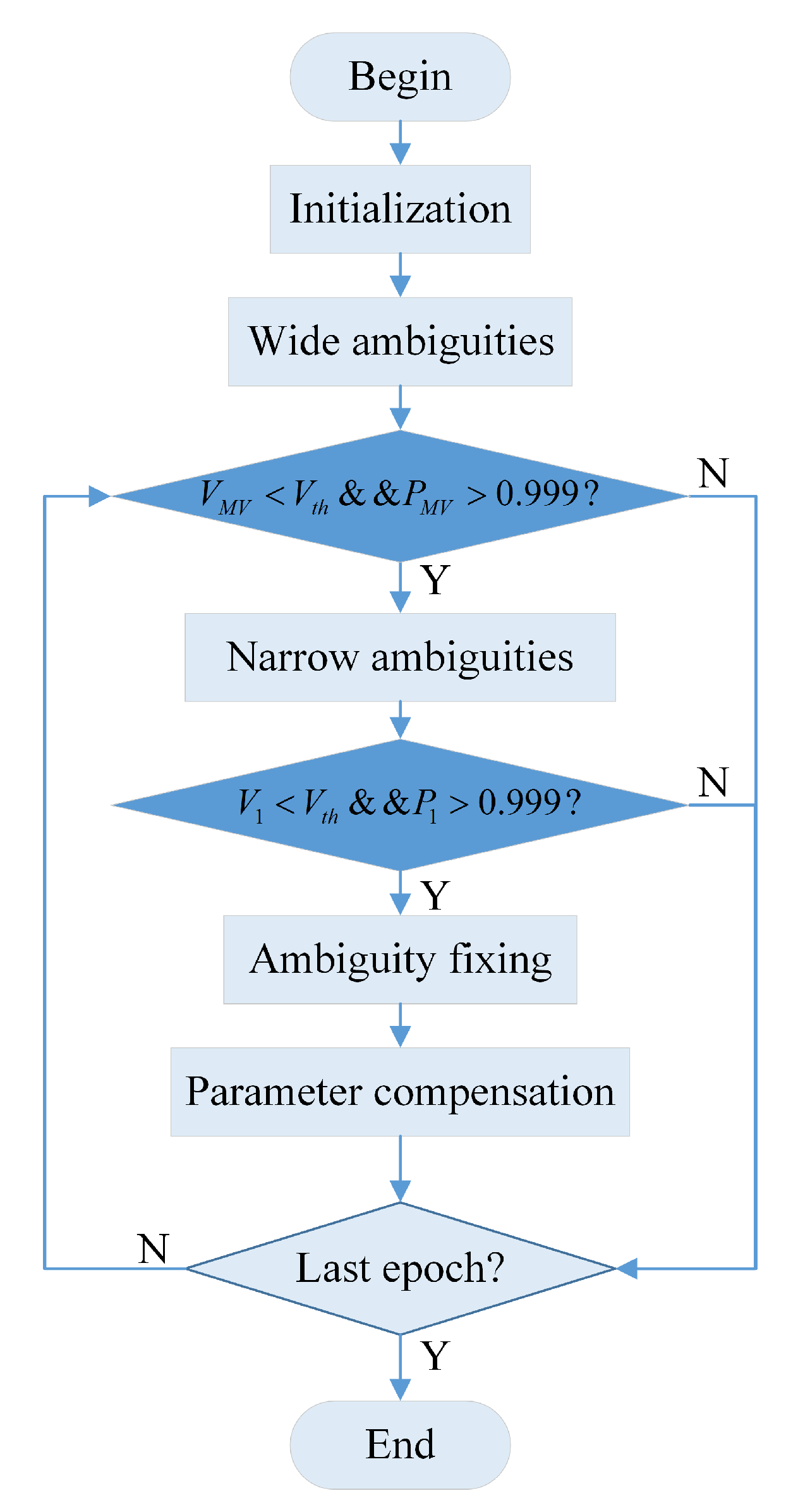
4. Partial Ambiguity Resolution
4.1. Ambiguity Residual Characteristic
4.1.1. Monotonicity
4.1.2. Convexity
4.2. Ambiguity Subset Screening
5. PPP Experiment
5.1. Experimental Configuration
5.2. Post-Processing PPP Experiment
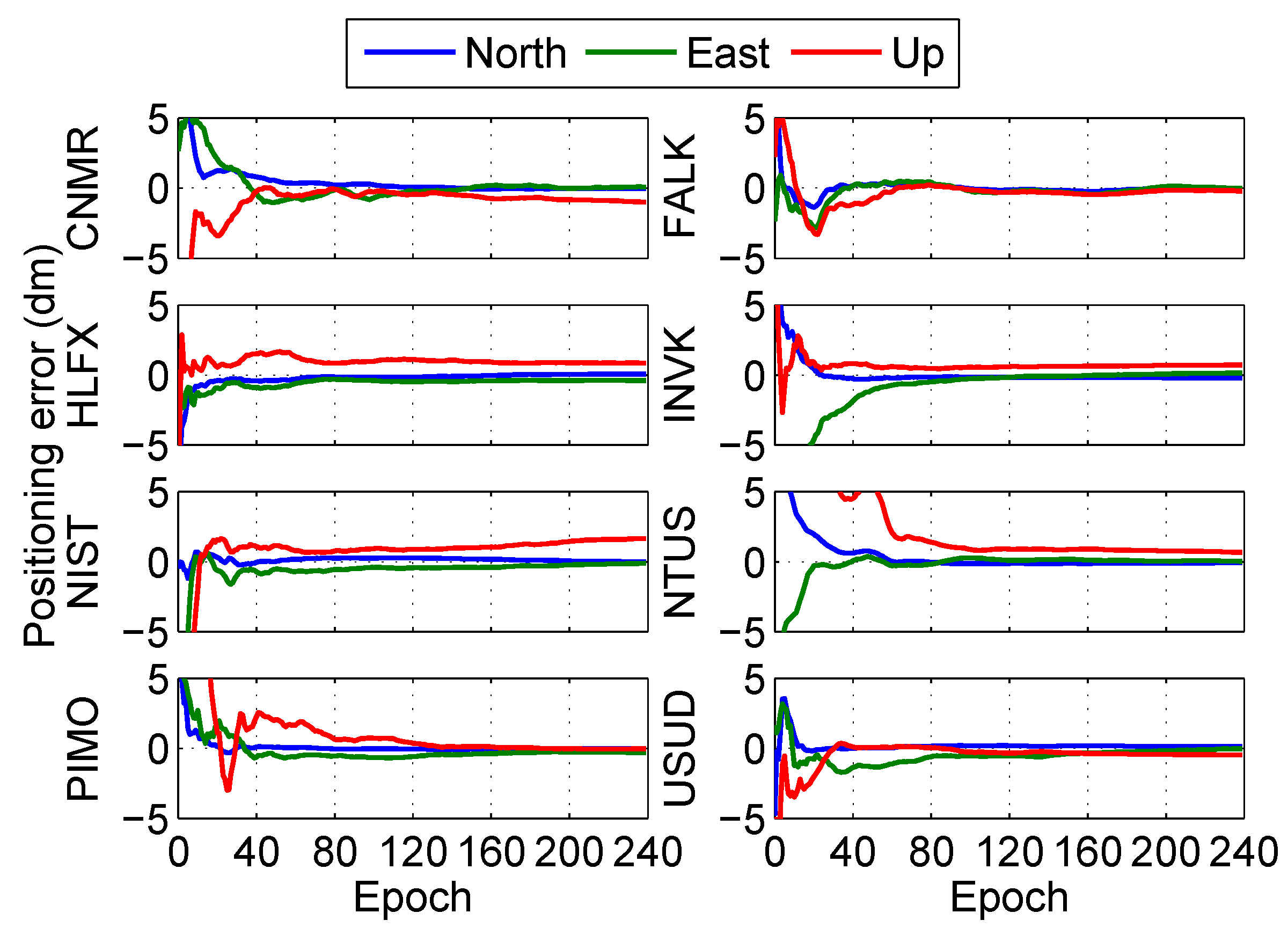
5.2.1. Stations Selection
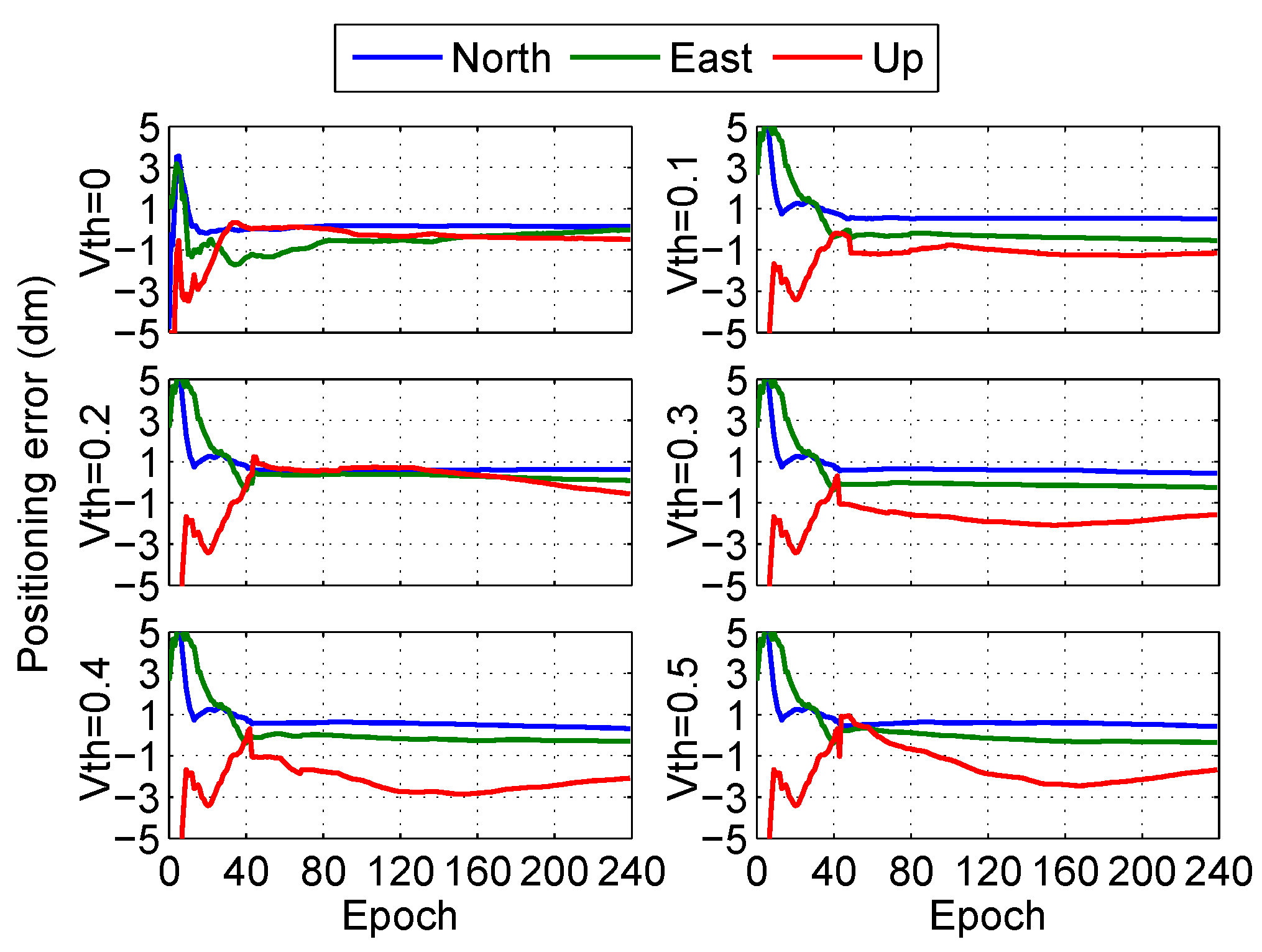
5.2.2. Determination of the Threshold
5.2.3. Performance Analysis at Multiple Stand-Alone Stations
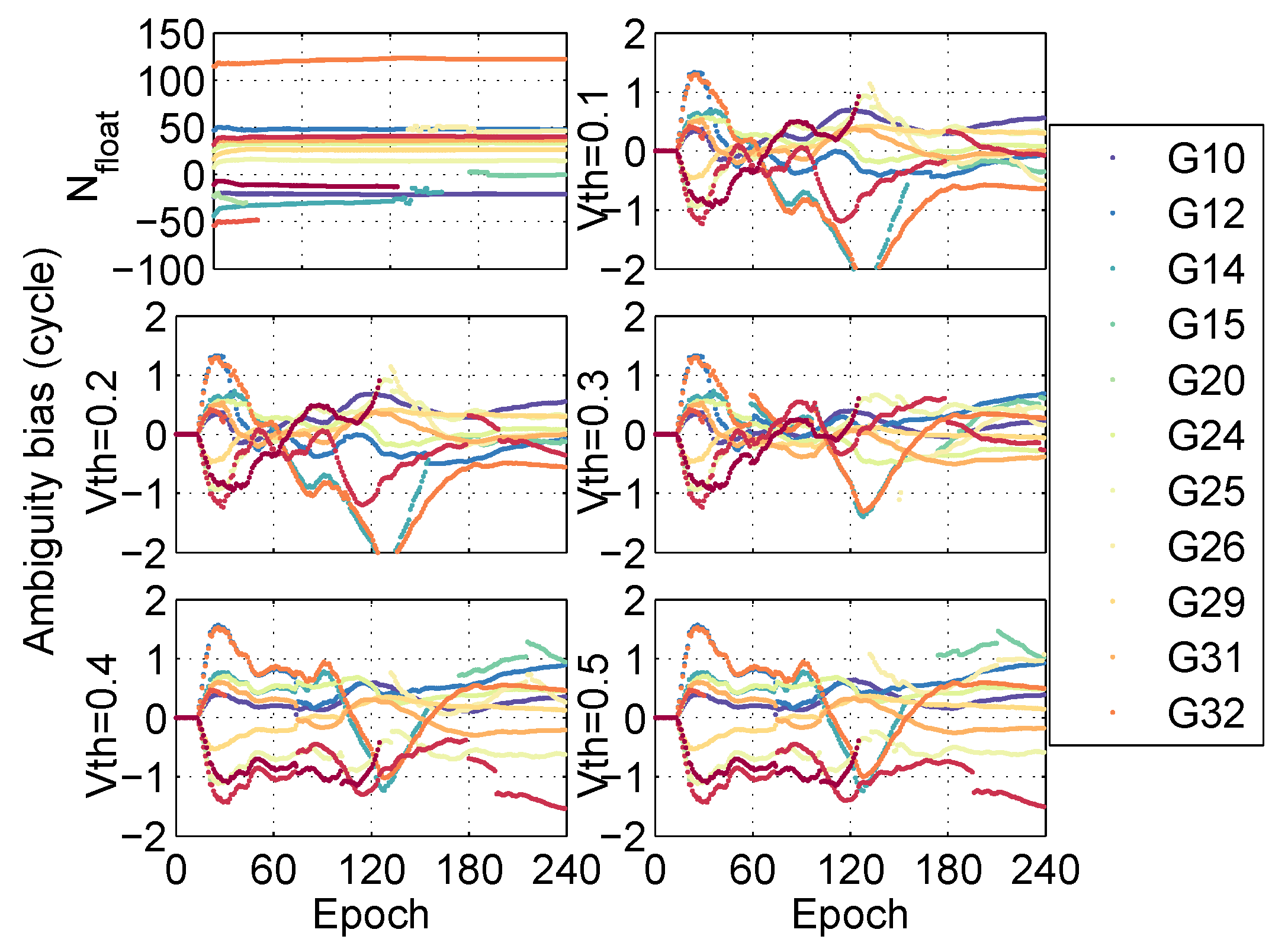
5.2.4. Ambiguity Analysis
5.3. Real-Time PPP Experiment
5.3.1. Stations Selection
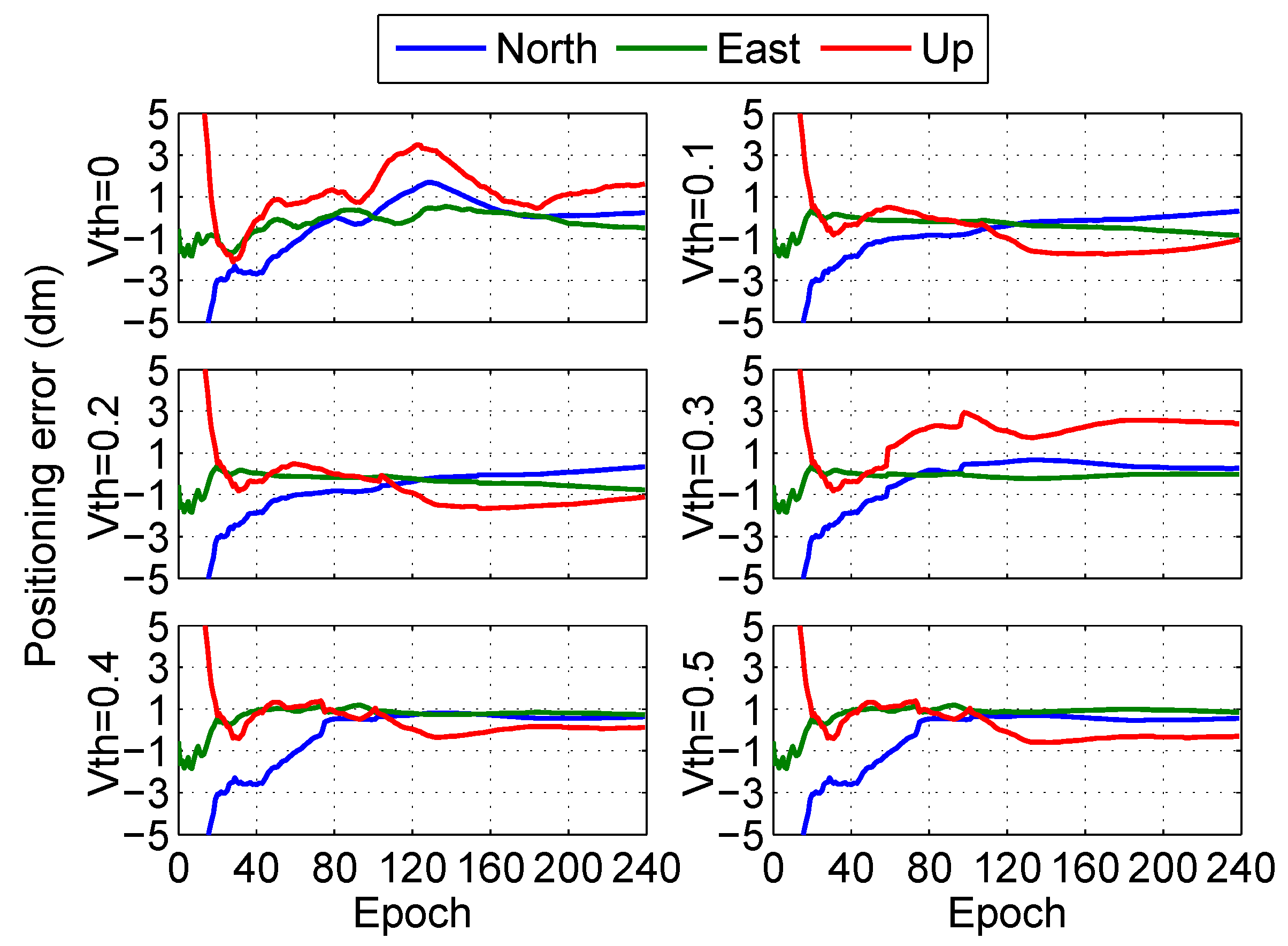
5.3.2. Determination of the Threshold
5.3.3. Performance Analysis at Multiple Stand-Alone Stations
5.3.4. Ambiguity Analysis
5.4. Extensibility Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CORS | continuously operating reference station |
| DSC | decoupled satellite clock |
| DCB | differential code bias |
| FCB | fractional cycle bias |
| GMF | Global Mapping Function |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GPST | Global Positioning System Time |
| IRC | integer recovery clock |
| M-W | Melbourne-Wubbena detecting |
| PCO | Antenna Phase Center Offsets |
| PCV | Antenna Phase Center Variations |
| PPP | precise point positioning |
| PPP-AR | PPP with ambiguity resolution |
| PPP-PAR | PPP with partial ambiguity resolution |
| PPP-PARC | ambiguity residual constraint-based PPP with partial ambiguity resolution |
| PPP-RTK | PPP with real-time kinematic |
| SA | selective availability |
| UHD | uncalibrated Hardware Delay |
| UPD | uncalibrated phase delay |
| UTC | Universal Time Coordinated |
References
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise Point Positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise Point Positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current state of precise point positioning and future prospects and limitations. In Observing Our Changing Earth; Springer: Berlin/Heidelberg, Germany, 2009; pp. 615–623. [Google Scholar] [CrossRef]
- Gao, Y.; Shen, X. A New Method for Carrier-Phase-Based Precise Point Positioning. Navigation 2002, 49, 109–116. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System: Theory and Practice; Springer: Wien, Austria, 2012. [Google Scholar] [CrossRef]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 11–80. [Google Scholar] [CrossRef]
- Teunissen, P.; Kleusberg, A. GPS for Geodesy; Springer: Berlin/Heidelberg, Germany, 1998; pp. 187–229. [Google Scholar] [CrossRef]
- Abdel-Salam, M.A.T. Precise Point Positioning Using Un-Differenced Code and Carrier Phase Observations. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Teunissen, P.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviation. Ser. A 2010, 42, 223–229. [Google Scholar]
- Liu, P.; Qin, H.; Cong, L. The Feasible Combining Observation Models and Equivalence in Dual-Frequency Precise Point Positioning. IEEE Access 2019, 7, 38618–38629. [Google Scholar] [CrossRef]
- Qin, H.; Liu, P.; Cong, L.; Ji, W. Triple-Frequency Combining Observation Models and Performance in Precise Point Positioning using Real BDS Data. IEEE Access 2019, 69826–69836. [Google Scholar] [CrossRef]
- Collins, P.; Lahaye, F.; Héroux, P.; Bisnath, S. Precise point positioning with ambiguity resolution using the decoupled clock model. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.A.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Gabor, M.J. GPS Carrier Phase Ambiguity Resolution Using Satellite-Satellite Single Differences. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1999. [Google Scholar]
- Teunissen, P.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Yang, Y.; Zhang, Q.; Gao, Y.; Xiao, G. FCB estimation with three different PPP models: Equivalence analysis and experiment tests. GPS Solut. 2019, 23, 93. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Khodabandeh, A.; Teunissen, P.J.G. An analytical study of PPP-RTK corrections: Precision, correlation and user-impact. J. Geod. 2015, 89, 1109–1132. [Google Scholar] [CrossRef]
- Landau, H.; Vollath, U.; Chen, X. Virtual reference station systems. J. Glob. Position. Syst. 2002, 1, 137–143. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; Volume 5, pp. 13–16. [Google Scholar]
- Mervart, L.; Lukes, Z.; Rocken, C.; Iwabuchi, T. Precise point positioning with ambiguity resolution in real-time. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; Volume 8, pp. 16–19. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Shi, C.; Meng, X.; Dodson, A.; Liu, J. Ambiguity resolution in precise point positioning with hourly data. GPS Solut. 2009, 13, 263–270. [Google Scholar] [CrossRef]
- Ge, M.; Zou, X.; Dick, G.; Jiang, W.; Wickert, J.; Liu, J. An alternative Network RTK approach based on undifferenced observation corrections. In Proceedings of the ION GNSS, Portland, OR, USA, 21–24 September 2010; Volume 2010. [Google Scholar]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.; Odijk, D. A novel un-differenced PPP-RTK concept. J. Navig. 2011, 64, S180–S191. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J. On the estimability of parameters in undifferenced, uncombined GN network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Khodabandeh, A.; Teunissen, P. Integer estimability in GNSS networks. J. Geod. 2019, 93, 1805–1819. [Google Scholar] [CrossRef]
- Liu, X.; Stone, M.; Memarzadeh, Y.; Goode, M.; Strandli, R. Integer Ambiguity Resolution Enabled RTK and PPP Solutions Using GPS and GLONASS Observations. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 12–16 September 2016. [Google Scholar] [CrossRef]
- Li, X.; Xin, L.; Yuan, Y.; Zhang, K.; Wickert, J. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo. J. Geod. 2018, 92, 579–608. [Google Scholar] [CrossRef]
- Hu, H. Research on Theory and Realization of GNSS Precise Point Positioning. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2013. (In Chinese). [Google Scholar]
- Liu, Y.; Ye, S.; Song, W.; Lou, Y.; Gu, S. Rapid PPP ambiguity resolution using GPS+GLONASS observations. J. Geod. 2017, 91, 441–455. [Google Scholar] [CrossRef]
- Xu, G.; Xu, Y. GPS: Theory, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 76–145. [Google Scholar] [CrossRef]
- Teunissen, P.J. An optimality property of the integer least-squares estimator. J. Geod. 1999, 73, 587–593. [Google Scholar] [CrossRef]
- Teunissen, P.; Joosten, P.; Tiberius, C. Geometry-free ambiguity success rates in case of partial fixing. In Proceedings of the ION-NTM, San Diego, CA, USA, 25–27 January 1999; pp. 25–27. [Google Scholar]
- Guo, F. Theory and Methodology of Quality Control and Quality Analysis for GPS Precise Point Positioning. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. (In Chinese). [Google Scholar]
- Ge, Y.; Zhou, F.; Sun, B.; Wang, S.; Shi, B. The Impact of Satellite Time Group Delay and Inter-Frequency Differential Code Bias Corrections on Multi-GNSS Combined Positioning. Sensors 2017, 17, 602. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Hu, C.; Gao, S.; Chen, Y.; Ding, X. Error correction models and their effects on GPS precise point positioning. Surv. Rev. 2009, 41, 238–252. [Google Scholar] [CrossRef]
- Choy, S.; Bisnath, S.; Rizos, C. Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut. 2017, 21, 13–22. [Google Scholar] [CrossRef]










| Error Corrections | Setting |
|---|---|
| Differential Code Biases(DCB) | CODE |
| Cycle slip | M-W and Ionosphere Residuals |
| Clock slip | M-W detection and integer repair [37] |
| Stochastic models | Sine function model [38] |
| Earth rotation | Sagnac effect |
| Relativistic effects | General relativistic function [34] |
| Troposphere | Random walk + Hopfield + GMF |
| Antenna phase center offsets | PCV + PCO |
| Phase windup | Windup compensation function [39] |
| Earth tides correction | Solid/Pole tide |
| Parameter | Setting |
|---|---|
| Rinex file | xxxx1000.18o |
| Precise orbit product | igs19962.sp3\ igu19962.sp3 |
| Precise clock product | igs19962.clk_30s |
| Pole shift/ut1-utc | igs19967.erp |
| Antenna phase center | igs14.atx |
| Positioning mode | Post-processing/real-time static |
| Estimation algorithm | Standard Kalman Filter |
| Observation models | dual-frequency ionosphere-free combination |
| Reference coordinate | igs18P1996_all.ssc |
| Sampling interval | 30 s |
| Elevation cutoff angle |
| Station | Method | CT (min) | Accuracy (mm) | Precision (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | |||
| CNMR | Float | 26.5 | 1.7 | −5.1 | −73 | 16.9 | 35.9 | 63.4 |
| Fixed | 23.5 | 59.7 | 27.4 | 23.9 | 59.3 | 30.6 | 52 | |
| FALK | Float | 24.5 | −3.5 | −8.5 | −23.5 | 16.2 | 26.6 | 29.5 |
| Fixed | 20.5 | 40.2 | −12.4 | 17 | 38 | 12.4 | 30.9 | |
| HLFX | Float | 35 | −3.1 | −40.6 | 91.3 | 9.5 | 40.9 | 93.5 |
| Fixed | 28 | 22.5 | 11.2 | 46 | 23.3 | 11.1 | 47.1 | |
| INVK | Float | 26.5 | −19.6 | −2.5 | 63.2 | 18.9 | 31.8 | 60.8 |
| Fixed | 21.5 | −50.6 | −27.8 | 35.4 | 49.9 | 30.5 | 48.7 | |
| NIST | Float | 28.5 | 10.2 | −30.3 | 124.8 | 18.8 | 42.2 | 113.3 |
| Fixed | 20 | 8.9 | −80.1 | 28.6 | 9.5 | 75.8 | 28.3 | |
| NTUS | Float | 47 | −11.9 | 8.6 | 79.3 | 12.3 | 12.4 | 82.5 |
| Fixed | 40 | 0.1 | −23.4 | 46.9 | 2.4 | 25 | 50.3 | |
| PIMO | Float | 38 | 4.9 | −35.6 | 7.1 | 5.6 | 44.5 | 36 |
| Fixed | 35.5 | −14.6 | −41.7 | 24.1 | 13.7 | 42 | 32.3 | |
| USUD | Float | 32.5 | 15 | −35.2 | −33.3 | 15.2 | 46.4 | 34.9 |
| Fixed | 28.5 | 34 | −24.7 | −6.8 | 33.1 | 30.3 | 9.8 | |
| Average | Float | 32.3 | −2 | −18.7 | 29.5 | 14.2 | 35.1 | 64.2 |
| Fixed | 27.2 | 12.5 | −21.4 | 26.9 | 28.7 | 32.2 | 37.4 | |
| Station | Method | CT (min) | Accuracy (mm) | Precision (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | |||
| BSHM | Float | 24.5 | 31.9 | −4.4 | 147.8 | 80 | 30.5 | 173.9 |
| fixed | 18.5 | −21.9 | −43.1 | −116.3 | 68.3 | 41.2 | 113.4 | |
| CUSV | Float | 71.5 | −19.2 | 82.2 | 64.1 | 23.7 | 86.5 | 105 |
| fixed | 60.5 | 64.5 | −5.9 | −173.5 | 64.3 | 6.8 | 173.3 | |
| DYNG | Float | 71 | 7.7 | 67 | 148.8 | 42.8 | 79.9 | 150 |
| fixed | 51 | −34.5 | 27.4 | 115.4 | 35.9 | 44.9 | 114.7 | |
| GMSD | Float | 98.5 | 42.6 | 155.7 | −86.4 | 43.2 | 159.2 | 96.1 |
| fixed | 67.5 | 100.5 | 49.1 | −111.5 | 100 | 49.3 | 130.6 | |
| LMMF | Float | 37 | −19 | −84.4 | 245.3 | 41 | 115.7 | 242.6 |
| fixed | 26.5 | 32.6 | 94.1 | 92.5 | 46.3 | 92.4 | 100.8 | |
| ULAB | Float | 30 | 68.5 | 64.5 | −138.8 | 81.6 | 64.9 | 144.2 |
| fixed | 21.5 | 64.7 | −76.3 | −32.7 | 66.3 | 77.8 | 56 | |
| VIS0 | Float | 28.5 | 66.4 | 32.6 | 89.6 | 76.8 | 77.6 | 143.8 |
| fixed | 26.5 | 32.8 | 117.5 | 115.8 | 36.7 | 122.3 | 119.7 | |
| WSRT | Float | 36.5 | 66.4 | 67.7 | 165.6 | 50.3 | 85.7 | 212 |
| fixed | 20.5 | 107.6 | −9.7 | −86.9 | 101.3 | 37.3 | 89.4 | |
| Average | Float | 49.7 | 27.4 | 47.6 | 79.5 | 54.9 | 87.5 | 158.4 |
| fixed | 36.6 | 43.3 | 19.1 | −24.7 | 64.9 | 59 | 112.2 | |
| Station | Positioning Type | Method | CT (min) | Accuracy (mm) | Precision (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||||
| BJFS, China | Post-processing | Float | 17.5 | −23.2 | −47.1 | 50.0 | 30.6 | 52.8 | 56.7 |
| fixed | 17.5 | −2.5 | 32.8 | −68.9 | 8.9 | 33.0 | 70.0 | ||
| Real-time | Float | 20.5 | 31.7 | −4.9 | 119.0 | 69.7 | 46.8 | 116.7 | |
| fixed | 20.5 | 135.3 | 182.0 | −79.6 | 135.5 | 164.8 | 98.8 | ||
| BZRG, Italy | Post-processing | Float | 21.5 | 24.4 | −11.9 | −38.6 | 22.9 | 32.7 | 41.6 |
| fixed | 21.5 | 12.7 | −35.9 | −30.1 | 14.4 | 39.0 | 42.2 | ||
| Real-time | Float | 51 | 63.1 | 35.2 | 13.7 | 97.9 | 65.1 | 600.9 | |
| fixed | 51 | 141.1 | 84.4 | 87.9 | 132.4 | 84.2 | 604.6 | ||
| CLRT, Canada | Post-processing | Float | 8.5 | −25.3 | −24.5 | 37.0 | 30.2 | 24.5 | 41.6 |
| fixed | 8.5 | −6.0 | −63.8 | 102.5 | 16.4 | 62.1 | 103.8 | ||
| Real-time | Float | 23 | −31.4 | −29.4 | 48.2 | 66.5 | 75.8 | 492.5 | |
| fixed | 27 | 63.3 | −58.8 | 204.4 | 69.3 | 73.6 | 523.2 | ||
| EIL4, USA | Post-processing | Float | 6 | −6.8 | 21.3 | 60.9 | 18.5 | 35.5 | 54.3 |
| fixed | 6 | −40.5 | 116.1 | 15.4 | 38.5 | 109.9 | 26.9 | ||
| Real-time | Float | 40 | −55.9 | 76.2 | 28.4 | 70.1 | 85.4 | 191.4 | |
| fixed | 40 | −83.7 | 80.2 | 44.7 | 81.7 | 86.9 | 190.6 | ||
| MAG0, Russia | Post-processing | Float | 26 | 16.7 | −29.8 | −40.1 | 15.7 | 40.0 | 42.7 |
| fixed | 26 | 18.4 | −57.3 | 55.9 | 17.6 | 57.4 | 62.9 | ||
| Real-time | Float | 38.5 | 49.6 | 68.2 | −199.0 | 57.5 | 67.9 | 261.4 | |
| fixed | 38.5 | 41.2 | 119.1 | 40.5 | 51.2 | 96.1 | 141.4 | ||
| OAK1, UK | Post-processing | Float | 7 | 25.0 | −24.5 | −35.2 | 24.2 | 33.3 | 34.1 |
| fixed | 7 | −25.7 | −23.1 | 58.7 | 25.1 | 31.4 | 55.8 | ||
| Real-time | Float | 26 | 63.0 | 45.7 | 180.2 | 62.4 | 59.2 | 256.9 | |
| fixed | 16.5 | −97.6 | 65.8 | 263.8 | 90.0 | 78.9 | 242.5 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Liu, P.; Cong, L.; Xue, X. Ambiguity of Residual Constraint-Based Precise Point Positioning with Partial Ambiguity Resolution under No Real-Time Network Corrections Using Real Global Positioning System (GPS) Data. Sensors 2020, 20, 3220. https://doi.org/10.3390/s20113220
Qin H, Liu P, Cong L, Xue X. Ambiguity of Residual Constraint-Based Precise Point Positioning with Partial Ambiguity Resolution under No Real-Time Network Corrections Using Real Global Positioning System (GPS) Data. Sensors. 2020; 20(11):3220. https://doi.org/10.3390/s20113220
Chicago/Turabian StyleQin, Honglei, Peng Liu, Li Cong, and Xia Xue. 2020. "Ambiguity of Residual Constraint-Based Precise Point Positioning with Partial Ambiguity Resolution under No Real-Time Network Corrections Using Real Global Positioning System (GPS) Data" Sensors 20, no. 11: 3220. https://doi.org/10.3390/s20113220
APA StyleQin, H., Liu, P., Cong, L., & Xue, X. (2020). Ambiguity of Residual Constraint-Based Precise Point Positioning with Partial Ambiguity Resolution under No Real-Time Network Corrections Using Real Global Positioning System (GPS) Data. Sensors, 20(11), 3220. https://doi.org/10.3390/s20113220





