Cellular Auxetic Structures for Mechanical Metamaterials: A Review
Abstract
1. Introduction
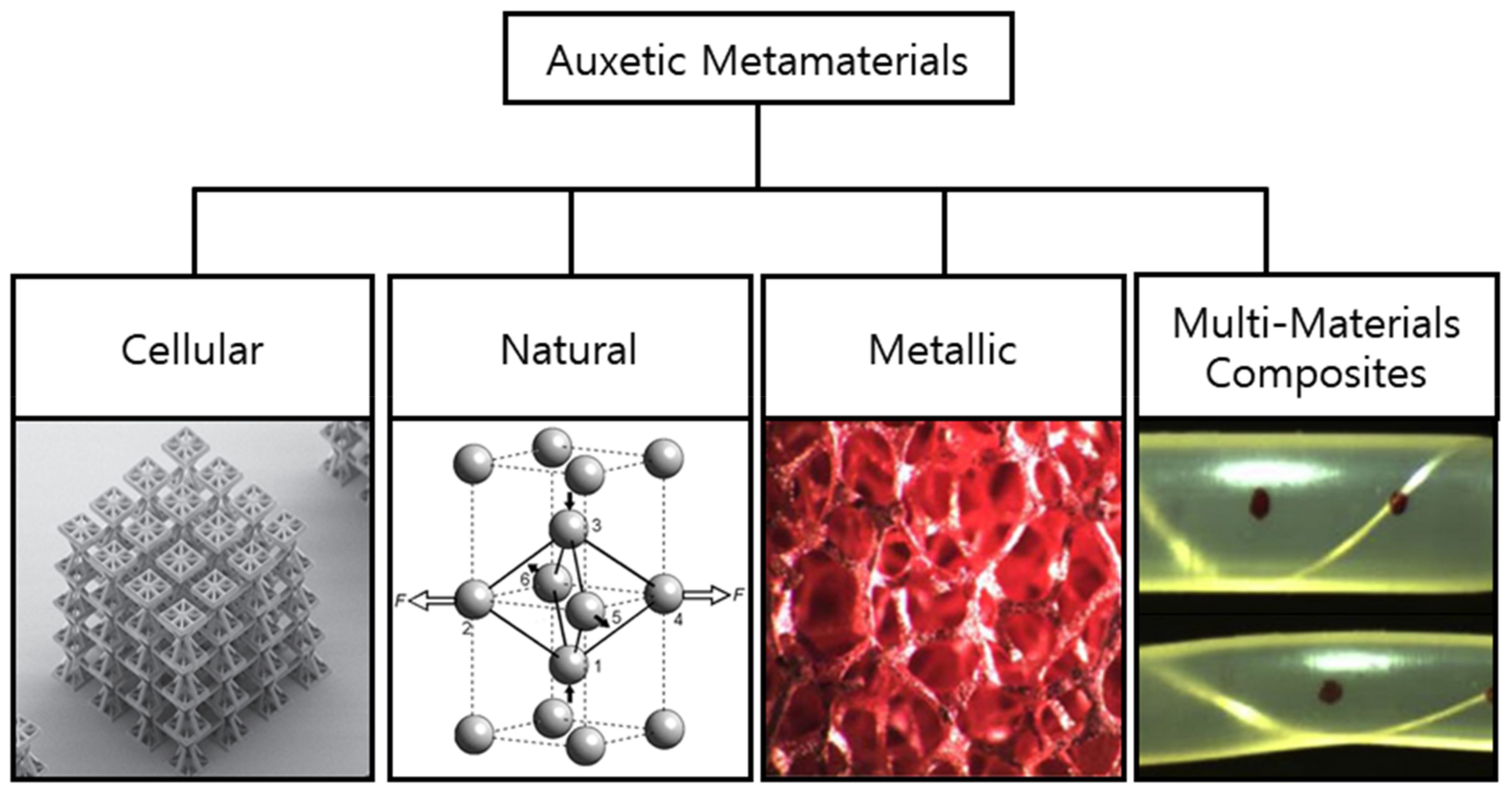
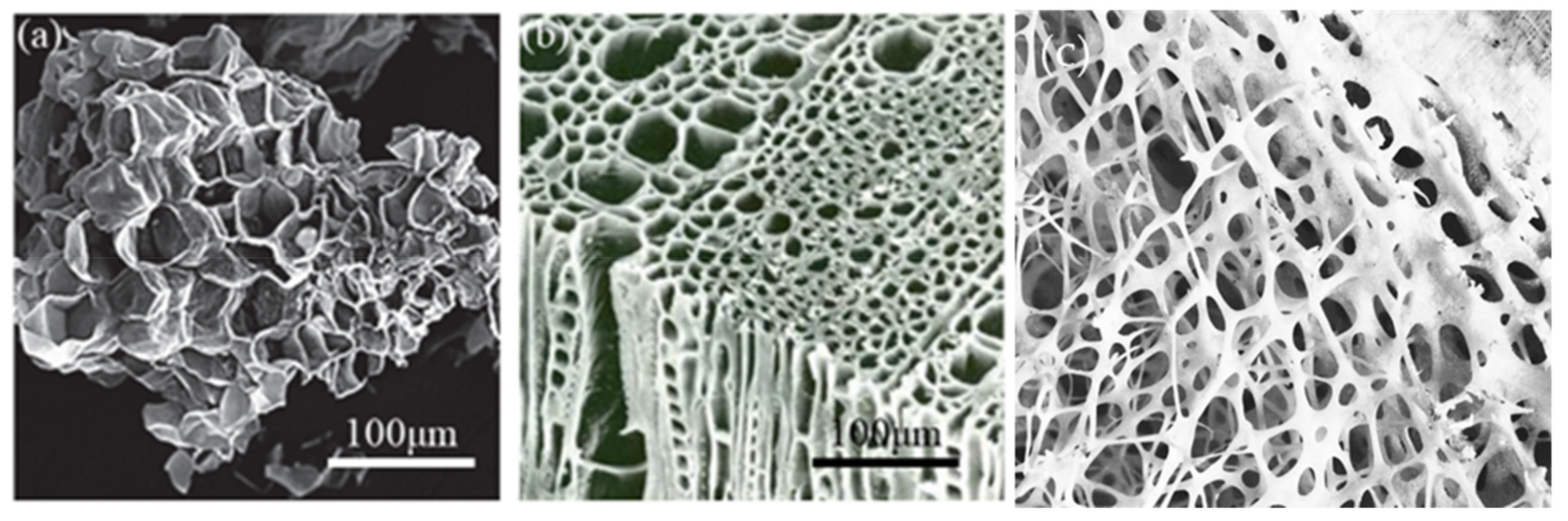
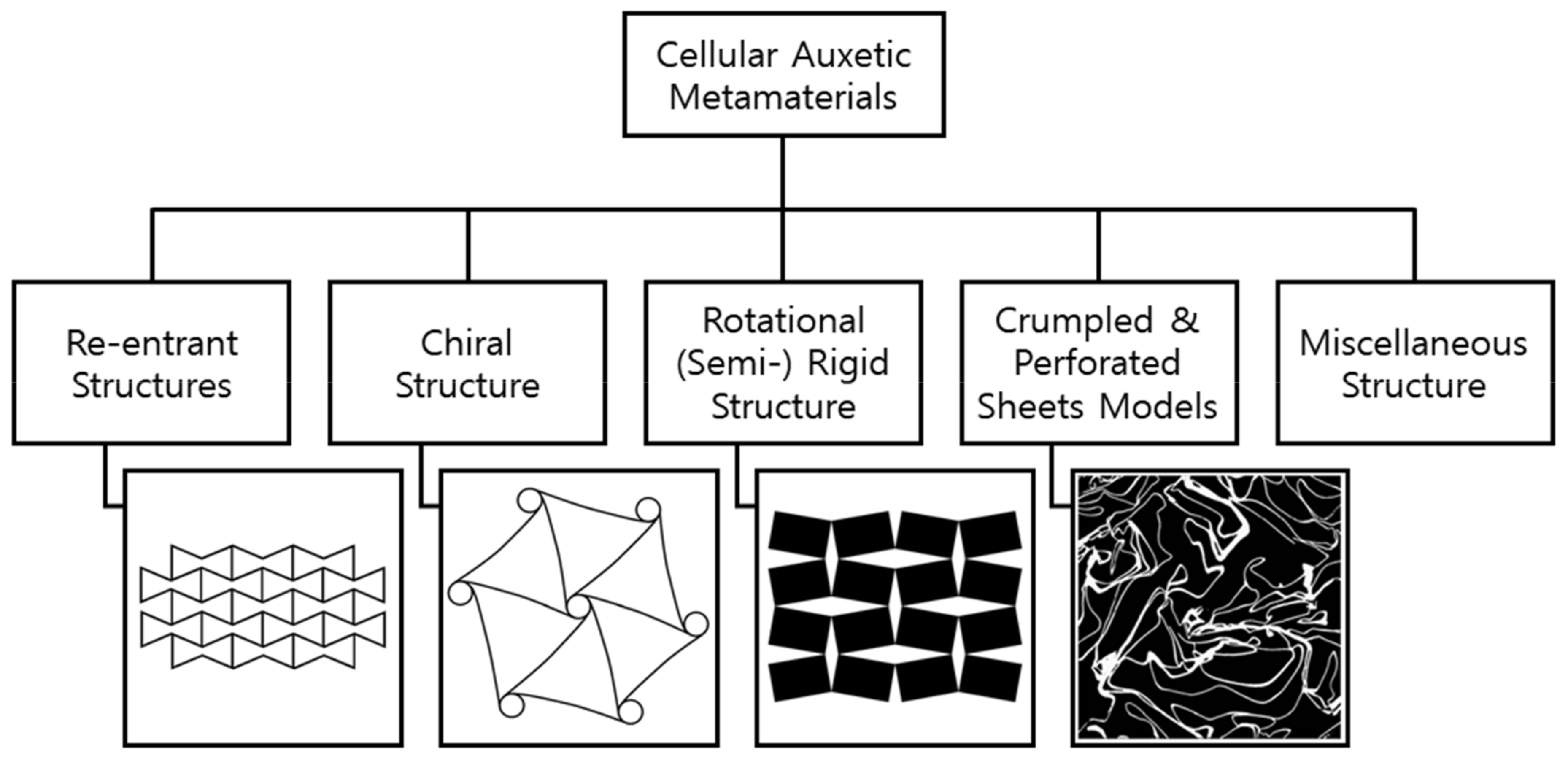
2. Cellular Auxetic Materials and Structures
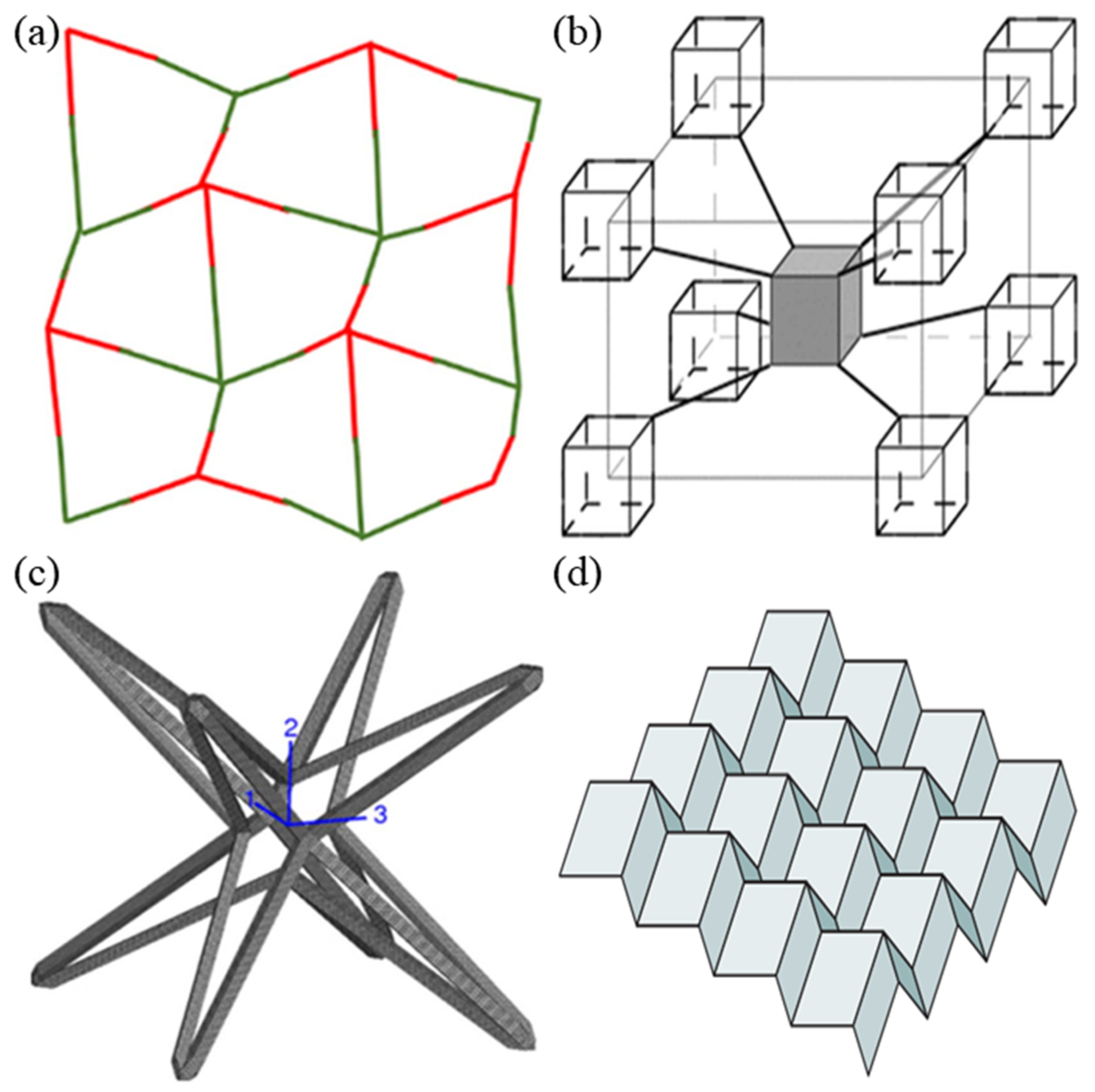
2.1. Re-Entrant Structures
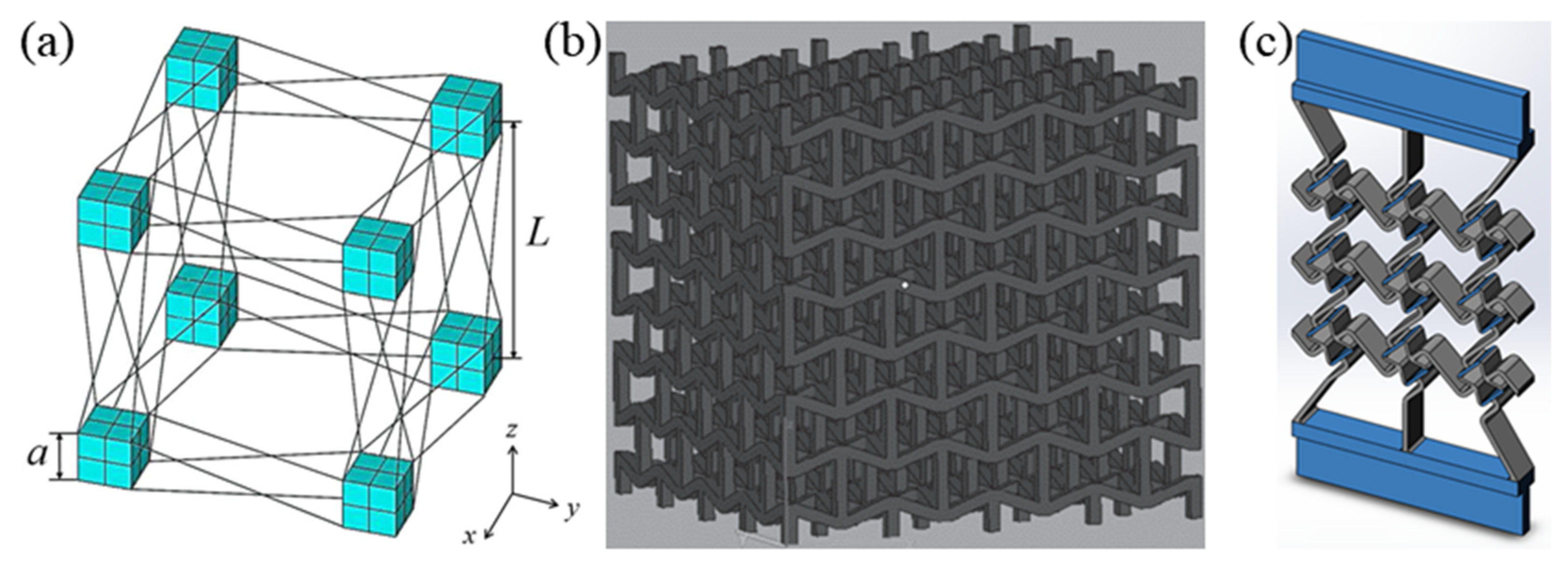
2.2. Chiral Structures
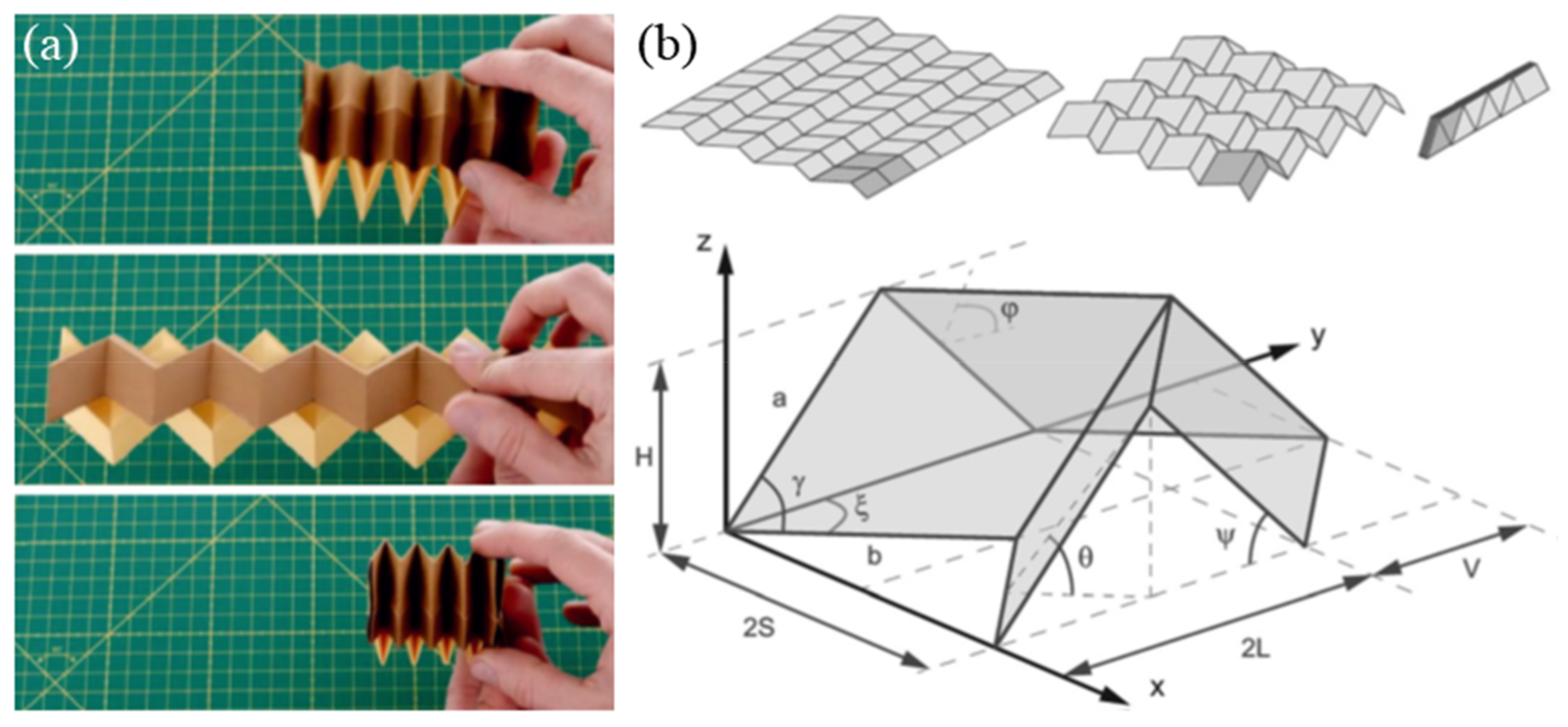
2.3. Crumpled and Perforated Sheets Models
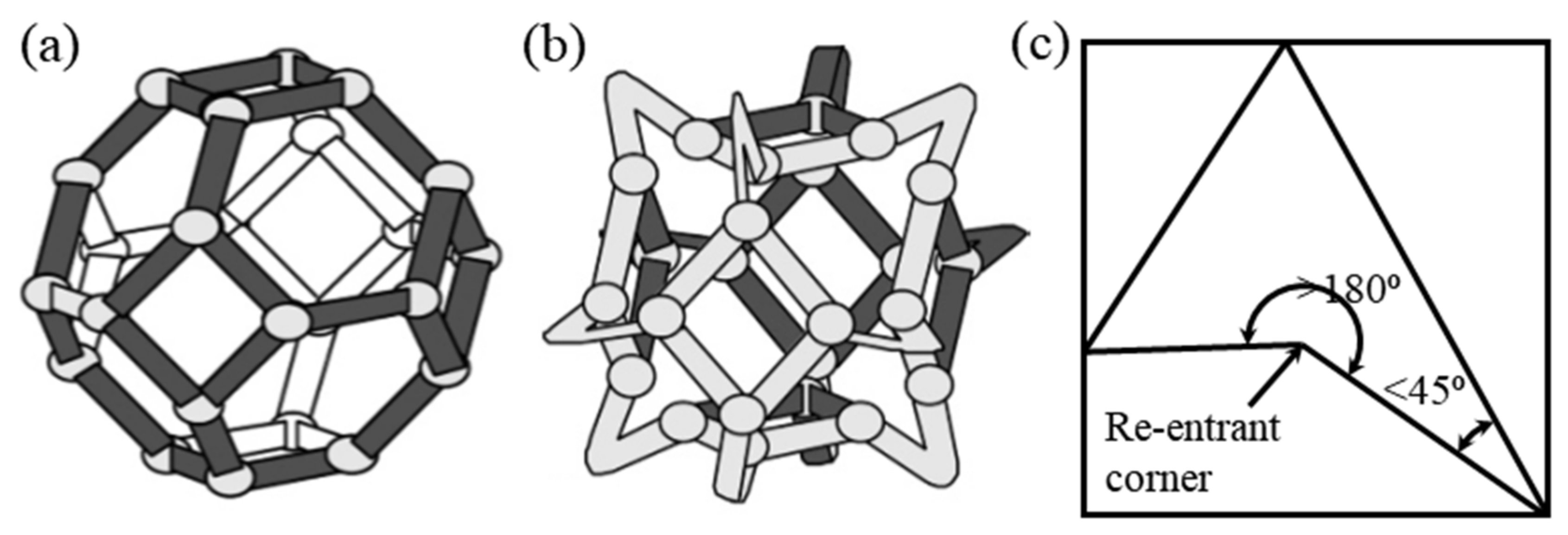
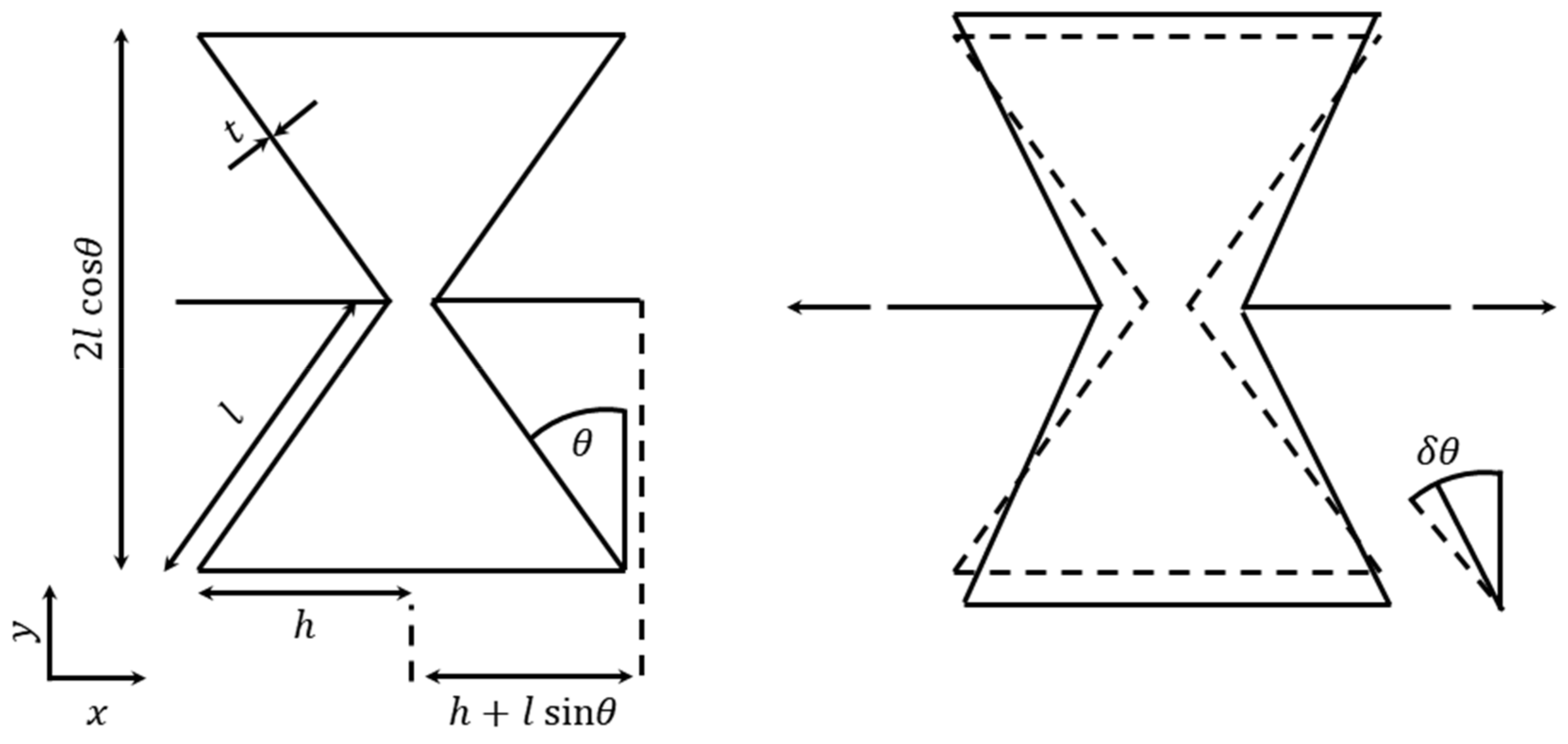
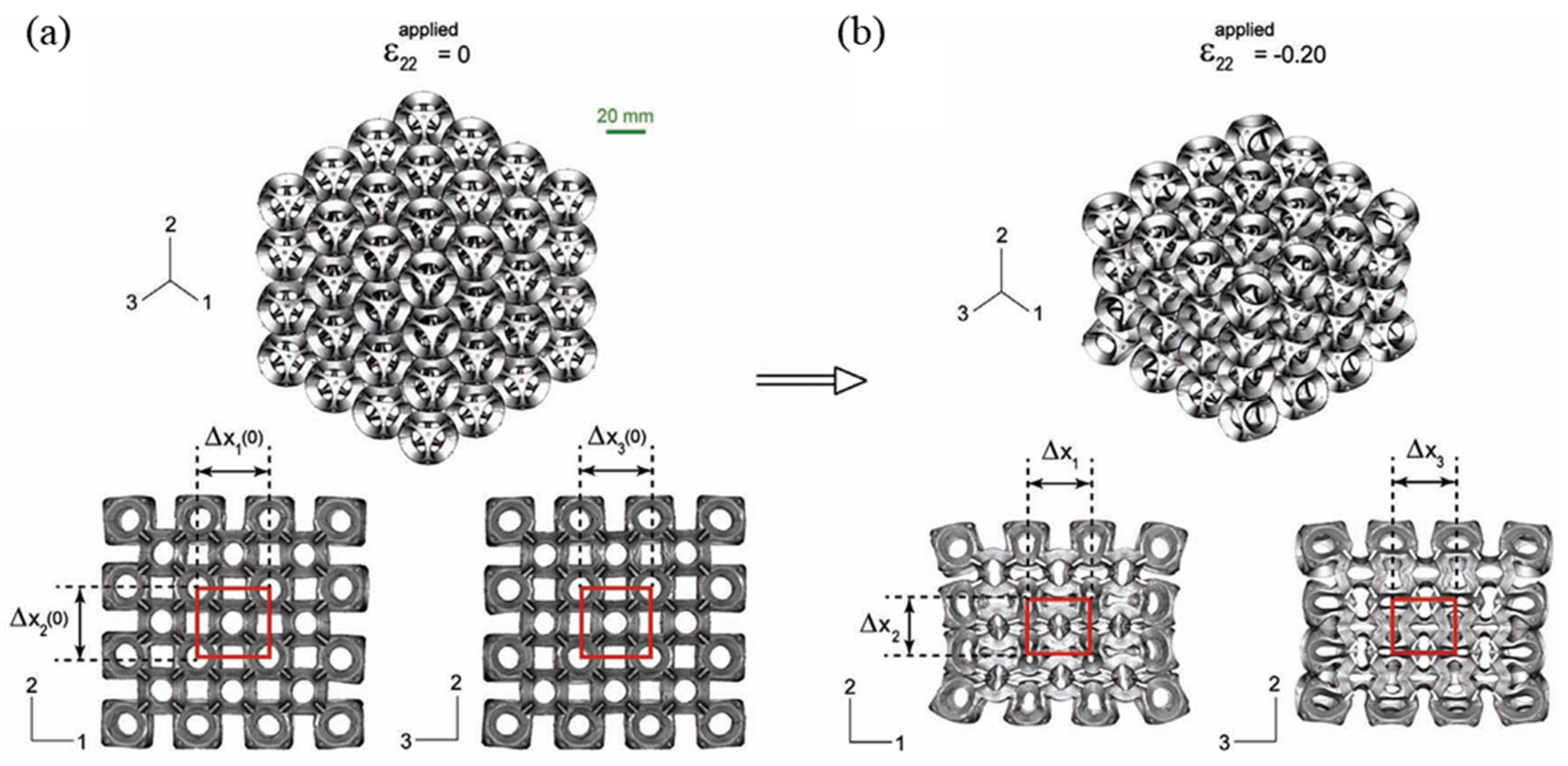
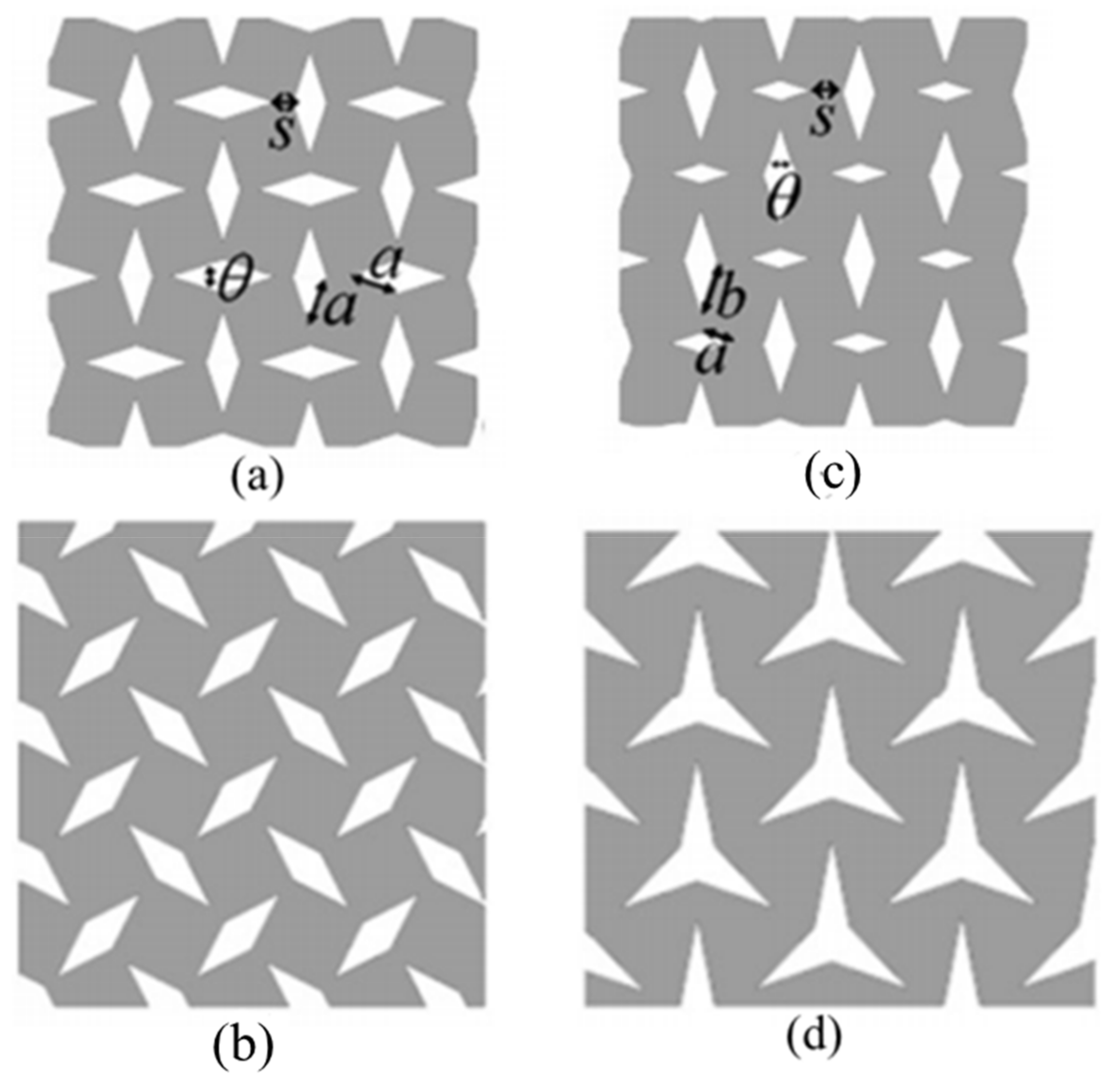
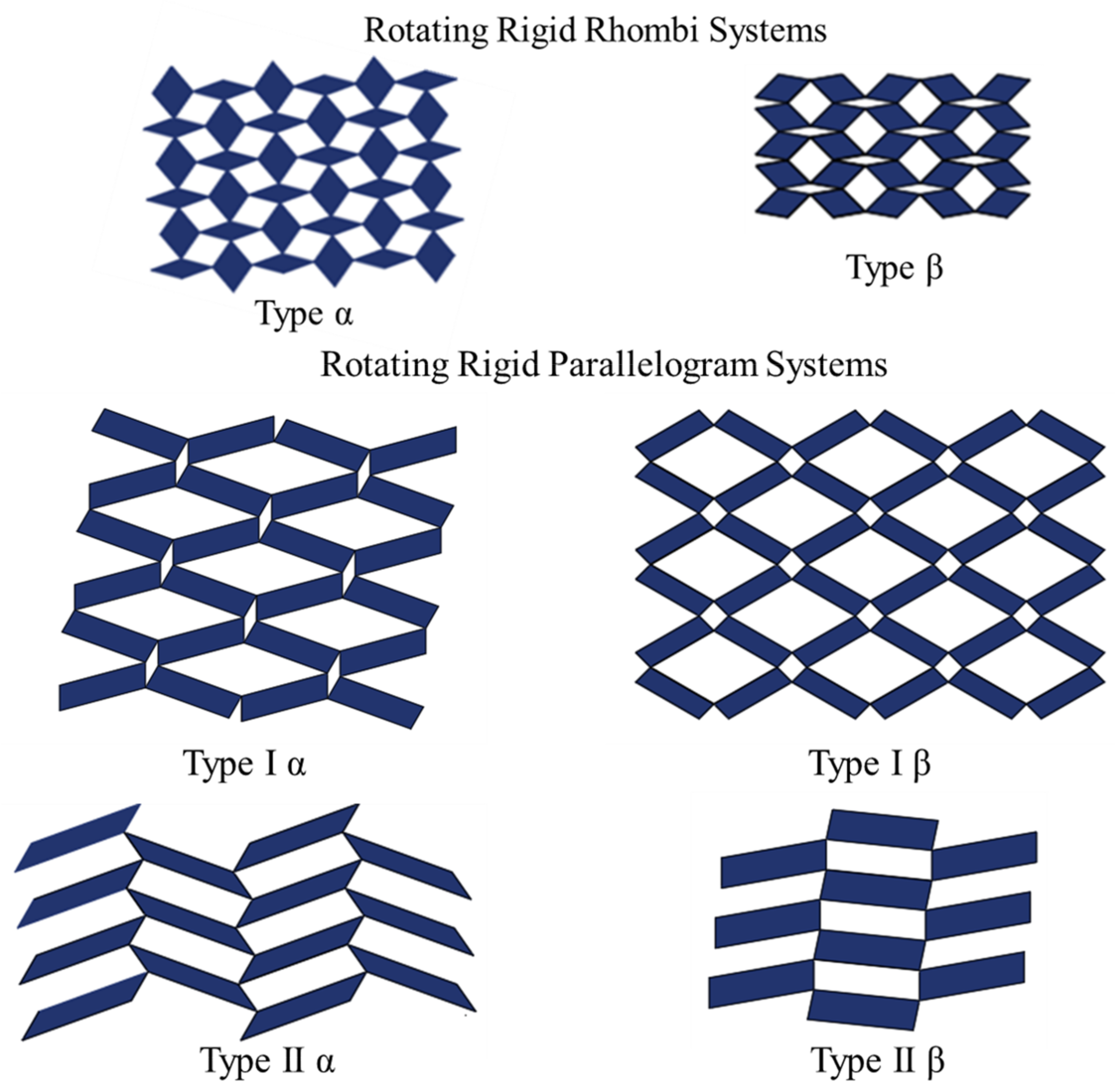
2.4. Rotational (Semi-) Rigid Structures
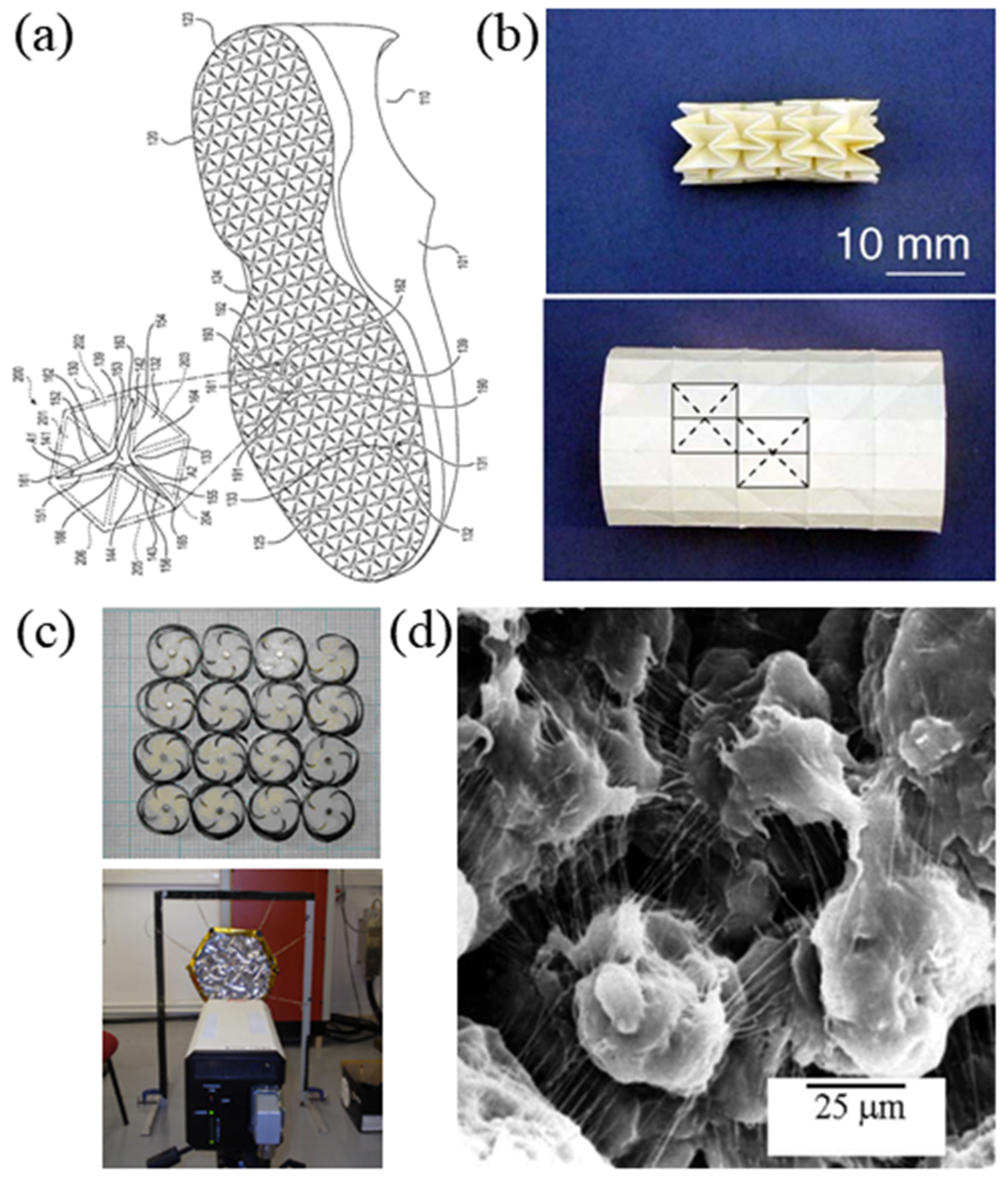
3. Applications of Auxetic Structures
- Poisson’s ratio being negative or zero.
- Large shear resistance.
- Hardness improvement.
- Lower fatigue crack propagation.
- Large toughness and modulus resilience.
- Vibration absorption.
3.1. Sports Science
3.2. Medical Industry
3.3. Sensors and Actuators
3.4. Textiles
3.5. Defence
4. Conclusions
4.1. Remarks
4.2. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pendry, J.B.; Holden, A.J.; Stewart, W.J.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76, 4773–4776. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation optics and metamaterials. Nat. Mater. 2010, 9, 387–396. [Google Scholar] [CrossRef]
- Kinoshita, S.; Yoshioka, S.; Fujii, Y.; Okamoto, N. Photophysics of structural color in the morpho butterflies. Forma 2002, 17, 103–121. [Google Scholar]
- Kinoshita, S.; Yoshioka, S.; Kawagoe, K. Mechanism of the structural color in Morpho butterflies. Seibutsu Butsuri 2001, 41, S213. [Google Scholar] [CrossRef]
- Choi, S.H.; Ku, Z.; Kim, S.; Choi, K.; Urbas, A.M.; Kim, Y.L. Silk is a natural metamaterial for self-cooling: An oxymoron? In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; pp. 1–2. [Google Scholar]
- Yan, Y. Developments in fibers for technical nonwovens. In Advances in Technical Nonwovens; Woodhead Publishing: Shaston, UK, 2016; pp. 19–96. ISBN 9780081005842. [Google Scholar]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Javadi, A.A.; Faramarzi, A.; Farmani, R. Design and optimization of microstructure of auxetic materials. Eng. Comput. (Swans. Wales) 2012, 29, 260–276. [Google Scholar] [CrossRef]
- Kurtz, S.M. Uhmwpe Biomaterials Handbook; William Andrew: Norwich, NY, USA, 2009; ISBN 9780123747211. [Google Scholar]
- Ting, T.C.T.; Chen, T. Poisson’s ratio for anisotropic elastic materials can have no bounds. Q. J. Mech. Appl. Math. 2005, 58, 73–82. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; Van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Dagdelen, J.; Montoya, J.; de Jong, M.; Persson, K. Computational prediction of new auxetic materials. Nat. Commun. 2017, 8, 323. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.B.; Lakes, R.S. Non-linear properties of metallic cellular materials with a negative Poisson’s ratio. J. Mater. Sci. 1992, 27, 5375–5381. [Google Scholar] [CrossRef]
- Argatov, I.I.; Guinovart-Díaz, R.; Sabina, F.J. On local indentation and impact compliance of isotropic auxetic materials from the continuum mechanics viewpoint. Int. J. Eng. Sci. 2012, 54, 42–57. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Fracture toughness of re-entrant foam materials with a negative Poisson’s ratio: Experiment and analysis. Int. J. Fract. 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Beg, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 23001. [Google Scholar] [CrossRef]
- Keskar, N.R.; Chelikowsky, J.R. Negative Poisson ratios in crystalline SiO2 from first-principles calculations. Nature 1992, 358, 222–224. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef]
- Kim, H.W.; Kim, T.Y.; Park, H.K.; You, I.; Kwak, J.; Kim, J.C.; Hwang, H.; Kim, H.S.; Jeong, U. Hygroscopic auxetic on-skin sensors for easy-to-handle repeated daily use. ACS Appl. Mater. Interfaces 2018, 10, 40141–40148. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Liu, Z.; Matsuhisa, N.; Qi, D.; Leow, W.R.; Yang, H.; Yu, J.; Chen, G.; Liu, Y.; Wan, C.; et al. Auxetic mechanical metamaterials to enhance sensitivity of stretchable strain sensors. Adv. Mater. 2018, 30, e1706589. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Bhullar, S.; Cho, Y.; Lee, P.C.; Byung-Guk Jun, M. Design and fabrication of auxetic stretchable force sensor for hand rehabilitation. Smart Mater. Struct. 2015, 24, 75027. [Google Scholar] [CrossRef]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of auxetic materials for sports applications: Expanding options in comfort and protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Sanami, M.; Ravirala, N.; Alderson, K.; Alderson, A. Auxetic materials for sports applications. Procedia Eng. 2014, 72, 453–458. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- AZoM Auxetic Materials—Applications. Available online: https://www.azom.com/article.aspx?ArticleID=168 (accessed on 17 August 2019).
- Burriesci, G.; Bergamasco, G. Annuloplasty Prosthesis with an Auxetic Structure; Jouve: Mayon, France, 2007; p. 11. [Google Scholar]
- Ali, M.N.; Rehman, I.U. An Auxetic structure configured as oesophageal stent with potential to be used for palliative treatment of oesophageal cancer; Development and in vitro mechanical analysis. J. Mater. Sci. Mater. Med. 2011, 22, 2573–2581. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2014, 25, 527–553. [Google Scholar] [CrossRef]
- Geng, L.C.; Ruan, X.L.; Wu, W.W.; Xia, R.; Fang, D.N. Mechanical properties of selective laser sintering (SLS) additive manufactured chiral Auxetic cylindrical stent. Exp. Mech. 2019, 59, 913–925. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of mechanics and applications of auxetic structures. Adv. Mater. Sci. Eng. 2014, 2014, 1–17. [Google Scholar] [CrossRef]
- Garber, A. Pyrolytic materials for thermal protection systems. Aerosp. Eng. 1963, 22, 126–137. [Google Scholar]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Novak, N.; Starčevič, L.; Vesenjak, M.; Ren, Z. Blast response study of the sandwich composite panels with 3D chiral auxetic core. Compos. Struct. 2019, 210, 167–178. [Google Scholar] [CrossRef]
- Ma, Z.-D.; Liu, Y.; Liu, X.; Sun, C.; Yushun, C. Ultralightweight Runflat Tires Based upon Negative Poisson Ratio (NPR) Auxetic Structures 2010. U.S. Patent 20110168313A1, 14 July 2011. [Google Scholar]
- Scheffler, M.; Colombo, P. Cellular Ceramics: Structure, Manufacturing, Properties and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; ISBN 3527313206. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure & Properties; Pergamon Press: Oxford, UK, 1989; pp. 165–166. ISBN 0-08-036607-4. [Google Scholar]
- Mazur, M.; Leary, M.; McMillan, M.; Sun, S.; Shidid, D.; Brandt, M. Mechanical properties of Ti6Al4V and AlSi12Mg lattice structures manufactured by Selective Laser Melting (SLM). Laser Addit. Manuf. 2017, 119–161. [Google Scholar] [CrossRef]
- Akhavan-Safar, A.; Barbosa, A.Q.; da Silva, L.F.M.; Ayatollahi, M.R. Micro failure analysis of adhesively bonded joints enhanced with natural cork particles: Impact of overlap length and particles volume fraction. Frat. Ed Integrità Strutt. 2018, 12, 266–274. [Google Scholar] [CrossRef]
- Ansell, M.P. Wood microstructure-A cellular composite. In Wood Composites; Woodhead Publishing: Shaston, UK, 2015; pp. 3–26. ISBN 9781782424772. [Google Scholar]
- Naboni, R.; Kunic, A. Design and Additive manufacturing of lattice-based cellular solids at building scale. Blucher Des. Proc. 2017, 3, 369–375. [Google Scholar]
- Alderson, A.; Evans, K.E. Modelling concurrent deformation mechanisms in auxetic microporous polymers. J. Mater. Sci. 1997, 32, 2797–2809. [Google Scholar] [CrossRef]
- Gaspar, N.; Smith, C.W.; Alderson, A.; Grima, J.N.; Evans, K.E. A generalised three-dimensional tethered-nodule model for auxetic materials. J. Mater. Sci. 2010, 46, 372–384. [Google Scholar] [CrossRef]
- Dirrenberger, J.; Forest, S.; Jeulin, D. Effective elastic properties of auxetic microstructures: Anisotropy and structural applications. Int. J. Mech. Mater. Des. 2012, 9, 21–33. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Smith, C.W.; Grima, J.N.; Evans, K.E. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Hearn, E.J. Introduction to the finite element method. Mech. Mater. 1997, 2, 300–380. [Google Scholar]
- Lakes, R. Response: Negative poisson’s ratio materials. Science 1987, 238, 551. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K.E. Fabrication methods for auxetic foams. J. Mater. Sci. 1997, 32, 5945–5953. [Google Scholar] [CrossRef]
- Quadrini, F.; Bellisario, D.; Ciampoli, L.; Costanza, G.; Santo, L. Auxetic epoxy foams produced by solid state foaming. J. Cell. Plast. 2015, 52, 441–454. [Google Scholar] [CrossRef]
- Bhullar, S.K. Three decades of auxetic polymers: A review. e-Polymers 2015, 15, 15. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson’s ratio. Int. J. Mech. Sci. 1995, 37, 51–59. [Google Scholar] [CrossRef]
- Lakes, R.S.; Elms, K. Indentability of conventional and negative poisson’s ratio foams. J. Compos. Mater. 1993, 27, 1193–1202. [Google Scholar] [CrossRef]
- Uchic, M.D.; Shade, P.A.; Dimiduk, D.M. Micro-compression testing of fcc metals: A selected overview of experiments and simulations. JOM 2009, 61, 36–41. [Google Scholar] [CrossRef]
- Hemker, K.J.; Sharpe, W.N. Microscale characterization of mechanical properties. Annu. Rev. Mater. Res. 2007, 37, 93–126. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Pathak, S. Determination of the effective zero-point and the extraction of spherical nanoindentation stress-strain curves. Acta Mater. 2008, 56, 3523–3532. [Google Scholar] [CrossRef]
- Gaspar, N.; Ren, X.J.; Smith, C.W.; Grima, J.N.; Evans, K.E. Novel honeycombs with auxetic behaviour. Acta Mater. 2005, 53, 2439–2445. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction through buckling in 2D periodic, soft and porous structures: Effect of pore shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- An isotropic three-dimensional structure with Poisson’s ratio = -1. J. Elast. 1985, 15, 427–430. [CrossRef]
- Korner, C.; Liebold-Ribeiro, Y. A systematic approach to identify cellular auxetic materials. Smart Mater. Struct. 2015, 24, 25013. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- Bückmann, T.; Stenger, N.; Kadic, M.; Kaschke, J.; Frölich, A.; Kennerknecht, T.; Eberl, C.; Thiel, M.; Wegener, M. Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography. Adv. Mater. 2012, 24, 2710–2714. [Google Scholar] [CrossRef]
- Li, D.; Dong, L.; Lakes, R.S. A unit cell structure with tunable Poisson’s ratio from positive to negative. Mater. Lett. 2016, 164, 456–459. [Google Scholar] [CrossRef]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D soft metamaterials with negative poisson’s ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.; Perdigou, C.; Chen, E.R.; Bertoldi, K.; Reis, P.M. Buckling-induced encapsulation of structured elastic shells under pressure. Proc. Natl. Acad. Sci. USA 2012, 109, 5978–5983. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Simple cubic three-dimensional auxetic metamaterials. Phys. Status Solidi 2014, 251, 1515–1522. [Google Scholar] [CrossRef]
- Lim, T.-C. A 3D auxetic material based on intersecting double arrowheads. Phys. Status Solidi 2016, 253, 1252–1260. [Google Scholar] [CrossRef]
- Rad, M.S.; Ahmad, Z.; Alias, A. Computational approach in formulating mechanical characteristics of 3D star honeycomb auxetic structure. Adv. Mater. Sci. Eng. 2015, 2015, 1–11. [Google Scholar]
- Wang, Y.-C.; Shen, M.-W.; Liao, S.-M. Microstructural effects on the poisson’s ratio of star-shaped two-dimensional systems. Phys. Status Solidi 2017, 254, 1700024. [Google Scholar] [CrossRef]
- Caddock, B.D.; Evans, K.E. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. J. Phys. D. Appl. Phys. 1989, 22, 1877–1882. [Google Scholar] [CrossRef]
- Pickles, A.P.; Alderson, K.L.; Evans, K.E. The effects of powder morphology on the processing of auxetic polypropylene (PP of negative poisson’s ratio). Polym. Eng. Sci. 1996, 36, 636–642. [Google Scholar] [CrossRef]
- Bellare, A.; Bistolfi, A.; Simis, K.; Pruitt, L. Physico-chemical characteristics of UHMWPE before and after processing. Available online: https://www.researchgate.net/publication/228588911_Physico-chemical_characteristics_of_UHMWPE_before_and_after_processing (accessed on 1 May 2020).
- Bhullar, S.; Çelik Bedeloğlu, A.; Jun, M. Characterization and Auxetic effect of Polytetrafluoroethylene Tubular structure. Int. J. Adv. Sci. Eng. 2014, 1, 8–13. [Google Scholar]
- Evans, K.E.; Alderson, A.; Christian, F.R. Auxetic two-dimensional polymer networks. An example of tailoring geometry for specific mechanical properties. J. Chem. Soc. Faraday Trans. 1995, 91, 2671. [Google Scholar] [CrossRef]
- Lakes, R. Deformation mechanisms in negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y. 3D printed Auxetic mechanical metamaterial with chiral cells and re-entrant cores. Sci. Rep. 2018, 8, 2397. [Google Scholar] [CrossRef] [PubMed]
- Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.-S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Ha, C.S.; Plesha, M.E.; Lakes, R.S. Chiral three-dimensional lattices with tunable Poisson’s ratio. Smart Mater. Struct. 2016, 25, 54005. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Haghpanah, B.; Ghosh, R.; Hamouda, A.M.; Nayeb-Hashemi, H.; Vaziri, A. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theor. Appl. Mech. Lett. 2016, 6, 81–96. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Farrugia, P.S.; Azzopardi, K.M.; Mizzi, L.; Brincat, J.P.; Grima, J.N. A realistic generic model for anti-tetrachiral systems. Phys. Status Solidi Basic Res. 2013, 250, 2012–2019. [Google Scholar] [CrossRef]
- Huang, H.H.; Wong, B.L.; Chou, Y.C. Design and properties of 3D-printed chiral auxetic metamaterials by reconfigurable connections. Phys. Status Solidi Basic Res. 2016, 253, 1557–1564. [Google Scholar] [CrossRef]
- Airoldi, A.; Bettini, P.; Panichelli, P.; Oktem, M.F.; Sala, G. Chiral topologies for composite morphing structures—Part I: Development of a chiral rib for deformable airfoils. Phys. Status Solidi Basic Res. 2015, 252, 1435–1445. [Google Scholar] [CrossRef]
- Airoldi, A.; Bettini, P.; Panichelli, P.; Sala, G. Chiral topologies for composite morphing structures—Part II: Novel configurations and technological processes. Phys. Status Solidi Basic Res. 2015, 252, 1446–1454. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Sudhir Sastry, Y.B.; Natarajan, R. Design concepts of an aircraft wing: Composite and morphing airfoil with auxetic structures. Front. Struct. Civ. Eng. 2016, 10, 394–408. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, H.; Liu, S.; Xu, B. Study of an auxetic structure made of tubes and corrugated sheets. Phys. Status Solidi 2013. [Google Scholar] [CrossRef]
- Hall, L.J.; Coluci, V.R.; Galvao, D.S.; Kozlov, M.E.; Zhang, M.; Dantas, S.O.; Baughman, R.H. Sign change of poisson’s ratio for carbon nanotube sheets. Science 2008, 320, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Adhikari, S.; Srikantha Phani, A. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology 2009, 20, 65709. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Winczewski, S.; Mizzi, L.; Grech, M.C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. Tailoring graphene to achieve negative poisson’s ratio properties. Adv. Mater. 2014, 27, 1455–1459. [Google Scholar] [CrossRef]
- Tan, H.; Yu, L.; Zhou, Z. Negative Poisson’s ratio in non-porous smooth curve sheet. Phys. Status Solidi 2017, 254, 1600612. [Google Scholar] [CrossRef]
- Lang, R.J. Origami Design Secrets; A.K. Peters: Natick, MA, USA, 2011. [Google Scholar]
- Castle, T.; Cho, Y.; Gong, X.; Jung, E.; Sussman, D.M.; Yang, S.; Kamien, R.D. Making the cut: Lattice kirigami rules. Phys. Rev. Lett. 2014, 113, 3276–3281. [Google Scholar] [CrossRef]
- Schenk, M.; Guest, S.D. Geometry of miura-folded metamaterials. Proc. Natl. Acad. Sci. USA 2013, 110, 3276–3281. [Google Scholar] [CrossRef]
- Silverberg, J.L.; Evans, A.A.; McLeod, L.; Hayward, R.C.; Hull, T.; Santangelo, C.D.; Cohen, I. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 2014, 345, 647–650. [Google Scholar] [CrossRef]
- Miura, K. Method of packaging and deployment of large membranes in space. Inst. Space Astronaut. Sci. 1985, 618, 1–9. [Google Scholar]
- Grima, J.N.; Gatt, R. Perforated sheets exhibiting negative poisson’s ratios. Adv. Eng. Mater. 2010, 12, 460–464. [Google Scholar] [CrossRef]
- Grima, J.N.; Mizzi, L.; Azzopardi, K.M.; Gatt, R. Auxetic perforated mechanical metamaterials with randomly oriented cuts. Adv. Mater. 2015, 28, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Negative poisson’s ratios from rotating rectangles. Comput. Methods Sci. Technol. 2004, 10, 137–145. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating triangles. J. Mater. Sci. 2006, 41, 3193–3196. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.-S.; Gatt, R.; Attard, D. On the auxetic properties of rotating rhombi and parallelograms: A preliminary investigation. Phys. Status Solidi 2008, 245, 521–529. [Google Scholar] [CrossRef]
- Grima, J.N.; Zammit, V.; Gatt, R.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating semi-rigid units. Phys. Status Solidi 2007, 244, 866–882. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Rotation and dilation deformation mechanisms for auxetic behaviour in the ?-cristobalite tetrahedral framework structure. Phys. Chem. Miner. 2001, 28, 711–718. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extrem. Mech. Lett. 2016, 9, 291–296. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. Auxetic behaviour from rotating rhombi. Phys. Status Solidi 2008, 245, 2395–2404. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Ellul, B.; Chetcuti, E. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations. J. Non. Cryst. Solids 2010, 356, 1980–1987. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Cross, T.; Hoffer, K.; Jones, D.; Kirsvhner, P.; Langvin, E.; Meschter, J. Auxetic Structures and Footwear with Soles Having Auxetic Structures. U.S. Patent 9402439B2, 2 August 2016. [Google Scholar]
- Kuribayashi, K.; Tsuchiya, K.; You, Z.; Tomus, D.; Umemoto, M.; Ito, T.; Sasaki, M. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Mater. Sci. Eng. A 2006, 419, 131–137. [Google Scholar] [CrossRef]
- Jacobs, S.; Coconnier, C.; Dimaio, D.; Scarpa, F.; Toso, M.; Martinez, J. Deployable auxetic shape memory alloy cellular antenna demonstrator: Design, manufacturing and modal testing. Smart Mater. Struct. 2012, 21, 75013. [Google Scholar] [CrossRef]
- Alderson, K.L.; Alderson, A.; Smart, G.; Simkins, V.R.; Davies, P.J. Auxetic polypropylene fibres Part 1—Manufacture and characterisation. Plast. Rubber Compos. 2002, 31, 344–349. [Google Scholar] [CrossRef]
- Toronjo, A. Articles of Apparel Including Auxetic Materials. U.S. Patent 20170099900A1, 13 April 2017. [Google Scholar]
- Qiao, J.X.; Chen, C.Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs. Int. J. Impact Eng. 2015, 83, 47–58. [Google Scholar] [CrossRef]
- Nike The New Dimensions of Nike Free. Available online: https://news.nike.com/news/nike-free-2016-running-training# (accessed on 1 April 2020).
- D3O Trust Nimbus Helmet Pad System. Available online: https://www.d3o.com/partner-support/products/trust-nimbus-helmet-pad-system/ (accessed on 1 April 2020).
- Hamzehei, R.; Rezaei, S.; Kadkhodapour, J.; Anaraki, A.P.; Mahmoudi, A. 2D triangular anti-trichiral structures and auxetic stents with symmetric shrinkage behavior and high energy absorption. Mech. Mater. 2020, 142, 103291. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, L.J.; Liu, Y.J.; Liu, L.W.; Leng, J.S. 4D printing of personalized shape memory polymer vascular stents with negative Poisson’s ratio structure: A preliminary study. Sci. China Technol. Sci. 2020, 63, 578–588. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Zeng, C.; Kramer, L.D.; Gillis, A. Prosthetic Socket Apparatus And Systems. U.S. Patent 9486333B2, 17 October 2013. [Google Scholar]
- Paxton, N.C.; Daley, R.; Forrestal, D.P.; Allenby, M.C.; Woodruff, M.A. Auxetic tubular scaffolds via melt electrowriting. Mater. Des. 2020, 108787. [Google Scholar] [CrossRef]
- Vijayavenkataraman, S.; Gopinath, A.; Lu, W.F. A new design of 3D-printed orthopedic bone plates with auxetic structures to mitigate stress shielding and improve intra-operative bending. Bio-Design Manuf. 2020, 3, 98–108. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, L.; Li, J.; Tian, S.; Zhang, M.; Fan, Y. A novel auxetic structure based bone screw design: Tensile mechanical characterization and pullout fixation strength evaluation. Mater. Des. 2020, 188, 108424. [Google Scholar] [CrossRef]
- Wong, J.; Gong, A.T.; Defnet, P.A.; Meabe, L.; Beauchamp, B.; Sweet, R.M.; Sardon, H.; Cobb, C.L.; Nelson, A. 3D printing ionogel auxetic frameworks for stretchable sensors. Adv. Mater. Technol. 2019, 4, 4. [Google Scholar] [CrossRef]
- De Bellis, M.L.; Bacigalupo, A. Auxetic behavior and acoustic properties of microstructured piezoelectric strain sensors. Smart Mater. Struct. 2017, 26, 085037. [Google Scholar] [CrossRef]
- Li, Y.; Luo, S.; Yang, M.C.; Liang, R.; Zeng, C. Poisson ratio and piezoresistive sensing: A new route to high-performance 3D flexible and stretchable sensors of multimodal sensing capability. Adv. Funct. Mater. 2016, 26, 2900–2908. [Google Scholar] [CrossRef]
- Taherkhani, B.; Azizkhani, M.B.; Kadkhodapour, J.; Anaraki, A.P.; Rastgordani, S. Highly sensitive, piezoresistive, silicone/carbon fiber-based auxetic sensor for low strain values. Sens. Actuators A Phys. 2020, 305, 111939. [Google Scholar] [CrossRef]
- Han, S.; Jung, S.; Jeong, S.; Choi, J.; Choi, Y.; Lee, S.Y. High-performance, biaxially stretchable conductor based on Ag composites and hierarchical auxetic structure. J. Mater. Chem. C 2020, 8, 1556–1561. [Google Scholar] [CrossRef]
- Farhangdoust, S.; Aghaei, S.M.; Amirahmadi, M.; Pala, N.; Mehrabi, A. Auxetic MEMS sensor. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2020, Orange, CA, USA, 27 April–1 May 2020; p. 36. [Google Scholar]
- Rossiter, J.; Takashima, K.; Scarpa, F.; Walters, P.; Mukai, T. Shape memory polymer hexachiral auxetic structures with tunable stiffness. Smart Mater. Struct. 2014, 23, 45007. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. Metamaterials with negative Poisson’s ratio and non-positive thermal expansion. Compos. Struct. 2017, 162, 70–84. [Google Scholar] [CrossRef]
- Sedal, A.; Memar, A.H.; Liu, T.; Menguc, Y.; Corson, N. Design of deployable soft robots through plastic deformation of kirigami structures. IEEE Robot. Autom. Lett. 2020, 5, 2272–2279. [Google Scholar] [CrossRef]
- Park, Y.; Loh, K.J. Surface morphing of geometrically patterned active skins. MRS Adv. 2020, 1–8, 743–750. [Google Scholar] [CrossRef]
- Dubbelday, P. Auxetic Materials: An Annotated Bibliography of Materials with Negative Poisson’s Ratio; PN: Stirling, UK, 1993. [Google Scholar]
- Sevick, E.M.; Williams, D.R.M. Porous membranes with grafted polymers: Valves and sensors. In Proceedings of the Materials Research Society Symposium, Boston, MA, USA, 13–14 November 1995; Volume 371, pp. 495–502. [Google Scholar]
- Grima, J.N.; Caruana-Gauci, R.; Dudek, M.R.; Wojciechowski, K.W.; Gatt, R. Smart metamaterials with tunable auxetic and other properties. Smart Mater. Struct. 2013, 22, 84016. [Google Scholar] [CrossRef]
- Lipton, J.I.; MacCurdy, R.; Manchester, Z.; Chin, L.; Cellucci, D.; Rus, D. Handedness in shearing auxetics creates rigid and compliant structures. Science 2018, 360, 632–635. [Google Scholar] [CrossRef] [PubMed]
- Lipton, J.I.; MacCurdy, R.; Chin, L.; Rus, D. Non-Planar Shearing Auxetic Structures, Devices, and Methods. U.S. Patent 20180311833A1, 1 November 2018. [Google Scholar]
- Lazarus, A.; Reis, P.M. Soft actuation of structured cylinders through auxetic behavior. Adv. Eng. Mater. 2015, 17, 815–820. [Google Scholar] [CrossRef]
- Hasse, A.; Mauser, K. Poisson induced bending actuator for soft robotic systems. Soft Robot. 2020, 7, 155–167. [Google Scholar] [CrossRef]
- Pfeil, A.; Barbé, L.; Wach, B.; Bruyas, A.; Geiskopf, F.; Nierenberger, M.; Renaud, P. A 3D-printed needle driver based on auxetic structure and inchworm kinematics. In Proceedings of the ASME Design Engineering Technical Conference, Quebec, QC, Canada, 26–29 August 2018;A; Volume 5. [Google Scholar]
- Bonfanti, S.; Guerra, R.; Clos, F.F.; Rayneau-Kirkhope, D.; Zapperi, S. Automatic Design of Mechanical Metamaterial Actuators. arXiv 2020, arXiv:2002.03032. [Google Scholar]
- Zhang, S.L.; Lai, Y.C.; He, X.; Liu, R.; Zi, Y.; Wang, Z.L. Auxetic foam-based contact-mode triboelectric nanogenerator with highly sensitive self-powered strain sensing capabilities to monitor human body movement. Adv. Funct. Mater. 2017, 27, 1606695. [Google Scholar] [CrossRef]
- Farhangdoust, S. Auxetic cantilever beam energy harvester. Sens. Actuators A: Phys. 2020, 282, 90–96. [Google Scholar]
- Eghbali, P.; Younesian, D.; Farhangdoust, S. Enhancement of piezoelectric vibration energy harvesting with auxetic boosters. Int. J. Energy Res. 2020, 44, 1179–1190. [Google Scholar] [CrossRef]
- Evans, K. Expanding Blast-Proof Curtain Will Reduce Impact of Bomb Explosions. Available online: https://epsrc.ukri.org/newsevents/casestudies/blastproofcurtain/ (accessed on 17 August 2019).
- Nagai, K. Narrow passage moving body structure. Japan Patent JP06137799, 1994. [Google Scholar]
- Stott, P.J.; Mitchell, R.; Alderson, K.; Alderson, A. A growth industry. Mater. World 2000, 8, 12–14. [Google Scholar]
- Ma, Z.; Arbor, A.; Hulbert, G.M. Functionally-graded Npr (Negative Poisson’s Ratio) material for a blast-protective deflector. Eng. Technol. 2010, 55909065. [Google Scholar]
- Yang, S.; Qi, C.; Wang, D.; Gao, R.; Hu, H.; Shu, J. A comparative study of ballistic resistance of sandwich panels with aluminum foam and auxetic honeycomb cores. Adv. Mech. Eng. 2013, 2013, 589216. [Google Scholar] [CrossRef]
- Qi, C.; Yang, S.; Wang, D.; Yang, L.J. Ballistic resistance of honeycomb sandwich panels under in-plane high-velocity impact. Sci. World J. 2013, 2013, 589216. [Google Scholar] [CrossRef] [PubMed]
- Madke, R.R.; Chowdhury, R. Anti-impact behavior of auxetic sandwich structure with braided face sheets and 3D re-entrant cores. Compos. Struct. 2020, 236, 111838. [Google Scholar] [CrossRef]
- Luo, F.; Zhang, S.; Yang, D. Anti-explosion performance of composite blastwall with an auxetic re-entrant honeycomb core for offshore platforms. J. Mar. Sci. Eng. 2020, 8, 182. [Google Scholar] [CrossRef]
- Lan, X.K.; Huang, Q.; Zhou, T.; Feng, S. Optimal design of a novel cylindrical sandwich panel with double arrow auxetic core under air blast loading. Def. Technol. 2020. [Google Scholar] [CrossRef]
- Auxetix. Available online: https://www.auxetix.com/ (accessed on 13 May 2020).
- Chen, Z.; Wu, X.; Wang, Z.; Shao, J. Concepts for morphing airfoil using novel auxetic lattices. Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2020; Volume 622, pp. 265–274. [Google Scholar]
- Zhao, Z.; Xu, H.; Wang, J.; Zhao, X.; Cai, M.; Yang, Q. Auxetic behavior of Beishan granite after thermal treatment: A microcracking perspective. Eng. Fract. Mech. 2020, 231, 107017. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The materials project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 11002. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python materials genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Brough, D.B.; Wheeler, D.; Kalidindi, S.R. Materials knowledge systems in python—A data science framework for accelerated development of hierarchical materials. Integr. Mater. Manuf. Innov. 2017, 6, 36–53. [Google Scholar] [CrossRef]
- Nazaré, F.; Alderson, A. Models for the prediction of Poisson’s ratio in the “α-cristobalite” tetrahedral framework. Phys. Status Solidi Basic Res. 2015, 252, 1465–1478. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelkar, P.U.; Kim, H.S.; Cho, K.-H.; Kwak, J.Y.; Kang, C.-Y.; Song, H.-C. Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors 2020, 20, 3132. https://doi.org/10.3390/s20113132
Kelkar PU, Kim HS, Cho K-H, Kwak JY, Kang C-Y, Song H-C. Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors. 2020; 20(11):3132. https://doi.org/10.3390/s20113132
Chicago/Turabian StyleKelkar, Parth Uday, Hyun Soo Kim, Kyung-Hoon Cho, Joon Young Kwak, Chong-Yun Kang, and Hyun-Cheol Song. 2020. "Cellular Auxetic Structures for Mechanical Metamaterials: A Review" Sensors 20, no. 11: 3132. https://doi.org/10.3390/s20113132
APA StyleKelkar, P. U., Kim, H. S., Cho, K.-H., Kwak, J. Y., Kang, C.-Y., & Song, H.-C. (2020). Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors, 20(11), 3132. https://doi.org/10.3390/s20113132