Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution and Paper Structure
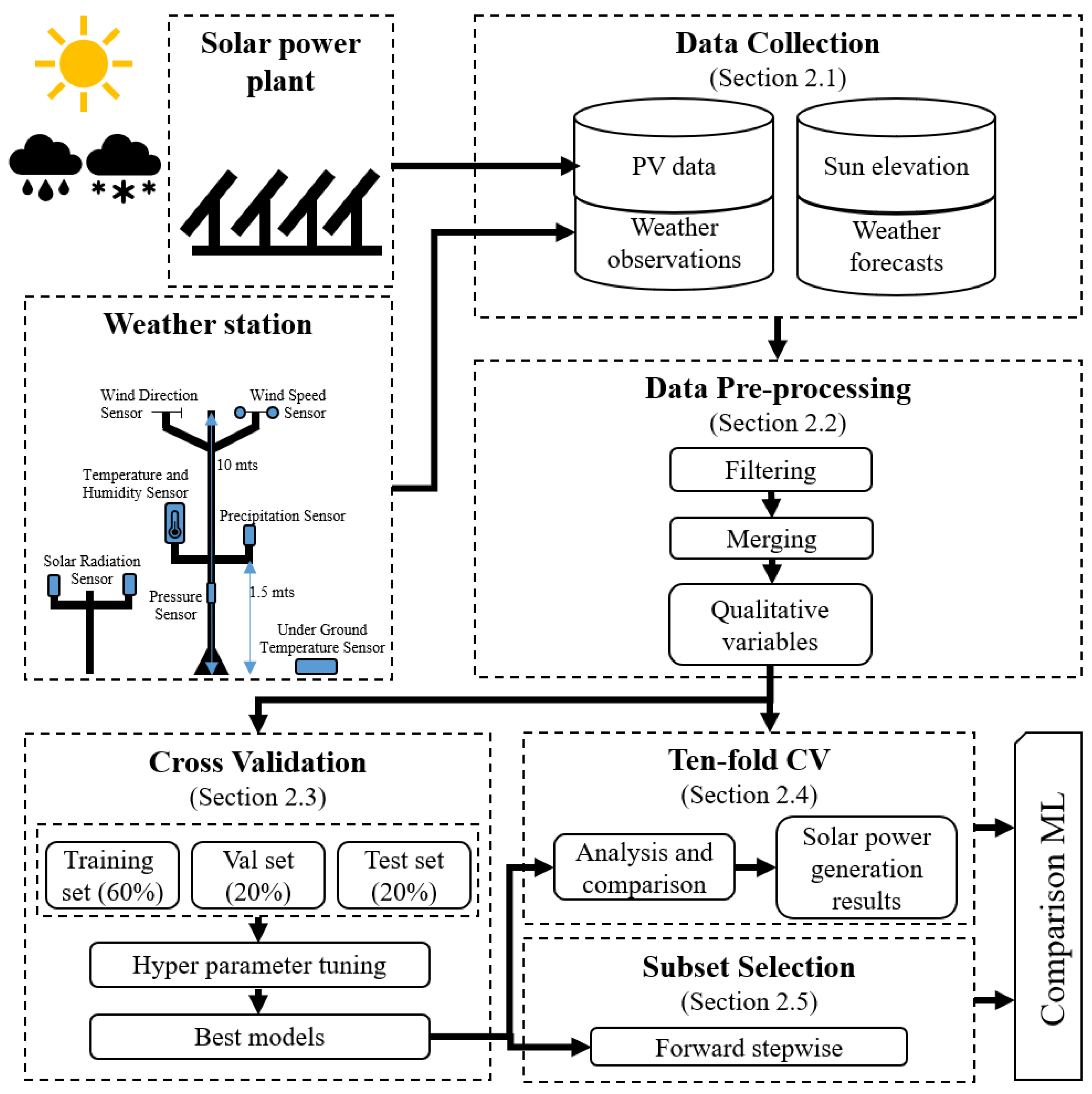
2. Research Framework
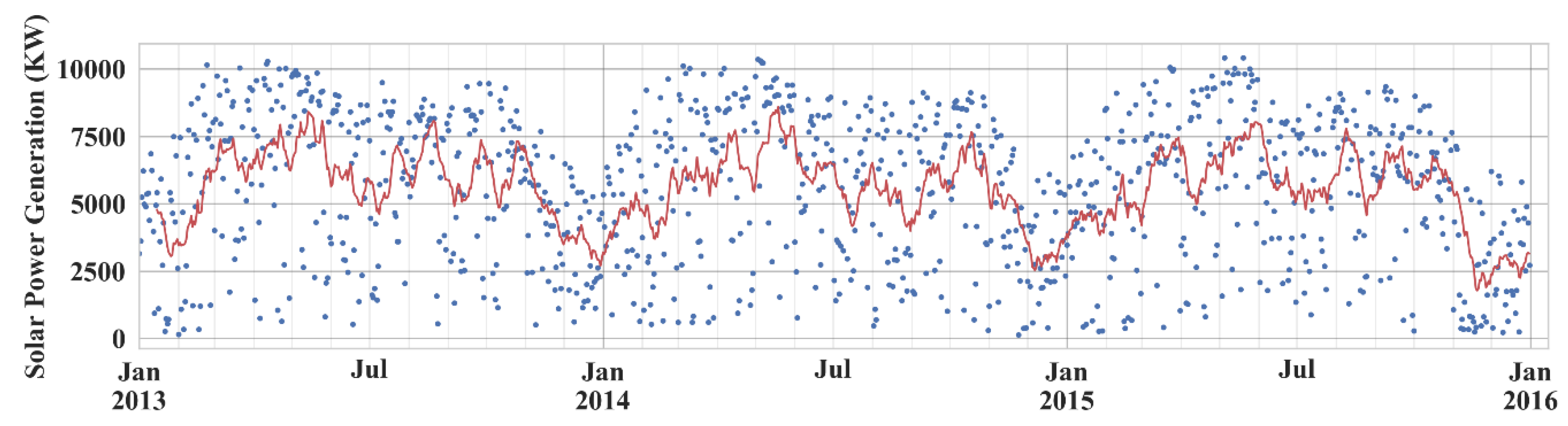
2.1. Framework and Data Collection
2.2. Data Preprocessing
2.3. Cross-Validation
2.4. Ten-Fold CV
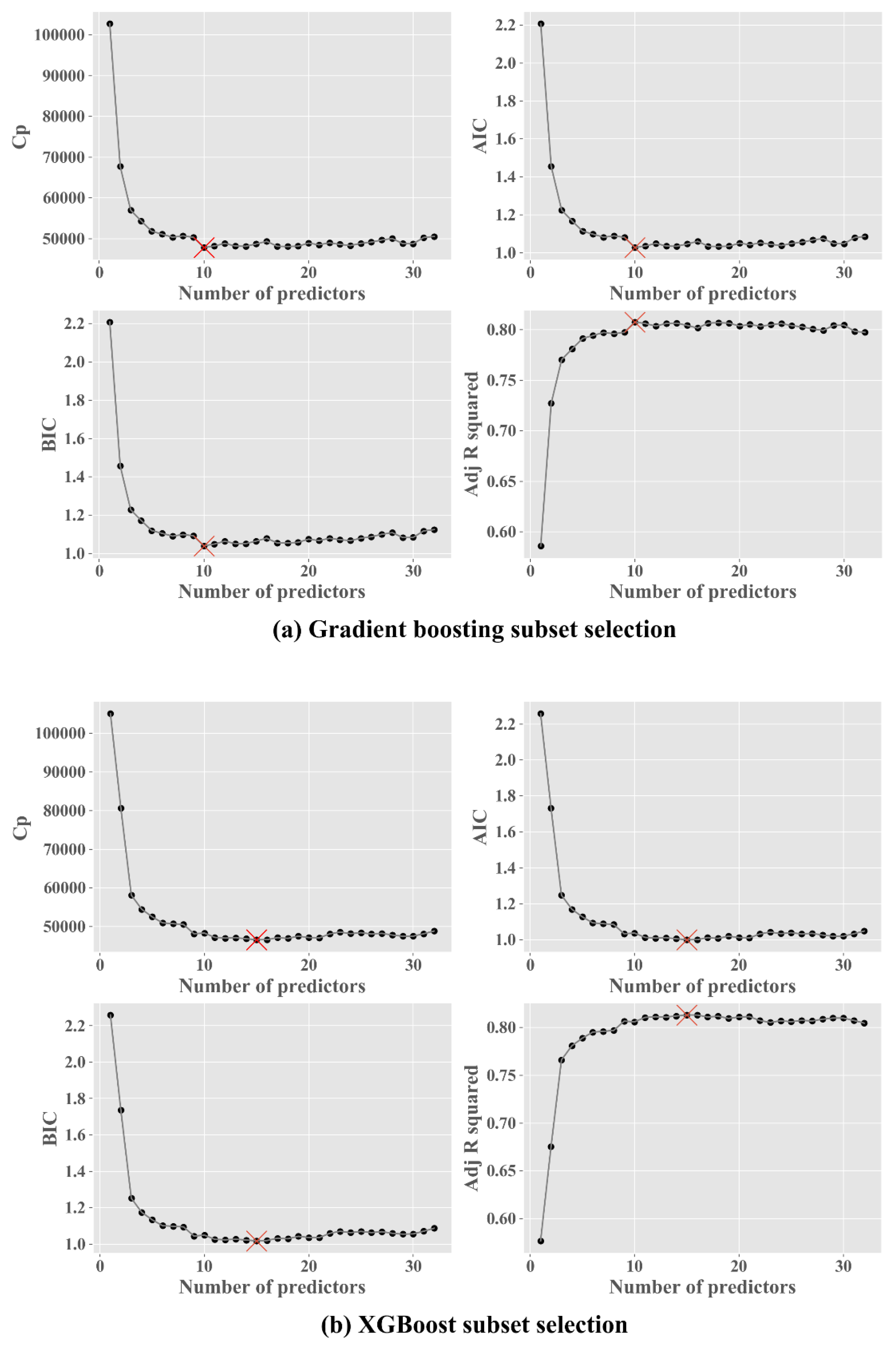
2.5. Subset Selection
3. Machine Learning Methods
3.1. Single Regression Methods
3.2. Bagging Ensemble Methods
3.3. Boosting Ensemble Methods
4. Experiment Results
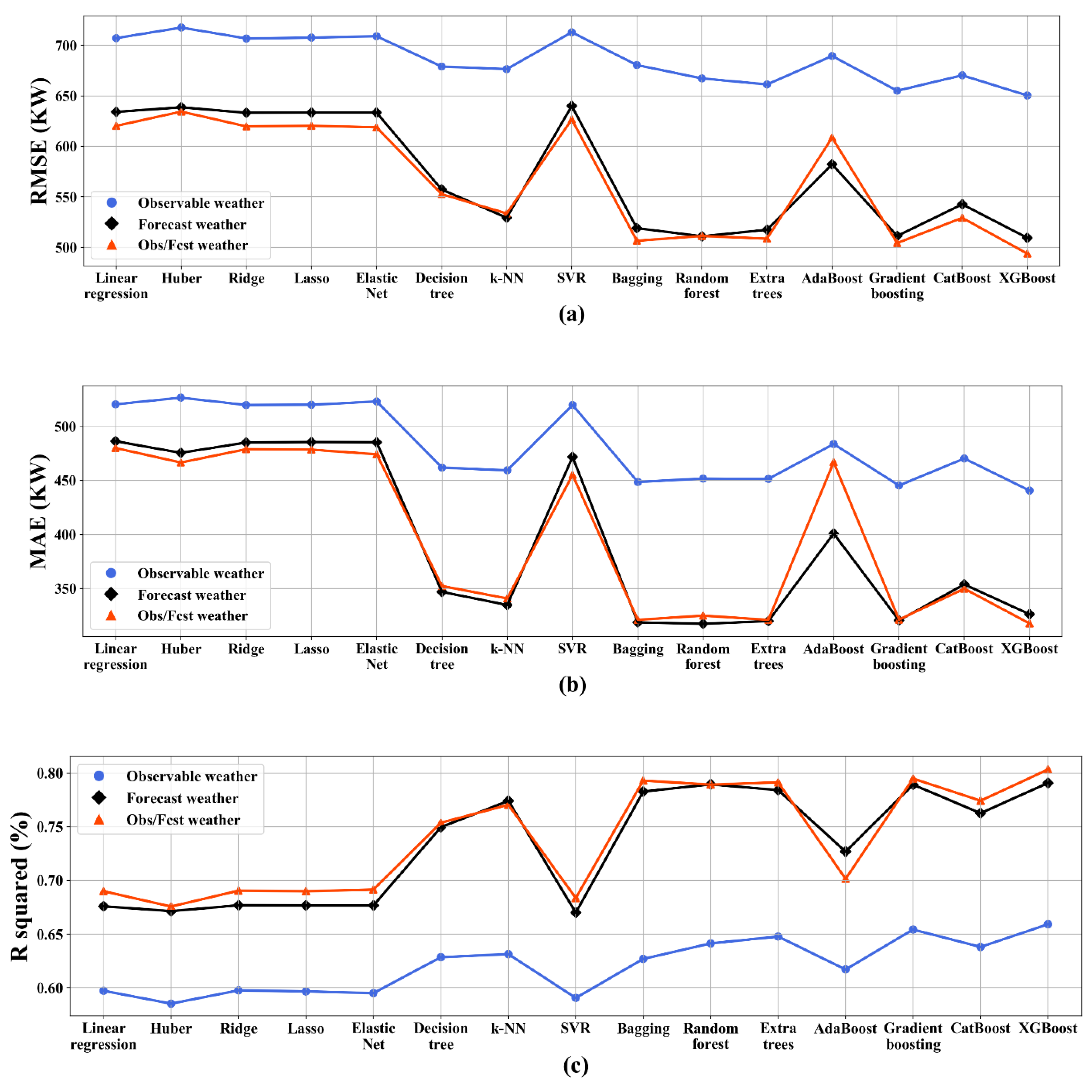
4.1. Performance Metrics
4.2. Cross-Validation
4.3. 10-Fold CV
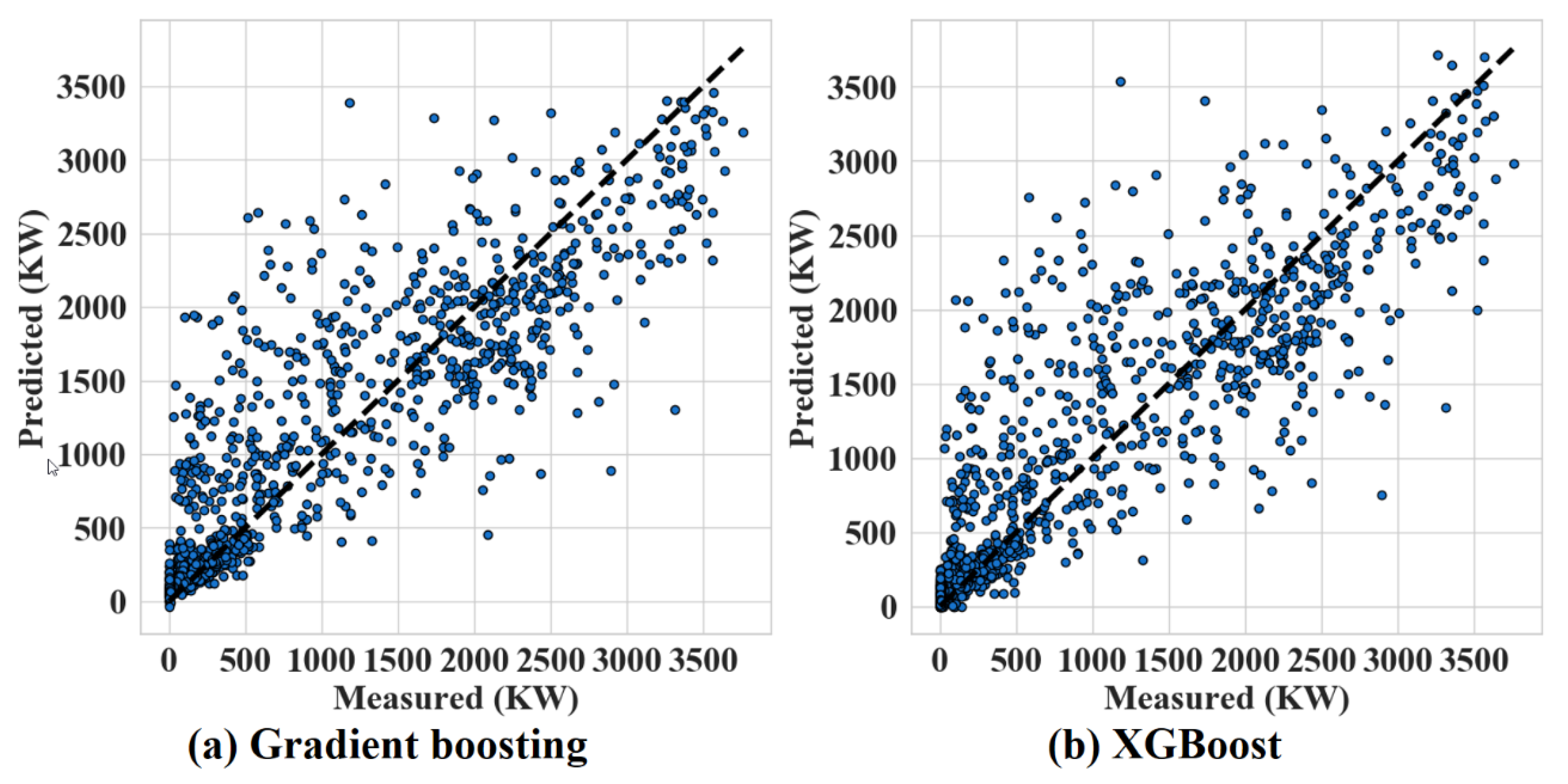
4.4. Subset Selection
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Input Data | Prediction Models | Evaluated Hyperparameters | |
|---|---|---|---|
| Observational data | Single regression models | Linear regression | N/A |
| Huber | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Ridge | α = {0.01, 0.02, 0.05, 0.1, 0.2, 0.3, 0.5, 0.8, 1.0, 2, 4, 10, 25} | ||
| Lasso | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Elastic net | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100}, max_iterations = {1, 5, 10}, L1= {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9} | ||
| Decision tree | max_depth = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} | ||
| k-NN | k = {5, 10, 15, 20, 40, 80} | ||
| SVR | C = {0.001, 0.01, 0.1, 1, 10}, γ = {0.001, 0.01, 0.1, 1} | ||
| Ensemble models (bagging) | Bagging | num_estimators = {5, 10, 15, 20, 40, 80} | |
| Random forest | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Extra trees | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | ||
| AdaBoost | N/A | ||
| Ensemble models (boosting) | Gradient boosting | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | |
| CatBoost | iterations = {50, 100, 1000}, learning_rate = {0.0001, 0.001, 0.01, 0.1}, depth = {2, 3, 4} | ||
| XGBoost | num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Forecast data | Linear regression | N/A | |
| Huber | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Single regression models | Ridge | α = {0.01, 0.02, 0.05, 0.1, 0.2, 0.3, 0.5, 0.8, 1.0, 2, 4, 10, 25} | |
| Lasso | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Elastic net | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100}, max_iterations = {1, 5, 10}, L1 = {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9} | ||
| Decision tree | max_depth= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} | ||
| k-NN | k = {5, 10, 15, 20, 40, 80} | ||
| SVR | C = {0.001, 0.01, 0.1, 1, 10}, γ = {0.001, 0.01, 0.1, 1} | ||
| Ensemble models (bagging) | Bagging | num_estimators = {5, 10, 15, 20, 40, 80} | |
| Random forest | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Extra trees | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | ||
| AdaBoost | N/A | ||
| Ensemble models (boosting) | Gradient boosting | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | |
| CatBoost | iterations = {50, 100, 1000}, learning_rate = {0.0001, 0.001, 0.01, 0.1}, depth = {2, 3, 4} | ||
| XGBoost | num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Forecast and observational data | Single regression models | Linear regression | N/A |
| Huber | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Ridge | α = {0.01, 0.02, 0.05, 0.1, 0.2, 0.3, 0.5, 0.8, 1.0, 2, 4, 10, 25} | ||
| Lasso | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100} | ||
| Elastic net | α = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100}, max_iterations = {1, 5, 10}, L1 = {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9} | ||
| Decision tree | max_depth = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} | ||
| k-NN | k = {5, 10, 15, 20, 40, 80} | ||
| SVR | C = {0.001, 0.01, 0.1, 1, 10}, γ = {0.001, 0.01, 0.1, 1} | ||
| Ensemble models (bagging) | Bagging | num_estimators = {5, 10, 15, 20, 40, 80} | |
| Random forest | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Extra trees | max_depth = {2, 5, 7, 9}, num_estimators = {5, 10, 15, 20, 40, 80}, | ||
| AdaBoost | N/A | ||
| Ensemble models (boosting) | Gradient boosting | max_depth = {2, 5, 7, 9} num_estimators = {5, 10, 15, 20, 40, 80} | |
| CatBoost | iterations = {50, 100, 1000}, learning_rate = {0.0001, 0.001, 0.01, 0.1}, depth = {2, 3, 4} | ||
| XGBoost | num_estimators = {5, 10, 15, 20, 40, 80} | ||
| Input Data | Prediction Models | Validation Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | ||||
| Observational data | Single regression models | Linear regression | Hyperparameters | 735.04 | 547.74 | 59.8% | 707.08 | 520.44 | 59.7% |
| Huber | α = 0.1 | 746.26 | 554.02 | 58.6% | 717.63 | 526.67 | 58.5% | ||
| Ridge | α = 0.8 | 735.06 | 547.32 | 59.8% | 706.76 | 519.81 | 59.8% | ||
| Lasso | α = 0.1 | 734.49 | 545.77 | 59.9% | 707.61 | 520.03 | 59.7% | ||
| Elastic net | α = 0.0001, L1 = 0.9, max_iterations = 10 | 734.66 | 541.45 | 59.9% | 709.04 | 523.10 | 59.5% | ||
| Decision tree | max_depth = 3 | 685.75 | 478.41 | 65.1% | 679.07 | 461.94 | 62.9% | ||
| k-NN | k = 15 | 683.80 | 475.89 | 65.3% | 676.44 | 459.42 | 63.1% | ||
| SVR | C = 10, γ = 0.001 | 741.87 | 546.58 | 59.1% | 712.95 | 519.84 | 59.1% | ||
| Ensemble models (bagging) | Bagging | num_estimators = 80 | 685.02 | 466.09 | 65.1% | 680.51 | 448.63 | 62.7% | |
| Random forest | max_depth = 7, num_estimators = 80 | 669.35 | 466.51 | 66.7% | 667.26 | 451.78 | 64.1% | ||
| Extra trees | max_depth = 7, num_estimators = 80 | 684.45 | 478.97 | 65.2% | 661.29 | 451.48 | 64.8% | ||
| AdaBoost | N/A | 707.59 | 507.44 | 62.8% | 689.47 | 483.75 | 61.7% | ||
| Ensemble models (boosting) | Gradient boosting | max_depth = 5, num_estimators = 80 | 673.19 | 473.28 | 66.3% | 655.07 | 445.37 | 65.4% | |
| CatBoost | depth = 3, iterations = 50, learning_rate = 0.1 | 690.14 | 497.52 | 64.6% | 670.36 | 470.36 | 63.8% | ||
| XGBoost | num_estimators = 80 | 681.32 | 474.58 | 65.5% | 650.36 | 440.67 | 65.9% | ||
| Forecast data | Single regression models | Linear regression | N/A | 657.30 | 509.97 | 67.9% | 634.18 | 486.35 | 67.6% |
| Huber | α = 0.01 | 671.02 | 505.89 | 66.5% | 638.68 | 475.59 | 67.1% | ||
| Ridge | α = 2.0 | 658.26 | 510.17 | 67.8% | 633.29 | 485.14 | 67.7% | ||
| Lasso | α = 1.0 | 657.79 | 509.97 | 67.8% | 633.44 | 485.52 | 67.7% | ||
| Elastic net | α = 0.001, L1 = 0.7, max_iterations = 10 | 658.03 | 510.02 | 67.8% | 633.46 | 485.34 | 67.7% | ||
| Decision tree | max_depth = 6 | 576.69 | 376.62 | 75.3% | 557.41 | 346.96 | 75.0% | ||
| k-NN | k = 15 | 537.32 | 358.39 | 78.5% | 529.37 | 334.78 | 77.4% | ||
| SVR | C = 10, γ = 0.001 | 678.00 | 507.18 | 65.8% | 640.00 | 471.79 | 67.0% | ||
| Bagging | num_estimators = 80 | 527.20 | 337.95 | 79.3% | 519.11 | 318.74 | 78.3% | ||
| Random forest | max_depth = 7, num_estimators = 80 | 518.98 | 335.68 | 80.0% | 510.96 | 317.40 | 79.0% | ||
| Extra trees | max_depth = 9, num_estimators = 80 | 537.02 | 351.18 | 78.6% | 517.46 | 319.89 | 78.4% | ||
| AdaBoost | N/A | 595.58 | 430.29 | 73.6% | 582.24 | 400.90 | 72.7% | ||
| Gradient boosting | max_depth = 5, num_estimators = 80 | 514.93 | 344.69 | 80.3% | 511.35 | 320.56 | 78.9% | ||
| CatBoost | depth = 3, iterations = 50, learning_rate = 0.1 | 543.21 | 372.91 | 78.1% | 542.67 | 353.85 | 76.3% | ||
| XGBoost | num_estimators = 80 | 525.21 | 349.87 | 79.5% | 509.44 | 326.25 | 79.1% | ||
| Forecast and observational data | Single regression models | Linear regression | N/A | 637.29 | 496.72 | 69.8% | 620.31 | 480.03 | 69.0% |
| Huber | α = 10 | 670.20 | 500.31 | 66.6% | 634.42 | 466.65 | 67.6% | ||
| Ridge | α = 1.0 | 637.95 | 496.44 | 69.8% | 619.79 | 478.94 | 69.1% | ||
| Lasso | α = 1.0 | 638.54 | 495.73 | 69.7% | 620.35 | 478.54 | 69.0% | ||
| Elastic net | α = 0.0001, L1 = 0.9, max_iterations = 10 | 639.79 | 494.39 | 69.6% | 618.82 | 474.22 | 69.2% | ||
| Decision tree | max_depth = 5 | 531.96 | 355.22 | 79.0% | 552.80 | 352.34 | 75.4% | ||
| k-NN | k = 15 | 548.95 | 368.00 | 77.6% | 533.59 | 340.86 | 77.1% | ||
| SVR | C = 10, γ = 0.001 | 660.39 | 487.39 | 67.6% | 626.68 | 455.21 | 68.4% | ||
| Ensemble models (bagging) | Bagging | num_estimators = 80 | 505.33 | 323.03 | 81.0% | 506.64 | 321.09 | 79.3% | |
| Random forest | max_depth = 7, num_estimators = 80 | 503.64 | 330.35 | 81.2% | 511.29 | 325.00 | 78.9% | ||
| Extra trees | max_depth = 7, num_estimators = 20 | 512.54 | 340.11 | 80.5% | 508.68 | 321.05 | 79.2% | ||
| AdaBoost | N/A | 622.54 | 487.11 | 71.2% | 608.63 | 466.95 | 70.2% | ||
| Ensemble models (boosting) | Gradient boosting | max_depth = 7, num_estimators = 80 | 501.84 | 336.85 | 81.3% | 504.33 | 321.25 | 79.5% | |
| CatBoost | depth = 3, iterations = 50, learning_rate = 0.1 | 521.38 | 365.95 | 79.8% | 529.27 | 349.92 | 77.4% | ||
| XGBoost | num_estimators = 80 | 518.16 | 340.40 | 80.0% | 493.85 | 317.70 | 80.4% | ||
Appendix B

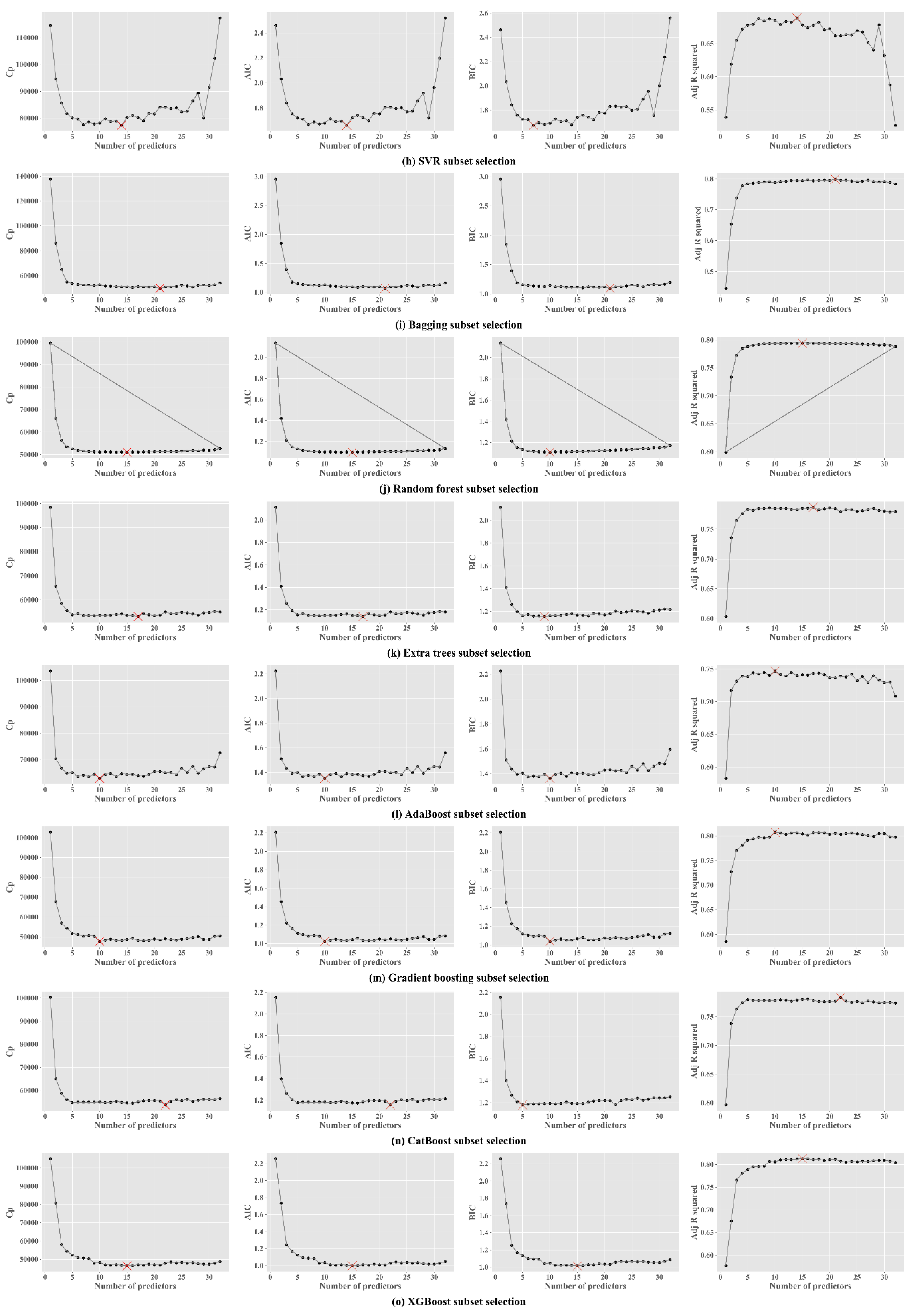
References
- Kim, S.-G.; Jung, J.-Y.; Sim, M.K. A two-step approach to solar power generation prediction based on weather data using machine learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very Short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.M.; Ichikawa, R.; Hayashi, H.; Nagasaka, K. neural network ensemble-based solar power generation short-term forecasting. World Acad. Sci. Eng. Technol. 2009, 3, 1258–1263. [Google Scholar] [CrossRef]
- Sharma, N.; Gummeson, J.; Irwin, D.; Shenoy, P. Cloudy computing: Leveraging weather forecasts in energy harvesting sensor systems. In Proceedings of the International Conference on SECON, Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Sharma, N.; Sharma, P.; Irwin, D.; Shenoy, P. Predicting solar generation from weather forecasts using machine learning. In Proceedings of the International Conference on SmartGridComm, Brussels, Belgium, 17–20 October 2011; pp. 528–533. [Google Scholar]
- Amrouche, B.; Le Pivert, X. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Shu, L. An ARMAX model for forecasting the power output of a grid connected photovoltaic system. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Aler, R.; Martín, R.; Valls, J.M.; Galván, I.M. A study of machine learning techniques for daily solar energy forecasting using numerical weather models. In Intelligent Distributed Computing VIII; Springer: Berlin/Heidelberg, Germany, 2015; pp. 269–278. [Google Scholar]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep learning for solar power forecasting — An approach using autoencoder and lstm neural networks. In Proceedings of the International Conference on SMC, Budapest, Hungary, 9–12 October 2016; pp. 2858–2865. [Google Scholar]
- Ahmed Mohammed, A.; Aung, Z. Ensemble learning approach for probabilistic forecasting of solar power generation. Energies 2016, 9, 1017. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving renewable energy forecasting with a grid of numerical weather predictions. Ieee Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Kim, J.-G.; Kim, D.-H.; Yoo, W.-S.; Lee, J.-Y.; Kim, Y.B. Daily prediction of solar power generation based on weather forecast information in Korea. IET Renew. Power Gener. 2017, 11, 1268–1273. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Improving combined solar power forecasts using estimated ramp rates: Data-driven post-processing approach. IET Renew. Power Gener. 2018, 12, 1127–1135. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. Comparison of training approaches for photovoltaic forecasts by means of machine learning. Appl. Sci. 2018, 8, 228. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-term solar power forecasting. Sol. Energy 2009, 83, 1772–1783. [Google Scholar] [CrossRef]
- Hossain, M.R.; Oo, A.M.T.; Ali, A.S. Hybrid prediction method of solar power using different computational intelligence algorithms. In Proceedings of the 22nd International Conference on AUPEC, Bali, Indonesia, 26–29 September 2012; pp. 1–6. [Google Scholar]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production, part I: Deterministic forecast of hourly production. Sol. Energy 2014, 105, 792–803. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar irradiance forecasting using deep neural networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Li, L.-L.; Cheng, P.; Lin, H.-C.; Dong, H. Short-term output power forecasting of photovoltaic systems based on the deep belief net. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of support vector machine and extreme gradient boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in china. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive modelling for solar thermal energy systems: A comparison of support vector regression, random forest, extra trees and regression trees. J. Clean. Prod. 2018, 203, 810–821. [Google Scholar] [CrossRef]
- Detyniecki, M.; Marsala, C.; Krishnan, A.; Siegel, M. Weather-based solar energy prediction. In Proceedings of the International Conference FUZZ-IEEE, Brisbane, Australia, 13 August 2012; pp. 1–7. [Google Scholar]
- Abedinia, O.; Raisz, D.; Amjady, N. Effective prediction model for hungarian small-scale solar power output. IET Renew. Power Gener. 2017, 11, 1648–1658. [Google Scholar] [CrossRef]
- Son, J.; Park, Y.; Lee, J.; Kim, H. Sensorless pv power forecasting in grid-connected buildings through deep learning. Sensors 2018, 18, 2529. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Kim, K. Recurrent neural network-based hourly prediction of photovoltaic power output using meteorological information. Energies 2019, 12, 215. [Google Scholar] [CrossRef]
- Carrera, B.; Sim, M.K.; Jung, J.-Y. PVHybNet: A hybrid framework for predicting photovoltaic power generation using both weather forecast and observation data. IET Renew. Power Gener. 2020, 1–11. [Google Scholar] [CrossRef]
- Pedro, H.T.; Coimbra, C.F. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.; Srikanth, N. Ensemble methods for wind and solar power forecasting—A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 82–91. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Cawley, G.C.; Talbot, N.L. On Over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]


| Category | Variable Name | Classification | Description (Unit) |
|---|---|---|---|
| Solar elevation (1) | Elevation | Continuous | Degrees (0°–76°) |
| Weather forecast (# variables: 7) (# features: 16) | Humidity | Continuous | (%) |
| PrecipitationProb | Continuous | (%) | |
| PrecipitationCat | Categorical | 0: none, 1: rain, 2: sleet, 3: snow | |
| SkyType | Categorical | 0: clear sky, 1: slightly cloudy, 2: partly cloudy, 3: overcast | |
| Temperature | Continuous | Celsius (°C) | |
| WindDirection | Categorical | N: 315°–45°, E: 45°–135°, W: 225°–315°, S: 135°–225° | |
| WindSpeed | Continuous | (m/s) |
| Category | Variable Name | Classification | Description (Unit) |
|---|---|---|---|
| Weather observation (# variables: 16) (# features: 19) | AirTemperature | Continuous | (°C) |
| AtmosPressure | Continuous | (hPa) | |
| DewPointTemperature | Continuous | (°C) | |
| GroundTemperature | Continuous | (°C) | |
| Humidity | Continuous | (%) | |
| Precipitation | Continuous | (mm) | |
| SeaLevelPressure | Continuous | (hPa) | |
| SolarRadiation | Continuous | (MJ/m2) | |
| SunlightTime | Continuous | (hr) | |
| VaporPressure | Continuous | (hPa) | |
| WindDirection | Categorical | N: 315°–45°, E: 45°–135°, W: 225°–315°, S: 135°–225° | |
| WindSpeed | Continuous | (m/s) | |
| 5cmDownTemperature | Continuous | Temperature below the ground surface (°C) | |
| 10cmDownTemperature | Continuous | ||
| 20cmDownTemperature | Continuous | ||
| 30cmDownTemperature | Continuous |
| Single Regression | Ensemble (Bagging) | Ensemble (Boosting) |
|---|---|---|
| Linear regression | Bagging | AdaBoost |
| Huber | Random forest | Gradient boosting |
| Ridge | Extra trees | CatBoost |
| Lasso | XGBoost | |
| Elastic Net | ||
| Decision tree | ||
| k-NN | ||
| SVR |
| Prediction Models | Observation Weather | Forecast Weather | Forecast and Observation Weather | |
|---|---|---|---|---|
| Single regression models | Linear regression | N/A | N/A | N/A |
| Huber | α = {0.1} | α = {0.01} | α = {10} | |
| Ridge | α = {0.8} | α = {2} | α = {1.0} | |
| Lasso | α = {0.1} | α = {1} | α = {1} | |
| Elastic net | α = {0.0001}, max_iterations = {10}, l1 = {0.9} | α = {0.001}, max_iterations = {10}, l1 = {0.7} | α = {0.0001}, max_iterations = {10}, l1 = {0.9} | |
| Decision tree | max_depth = {3} | max_depth= {6} | max_depth = {5} | |
| k-NN | k = {15} | k = {15} | k = {15} | |
| SVR | C = {10}, γ = {0.001} | C = {10}, γ = {0.001} | C = {10}, γ = {0.001} | |
| Ensemble models (bagging) | Bagging | num_estimators = {80} | num_estimators = {80} | num_estimators = {80} |
| Random forest | max_depth = {7}, num_estimators = {80} | max_depth = {7}, num_estimators = {80} | max_depth = {7}, num_estimators = {80} | |
| Extra trees | max_depth = {7}, num_estimators = {80} | max_depth = {9}, num_estimators = {80} | max_depth = {7}, num_estimators = {20}, | |
| AdaBoost | N/A | N/A | N/A | |
| Ensemble models (boosting) | Gradient boosting | max_depth = {5}, num_estimators = {80} | max_depth = {5}, num_estimators = {80} | max_depth = {7} num_estimators = {80} |
| CatBoost | iterations = {50}, learning_rate = {0.1}, depth = {3} | iterations = {50}, learning_rate = {0.1}, depth = {3} | iterations = {50}, learning_rate = {0.1}, depth = {3} | |
| XGBoost | num_estimators = {80} | num_estimators = {80} | num_estimators = {80} | |
| Prediction Models | RMSE | MAE | R2 | ||||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
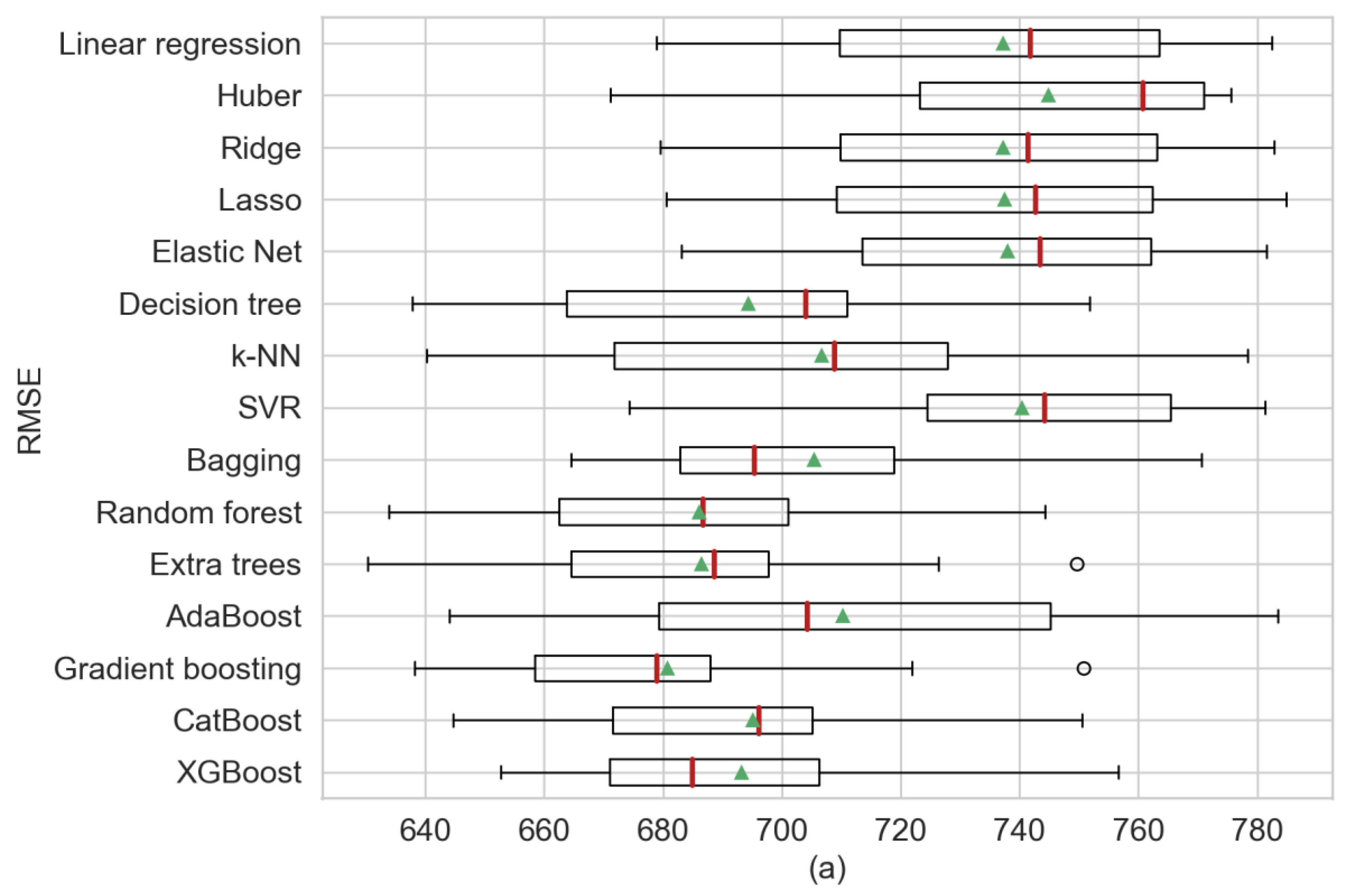
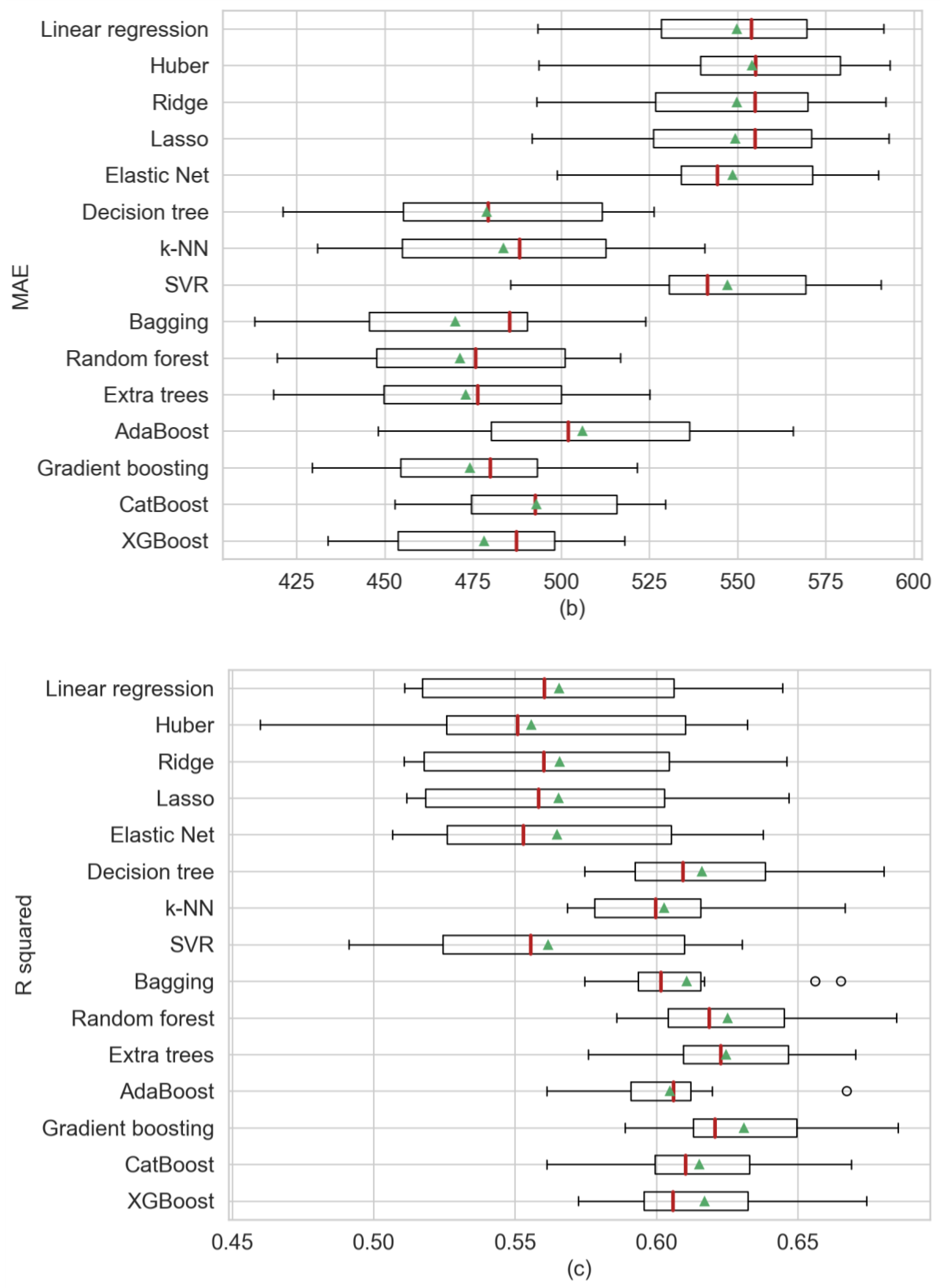
| Linear regression | 737.22 | 32.76 | 549.73 | 30.44 | 0.5656 | 0.0467 | |
| Single regression models | Huber | 744.82 | 32.95 | 554.09 | 29.9 | 0.5557 | 0.0561 |
| Ridge | 737.15 | 32.65 | 549.69 | 30.95 | 0.5656 | 0.0466 | |
| Lasso | 737.49 | 32.75 | 549.37 | 31.48 | 0.5653 | 0.0465 | |
| Elastic net | 737.9 | 29.79 | 548.56 | 28.3 | 0.5648 | 0.0449 | |
| Decision tree | 694.24 | 35.83 | 478.77 | 34.68 | 0.616 | 0.0312 | |
| k-NN | 706.65 | 42.12 | 483.64 | 36.71 | 0.6027 | 0.0299 | |
| SVR | 740.4 | 32.1 | 547.15 | 29.98 | 0.5615 | 0.0497 | |
| Ensemble models (bagging) | Bagging | 705.42 | 34.71 | 470.01 | 33.18 | 0.6106 | 0.0275 |
| Random forest | 685.97 | 33.71 | 471.31 | 33.8 | 0.6251 | 0.029 | |
| Extra trees | 686.43 | 32.87 | 472.94 | 34.51 | 0.6245 | 0.0295 | |
| AdaBoost | 710.19 | 43.01 | 506 | 38.73 | 0.6047 | 0.0266 | |
| Ensemble models (boosting) | Gradient boosting | 680.65 | 33 | 474.09 | 28.3 | 0.6309 | 0.028 |
| CatBoost | 695.07 | 33.49 | 492.89 | 26.7 | 0.6151 | 0.0294 | |
| XGBoost | 693.13 | 32.75 | 478.05 | 26.16 | 0.617 | 0.0318 | |
| Prediction Models | RMSE | MAE | R2 | ||||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
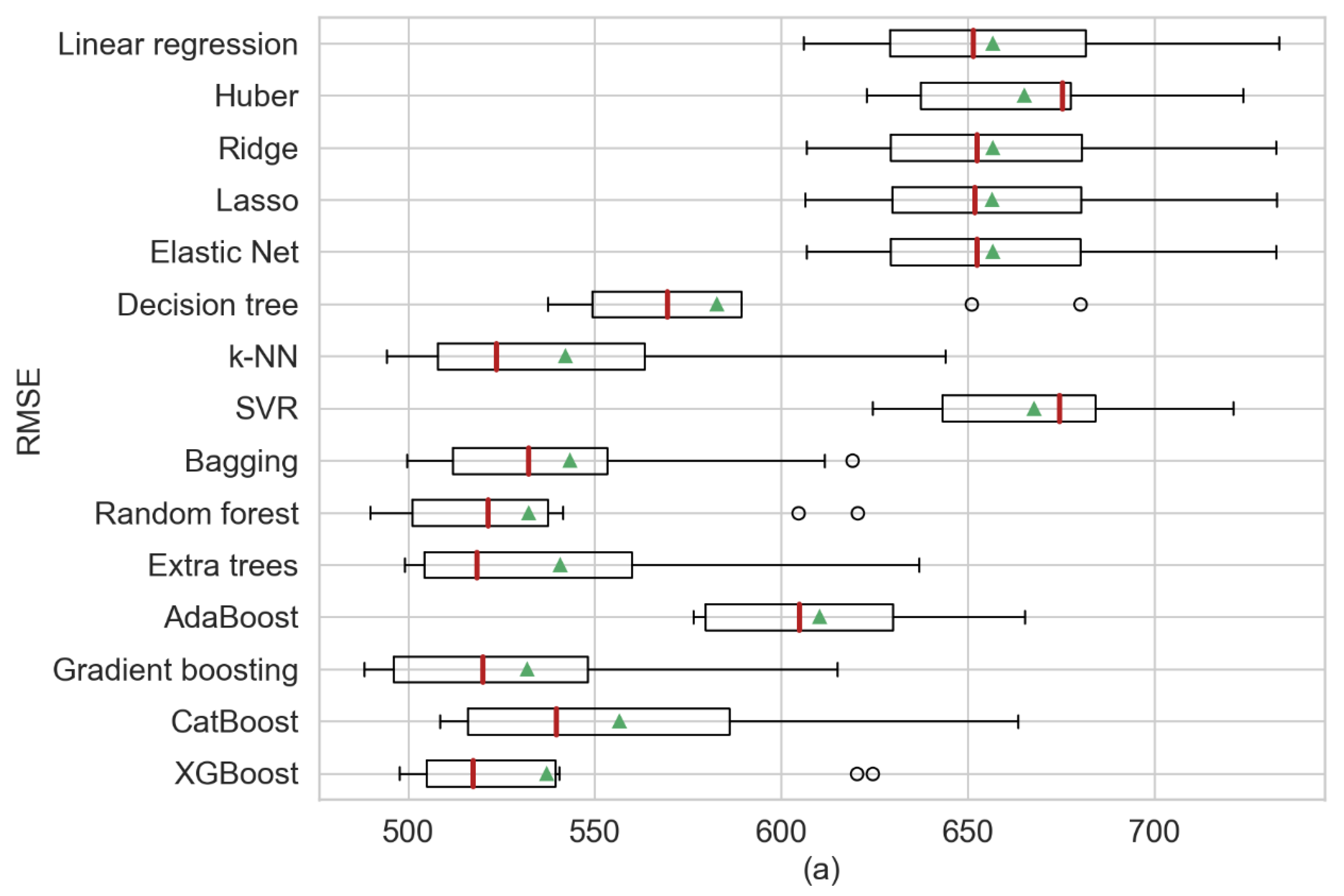
| Linear regression | 656.62 | 36.88 | 509.51 | 35.74 | 0.6558 | 0.0357 | |
| Single regression models | Huber | 665.09 | 30.53 | 501.79 | 28.61 | 0.6460 | 0.0414 |
| Ridge | 656.65 | 36.61 | 509.17 | 35.60 | 0.6557 | 0.0362 | |
| Lasso | 656.54 | 36.73 | 509.18 | 35.68 | 0.6558 | 0.0364 | |
| Elastic net | 656.62 | 36.57 | 509.07 | 35.58 | 0.6557 | 0.0362 | |
| Decision tree | 582.60 | 45.43 | 384.15 | 32.12 | 0.7295 | 0.0299 | |
| k-NN | 542.09 | 47.76 | 350.20 | 29.78 | 0.7661 | 0.0276 | |
| SVR | 667.79 | 29.18 | 500.79 | 27.48 | 0.6429 | 0.0430 | |
| Ensemble models (bagging) | Bagging | 543.32 | 39.60 | 347.18 | 25.03 | 0.7671 | 0.0203 |
| Random forest | 532.20 | 43.19 | 340.77 | 24.11 | 0.7746 | 0.0230 | |
| Extra trees | 540.77 | 46.86 | 348.29 | 28.70 | 0.7673 | 0.0262 | |
| AdaBoost | 610.32 | 32.46 | 439.47 | 26.32 | 0.7061 | 0.0232 | |
| Ensemble models (boosting) | Gradient boosting | 531.85 | 42.73 | 347.75 | 24.67 | 0.7749 | 0.0227 |
| CatBoost | 556.66 | 49.60 | 375.19 | 32.40 | 0.7532 | 0.0301 | |
| XGBoost | 537.06 | 44.69 | 355.67 | 28.67 | 0.7707 | 0.0219 | |
| Prediction Models | RMSE | MAE | R2 | ||||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
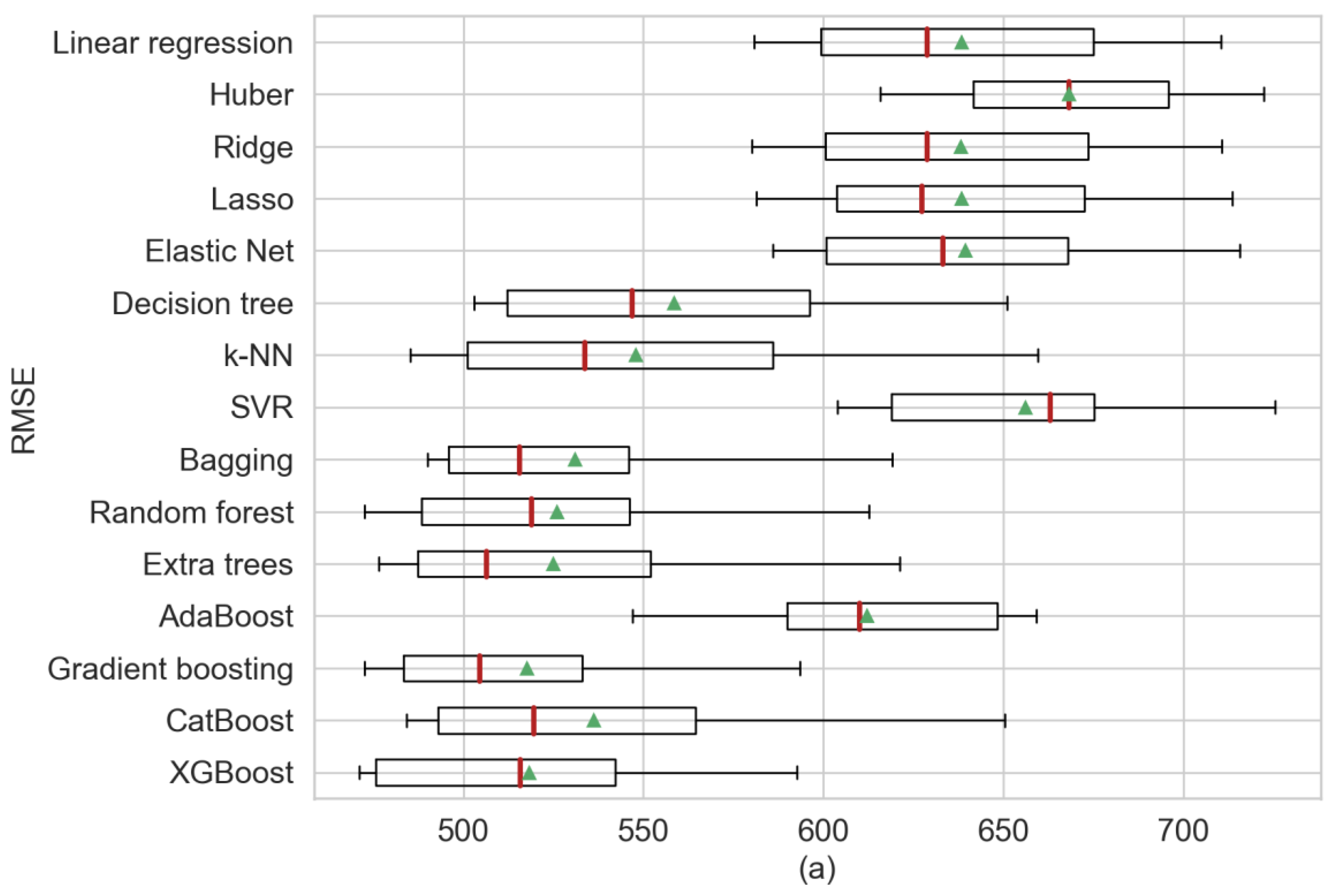
| Single regression models | Linear regression | 638.18 | 43.81 | 497.20 | 38.50 | 0.6741 | 0.0440 |
| Huber | 668.09 | 34.30 | 497.38 | 25.83 | 0.6419 | 0.0494 | |
| Ridge | 638.06 | 43.62 | 496.58 | 38.22 | 0.6742 | 0.0440 | |
| Lasso | 638.36 | 43.61 | 495.98 | 38.02 | 0.6740 | 0.0437 | |
| Elastic net | 639.37 | 42.45 | 495.47 | 35.45 | 0.6727 | 0.0445 | |
| Decision tree | 558.35 | 49.92 | 366.54 | 36.39 | 0.7512 | 0.0354 | |
| k-NN | 547.79 | 56.24 | 358.28 | 31.88 | 0.7601 | 0.0395 | |
| SVR | 656.00 | 38.92 | 483.36 | 29.68 | 0.6551 | 0.0472 | |
| Ensemble models (bagging) | Bagging | 530.90 | 42.84 | 338.03 | 27.46 | 0.7770 | 0.0295 |
| Random forest | 525.88 | 46.17 | 339.20 | 29.82 | 0.7791 | 0.0324 | |
| Extra trees | 524.92 | 48.44 | 340.73 | 31.94 | 0.7805 | 0.0287 | |
| AdaBoost | 612.09 | 38.51 | 454.29 | 40.33 | 0.7088 | 0.0416 | |
| Ensemble models (boosting) | Gradient boosting | 517.56 | 42.09 | 341.22 | 24.99 | 0.7864 | 0.0267 |
| CatBoost | 536.23 | 52.59 | 364.20 | 32.35 | 0.7704 | 0.0353 | |
| XGBoost | 518.30 | 43.45 | 343.65 | 25.59 | 0.7850 | 0.0324 | |
| Category | Variable Name | Classification | Description (unit) |
|---|---|---|---|
| Solar elevation (1) | Elevation | Continuous | Degrees (0°–76°) |
| Weather forecast (Features: 5) | Humidity | Continuous | (%) |
| PrecipitationProb | Continuous | (%) | |
| PrecipitationCat | Categorical | 0: none | |
| Temperature | Continuous | Celsius (°C) | |
| WindSpeed | Continuous | (m/s) | |
| Weather observation (Features: 4) | AtmosPressure | Continuous | (hPa) |
| SolarRadiation | Continuous | (MJ/m2) | |
| WindDirection | Categorical | W: 225°–315° | |
| 5cmDownTemperature | Continuous | Temperature below the ground surface (°C) |
| Category | Variable Name | Classification | Description (unit) |
|---|---|---|---|
| Solar elevation (1) | Elevation | Continuous | Degrees (0°–76°) |
| Weather forecast (Features: 8) | Humidity | Continuous | (%) |
| PrecipitationProb | Continuous | (%) | |
| PrecipitationCat | Categorical | 1: rain | |
| Temperature | Continuous | Celsius (°C) | |
| WindDirection | Categorical | E: 45°–135°, W: 225°–315°, S: 135°–225° | |
| WindSpeed | Continuous | (m/s) | |
| Weather observation (Features: 6) | Humidity | Continuous | (%) |
| SolarRadiation | Continuous | (MJ/m2) | |
| WindDirection | Categorical | S: 135°–225° | |
| GroundTemperature | Continuous | Celsius (°C) | |
| 5cmDownTemperature | Continuous | Temperature below the ground surface (°C) | |
| 20cmDownTemperature | Continuous |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrera, B.; Kim, K. Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data. Sensors 2020, 20, 3129. https://doi.org/10.3390/s20113129
Carrera B, Kim K. Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data. Sensors. 2020; 20(11):3129. https://doi.org/10.3390/s20113129
Chicago/Turabian StyleCarrera, Berny, and Kwanho Kim. 2020. "Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data" Sensors 20, no. 11: 3129. https://doi.org/10.3390/s20113129
APA StyleCarrera, B., & Kim, K. (2020). Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data. Sensors, 20(11), 3129. https://doi.org/10.3390/s20113129




