Hybrid Temperature and Stress Monitoring of Woven Fabric Thermoplastic Composite Using Fiber Bragg Grating Based Sensing Technique
Abstract
1. Introduction
2. Sensor
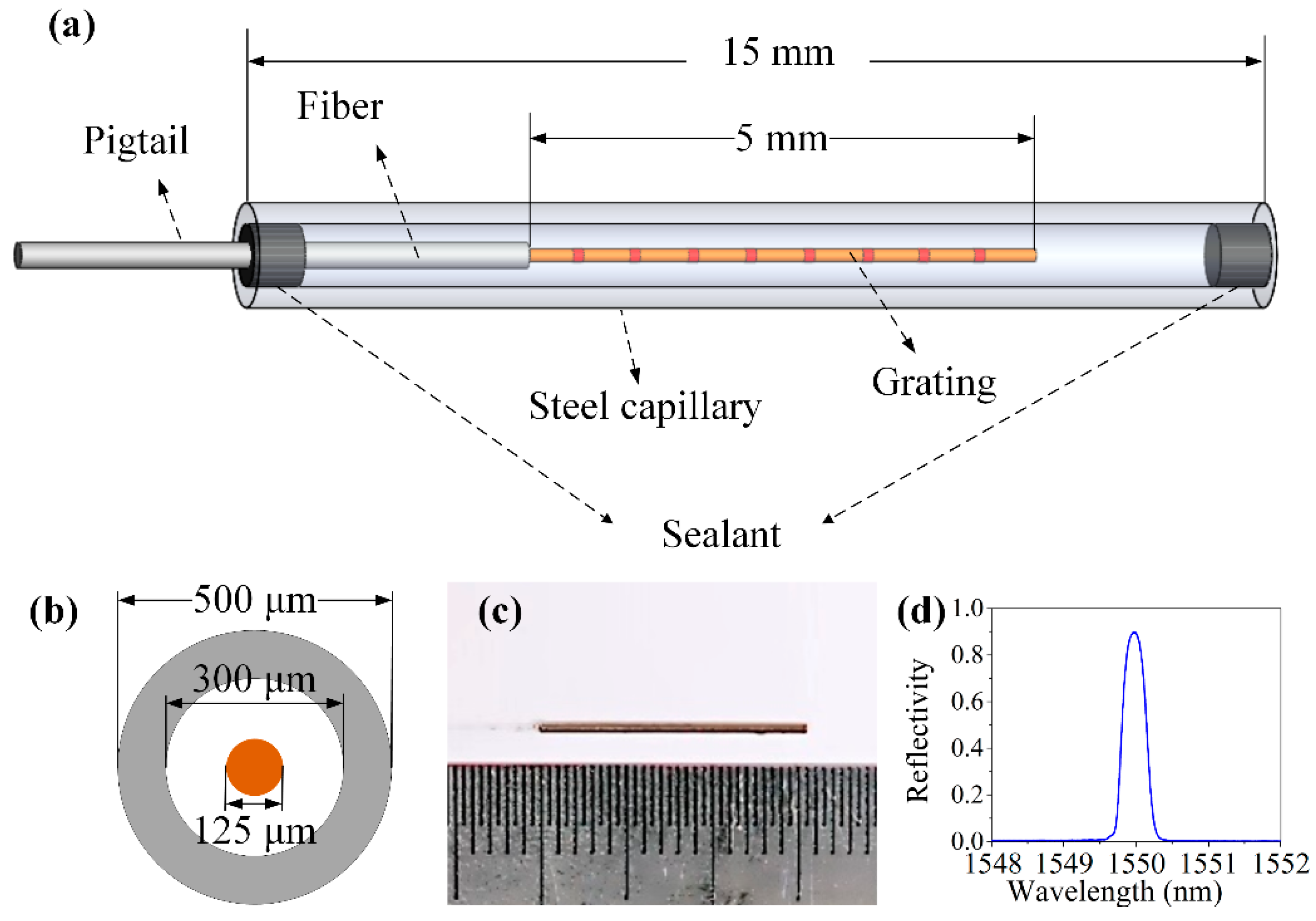
2.1. Structure of EFBG Sensor
2.2. Calibration Results
3. Experiment
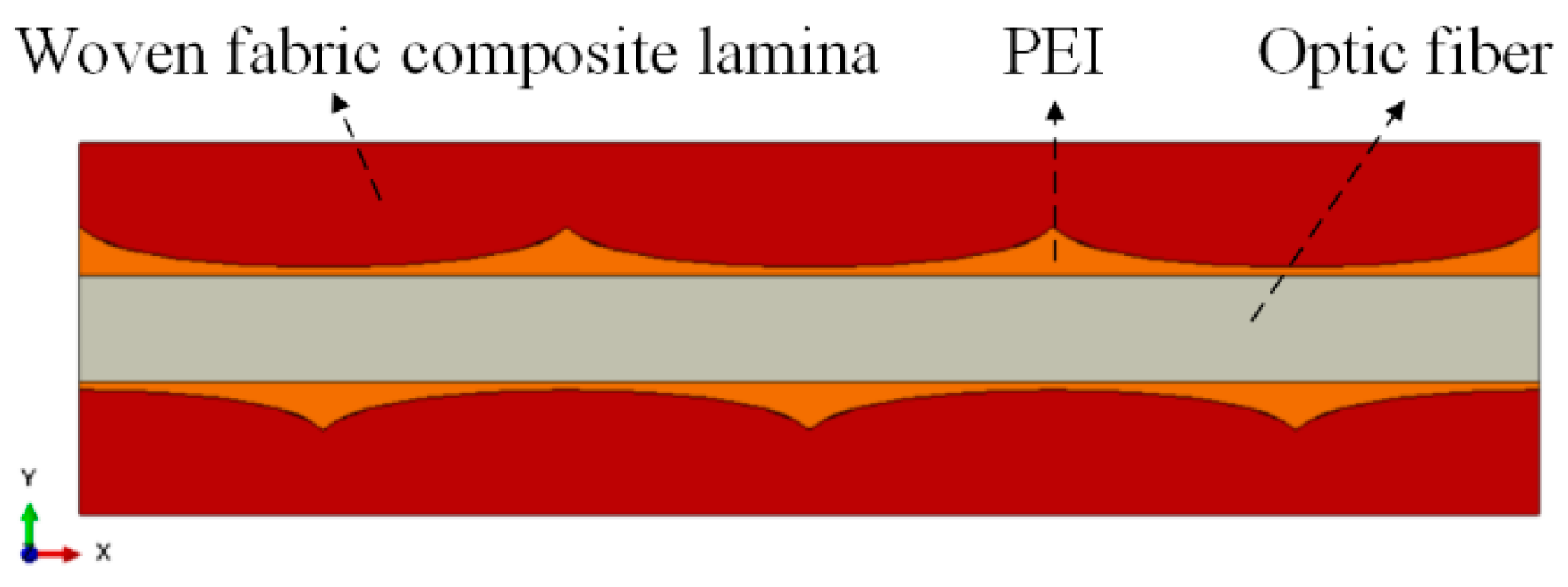
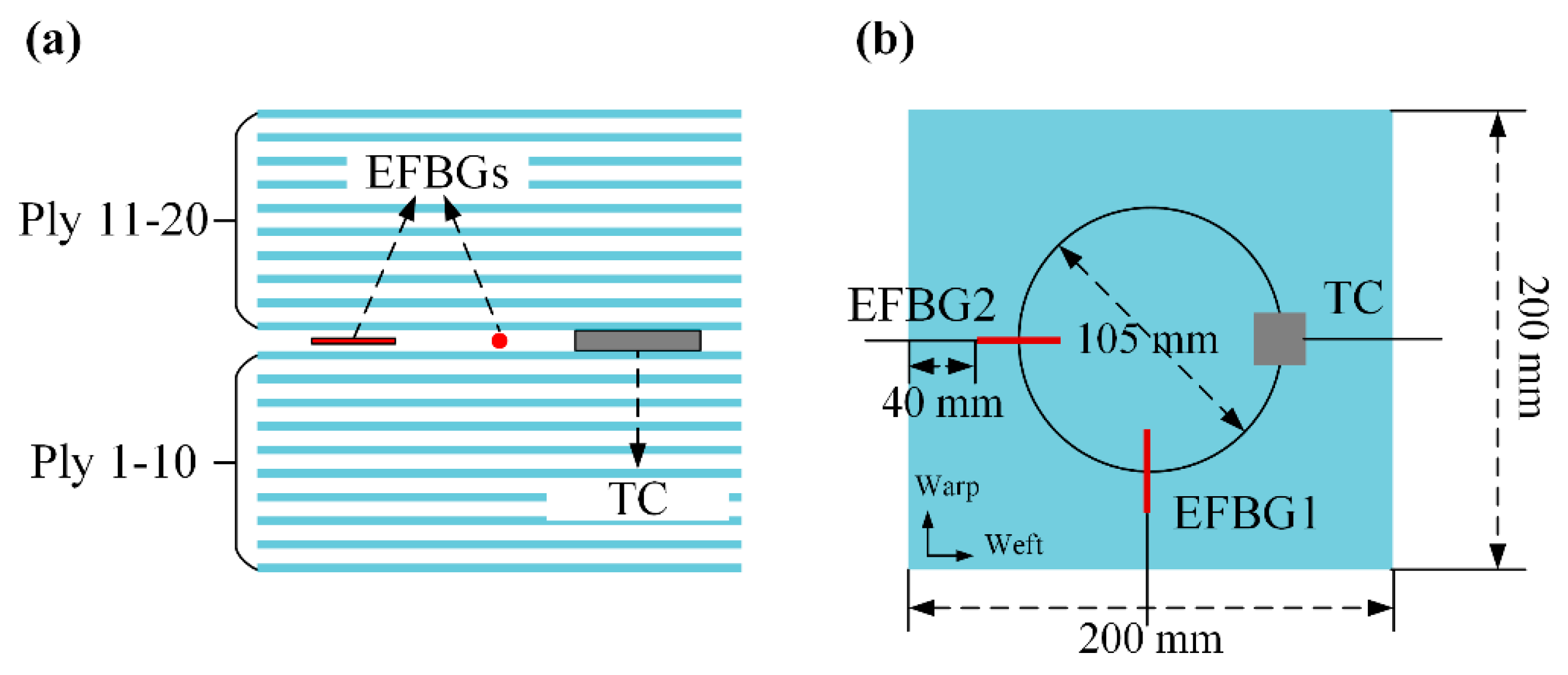
3.1. FRTP Laminate
3.2. Forming Procedure
3.3. Manufactured Laminate
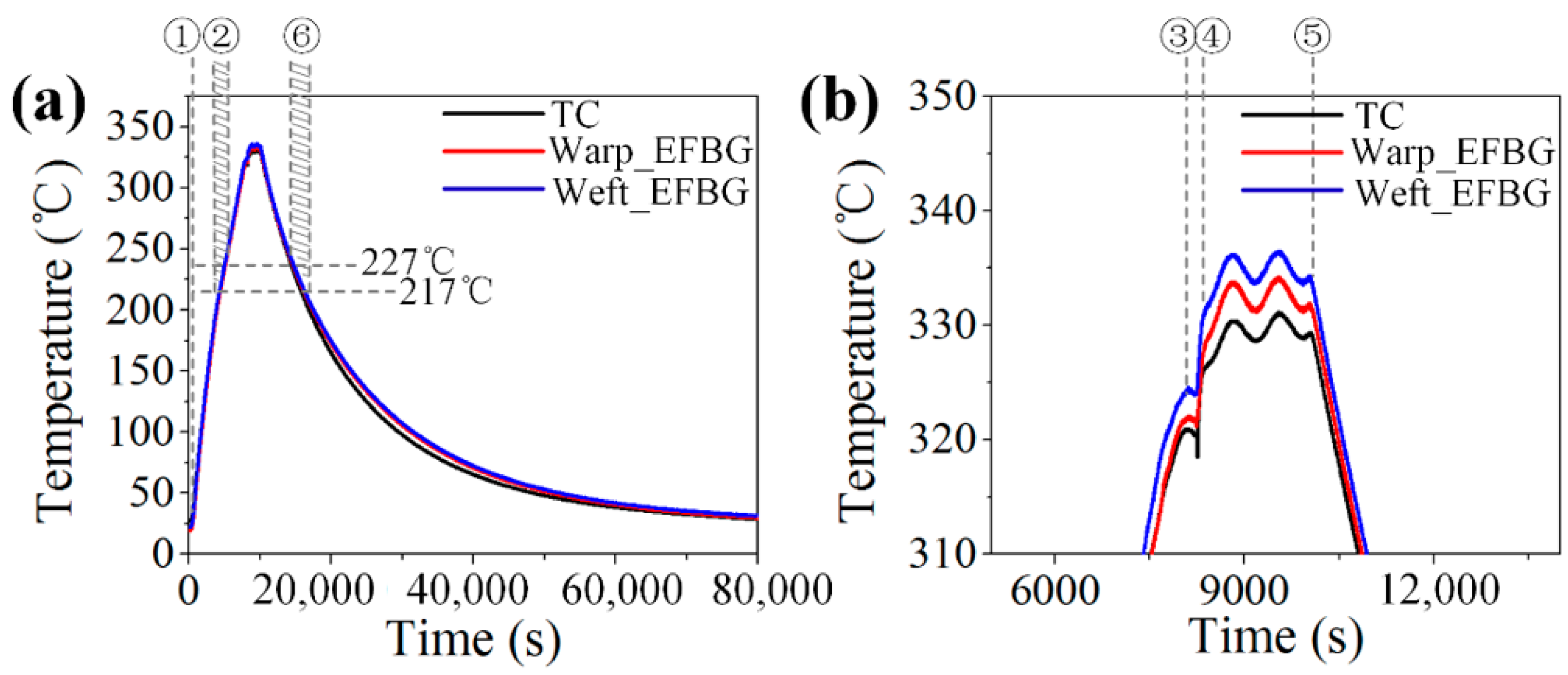
4. Temperature Monitoring Using Wavelength Shift
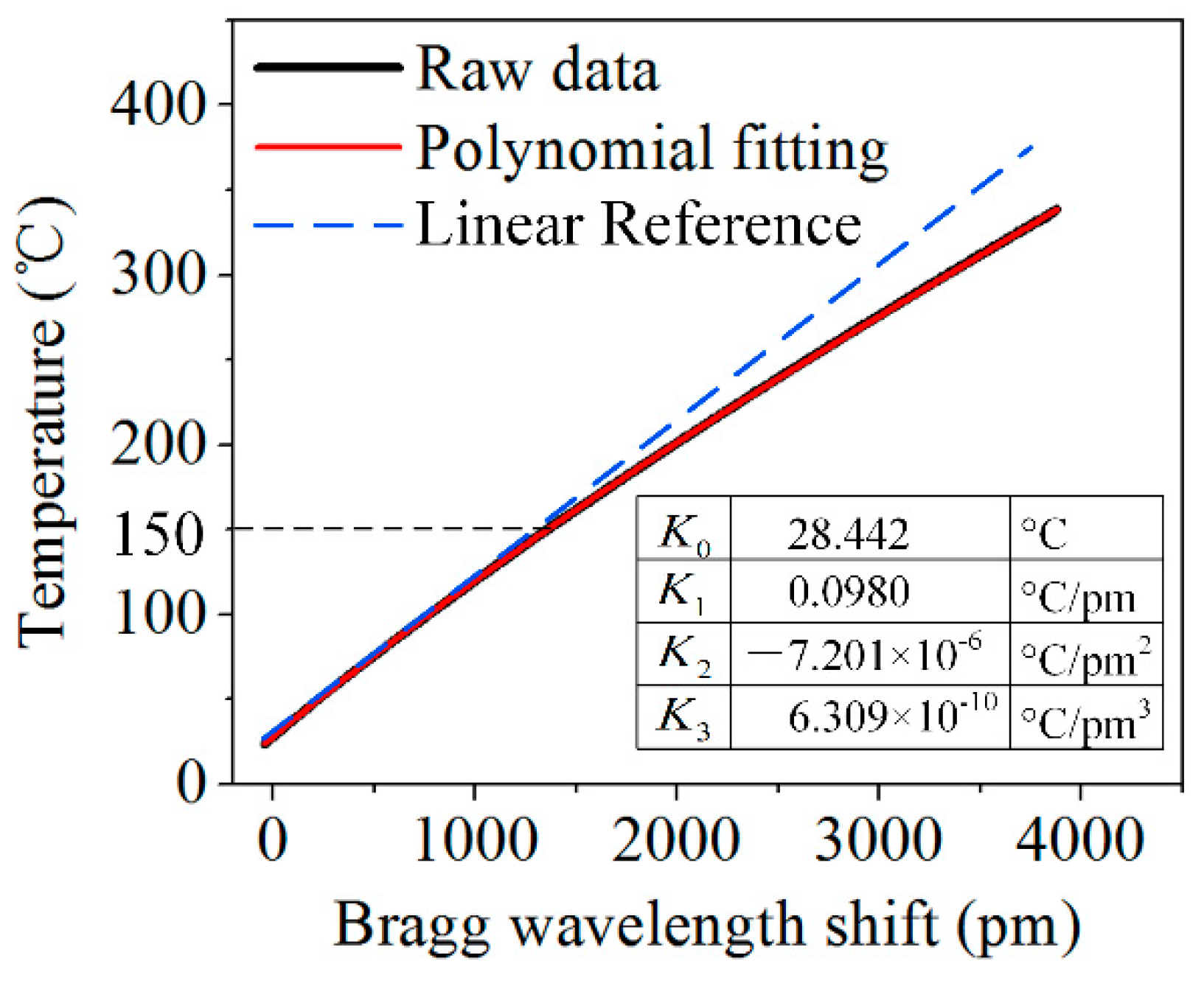
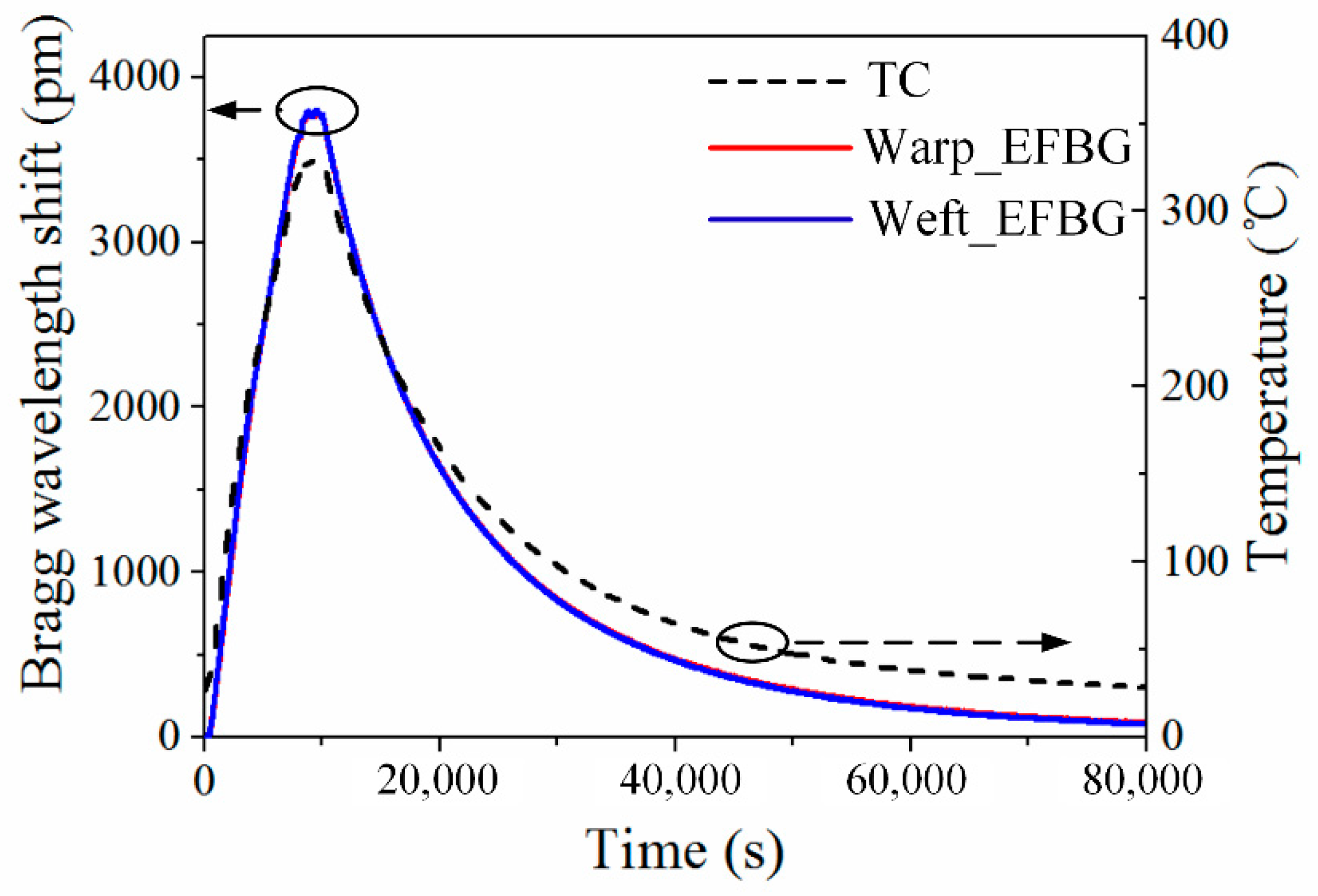
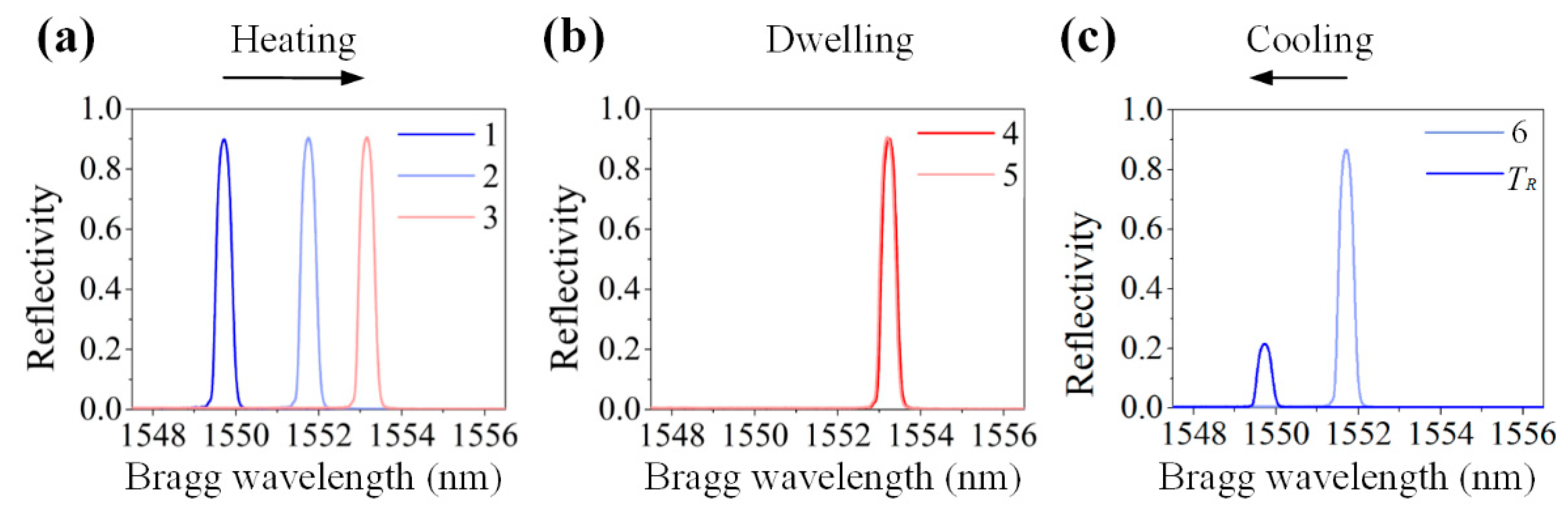
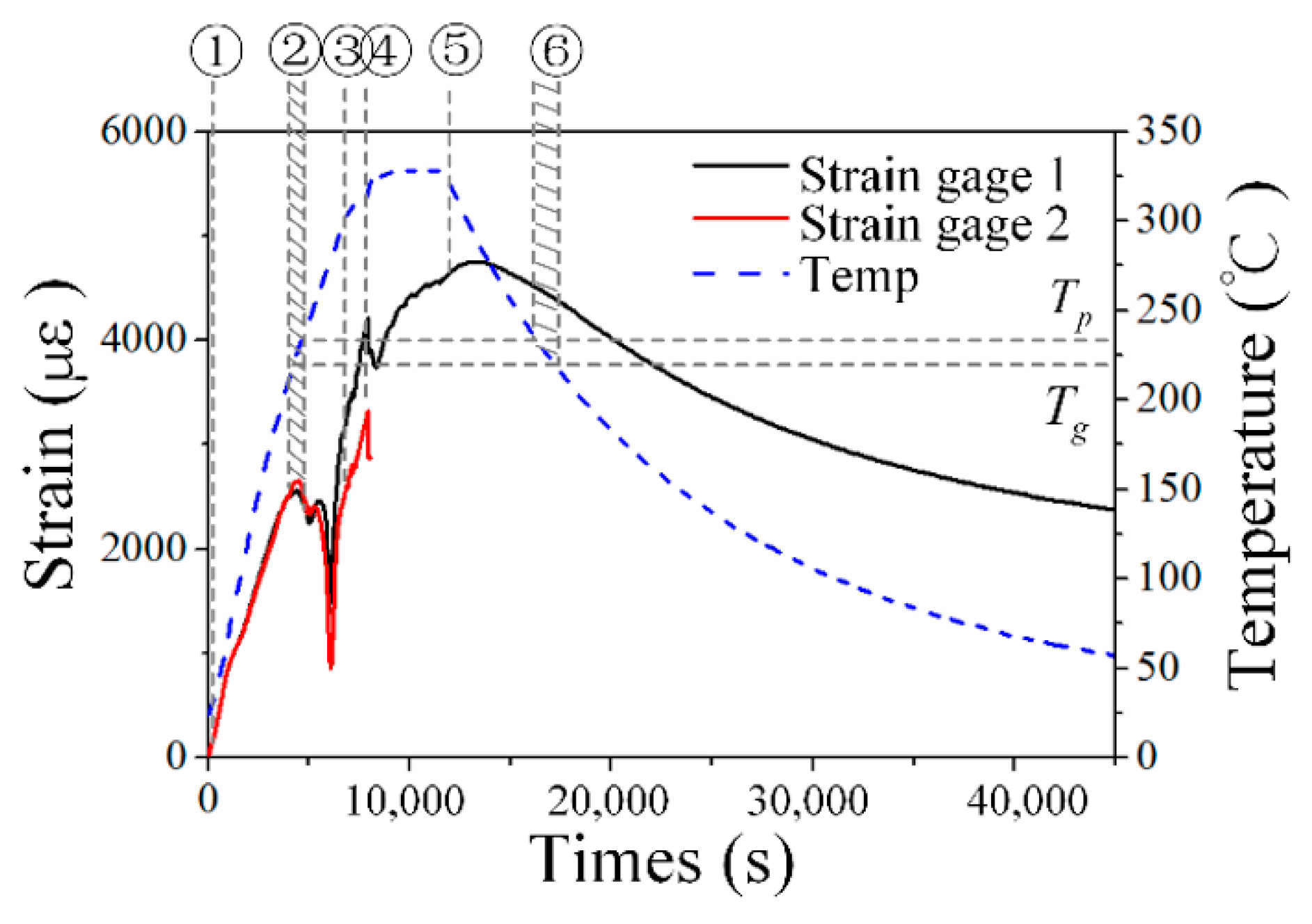
4.1. Bragg Wavelength Shift
4.2. Temperature Reconstruction
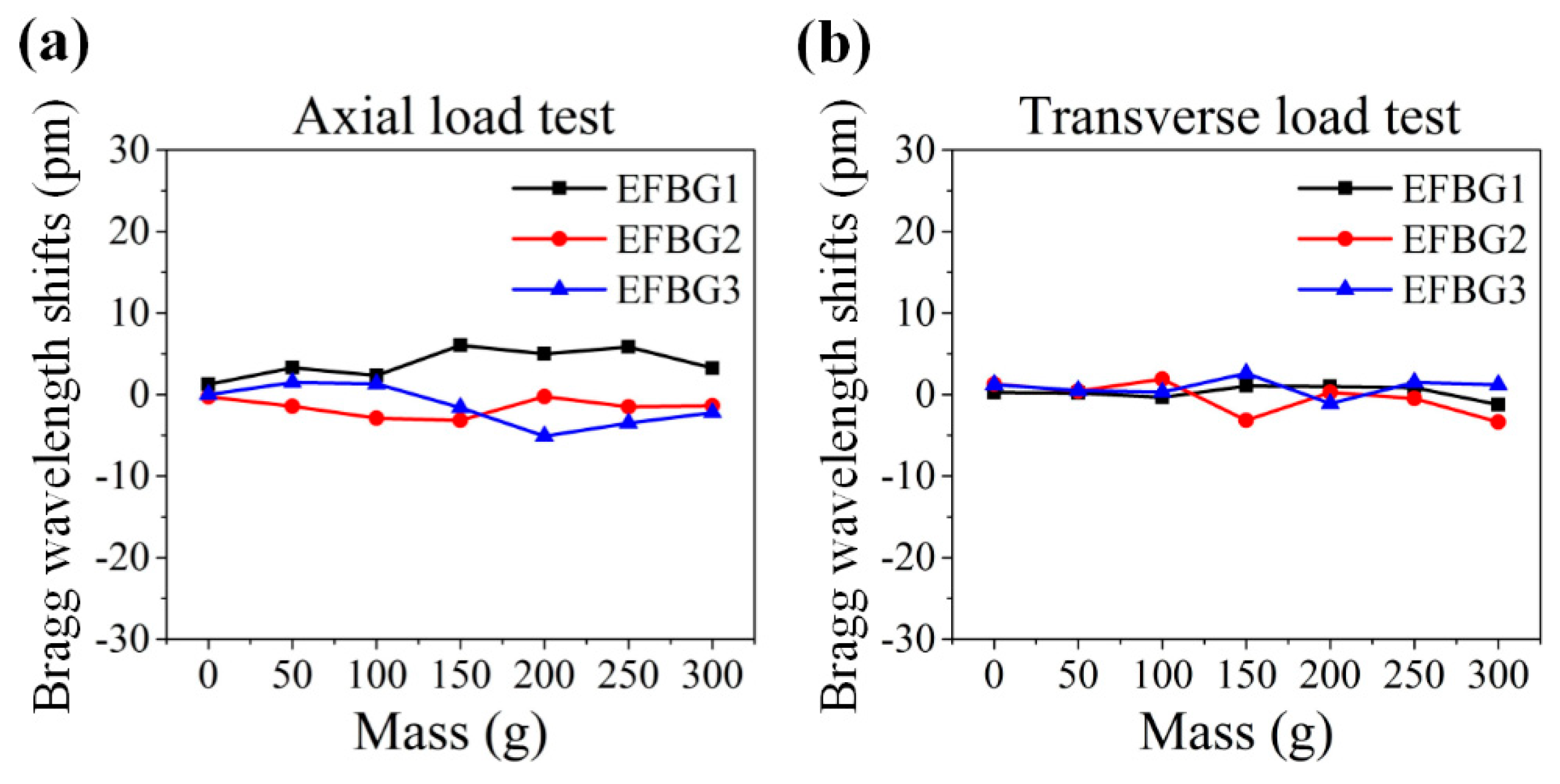
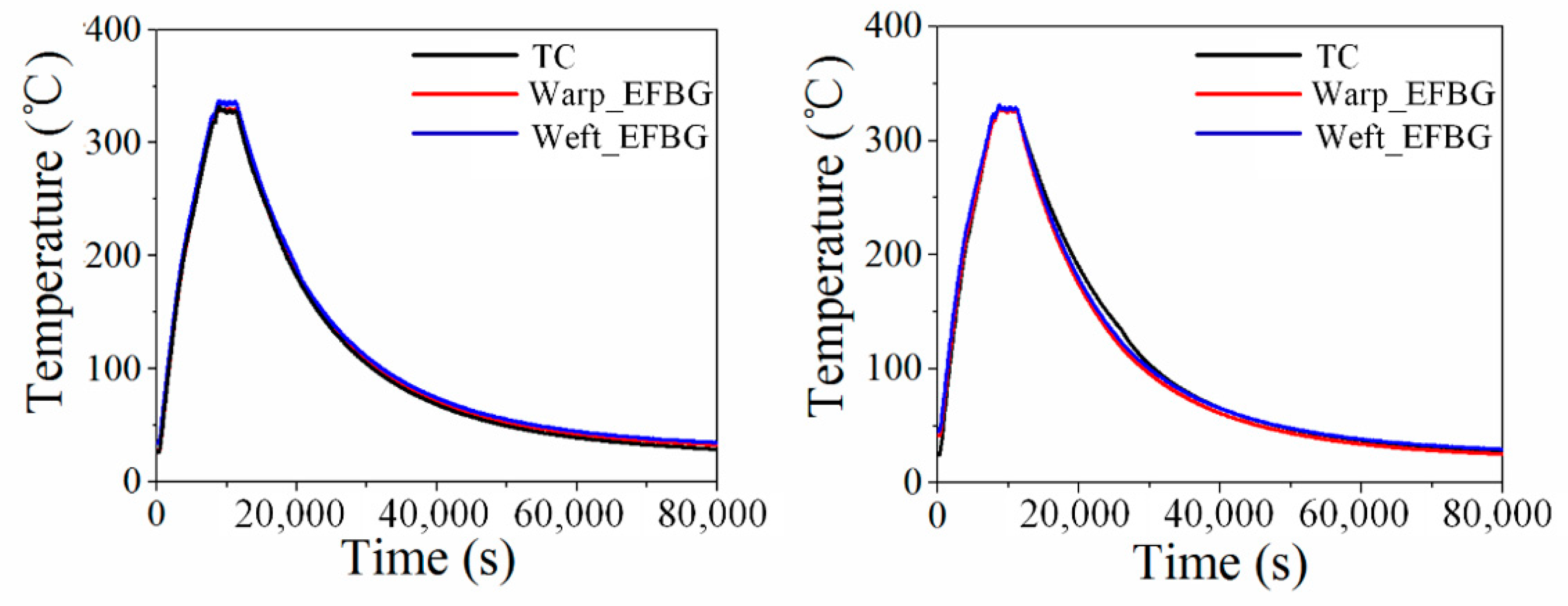
4.3. Repeatability Validation
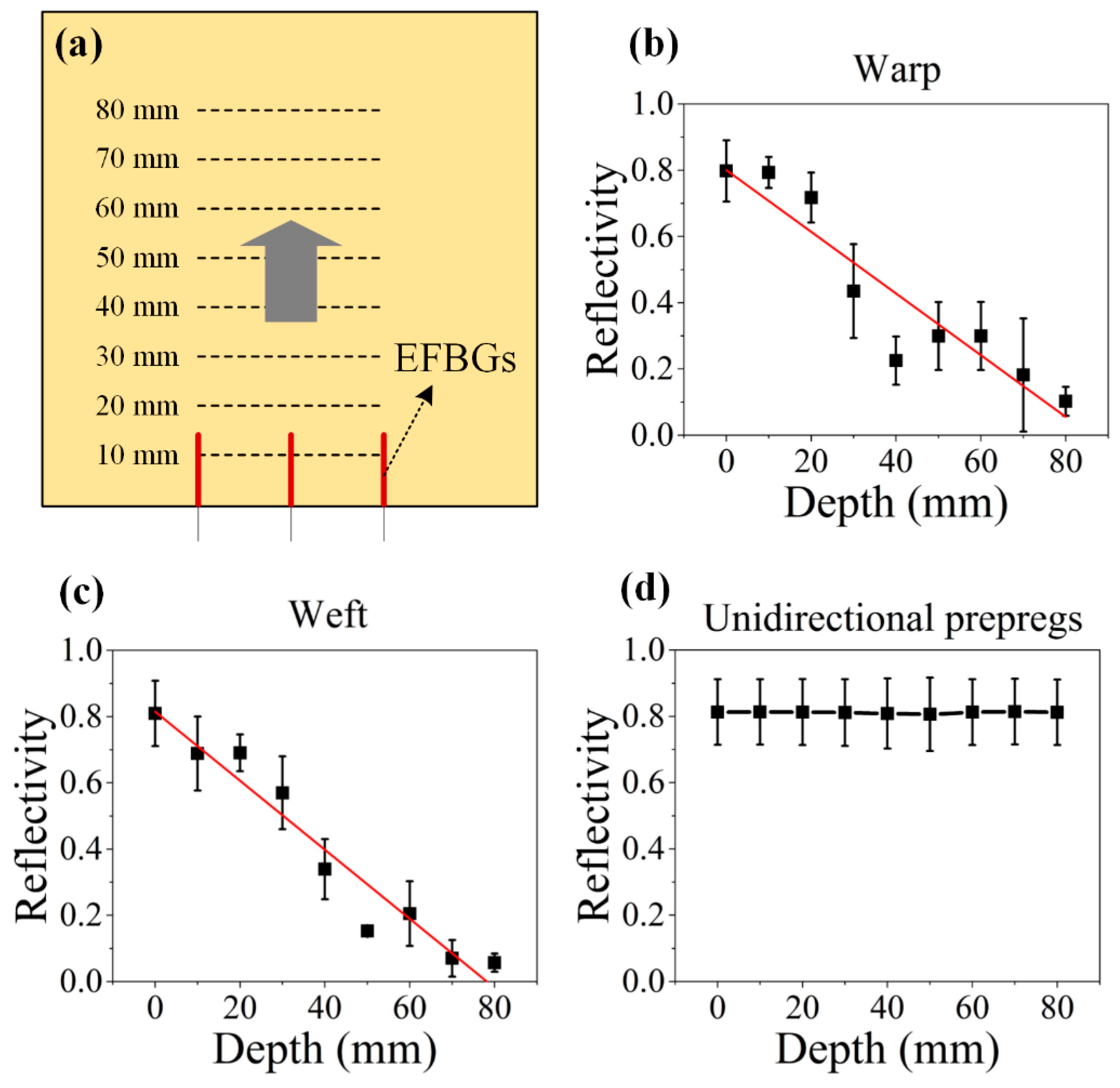
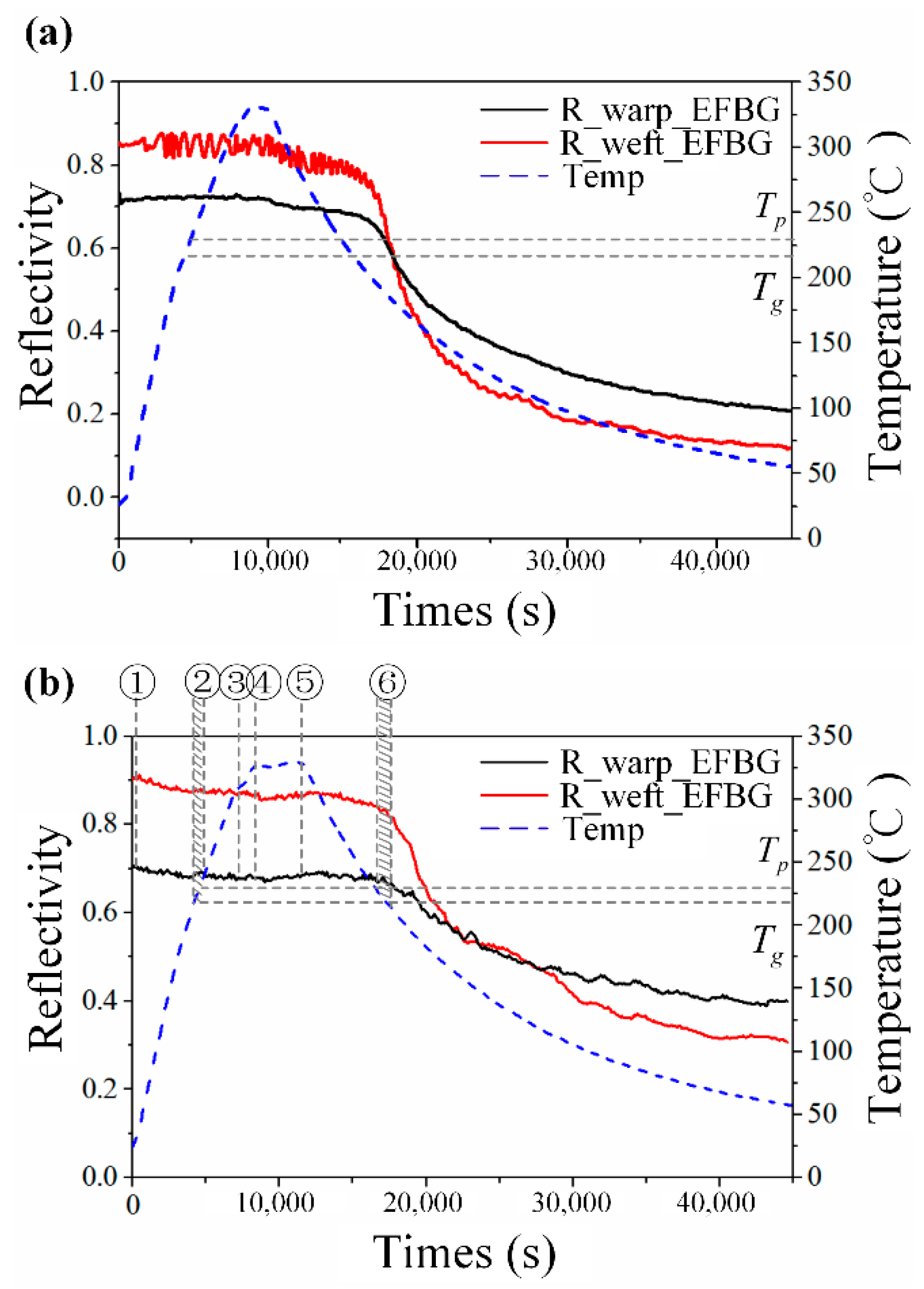
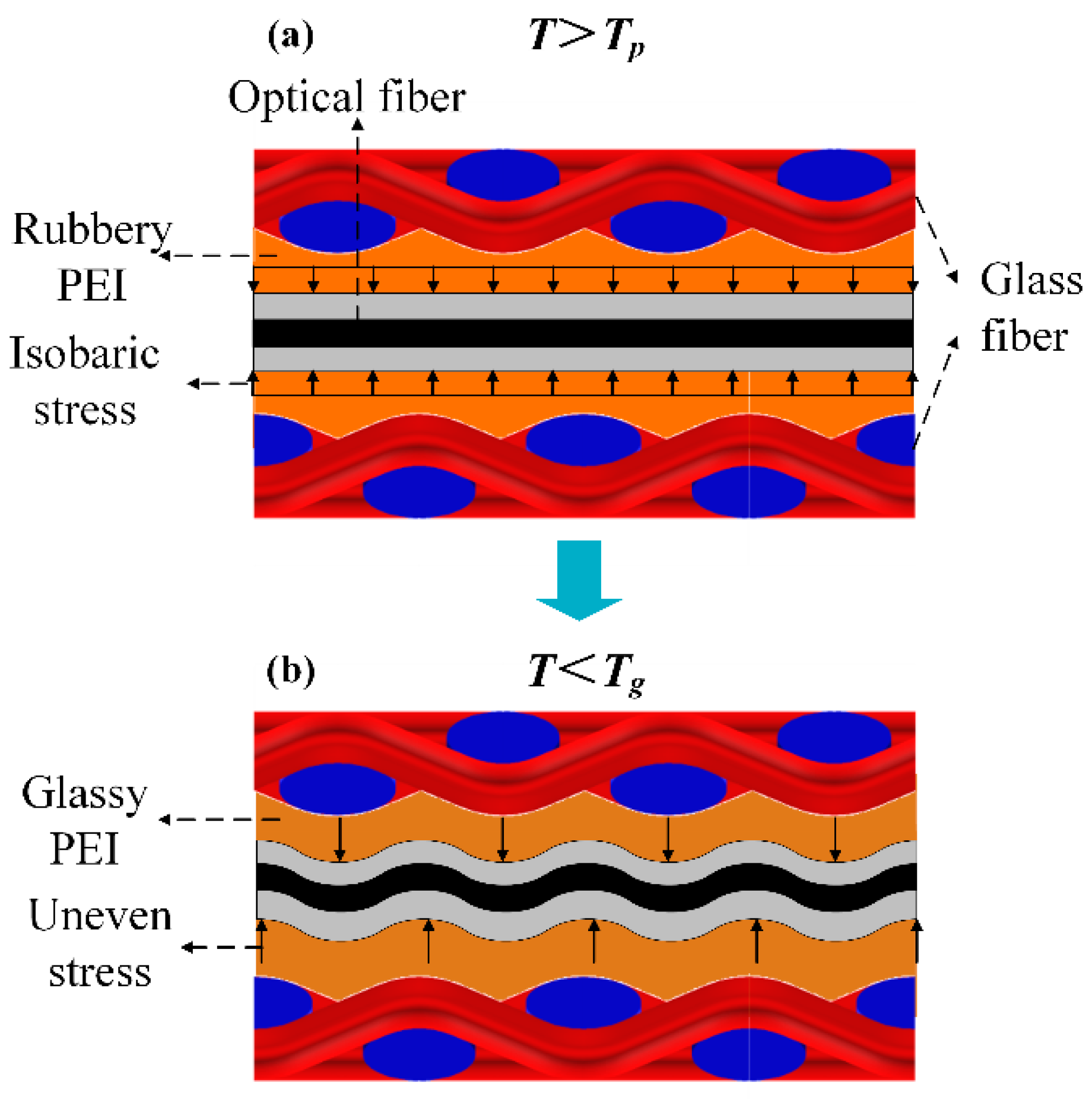
5. Stress Reflection Using Reflectivity Change
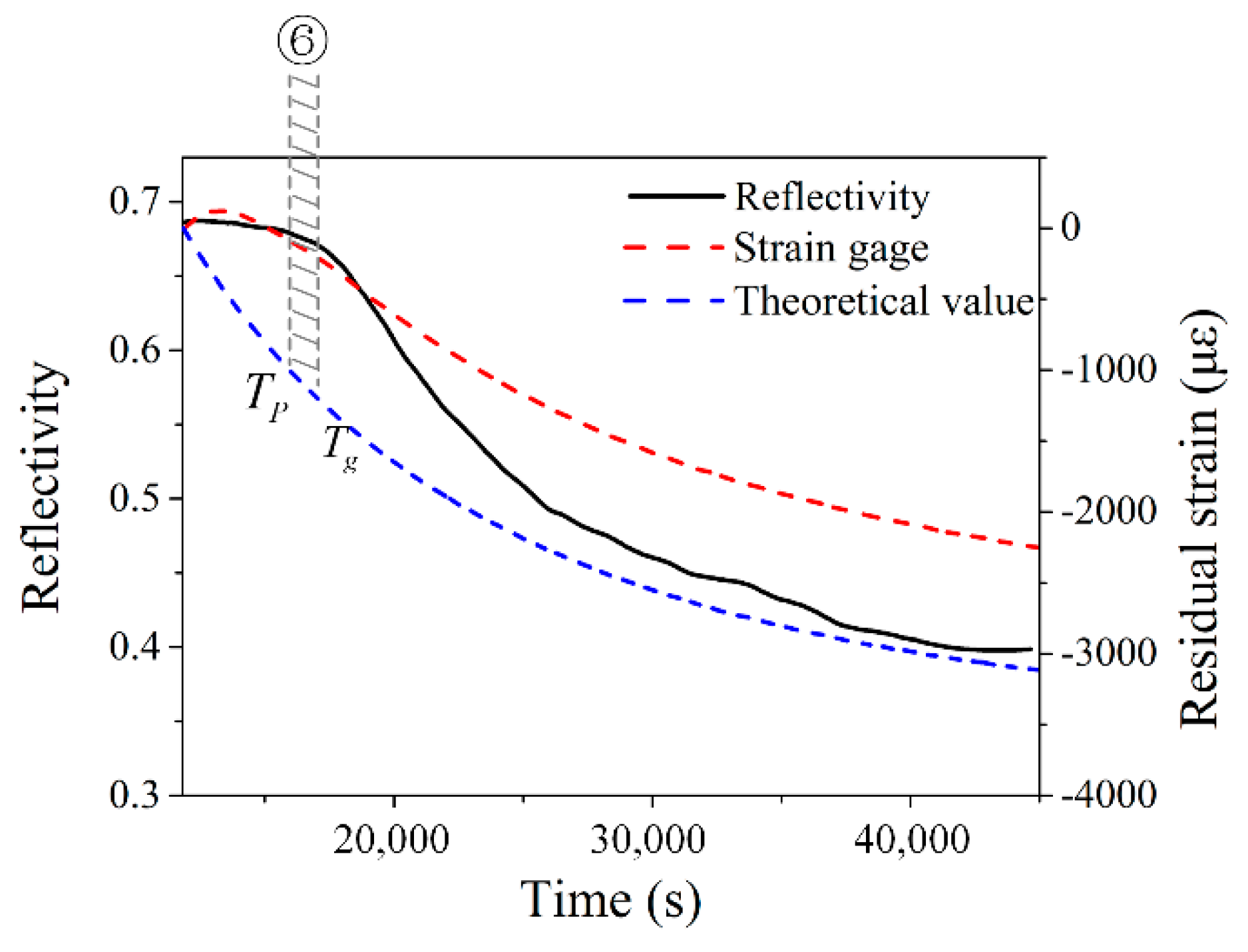
5.1. Reflectivity Change
5.2. Internal Strain Change
5.3. Comparison of Reflectivity and Strain
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Nielsen, A.S.; Pyrz, R. The effect of cooling rate on thermal residual strains in carbon/polypropylene microcomposites. Sci. Eng. Compos. Mater. 1998, 7, 1–22. [Google Scholar] [CrossRef]
- Guillen, J.; Cantwell, W. The influence of cooling rate on the fracture properties of a glass reiforced/nylon fiber–metal laminate. Polym. Compos. 2002, 23, 839–851. [Google Scholar] [CrossRef]
- Youssef, Y.; Denault, J. Thermoformed glass fiber reinforced polypropylene: Microstructure, mechanical properties and residual stresses. Polym. Compos. 2010, 19, 301–309. [Google Scholar]
- Gelb, G.H.; Marcus, B.D.; Dropkin, D. Manufacture of fine wire thermocouple probes. Rev. Sci. Instrum. 1964, 35, 80–81. [Google Scholar] [CrossRef]
- Zhang, B.; Kahrizi, M. High-temperature resistance fiber Bragg grating temperature sensor fabrication. IEEE Sens. J. 2007, 7, 586–591. [Google Scholar]
- Parne, S.R.; Ravinuthala, L.N.S.P.; Dipankar, S.G.; Madhuvarasu, S.S.; Kamineni, S.N.; Putha, K. Encapsulated fiber Bragg grating sensor for high temperature measurements. Opt. Eng. 2011, 55, 4401. [Google Scholar]
- Takeda, S.I.; Mizutani, T.; Nishi, T.; Uota, N.; Hirano, Y.; Iwahori, Y.; Nagao, Y.; Takeda, N. Monitoring of a CFRP-stiffened panel manufactured by VaRTM using fiber-optic sensors. Adv. Compos. Mater. 2008, 17, 125–137. [Google Scholar] [CrossRef]
- Guo, Z.S. Strain and temperature monitoring of asymmetric composite laminate using FBG hybrid sensors. Struct. Health Monit. 2007, 6, 191–197. [Google Scholar] [CrossRef]
- Molimard, J.; Vacher, S.; Vautrin, A. Monitoring LCM Process by FBG sensor under birefringence. Strain 2011, 47, 364–373. [Google Scholar] [CrossRef]
- Zhan, Y.; Feng, C.; Shen, Z.; Xie, N.; Liu, H.; Xiong, F.; Wang, S.; Sun, Z.; Yu, M. Fiber Bragg grating monitoring for composites in the out-of-autoclave curing process. J. Opt. Technol. 2018, 85, 371–376. [Google Scholar] [CrossRef]
- Ding, G.; Cao, H.; Xie, C. Multipoint cure monitoring of temperature and strain of carbon fibre-reinforced plastic shafts using fibre Bragg grating sensors. Nondestr. Test. Eval. 2019, 34, 117–134. [Google Scholar] [CrossRef]
- Mulle, M.; Wafai, H.; Yudhanto, A.; Lubineau, G.; Yaldiz, R.; Schijve, W.; Verghese, N. Process monitoring of glass reinforced polypropylene laminates using fiber Bragg gratings. Compos. Sci. Technol. 2016, 123, 143–150. [Google Scholar] [CrossRef]
- Guillaume, L.; Romain, C.; Nicolas, R.; Rudy, D.; Stephane, R. Temperature resistant fiber Bragg gratings for on-line and structural health monitoring of the next-generation of nuclear reactors. Sensors 2018, 18, 1791. [Google Scholar]
- Tu, Y.; Qi, Y.H.; Tu, S.T. Fabrication and thermal characteristics of multilayer metal-coated regenerated grating sensors for high-temperature sensing. Smart Mater. Struct. 2013, 22, 075026. [Google Scholar] [CrossRef]
- Wu, Q.; Ogasawara, T.; Yoshikawa, N.; Zhai, H.Z. Modeling the viscoelasticity of polyetherimide. J. Appl. Polym. Sci. 2018, 135, 46102. [Google Scholar] [CrossRef]
- Michael, W.N.; Jacob, W.S.; Jacob, H.H.; Jacob, P.W.; Jesper, H.H.; Tom, L.A.; Christen, M.M. Life cycle strain monitoring in glass fibre reinforced polymer laminates using embedded fibre Bragg grating sensors from manufacturing to failure. J. Compos. Mater. 2014, 48, 365–381. [Google Scholar]
- Tsukada, T.; Minakuchi, S.; Takeda, N. Identification of process-induced residual stress/strain distribution in thick thermoplastic composites based on in situ strain monitoring using optical fiber sensors. J. Compos. Mater. 2019, 53, 3445–3458. [Google Scholar] [CrossRef]
- Takeda, S.I.; Tsukada, T.; Minakuchi, S.; Takeda, N.; Iwahori, Y. Fiber-optic sensing for press forming of L-shaped thermoplastic composites. Procedia Eng. 2017, 188, 348–353. [Google Scholar] [CrossRef]
- Tsukada, T.; Takeda, S.I.; Minakuchi, S.; Iwahori, Y.; Takeda, N. Evaluation of the influence of cooling rate on residual strain development in unidirectional carbon fibre/polyphenylenesulfide laminates using embedded fibre Bragg grating sensors. J. Compos. Mater. 2016, 0, 1–11. [Google Scholar] [CrossRef]
- Leng, J.S.; Asundi, A. Stuctural health monitoring of smart composite materails by using EFPI and FBG sensors. Sens. Actuators A 2003, 103, 330–340. [Google Scholar] [CrossRef]
- Minakuchi, S. In situ characterization of direction-dependent cure-induced shrinkage in thermoset composite laminates with fiber-optic sensors embedded in through-thickness and in-plane directions. J. Compos. Mater. 2015, 49.9, 1021–1034. [Google Scholar] [CrossRef]
- Wisnom, M.R.; Gigliotti, M.; Ersoy, N.; Campbell, M.; Potter, K.D. Mechanisms generating residual stresses and distortion during manufacture of polymer-matrix composite structures. Compos. Part A 2006, 37, 522–529. [Google Scholar] [CrossRef]
- Johnston, A.; Vaziri, R.; Poursartip, A. A plane strain model for process-induced deformation of laminated composite structures. J. Compos. Mater. 2001, 35, 1435–1469. [Google Scholar] [CrossRef]
- Svanberg, J.M.; Holmberg, J.A. An experimental investigation on mechanisms for manufacturing induced shape distortions in homogeneous and balanced laminates. Compos. Part A 2001, 32, 827–838. [Google Scholar] [CrossRef]
- Venkatesan, V.N.; Weiss, K.P.; Bharti, R.P.; Neumann, H.; Ramalingam, R. Strain Calibration of Substrate-Free FBG Sensors at Cryogenic Temperature; Springer: Cham, Switzerland, 2015; pp. 191–202. [Google Scholar]
- Gayan, C.K.; Jayantha, E.; Wang, H.; Lau, K.T. Use of FBG Sensors for SHM in Aerospace Structures. Photonic Sens. 2012, 2, 203–214. [Google Scholar]
- Huang, Y.K.; Tu, Y.; Tu, S.T. Monitoring of bolt clamping force at high temperatures using metal-packaged regenerated fiber Bragg grating strain sensors. In AOPC 2017: Fiber Optic Sensing and Optical Communications, Proceedings of the Applied Optics and Photonics China (AOPC2017), Beijing, China, 4–6 June 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; p. 1046412. [Google Scholar]
- Zhang, W.; Lei, X.; Chen, W.; Wang, A. Modeling of spectral changes in bent fiber Bragg gratings. Opt. Lett. 2015, 40, 3260–3263. [Google Scholar] [CrossRef]
- Davis, C.; Philips, A.; Norman, P.; Rajic, N. Effect of gauge length on embedded fibre Bragg grating sensor response in woven fibre composites. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace System: International Society for Optics and Photonics; SPIE: Portland, OR, USA, 2017. [Google Scholar]
- Jay, J.A. An overview of macrobending and microbending of optical fibers. White Pap. Corning 2010, 1–21. [Google Scholar]
- Beukema, R.P. Embedding technologies of FBG sensors in composites: Technologies, applications and practical use. In Proceedings of the 6th European Workshop on Structural Health Monitoring, Dresden, Germany, 3–6 July 2012. [Google Scholar]
- Wu, Q.; Ogasawara, T.; Yoshikawa, N.; Zhai, H.Z. Stress evolution of amorphous thermoplastic plate during forming process. Materials 2018, 11, 464. [Google Scholar] [CrossRef]
- Kwon, Y.I.; Kang, T.J.; Chung, K.; Youn, J.R. Prediction and measurement of residual stresses in injection molded parts. Fibers Polym. 2001, 2, 203–211. [Google Scholar] [CrossRef]
- Nguyen, Q.; Chen, X.; Lam, Y.; Yue, C.Y. Effects of polymer melt compressibility on mold filling in micro-injection molding. J. Micromech. Microeng. 2011, 21, 095019. [Google Scholar] [CrossRef]
- Askeland, D.R.; Fulay, P.P.; Wright, W.J. The Science and Engineering of Materials; Nelson Education: Scarborough, ON, Canada, 2011. [Google Scholar]
- Akkerman, R.; de Vries, R.S. Thermomechanical properties of woven fabric composites. In Proceedings of the International Conference on Fibre Reinforced Composites, Newcastle, UK, 15–17 April 1998; pp. 422–429. [Google Scholar]
- Abaqus, G. Abaqus 6.11; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2011. [Google Scholar]
- Hartman, D.R.; Greenwood, M.E.; Miller, D.M. High Strength Glass Fibers; AGY: Aiken, SC, USA, 1996. [Google Scholar]


| Parameter | PEI | Glass Fiber |
|---|---|---|
| Tensile modulus (MPa) | 3276 | 73,000 |
| Poisson’s ratio | 0.36 | 0.23 |
| Coefficient of thermal expansion (°C−1) | 5.58 × 10−6 | 5.40 × 10−6 |
| Glass-transition temperature Tg (°C) | 217 | |
| Rubbery plateau beginning temperature Tp (°C) | 227 | |
| Melt index (g/min) | 0.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Wu, Q.; Xiong, K.; Zhai, H.; Yoshikawa, N.; Wang, R. Hybrid Temperature and Stress Monitoring of Woven Fabric Thermoplastic Composite Using Fiber Bragg Grating Based Sensing Technique. Sensors 2020, 20, 3081. https://doi.org/10.3390/s20113081
Chen C, Wu Q, Xiong K, Zhai H, Yoshikawa N, Wang R. Hybrid Temperature and Stress Monitoring of Woven Fabric Thermoplastic Composite Using Fiber Bragg Grating Based Sensing Technique. Sensors. 2020; 20(11):3081. https://doi.org/10.3390/s20113081
Chicago/Turabian StyleChen, Changhao, Qi Wu, Ke Xiong, Hongzhou Zhai, Nobuhiro Yoshikawa, and Rong Wang. 2020. "Hybrid Temperature and Stress Monitoring of Woven Fabric Thermoplastic Composite Using Fiber Bragg Grating Based Sensing Technique" Sensors 20, no. 11: 3081. https://doi.org/10.3390/s20113081
APA StyleChen, C., Wu, Q., Xiong, K., Zhai, H., Yoshikawa, N., & Wang, R. (2020). Hybrid Temperature and Stress Monitoring of Woven Fabric Thermoplastic Composite Using Fiber Bragg Grating Based Sensing Technique. Sensors, 20(11), 3081. https://doi.org/10.3390/s20113081





