The Power Gain Difference Method Analysis
Abstract
1. Introduction
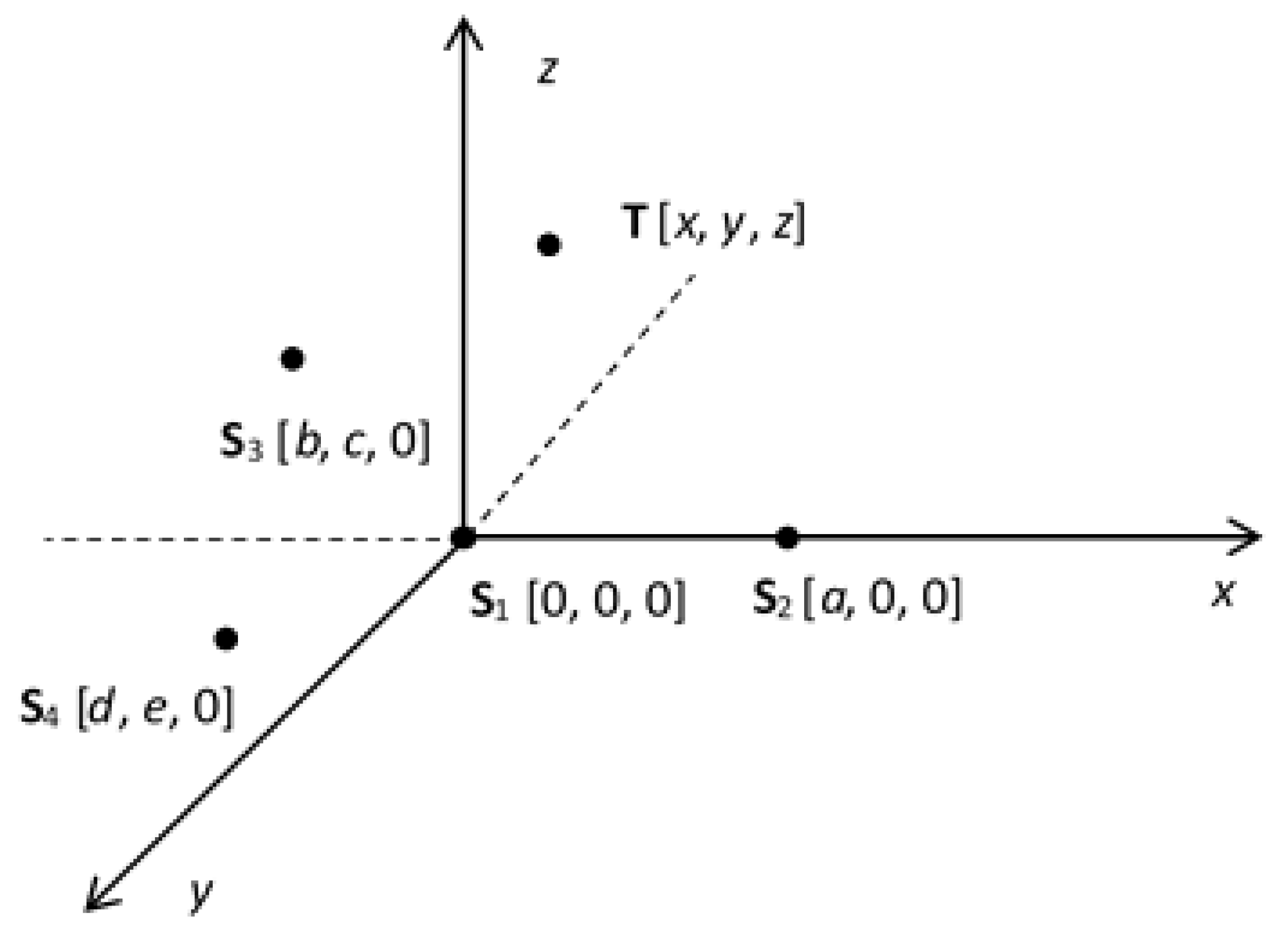
2. The Geometric Representation and the Analytical Solution of the Power Gain Difference (PGD) Technique Model
3. The PGD Technique Accuracy Analysis
3.1. The Theoretical Basis of the Accuracy Analysis
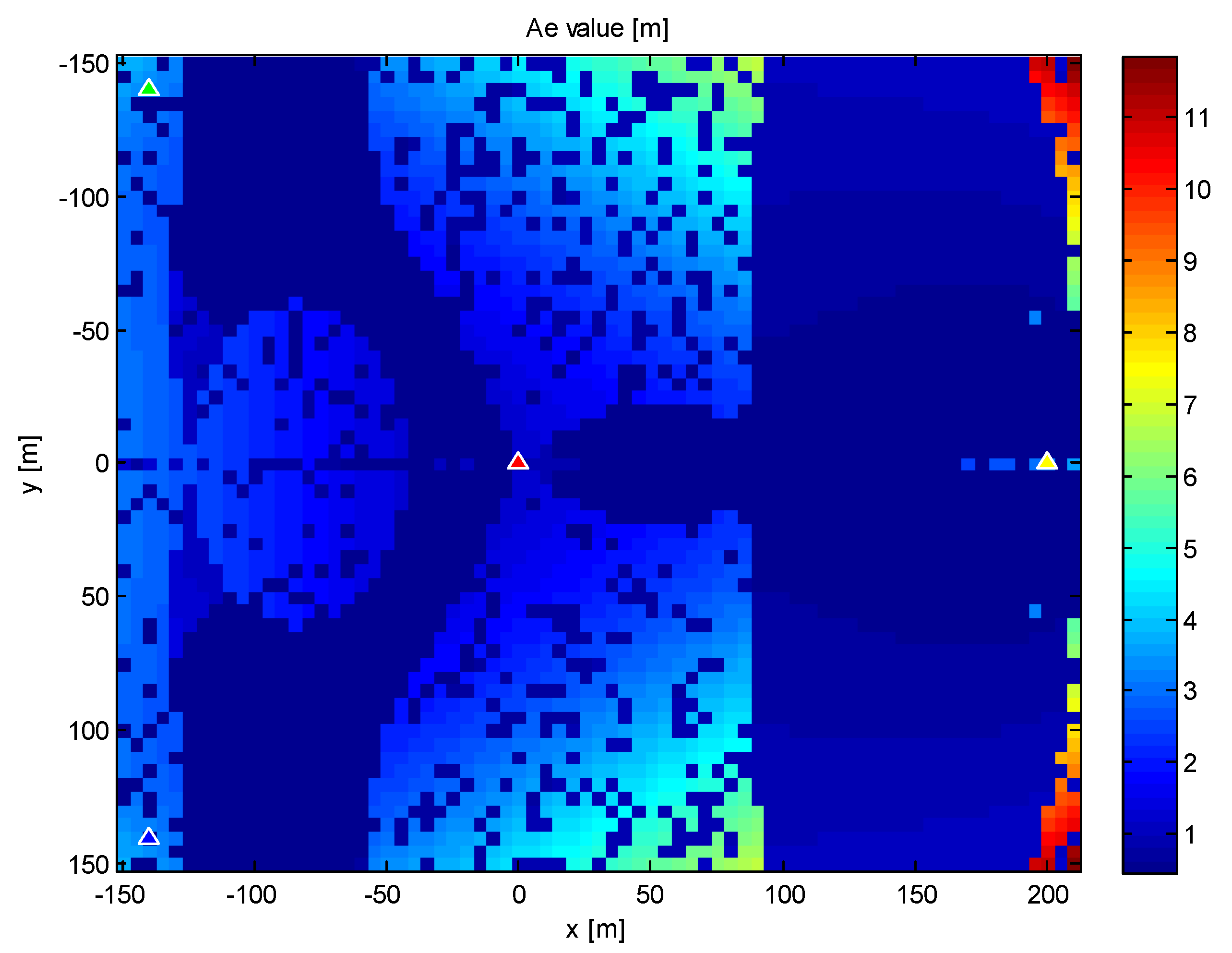
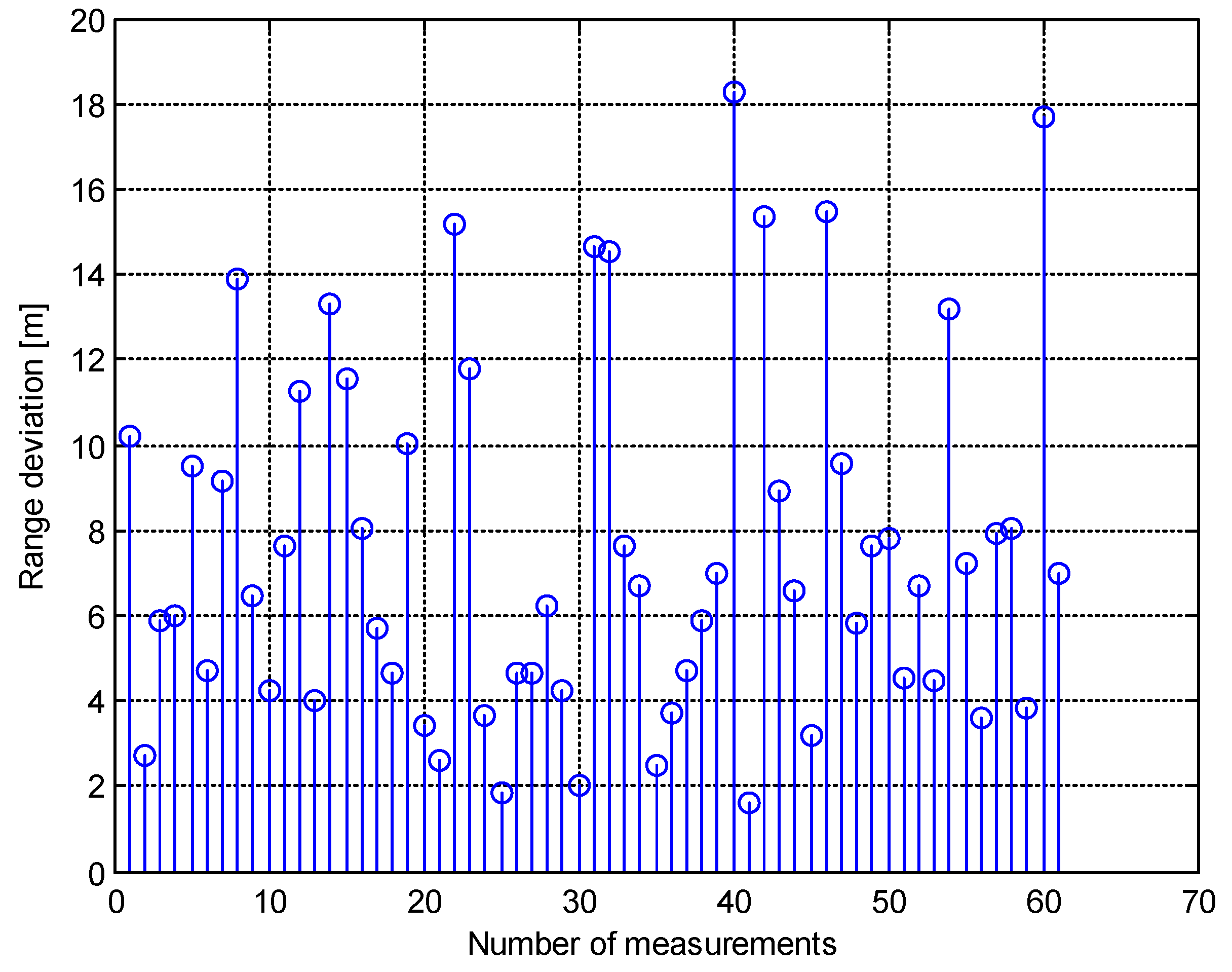
3.2. The Results of the Error Analysis of the PGD Method
- Aemin = 0.47 m, Aemax = 5.84 m,
- Bemin = 0.46 m, Bemax = 4.09 m,
- Cemin = 0.47 m, Cemax = 8.97 m.
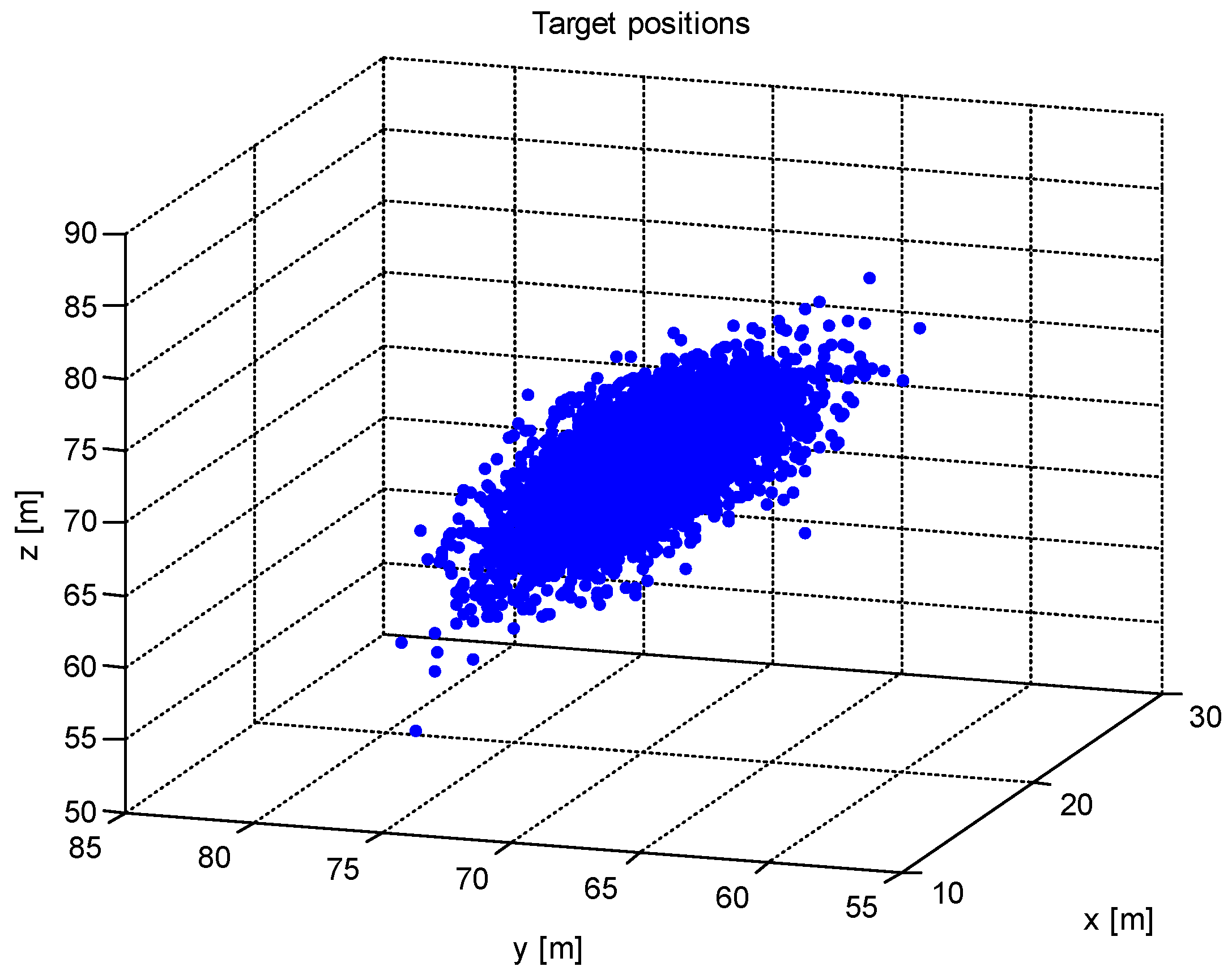
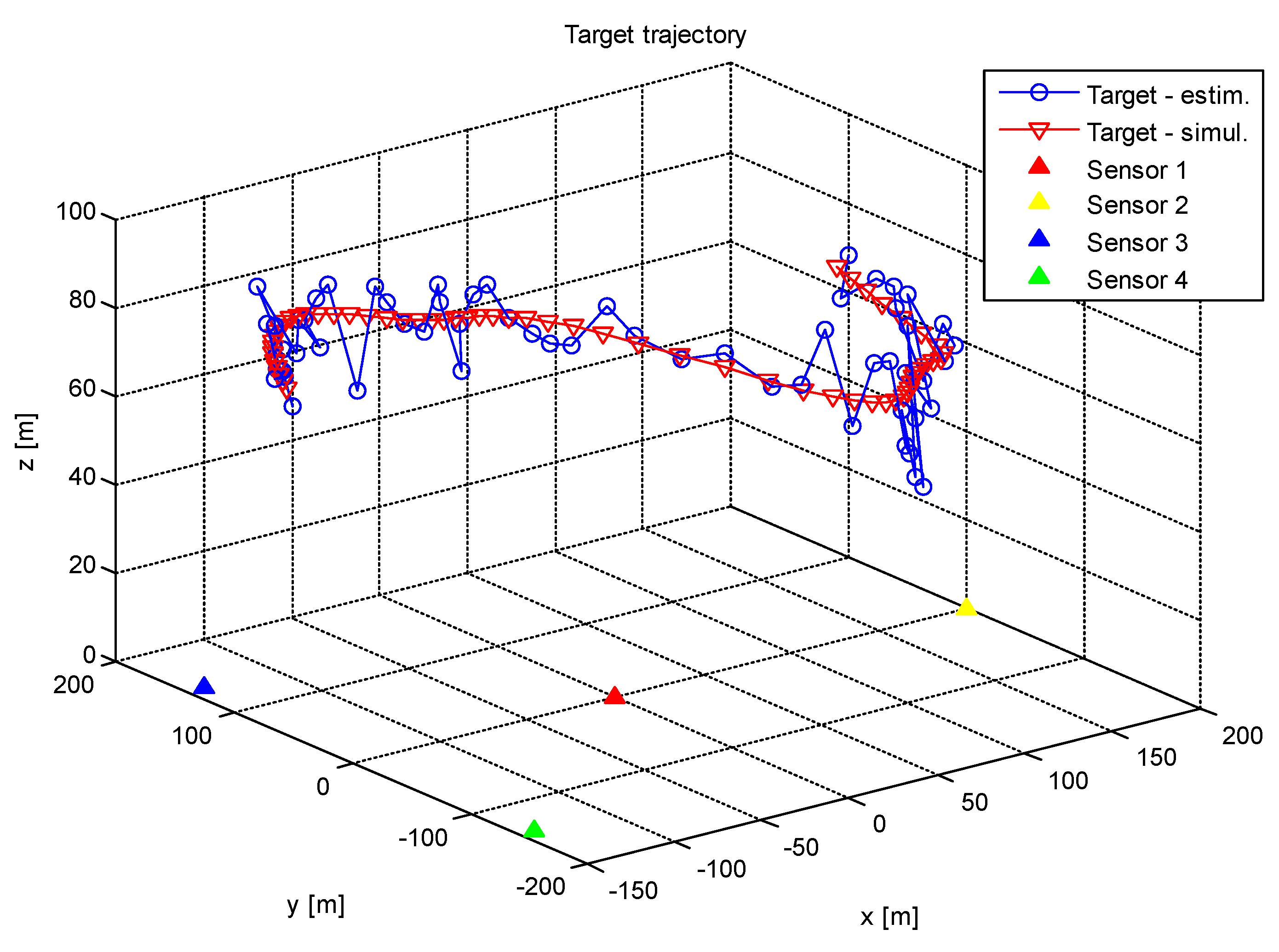
4. The Simulation of the Method Performance
- ,
- ,
- ,
- .
- ,
- ,
- ,
- .
5. Discussion
- The target position can be estimated by the standard RSS method in the case that only three receiver sensors are irradiated by the target (for example, due to the shadowing effect).
- The target position can be estimated by the fusion of the localization data that the PGD and the RSS methods provide in the case that four or more sensors are irradiated.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Gu, Y.; Lo, A.; Niemegeers, I. A survey of indoor positioning systems for wireless personal networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.Y.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef]
- Poisel, R. Electronic Warfare Target Location Methods, 2nd. ed.; Artech House: Boston, MA, USA, 2012; ISBN 9781608075232. [Google Scholar]
- Rong, P.; Sichitiu, M.L. Angle of Arrival Localization for Wireless Sensor Networks. In Proceedings of the 2006 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 28 September 2006; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; Volume 1, pp. 374–382. [Google Scholar]
- Alma’Aitah, A.; Alsaify, B.; Bani-Hani, R. Three-Dimensional Empirical AoA Localization Technique for Indoor Applications. Sensors 2019, 19, 5544. [Google Scholar] [CrossRef] [PubMed]
- Nemati, M.; Baykas, T.; Choi, J. Performance of TDOA and AOA Localization Techniques for Different Base-Stations Topologies. In Proceedings of the 13th International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, Australia, 16–18 December 2019; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; pp. 1–7. [Google Scholar]
- Jeong, S.; Sung, T.-K.; Lee, K.E.; Kang, J. Joint TOA/AOA-based localization in wireless sensor networks. In Proceedings of the 8th International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, Australia, 15–17 December 2014; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Foy, W. Position-Location Solutions by Taylor-Series Estimation. IEEE Trans. Aerosp. Electron. Syst. 1976, 187–194. [Google Scholar] [CrossRef]
- Ho, K.C.; Lu, X.; Kovavisaruch, L. Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors: Analysis and Solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Ho, K.C.; Xu, W. An Accurate Algebraic Solution for Moving Source Location Using TDOA and FDOA Measurements. IEEE Trans. Signal Process. 2004, 52, 2453–2463. [Google Scholar] [CrossRef]
- Kang, S.; Kim, T.; Chung, W. Hybrid RSS/AOA Localization using Approximated Weighted Least Square in Wireless Sensor Networks. Sensors 2020, 20, 1159. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Cabric, D. Cramer-Rao Bounds for Joint RSS/DoA-Based Primary-User Localization in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2013, 12, 1363–1375. [Google Scholar] [CrossRef]
- Sadowski, S.; Spachos, P. RSSI-Based Indoor Localization with the Internet of Things. IEEE Access 2018, 6, 30149–30161. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, J.; Xiao, Y.; Peng, M. Robust Localization Algorithm Based on the RSSI Ranging Scope. Int. J. Distrib. Sens. Netw. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Zou, R.; Kalivarapu, V.; Winer, E.; Oliver, J.; Bhattacharya, S. Particle Swarm Optimization-Based Source Seeking. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1–11. [Google Scholar] [CrossRef]
- Yiu, S.; Dashti, M.; Claussen, H.; Perez-Cruz, F. Wireless RSSI fingerprinting localization. Signal Process. 2017, 131, 235–244. [Google Scholar] [CrossRef]
- Stoyanova, T.; Kerasiotis, F.; Efstathiou, K.; Papadopoulos, G. Modeling of the RSS Uncertainty for RSS-Based Outdoor Localization and Tracking Applications in Wireless Sensor Networks. In Proceedings of the 4th International Conference on Sensor Technologies and Applications, Venice, Italy, 18–25 July 2010; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; pp. 45–50. [Google Scholar]
- Graefenstein, J.; Bouzouraa, M.E. Robust method for outdoor localization of a mobile robot using received signal strength in low power wireless networks. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; pp. 33–38. [Google Scholar]
- Zhu, X.; Feng, Y. RSSI-based Algorithm for Indoor Localization. Commun. Netw. 2013, 5, 37–42. [Google Scholar] [CrossRef]
- Bae, Y. Robust Localization for Robot and IoT Using RSSI. Energies 2019, 12, 2212. [Google Scholar] [CrossRef]
- Kokkinis, A.; Kanaris, L.; Liotta, A.; Stavrou, S. RSS Indoor Localization Based on a Single Access Point. Sensors 2019, 19, 3711. [Google Scholar] [CrossRef]
- Koneru, A.; Li, X.; Varanasi, M. Comparative study of RSS-based collaborative localization methods in sensor networks. In Proceedings of the IEEE Region 5 Conference, San Antonio, TX, USA, 7–9 April 2006; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA; pp. 243–248. [Google Scholar]
- Huang, J.; Liu, P.; Lin, W.; Gui, G. RSS-Based Method for Sensor Localization with Unknown Transmit Power and Uncertainty in Path Loss Exponent. Sensors 2016, 16, 1452. [Google Scholar] [CrossRef]
- Li, X. Collaborative Localization with Received-Signal Strength in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2007, 56, 3807–3817. [Google Scholar] [CrossRef]
- Wang, G.; Yang, K. A New Approach to Sensor Node Localization Using RSS Measurements in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2011, 10, 1389–1395. [Google Scholar] [CrossRef]
- Torrieri, D. Statistical Theory of Passive Location Systems. IEEE Trans. Aerosp. Electron. Syst. 1984, 20, 183–198. [Google Scholar] [CrossRef]
- Laaraiedh, M.; Avrillon, S.; Uguen, B. Cramer-Rao lower bounds for nonhybrid and hybrid localisation techniques in wireless networks. Eur. Trans. Telecommun. 2011. [Google Scholar] [CrossRef]
- Schervish, M.J. Theory of Statistics; Corr. 2nd printing 1996 Edition; Springer: New York, NY, USA, 1997; ISBN 978-0-387-94546-0. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1993; ISBN 0133457117. [Google Scholar]
- Li, Y.-Y.; Wang, C.-C.; Qi, G.-Q.; Sheng, A.-D. Closed-form formula of Cramer–Rao lower bound for 3D TOA target localisation. Electron. Lett. 2020, 56, 43–45. [Google Scholar] [CrossRef]
- Pogliano, U. Use of integrative analog-to-digital converters for high-precision measurement of electrical power. IEEE Trans. Instrum. Meas. 2001, 50, 1315–1318. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veselý, J.; Hubáček, P.; Olivová, J. The Power Gain Difference Method Analysis. Sensors 2020, 20, 3018. https://doi.org/10.3390/s20113018
Veselý J, Hubáček P, Olivová J. The Power Gain Difference Method Analysis. Sensors. 2020; 20(11):3018. https://doi.org/10.3390/s20113018
Chicago/Turabian StyleVeselý, Jiří, Petr Hubáček, and Jana Olivová. 2020. "The Power Gain Difference Method Analysis" Sensors 20, no. 11: 3018. https://doi.org/10.3390/s20113018
APA StyleVeselý, J., Hubáček, P., & Olivová, J. (2020). The Power Gain Difference Method Analysis. Sensors, 20(11), 3018. https://doi.org/10.3390/s20113018




