Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator
Abstract
1. Introduction
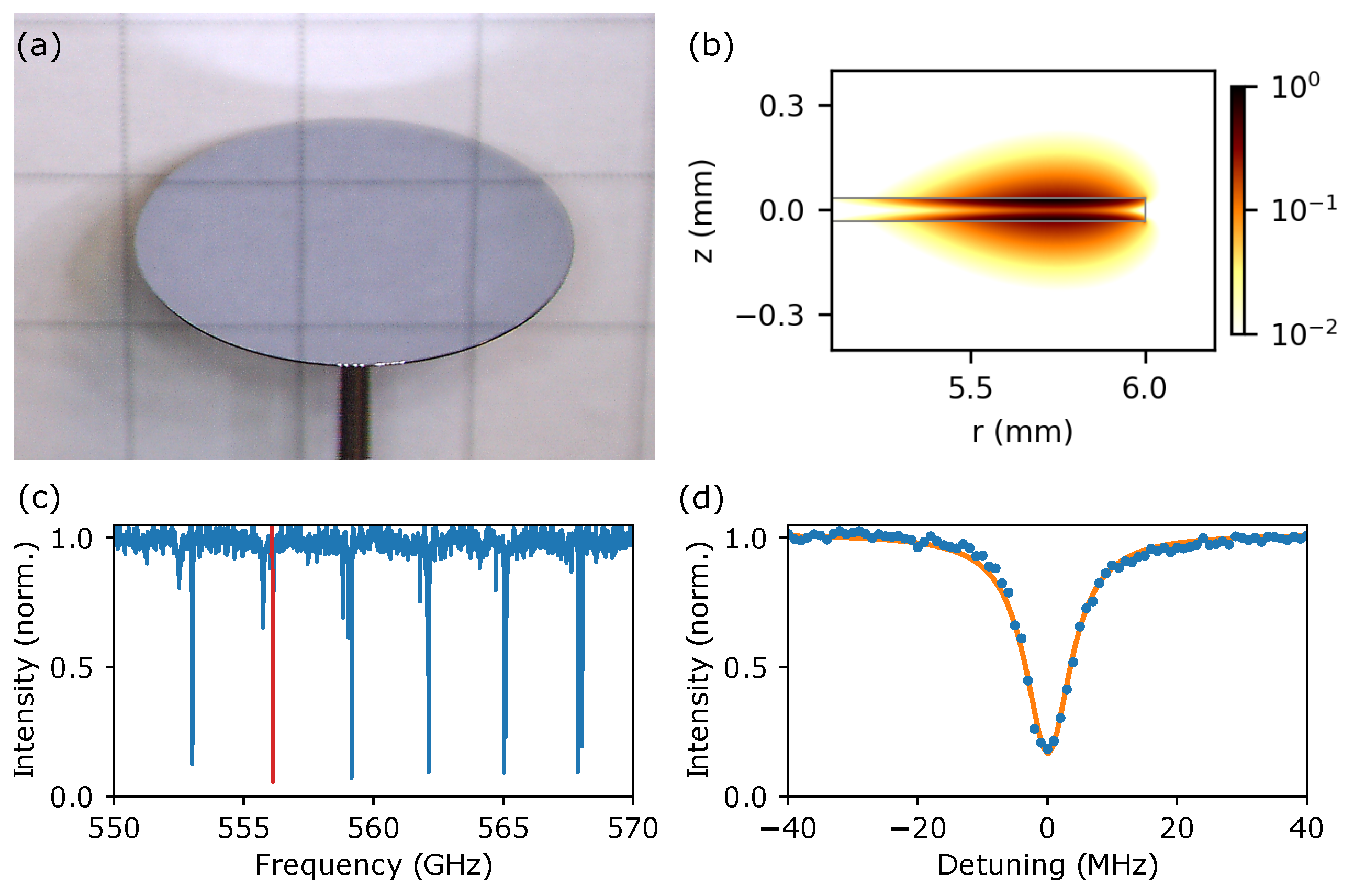
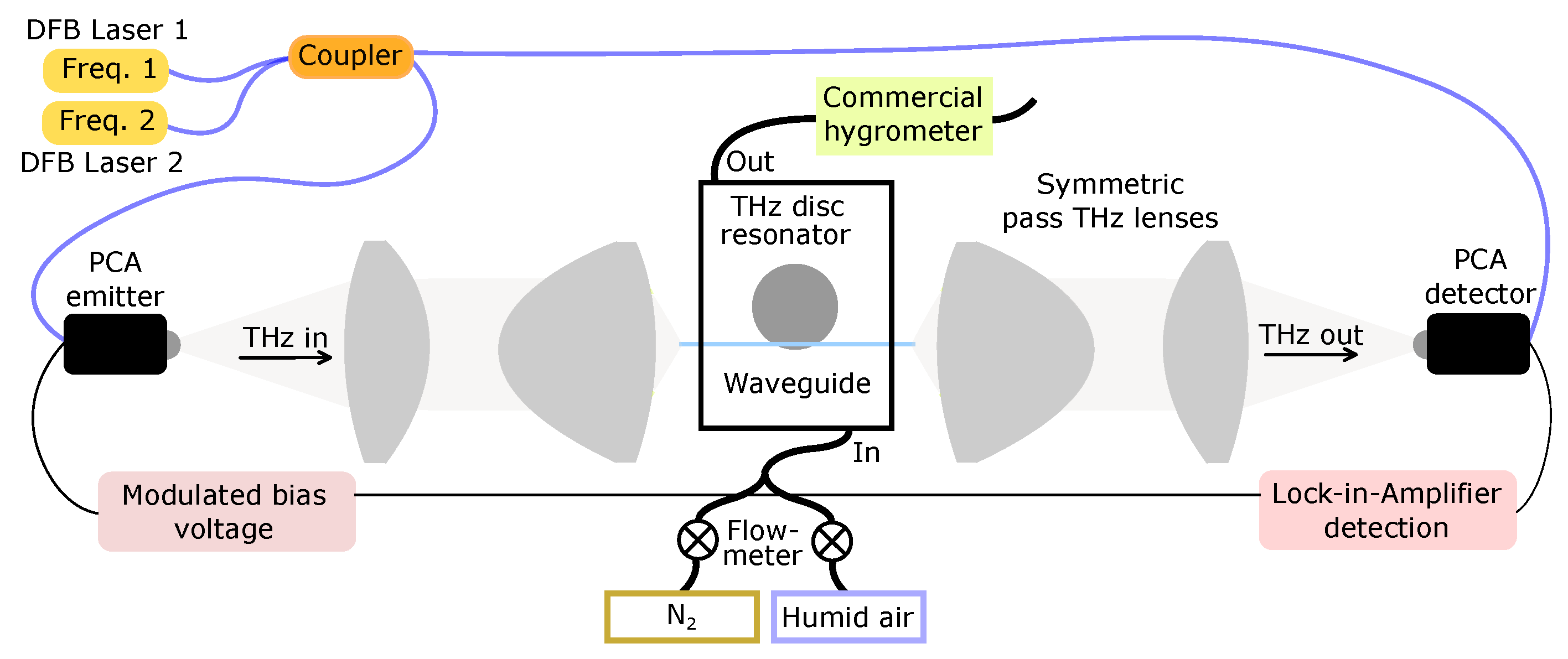
2. Materials and Methods
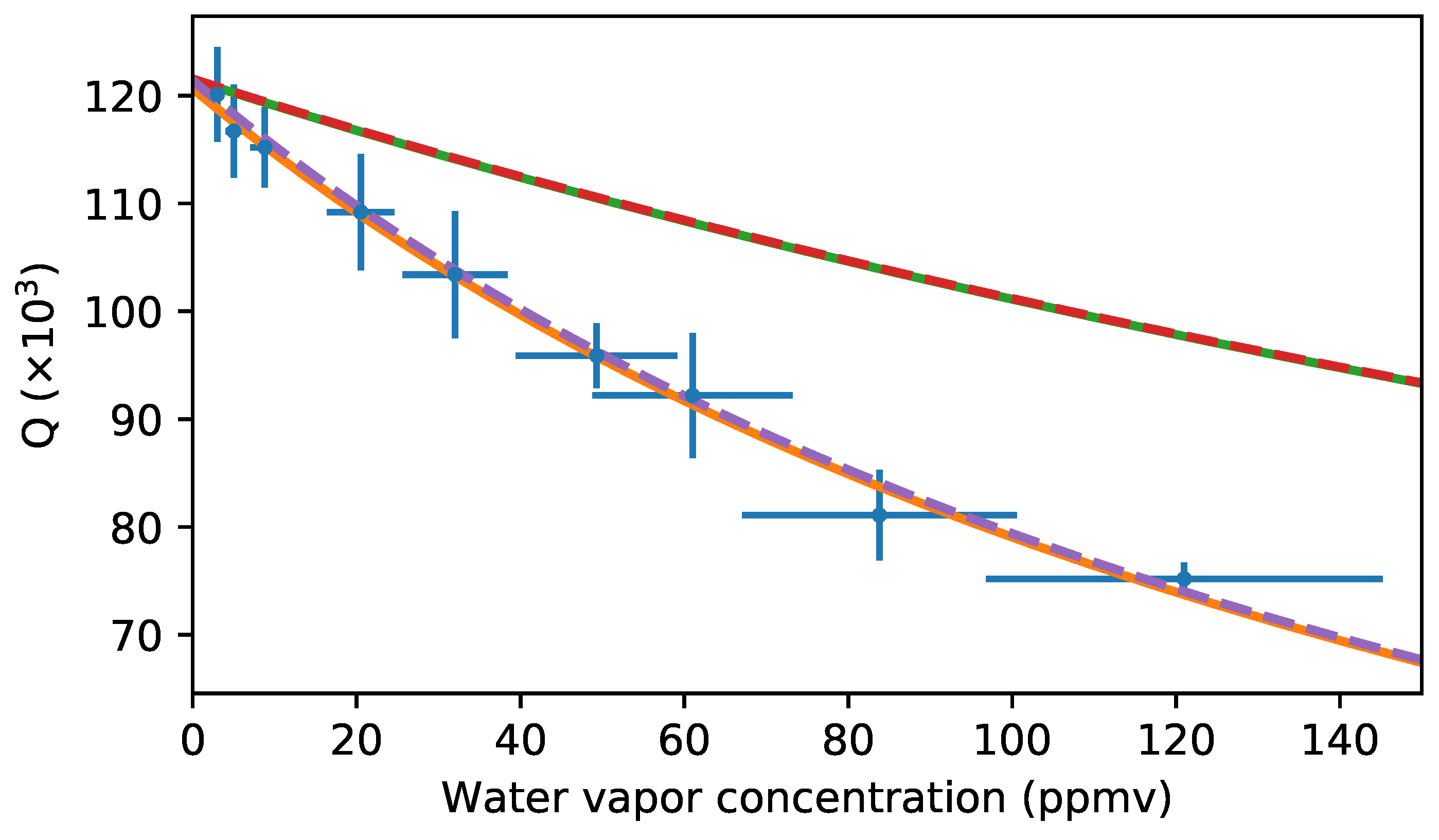
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory. Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef]
- Chan, W.L.; Deibel, J.; Mittleman, D.M. Imaging with terahertz radiation. Rep. Prog. Phys. 2007, 70, 1325. [Google Scholar] [CrossRef]
- Pickwell, E.; Cole, B.E.; Fitzgerald, A.; Pepper, M.; Wallace, V. In vivo study of human skin using pulsed terahertz radiation. Phys. Med. Biol. 2004, 49, 1595. [Google Scholar] [CrossRef]
- Fukunaga, K.; Ogawa, Y.; Hayashi, S.; Hosako, I. Terahertz spectroscopy for art conservation. IEICE Electron. Express 2007, 4, 258–263. [Google Scholar] [CrossRef]
- Kemp, M.C.; Taday, P.; Cole, B.E.; Cluff, J.; Fitzgerald, A.J.; Tribe, W.R. Security applications of terahertz technology. Proc. SPIE 2003, 5070. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Smith, R.M.; Arnold, M.A. Selectivity of terahertz gas-phase spectroscopy. Anal. Chem. 2015, 87, 10679–10683. [Google Scholar] [CrossRef]
- Neumaier, P.; Schmalz, K.; Borngräber, J.; Kissinger, D.; Hübers, H.W. Terahertz gas-sensors: Gas-phase spectroscopy and multivariate analysis for medical and security applications. In Proceedings of the 2015 IEEE SENSORS, Busan, Korea, 1–4 November 2015. [Google Scholar]
- Rothbart, N.; Holz, O.; Koczulla, R.; Schmalz, K.; Hübers, H.W. Analysis of human breath by millimeter-wave/terahertz spectroscopy. Sensors 2019, 19, 2719. [Google Scholar] [CrossRef]
- Hepp, C.; Lüttjohann, S.; Roggenbuck, A.; Deninger, A.; Nellen, S.; Göbel, T.; Jörger, M.; Harig, R. A cw-terahertz gas analysis system with ppm detection limits. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; pp. 1–2. [Google Scholar]
- Hindle, F.; Bocquet, R.; Pienkina, A.; Cuisset, A.; Mouret, G. Terahertz gas phase spectroscopy using a high-finesse Fabry–Pérot cavity. Optica 2019, 6, 1449–1454. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Spillane, S.; Kippenberg, T.; Vahala, K.; Goh, K.; Wilcut, E.; Kimble, H. Ultrahigh-Q toroidal microresonators for cavity quantum electrodynamics. Phys. Rev. A 2005, 71, 013817. [Google Scholar] [CrossRef]
- Herr, T.; Hartinger, K.; Riemensberger, J.; Wang, C.; Gavartin, E.; Holzwarth, R.; Gorodetsky, M.; Kippenberg, T. Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nat. Photonics 2012, 6, 480–487. [Google Scholar] [CrossRef]
- Del’Haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T.J. Optical frequency comb generation from a monolithic microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Armani, D.; Kippenberg, T.; Spillane, S.; Vahala, K. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef]
- Xiao, S.; Khan, M.H.; Shen, H.; Qi, M. Multiple-channel silicon micro-resonator based filters for WDM applications. Opt. Express 2007, 15, 7489–7498. [Google Scholar] [CrossRef]
- Shitikov, A.; Bilenko, I.; Kondratiev, N.; Lobanov, V.; Markosyan, A.; Gorodetsky, M. Billion Q-factor in silicon WGM resonators. Optica 2018, 5, 1525–1528. [Google Scholar] [CrossRef]
- Mathai, C.; Jain, R.; Achanta, V.; Duttagupta, S.; Ghindani, D.; Joshi, N.; Pinto, R.; Prabhu, S. Sensing at terahertz frequency domain using a sapphire whispering gallery mode resonator. Opt. Lett. 2018, 43, 5383–5386. [Google Scholar] [CrossRef] [PubMed]
- Vogt, D.W.; Leonhardt, R. Terahertz whispering gallery mode bubble resonator. Optica 2017, 4, 809–812. [Google Scholar] [CrossRef][Green Version]
- Vogt, D.W.; Jones, A.H.; Schwefel, H.G.; Leonhardt, R. Prism coupling of high-Q terahertz whispering-gallery-modes over two octaves from 0.2 THz to 1.1 THz. Opt. Express 2018, 26, 31190–31198. [Google Scholar] [CrossRef] [PubMed]
- Preu, S.; Schwefel, H.; Malzer, S.; Döhler, G.; Wang, L.; Hanson, M.; Zimmerman, J.; Gossard, A. Coupled whispering gallery mode resonators in the Terahertz frequency range. Opt. Express 2008, 16, 7336–7343. [Google Scholar] [CrossRef]
- Vogt, D.W.; Leonhardt, R. Fano resonances in a high-Q terahertz whispering-gallery mode resonator coupled to a multi-mode waveguide. Opt. Lett. 2017, 42, 4359–4362. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, X.; Zang, X.; Cheng, Q.; Chen, L.; Zhu, Y. Terahertz integrated device: High-Q silicon dielectric resonators. Opt. Mater. Express 2018, 8, 50–58. [Google Scholar] [CrossRef]
- Vogt, D.W.; Leonhardt, R. Ultra-high Q terahertz whispering-gallery modes in a silicon resonator. APL Photonics 2018, 3, 051702. [Google Scholar] [CrossRef]
- Vogt, D.W.; Jones, A.H.; Schwefel, H.G.; Leonhardt, R. Anomalous blue-shift of terahertz whispering-gallery modes via dielectric and metallic tuning. Opt. Lett. 2019, 44, 1319–1322. [Google Scholar] [CrossRef]
- Vogt, D.W.; Jones, A.H.; Leonhardt, R. Free-space coupling to symmetric high-Q terahertz whispering-gallery mode resonators. Opt. Lett. 2019, 44, 2220–2223. [Google Scholar] [CrossRef]
- COMSOL, A.B.; Stockholm, S. COMSOL Multiphysics® Software. Available online: www.comsol.com (accessed on 25 May 2020).
- Gorodetsky, M.L.; Ilchenko, V.S. Optical microsphere resonators: Optimal coupling to high-Q whispering-gallery modes. JOSA B 1999, 16, 147–154. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Vogt, D.W.; Jones, A.H.; Haase, T.A.; Leonhardt, R. Sub-wavelength thick ultrahigh-Q terahertz disc microresonators. Photonics Res. 2020, accepted. [Google Scholar] [CrossRef]
- Deninger, A.J.; Roggenbuck, A.; Schindler, S.; Preu, S. 2.75 THz tuning with a triple-DFB laser system at 1550 nm and InGaAs photomixers. J. Infrared Millim. Terahertz Waves 2015, 36, 269–277. [Google Scholar] [CrossRef]
- Vogt, D.W.; Erkintalo, M.; Leonhardt, R. Coherent Continuous Wave Terahertz Spectroscopy Using Hilbert Transform. J. Infrared Millim. Terahertz Waves 2019, 40, 524–534. [Google Scholar] [CrossRef]
- Vogt, D.W.; Leonhardt, R. High resolution terahertz spectroscopy of a whispering gallery mode bubble resonator using Hilbert analysis. Opt. Express 2017, 25, 16860–16866. [Google Scholar] [CrossRef] [PubMed]
- Lo, Y.H.; Leonhardt, R. Aspheric lenses for terahertz imaging. Opt. Express 2008, 16, 15991–15998. [Google Scholar] [CrossRef] [PubMed]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering gallery mode sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [PubMed]
- Vogt, D.W.; Jones, A.H.; Leonhardt, R. Thermal tuning of silicon terahertz whispering-gallery mode resonators. Appl. Phys. Lett. 2018, 113, 011101. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, G.; Yuan, S.; Chen, L.; Wu, X.; Zhang, X. Voltage-actuated thermally tunable on-chip terahertz filters based on a whispering gallery mode resonator. Opt. Lett. 2019, 44, 4670–4673. [Google Scholar] [CrossRef]
- Puppe, T.A.; Mayzlin, Y.; Robinson-Tait, J.; Wilk, R. Comb-locked Frequency-domain terahertz spectrometer. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; p. 1. [Google Scholar]
- Yang, Y.; Mandehgar, M.; Grischkowsky, D. Determination of the water vapor continuum absorption by THz-TDS and Molecular Response Theory. Opt. Express 2014, 22, 4388–4403. [Google Scholar] [CrossRef]
- Ro/nne, C.; Thrane, L.; Åstrand, P.O.; Wallqvist, A.; Mikkelsen, K.V.; Keiding, S.R. Investigation of the temperature dependence of dielectric relaxation in liquid water by THz reflection spectroscopy and molecular dynamics simulation. J. Chem. Phys. 1997, 107, 5319–5331. [Google Scholar] [CrossRef]
- Asay, D.B.; Kim, S.H. Evolution of the adsorbed water layer structure on silicon oxide at room temperature. J. Phys. Chem. B 2005, 109, 16760–16763. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Huang, L.; Guo, Z.; Rossmann, T. Spectral shift response of optical whispering-gallery modes due to water vapor adsorption and desorption. Meas. Sci. Technol. 2010, 21, 115206. [Google Scholar] [CrossRef]
- Vernooy, D.; Ilchenko, V.S.; Mabuchi, H.; Streed, E.; Kimble, H. High-Q measurements of fused-silica microspheres in the near infrared. Opt. Lett. 1998, 23, 247–249. [Google Scholar] [CrossRef]
- Su, J. Label-free biological and chemical sensing using whispering gallery mode optical resonators: Past, present, and future. Sensors 2017, 17, 540. [Google Scholar] [CrossRef]
- Mallik, A.K.; Farrell, G.; Liu, D.; Kavungal, V.; Wu, Q.; Semenova, Y. Silica gel coated spherical micro resonator for ultra-high sensitivity detection of ammonia gas concentration in air. Sci. Rep. 2018, 8, 1620. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogt, D.W.; Jones, A.H.; Leonhardt, R. Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator. Sensors 2020, 20, 3005. https://doi.org/10.3390/s20103005
Vogt DW, Jones AH, Leonhardt R. Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator. Sensors. 2020; 20(10):3005. https://doi.org/10.3390/s20103005
Chicago/Turabian StyleVogt, Dominik Walter, Angus Harvey Jones, and Rainer Leonhardt. 2020. "Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator" Sensors 20, no. 10: 3005. https://doi.org/10.3390/s20103005
APA StyleVogt, D. W., Jones, A. H., & Leonhardt, R. (2020). Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator. Sensors, 20(10), 3005. https://doi.org/10.3390/s20103005





