Comparison of Trotting Stance Detection Methods from an Inertial Measurement Unit Mounted on the Horse’s Limb
Abstract
1. Introduction
2. Materials and Methods
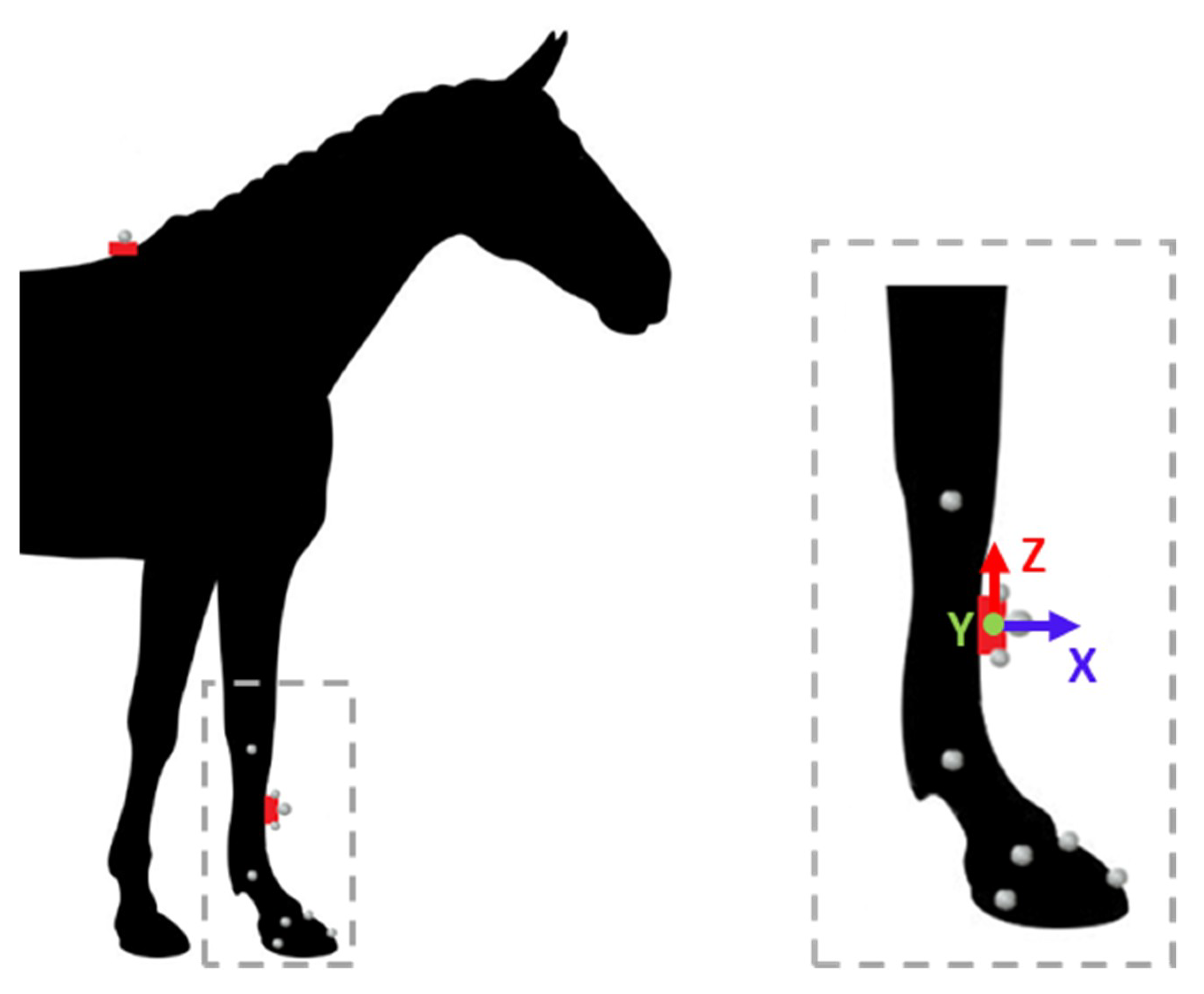
2.1. Animals
2.2. Data Acquisition
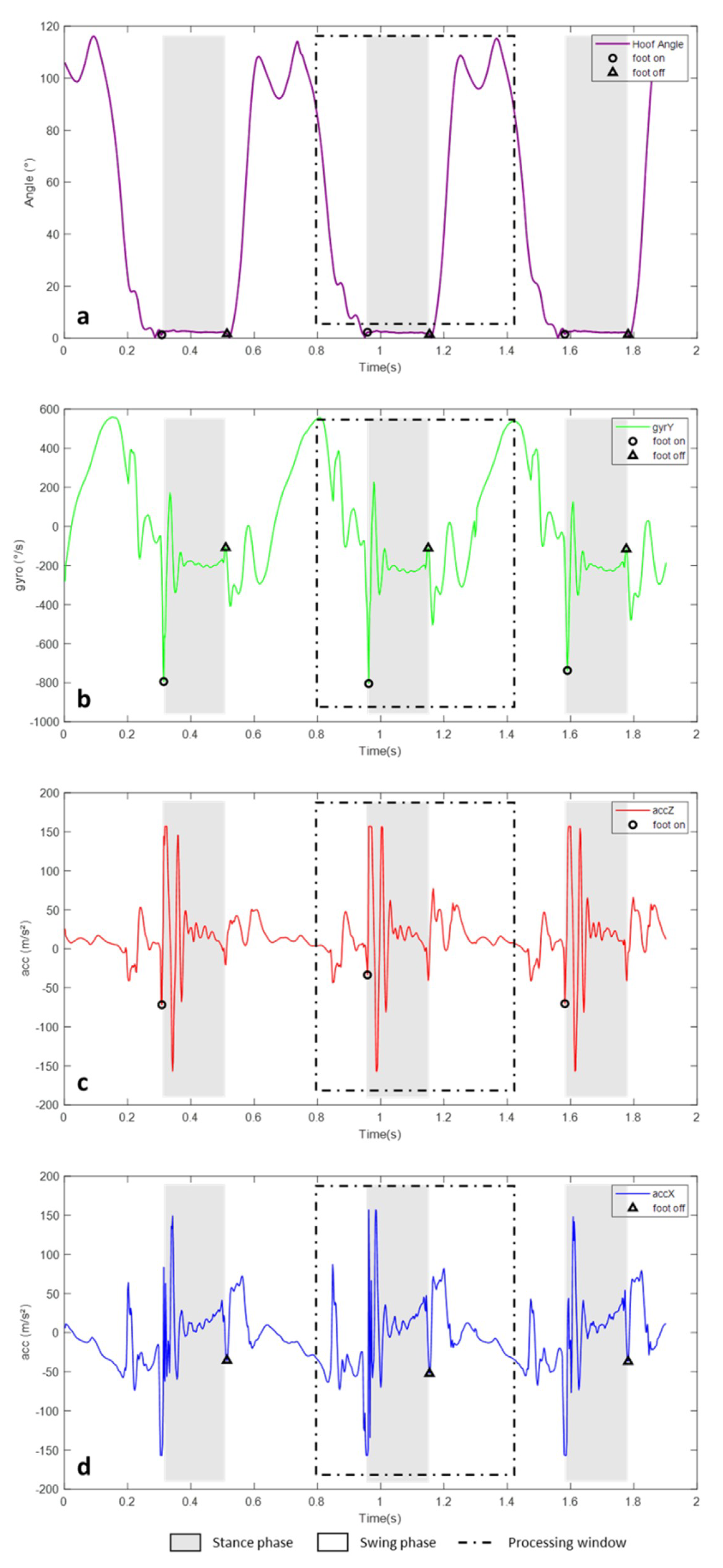
2.3. Data Processing
3. Results
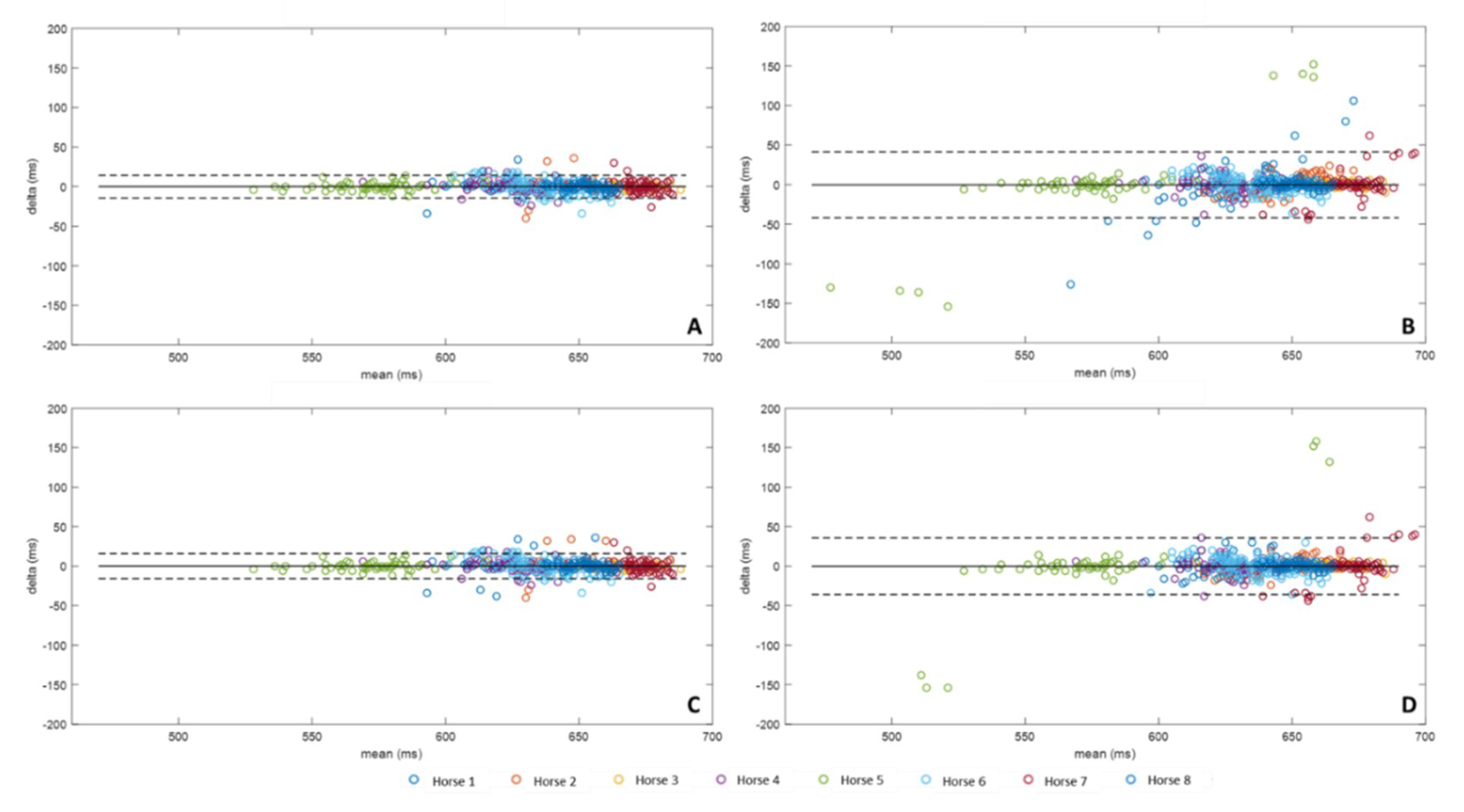
3.1. Foot on Detections
3.2. Foot Off Detections
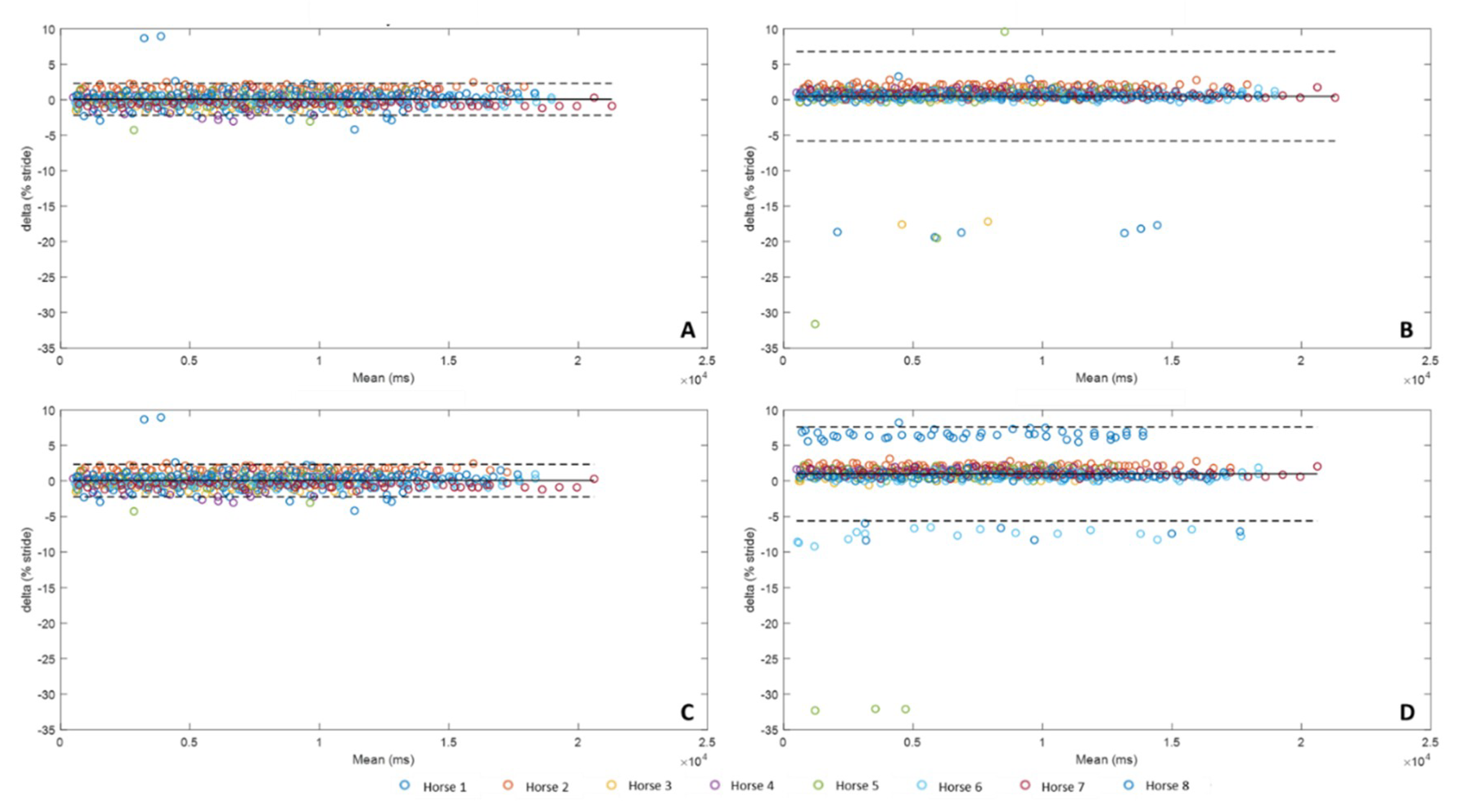
3.3. Stride Durations
3.4. Stance Durations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barrey, E. Methods, Applications and Limitations of Gait Analysis in Horses. Vet. J. 1999, 157, 7–22. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wilson, A.M.; Watson, J.C.; Lichtwark, G.A. Biomechanics: A catapult action for rapid limb protraction. Nature 2003, 421, 35–36. [Google Scholar] [CrossRef] [PubMed]
- Biewener, A.A.; Thomason, J.; Goodship, A.; Lanyon, L.E. Bone stress in the horse forelimb during locomotion at different gaits: A comparison of two experimental methods. J. Biomech. 1983, 16, 565–576. [Google Scholar] [CrossRef]
- Crevier-Denoix, N.; Falala, S.; Holden-Douilly, L.; Camus, M.; Martino, J.; Ravary-Plumioen, B.; Vergari, C.; Desquilbet, L.; Denoix, J.-M.; Chateau, H. Comparative kinematic analysis of the leading and trailing forelimbs of horses cantering on a turf and a synthetic surface: Forelimb kinematics at the canter on turf and synthetic surfaces. Equine Vet. J. 2013, 45, 54–61. [Google Scholar] [CrossRef]
- Murray, R.C.; Dyson, S.J.; Tranquille, C.; Adams, V. Association of type of sport and performance level with anatomical site of orthopaedic injury diagnosis. Equine Vet. J. 2006, 38, 411–416. [Google Scholar] [CrossRef] [PubMed]
- Meershoek, L.S.; Roepstorff, L.; Schamhardt, H.C.; Johnston, C.; Bobbert, M.F. Joint moments in the distal forelimbs of jumping horses during landing. Equine Vet. J. 2010, 33, 410–415. [Google Scholar] [CrossRef]
- Singer, E.R.; Barnes, J.; Saxby, F.; Murray, J.K. Injuries in the event horse: Training versus competition. Vet. J. 2008, 175, 76–81. [Google Scholar] [CrossRef]
- Buchner, H.H.F.; Savelberg, H.H.C.M.; Schamhardt, H.C.; Barneveld, A. Head and trunk movement adaptations in horses with experimentally induced fore-or hindlimb lameness. Equine Vet. J. 1996, 28, 71–76. [Google Scholar] [CrossRef]
- Kramer, J.; Keegan, K.G.; Wilson, D.A.; Smith, B.K.; Wilson, D.J. Kinematics of the hind limb in trotting horses after induced lameness of the distal intertarsal and tarsometatarsal joints and intra-articular administration of anesthetic. Am. J. Vet. Res. 2000, 61, 1031–1036. [Google Scholar] [CrossRef]
- Keegan, K.G.; Pai, P.F.; Wilson, D.A.; Smith, B.K. Signal decomposition method of evaluating head movement to measure induced forelimb lameness in horses trotting on a treadmill. Equine Vet. J. 2001, 33, 446–451. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Mun, K.R.; Jung, D.; Han, J.; Park, M.; Kim, J.; Kim, J. IMU-based Spectrogram Approach with Deep Convolutional Neural Networks for Gait Classification. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 4–6 January 2020; pp. 1–6. [Google Scholar]
- Sahoo, S.; Saboo, M.; Pratihar, D.K.; Mukhopadhyay, S. Real-Time Detection of Actual and Early Gait Events During Level-Ground and Ramp Walking. IEEE Sens. J. 2020. [Google Scholar] [CrossRef]
- Tumkur, K.; Subbiah, S. Modeling Human Walking for Step Detection and Stride Determination by 3-Axis Accelerometer Readings in Pedometer. In Proceedings of the 2012 Fourth International Conference on Computational Intelligence, Modelling and Simulation, Kuantan, Malaysia, 25–27 September 2012; pp. 199–204. [Google Scholar]
- Anwary, A.R.; Yu, H.; Vassallo, M. Optimal Foot Location for Placing Wearable IMU Sensors and Automatic Feature Extraction for Gait Analysis. IEEE Sens. J. 2018, 18, 2555–2567. [Google Scholar] [CrossRef]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.G.; Dehollain, C.; Blanc, Y.; Burkhard, P.R.; Aminian, K. Gait Assessment in Parkinson’s Disease: Toward an Ambulatory System for Long-Term Monitoring. IEEE Trans. Biomed. Eng. 2004, 51, 1434–1443. [Google Scholar] [CrossRef]
- Doheny, E.P.; Foran, T.G.; Greene, B.R. A single gyroscope method for spatial gait analysis. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1300–1303. [Google Scholar]
- Caramia, C.; De Marchis, C.; Schmid, M. Optimizing the Scale of a Wavelet-Based Method for the Detection of Gait Events from a Waist-Mounted Accelerometer under Different Walking Speeds. Sensors 2019, 19, 1869. [Google Scholar] [CrossRef] [PubMed]
- Sapone, M.; Martin, P.; Chateau, H.; Parmentier, J.; Ben Mansour, K.; Marin, F. Sizing of inertial sensors adapted to measurement of locomotor parameters in horses using motion capture. 44th Congress of the Société de Biomécanique, Poitiers, France, 2019 October. Comput. Methods Biomech. Biomed. Eng. 2019, 22, S1–S393. [Google Scholar]
- Drevemo, S.; Dalin, G.; Fredricson, I.; Hjerten, G. Equine locomotion: 1. The analysis of linear and temporal stride characteristics of trotting Standardbreds. Equine Vet. J. 1980, 12, 60–65. [Google Scholar] [CrossRef]
- Olsen, E.; Haubro Andersen, P.; Pfau, T. Accuracy and Precision of Equine Gait Event Detection during Walking with Limb and Trunk Mounted Inertial Sensors. Sensors 2012, 12, 8145–8156. [Google Scholar] [CrossRef]
- Hodson, E.; Clayton, H.M.; Lanovaz, J.L. The forelimb in walking horses: 1. Kinematics and ground reaction forces. Equine Vet. J. 2000, 32, 287–294. [Google Scholar] [CrossRef]
- Merkens, H.W.; Schamhardt, H.C. Relationships between ground reaction force patterns and kinematics in the walking and trotting horse. Equine Vet. J. 1994, 26, 67–70. [Google Scholar] [CrossRef]
- Witte, T.H. Determination of peak vertical ground reaction force from duty factor in the horse (Equus caballus). J. Exp. Biol. 2004, 207, 3639–3648. [Google Scholar] [CrossRef]
- Boye, J.K.; Thomsen, M.H.; Pfau, T.; Olsen, E. Accuracy and precision of gait events derived from motion capture in horses during walk and trot. J. Biomech. 2014, 47, 1220–1224. [Google Scholar] [CrossRef] [PubMed]
- Galisteo, A.M.; Garrido-Castro, J.L.; Miró, F.; Plaza, C.; Medina-Carnicer, R. Assessment of a method to determine the stride phases in trotting horses from video sequences under field conditions. Wien. Tierarztl. Mon. 2010, 97, 65–73. [Google Scholar]
- Starke, S.D.; Clayton, H.M. A universal approach to determine footfall timings from kinematics of a single foot marker in hoofed animals. PeerJ 2015, 3, e783. [Google Scholar] [CrossRef] [PubMed]
- Bosch, S.; Serra Bragança, F.; Marin-Perianu, M.; Marin-Perianu, R.; van der Zwaag, B.; Voskamp, J.; Back, W.; van Weeren, R.; Havinga, P. EquiMoves: A Wireless Networked Inertial Measurement System for Objective Examination of Horse Gait. Sensors 2018, 18, 850. [Google Scholar] [CrossRef] [PubMed]
- Pfau, T.; Starke, S.D.; Tröster, S.; Roepstorff, L. Estimation of vertical tuber coxae movement in the horse from a single inertial measurement unit. Vet. J. 2013, 198, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Moorman, V.J.; Reiser II, R.F.; McIlwraith, C.W.; Kawcak, C.E. Validation of an equine inertial measurement unit system in clinically normal horses during walking and trotting. Am. J. Vet. Res. 2012, 73, 1160–1170. [Google Scholar] [CrossRef]
- Cruz, A.M.; Maninchedda, U.E.; Burger, D.; Wanda, S.; Vidondo, B. Repeatability of gait pattern variables measured by use of extremity-mounted inertial measurement units in nonlame horses during trotting. Am. J. Vet. Res. 2017, 78, 1011–1018. [Google Scholar] [CrossRef]
- Bragança, F.M.; Bosch, S.; Voskamp, J.P.; Marin-Perianu, M.; Van der Zwaag, B.J.; Vernooij, J.C.M.; van Weeren, P.R.; Back, W. Validation of distal limb mounted inertial measurement unit sensors for stride detection in Warmblood horses at walk and trot. Equine Vet. J. 2017, 49, 545–551. [Google Scholar] [CrossRef]
- Robert, C.; Valette, J.P.; Denoix, J.M. The effects of treadmill inclination and speed on the activity of two hindlimb muscles in the trotting horse. Equine Vet. J. 2000, 32, 312–317. [Google Scholar] [CrossRef]
- Robert, C.; Valette, J.P.; Pourcelot, P.; Audigie, F.; Denoix, J.M. Effects of trotting speed on muscle activity and kinematics in saddlehorses. Equine Vet. J. 2002, 34, 295–301. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Jobert, M.; Tismer, C.; Poiseau, E.; Schulz, H. Wavelets—A new tool in sleep biosignal analysis. J. Sleep Res. 1994, 3, 223–232. [Google Scholar] [CrossRef]
- Pang, Y.; Christenson, J.; Jiang, F.; Lei, T.; Rhoades, R.; Kern, D.; Thompson, J.A.; Liu, C. Automatic detection and quantification of hand movements toward development of an objective assessment of tremor and bradykinesia in Parkinson’s disease. J. Neurosci. Methods 2020, 333, 108576. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Agreement between Methods of Measurement with Multiple Observations Per Individual. J. Biopharm. Stat. 2007, 17, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Nez, A.; Fradet, L.; Laguillaumie, P.; Monnet, T.; Lacouture, P. Simple and efficient thermal calibration for MEMS gyroscopes. Med. Eng. Phys. 2018, 55, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Lepetit, K.; Ben Mansour, K.; Boudaoud, S.; Kinugawa-Bourron, K.; Marin, F. Evaluation of the kinetic energy of the torso by magneto-inertial measurement unit during the sit-to-stand movement. J. Biomech. 2018, 67, 172–176. [Google Scholar] [CrossRef] [PubMed]
- Verlinde, D.; Beckers, F.; Ramaekers, D.; Aubert, A.E. Wavelet decomposition analysis of heart rate variability in aerobic athletes. Auton. Neurosci. 2001, 90, 138–141. [Google Scholar] [CrossRef]
- Soangra, R.; Lockhart, T.E.; Van de Berge, N. An approach for identifying gait events using wavelet denoising technique and single wireless IMU. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2011, 55, 1990–1994. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, S.W.; Park, U. R Peak Detection Method Using Wavelet Transform and Modified Shannon Energy Envelope. J. Healthc. Eng. 2017, 2017, 4901017. [Google Scholar] [CrossRef]
- Benson, L.; Clermont, C.; Watari, R.; Exley, T.; Ferber, R. Automated Accelerometer-Based Gait Event Detection during Multiple Running Conditions. Sensors 2019, 19, 1483. [Google Scholar] [CrossRef]
- Boutaayamou, M.; Schwartz, C.; Stamatakis, J.; Denoël, V.; Maquet, D.; Forthomme, B.; Croisier, J.L.; Macq, B.; Verly, J.G.; Garraux, G.; et al. Development and validation of an accelerometer-based method for quantifying gait events. Med. Eng. Phys. 2015, 37, 226–232. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, C.M.; Thorpe, S.K.; O’Malley, M.J.; Vaughan, C.L. Automatic detection of gait events using kinematic data. Gait Posture 2007, 25, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Hernlund, E.; Egenvall, A.; Peterson, M.L.; Mahaffey, C.A.; Roepstorff, L. Hoof accelerations at hoof-surface impact for stride types and functional limb types relevant to show jumping horses. Vet. J. 2013, 198, e27–e32. [Google Scholar] [CrossRef] [PubMed]
- Boyer, K.A.; Nigg, B.M. Soft tissue vibrations within one soft tissue compartment. J. Biomech. 2006, 39, 645–651. [Google Scholar] [CrossRef] [PubMed]
- Pacini Panebianco, G.; Bisi, M.C.; Stagni, R.; Fantozzi, S. Analysis of the performance of 17 algorithms from a systematic review: Influence of sensor position, analysed variable and computational approach in gait timing estimation from IMU measurements. Gait Posture 2018, 66, 76–82. [Google Scholar] [CrossRef]
- Back, W.; Schamhardt, H.C.; Savelberg, H.H.C.M.; Bogert, A.J.; Bruin, G.; Hartman, W.; Barneveld, A. How the horse moves: 1. Significance of graphical representations of equine forelimb kinematics. Equine Vet. J. 1995, 27, 31–38. [Google Scholar] [CrossRef]
- Clayton, H.M. The effect of an acute hoof wall angulation on the stride kinematics of trotting horses. Equine Vet. J. 1990, 22, 86–90. [Google Scholar] [CrossRef]
- Cano, M.R.; Vivo, J.; MirÓ, F.; Morales, J.L.; Galisteo, A.M. Kinematic characteristics of Andalusian, Arabian and Anglo-Arabian horses: A comparative study. Res. Vet. Sci. 2001, 71, 147–153. [Google Scholar] [CrossRef]
- Chateau, H.; Degueurce, C.; Denoix, J.-M. Three-dimensional kinematics of the distal forelimb in horses trotting on a treadmill and effects of elevation of heel and toe. Equine Vet. J. 2010, 38, 164–169. [Google Scholar] [CrossRef]
- Buchner, H.H.F.; Savelberg, H.H.C.M.; Schamhardt, H.C.; Merkens, H.W.; Barneveld, A. Kinematics of treadmill versus overground locomotion in horses. Vet. Q. 1994, 16, 87–90. [Google Scholar] [CrossRef]
- Rezvanian, S.; Lockhart, T. Towards Real-Time Detection of Freezing of Gait Using Wavelet Transform on Wireless Accelerometer Data. Sensors 2016, 16, 475. [Google Scholar] [CrossRef] [PubMed]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapone, M.; Martin, P.; Ben Mansour, K.; Château, H.; Marin, F. Comparison of Trotting Stance Detection Methods from an Inertial Measurement Unit Mounted on the Horse’s Limb. Sensors 2020, 20, 2983. https://doi.org/10.3390/s20102983
Sapone M, Martin P, Ben Mansour K, Château H, Marin F. Comparison of Trotting Stance Detection Methods from an Inertial Measurement Unit Mounted on the Horse’s Limb. Sensors. 2020; 20(10):2983. https://doi.org/10.3390/s20102983
Chicago/Turabian StyleSapone, Marie, Pauline Martin, Khalil Ben Mansour, Henry Château, and Frédéric Marin. 2020. "Comparison of Trotting Stance Detection Methods from an Inertial Measurement Unit Mounted on the Horse’s Limb" Sensors 20, no. 10: 2983. https://doi.org/10.3390/s20102983
APA StyleSapone, M., Martin, P., Ben Mansour, K., Château, H., & Marin, F. (2020). Comparison of Trotting Stance Detection Methods from an Inertial Measurement Unit Mounted on the Horse’s Limb. Sensors, 20(10), 2983. https://doi.org/10.3390/s20102983





