Phase Synchrony Analysis of Rolling Bearing Vibrations and Its Application to Failure Identification
Abstract
1. Introduction
2. Method and Principles of PSA
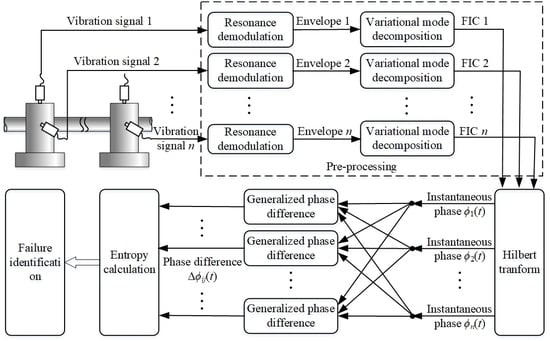
2.1. PSA Method for Analyzing Rolling Bearing Vibrations
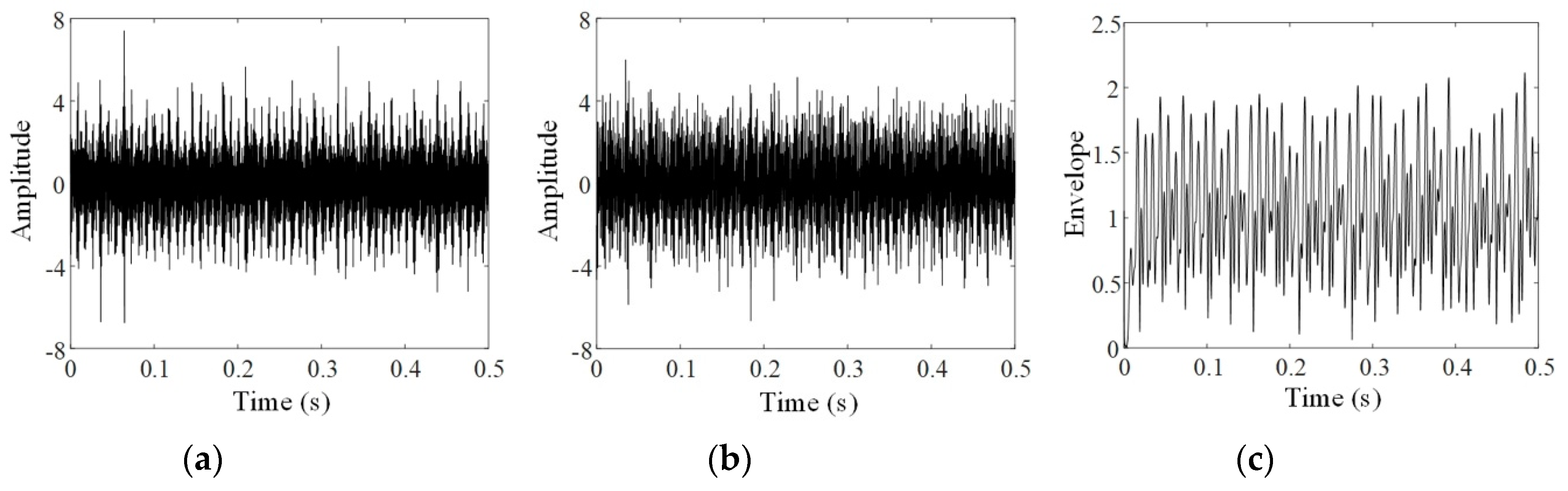
2.2. Resonance Demodulation
2.3. Variational Mode Decomposition
- (1)
- Initialize , , , and .
- (2)
- Update and according to Equations (4) and (5).
- (3)
- Perform a dual ascent operation for all as
- (4)
- Repeat steps 2 and 3 until the following convergence condition is satisfied.
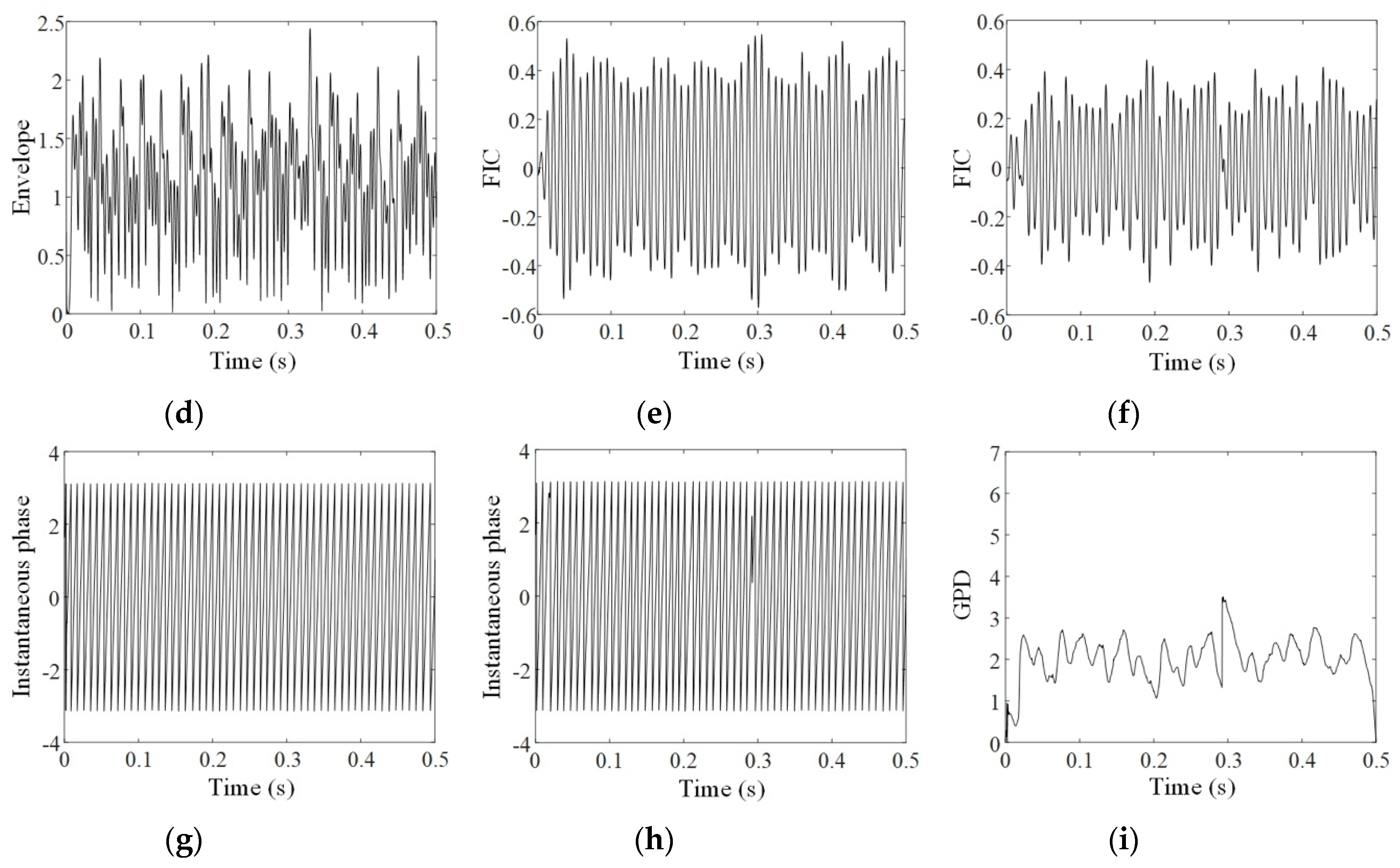
2.4. PSA
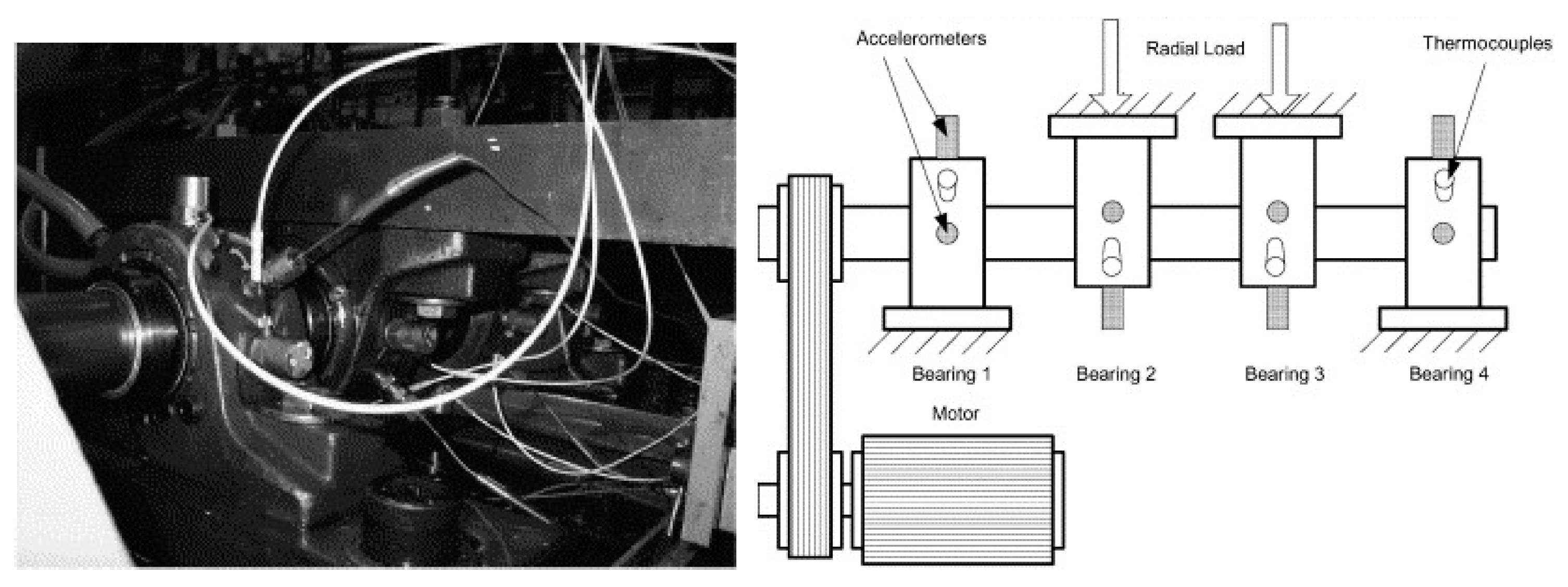
3. Application Case Studies
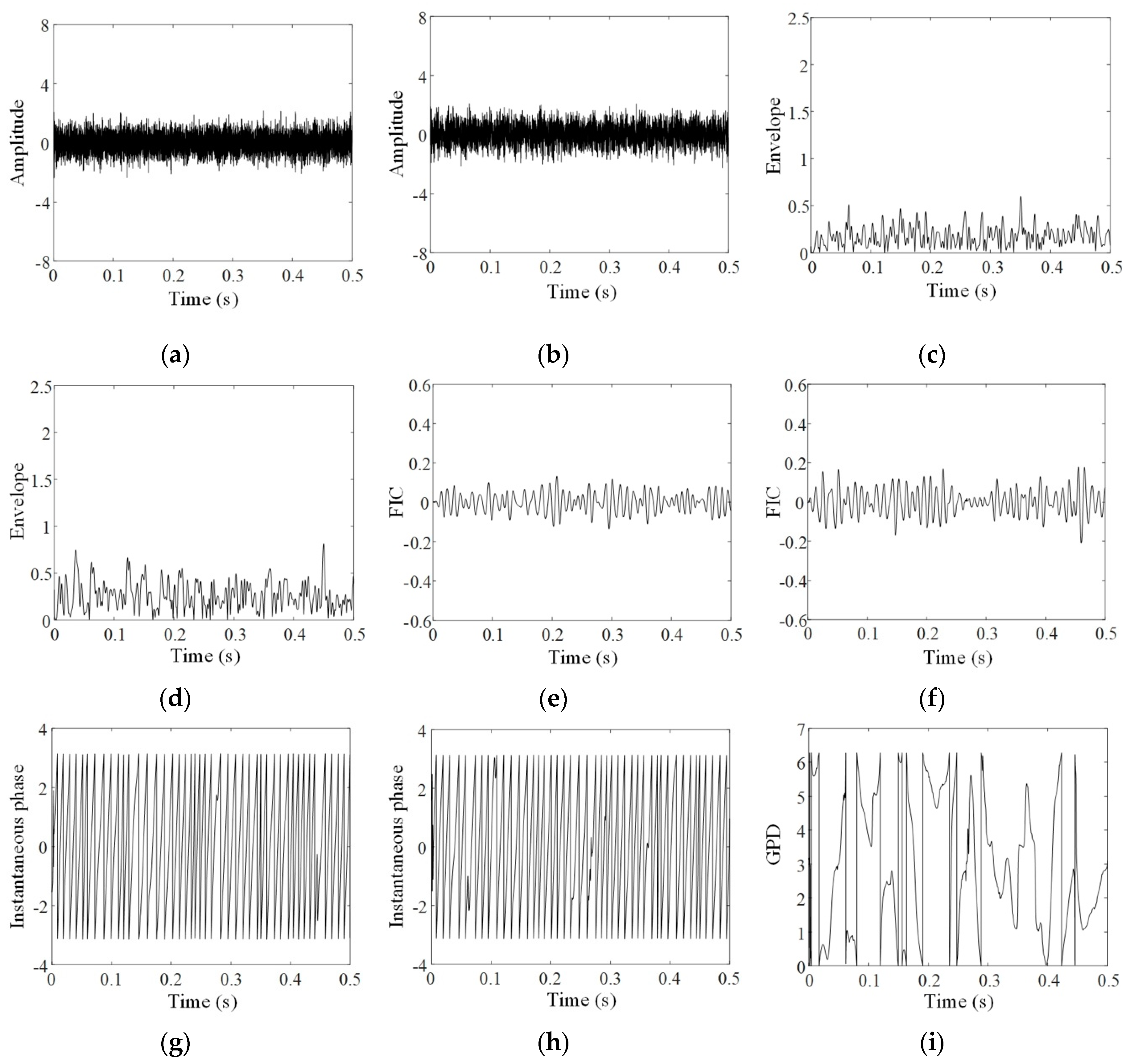
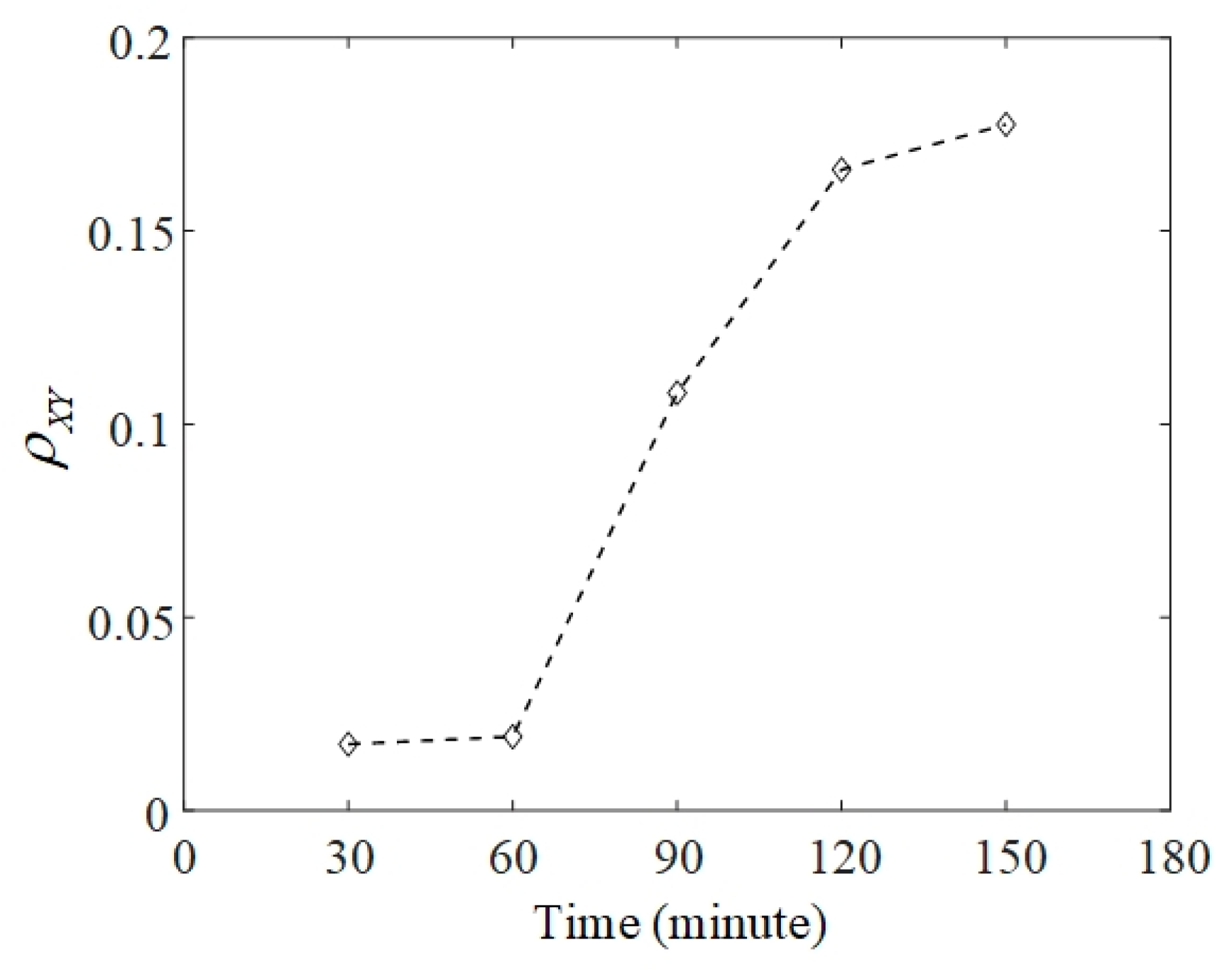
3.1. Application to Accelerated Bearing Failure
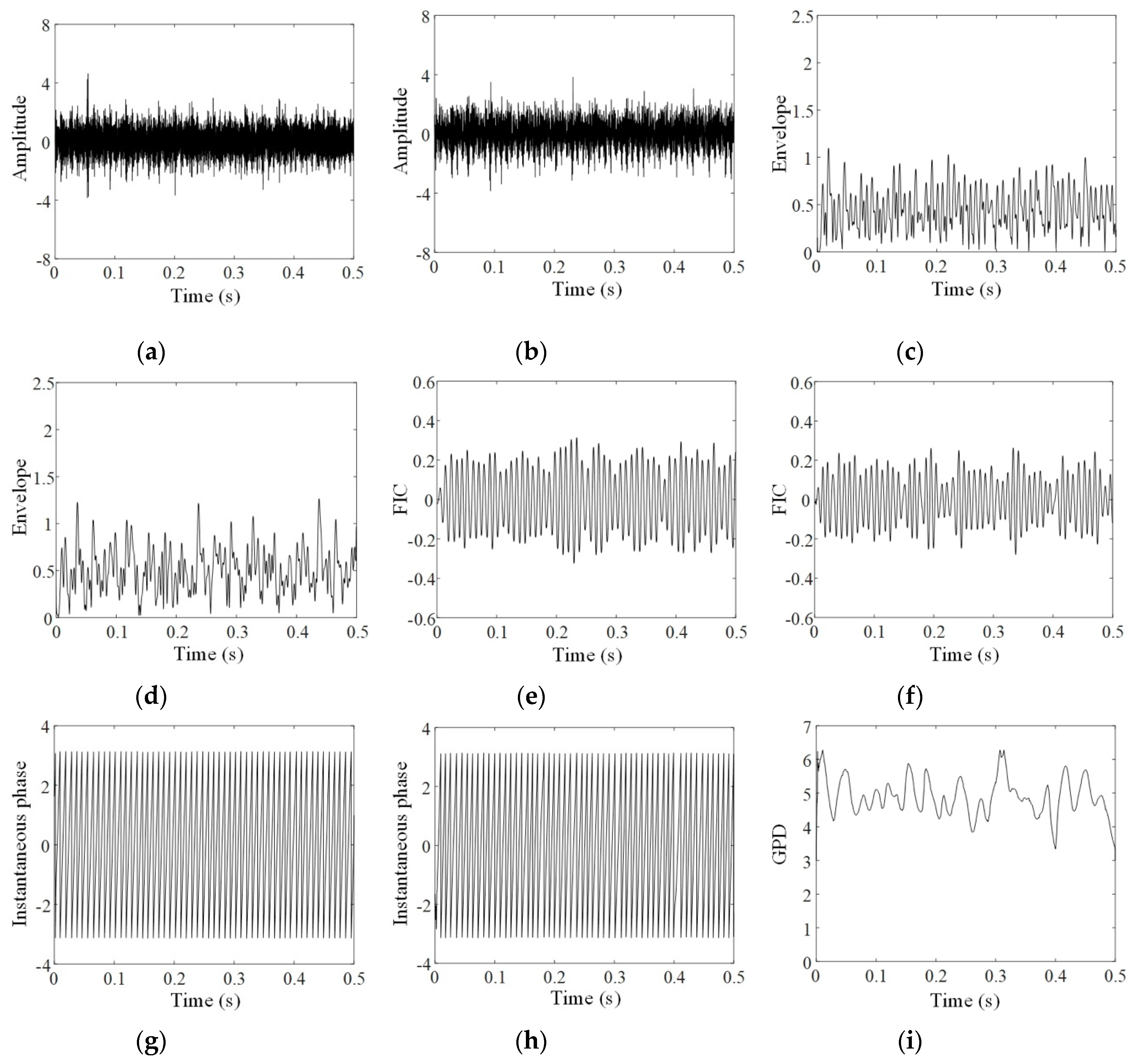
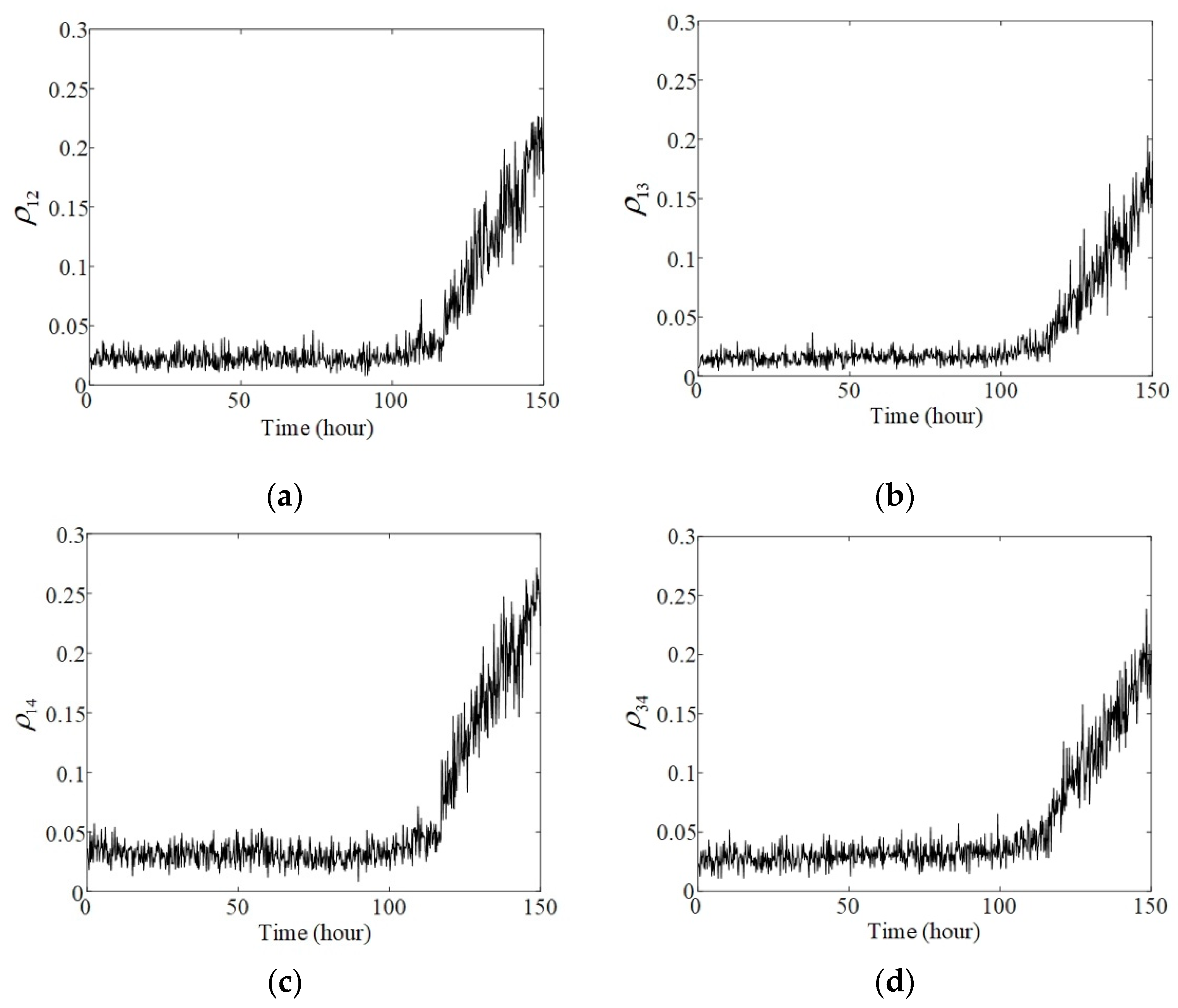
3.2. Application to Natural Failure of Bearing
4. Discussion and Conclusions
- (1)
- A mono-component FIC is extracted from vibration signals through a pre-processing step including resonance demodulation and VMD. The interference components mixed in multiplicative and additive forms are removed to obtain an optimal band-limited FIC, whose instantaneous phase can be solved using Hilbert transformation.
- (2)
- The indicator, which is the entropy of the GPD between FICs, is constructed to quantitatively evaluate phase synchronization of vibration signals. Despite the chaotic behavior of the signals, the phase synchronization indicator could identify bearing failure during the initial stage in a robust manner.
Author Contributions
Funding
Conflicts of Interest
References
- Gu, X.; Yang, S.; Liu, Y.; Hao, R.; Liu, Z. Multi-objective informative frequency band selection based on negentropy-induced grey wolf optimizer for fault diagnosis of rolling element bearings. Sensors 2020, 20, 1845. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, B.; Feng, F.; Jiang, P. Optimal resonant band demodulation based on an improved correlated kurtosis and its application in bearing fault diagnosis. Sensors 2017, 17, 360. [Google Scholar] [CrossRef] [PubMed]
- McFadden, P.D.; Smith, J.D. Vibration monitoring of rolling element bearing by the high-frequency resonance technique—A review. Tribol. Int. 1984, 17, 3–10. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced kurtogram for fault diagnosis of rolling element bearing. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Chen, X.; Feng, F.; Zhang, B. Weak fault feature extraction of rolling bearing based on an improved kurtogram. Sensors 2016, 16, 1482. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zhao, X.; Kou, L.L.; Qin, Y.; Zhao, Y.; Tsui, K.L. A simple and fast guideline for generating enhanced/squared envelope spectra from spectral coherence for bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 122, 754–768. [Google Scholar] [CrossRef]
- Harsha, S.P.; Sandeep, K.; Prakash, R. The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings. Int. J. Mech. Sci. 2003, 45, 725–740. [Google Scholar] [CrossRef]
- Ahmadi, A.M.; Petersen, D.; Howard, C. A nonlinear dynamic vibration model of defective bearings- the importance of modelling the finite size of rolling elements. Mech. Syst. Signal Process. 2015, 52–53, 309–326. [Google Scholar] [CrossRef]
- Zhao, X.; Patel, T.H.; Zuo, M.J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery. Mech. Syst. Signal Process. 2012, 27, 712–728. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and localization diagnosis of a defective ball bearing based on vertical-horizontal synchronization signal analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8706. [Google Scholar] [CrossRef]
- Pikovsky, A.S.; Rosenblum, M.G.; Osipov, G.V.; Kurths, J. Phase synchronization of chaotic oscillators by external driving. Physica D 1997, 104, 219–238. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Pereda, E.; Quiroga, R.Q.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005, 77, 1–37. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, M.; Omidvarnia, A.; Zalesky, A.; Jackson, G.D. On the relationship between instantaneous phase synchrony and correlation-based sliding windows for time-resolved fMRI connectivity analysis. NeuroImage. 2018, 181, 85–94. [Google Scholar] [CrossRef]
- Baboukani, P.S.; Azemi, G.; Boashash, B.; Colditz, P.; Omidvarnia, A. A novel multivariate phase synchrony measure: Application to multichannel newborn EEG analysis. Digit. Signal Process. 2019, 84, 59–68. [Google Scholar] [CrossRef]
- Farahmand, S.; Sobayo, T.; Mogui, D.J. Noise-assisted multivariate EMD-based mean-phase coherence analysis to evaluate phase-synchrony dynamics in epilepsy patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2270–2279. [Google Scholar] [CrossRef]
- Chavez, M.; Besserve, M.; Adam, C.; Martinerie, J. Towards a proper estimation of phase synchronization from time series. J. Neurosci. Methods. 2006, 154, 149–160. [Google Scholar] [CrossRef]
- Barszcz, T.; Jalonski, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Dragomireskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar]
- Tang, G.; Luo, G.; Zhang, W.; Yang, C.; Wang, H. Underdetermined blind source separation with variational mode decomposition for compound roller bearing fault signals. Sensors 2016, 16, 897. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Sun, C.; Jin, Q. Intelligent detection of a planetary gearbox composite fault based on adaptive separation and deep learning. Sensors 2019, 19, 5222. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Wang, G.; Dong, Y.; Zhang, Q.; Sang, L. Early chatter identification based on an optimized variational mode decomposition. Mech. Syst. Signal Process. 2019, 115, 238–254. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mech. Syst. Signal Process. 2019, 134, 106330. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Jiang, T.; Yan, J.D. Phase Synchrony Analysis of Rolling Bearing Vibrations and Its Application to Failure Identification. Sensors 2020, 20, 2964. https://doi.org/10.3390/s20102964
Zhang Q, Jiang T, Yan JD. Phase Synchrony Analysis of Rolling Bearing Vibrations and Its Application to Failure Identification. Sensors. 2020; 20(10):2964. https://doi.org/10.3390/s20102964
Chicago/Turabian StyleZhang, Qing, Tingting Jiang, and Joseph D. Yan. 2020. "Phase Synchrony Analysis of Rolling Bearing Vibrations and Its Application to Failure Identification" Sensors 20, no. 10: 2964. https://doi.org/10.3390/s20102964
APA StyleZhang, Q., Jiang, T., & Yan, J. D. (2020). Phase Synchrony Analysis of Rolling Bearing Vibrations and Its Application to Failure Identification. Sensors, 20(10), 2964. https://doi.org/10.3390/s20102964