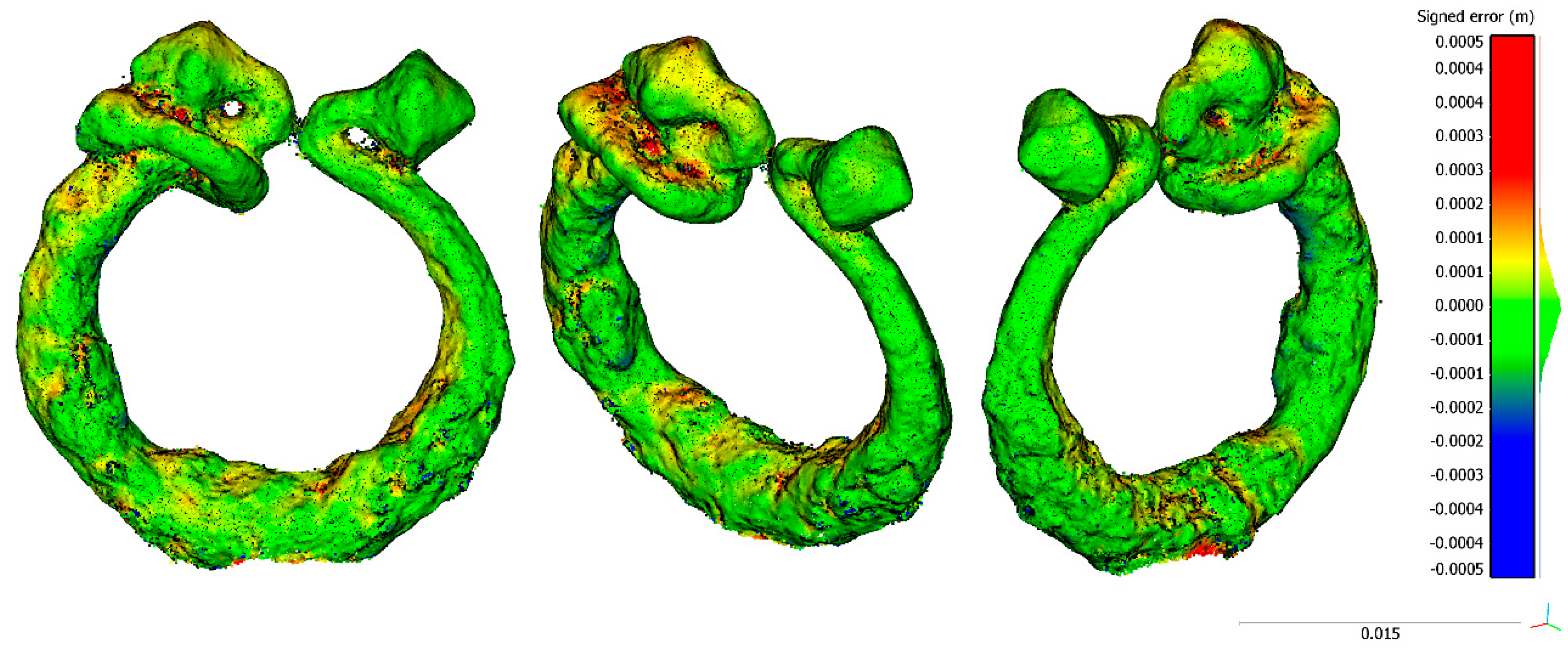1. Introduction
Geotechnologies encompass different sensors and computer algorithms for the acquisition, modeling, and/or analysis of spatial features [
1]. Moreover, different geotechnologies are available to document, model, and analyze small objects. Recent advances in geotechnologies has enabled the use of a wide range of sensors that record, catalog, and study cultural heritage sites [
2,
3,
4]. Some of these geotechnologies include laser scanning, structured light systems, and photogrammetry. In recent years, these techniques have demonstrated value to visual inspection [
5]. The generation of three-dimensional (3D) digital models of heritage assets such as monuments or excavations is an important task in areas such as heritage documentation [
6]; inspection, and restoration [
7]; project planning and management [
8]; virtual and augmented reality [
9]; and other areas of scientific research [
10].
Heritage is an important cultural, social, and economic resource that enriches societies who appreciates and know how to maintain a site’s authenticity, integrity, and/or the memory of its original state, as well as the probable evolution to its current state. A high accuracy 3D model of a heritage element is of great value for documenting, evaluating, analyzing, and monitoring the heritage. Its physical properties [
11,
12], and its virtualization. Moreover, a 3D model acts as a base to reestablish missing elements in a reconstruction of a heritage element’s current remains, which achieves a complete virtual 3D reconstruction of the element [
13]. Based on geometry modelling applications (e.g., Maya, 3D Studio Mark), we can generate virtual models similar to real ones. However, these applications require considerable learning [
10] and working time. Furthermore, while using these applications it is not possible to reconstruct a heritage artifact with total geometric and chromatic fidelity.
The documentation of heritage models as 3D models can be done with different techniques such as laser scanning with portable mobile mapping systems (PMMS), static laser systems [
6], structured light systems [
14], and photogrammetry [
15]. For small size objects, only three techniques can be used for an accurate three-dimensional reconstruction: laser scanning, structured light system (white, blue, or infrared (IR) light), and photogrammetry. This is true even for industrial tasks such as non-invasive quality control and documentation [
16,
17,
18].
Laser scanning is a technique based on the use of a controlled light source (active technique) to sweep the object’s surface and analyze the reflected energy [
17]. This type of system has a price between 80–100 times the cost of a basic photogrammetric equipment to achieve a submillimeter resolution [
19]. Structured light-based depth cameras project specific light patterns that extract the geometric information of the scene based on the structured-light triangulation principle [
20]. These systems are versatile and provide good results, but the reflections generate zones without information in the model, which can create problems in the 3D documentation process [
18]. In combination with Structure for Motion (SfM) techniques, photogrammetry has been developed in recent years and is an attractive alternative to laser scanning systems [
21,
22] and structured light systems. The input for this process is the collection of single images acquired using an off-the-shelf camera, which can be even equipped in platforms such as drones [
23]. In recent years, the image-based modelling strategy (SfM) has positioned itself as an attractive alternative to active scanning systems. On the one hand, it is flexible; it can be integrated into different types of platforms (e.g., drones [
24]) and employed to document a wide range of scenarios and objects [
25]. On the other hand, it is low-cost because the necessary hardware is a standard photographic camera and lens. It is also worth highlighting that the features of the generated dense point cloud (in terms of radiometric information provided, high spatial density, and precision) place SfM at a vantage position in the evaluation of heritage buildings and elements by integrating advantages of computer vision (automation and flexibility) and photogrammetry (accuracy and reliability) [
26] to obtain high density 3D models whose accuracy can compete with laser scanner systems [
27,
28].
The main weakness of this technique is the dependence of a specialized camera operator who can configure the camera parameters and obtain images in the right way (e.g., properly focused, without blurring, with proper exposition, low noise level, etc.). If the images are not acquired adequately, the subsequent 3D reconstruction will be affected by the presence of significant noise and/or reconstruction errors. Moreover, the positioning of the control points and their marking in the image are also critical steps to assure the accurate reconstruction with metric units. The latter is significant for the assembly of dismantled heritage elements and/or missing parts [
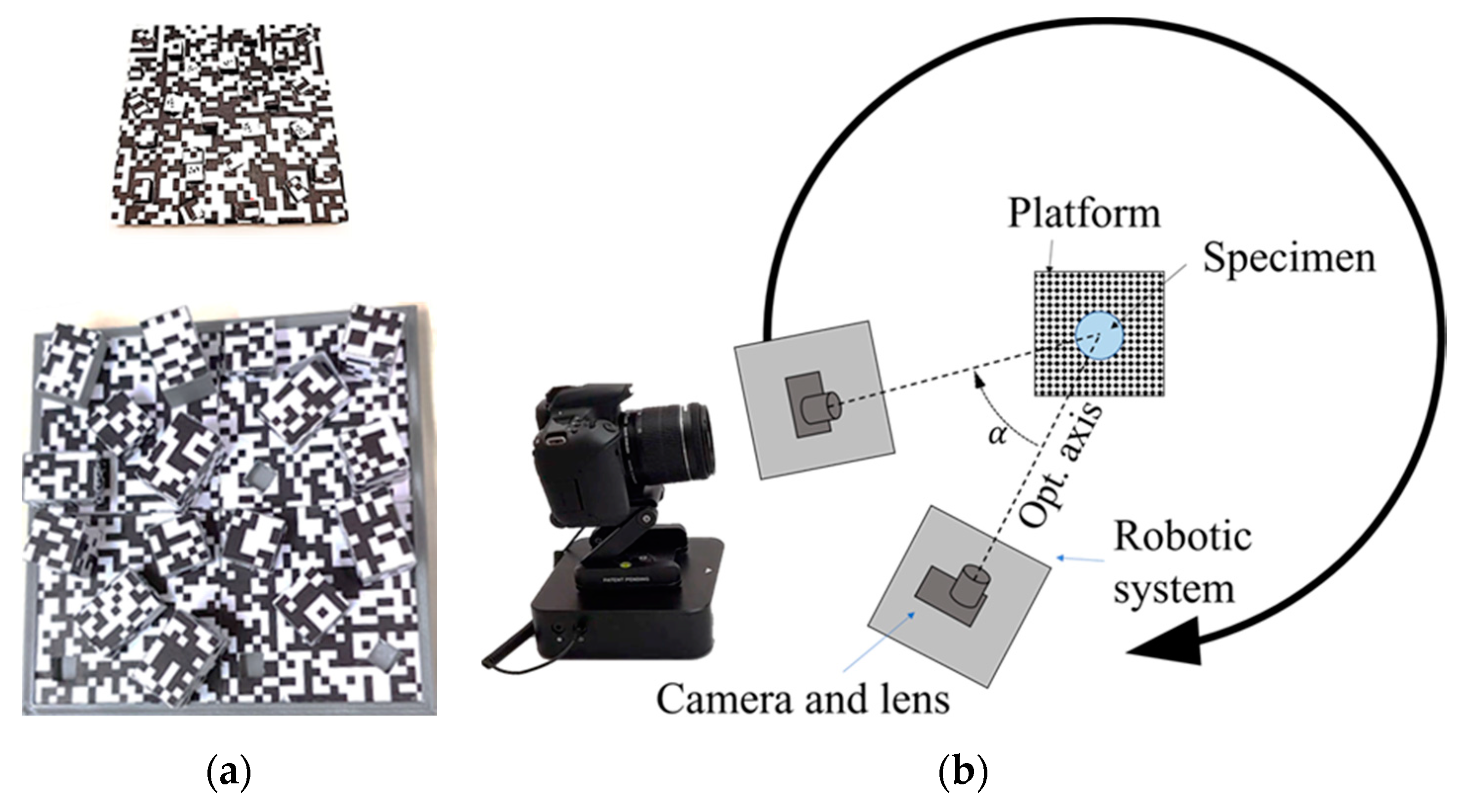
29]. To obtain the complete geometry of an object (360° image acquisition), it is necessary to take shots around it according to a specific path or, alternatively, keep the camera fixed and rotate the object at predefined angle steps [
30,
31]. Nevertheless, this last approach implies higher preprocessing times since the background has to be removed from the images so that it does not take part in the reconstruction process. However, the main challenges include optimizing the number of images to avoid excessive processing times, stabilizing the camera due to long exposure times in low-light conditions, considering the presence of hard reflections due to direct light sources, and, finally, establishing the camera-object distance as a constant. The latter is of special significance for very small objects and/or very high spatial resolutions due to the limited depth of field of macro lenses [
32,
33]. Including a reference element in the scene that remains static during the capture process can be a cumbersome task in some cases and can even hide details of the piece itself.
Different free packages are available for the generation of photogrammetric models such as GRAPHOS [
34], MICMAC [
35], Regard3D [
36], and ColMAP [
37]. Nevertheless, these applications could be difficult to use for researchers and professionals in the cultural heritage field, especially for those who are not experts in photogrammetry. A comparison of some open-access software such as Metashape [
38] takes into account applications for mesh generation, 3D sharing, and visualization tools. Metashape [
39] is one of the most used commercial photogrammetric and SfM packages. It has been used as ground through for comparatives with respect to other applications [
10,
38]. In this case, Metashape software is taken as reference for this experimentation due to its popularity among non-experts in photogrammetry, conservation, and cultural heritage documentation.
Finally, it should be noted that in the Mosul project, crowd-sourced photogrammetry was proposed as an opportunity to visualize and document lost heritage using images with unknown parameters taken without photogrammetric knowledge [
40,
41]. Such occurrences are an example of the scientific community’s interest in extending the photogrammetric process to non-expert users to preserve and document cultural heritage.
This article aims to provide an automatic workflow for image acquisition with a commercial digital single lens reflex (DSLR) camera. We apply a robust statistical comparison methodology to real small size archaeological pieces obtained with two different lenses and with different calibration processes (pre-calibration and self-calibration). Herein, this article advises non-experts in photogrammetry and heritage specialists working in data acquisition and small archaeological artifact modelling.
3. Results
Firstly, different empirical pre-tests were carried out in situ to obtain optimal camera parameters in relation to scene illumination and limited depth of field of the macro lens. The focal length of the zoom lens was fixed at 35 mm as a compromise between image definition and field of view, considering the space available inside the light. ISO sensibility was set at ISO-100 to reduce sensor noise as much as possible, which could have affected the photogrammetric process. The aperture was established at f/14 for all experiments to achieve an adequate depth of field (especially for the macro lens) without excessively affecting the exposition of the scene. The shutter speed was set to automatic, since the robotic device stopped at every position and avoided camera vibrations. The external reference frame was established by four reference points distributed on the base and on the edges of the platform whose coordinates were integrated in the photogrammetric process.
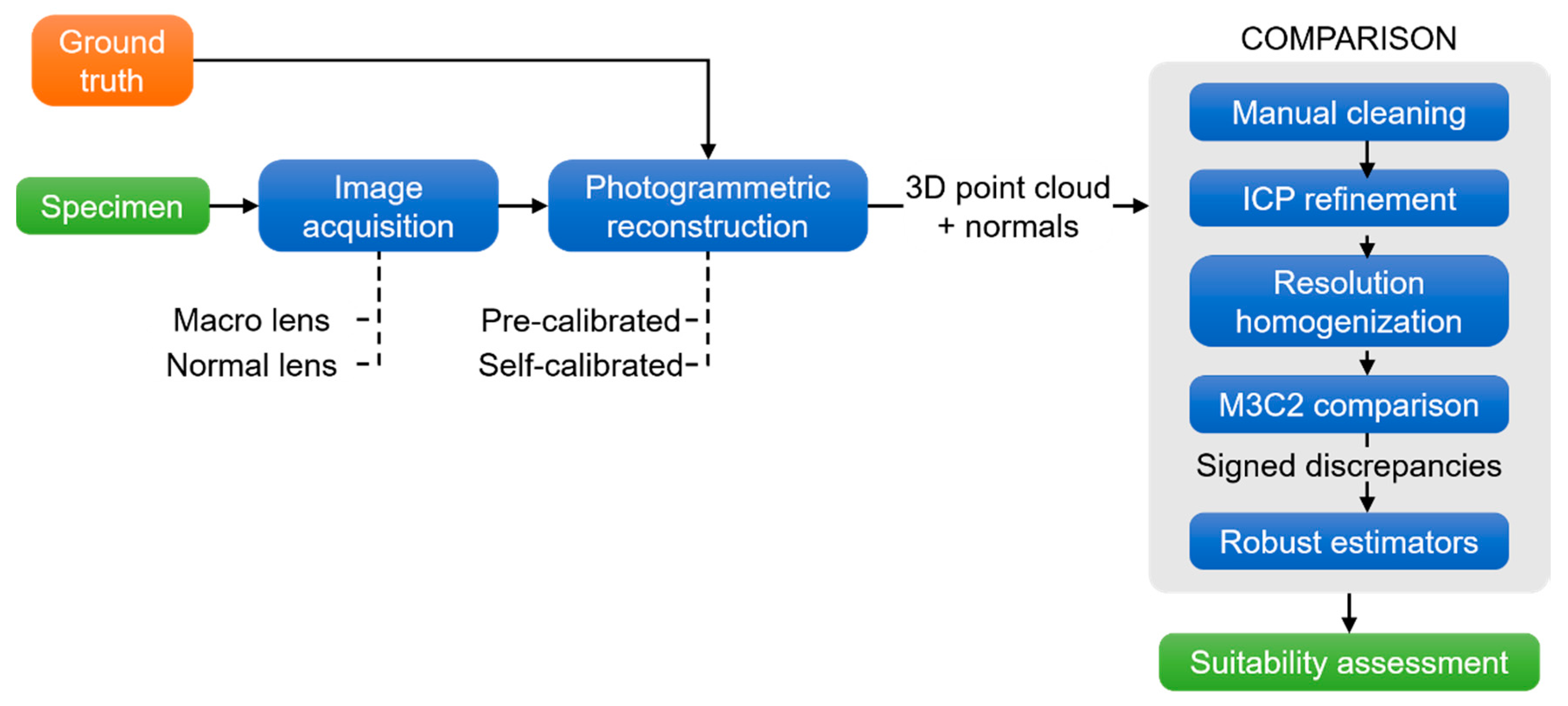
The photogrammetric reconstruction was performed following the steps described in
Section 2.2.1. In this way, four different point clouds were obtained for each specimen, one for each lens, and one for each camera calibration process (pre-calibrated vs. self-calibrated). An example of dense point clouds for each specimen (geometry and texture) is shown in
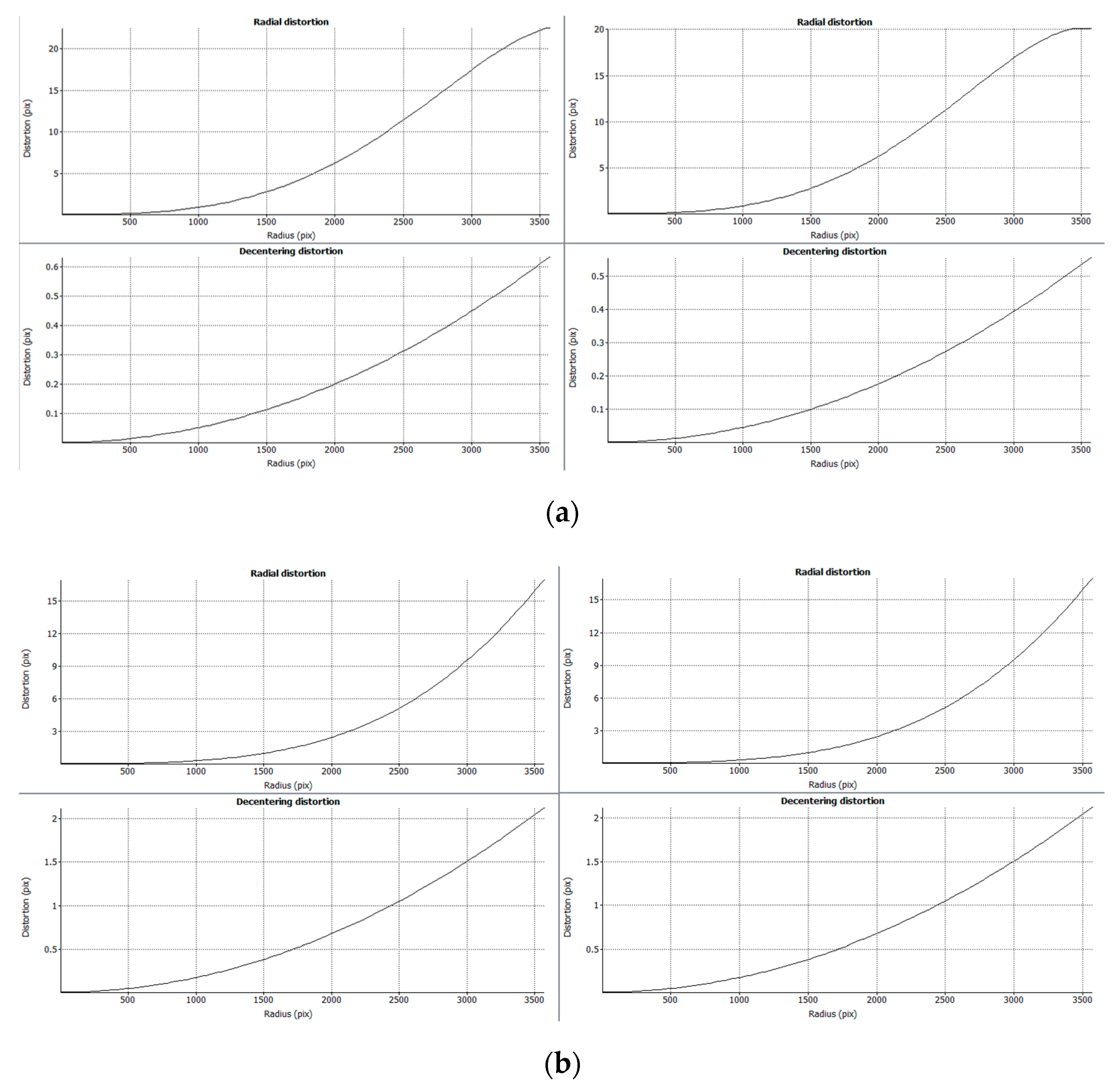
Figure 5. During the calibration process, a radial and decentered distortion curve were obtained (
Figure 6).
The distortion curves of the zoom lens (
Figure 6a) show differences in the last one-third of the diagonal, whereas for the macro lens (
Figure 6b) there are no significant differences. One of the aims of this research was to evaluate if these differences significantly impact the reconstruction process. The initial hypothesis was that, due to the higher field of view of the zoom lens, during the self-calibration the edges of the images would not contribute with key points for the camera orientation and internal parameter determination step. Yet, since reconstruction was carried out near to the center of the images, this difference was not relevant in terms of geometric discrepancies.
Additionally, in
Table 4 and
Table 5, the main summary of the reconstruction process is shown. In
Table 4, the results of the bundle adjustment solution for each case are presented, using four GCPs as reference points to scale the model and the rest of available GCPs as check points. The accuracy reported by the check points was increased due to the oblique point of view of the GCPs distributed in the base. Please note that since photogrammetric models’ alignment was refined based on ICP (as stated in
Section 2.2.2.) the error reported by the check points does not affect the subsequent analyses.
Table 5 lists the average point density achieved according to an ideal equilateral triangular distribution for a circular neighborhood [
51]. It is shown that the zooms lens, for the same photogrammetric reconstruction parameters, achieved a lower spatial resolution. According to the focal length reaction (35 mm vs. 60 mm), the GSD of the zoom lens was approximately 71% higher than the macro lens. It was expected that the macro lens would achieve a resolution 2.9 times higher than the zoom lens. However, in
Table 5, this relation is not achieved due to the different specimen shapes.
After carrying out the ICP refinement to dismiss any possible error due to movement of the archaeological sample in the base, a point density reduction was applied. Due to the high number of points of each sample (
Table 5), in order to speed up the computation process, a spatial subsampling at 0.1 mm was carried out using the function incorporated in CloudCompare [
43]. Additionally, a manual cleaning was applied to all point clouds to remove the points related to the base and reusable adhesive putty. The discrepancies were computed using the M3C2 algorithm [
48] and exported to the obtention of the statistical estimators.
The above steps are applied for the next subsections: comparison between pre-calibration and self-calibration (
Section 3.1) and comparison between the use of macro and zoom lenses (
Section 3.2).
3.1. Calibration Comparison
To establish a range of confidentiality during the comparison between both photogrammetric point clouds (pre-calibrated vs. self-calibrated), a statistical analysis was carried out (
Table 6 and
Table 7). The Gaussian estimation was provided by the mean and the standard deviation. Regarding the robust estimation, the central tendency of the error was estimated by the median and the error dispersion as the square root of the biweight midvariance (2) and NMAD, or normalized MAD (1).
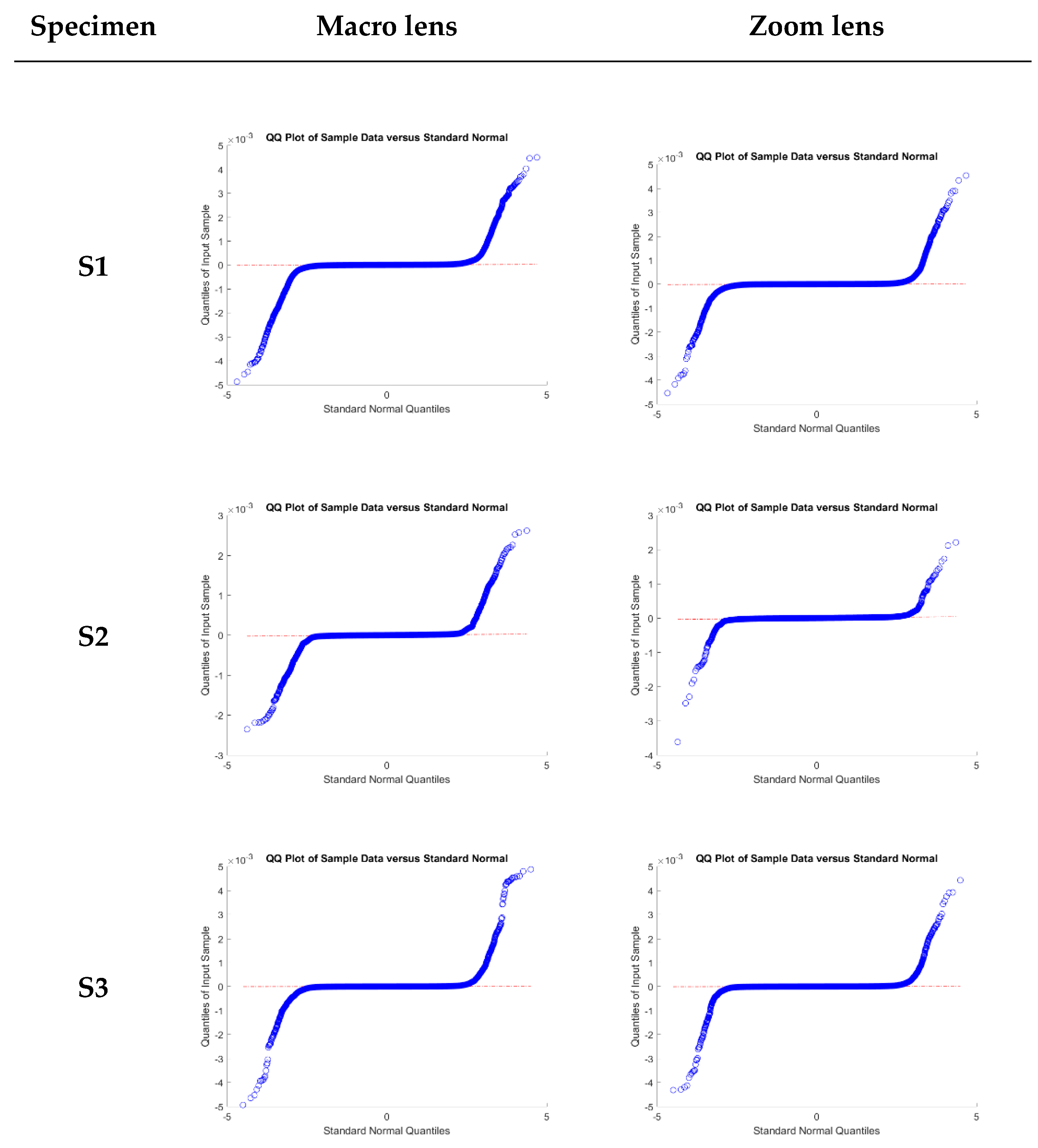
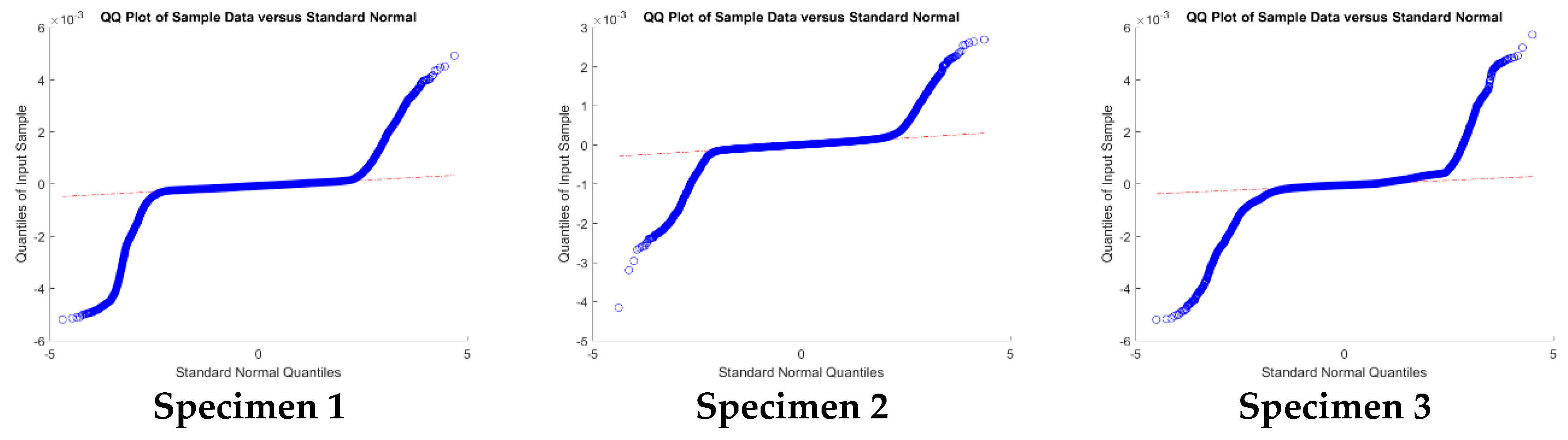
As a global conclusion, there were no significant differences for all the tested configurations, being that the discrepancies in all cases compatible with zero. Please note that the overestimation of error, both for the macro and zoom lens, for the classical Gaussian approach and the normality condition was not met in any of the six tested cases, as illustrated in
Figure 7, where the Q-Q plot to confirm the non-normality of the samples.
The absolute inter-percentile range at different confidence intervals (
Table 7) provides an additional insight into the reconstruction differences for both approaches (pre-calibrated/self-calibrated). It can be noted that at a 95% confidence level (difference of the percentile 2.5% and 97.5%) is compatible with zero (a value lower than the ACMM precision).
Finally, in
Table 7, the Gaussian confidence intervals overestimate the error range in all cases, stressing the importance of a normality assessment and the use of robust estimators for the geomatic products evaluated.
3.2. Lens Comparison
The comparison carried out in the previous subsection was repeated, but in this case for the pre-calibrated point clouds of the macro and zoom lenses. In
Table 8, the median values were expected to be close to zero after the application of the ICP registration algorithm. A slightly higher value was appreciated for specimens 1 and 3, which points out some registration error or reconstruction deformation. Despite their small value (lower than 0.1 mm), they could be of relevance in the high detail reconstructions of small archaeological objects.
In
Table 8, the robust dispersion values (NMAD and BWMV) are a good indicator of the precision degradation due to the use of a conventional zoom lens in relation to the macro lens best suited for small artifacts. In all cases, the dispersion value was almost ±0.1 mm, which matches the applied subsamples. As in
Section 3.1, the Gaussian error dispersion was overestimated due to the asymmetrical shape of the discrepancy distribution, highlighting the importance of an adequate statistical parameter election.
The obtained values were analyzed with a Q-Q plot to confirm the non-normality of the sample (
Figure 8). This fact was hinted by the percentile values and the skewness and kurtosis parameters (these two are not listed in the table). The samples do not follow a normal distribution (
Figure 8); it is not possible to infer the central tendency and dispersion of the population according to Gaussian statistics parameters like the mean and standard deviation. For that reason, the accuracy assessment was carried out based on robust alternatives, using non-parametric assumptions such as the median value and the square root of the biweight midvariance (2) (
Table 8).
Moreover, the robust estimators provide a clearer view of the error distribution, as for example the absolute inter-percentile range at different confidence intervals (
Table 9).
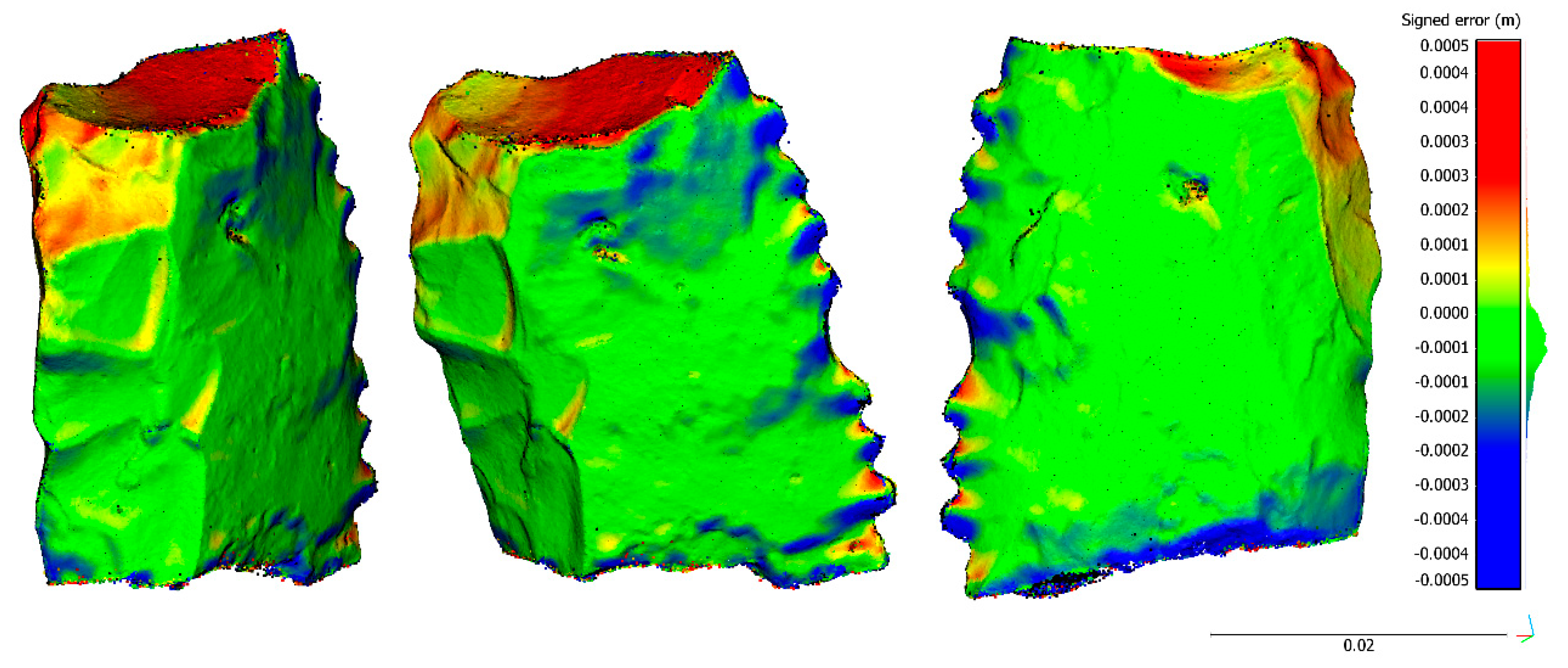
The difference of the percentile, 2.5% and 97.5%, (95% confidence level) is approximately 0.35 mm for the two cases, and 0.84 mm for the S3 case (racloir). The high error of the last specimen (S3-racloir) was caused by the top part of the sample (
Figure 9), which was a weak area due to the camera configuration. The acquisition of complementary nadiral images reduced the error. Additionally, the sharp edges of the specimen show a negative error pattern (blue colors) related to the difficulties of the automatic matching process in this area where the useful surface is very limited.
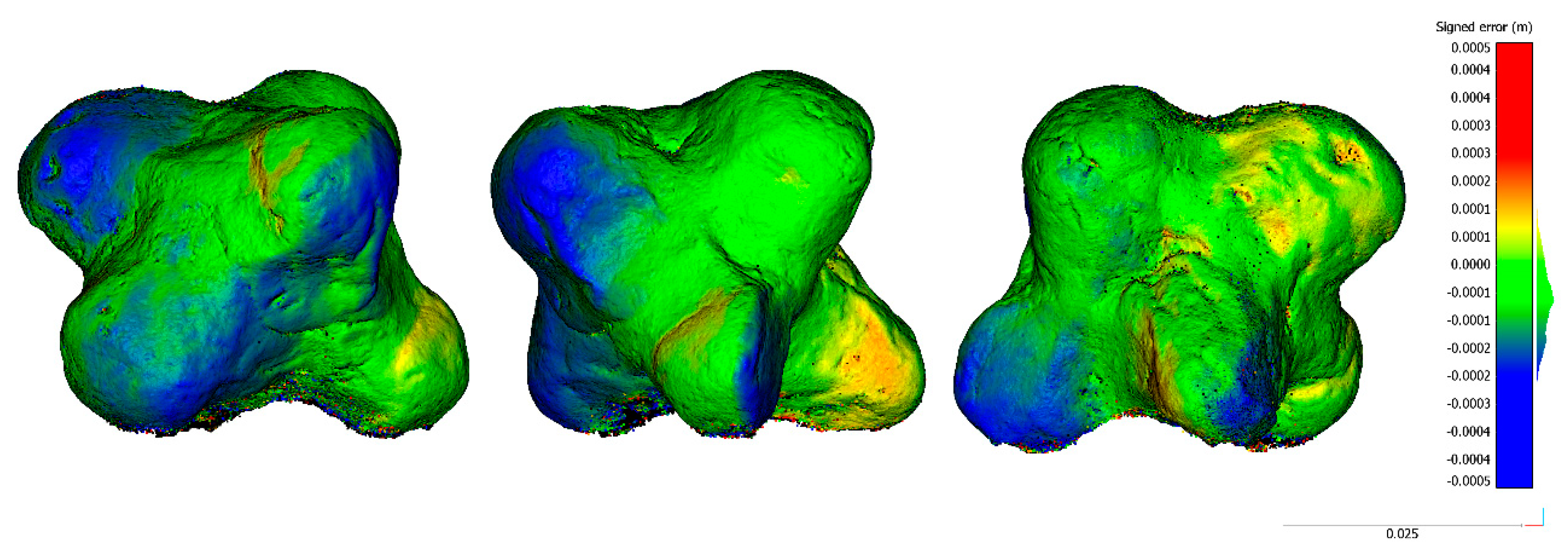
Regarding specimens 1 and 2, as shown in
Figure 10 and
Figure 11, there are no significant error distributions. For specimen 1, in one of the laterals of the ends, there is a systematic negative discrepancy that could be related to the central tendency’s bias stated in
Table 8. Regarding specimen 2, no bias was seen as expected by the median value compatible with zero (
Table 8). The only significative discrepancies were in the top part, which could be caused by the challenging point of view for data acquisition.
Finally, the error increase from IPR 95% to IPR 99% (
Table 9) was caused by the outliers of the manual cleaning of the rotating base and reusable adhesive putty. Therefore, the outliers should be taken into account in the evaluation of the photogrammetric configuration.
The lower spatial resolution and image definition of the zoom lenses would affect the GCP identification and therefore change the final 3D reconstruction. Since an ICP was applied, the rotation changes were dismissed in the analysis, remaining only shape deformation due to the error propagated by the GCPs. For all cases, the number of images and camera orientation was the same (therefore the baseline-to-depth ratio) and the lighting condition was controlled by the lightbox, which was the only significant error source is the employed lens. Regarding the GCP definition with the ACMM, the precision provided by this metrological instrument was higher than the photogrammetric reconstruction, thus it can be considered negligible. Remember that in both cases (
Section 3.2) they were pre-calibrated independently.
4. Conclusions
In the present article, a new automatic protocol for the photogrammetric data acquisition is presented and evaluated. This protocol allows us to capture the images in a convergent path at equal angular intervals around a specimen. This configuration allows us to implement the data acquisition protocol of reconstructed small size archeological objects even if the operator is not an expert in photogrammetry, as is the case in an interdisciplinary field like archaeology. Furthermore, the images acquired using this protocol fully cover the geometry of the specimen without manually repositioning the camera, while providing an adequate dataset for the photogrammetric process using open [
34,
35,
36,
37] or commercial software [
39]. The widely extended commercial application of Metashape [
39] was chosen for this research due to its popularity and reduced complexity for final users (non-experts in photogrammetry). Both were chosen for their intuitive software interfaces and available documentation about use. The present approach is significant for three main reasons: aids in the reconstruction of small archaeological parts for documentation purposes [
52]; helps assemble dismantled heritage elements and/or missing parts [
29]; and generates didactical models for the acquisition of competences in an e-learning context [
53] and can be included in products like augmented or virtual reality (AR/VR) applications for awareness-raising [
6].
In this research, the variables that impact the photogrammetric reconstruction process was established as independent (e.g., luminosity, spatial reference system, specimen position, camera path, and photogrammetric reconstruction parameters). Only lens and calibration process were modified for the different experiments performed. Dense point clouds are generated for each case and there were control point errors for the pre-calibrated configurations between 0.072 and 0.204 mm. In this manner, a comparison between the point clouds obtained for the two lenses (macro and zoom) and the two calibration processes (pre-calibration and self-calibration) were implemented using a robust statistical analysis technique. Results show that the use of a non-macro lens does not substantially affect the geometric accuracy of the final 3D point cloud. However, when using a macro lens, the 3D model obtained is denser and can better reflect better small details of the geometry due to the smaller object sample distance (or GSD). In this regard, it should be noted that for the use of a macro lens, the establishment of an adequate depth of field allows for a proper focus of the entire object, which is a critical aspect that may not be easily solved by users without macro-photography experience. Therefore, and since the conventional zoom lens provided compatible results in terms of geometric error, they are more versatile and adequate for final users. Furthermore, as shown in the experimental results, a previous initial camera pre-calibration does not significantly improve the results for either lens, possibly due to the automated image acquisition, thanks to the robotic device. Moreover, the calibrated GCPs of the platform assure the metric quality of the 3D point cloud.
The results of the present research are expected to advise heritage specialists, which are non-experts in photogrammetry, about the data acquisition, lens selection, and modelling of small archaeological samples. With regard to future perspectives, there will be more test lenses and cameras with different sensor resolutions and specifications that use new comparison/validation techniques, which will thus increase the scope of the present work.