Abstract
The present paper aims to investigate the influence of perforated membrane geometry on the performance of biosensors. For this purpose, a 2-D axisymmetric model of an amperometric biosensor is analyzed. The governing equations describing the reaction-diffusion equations containing a nonlinear term related to the Michaelis–Menten kinetics of the enzymatic reaction are introduced. The partial differential governing equations, along with the boundary conditions, are first non-dimensionalized by using appropriate dimensionless variables and then solved in a non-uniform unstructured grid by employing the Galerkin Finite Element Method. To examine the impact of the hole-geometry of the perforated membrane, seven different geometries—including cylindrical, upward circular cone, downward circular cone, upward paraboloid, downward paraboloid, upward concave paraboloid, and downward concave paraboloid—are studied. Moreover, the effects of the perforation level of the perforated membrane, the filling level of the enzyme on the transient and steady-state current of the biosensor, and the half-time response are presented. The results of the simulations show that the transient and steady-state current of the biosensor are affected by the geometry dramatically. Thus, the sensitivity of the biosensor can be influenced by different hole-geometries. The minimum and maximum output current can be obtained from the cylindrical and upward concave paraboloid holes. On the other hand, the least half-time response of the biosensor can be obtained in the cylindrical geometry.
1. Introduction
The detection of bio-particles (like nucleic acids, proteins, bacteria, and viruses) plays a crucial role in the early diagnosis and prevention of various diseases, such as breast and prostate cancers. Nowadays, the start of diseases and their progress can be rapidly assessed using biosensors [1,2]. A quick and precise detection can lead to the administration of appropriate medicine and reduces the possibility of reaching a critical stage of the disease [3]. Therefore, the study of such biosensors has drawn the attention of the investigators to examine the effects of bioparticle detection by carrying out analytical, numerical, and experimental research.
Typically, biosensors are made up of two elements. First, the specific biological element, usually an enzyme, is responsible for detecting a sample solution. The second element that translates biorecognition is called a transducer event into an electrical signal [4]. Amperometric biosensors work by measuring electrical current. Stability is a crucial characteristic of biosensors. The operational stability of a biosensor mainly depends on the geometry of the sensor and the applied transducer. Amperometric biosensors are reliable and relatively cheap with high sensitivity, making them practical for industrial, medical, and environmental applications [5,6]; they have been a main focus of attention mostly because of the wide range of oxidase substrates they can measure, like alcohol and cholesterol [7,8,9].
Numerous studies can be found regarding the mathematical modeling of amperometric biosensors. Early works were mainly devoted to simple geometries and one-dimensional-in-space models. The mathematical models are based on time-dependent diffusion equations with a non-linear term associated with the Michaelis-Menten kinetics of the enzymatic reaction. For instance, Baronas et al. [10] studied the impact of enzyme membrane thickness on the response of an amperometric biosensor in a simple enzyme-catalyzed reaction. They employed the Finite Difference Method (FDM) for solving a set of non-linear 1-D equations and showed that the maximum current of the biosensor is a non-monotonic function of the membrane thickness. Meena and Rajendran [6] developed the 1-D mathematical modeling of amperometric and potentiometric biosensors. They used the Homotopy perturbation method to solve the non-linear differential equations and discussed the biosensor steady-state current concerning the Damköhler number (σ). Djaalab et al. [11] surveyed the mathematical modeling of highly sensitive enzyme biosensor kinetics. They employed the Laplace transform method and the Heaviside expansion theorem for solving the set of time-dependent reaction-diffusion equations in a one-dimensional-in-space model of the biosensor. Djaalab et al. [11] also showed that in highly sensitive biosensors, reducing the Damköhler number leads to an increase in the substrate concentration degradation. Loghambal and Rajendran [12] developed a theoretical model for the simulation of a mediated enzyme electrode in the presence of oxygen. The homotopy perturbation method was employed to solve the system of coupled, steady-state, non-linear reaction-diffusion equations. Their results showed that the thickness of the enzyme electrode caused a significant change in both the magnitude of the current response and the general behavior of the system. Croce et al. [13] surveyed the mathematical modeling of an amperometric glucose biosensor coated with layer-by-layer outer membranes and compared the diffusion profiles of various participating species and their impact on the performance of the biosensors. They utilized the FDM scheme for their numerical simulation. Croce et al. [13] compared a humic acids/ferric cations (HAs/Fe3+) membrane (with a high permeability to glucose) with a poly(styrene sulfonate)/poly(diallyldimethylammonium chloride) (PSS/PDDA) membrane (as a low permeable membrane to glucose) and showed that the biosensor response for the low glucose permeable membrane (PSS/PDDA) was about 30% higher than the one with a high permeability to glucose.
Extensive studies have been devoted to the mathematical modeling of the so-called sandwich-type amperometric biosensors with multiple layers. In these devices, the enzyme layer is trapped between two membranes. These membranes control the diffusion transport of the species and also diminish the potential interferences [14]. Aziz [15] developed a 1-D mathematical model to investigate the influence of membrane permeability and also selectivity on peroxide-based glucose biosensors. Their studied biosensor layout consists of three layers of selective membrane (as interferant retardant), an enzyme layer, and also the outer layer (diffusion layer). They used FDM for the numerical simulation and revealed that the selectivity of the selective membrane plays a major role in reducing interference. Romero et al. [14] investigated the mathematical modeling of sandwich-type amperometric biosensors. They studied the reaction-diffusion mechanism within the enzymatic membrane by considering oxygen as the mediator. Romero et al. [14] employed the FDM and Fortran programming language for numerical simulation and revealed that the permeability to the analyte of the external membrane and its thickness are the most influential parameters for enhancing the response time of sandwich-type biosensors.
An outer porous or perforated membrane is mainly utilized in practical biosensors for increasing their stability and also prolonging their calibration curves [16,17,18]. Schulmeister and Pfeiffer [19] developed the mathematical modeling of a biosensor in the presence of a perforated membrane. However, the geometry of the membrane was not considered in their 1-D model. The two-dimensional-in-space mathematical modeling of biosensors was proposed by Baronas et al. [20,21]. In [21], Baronas et al. investigated the influence of the presence of a cylindrical perforated membrane on the performance of the biosensor. They assumed that the perforated membrane was completely filled with enzymes and showed that the perforation level of the membrane could strongly affect the steady-state and also half-time response of the biosensor. In the other study, Baronas et al. [20] surveyed the influence of the filling level of enzymes in the perforated membrane and revealed that the impact of the filling level on the biosensor response diminished as the radius of the hole decreased.
It is worth noting that in comparison to 1-D cases, the 2-D modeling of biosensors is highly computationally demanding and may not be efficient in some situations. As such, in another study, Baronas et al. [22] evaluated the conditions in which 1-D models are accurate enough to be employed for the mathematical modeling of biosensors. They found that 1-D models cannot be used when the hole of the perforated membrane is very small; thus, in such cases, 2-D models should be utilized to obtain accurate outcomes. In addition to this, the geometry of the perforated membrane governs the mass transport by the diffusion process and thus can affect the overall performance of amperometric biosensors. Previous surveys have significantly increased knowledge about the impact of influential parameters on the performance of biosensors. However, in all of the studies to date, only cylindrical perforated membranes have been analyzed and, to the best of the authors’ knowledge, the impact of the shape of the mentioned membrane on the steady-state current and time response of biosensors has not been addressed yet.
With the above literature review, it is now clear that this study aims to numerically survey the influence of the geometry of the perforated membrane on the performance of biosensors. For this purpose, a 2-D axisymmetric amperometric biosensor with selective and perforated membranes was analyzed. Seven different geometries were designed and modeled. The governing equations were solved using the Galerkin Finite Element Method. The results were first compared and validated with four different works. Then, the influence of the geometry of the perforated membranes on the steady-state current and also the time response of the biosensor was discussed.
2. Structure of the Biosensor
The schematic view of the biosensor is provided in Figure 1. It is assumed that the thickness of the perforated and selective membranes is much lower than the length and width of the biosensor. The holes in the perforated membrane can be modeled to form the same unit cells with hexagonal patterns. Only half of the cross-section of the mentioned unit cell is studied because of its symmetry [20,21].
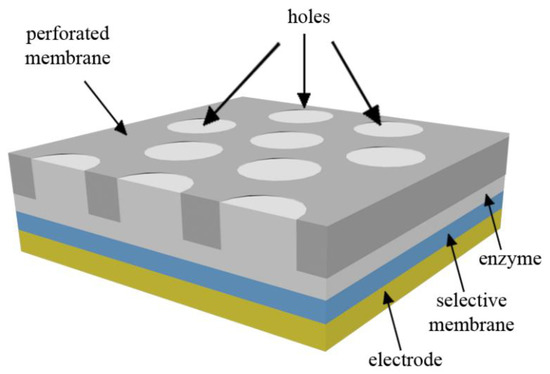
Figure 1.
Schematic view of the biosensor with cylindrical holes.
Scheme 1 illustrates various regions of the biosensor. While in the bulk solution region both convection and diffusion mechanisms (without reaction) can be found, the diffusion mode governs the other layers [14,23]. The enzyme-catalyzed reaction takes place in the enzyme region. In the selective membrane, the production detection process is performed. Finally, in the electrode, the biochemical energy from the enzyme reaction is converted by the transducer to the output current.
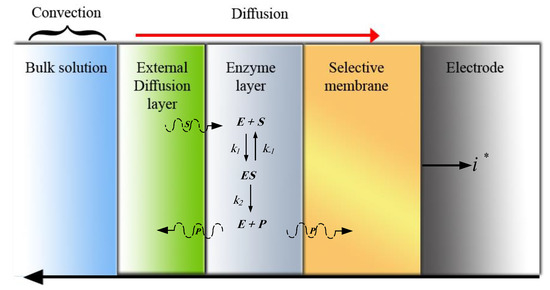
Scheme 1.
Different regions of an amperometric biosensor.
3. Formulation of the Problem
The biosensor can be mathematically modeled in a 2-D domain consisting of the discussed regions. The Michaelis–Menten model is utilized for the study of the kinetics of enzymes [24]. According to the Michaelis–Menten model, the substrate (S) binds to the enzyme (E) with the reaction rate of k1 and converts to the ES. The formed complex (ES) then dissociates during the second reaction with the reaction rate of k2 and produces the product (P), regenerating the enzyme [20]. It is worth noting that the rate of forward reaction rate (k2) for is much higher than the reverse one, and thus the reverse reaction can be neglected. Following Baronas et al. [25], the reaction model can be shown as follows:
Since the concentration of the substrate is much more than the ES, it is reasonable to consider a constant concentration for the ES. Thus, the concentration of the enzyme production can be calculated using the following equation [26]:
where S, E, and ES represent the concentrations of the substrate, enzyme, and the enzyme–substrate complex, respectively. E0 is the initial concentration of the enzyme. By replacing the expression E = E0 − ES in Equation (2), the production rate (v) can be written as follows [25,27]:
In Equation (3), P represents the concentration of the product. Moreover, the reaction rate approaches the saturated reaction rate when the E0 = ES. For this case, represents the maximum reaction rate and is the Michaelis-Menten constant, showing the concentration of the substrate when the reaction velocity is equal to one half of the maximal velocity of the reaction. The mass diffusion in the layers can be expressed over time with Fick’s law of diffusion in two or three dimensions, as follows:
where t is the time, Δ is the Laplace operator, c is the concentration of a component, and D is the corresponding diffusion coefficient. The value of the diffusion coefficient indicates the quality of the transfer, which means that the larger the diffusion coefficient, the better the diffusion mass transfer.
Shown in Figure 2 are the seven studied unit cells with different geometrical designs. Except for the cylindrical one (Figure 2a), the perforated membranes were designed to be in upward or downward pairs of a circular cone, paraboloid, and concave paraboloid. As such, the minimum and maximum radii of the perforated membranes are set to be and , respectively. Moreover, corresponds to the hole radius. The thickness of the selective membrane is . and are the perforated membrane thickness and the diffusion layer thickness, respectively. The filling level of enzymes is shown with b3. Region Ω1 indicates the selective membrane, Ω2 specifies the layer occupied with the enzymes, Ω3 is the external diffusion layer, and Ω4 is the impermeable carrier of the perforated membrane.
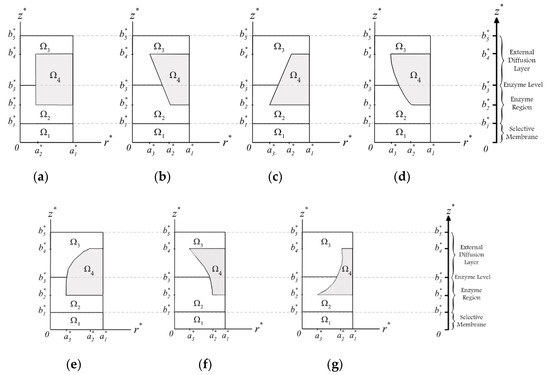
Figure 2.
The geometries of the biosensor unit cell: (a) cylindrical, (b) upward circular cone, (c) downward circular cone, (d) upward paraboloid, (e) downward paraboloid, (f) upward concave paraboloid, and (g) downward concave paraboloid. Figures are not to scale.
It is assumed that the selected layer has a uniform thickness, and the thicknesses of both the perforated membrane and the selective membrane in the biosensor are much less than its length and width. The volume of the bulk solution is considered to be extremely high, while the substrate concentration can be assumed to be constant [28,29]. The concentration of the ES form can be assumed to be constant because the biosensor reached the steady-state condition in a short time. By using Equation (2), the maximum rate of enzymatic reaction can be obtained. Therefore, according to Figure 2, the biosensor described from the process starts (t* > 0) with the system of reaction-diffusion equations as follows:
where and are the product and substrate concentrations, respectively. The symbols r* and z* indicate the radial and axial distances, respectively, and t* denotes elapsed time. is the product concentration on the surface of the electrode; this concentration and its variation are important for measuring the change in the current of the biosensor (see Equation (26)). Here, and represent the product concentrations of the enzyme and external diffusion layers, respectively. Since the reaction product oxidizes at the electrode surface rapidly, it can be assumed that its concentration at the electrode surface is zero [21].
At the interface between the bulk solution and the biosensor , the concentration of the enzyme reaction is assumed to be zero because the reaction has not yet occurred. and are the substrate concentration on the selective membrane and the perforated membrane. , , and represent the diffusion coefficient in these regions.
The initial conditions are described as :
where is the substrate concentration in the solution, is the area of each layer, and is the upper surface of . Due to the oxidation of the reaction product at the electrode surface, its concentration at the electrode surface is considered to be zero ():
Since no reaction has occurred on the boundary, , the concentration of the enzymatic product, has to be constant and zero. During the biosensor operation, the substrate concentration, as well as the product over the enzyme surface (bulk solution and membrane interface), remains constant; therefore ():
The non-leakage condition for the symmetric boundaries of the unit cell is considered as follows:
where n denotes the normal vector of the hole surface. At the boundary between the two regions, it is necessary to apply matching conditions. According to the conservation of mass, the mass flux of particles at the interfaces is equal on both sides. In addition to this, it can be assumed that the substrate concentration and the enzyme product on the boundaries are equal for both sides:
In physical experiments, the anodic current generated at the electrode surface is considered as the amperometric biosensor response, which is a linear function of the reaction product gradient at the surface of the electrode. According to the Faraday and Fick laws, the current density on the electrode surface can be obtained as:
where is the number of electrons involved in a charge transfer at the electrode surface and F is the Faraday constant [4]. The steady-state current I* can be obtained when the concentration of the production remains constant at the sensor surface:
Finally, in the present study, , half of the required time to reach the steady-state current, is used to evaluate the dynamics of the biosensor operation [25]:
4. Dimensionless Mathematical Model
The governing Equations (6) and the corresponding boundary and initial conditions (7)–(11) are non-dimensionalized by introducing the following set of dimensionless variables:
Substituting Equation (16) into the governing Equation (5), the dimensionless nonlinear reaction-diffusion equations can be summarized as follows:
where is the dimensionless diffusion coefficient and is the diffusion modulus (Damköhler number), which compares the rate of enzyme reaction () with the mass transport through the enzyme layer () [25]. In fact, for high values of , the diffusion mechanism is considered to control the biosensor response, while, when it approaches zero, the enzyme kinetics prevail in the response [6,21]. The non-dimensional initial conditions are as follows:
and the dimensionless boundary conditions read:
The non-dimensional matching conditions are:
and the non-dimensional density of the current is given by:
and the dimensionless output current reads as:
To compare the effects of hole-geometry and filling level on the i(t) and I in different geometries, the following parameters are used [20,21,22]:
where γ is the level of the enzyme filling within the holes. For instance, represents a case where half of the perforated membrane is filled with the enzyme. α represents the perforation level of the perforated membrane. For the set of studied geometrical designs, the maximum radius of the holes (a3) is considered to be constant, and thus α is a measure of the volume fraction of the holes in the perforated membrane. In other words, increasing the perforation level (α) augments the surface area of the impermeable part of the perforated membrane (Ω4).
5. Numerical Approach
The partial differential governing Equation (17) and the corresponding initial and boundary conditions (18)–(20) are solved numerically utilizing the Galerkin method. Using the basis set , the product and the enzyme concentrations can be expanded as follows:
It should be noted that the function is the same for both variables. By substituting in Equation (17), the following residual equations can be obtained at the internal domain nodes:
In order to numerically evaluate the integral terms, the bi-quadratic function with three-point Gaussian quadrature is employed. Then, the Newton-Raphson method is used to evaluate the coefficients and in the nonlinear residual Equation (26). More details about the solution procedure can be found in the Reddy studies [30]. The iterative process is stopped when the convergence criterion is reached. Moreover, a time step of 0.01 s is used to evaluate the half-time response of the biosensor.
6. Validation of Computations
To ensure about the validity of the solution, the results of the present study have been compared against the different numerical and experimental results of previously published surveys. Shown in Figure 3 are the comparisons of the results of the present study with those provided by Baronas et al. [10] for a 1-D case without perforated and selective membranes (Ds = Dp = 3.010−6 cm3/s, Km = 10−7 cm3/s). Baronas et al. [10] employed FDM for solving the set of non-linear equations. Further, to compare the accuracy of concentration profiles, we have compared our numerical code with the concentration and current profiles of a Glucose sensor [13]. Figure 4a shows glucose and H2O2 concentration profiles in the multi-layer sensor system consisting of GOx/PPD and HAs/Fe3+ as the first and second layers. Additionally, Figure 4b, depicts the dependency of the current density of the biosensor on the concentration of the glucose. All of the simulation parameters for comparison can be found in Table 2 of [13]. In addition, to ensure the outcomes in the presence of a perforated membrane and also the perforation level (α) and the level of the enzyme filling (γ) for a cylindrical geometry (Figure 2a), the results of the present study have been validated with the work of Baronas [20] in Figure 5. Finally, to compare the presented model with an experimental study, we have developed our FEM code to take into account the influence of the mediator layer and compared our modeling with the experimental data provided by Šimelevičius et al. [31] for mediator oxidization in an amperometric glucose biosensor. The maximum value of the residual sum of squares (RSS) for Figure 3, Figure 4 and Figure 5 (comparisons with numerical approaches) are below 0.01, and for Figure 6 (comparison with the experimental data) it is around 0.35. In addition to this, the minimum value of R-square representing the similarity between the obtained results of the present study and those mentioned above is 99.8% for the numerical validations and 86.5% for the experimental comparison. This indicates an admissible agreement and very low discrepancies between the present model and all of the analyzed literature.
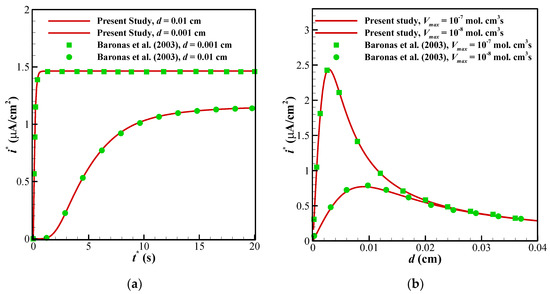
Figure 3.
Comparison between the results of the present study with [10]: (a) variation in the dynamic current of the biosensor with the time and thickness of the enzyme membrane (d) for Vmax = 10−7 mol/cm3s; (b) dependency of the maximal current of the biosensor on the maximal enzymatic rate (Vmax) and the thickness of the enzyme membrane.
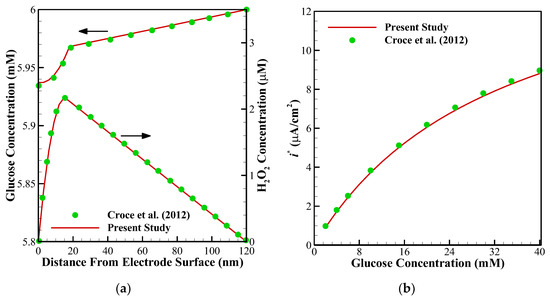
Figure 4.
Comparison between the results of the present study with [13]: (a) concentration profiles of glucose and H2O2 in a multi-layer sensor system consisting of GOx/PPD (20 nm) and HAs/Fe3+ (100 nm); (b) dependency of the maximal current of the biosensor on the glucose concentration with 20 nm of GOx/PPD and 100 nm of HAs/Fe3+.
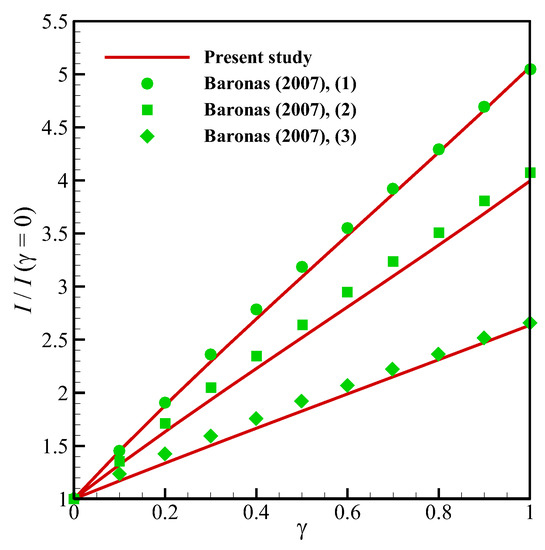
Figure 5.
Comparison between the results of the present study and Baronas [20] in cylindrical geometry for different values of the enzyme filling level (γ) and the perforation level (α): Vmax = 100 μM. (1) a1 = 1 μm, S0 = 1 μM; (2) a1 = 0.8 μm, S0 = 100 μM; (3) a1 = 0.4 μm, S0 = 100 μM.
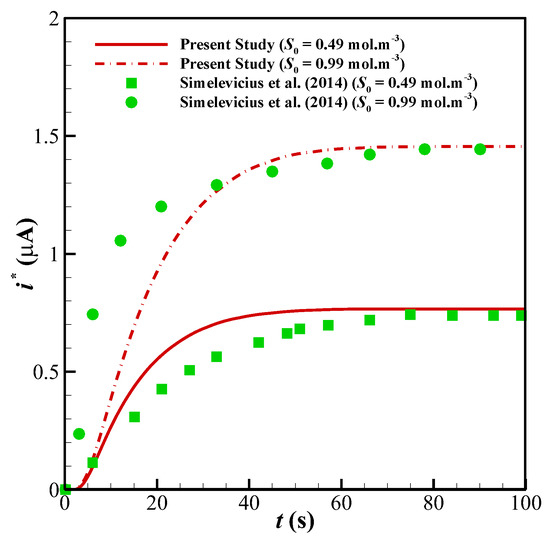
Figure 6.
Comparison between the results of the present study with the experimental data of [31]; variation in the dynamic current of the biosensor with time and for two substrate concentrations: S0 = 0.49 and 0.99 mol/m3.
7. Results and Discussion
To study the impact of geometry on the biosensor performance, seven geometries—including cylindrical, upward circular cone, downward circular cone, upward paraboloid, downward paraboloid, upward concave paraboloid, and downward concave paraboloid—are considered. The effects of the enzyme filling level and the perforation level in these holes on the transient and steady-state current and the half-time response of the biosensor have been investigated for a range of geometrical parameters. The values of parameters are considered as , , , and .
The effects of the perforation level on the transient current are shown in Figure 7a,b for various geometries. It is clear that the geometry has a significant influence on the output current of the biosensor, and the transient current is higher for the upward geometries than the downward ones. In addition to this, increasing the perforation level boosts the output current strongly. However, the difference between the current in the upward and downward geometries decreased by increasing the level of perforation for the concave paraboloid and circular cone geometries. The maximum current can be obtained from the upward concave paraboloid holes. Figure 7c,d compares the effect of the enzyme filling level on the transient current of the biosensors with different geometries. It is clear that the γ affects both the biosensor response time and current. The current of the biosensor for high values of γ is up to three times higher than that obtained when the enzyme filling level approaches zero. Moreover, the difference between the upward and downward geometries vanishes for a low level of enzyme. Finally, the minimum current is produced in the cylindrical geometry.
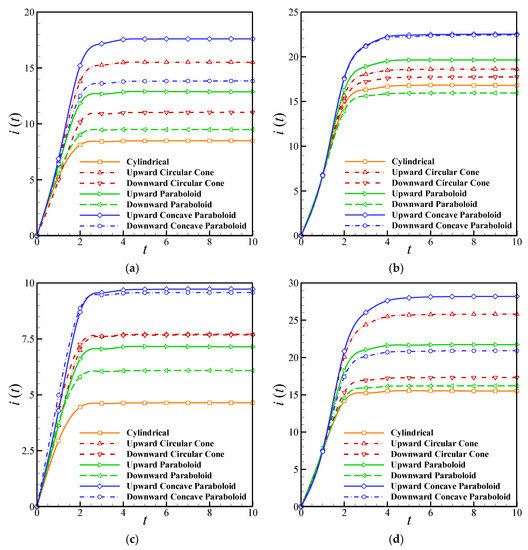
Figure 7.
Dependency of the output current on the perforation level (): (a) , (b) . The enzyme filling level (); (c) ; (d) .
Figure 8 depicts the effect of the perforation level and enzyme filling level on the non-dimensional output current of the biosensor. Obviously, the current increases with the level of perforation exponentially, and the current is highly sensitive to α when it approaches 1. Moreover, increasing the perforation level reduces the difference between the maximum and minimum steady-state currents of the hole-geometries, indicating that the impact of the hole-geometry on the output current decreases as α increases. In contrast with α, the output current increases with the increment of the enzyme filling level almost linearly.
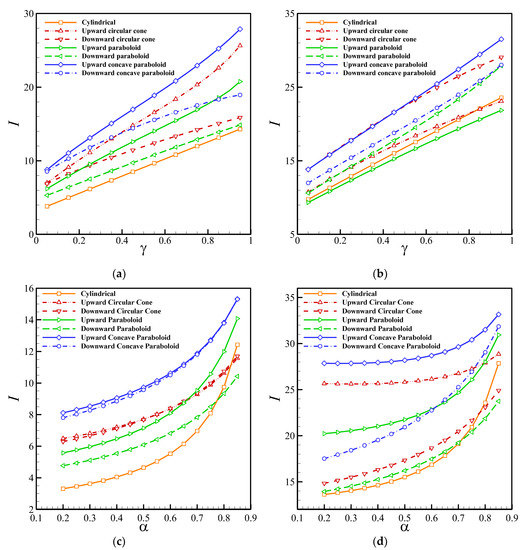
Figure 8.
Dependency of the steady-state biosensor current on the perforation level: (a) , (b) . The enzyme filling level: (c) , (d) .
Table 1 compares the effect of the perforation level and enzyme filling level on the half-time response of the biosensor. It is evident that the cylindrical and upward concave paraboloid holes require the lowest and highest time intervals to reach the steady-state condition. In addition to this, T0.5 is a monotonous function of the enzyme filling level and perforation level, and it increases with the increment of α and γ.

Table 1.
Influence of the α and γ on the time response (T0.5) for all of the geometries.
8. Conclusions
The influence of the perforated membrane geometry on the performance of a biosensor is studied in the case of a 2-D axisymmetric model of an amperometric biosensor. For this aim, seven practical geometries—including cylindrical, upward circular cone, downward circular cone, upward paraboloid, downward paraboloid, upward concave paraboloid, and downward concave paraboloid—are taken into consideration. In addition to this, the effects of the perforation level of the perforated membrane and the filling level of the enzyme level on the transient and steady-state current of the biosensor and the half-time response are studied. The results show that the geometry of the biosensor strongly influences the sensitivity and time response of the biosensor, specifying the potential of future experimental studies. The outcomes reveal that the maximum and minimum current can be obtained from the upward concave paraboloid and circular holes, respectively. Moreover, increasing the perforation level and enzyme filling level boosts the output current strongly. On the other hand, the time response of the studied biosensor for the cylindrical geometry is lower than that for other geometries.
Author Contributions
Conceptualization, A.N.; Data curation, S.M.H.Z. and M.H.; Formal analysis, S.M.H.Z.; Funding acquisition, M.H.; Investigation, S.M.H.Z., M.H. and M.S.P.; Methodology, S.M.H.Z., M.H., M.G. and A.N.; Resources, M.S.P.; Software, S.M.H.Z. and M.H.; Supervision, M.G., A.N. and M.S.P.; Validation, S.M.H.Z. and M.H.; Visualization, S.M.H.Z. and M.H.; Writing—original draft, S.M.H.Z. and M.H.; Writing—review & editing, M.G. and M.S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arefin, M.S.; Porter, T.L. An ac electroosmosis device for the detection of bioparticles with piezoresistive microcantilever sensors. J. Appl. Phys. 2012, 111, 054919. [Google Scholar] [CrossRef]
- Metkar, S.K.; Girigoswami, K. Diagnostic biosensors in medicine—A review. Biocatal. Agric. Biotechnol. 2019, 17, 271–283. [Google Scholar] [CrossRef]
- Kumar, P.; Narwal, V.; Jaiwal, R.; Pundir, C.S. Construction and application of amperometric sarcosine biosensor based on SOxNPs/AuE for determination of prostate cancer. Biosens. Bioelectron. 2018, 122, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Scheller, F.W.; Schubert, F. Techniques and Instrumentation in Analytical Chemistry, Biosensors; Elsevier: Amsterdam, The Netherlands, 1992; Volume 11. [Google Scholar]
- Coulet, P.R. Polymeric membranes and coupled enzymes in the design of biosensors. J. Membr. Sci. 1992, 68, 217–228. [Google Scholar] [CrossRef]
- Meena, A.; Rajendran, L. Mathematical modeling of amperometric and potentiometric biosensors and system of non-linear equations—Homotopy perturbation approach. J. Electroanal. Chem. 2010, 644, 50–59. [Google Scholar] [CrossRef]
- Chinnadayyala, S.R.; Santhosh, M.; Singh, N.K.; Goswami, P. Alcohol oxidase protein mediated in-situ synthesized and stabilized gold nanoparticles for developing amperometric alcohol biosensor. Biosens. Bioelectron. 2015, 69, 155–161. [Google Scholar] [CrossRef]
- Lata, K.; Dhull, V.; Hooda, V. Fabrication and optimization of ChE/ChO/HRP-AuNPs/c-MWCNTs based silver electrode for determining total cholesterol in serum. Biochem. Res. Int. 2016, 2016, 1545206. [Google Scholar] [CrossRef]
- Vadgama, P. Membrane based sensors: A review. J. Membr. Sci. 1990, 50, 141–152. [Google Scholar] [CrossRef]
- Baronas, R.; Ivanauskas, F.; Kulys, J. The influence of the enzyme membrane thickness on the response of amperometric biosensors. Sensors 2003, 3, 248–262. [Google Scholar] [CrossRef]
- Djaalab, E.; Samar, M.E.H.; Zougar, S. Mathematical modeling of the kinetics of a highly sensitive enzyme biosensor. React. Kinet. Mech. Catal. 2019, 126, 49–59. [Google Scholar] [CrossRef]
- Loghambal, S.; Rajendran, L. Mathematical modeling in amperometric oxidase enzyme–membrane electrodes. J. Membr. Sci. 2011, 373, 20–28. [Google Scholar] [CrossRef]
- Croce, R.A.; Vaddiraju, S.; Papadimitrakopoulos, F.; Jain, F.C. Theoretical analysis of the performance of glucose sensors with layer-by-layer assembled outer membranes. Sensors 2012, 12, 13402–13416. [Google Scholar] [CrossRef] [PubMed]
- Romero, M.R.; Baruzzi, A.M.; Garay, F. Mathematical modeling and experimental results of a sandwich-type amperometric biosensor. Sens. Actuators B Chem. 2012, 162, 284–291. [Google Scholar] [CrossRef]
- Aziz, A.A. Mathematical modeling of an amperometric glucose sensor: The effect of membrane permeability and selectivity on performance. J. Teknol. 2009, 51, 77–94. [Google Scholar]
- Ahammad, A.; Lee, J.-J.; Rahman, M. Electrochemical sensors based on carbon nanotubes. Sensors 2009, 9, 2289–2319. [Google Scholar] [CrossRef]
- Baronas, R.; Kulys, J.; Petrauskas, K.; Razumiene, J. Modelling carbon nanotube based biosensor. J. Math. Chem. 2011, 49, 995–1010. [Google Scholar] [CrossRef]
- Turner, A.; Karube, I.; Wilson, G.S. Biosensors: Fundamentals and Applications; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Schulmeister, T.; Pfeiffer, D. Mathematical modelling of amperometric enzyme electrodes with perforated membranes. Biosens. Bioelectron. 1993, 8, 75–79. [Google Scholar] [CrossRef]
- Baronas, R. Numerical simulation of biochemical behaviour of biosensors with perforated membrane. In Proceedings of the 21st European Conference on Modelling and Simulation ECMS, Prague, Czech Republic, 4–6 June 2007; pp. 214–217. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Computational modelling of biosensors with perforated and selective membranes. J. Math. Chem. 2006, 39, 345–362. [Google Scholar] [CrossRef]
- Petrauskas, K.; Baronas, R. Computational modelling of biosensors with an outer perforated membrane. Nonlinear Anal. Model. Control 2009, 14, 85–102. [Google Scholar] [CrossRef]
- Achi, F.; Bourouina-Bacha, S.; Bourouina, M.; Amine, A. Mathematical model and numerical simulation of inhibition based biosensor for the detection of Hg(II). Sens. Actuators B Chem. 2015, 207, 413–423. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.L. Die kinetik der invertinwirkung. Biochem. Z 1913, 49, 333–369, 352. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. Mathematical Modeling of Biosensors: An Introduction for Chemists and Mathematicians; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 9. [Google Scholar]
- Briggs, G.E.; Haldane, J.B.S. A note on the kinetics of enzyme action. Biochem. J. 1925, 19, 338. [Google Scholar] [CrossRef] [PubMed]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; W.H. Freeman: New York, NY, USA, 2002. [Google Scholar]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Seibert, E.; Tracy, T.S. Fundamentals of enzyme kinetics. Enzyme kinetics in drug metabolism: Fundamentals and applications. In Enzyme Kinetics in Drug Metabolism; Humana Press: Totowa, NJ, USA, 2014; pp. 9–22. [Google Scholar]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993; Volume 2. [Google Scholar]
- Šimelevičius, D.; Petrauskas, K.; Baronas, R.; Razumienė, J. Computational modeling of mediator oxidation by oxygen in an amperometric glucose biosensor. Sensors 2014, 14, 2578–2594. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).