Fingerprinting-Based Indoor Localization Using Interpolated Preprocessed CSI Phases and Bayesian Tracking
Abstract
1. Introduction
2. Choice of Fingerprints
2.1. Channel State Information
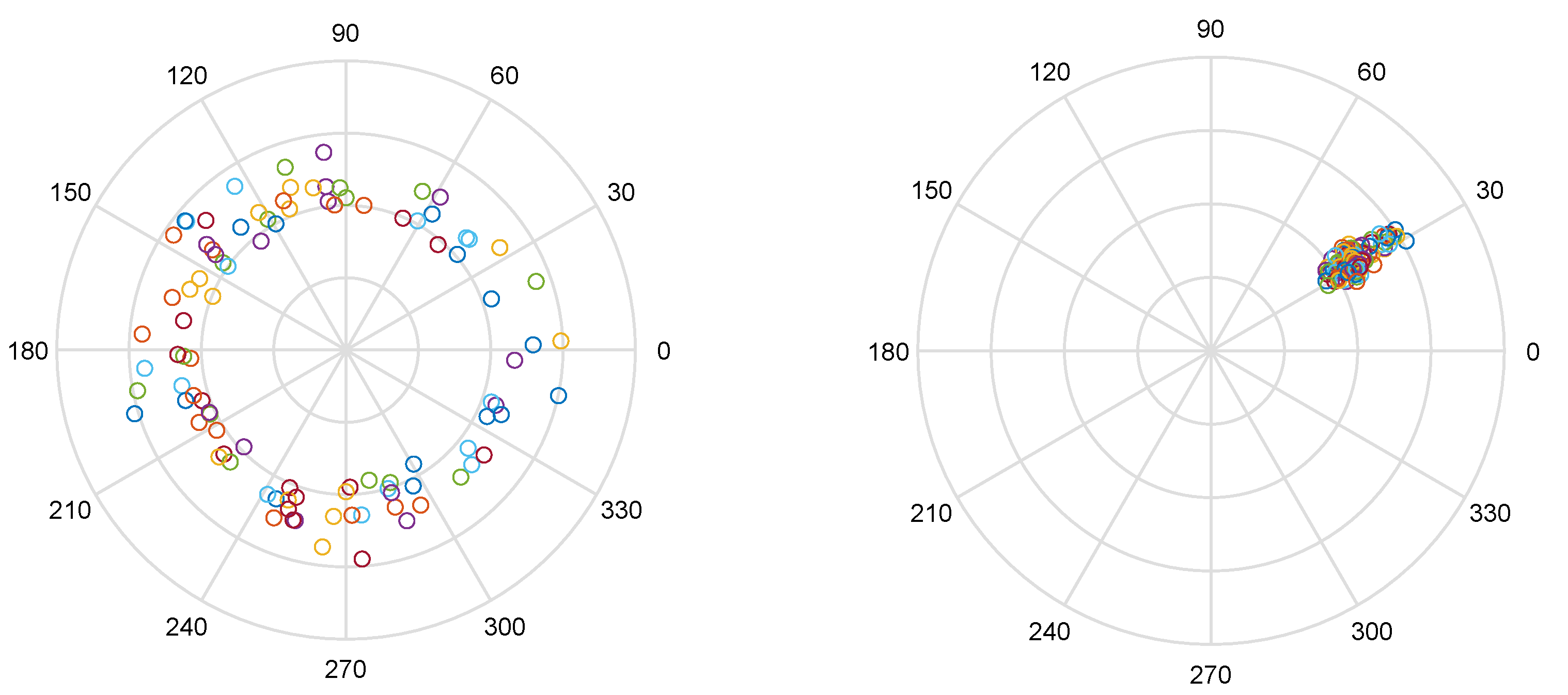
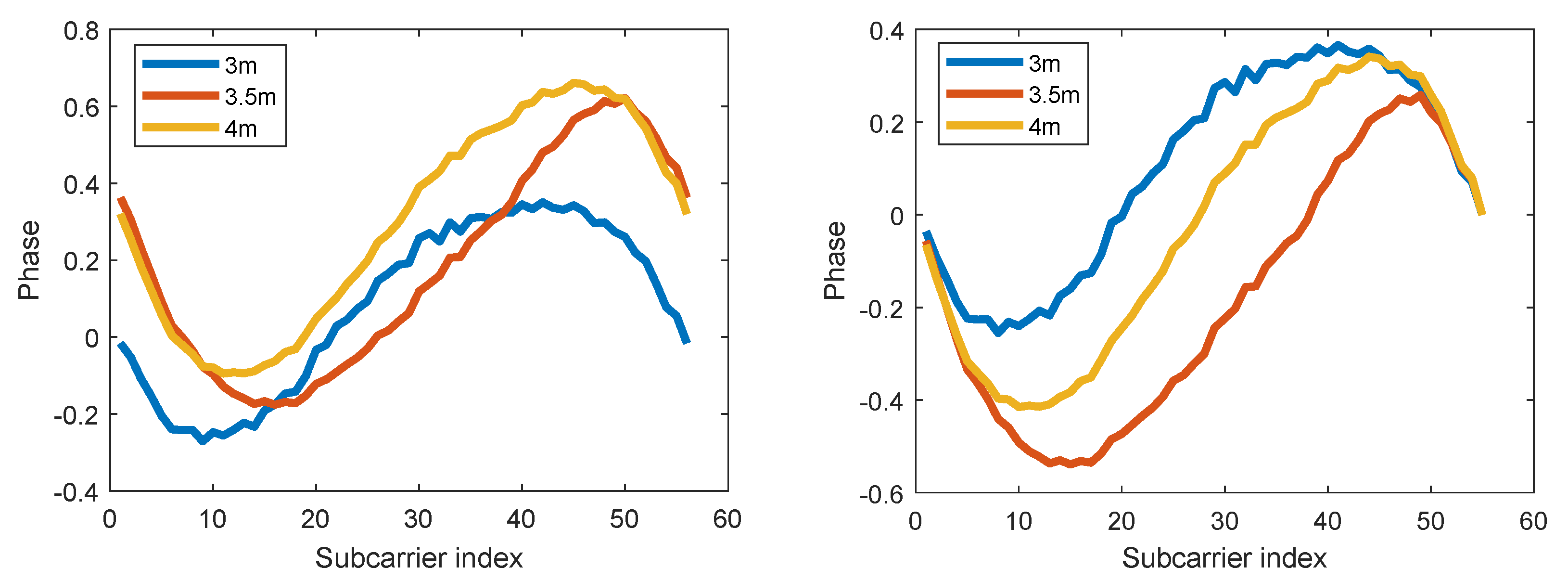
2.2. Phase Information
2.3. Phase Differences
3. Problem Description
4. Proposed Positioning Method
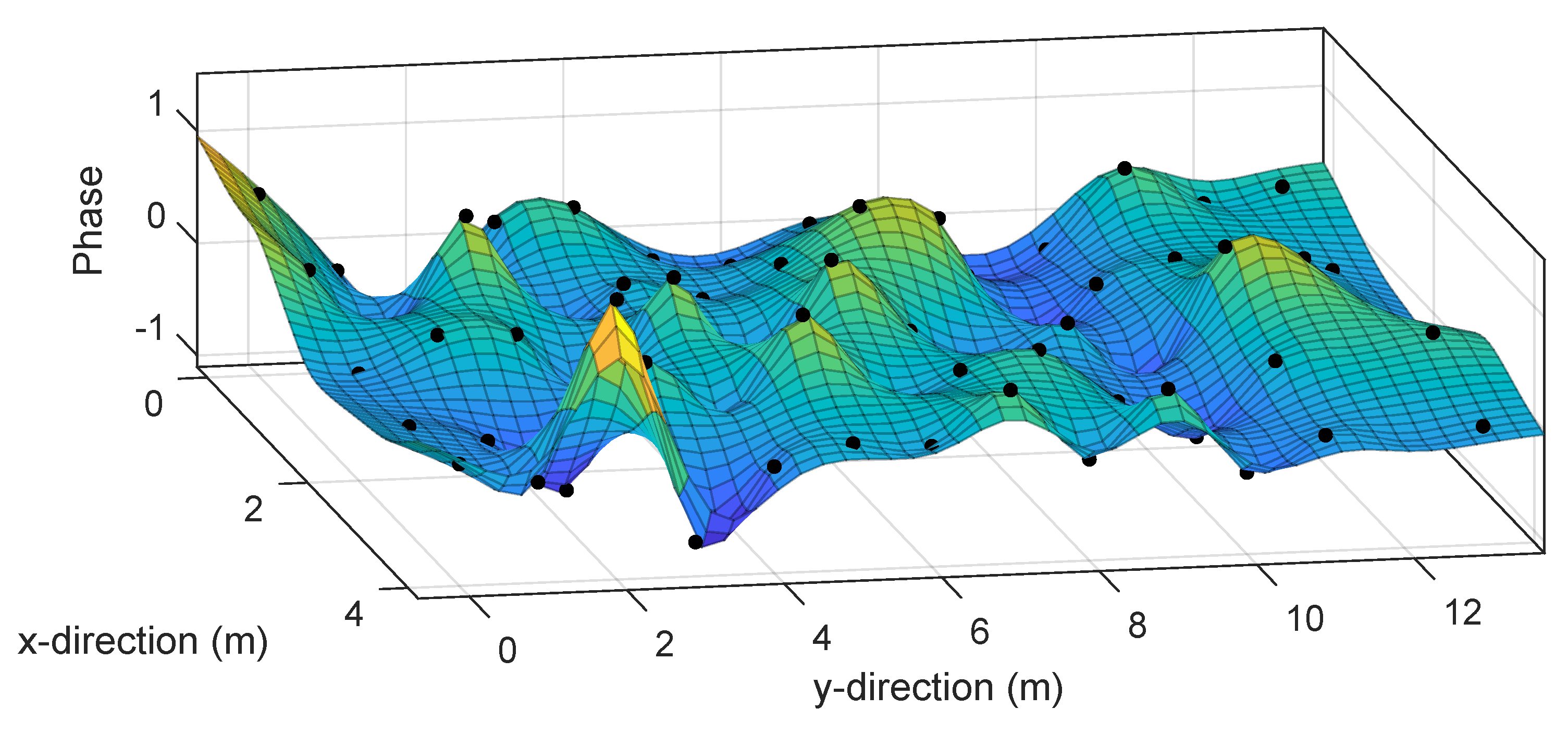
4.1. Fingerprint Modeling
4.2. Static Positioning
4.3. Dynamic Positioning
4.3.1. Prediction
4.3.2. Update
4.3.3. Final Step
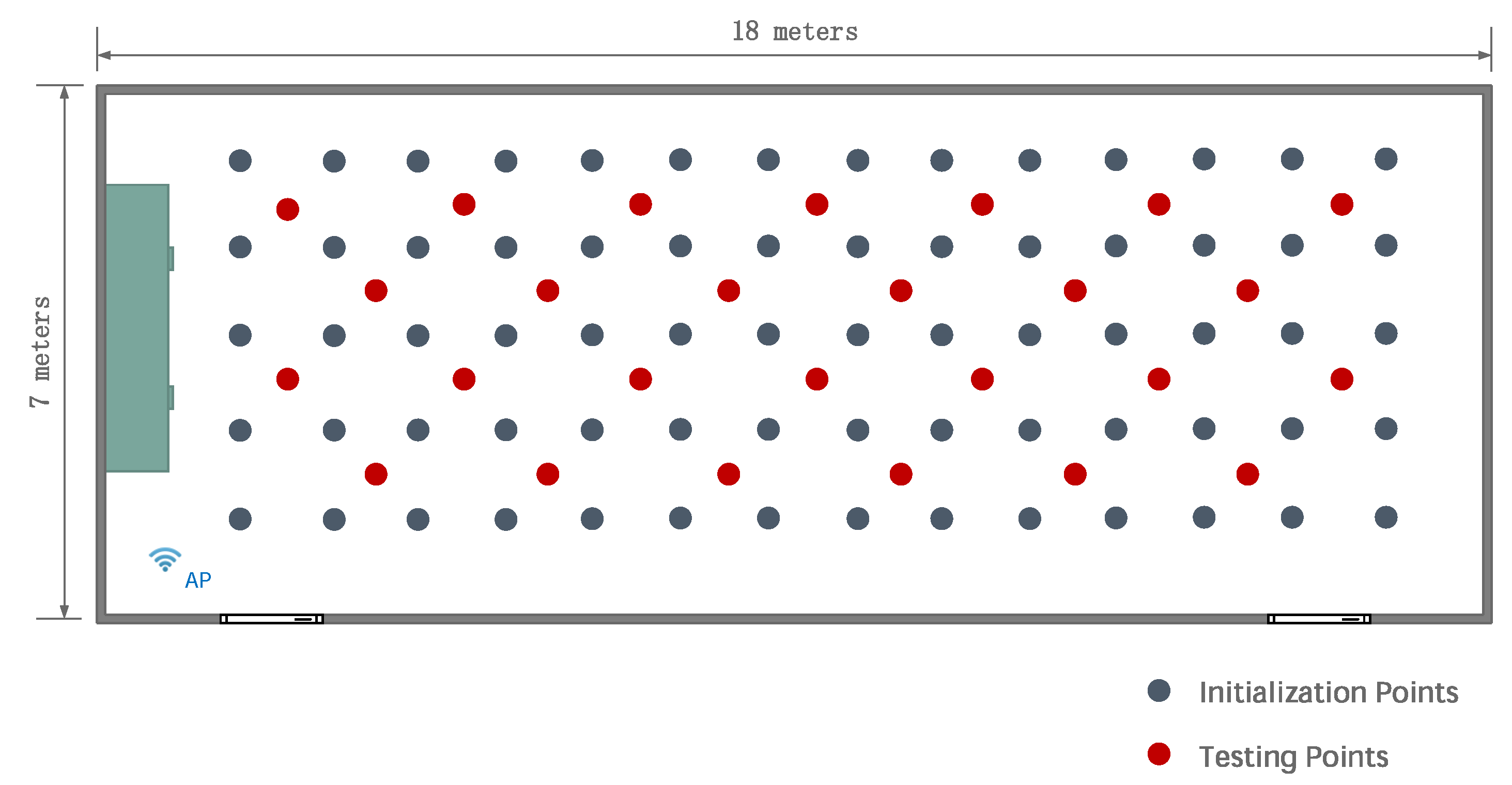
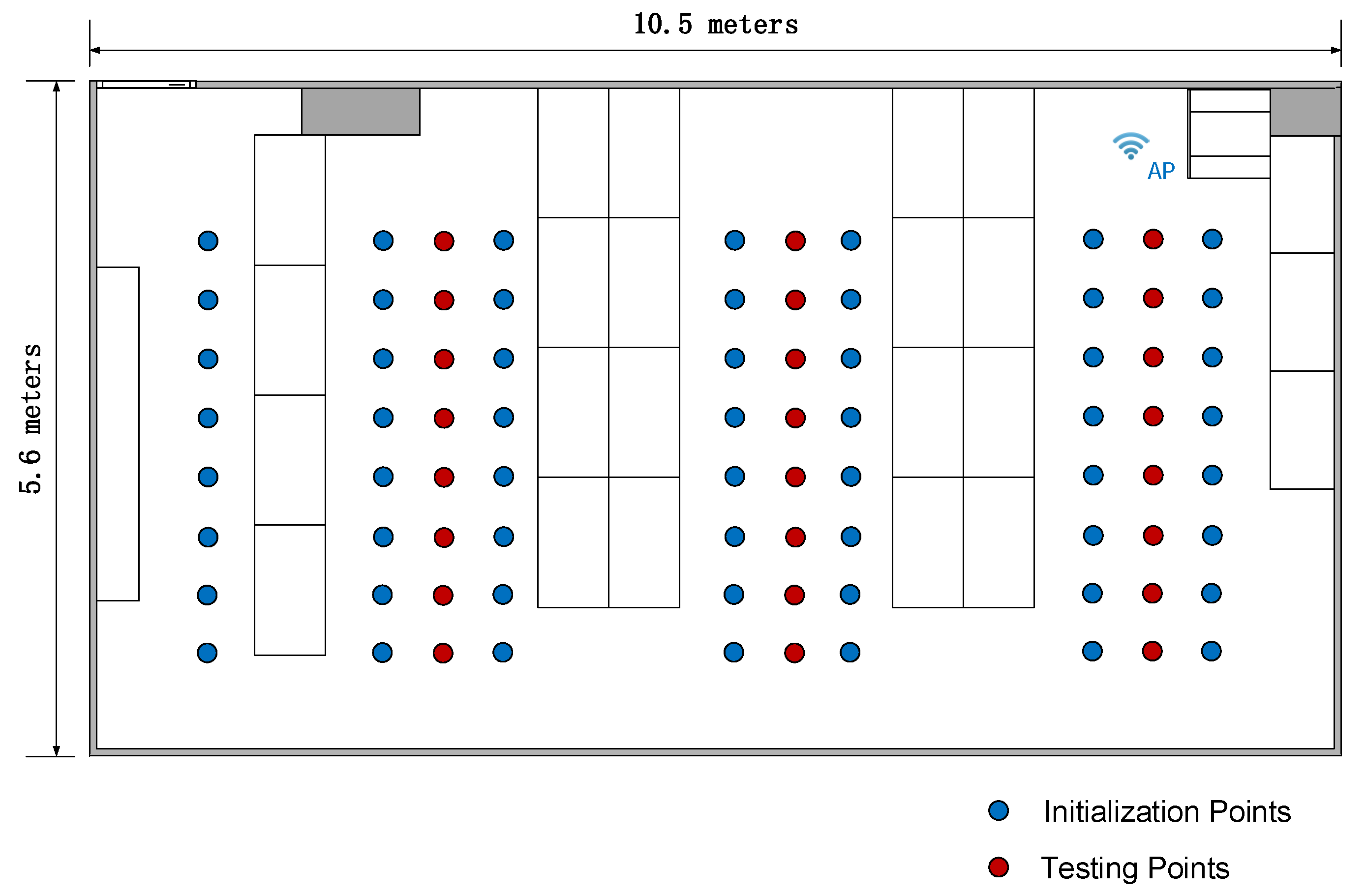
5. Experiments
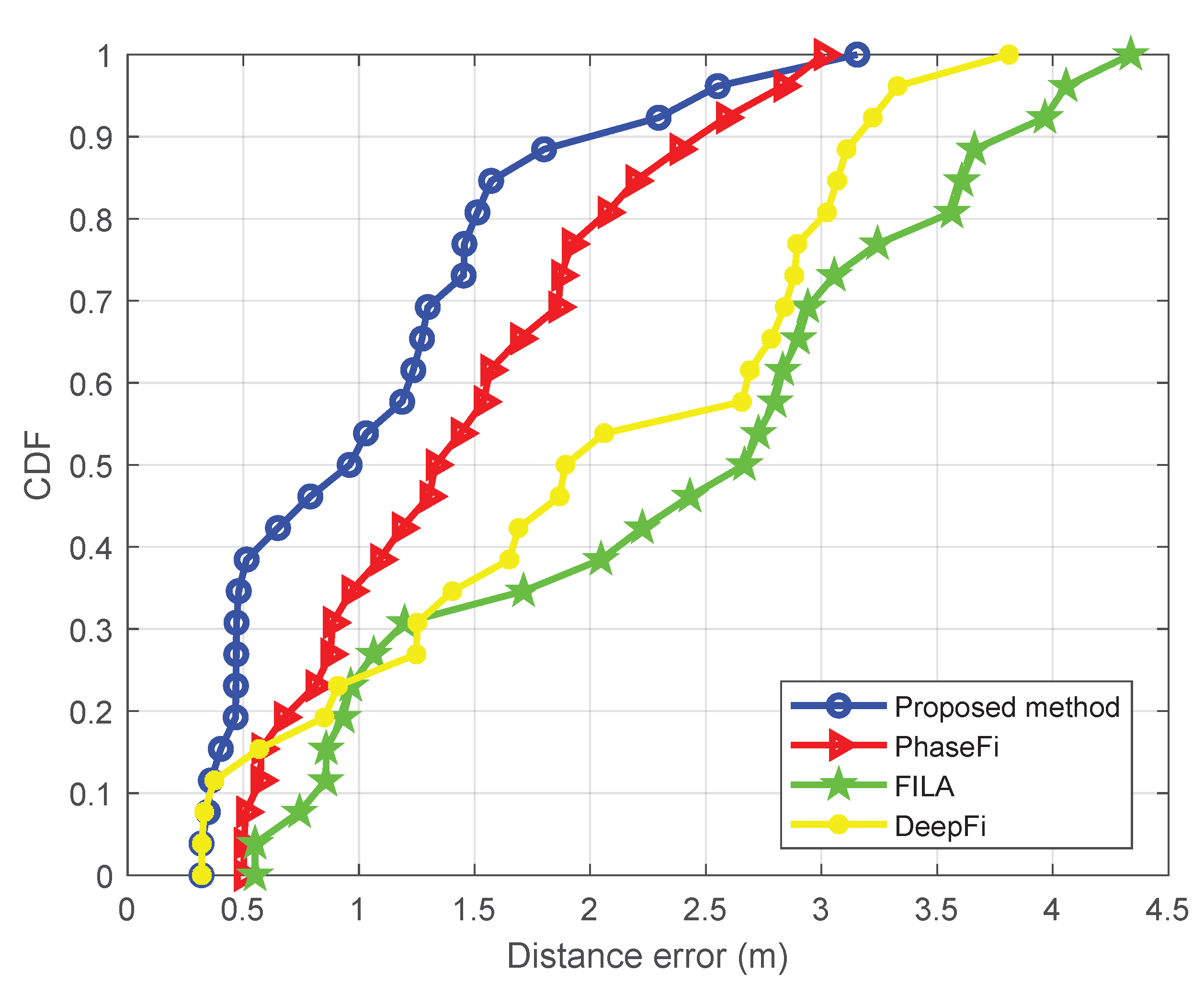
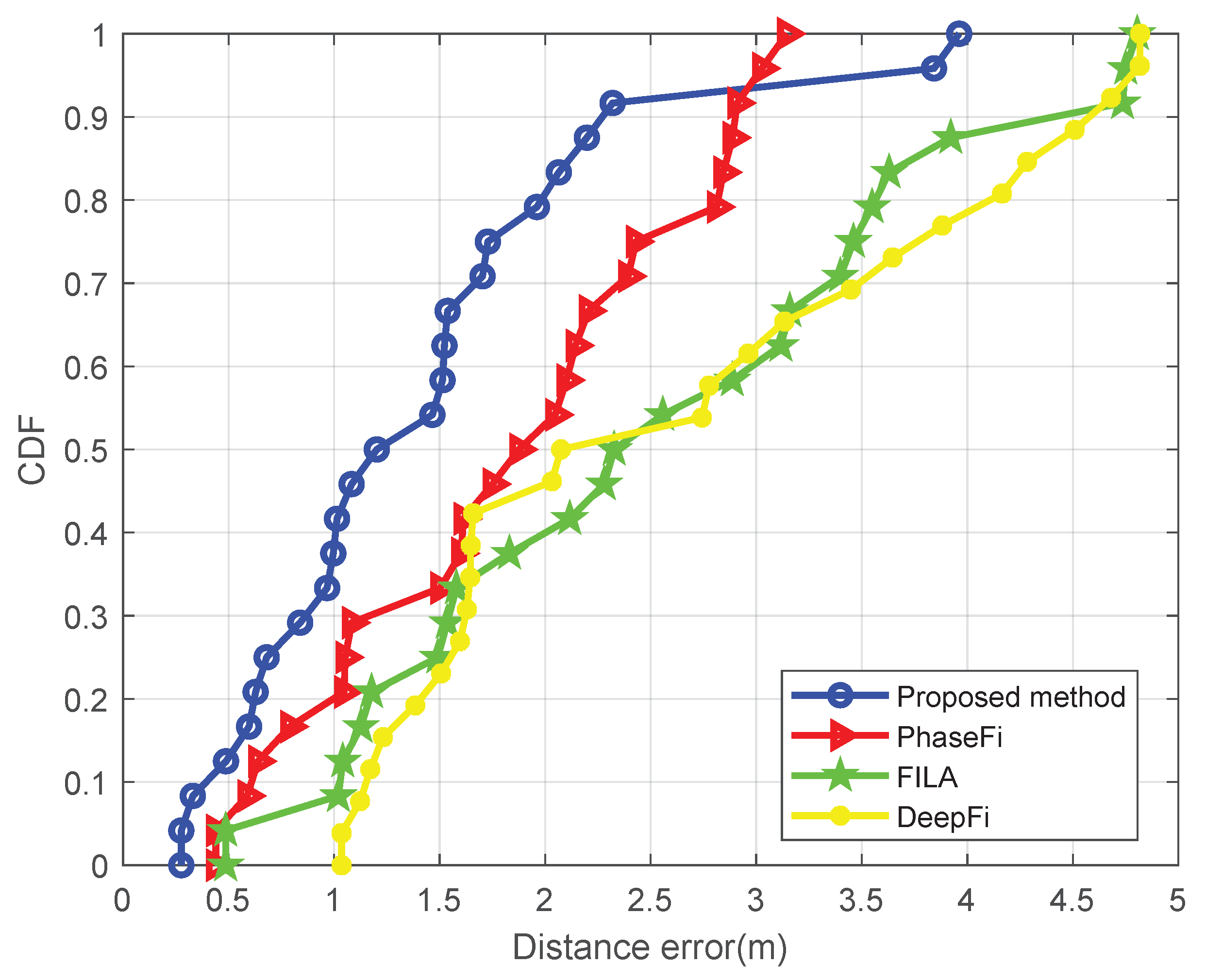
5.1. Static Positioning
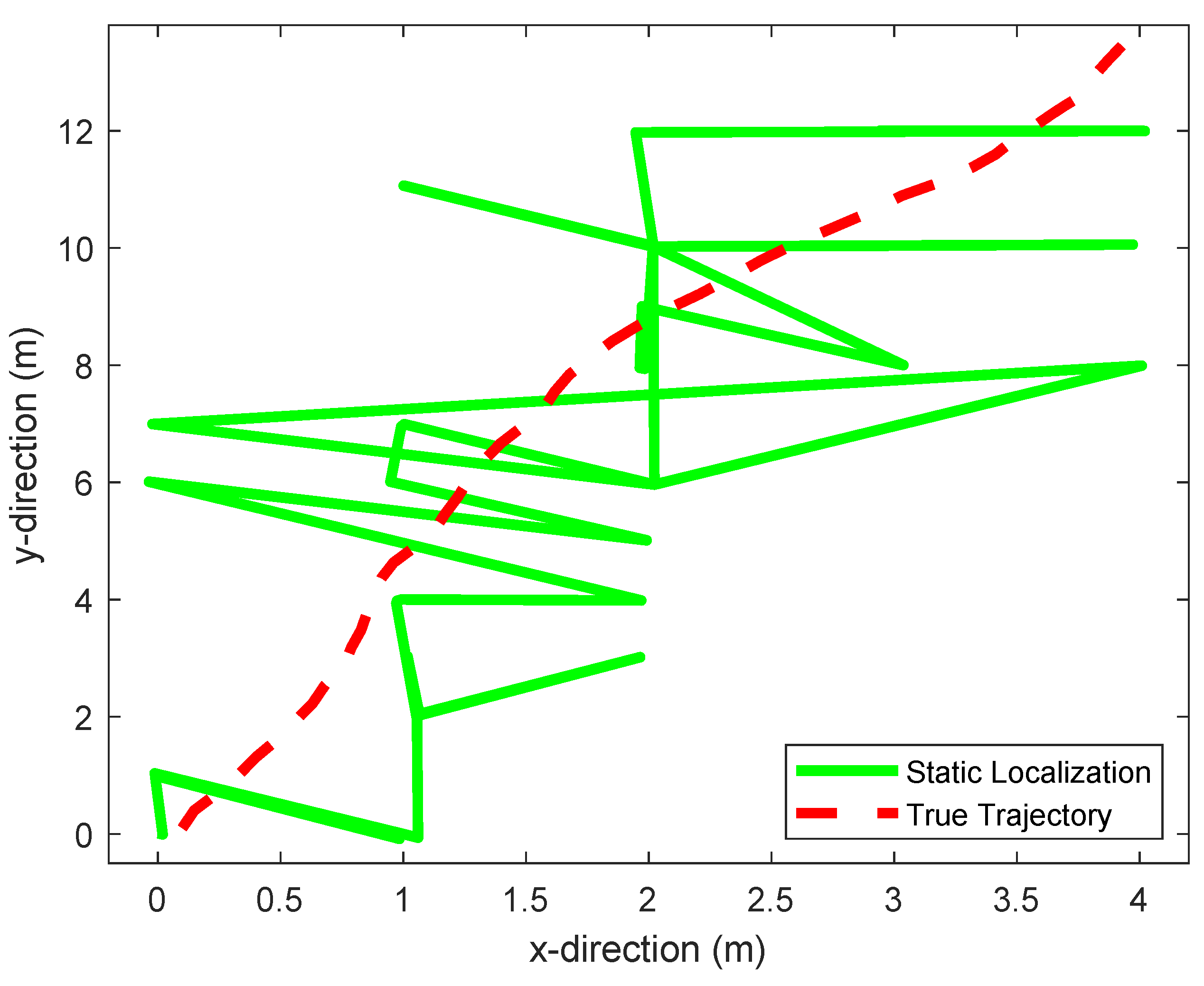
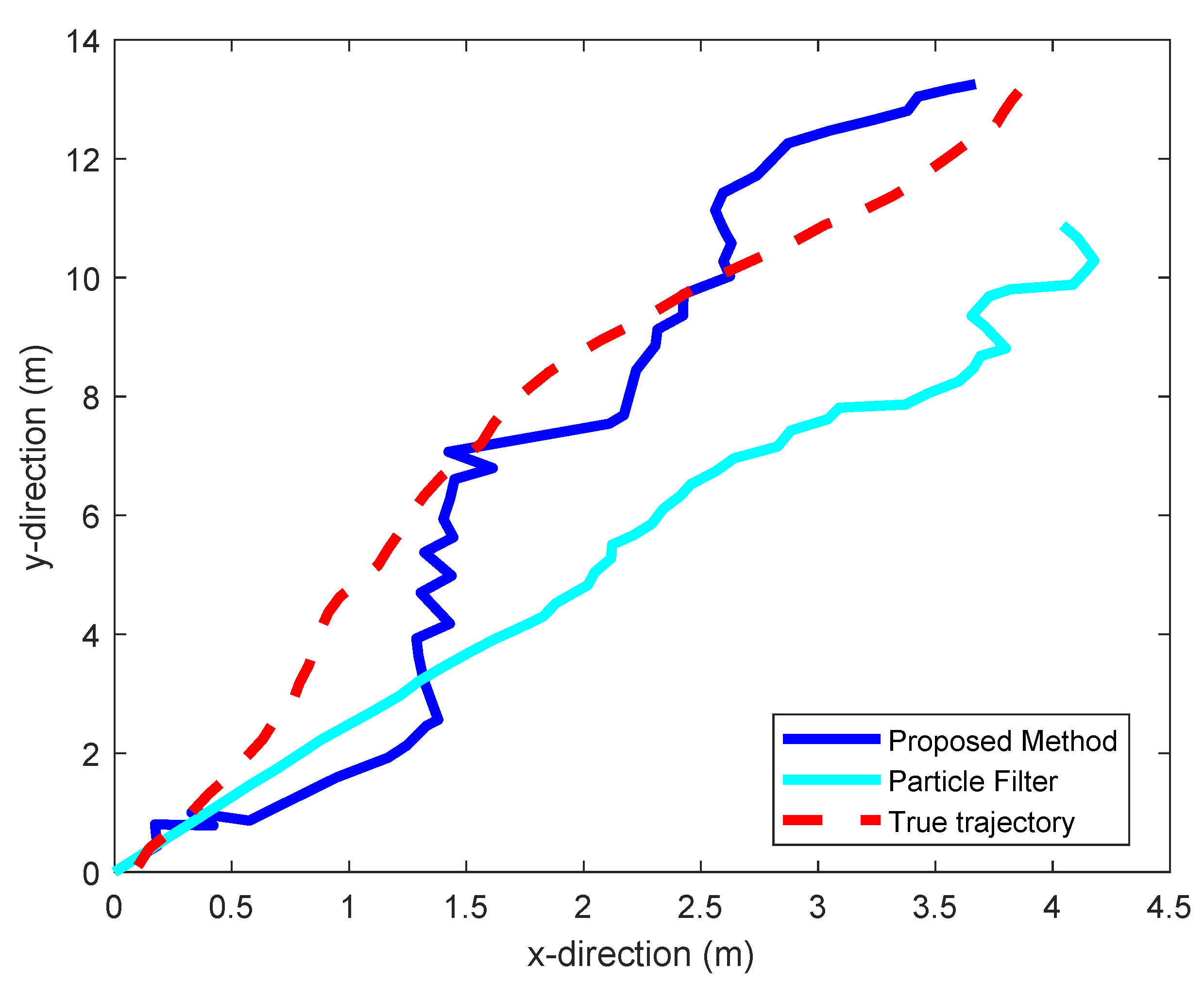
5.2. Dynamic Positioning
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bensky, A. Wireless Positioning Technologies and Applications; Artech House: Norwood, MA, USA, 2016. [Google Scholar]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Sahinoglu, Z.; Gezici, S.; Guvenc, I. Ultra-Wideband Positioning Systems; Cambridge: New York, NY, USA, 2008. [Google Scholar]
- Shi, G.; Ming, Y. Survey of Indoor Positioning Systems Based on Ultra-Wideband (UWB) Technology; Springer: Berlin, Germany, 2016; pp. 1269–1278. [Google Scholar]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zhou, Z.; Liu, Y. From RSSI to CSI:Indoor localization via channel response. ACM Comput. Surv. 2013, 46, 1–32. [Google Scholar]
- Ma, R.; Guo, Q.; Hu, C.; Xue, J. An improved WiFi indoor positioning algorithm by weighted fusion. Sensors 2015, 15, 21824–21843. [Google Scholar] [CrossRef]
- Liu, H.H.; Liu, C. Implementation of Wi-Fi signal sampling on an android smartphone for indoor positioning systems. Sensors 2018, 18, 3. [Google Scholar] [CrossRef]
- Feldmann, S.; Kyamakya, K.; Zapater, A.; Lue, Z. An indoor bluetooth-based positioning system: Concept, implementation and experimental evaluation. In Proceedings of the International Conference on Wireless Networks, Las Vegas, NV, USA, 23–26 June 2003; Volume 272. [Google Scholar]
- Li, X.; Wang, J.; Liu, C. A Bluetooth/PDR integration algorithm for an indoor positioning system. Sensors 2015, 15, 24862–24885. [Google Scholar] [CrossRef]
- Chon, H.D.; Jun, S.; Jung, H.; An, W. Using RFID for accurate positioning. Positioning 2004, 3, 32–39. [Google Scholar] [CrossRef]
- Jechlitschek, C. A survey paper on Radio Frequency Identification (RFID) trends. Radio Freq. IDentif. 2010, 100, 765–768. [Google Scholar]
- Seco, F.; Jiménez, A.R. Smartphone-based cooperative indoor localization with RFID technology. Sensors 2018, 18, 266. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Qiu, Z.; Cao, M.; Nguyen, T.H.; Xie, L. Single landmark distance-based navigation. IEEE Trans. Control Syst. Technol. 2019, 1–8. [Google Scholar] [CrossRef]
- Kotaru, M.; Joshi, K.; Bharadia, D.; Katti, S. SpotFi:Decimeter Level Localization Using WiFi. ACM Sigcomm Comput. Commun. Rev. 2015, 45, 269–282. [Google Scholar] [CrossRef]
- Tian, Z.; Li, Z.; Zhou, M.; Jin, Y.; Wu, Z. PILA: Sub-meter localization using CSI from commodity Wi-Fi devices. Sensors 2016, 16, 1664. [Google Scholar] [CrossRef] [PubMed]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM 2000: Conference on Computer Communications, Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No.00CH37064), Tel Aviv, Israel, 26–30 March 2000. [Google Scholar]
- Jan, S.S.; Yeh, S.J.; Liu, Y.W. Received signal strength database interpolation by Kriging for a Wi-Fi indoor positioning system. Sensors 2015, 15, 21377–21393. [Google Scholar] [CrossRef]
- Youssef, M.; Agrawala, A. The Horus WLAN location determination system. In Proceedings of the 3rd International Conference on Mobile Systems, Applications, and Services, Seattle, WA, USA, 6–8 June 2005; pp. 205–218. [Google Scholar]
- Marelli, D.; Fu, M. Asymptotic Properties of Statistical Estimators using Multivariate Chi-squared Measurements. Digit. Signal Process. 2020, submitted. [Google Scholar]
- Wu, K.; Jiang, X.; Yi, Y.; Chen, D.; Luo, X.; Ni, L.M. CSI-Based Indoor Localization. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1300–1309. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. DeepFi: Deep learning for indoor fingerprinting using channel state information. In Proceedings of the IEEE Wireless Communications & Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015. [Google Scholar]
- Song, Q.; Guo, S.; Liu, X.; Yang, Y. CSI amplitude fingerprinting-based NB-IoT indoor localization. IEEE Internet Things J. 2017, 5, 1494–1504. [Google Scholar] [CrossRef]
- Wang, W.; Marelli, D.; Fu, M. A statistical CSI model for indoor positioning using fingerprinting. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 3630–3633. [Google Scholar]
- Chapre, Y.; Ignjatovic, A.; Seneviratne, A.; Jha, S. CSI-MIMO: Indoor Wi-Fi fingerprinting system. In Proceedings of the 39th Annual IEEE Conference on Local Computer Networks, Edmonton, AB, Canada, 8–11 September 2014. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S. CSI Phase Fingerprinting for Indoor Localization with a Deep Learning Approach. IEEE Internet Things J. 2017, 3, 1113–1123. [Google Scholar] [CrossRef]
- Bernas, M.; Płaczek, B. Fully connected neural networks ensemble with signal strength clustering for indoor localization in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2015, 11, 403242. [Google Scholar] [CrossRef]
- Wang, Y.; Xiu, C.; Zhang, X.; Yang, D. WiFi indoor localization with CSI fingerprinting-based random forest. Sensors 2018, 18, 2869. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S. BiLoc: Bi-modal deep learning for indoor localization with commodity 5GHz WiFi. IEEE Access 2017, 5, 4209–4220. [Google Scholar] [CrossRef]
- Khatab, Z.E.; Hajihoseini, A.; Ghorashi, S.A. A fingerprint method for indoor localization using autoencoder based deep extreme learning machine. IEEE Sens. Lett. 2017, 2, 1–4. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Mao, S. CiFi: Deep convolutional neural networks for indoor localization with 5 GHz Wi-Fi. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Figueiras, J.; Frattasi, S. Mobile Positioning and Tracking; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Dardari, D.; Closas, P.; Djuric, P.M. Indoor Tracking: Theory, Methods, and Technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef]
- Van Der Merwe, R.; Wan, E. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, OGI School of Science & Engineering at OHSU, Portland, OR, USA, 2004. [Google Scholar]
- Leppäkoski, H.; Collin, J.; Takala, J. Pedestrian navigation based on inertial sensors, indoor map, and WLAN signals. J. Signal Process. Syst. 2013, 71, 287–296. [Google Scholar] [CrossRef]
- Chen, Z.; Zou, H.; Jiang, H.; Zhu, Q.; Soh, Y.C.; Xie, L. Fusion of WiFi, smartphone sensors and landmarks using the Kalman filter for indoor localization. Sensors 2015, 15, 715–732. [Google Scholar] [CrossRef] [PubMed]
- Marelli, D.; Fu, M.; Ninness, B. Asymptotic Optimality of the Maximum-Likelihood Kalman Filter for Bayesian Tracking With Multiple Nonlinear Sensors. IEEE Trans. Signal Process. 2015, 63, 4502–4515. [Google Scholar] [CrossRef]
- Sen, S.; Radunovic, B.; Choudhury, R.R.; Minka, T. You are facing the Mona Lisa: Spot localization using PHY layer information. In Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services, Low Wood Bay, Lake District, UK, 25–29 June 2012. [Google Scholar]
- Hardle, W. Kernel Density Estimation; Springer-Verlag New York Inc.: New York, NY, USA, 1991. [Google Scholar]
- Xie, Y.; Li, Z.; Li, M. Precise power delay profiling with commodity Wi-Fi. IEEE Trans. Mob. Comput. 2018, 18, 1342–1355. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
| Methods | Mean Error [meters] | Minimum Error [meters] |
|---|---|---|
| Static positioning | 1.0970 | 0.3196 |
| PhaseFi | 1.4722 | 0.5021 |
| FILA | 2.3825 | 0.5511 |
| DeepFi | 2.0283 | 0.3210 |
| Methods | Mean Error [meters] | Minimum Error [meters] |
|---|---|---|
| Static positioning | 1.4551 | 0.2763 |
| PhaseFi | 1.8722 | 0.4395 |
| FILA | 2.5826 | 0.4863 |
| DeepFi | 2.6770 | 1.0355 |
| Methods | Mean Error [meters] | Maximum Error [meters] |
|---|---|---|
| Static positioning | 0.9879 | 2.4325 |
| Particle filter | 1.6475 | 2.8131 |
| Dynamic positioning | 0.4602 | 1.0706 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Marelli, D.; Fu, M. Fingerprinting-Based Indoor Localization Using Interpolated Preprocessed CSI Phases and Bayesian Tracking. Sensors 2020, 20, 2854. https://doi.org/10.3390/s20102854
Wang W, Marelli D, Fu M. Fingerprinting-Based Indoor Localization Using Interpolated Preprocessed CSI Phases and Bayesian Tracking. Sensors. 2020; 20(10):2854. https://doi.org/10.3390/s20102854
Chicago/Turabian StyleWang, Wenxu, Damián Marelli, and Minyue Fu. 2020. "Fingerprinting-Based Indoor Localization Using Interpolated Preprocessed CSI Phases and Bayesian Tracking" Sensors 20, no. 10: 2854. https://doi.org/10.3390/s20102854
APA StyleWang, W., Marelli, D., & Fu, M. (2020). Fingerprinting-Based Indoor Localization Using Interpolated Preprocessed CSI Phases and Bayesian Tracking. Sensors, 20(10), 2854. https://doi.org/10.3390/s20102854





