Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction
Abstract
1. Introduction
2. Methodology
2.1. Problem Definition
2.2. Accelerated Algorithm Using the Proximal Splitting with Passty’s Framework
 |
2.3. Optimization
2.3.1. Update the Data-Fidelity Term
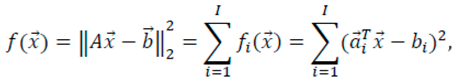
 , the above minimization problem for each subfunction can be converted into the constrained minimization below
, the above minimization problem for each subfunction can be converted into the constrained minimization below

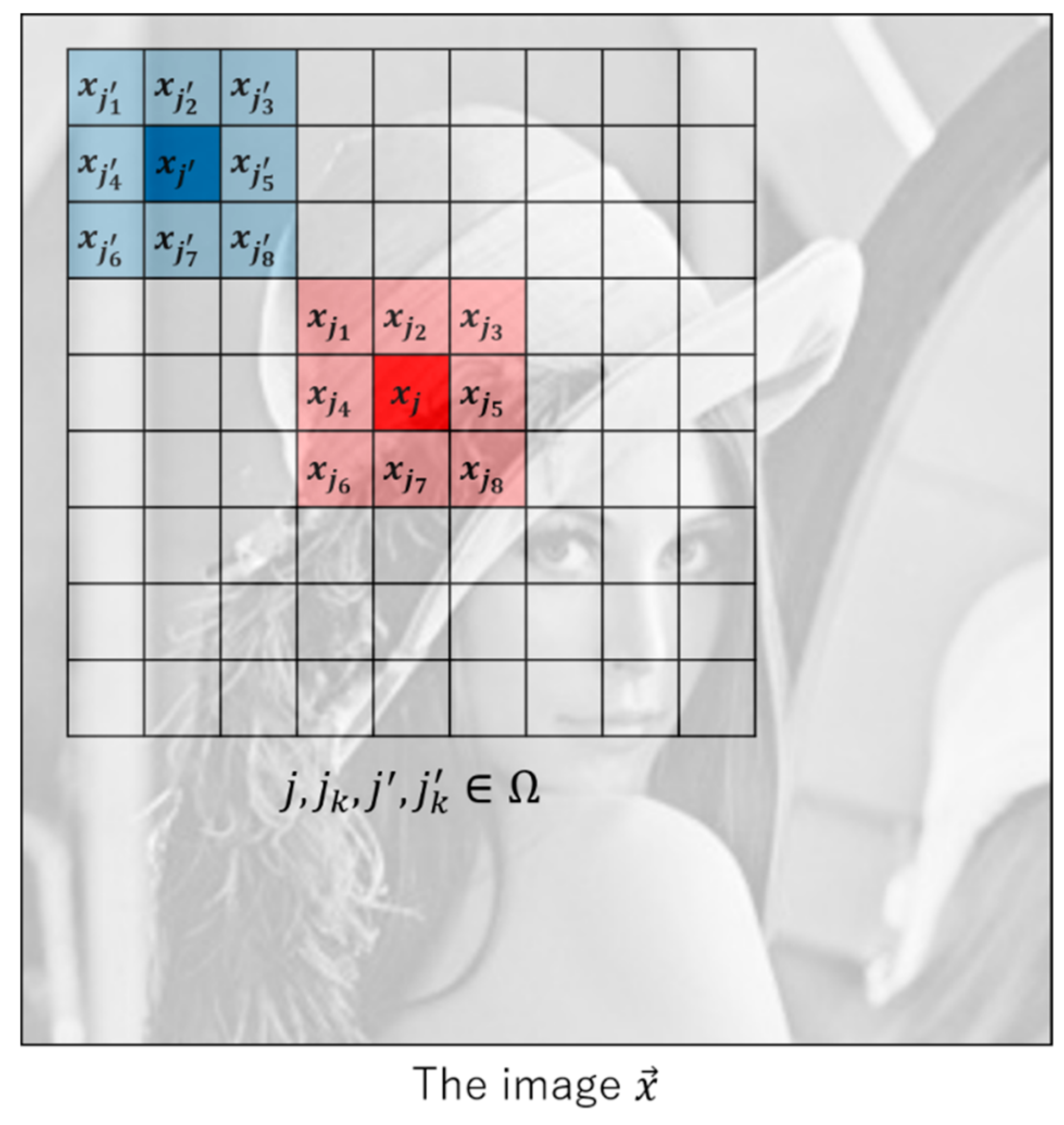
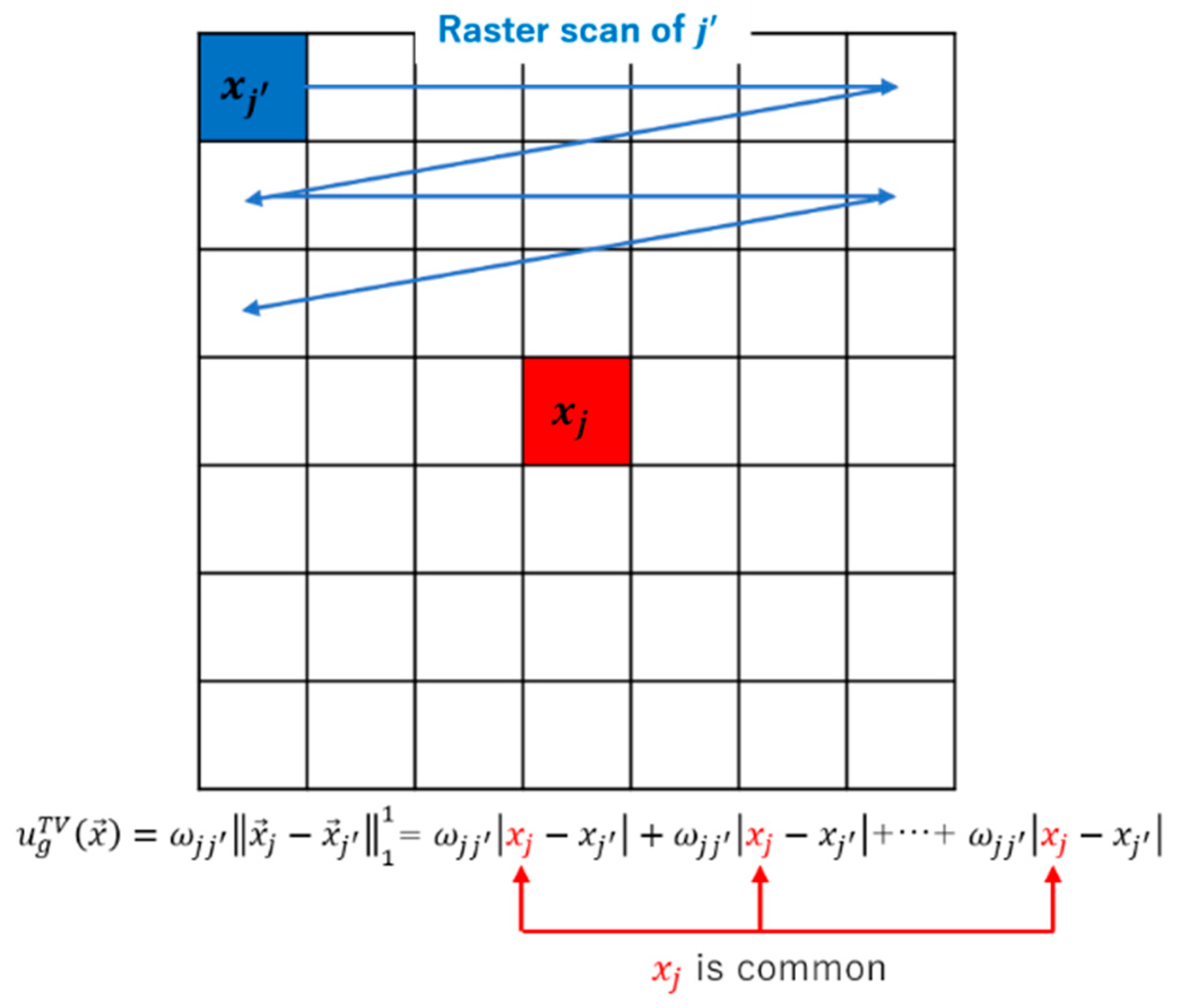
2.3.2. Update the Regularization Term
2.3.3. The Weight

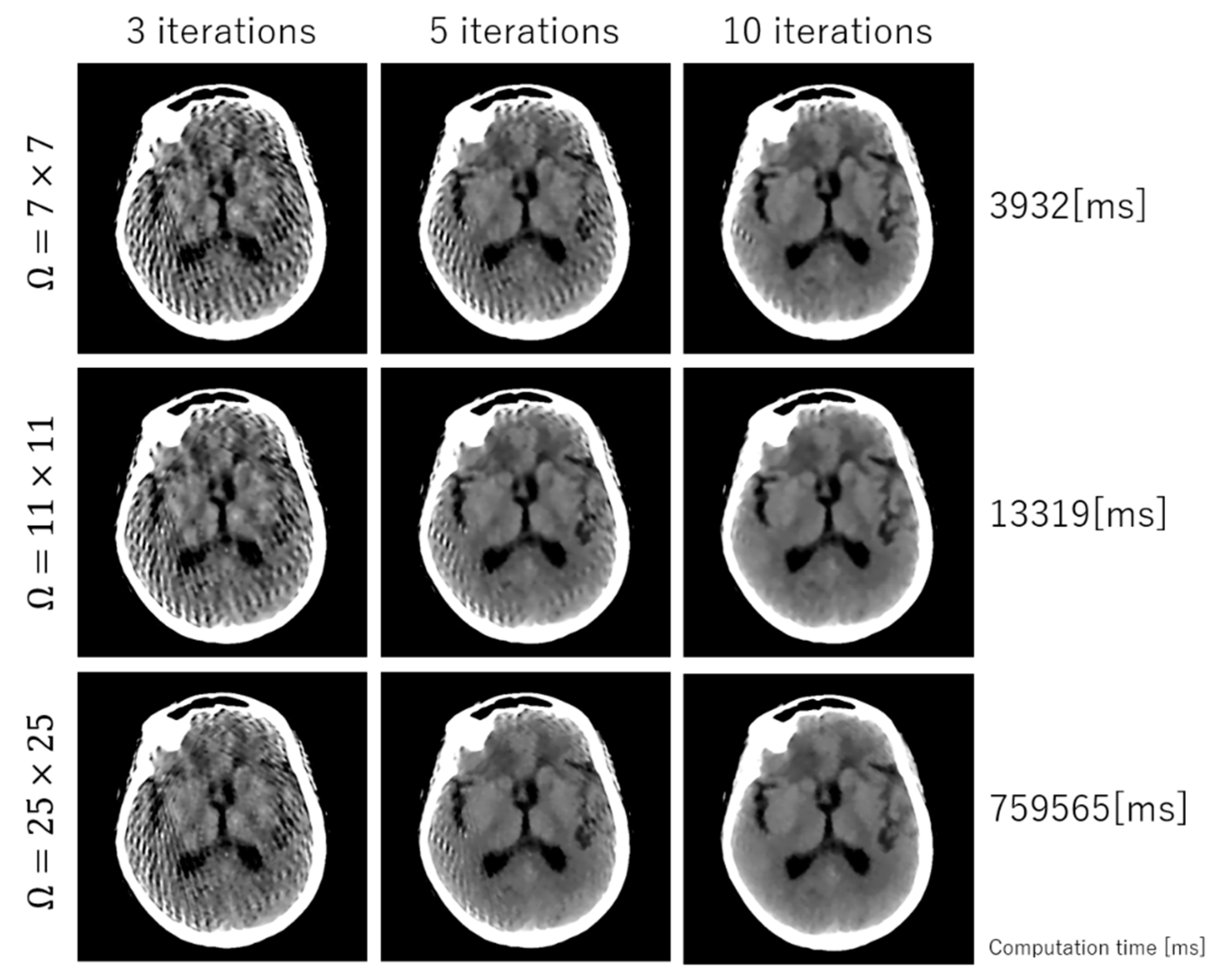
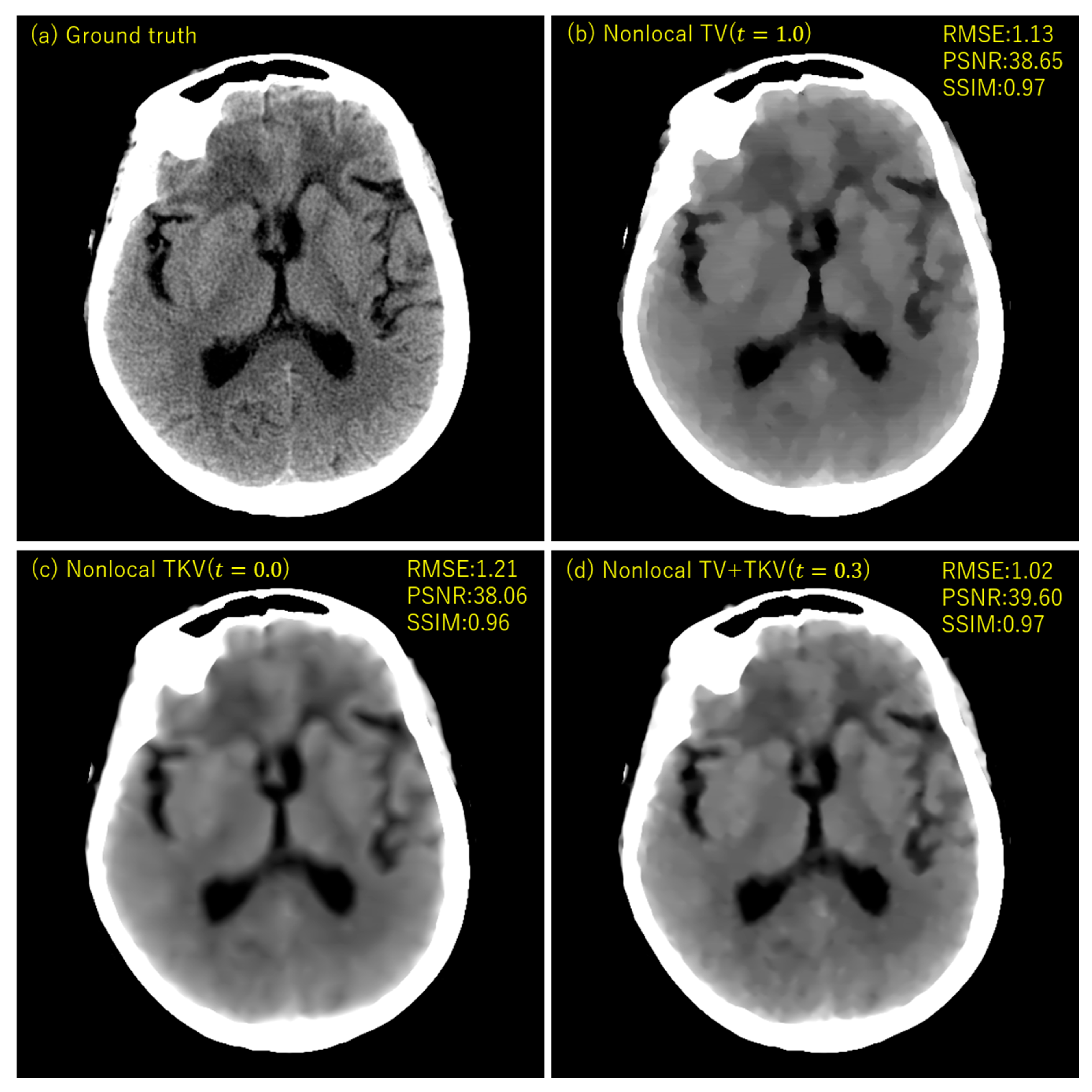
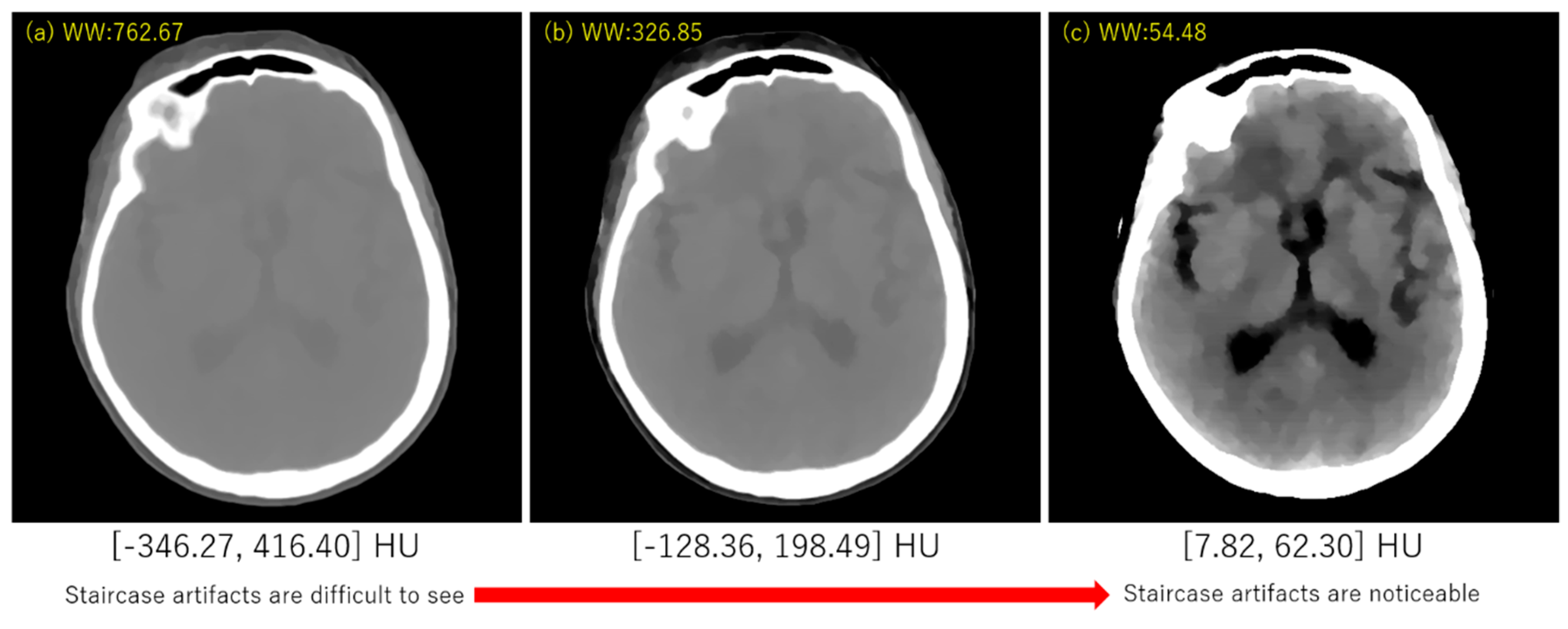
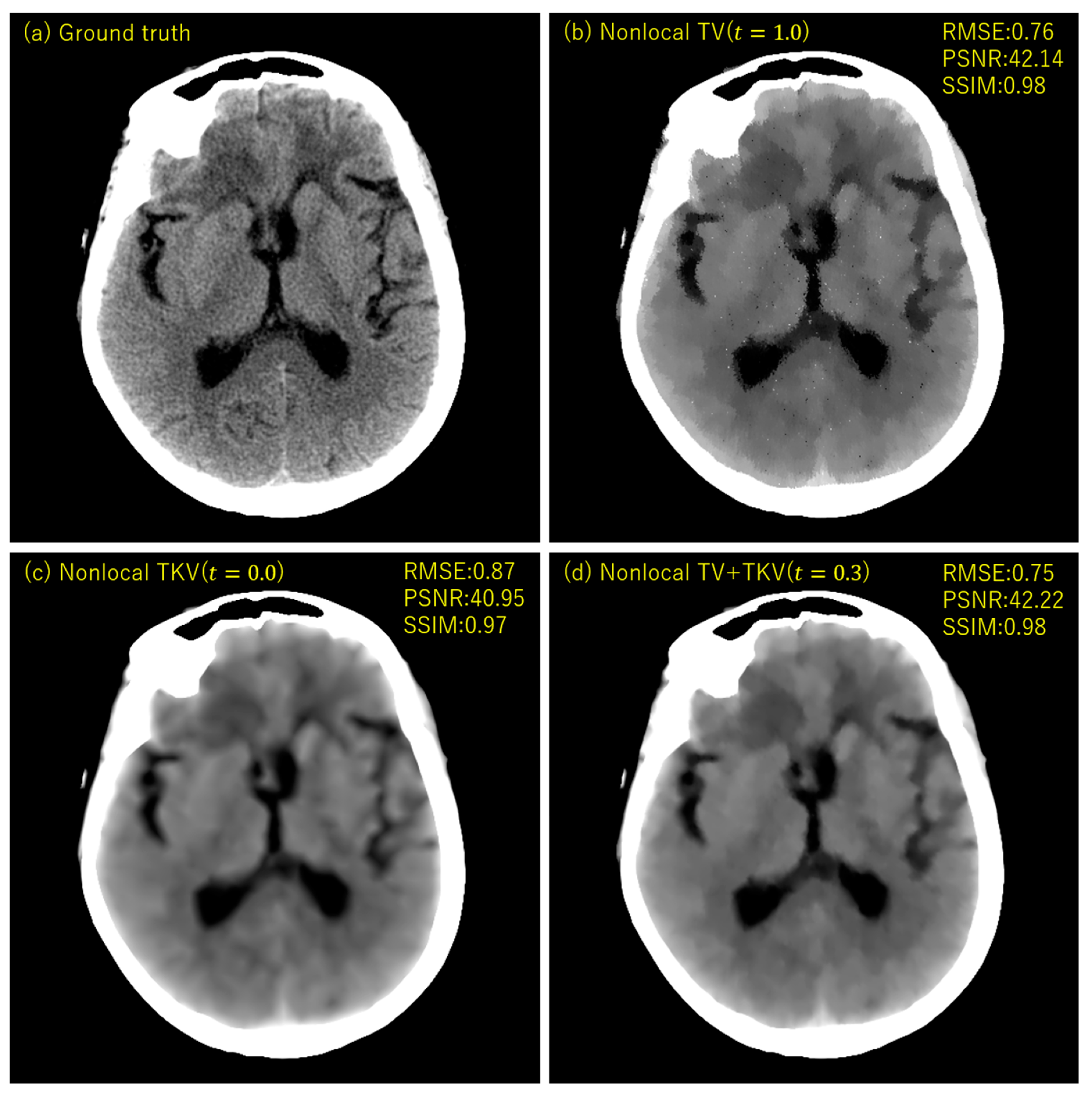
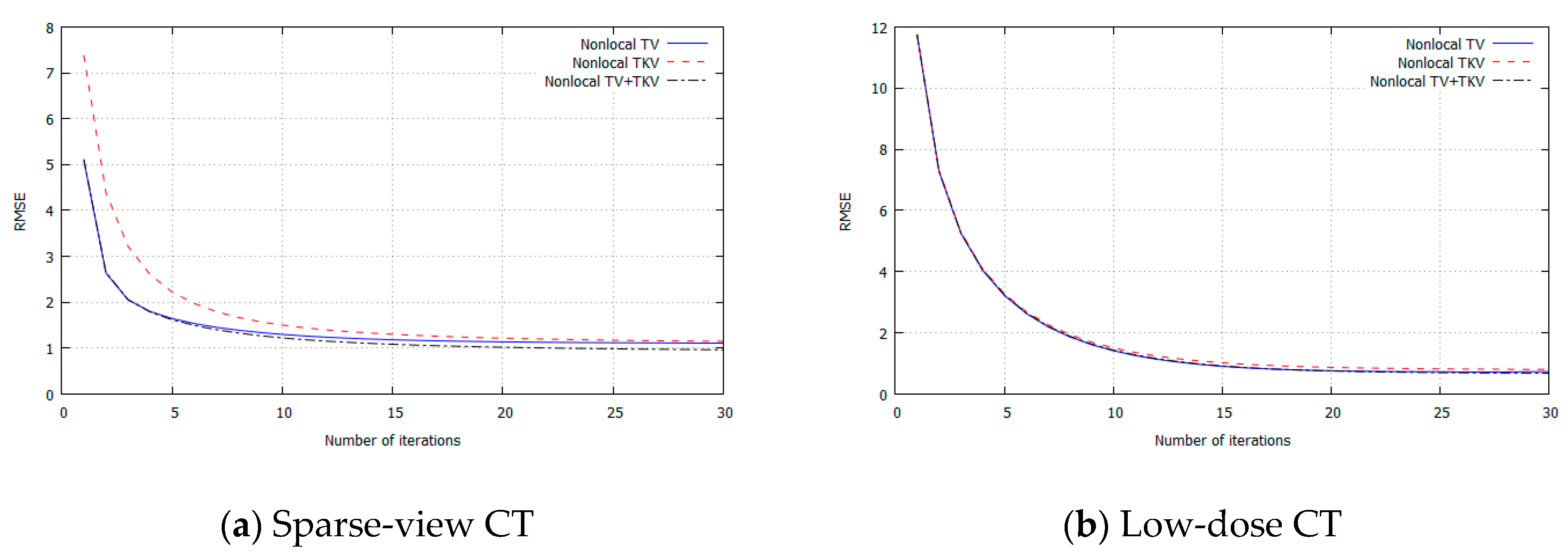
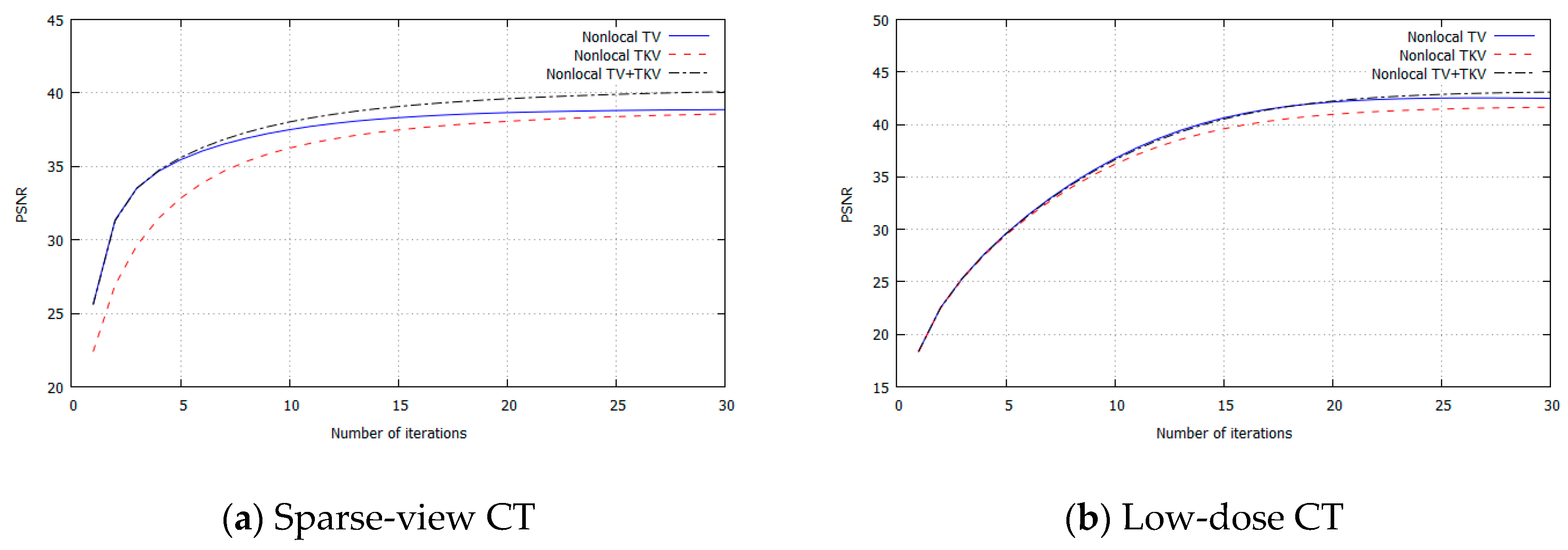
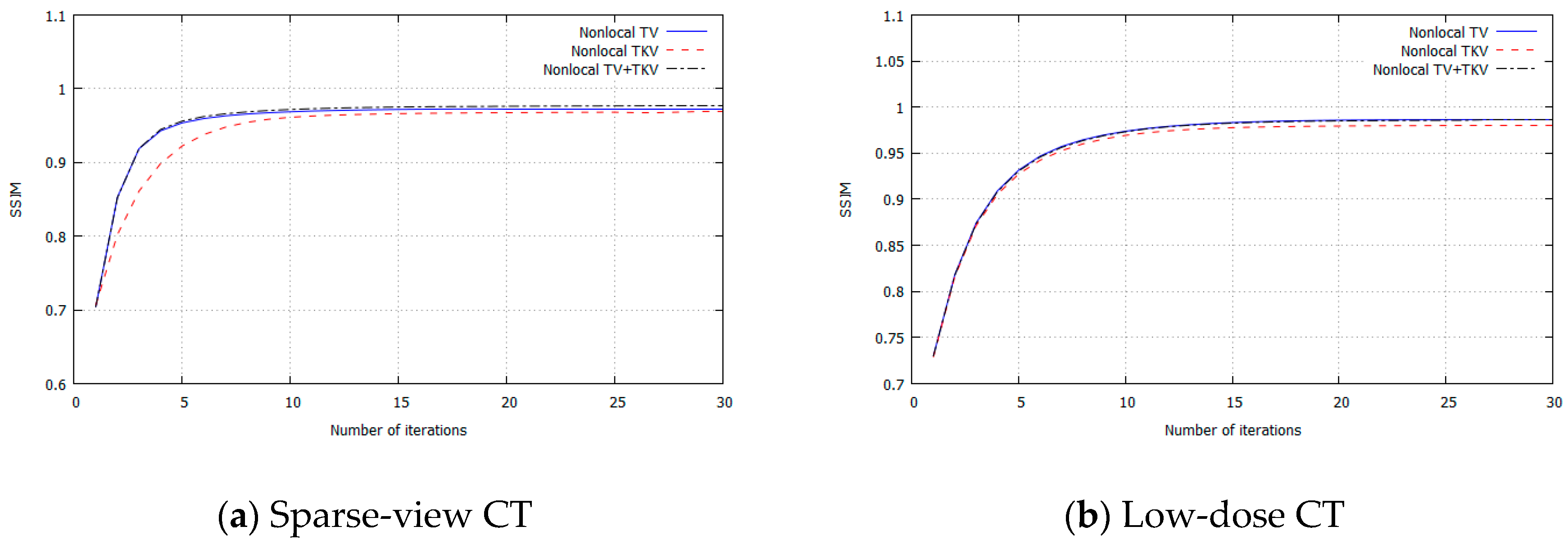
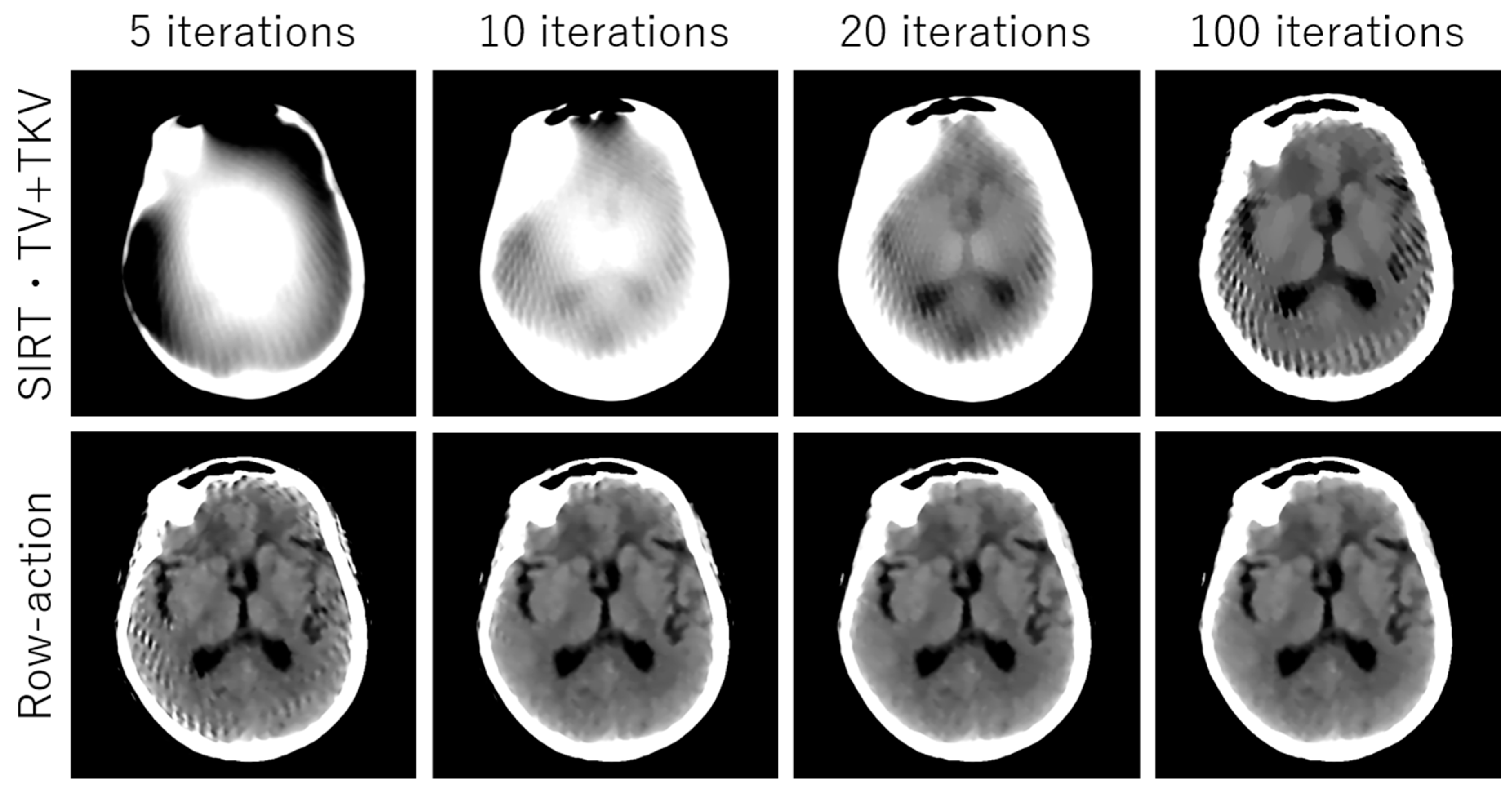
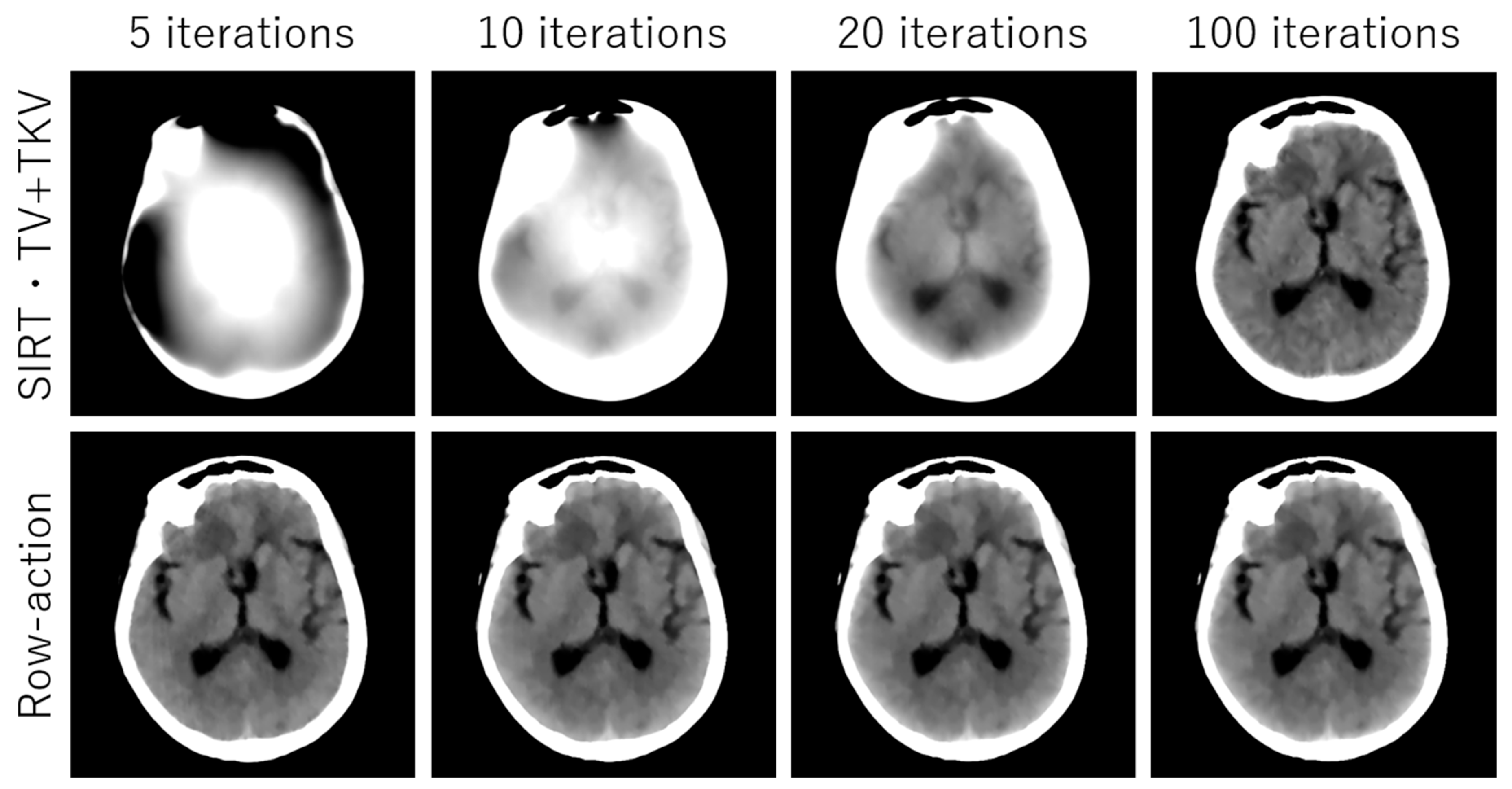
3. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, Y.; Kudo, H.; Chigita, K.; Lian, S. Image reconstruction in sparse-view CT using improved nonlocal total variation regularization. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 10 September 2019. [Google Scholar]
- Kim, H.; Chen, J.; Wang, A.; Chuang, C.; Held, M.; Pouliot, J. Non-local total-variation (NLTV) minimization combined with reweighted L1-norm for compressed sensing CT reconstruction. Phys. Med. Biol. 2016, 61, 6878–6891. [Google Scholar] [CrossRef]
- Kim, K.; El Fakhri, G.; Li, Q. Low-dose CT reconstruction using spatially encoded nonlocal penalty. Med. Phys. 2017, 44, e376–e390. [Google Scholar] [CrossRef] [PubMed]
- Lv, D.; Zhou, Q.; Choi, J.K.; Li, J.; Zhang, X. NLTG Priors in Medical Image: Nonlocal TV-Gaussian (NLTG) prior for Bayesian inverse problems with applications to Limited CT Reconstruction. Inverse Prob. Imaging 2019, 14, 117–132. [Google Scholar] [CrossRef]
- Gilboa, G.; Osher, S. Nonlocal Operators with Applications to Image Processing. Multiscale Model. Simul. 2009, 7, 1005–1028. [Google Scholar] [CrossRef]
- Bresson, X. A Short Note for Nonlocal TV Minimization. Technical Report. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.210.471&rep=rep1&type=pdf (accessed on 15 June 2020).
- Chambolle, A. An algorithm for Total variation Regularization and Denoising. J. Math. Imaging. 2004, 20, 89–97. [Google Scholar]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, L. Sequentially reweighted TV minimization for CT metal artifact reduction. Med. Phys. 2013, 40, 1–12. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imag. Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Ranftl, R.; Bredies, K.; Pock, T. Non-local total generalized variation for optical flow estimation. Lect. Notes Comput. Sci. 2014, 8689, 439–454. [Google Scholar]
- Parikh, N.; Boyd, S. Proximal Algorithms. Available online: https://web.stanford.edu/~boyd/papers/pdf/prox_algs.pdf (accessed on 15 June 2020).
- Combettes, P.L.; Pesquet, J.C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: New York, NY, USA, 2011. [Google Scholar]
- Passty, G.B. Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 1979, 72, 383–390. [Google Scholar] [CrossRef]
- Herman, G.T.; Meyer, L.B. Algebraic reconstruction techniques can be made computationally efficient (positron emission tomography application). IEEE Trans. Med. Imaging 1993, 12, 600–609. [Google Scholar] [CrossRef]
- Tanaka, E.; Kudo, H. Subset-dependent relaxation in block-iterative algorithms for image reconstruction in emission tomography. Phys. Med. Biol. 2003, 48, 1405–1422. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Jiang, M. Ordered subset simultaneous algebraic reconstruction techniques (OS SART). J. of X Ray Sci. Technol. 2004, 12, 169–177. [Google Scholar]
- Dong, J.; Kudo, H. Proposal of Compressed Sensing Using Nonlinear Sparsifying Transform for CT Image Reconstruction. Med. Imaging Technol. 2016, 34, 235–244. [Google Scholar]
- Dong, J.; Kudo, H. Accelerated Algorithm for Compressed Sensing Using Nonlinear Sparsifying Transform in CT Image Reconstruction. Med. Imaging Technol. 2017, 35, 63–73. [Google Scholar]
- Dong, J.; Kudo, H.; Kim, Y. Accelerated Algorithm for the Classical SIRT Method in CT Image Reconstruction. In Proceedings of the 5th International Conference on Multimedia and Image Processing, Nanjing, China, 10–12 January 2020; pp. 49–55. [Google Scholar]
- Kudo, H.; Takaki, K.; Yamazaki, F.; Nemoto, T. Proposal of fault-tolerant tomographic image reconstruction. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 3 October 2016. [Google Scholar]
- Kudo, H.; Dong, J.; Chigita, K.; Kim, Y. Metal artifact reduction in CT using fault-tolerant image reconstruction. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 10 September 2019. [Google Scholar]
- Li, M.; Yang, H.; Kudo, H. An accurate iterative reconstruction algorithm for sparse objects: Application to 3 D blood vessel reconstruction from a limited number of projections. Phys. Med. Biol. 2002, 47, 2599–2609. [Google Scholar] [CrossRef] [PubMed]
- Kudo, H.; Suzuki, T.; Rashed, E.A. Image reconstruction for sparse-view CT and interior CT-introduction to compressed sensing and differentiated backprojection. Quant. Imaging Med. Surg. 2013, 3. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. On image denoising methods. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.100.81&rep=rep1&type=pdf (accessed on 15 June 2020).
- Sidky, E.Y.; Jørgensen, J.H.; Pan, X. Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle–Pock algorithm. Phys. Med. Biol. 2012, 57, 3065–3091. [Google Scholar] [CrossRef]
- Han, Y.; Ye, J.C. Framing U-Net via Deep Convolutional Framelets: Application to Sparse-View CT. IEEE Trans. Med. Imaging 2018, 37, 1418–1429. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep Convolutional Neural Network for Inverse Problems in Imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Shi, F.; Cheng, J.; Wang, L.; Yap, P.-T.; Shen, D. Low-Rank Total Variation for Image Super-Resolution. Med. Image Comput. Comput. Assist. Interv. 2013, 16, 155–162. [Google Scholar] [PubMed]
- Niu, S.; Yu, G.; Ma, J.; Wang, J. Nonlocal low-rank and sparse matrix decomposition for spectral CT reconstruction. Inverse Probl. 2018, 34. [Google Scholar] [CrossRef] [PubMed]


| Nonlocal TV | Nonlocal TKV | Nonlocal TV + TKV | |
|---|---|---|---|
| Convergence | Good | Not bad | Good |
| High contrast | Yes | No | Yes |
| Smooth intensity change | No | Yes | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Kudo, H. Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction. Sensors 2020, 20, 3494. https://doi.org/10.3390/s20123494
Kim Y, Kudo H. Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction. Sensors. 2020; 20(12):3494. https://doi.org/10.3390/s20123494
Chicago/Turabian StyleKim, Yongchae, and Hiroyuki Kudo. 2020. "Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction" Sensors 20, no. 12: 3494. https://doi.org/10.3390/s20123494
APA StyleKim, Y., & Kudo, H. (2020). Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction. Sensors, 20(12), 3494. https://doi.org/10.3390/s20123494





