Static Tactile Sensing for a Robotic Electronic Skin via an Electromechanical Impedance-Based Approach
Abstract
1. Introduction
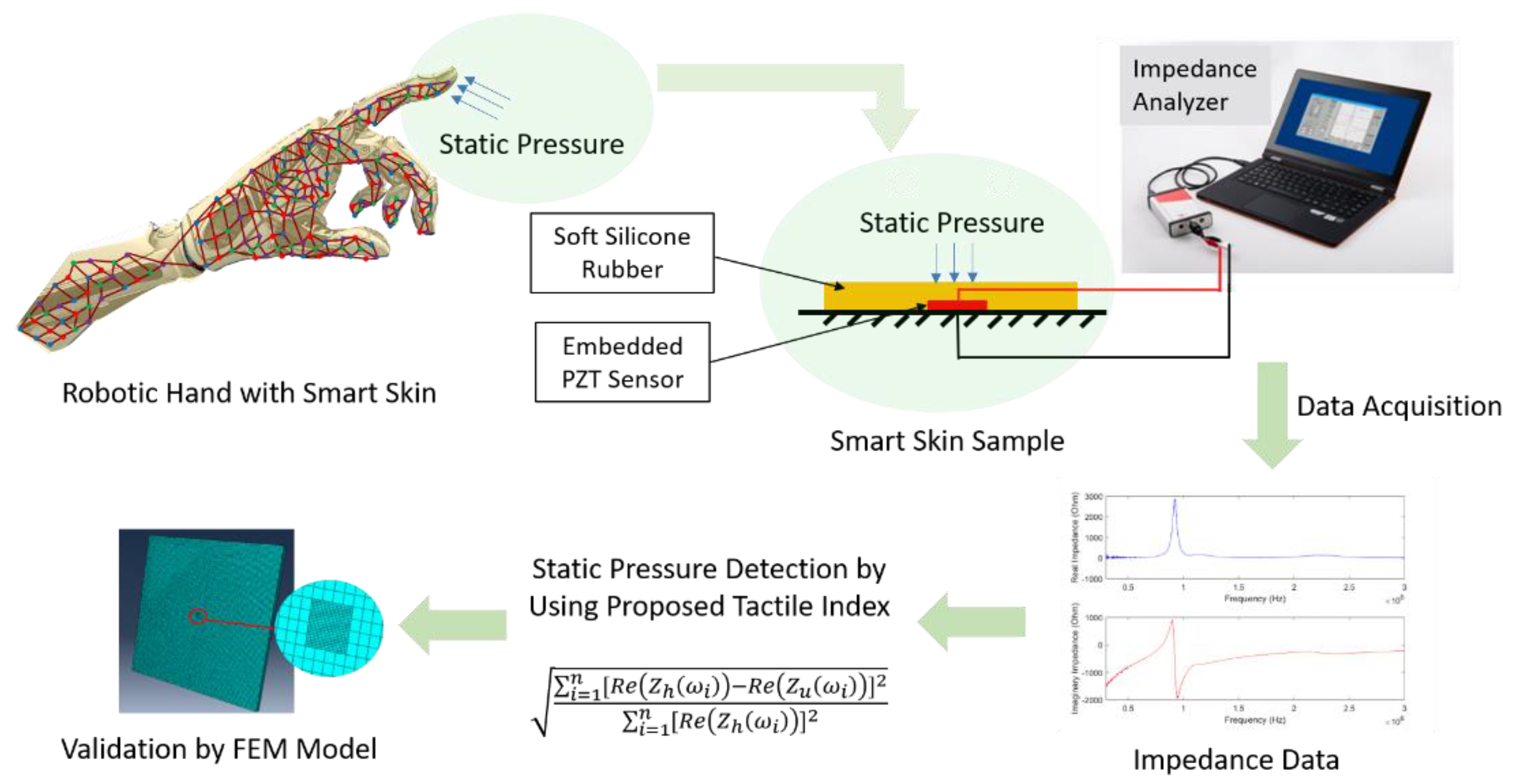
2. Problem Statement
3. Method of Approach
4. Experiment and Results
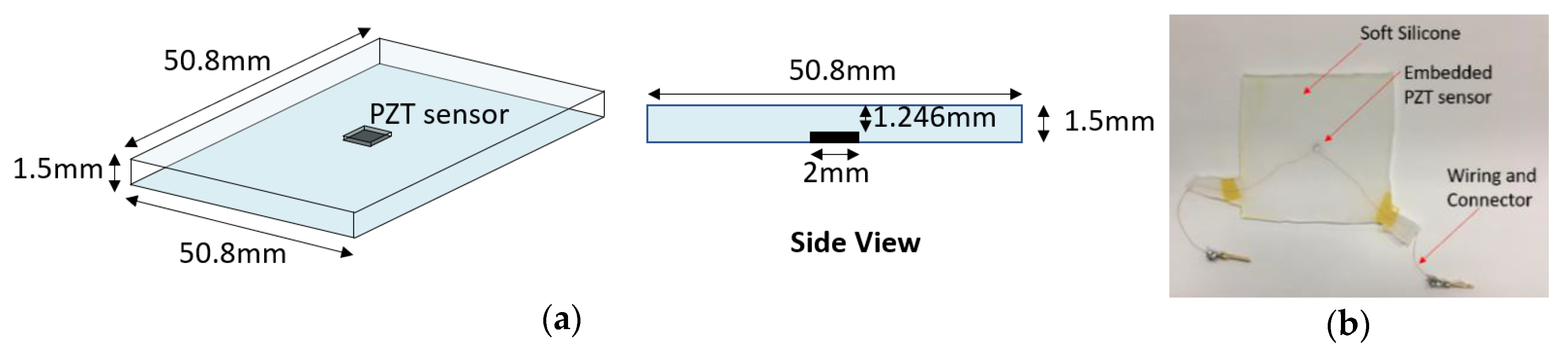
4.1. Smart Skin Sample Development
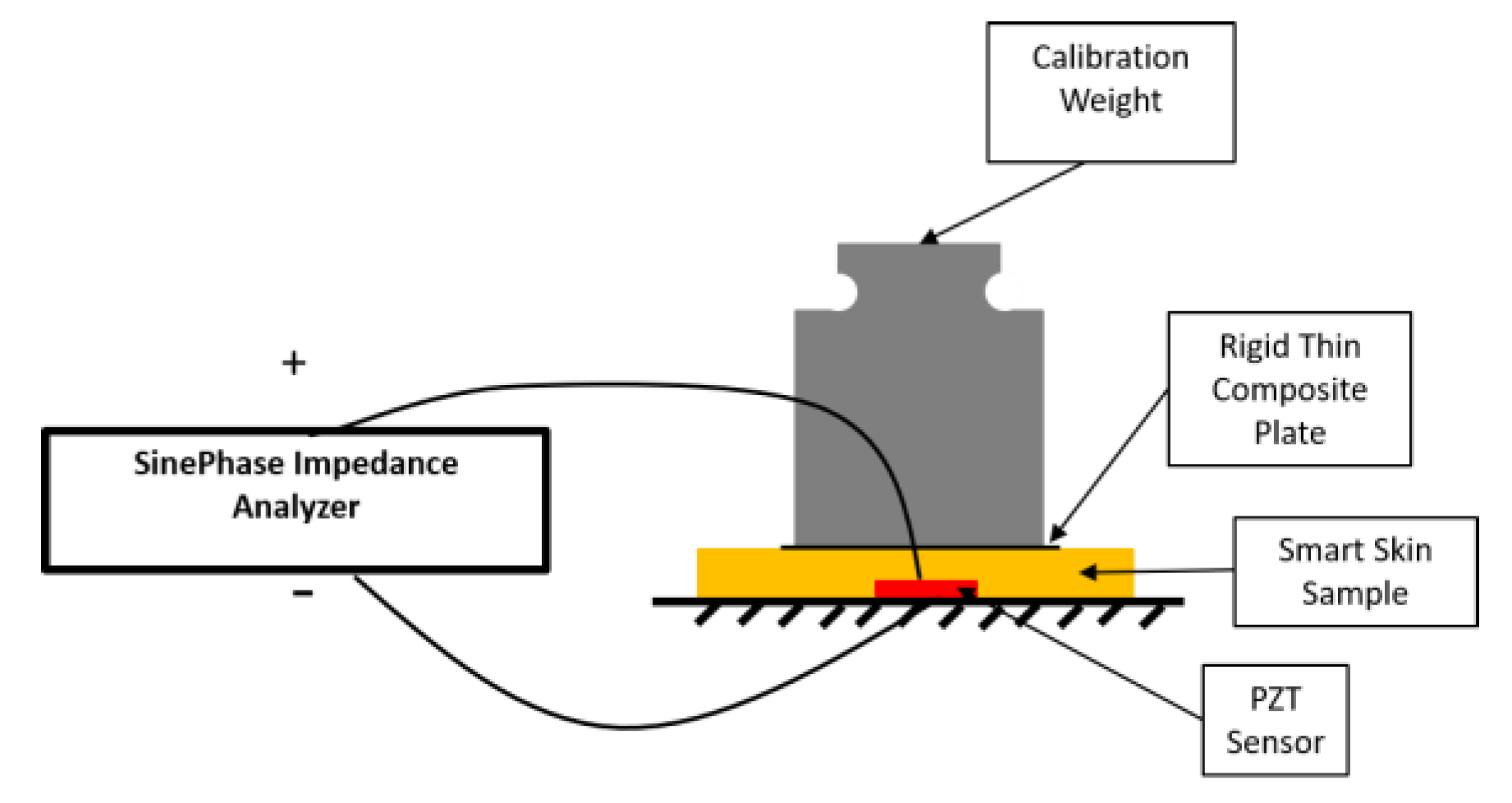
4.2. Test Procedure
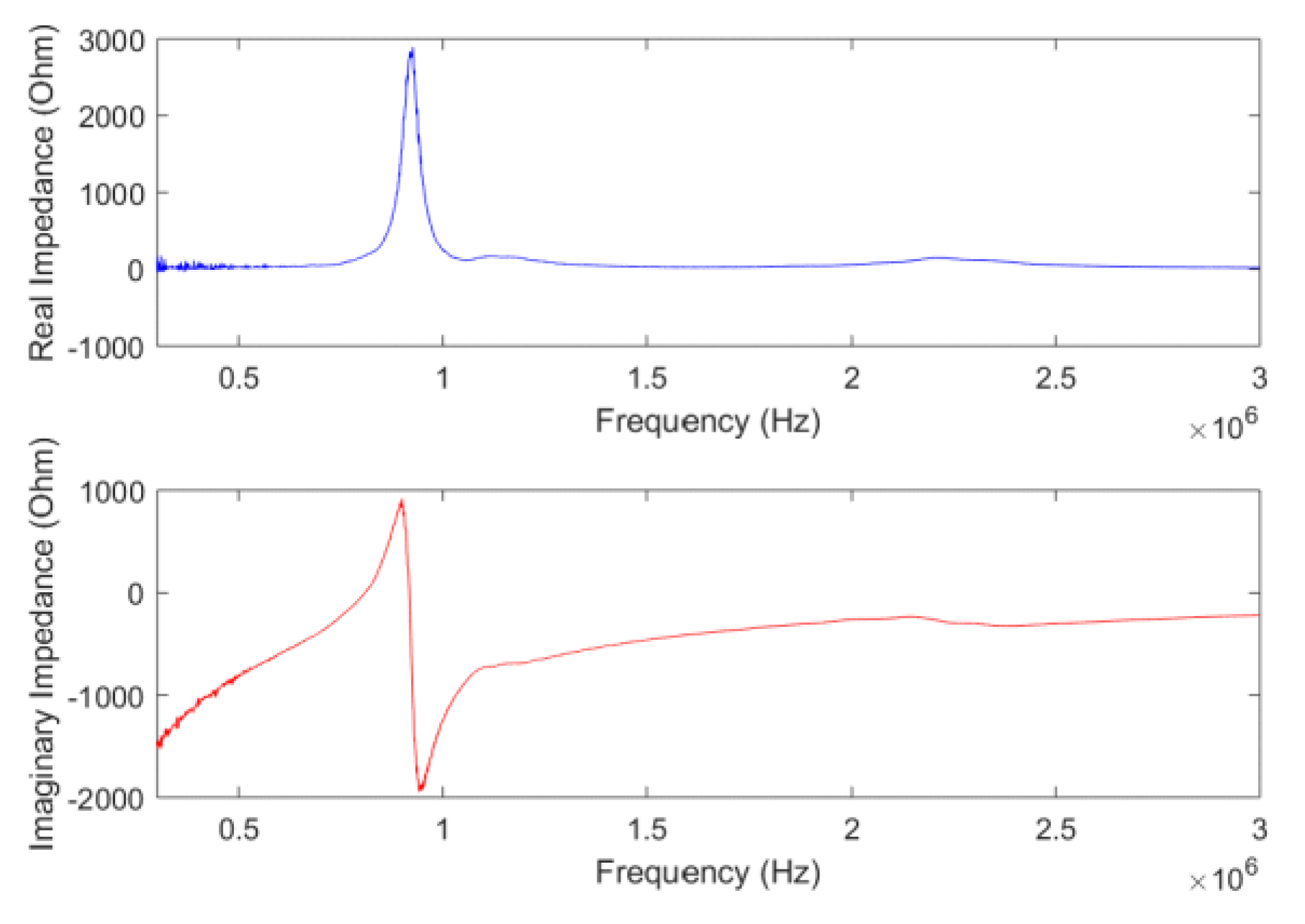
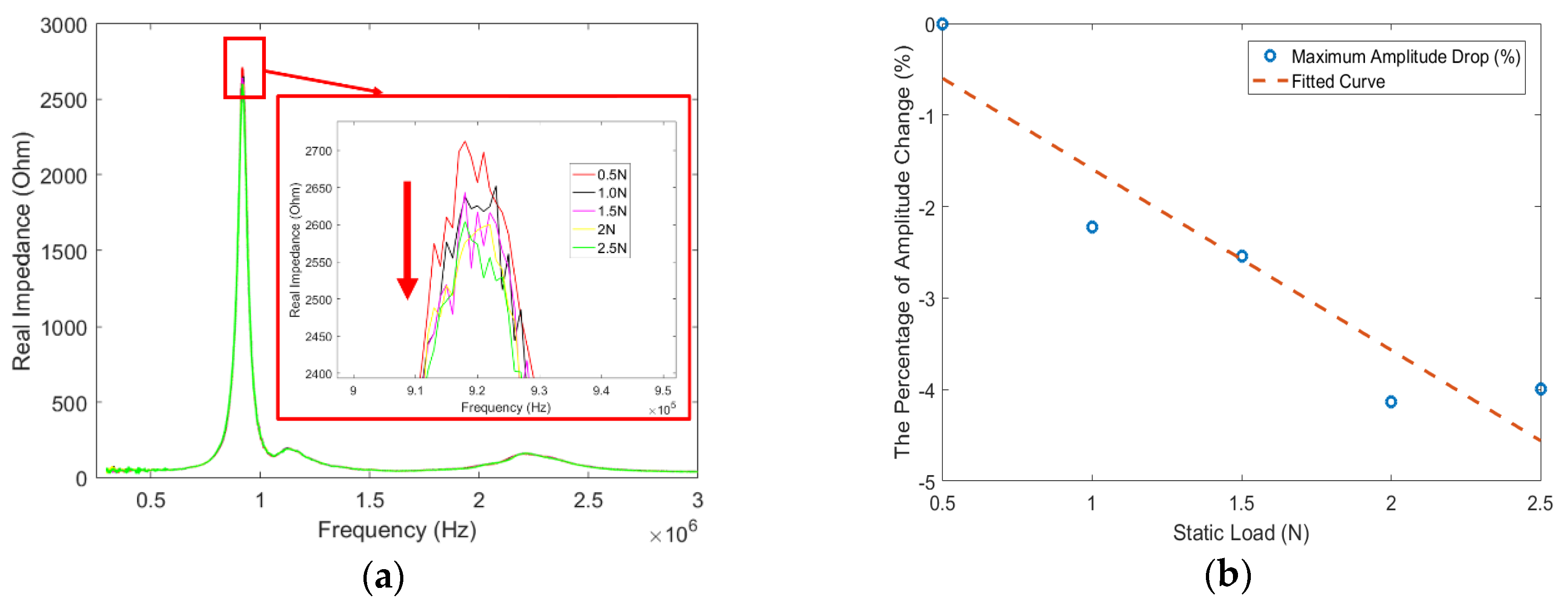
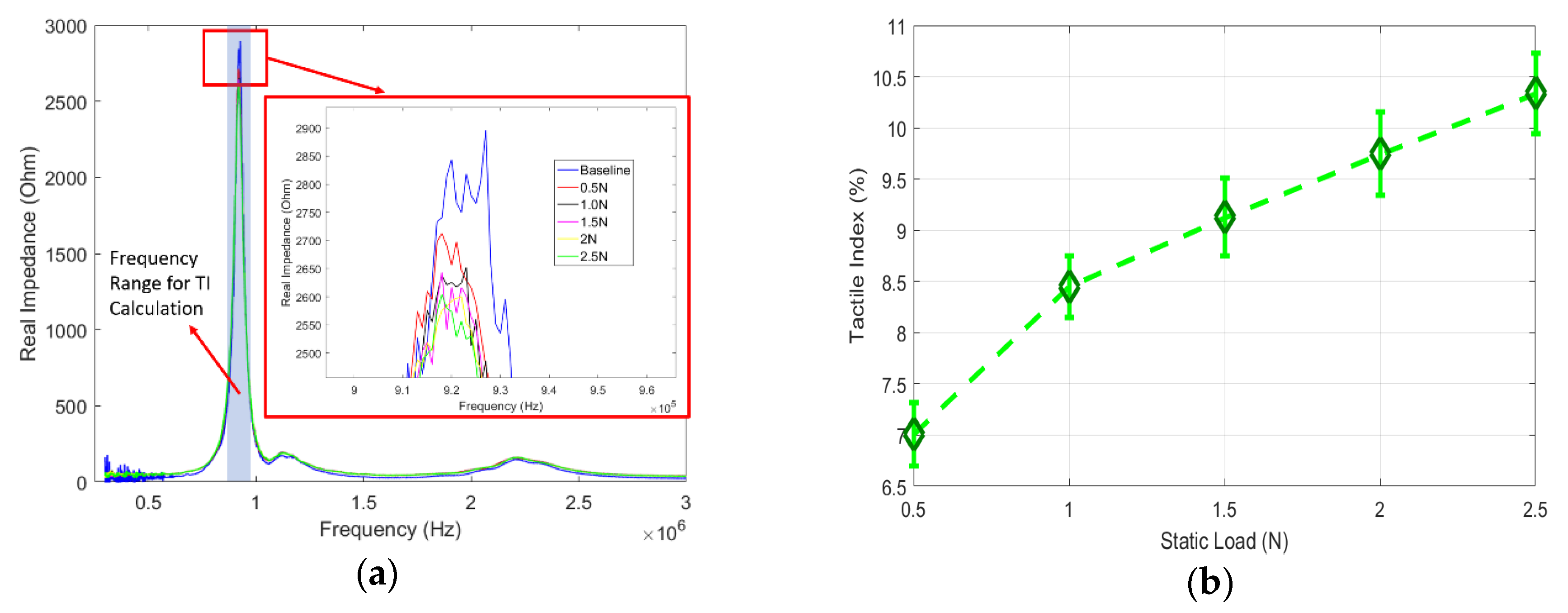
4.3. Results of Impedance Response to Static Pressure Loads
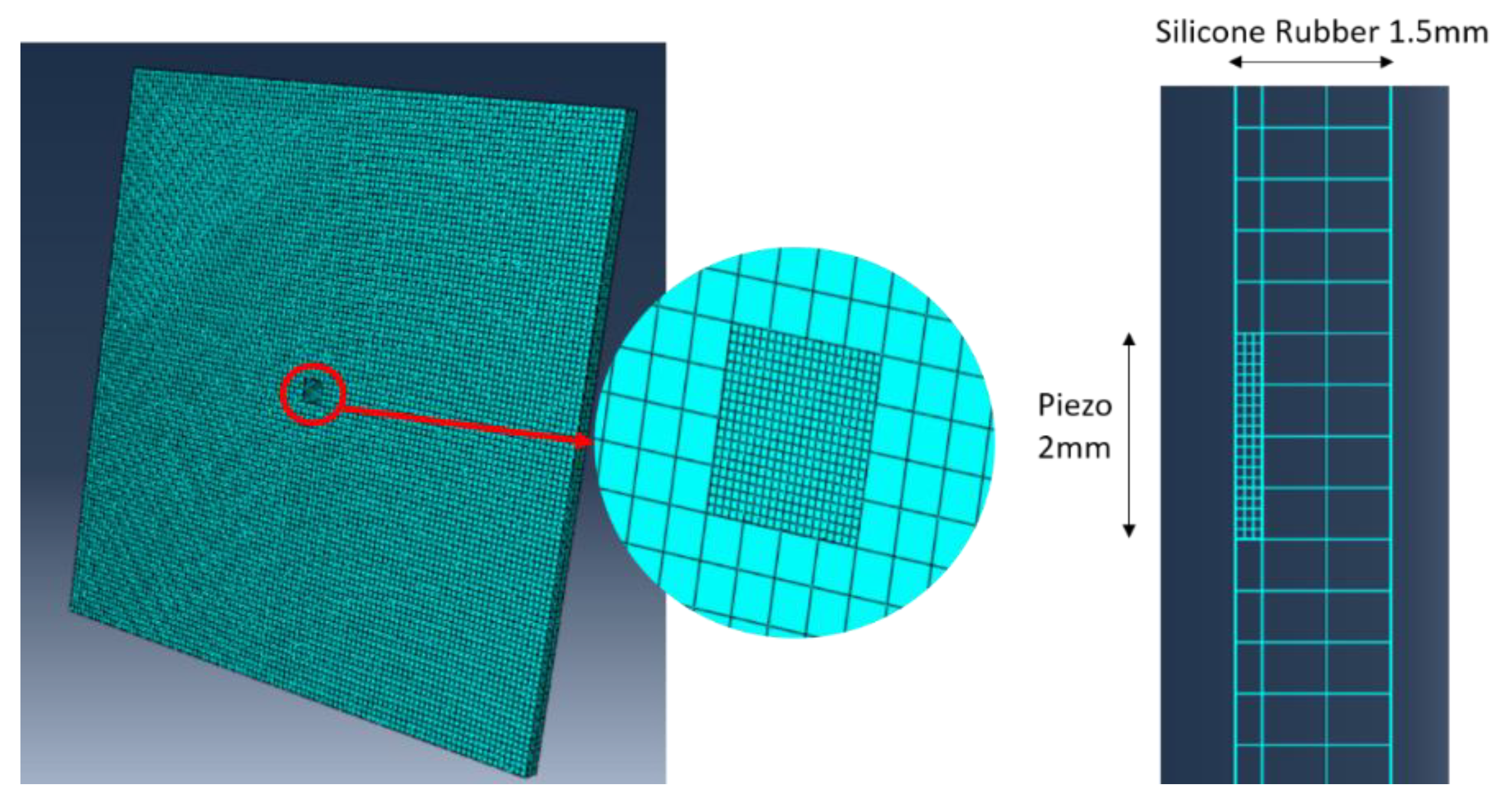
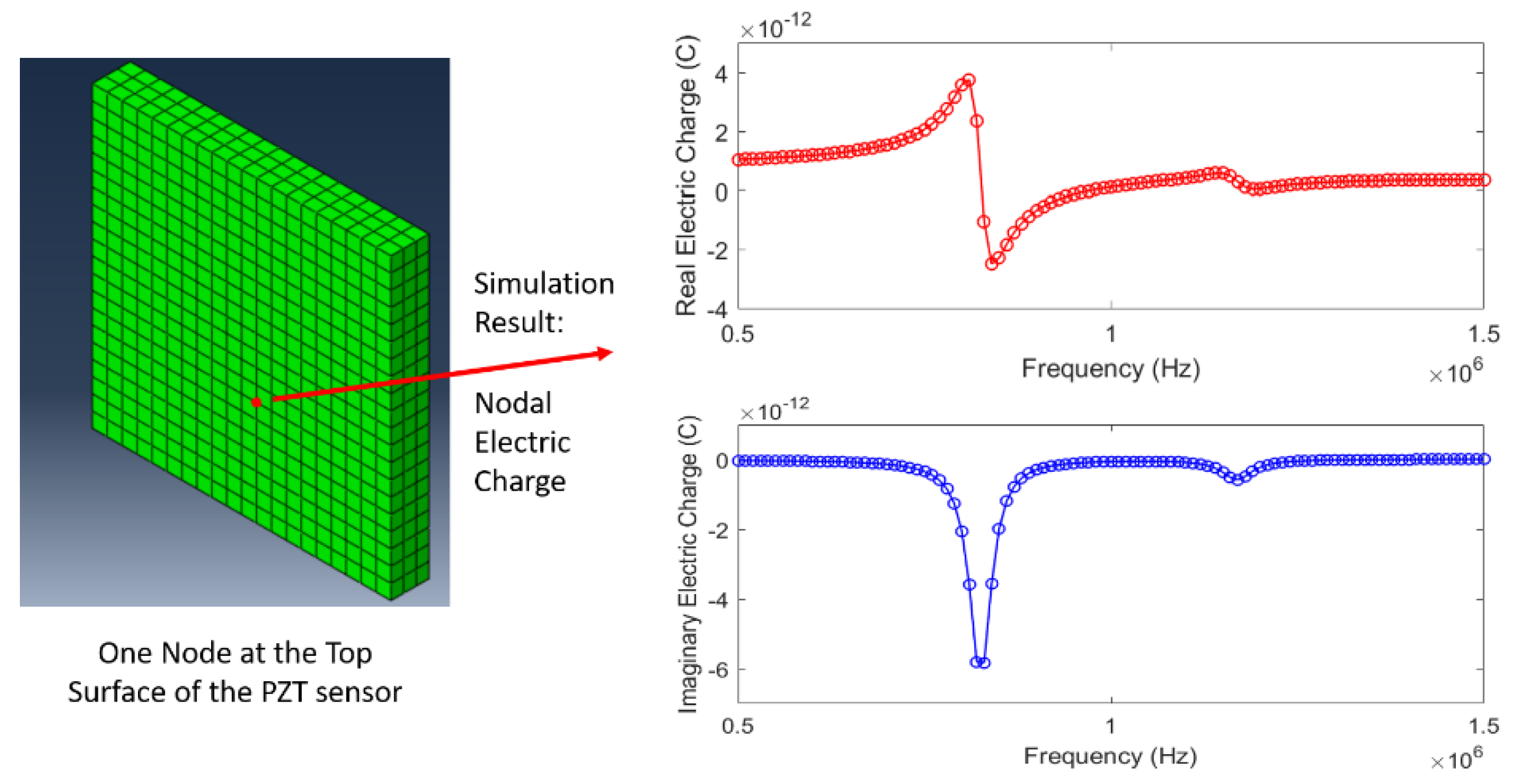
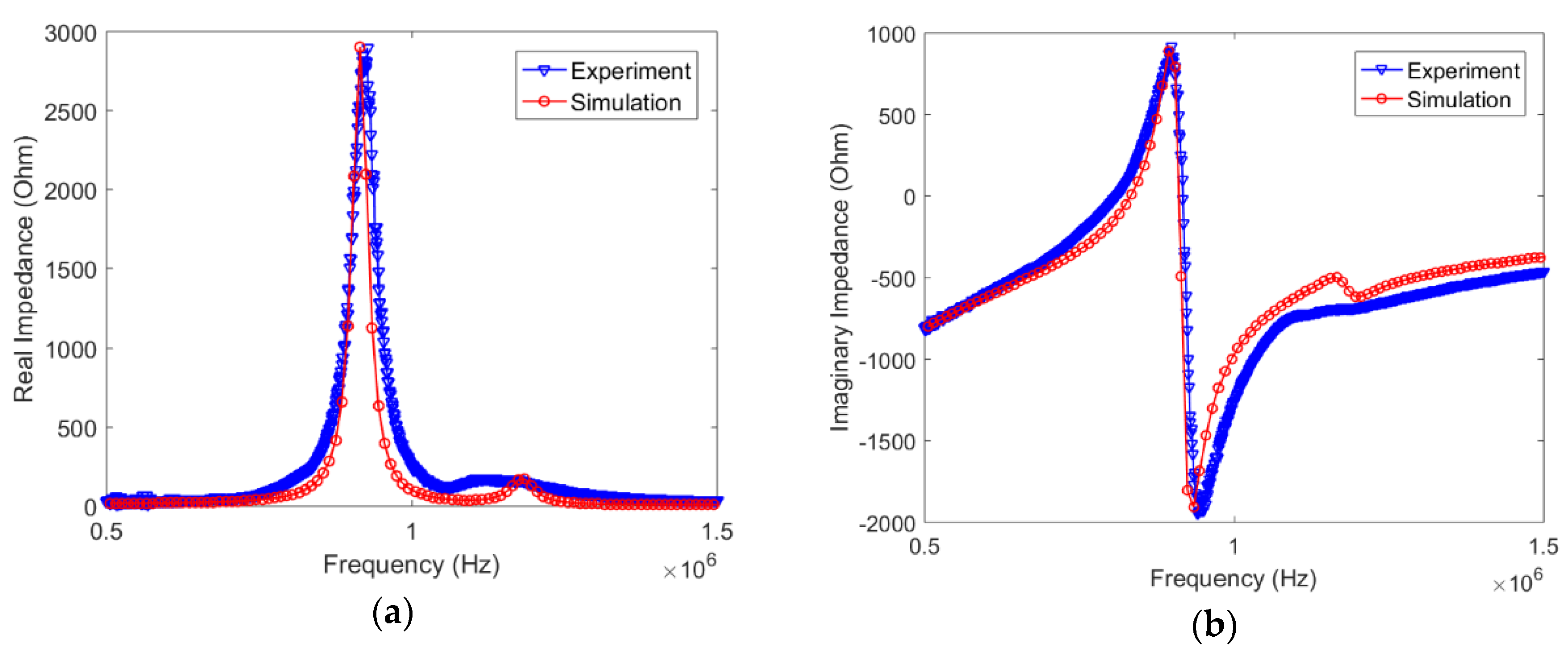
5. Finite Element Simulation Study
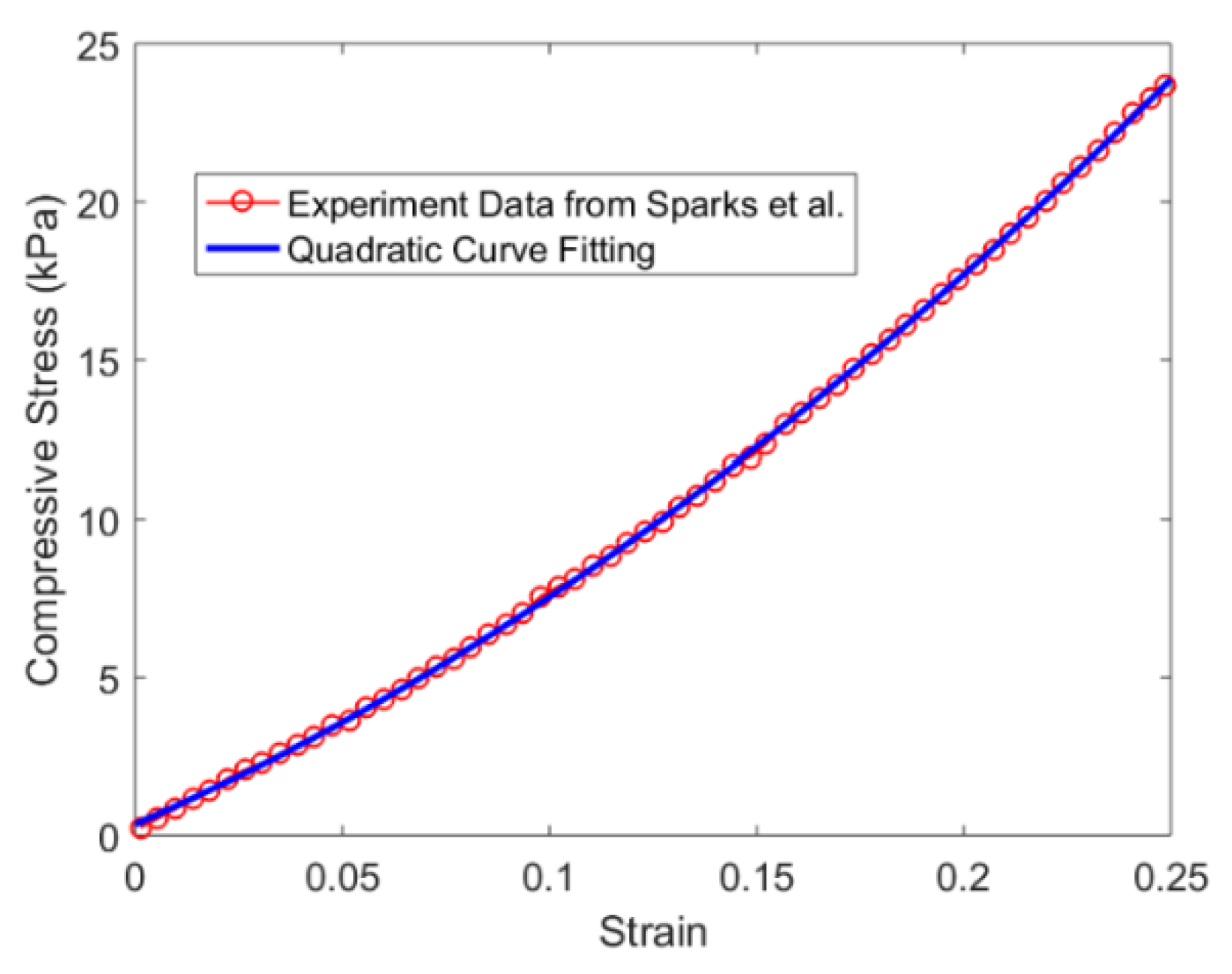
5.1. Hyperelastic Material Property of Silicone Rubber
5.2. Dynamic Compressive Behavior of Silicone Rubber Material
5.3. A Direct Steady-State Dynamic Analysis for Simulating Impedance Behavior
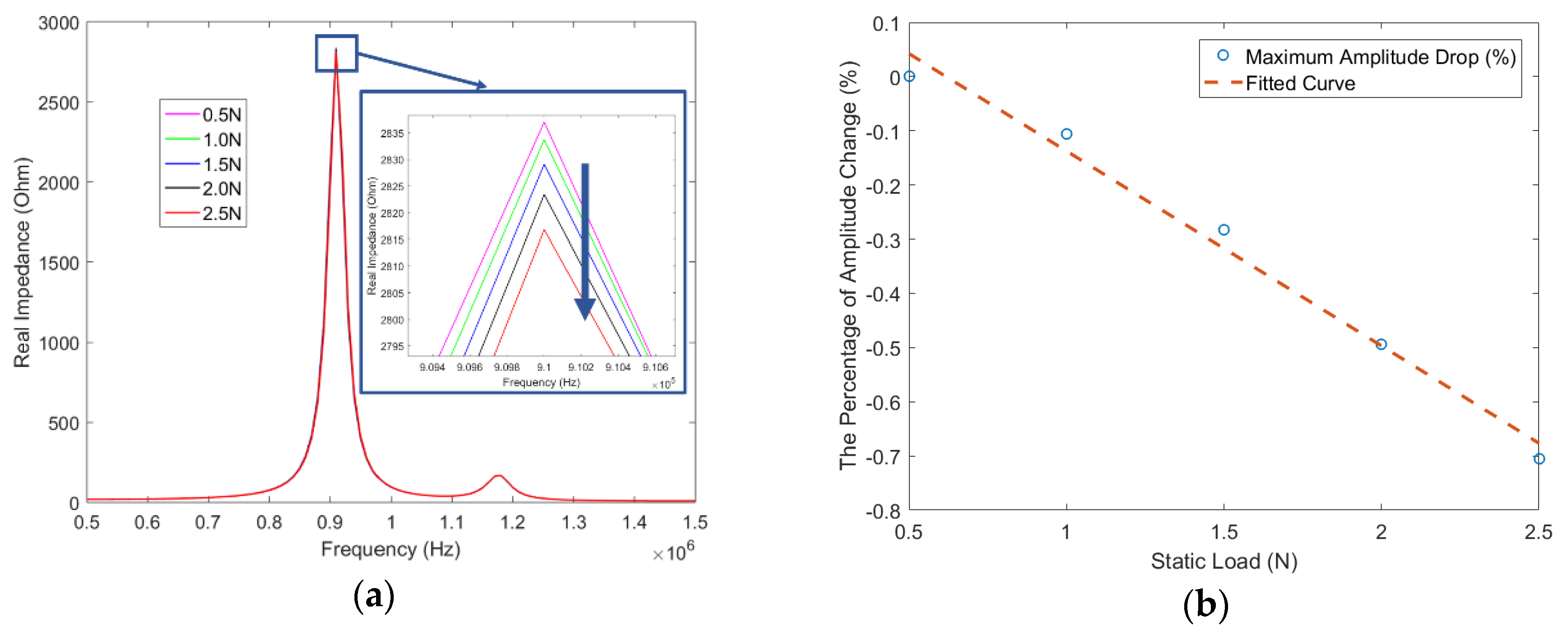
5.4. The Effect of the Silicone Rubber Stiffness to the Impedance Response
6. Discussions Based on the Theoretical Model
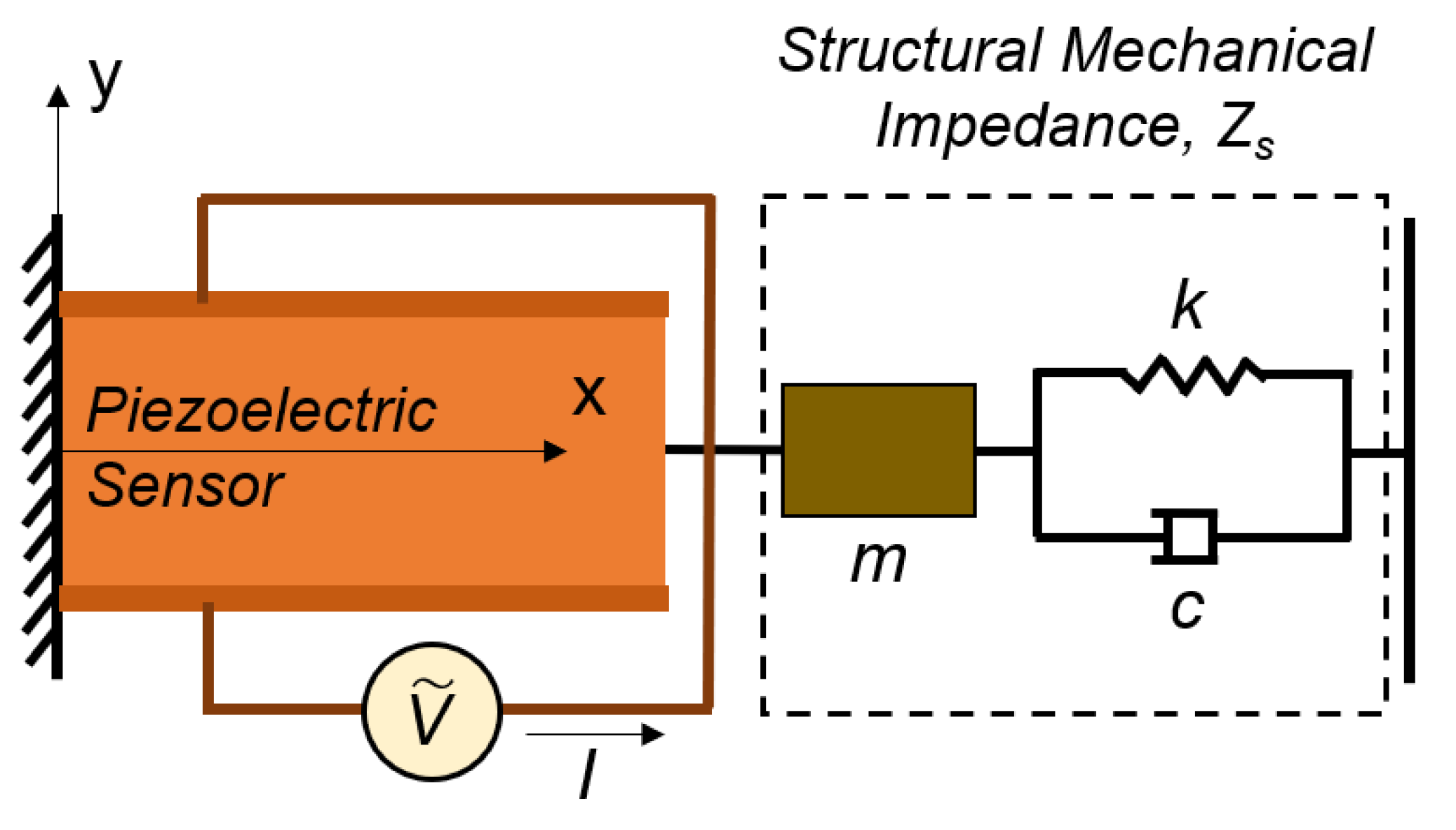
6.1. Analytical Model: Dynamic Interaction between the PZT Sensor and Structure
6.2. The Effect of Stress on PZT Material Properties to Impedance Response
6.3. The Effect of Stress on PZT Geometry Change to Impedance Response
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jacobsen, S.C.; Wood, J.E.; Knutti, D.; Biggers, K.B. The UTAH/MIT dextrous hand: Work in progress. Int. J. Robot. Res. 1984, 3, 21–50. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—From humans to humanoids. IEEE Trans. Robot. 2009, 26, 1–20. [Google Scholar] [CrossRef]
- Lee, M.H. Tactile sensing: New directions, new challenges. Int. J. Robot. Res. 2000, 19, 636–643. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Howe, R.D.; Provancher, W.R. Force and Tactile Sensors. Springer Handb. Robot. 2008, 100, 455–476. [Google Scholar]
- Howe, R.D. Tactile sensing and control of robotic manipulation. Adv. Robot. 1993, 8, 245–261. [Google Scholar] [CrossRef]
- Chen, X.; Topac, T.; Smith, W.; Ladpli, P.; Liu, C.; Chang, F.-K. Characterization of Distributed Microfabricated Strain Gauges on Stretchable Sensor Networks for Structural Applications. Sensors 2018, 18, 3260. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z. Robust Design and Fabrication of Highly Stretchable Sensor Networks for the Creation of Intelligent Materials; Stanford University: Stanford, CA, USA, 2014. [Google Scholar]
- Stassi, S.; Cauda, V.; Canavese, G.; Pirri, C.F. Flexible tactile sensing based on piezoresistive composites: A review. Sensors 2014, 14, 5296–5332. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Ge, C.; Wang, Z.J.; Cretu, E.; Li, X. Novel tactile sensor technology and smart tactile sensing systems: A review. Sensors 2017, 17, 2653. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.; Sun, X.; Xue, N.; Li, T.; Liu, C. Recent progress in technologies for tactile sensors. Sensors 2018, 18, 948. [Google Scholar] [CrossRef]
- Huh, T.M.; Liu, C.; Hashizume, J.; Chen, T.G.; Suresh, S.A.; Chang, F.-K.; Cutkosky, M.R. Active sensing for measuring contact of thin film gecko-inspired adhesives. IEEE Robot. Autom. Lett. 2018, 3, 3263–3270. [Google Scholar] [CrossRef]
- Almassri, A.M.; Wan Hasan, W.; Ahmad, S.A.; Ishak, A.J.; Ghazali, A.; Talib, D.; Wada, C. Pressure sensor: State of the art, design, and application for robotic hand. J. Sens. 2015, 2015. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, D.; Hao, S.; Jie, Y.; Cao, X.; Wang, N.; Wang, Z.L. Highly stretchable triboelectric tactile sensor for electronic skin. Nano Energy 2019, 64, 103907. [Google Scholar] [CrossRef]
- Shin, K.; Lee, S.; Min, K.; Ko, D.; Mun, J.H. Methodology for Force Measurement Using Piezoelectric Ceramic; World Congress on Medical Physics and Biomedical Engineering 2006, 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 853–856. [Google Scholar]
- Safour, S.; Bernard, Y. Static force transducer based on resonant piezoelectric structure: Root cause investigation. Smart Mater. Struct. 2017, 26, 055012. [Google Scholar] [CrossRef]
- Ozeri, S.; Shmilovitz, D. Static Force Measurement by Piezoelectric Sensors, 2006 IEEE International Symposium on Circuits and Systems, 2006; IEEE: Island of Kos, Greece, 2006; p. 4. [Google Scholar]
- Sparks, J.L.; Vavalle, N.A.; Kasting, K.E.; Long, B.; Tanaka, M.L.; Sanger, P.A.; Schnell, K.; Conner-Kerr, T.A. Use of silicone materials to simulate tissue biomechanics as related to deep tissue injury. Adv. Skin Wound Care 2015, 28, 59–68. [Google Scholar] [CrossRef]
- Zhuang, Y.; Kopsaftopoulos, F.; Dugnani, R.; Chang, F.-K. Integrity monitoring of adhesively bonded joints via an electromechanical impedance-based approach. Struct. Health Monit. 2018, 17, 1031–1045. [Google Scholar] [CrossRef]
- Folds, D. Speed of sound and transmission loss in silicone rubbers at ultrasonic frequencies. J. Acoust. Soc. Am. 1974, 56, 1295–1296. [Google Scholar] [CrossRef]
- Mohamed, M.; Samy, A.; Ali, W. Friction coefficient of rubber shoes sliding against ceramic flooring. KGK-Kautsch. Gummi Kunstst. 2012, 65, 52. [Google Scholar]
- Elsayed, Y.; Vincensi, A.; Lekakou, C.; Geng, T.; Saaj, C.; Ranzani, T.; Cianchetti, M.; Menciassi, A. Finite element analysis and design optimization of a pneumatically actuating silicone module for robotic surgery applications. Soft Robot. 2014, 1, 255–262. [Google Scholar] [CrossRef]
- Song, B.; Chen, W. One-Dimensional dynamic compressive behavior of EPDM rubber. J. Eng. Mater. Technol. 2003, 125, 294–301. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled electro-mechanical analysis of adaptive material systems-determination of the actuator power consumption and system energy transfer. J. Intell. Mater. Syst. Struct. 1997, 8, 335–343. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Zhao, J. Electromechanical properties of lead zirconate titanate piezoceramics under the influence of mechanical stresses. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1518–1526. [Google Scholar] [CrossRef] [PubMed]


| Density | Young’s Modulus E11 | Young’s Modulus E33 | Relative Dielectric Constant KT | Piezo Charge Constant d33 | Piezo Voltage Constant g33 |
|---|---|---|---|---|---|
| 7.6 g/cm3 | 63 GPa | 54 GPa | 1700 | 400 pC/N | 24.8 mV-m/N |
| Property | Unit | Piezo PZT-5A |
|---|---|---|
| E11 | GPa | 60.97 |
| E22 | GPa | 60.97 |
| E33 | GPa | 53.19 |
| G23 | GPa | 21.05 |
| G31 | GPa | 21.05 |
| G12 | GPa | 22.57 |
| v23 | 0.4402 | |
| v13 | 0.4402 | |
| v12 | 0.3500 | |
| ρ | kg/m3 | 7750 |
| Static Load (N) | Stress (kPa) | Strain | Stiffness (kPa) |
|---|---|---|---|
| 0.5 | 1.2875 | 0.01563 | 61.757 |
| 1.0 | 2.5375 | 0.03498 | 67.473 |
| 1.5 | 3.7875 | 0.05281 | 72.740 |
| 2.0 | 5.0375 | 0.06943 | 77.650 |
| 2.5 | 6.2875 | 0.08506 | 82.267 |
| Static Load (N) | Dynamic Stiffness (kPa) |
|---|---|
| 0.5 | 431.27 |
| 1.0 | 472.25 |
| 1.5 | 509.12 |
| 2.0 | 543.46 |
| 2.5 | 575.78 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Zhuang, Y.; Nasrollahi, A.; Lu, L.; Haider, M.F.; Chang, F.-K. Static Tactile Sensing for a Robotic Electronic Skin via an Electromechanical Impedance-Based Approach. Sensors 2020, 20, 2830. https://doi.org/10.3390/s20102830
Liu C, Zhuang Y, Nasrollahi A, Lu L, Haider MF, Chang F-K. Static Tactile Sensing for a Robotic Electronic Skin via an Electromechanical Impedance-Based Approach. Sensors. 2020; 20(10):2830. https://doi.org/10.3390/s20102830
Chicago/Turabian StyleLiu, Cheng, Yitao Zhuang, Amir Nasrollahi, Lingling Lu, Mohammad Faisal Haider, and Fu-Kuo Chang. 2020. "Static Tactile Sensing for a Robotic Electronic Skin via an Electromechanical Impedance-Based Approach" Sensors 20, no. 10: 2830. https://doi.org/10.3390/s20102830
APA StyleLiu, C., Zhuang, Y., Nasrollahi, A., Lu, L., Haider, M. F., & Chang, F.-K. (2020). Static Tactile Sensing for a Robotic Electronic Skin via an Electromechanical Impedance-Based Approach. Sensors, 20(10), 2830. https://doi.org/10.3390/s20102830








