A Novel Fault Diagnosis Scheme for Rolling Bearing Based on Convex Optimization in Synchroextracting Chirplet Transform
Abstract
1. Introduction
2. Theory Description
2.1. Convex Optimization Based on GMC Penalty
2.2. Synchroextracting Chirplet Transform
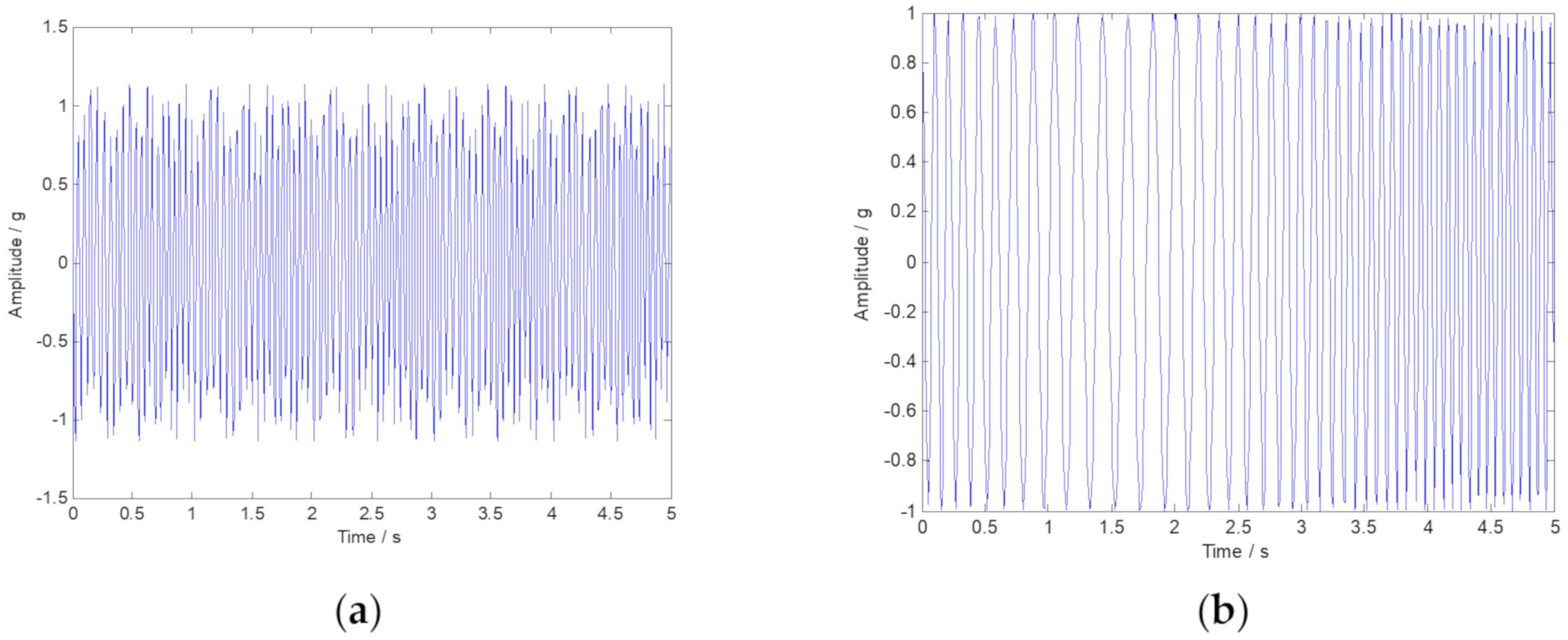
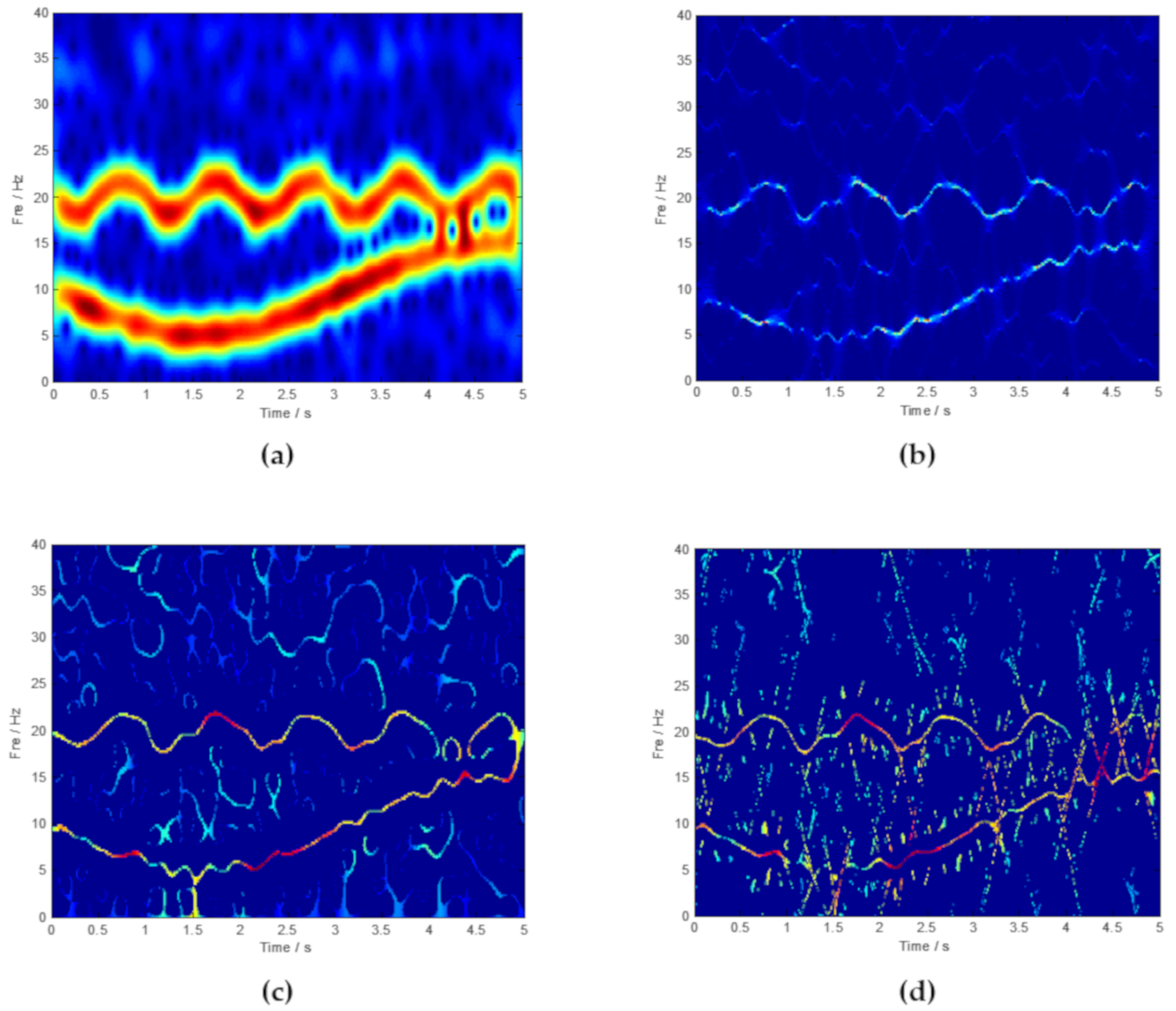
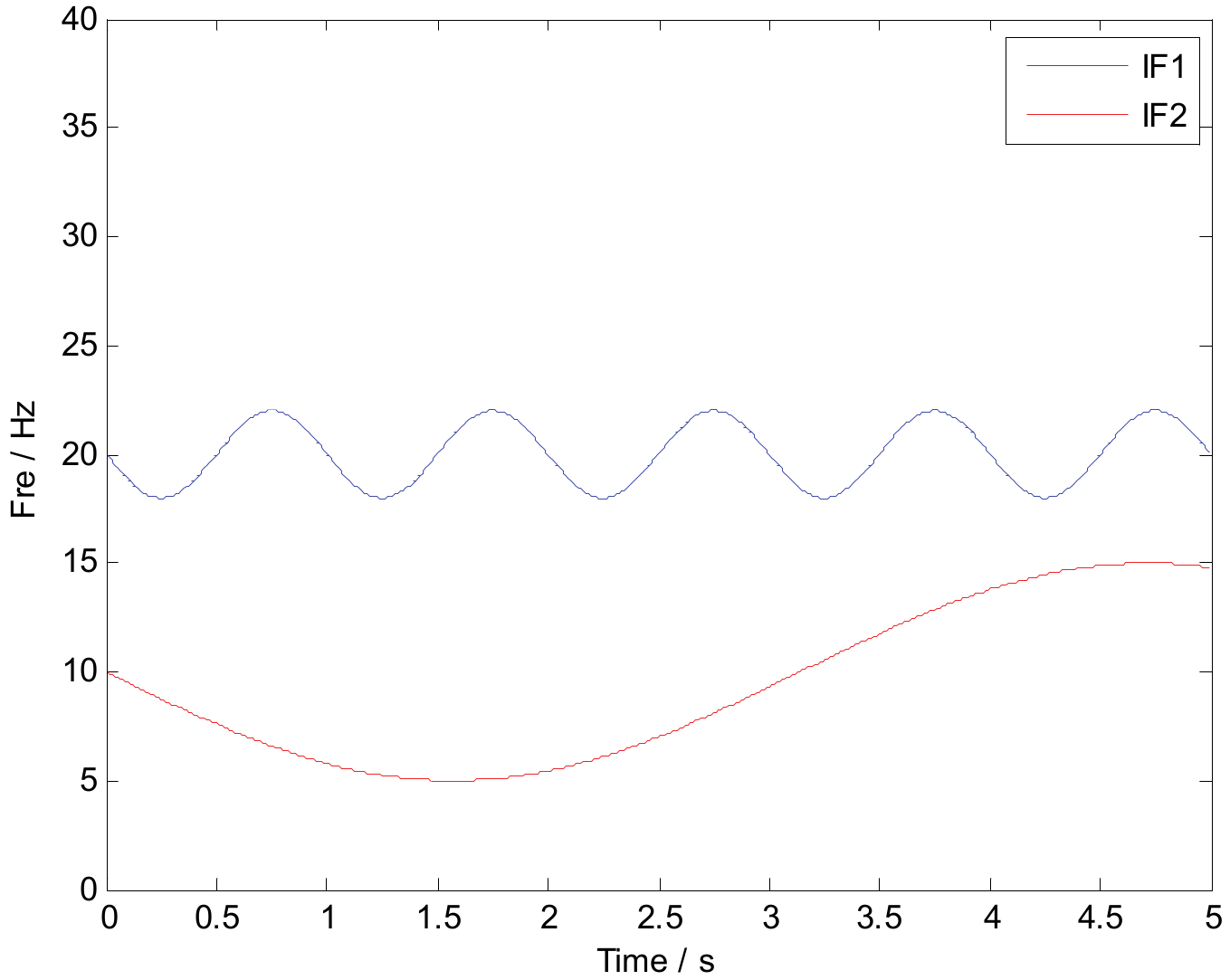
3. Simulated Signal Analysis
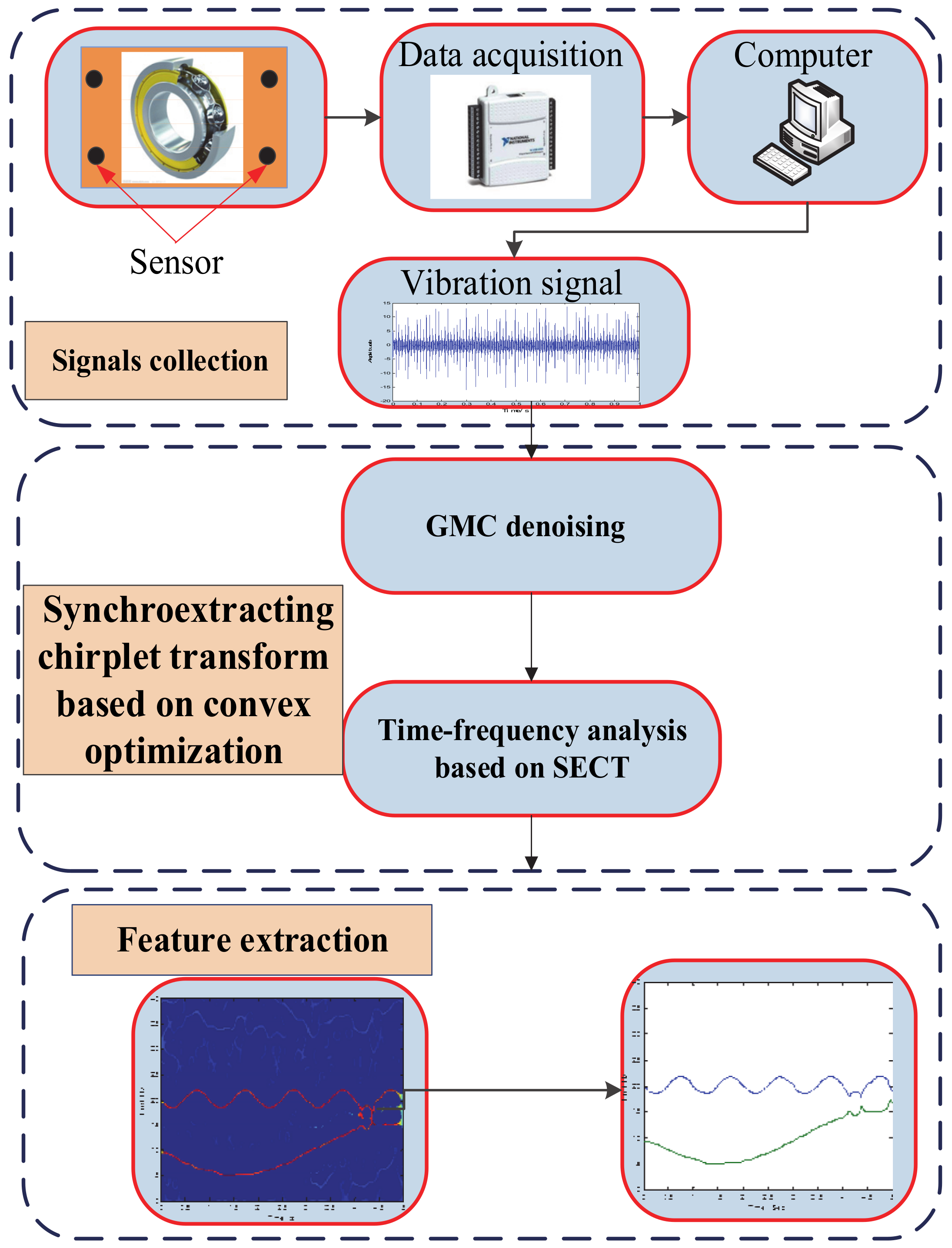
4. Experimental Data Analysis
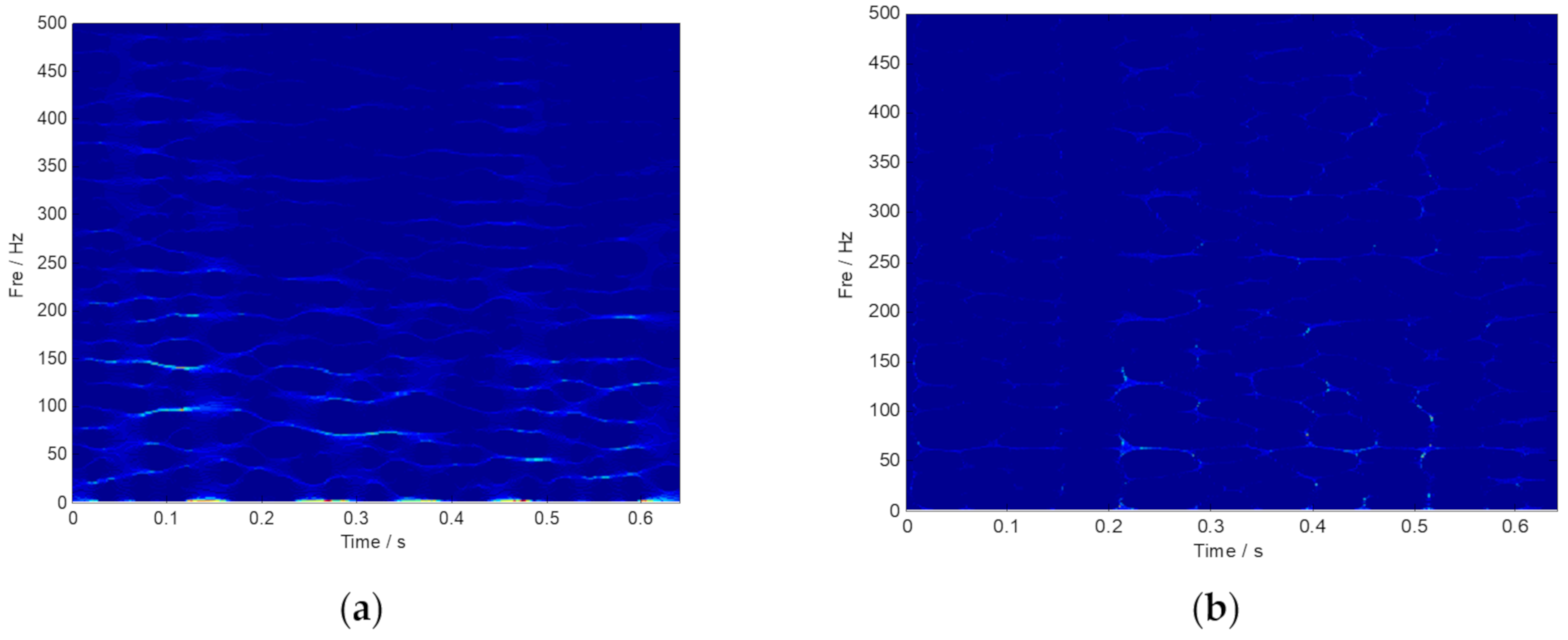
4.1. Case 1: Data Analysis of a Fault Test Rig
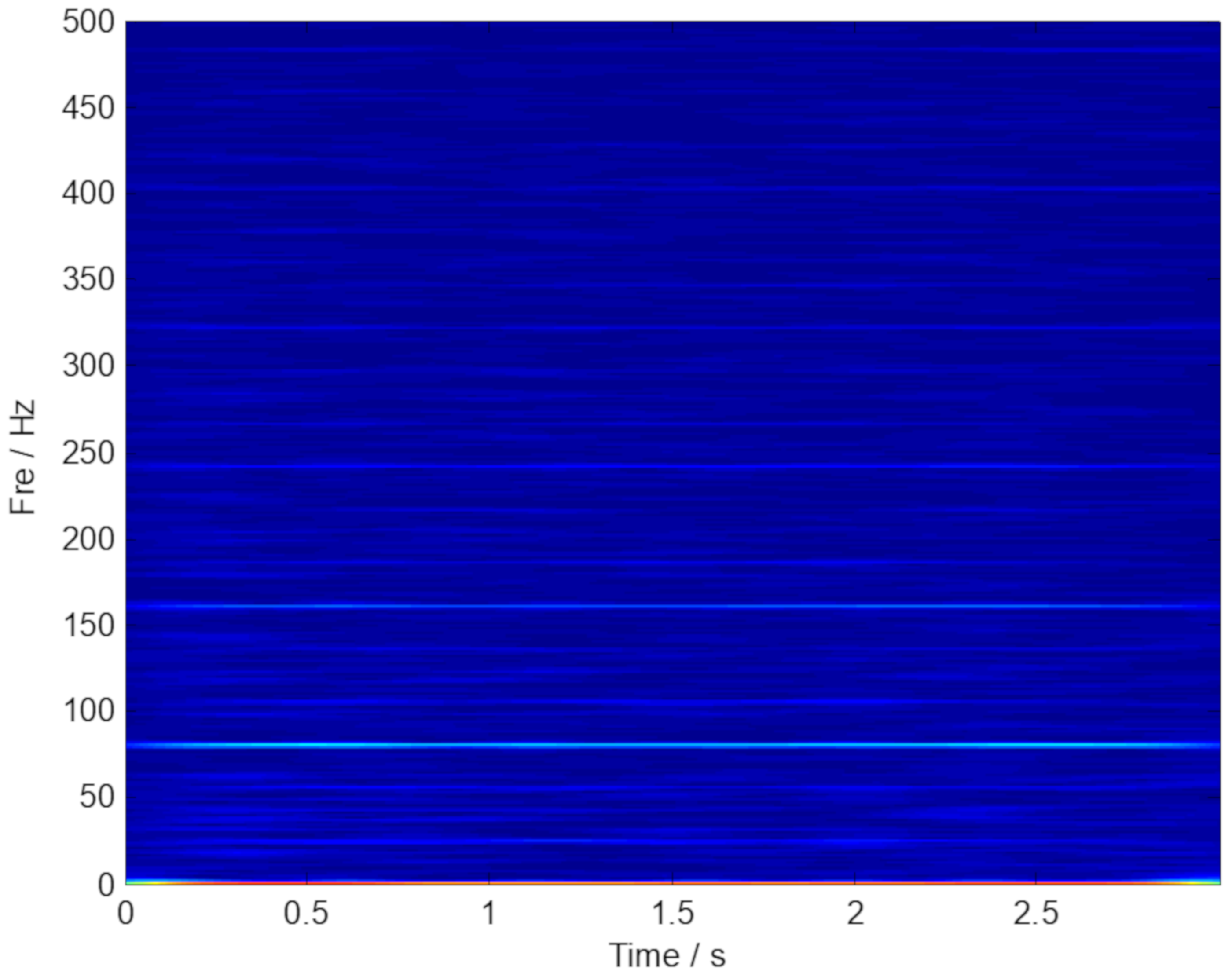
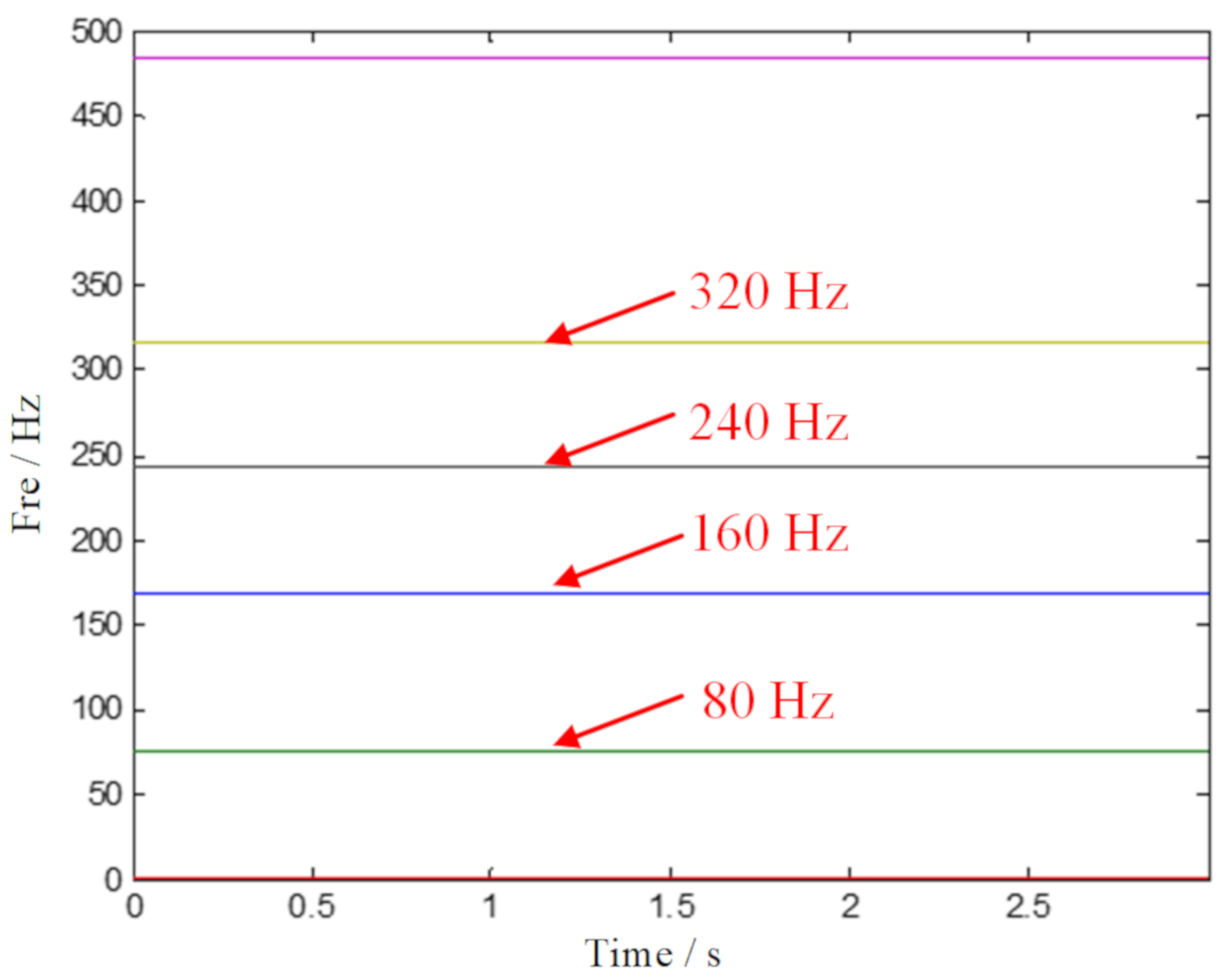
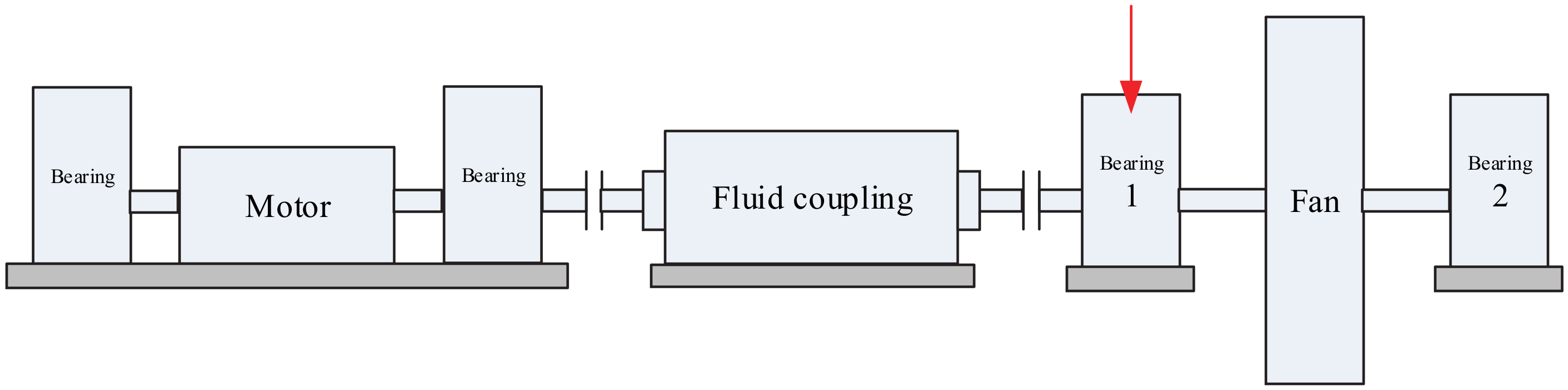
4.2. Case 2: Data Analysis of a Large Desulfurization Fan
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, H.; Baddour, N.; Liang, M. Bearing fault diagnosis under unknown time-varying rotational speed conditions via multiple time-frequency curve extraction. J. Sound Vib. 2018, 414, 43–60. [Google Scholar] [CrossRef]
- Wang, S.; Selesnick, I.; Cai, G.; Feng, Y.; Sui, X.; Chen, X. Nonconvex Sparse Regularization and Convex Optimization for Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7332–7342. [Google Scholar] [CrossRef]
- Zhong, D.; Yi, C.; Xiao, H.; Zhang, H.; Wu, A. A Novel Fault Diagnosis Method for Rolling Bearing Based on Improved Sparse Regularization via Convex Optimization. Complexity 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Abboud, D.; Antoni, J. Order-frequency analysis of machine signals. Mech. Syst. Signal Process. 2017, 87, 229–258. [Google Scholar] [CrossRef]
- Iatsenko, D.; McClintock, P.; Stefanovska, A. Linear and synchrosqueezed time-frequency representations revisited: Overview, standards of use, resolution, reconstruction, concentration, and algorithms. Digit. Signal Process. 2015, 42, 1–26. [Google Scholar] [CrossRef]
- Li, X.; Jia, X.-D.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Intelligent cross-machine fault diagnosis approach with deep auto-encoder and domain adaptation. Neurocomputing 2020, 383, 235–247. [Google Scholar] [CrossRef]
- Colominas, M.A.; Meignen, S.; Pham, D.H. Time-Frequency Filtering Based on Model Fitting in the Time-Frequency Plane. IEEE Signal Process. Lett. 2019, 26, 660–664. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.H. Retrieval of the Modes of Multicomponent Signals From Downsampled Short-Time Fourier Transform. IEEE Trans. Signal Process. 2018, 66, 6204–6215. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Soleymani, R.; Selesnick, I.W.; Landsberger, D.M. SEDA: A tunable Q-factor wavelet-based noise reduction algorithm for multi-talker babble. Speech Commun. 2017, 96, 102–115. [Google Scholar] [CrossRef] [PubMed]
- Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z. A Fault Diagnosis Scheme for Rolling Bearing Based on Particle Swarm Optimization in Variational Mode Decomposition. Shock. Vib. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Dugnol, B.; Fernandez, C.; Galiano, G.; Velasco, J. Implementation of a diffusive differential reassignment method for signal enhancement: An application to wolf population counting. Appl. Math. Comput. 2007, 193, 374–384. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; Huang, T.; You, G. Multisensor signal denoising based on matching synchrosqueezing wavelet transform for mechanical fault condition assessment. Meas. Sci. Technol. 2018, 29, 045104. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.H.; McLaughlin, S. On Demodulation, Ridge Detection, and Synchrosqueezing for Multicomponent Signals. IEEE Trans. Signal Process. 2017, 65, 2093–2103. [Google Scholar] [CrossRef]
- Pham, D.H.; Meignen, S. High-Order Synchrosqueezing Transform for Multicomponent Signals Analysis—With an Application to Gravitational-Wave Signal. IEEE Trans. Signal Process. 2017, 65, 1. [Google Scholar] [CrossRef]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Trans. Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Liu, H.; Xiang, J. Kernel regression residual decomposition-based synchroextracting transform to detect faults in mechanical systems. ISA Trans. 2019, 87, 251–263. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Z.; Gao, J.; Li, B.; Li, Z.; Huang, X.; Wen, G. Synchroextracting chirplet transform for accurate IF estimate and perfect signal reconstruction. Digit. Signal Process. 2019, 93, 172–186. [Google Scholar] [CrossRef]
- Peng, Z.; Meng, G.; Chu, F.L.; Lang, Z.-Q.; Zhang, W.M.; Yang, Y. Polynomial Chirplet Transform With Application to Instantaneous Frequency Estimation. IEEE Trans. Instrum. Meas. 2011, 60, 3222–3229. [Google Scholar] [CrossRef]
- Yu, G.; Zhou, Y. General linear chirplet transform. Mech. Syst. Signal Process. 2016, 70, 958–973. [Google Scholar] [CrossRef]
- Selesnick, I. Total Variation Denoising Via the Moreau Envelope. IEEE Signal Process. Lett. 2017, 24, 216–220. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H.; Yu, X. Quaternion singular spectrum analysis using convex optimization and its application to fault diagnosis of rolling bearing. Measurement 2017, 103, 321–332. [Google Scholar] [CrossRef]
- Selesnick, I. Sparse Regularization via Convex Analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- Cai, G.; Selesnick, I.W.; Wang, S.; Dai, W.; Zhu, Z. Sparsity-enhanced signal decomposition via generalized minimax-concave penalty for gearbox fault diagnosis. J. Sound Vib. 2018, 432, 213–234. [Google Scholar] [CrossRef]
- Boţ, R.I.; Csetnek, E.R.; Laszlo, S.C. An inertial forward-backward algorithm for the minimization of the sum of two nonconvex functions. EURO J. Comput. Optim. 2015, 4, 3–25. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Bechhoefer, E. A Quick Introduction to Bearing Envelope Analysis, MFPT Data. Available online: http://www.mfpt.org/FaultData/FaultData.htm.Set (accessed on 10 March 2020).
- Antoni, J.; Randall, R.B. A Stochastic Model for Simulation and Diagnostics of Rolling Element Bearings With Localized Faults. J. Vib. Acoust. 2003, 125, 282–289. [Google Scholar] [CrossRef]









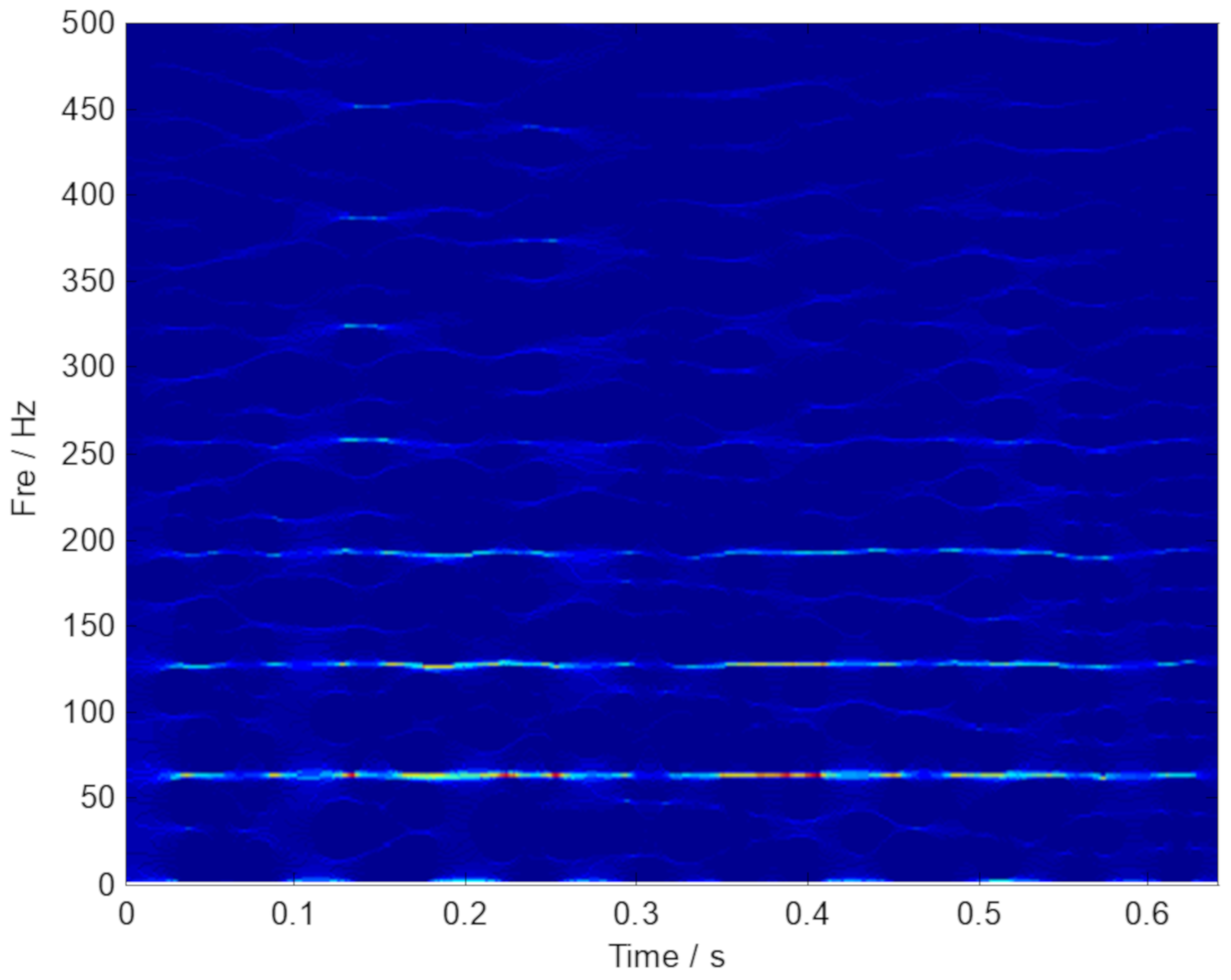
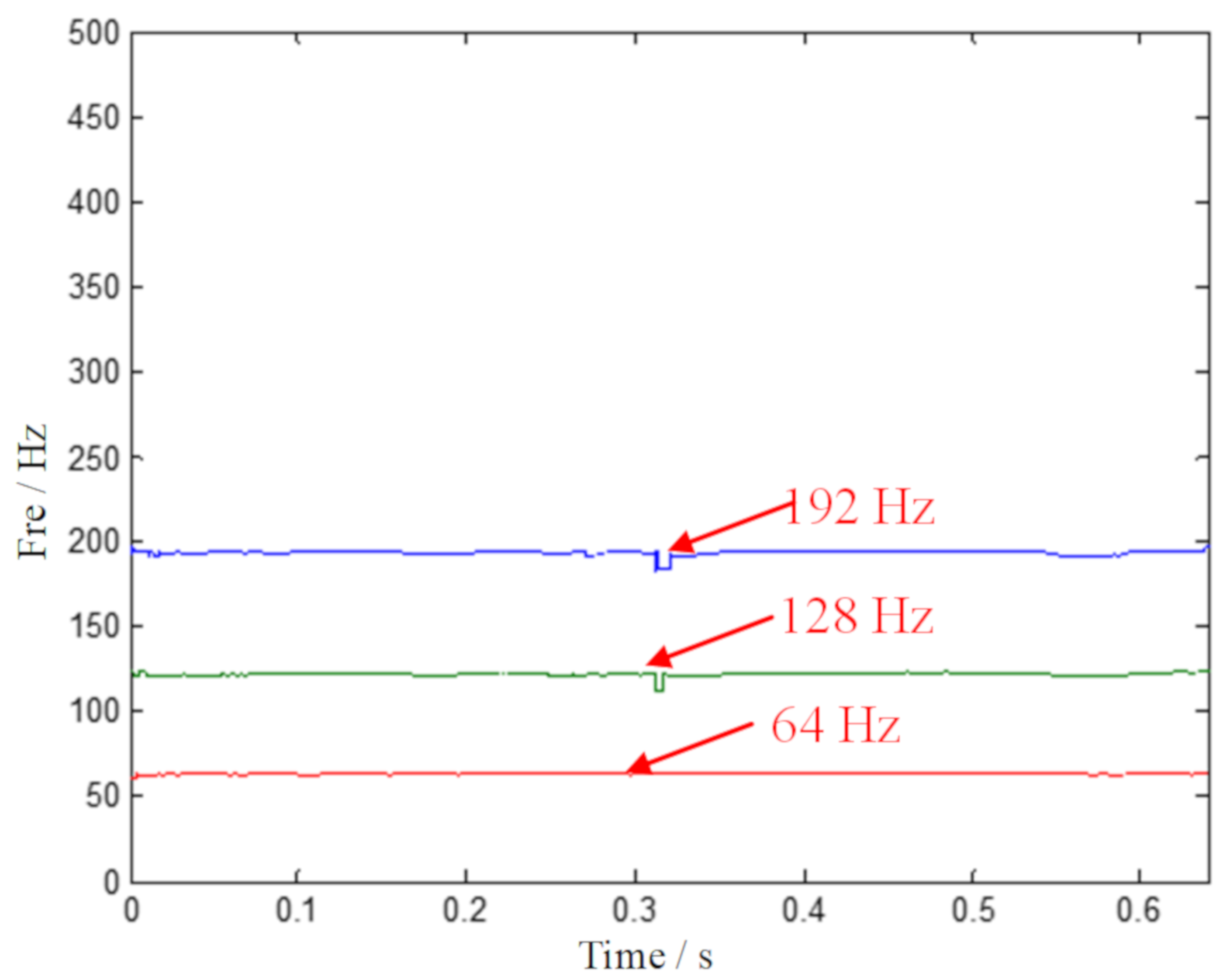
| Methods | STFT | SST | SET | SECT | Proposed ISECT |
|---|---|---|---|---|---|
| Rayleigh entropy | 15.78 | 12.12 | 11.49 | 11.46 | 11.01 |
| Roller Diameter | Pitch Diameter | Number of Elements | Contact Angle |
|---|---|---|---|
| 0.235 | 1.245 | 8 | 0 |
| Speed r/min | Rotational Frequency/Hz | Sampling Frequency/Hz | Sampling Time/s | Outer/Hz | Inner/Hz | Rolling Ball/Hz | Container/Hz |
|---|---|---|---|---|---|---|---|
| 740 | 12.3 | 25600 | 0.64 | 64.1 | 96.2 | 34.4 | 5.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, G.; Lv, Y.; Jiang, Y.; Yi, C. A Novel Fault Diagnosis Scheme for Rolling Bearing Based on Convex Optimization in Synchroextracting Chirplet Transform. Sensors 2020, 20, 2813. https://doi.org/10.3390/s20102813
You G, Lv Y, Jiang Y, Yi C. A Novel Fault Diagnosis Scheme for Rolling Bearing Based on Convex Optimization in Synchroextracting Chirplet Transform. Sensors. 2020; 20(10):2813. https://doi.org/10.3390/s20102813
Chicago/Turabian StyleYou, Guanghui, Yong Lv, Yefeng Jiang, and Cancan Yi. 2020. "A Novel Fault Diagnosis Scheme for Rolling Bearing Based on Convex Optimization in Synchroextracting Chirplet Transform" Sensors 20, no. 10: 2813. https://doi.org/10.3390/s20102813
APA StyleYou, G., Lv, Y., Jiang, Y., & Yi, C. (2020). A Novel Fault Diagnosis Scheme for Rolling Bearing Based on Convex Optimization in Synchroextracting Chirplet Transform. Sensors, 20(10), 2813. https://doi.org/10.3390/s20102813





