Optimal Design of Switchable Wearable Antenna Array for Wireless Sensor Networks
Abstract
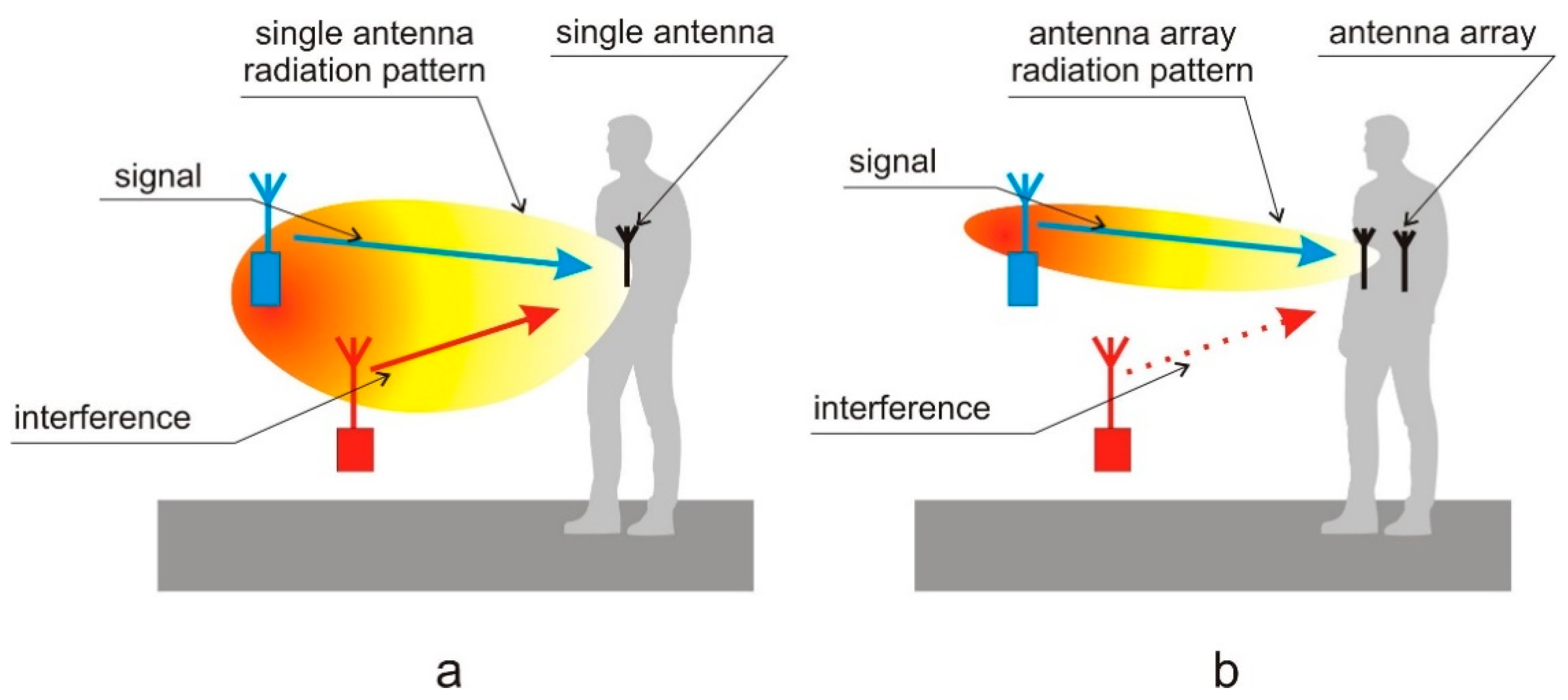
1. Introduction
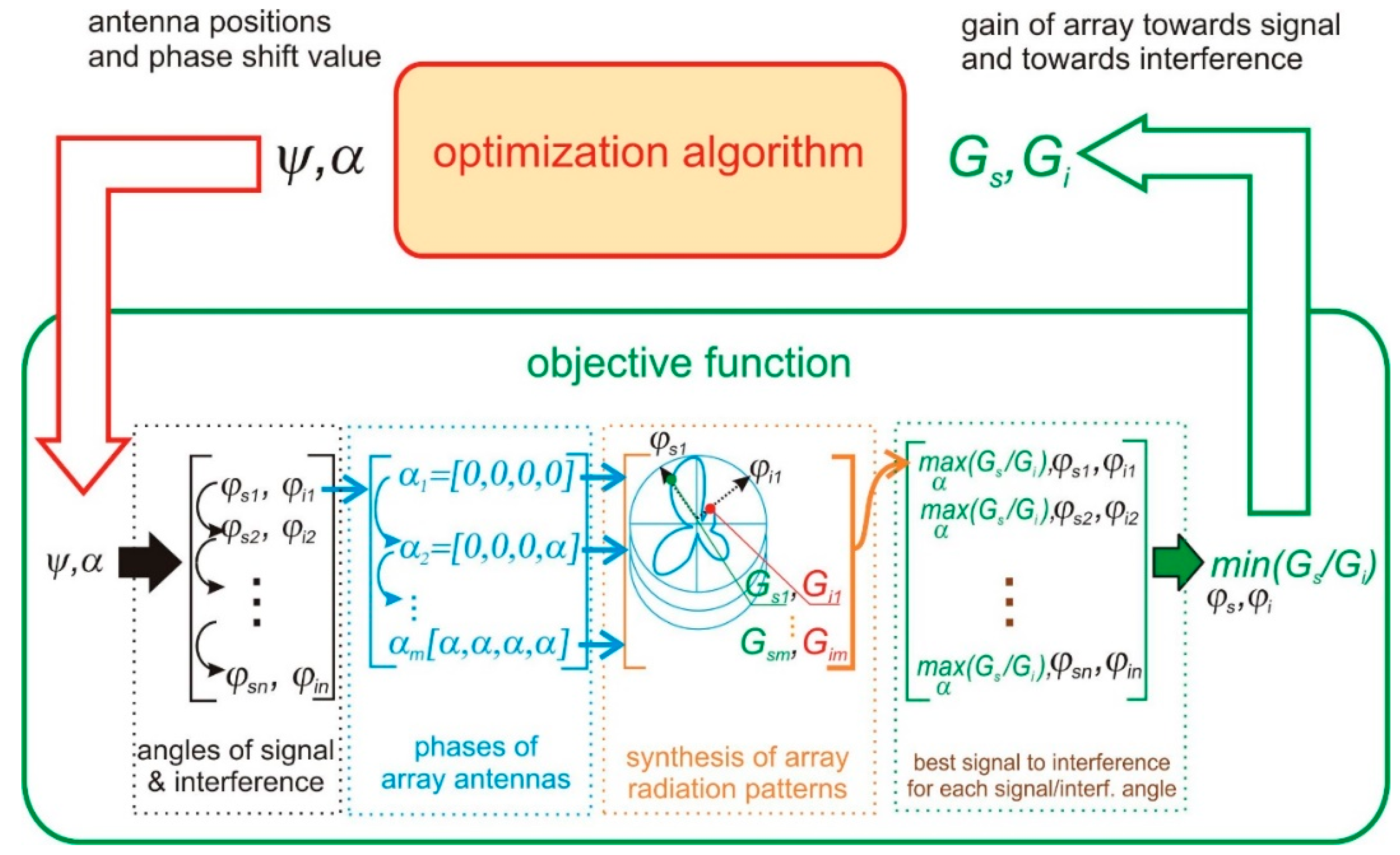
2. Models and Methods
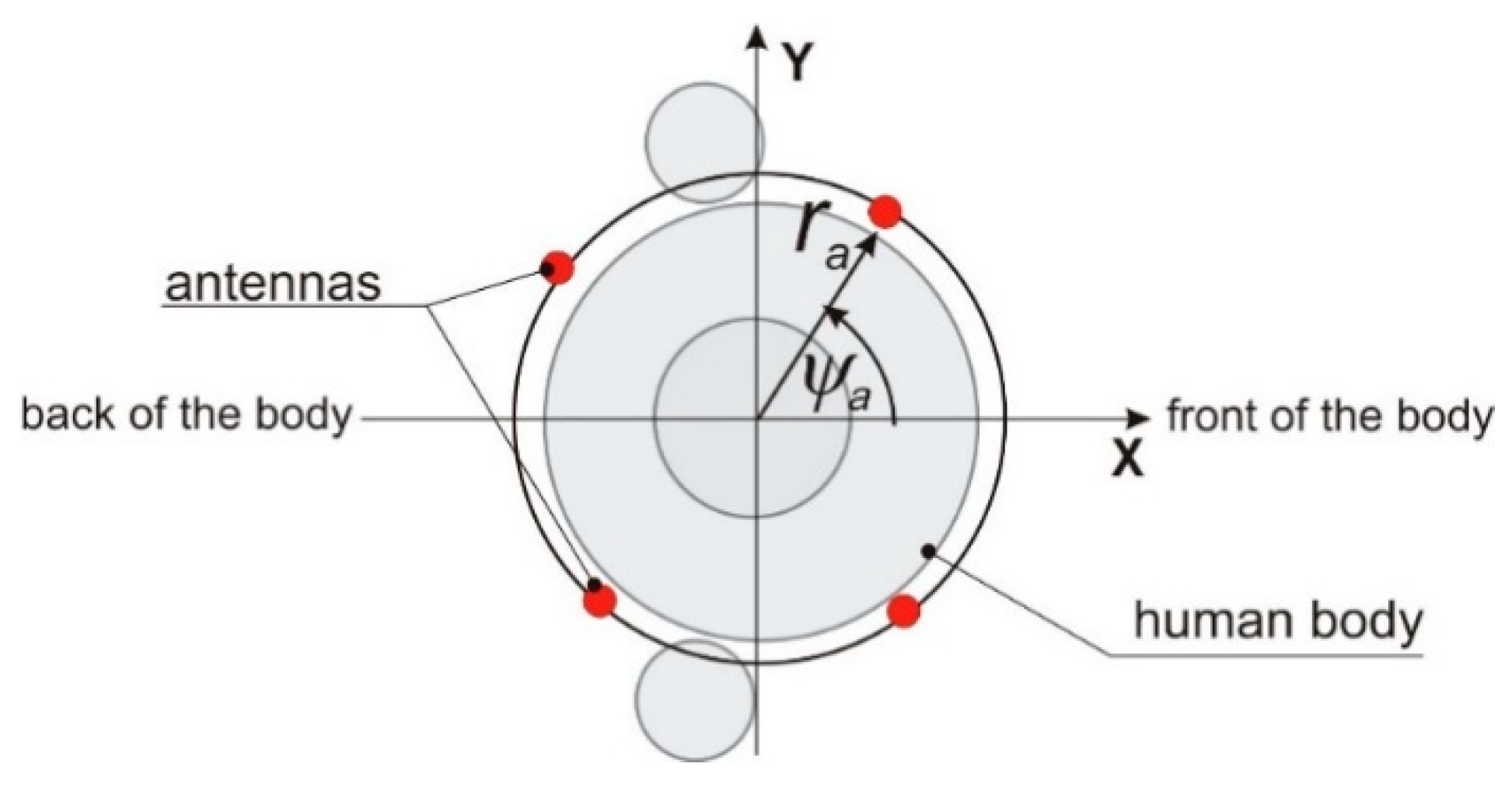
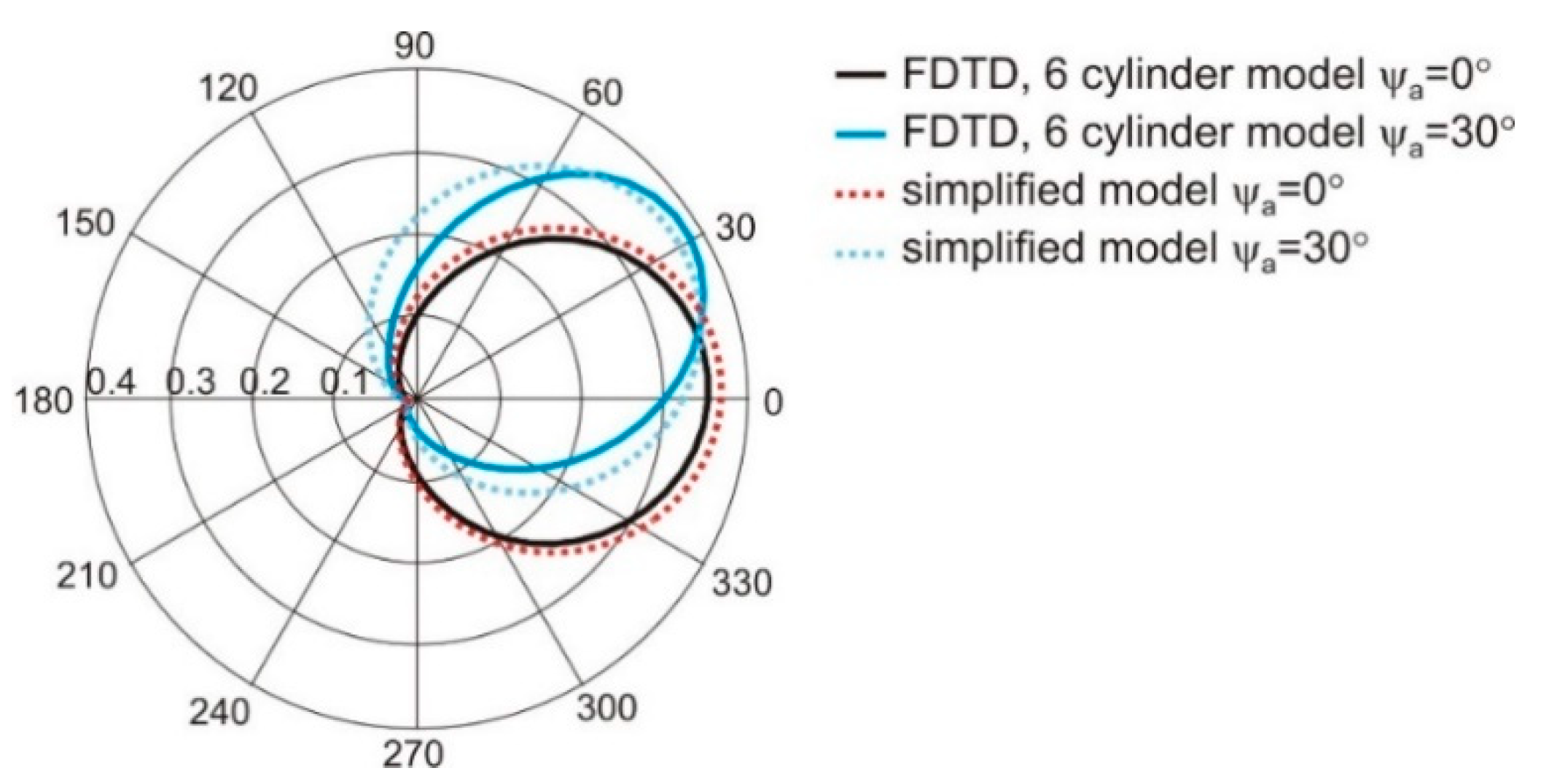
2.1. Direct Problem Formulation
2.2. Inverse Problem Formulation
2.2.1. Min-Max Approach
2.2.2. Nadir Point Distance Maximization
- -
- utopia U, i.e., the point the coordinates of which are the best values of each objective (in our case, Us is the maximum of Gs function, independently considered and subject to the problem constraints; a similar explanation holds for Ui);
- -
- nadir R, i.e., the point the coordinates of which are the worst values of each objective.
2.2.3. Utopia Point Distance Minimization
2.2.4. Full Pareto-Like Optimization: P-EStra
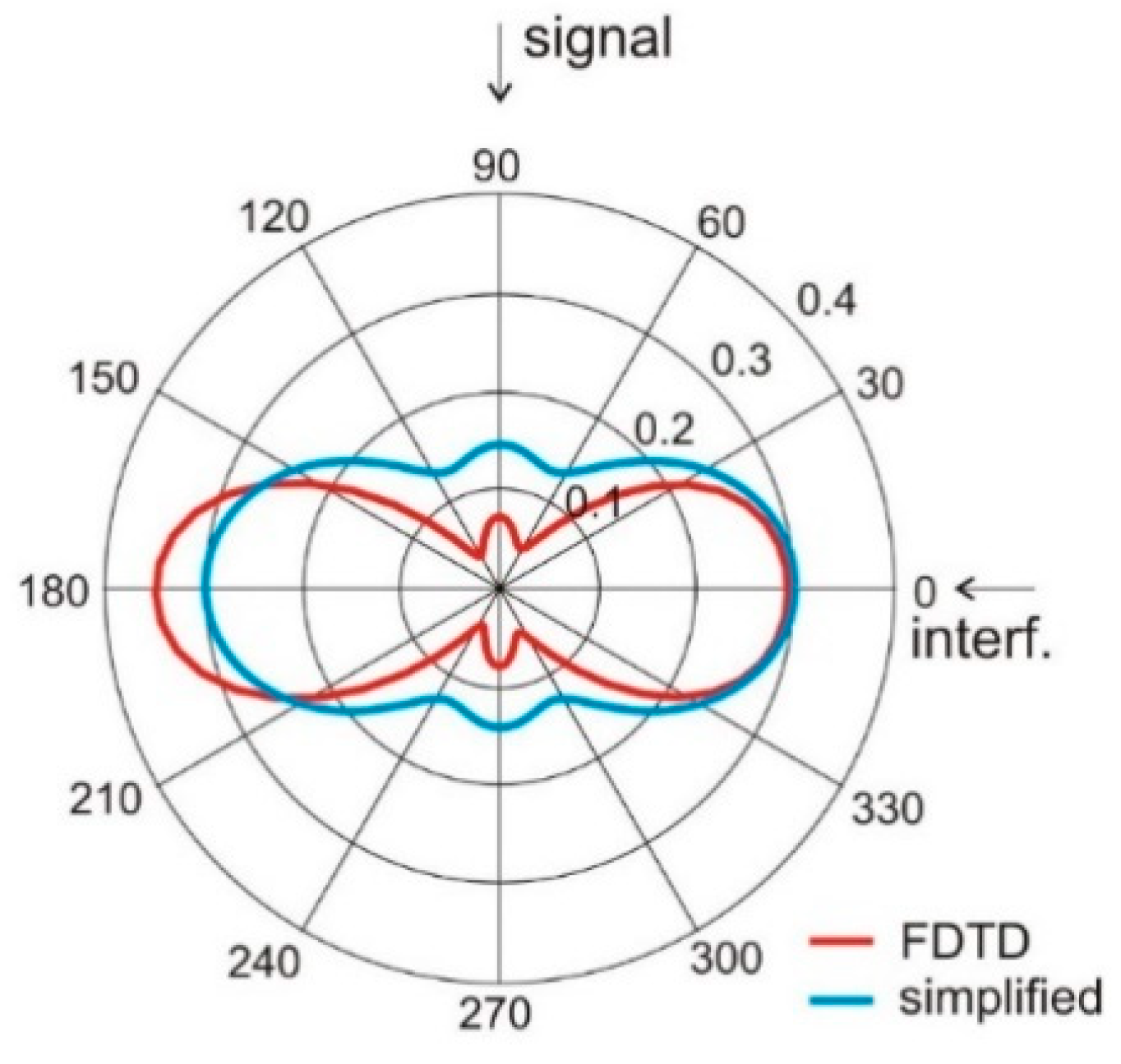
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fahmy, H.M.A. Wireless Sensor Networks—Concepts, Applications, Experimentation and Analysis; Springer: Berlin, Germany, 2016. [Google Scholar]
- Ghamari, M.; Janko, B.; Sherratt, R.S.; Harwin, W.; Piechockic, R.; Soltanpur, C. A Survey on Wireless Body Area Networks for eHealthcare Systems in Residential Environments. Sensors 2016, 16, 831. [Google Scholar] [CrossRef] [PubMed]
- Januszkiewicz, Ł. The analysis of influence of textile antenna location on its performance. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–5. [Google Scholar]
- Chandran, A.R.; Morris, S.; Timmons, N.; Morrison, J. Antenna with switchable propagating modes for WBAN applications. In Proceedings of the 2015 Loughborough Antennas Propagation Conference (LAPC), Loughborough, UK, 2–3 November 2015; pp. 1–3. [Google Scholar]
- Sánchez-Montero, R.; Camacho-Gómez, C.; López-Espí, P.-L.; Salcedo-Sanz, S. Optimal Design of a Planar Textile Antenna for Industrial Scientific Medical (ISM) 2.4 GHz Wireless Body Area Networks (WBAN) with the CRO-SL Algorithm. Sensors 2018, 18, 1982. [Google Scholar] [CrossRef]
- Ngamjanyaporn, P.; Phongcharoenpanich, C.; Akkaraekthalin, P.; Krairiksh, M. Signal-to-interference ratio improvement by using a phased array antenna of switched-beam elements. IEEE Trans. Antennas Propag. 2005, 53, 1819–1828. [Google Scholar] [CrossRef]
- Tong, X.; Liu, C.; Liu, X.; Guo, H.; Yang, X. Switchable ON-/OFF-Body Antenna for 2.45 GHz WBAN Applications. IEEE Trans. Antennas Propag. 2018, 66, 967–971. [Google Scholar] [CrossRef]
- Mohamadzade, B.; Simorangkir, R.B.V.B.; Hashmi, R.M.; Shrestha, S. Low-profile Pattern Reconfigurable Antenna for Wireless Body Area Networks. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 546–547. [Google Scholar]
- Sotiriou, A.I.; Trakadas, P.T.; Capsalis, C.N. Uplink Carrier-to-Interference Improvement in a Cellular Telecommunication System When a Six-Beam Switched Parasitic Array Is Implemented. Progress Electromagn. Res. B 2008, 5, 303–321. [Google Scholar] [CrossRef][Green Version]
- Basu, B.; Mahanti, G.K. A comparative study of Modified Particle Swarm Optimization, Differential Evolution and Artificial Bees Colony optimization in synthesis of circular array. In Proceedings of the 2010 International Conference on Power, Control and Embedded Systems; Allahabad, India, 29 November–1 December 2010, IEEE: Piscataway, NJ, USA, 2010; pp. 1–5. [Google Scholar]
- Bhargav, A.; Gupta, N. Multiobjective Genetic Optimization of Nonuniform Linear Array with Low Sidelobes and Beamwidth. Antennas Wirel. Propag. Lett. 2013, 12, 1547–1549. [Google Scholar] [CrossRef]
- Jang, C.-H.; Hu, F.; He, F.; Wu, L. A Novel Circular Array Structure and Particle Swarm Optimization in Aperture Synthesis Radiometers. Antennas Wirel. Propag. Lett. 2015, 14, 1758–1761. [Google Scholar] [CrossRef]
- Khodier, M.M.; Al-Aqeel, M. Linear and circular array optimization: A study using particle swarm intelligence. PIER B 2009, 15, 347–373. [Google Scholar] [CrossRef]
- Panduro, M.A.; Brizuela, C.A.; Balderas, L.I.; Acosta, D.A. A comparison of genetic algorithms, particle swarm optimization and the differential evolution method for the design of scannable circular antenna arrays. PIER B 2009, 13, 171–186. [Google Scholar] [CrossRef]
- Sengupta, A.; Chakraborti, T.; Konar, A.; Nagar, A.K. A multi-objective memetic optimization approach to the circular antenna array design problem. PIER B 2012, 42, 363–380. [Google Scholar] [CrossRef][Green Version]
- Zhao, X.; Yang, Q.; Zhang, Y. Design of non-uniform circular antenna arrays by convex optimization. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP); Davos, Switzerland, 10–15 April 2016, IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Januszkiewicz, Ł. The analysis of textile antenna array radiation pattern. In Proceedings of the 18-th International Conference on Microwaves, Radar and Wireless Communications, Vilnius, Lithuania, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Remcom Inc. XFDTD Reference Manual, Release 7.6.0; Remcom Inc.: State College, PA, USA, 2016. [Google Scholar]
- Januszkiewicz, Ł.; Hausman, S. Simplified human phantoms for narrowband and ultra-wideband body area network modelling. COMPEL 2015, 34, 439–447. [Google Scholar] [CrossRef]
- Januszkiewicz, Ł.; Hausman, S. Simplified human phantoms for wireless body area network modelling. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–4. [Google Scholar]
- Januszkiewicz, Ł. Simplified human body models for interference analysis in the cognitive radio for medical body area networks. In Proceedings of the 2014 8th International Symposium on Medical Information and Communication Technology (ISMICT), Firenze, Italy, 2–4 April 2014; pp. 1–5. [Google Scholar]
- Januszkiewicz, Ł.; Di Barba, P.; Hausman, S. Optimization of wireless body area network performance with simplified electromagnetic model of the body. JAE 2018, 57, 143–154. [Google Scholar] [CrossRef]
- Januszkiewicz, Ł.; Di Barba, P.; Hausman, S. Multi-Objective Optimization of a Wireless Body Area Network for Varying Body Positions. Sensors 2018, 18, 3406. [Google Scholar] [CrossRef] [PubMed]
- Balanis, C.A. Antenna Theory, Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Di Barba, P. A fast evolutionary method for identifying non-inferior solutions in multicriteria shape optimisation of a shielded reactor. Int. J. Comput. Math. Electr. Electron. Eng. 2001, 20, 762. [Google Scholar] [CrossRef]
- Di Barba, P. Muliobjective Shape Design in Electricity and Magnetism; Springer: Berlin, Germany, 2010. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/help/matlab/ref/fminsearch.html (accessed on 20 April 2020).
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 20 April 2020).
- Powell, M.J.D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]






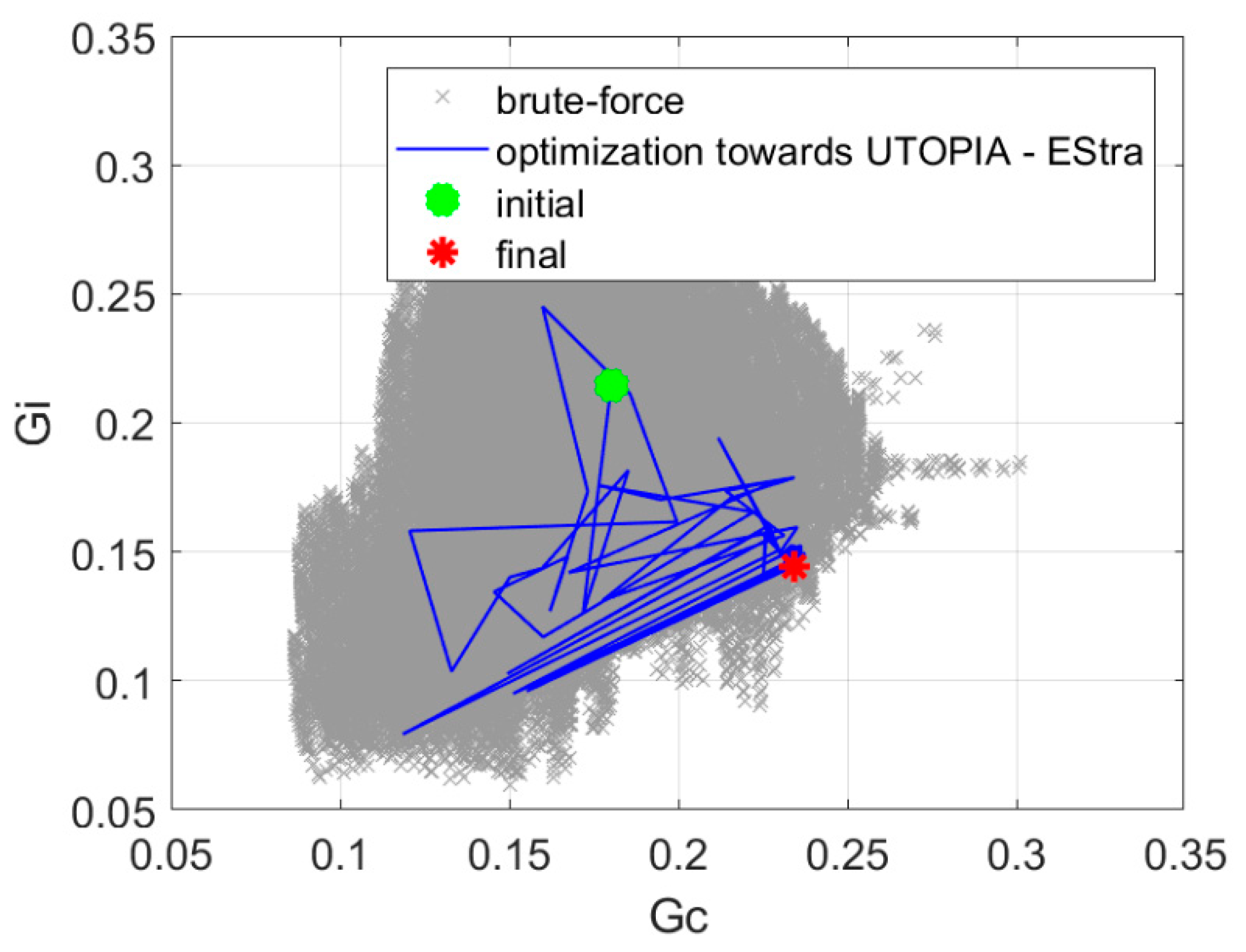
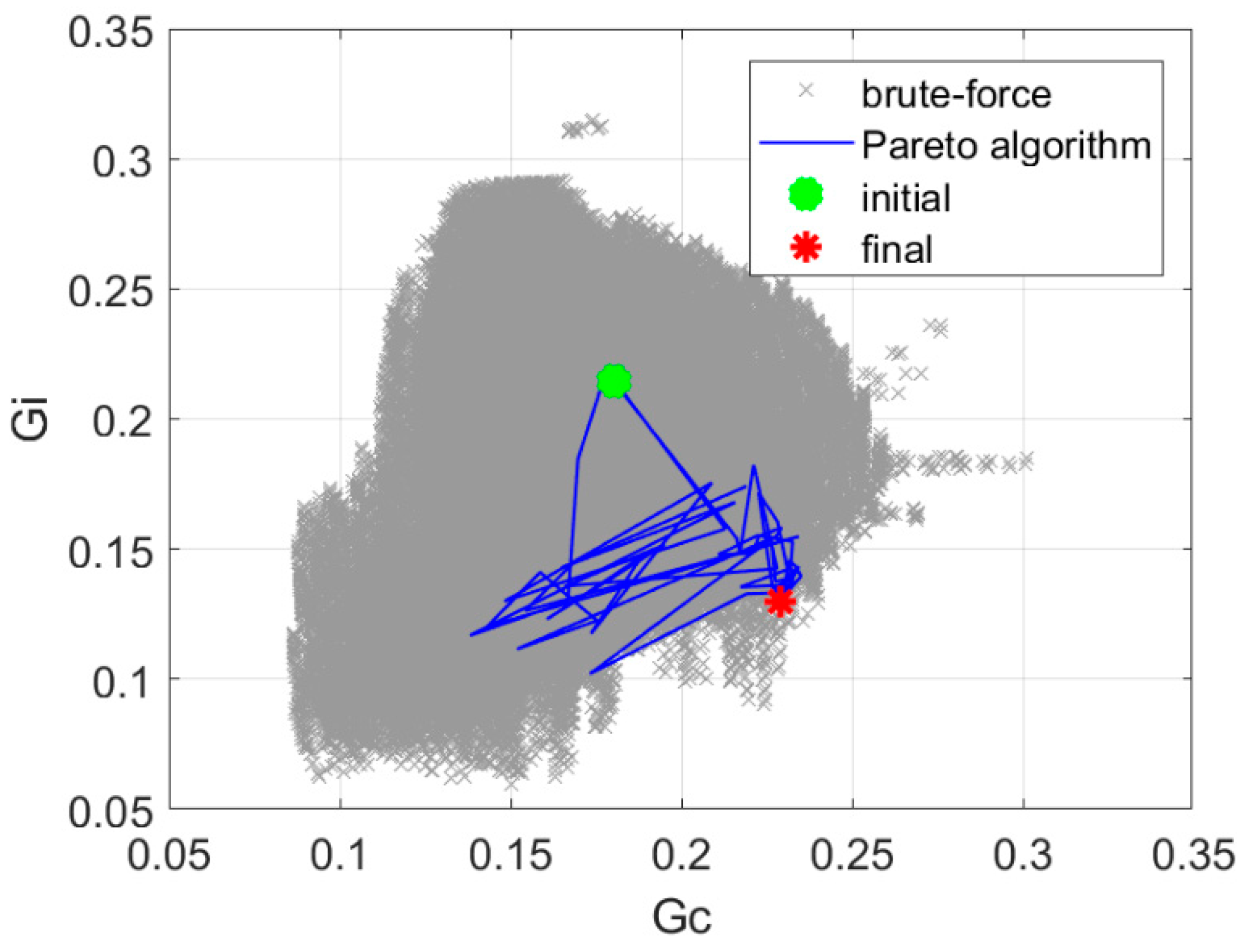
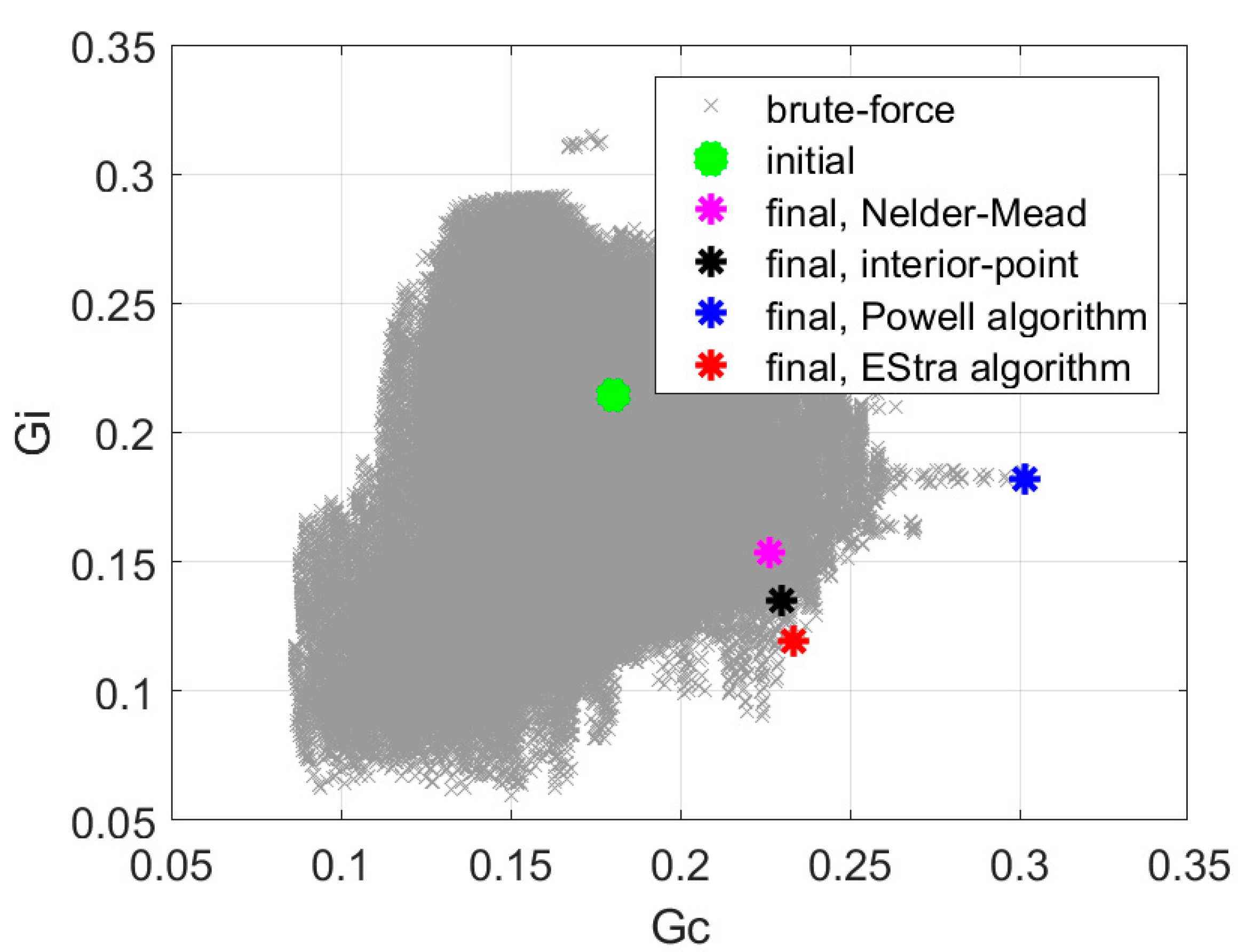
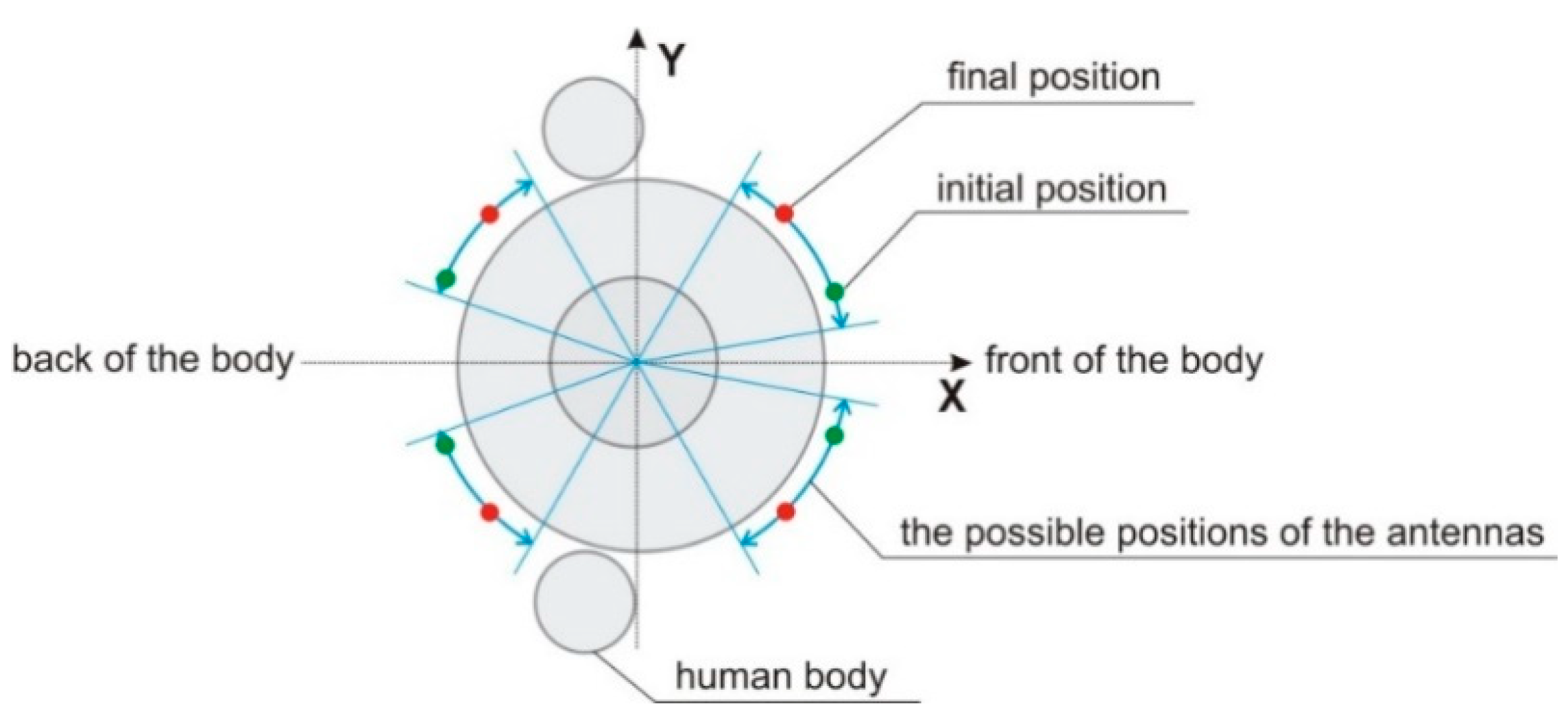

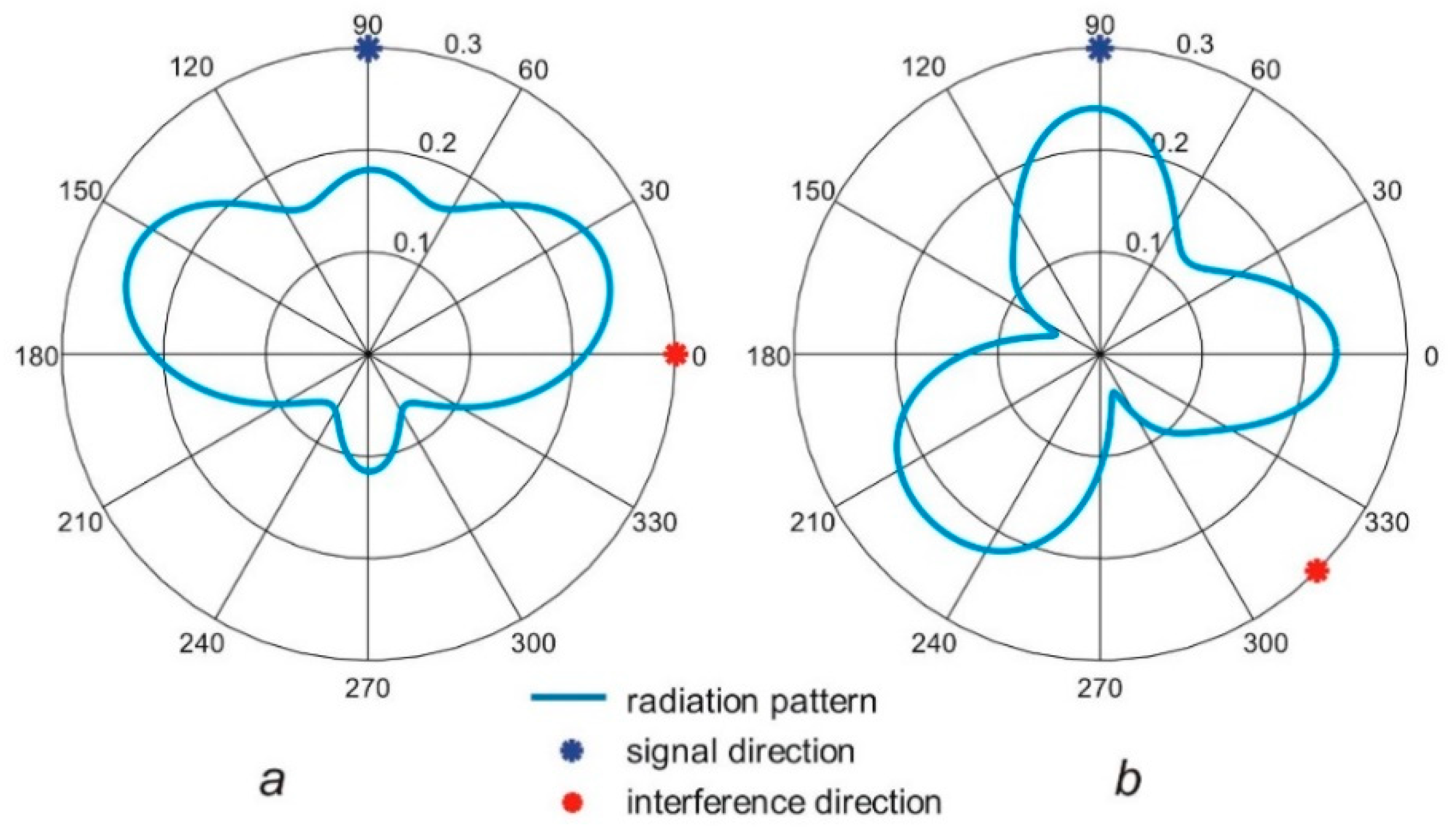
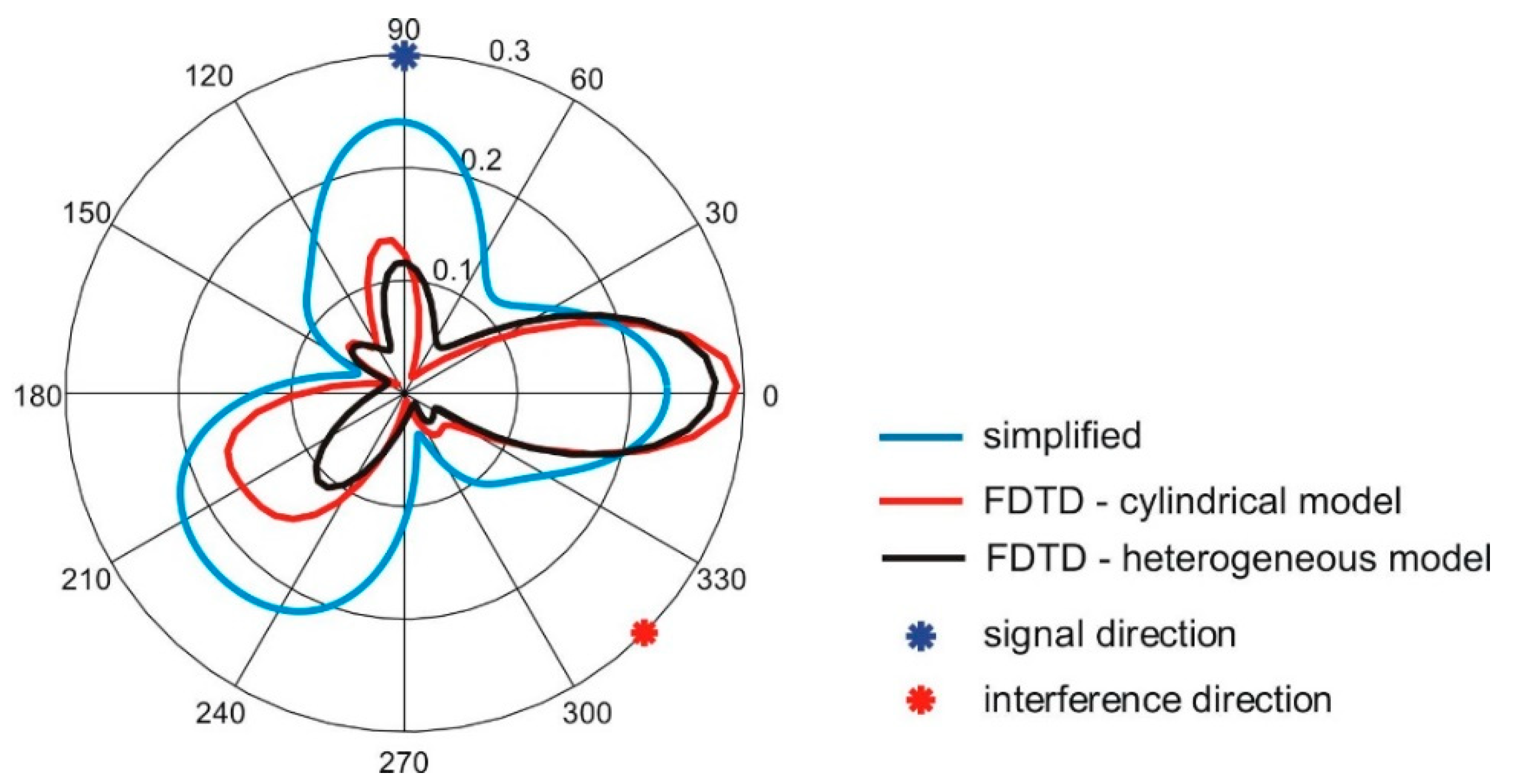
| Variant of the Optimization Algorithm | Objective Function Value | Number of Iterations |
|---|---|---|
| Min-max | fm = 1.96 | 109 |
| Nadir point distance maximization | fr = 1.87 | 145 |
| Utopia point distance minimization | fu = 1.62 | 71 |
| Pareto-like optimization | fp = 1.76 | 56 |
| Algorithm | Number of Iterations | Objective Function Value |
|---|---|---|
| EStra | 109 | 1.96 |
| Nelder–Mead simplex (Matlab function fminsearch) | 445 | 1.47 |
| Interior-point (Matlab function fmincon) | 628 | 1.70 |
| Powell | 415 | 1.66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Januszkiewicz, Ł.; Di Barba, P.; Hausman, S. Optimal Design of Switchable Wearable Antenna Array for Wireless Sensor Networks. Sensors 2020, 20, 2795. https://doi.org/10.3390/s20102795
Januszkiewicz Ł, Di Barba P, Hausman S. Optimal Design of Switchable Wearable Antenna Array for Wireless Sensor Networks. Sensors. 2020; 20(10):2795. https://doi.org/10.3390/s20102795
Chicago/Turabian StyleJanuszkiewicz, Łukasz, Paolo Di Barba, and Sławomir Hausman. 2020. "Optimal Design of Switchable Wearable Antenna Array for Wireless Sensor Networks" Sensors 20, no. 10: 2795. https://doi.org/10.3390/s20102795
APA StyleJanuszkiewicz, Ł., Di Barba, P., & Hausman, S. (2020). Optimal Design of Switchable Wearable Antenna Array for Wireless Sensor Networks. Sensors, 20(10), 2795. https://doi.org/10.3390/s20102795







