SteadEye-Head—Improving MARG-Sensor Based Head Orientation Measurements Through Eye Tracking Data
Abstract
1. Introduction
1.1. State of the Art in MARG Based Orientation Measurements
1.2. State of the Art in Eye Tracking
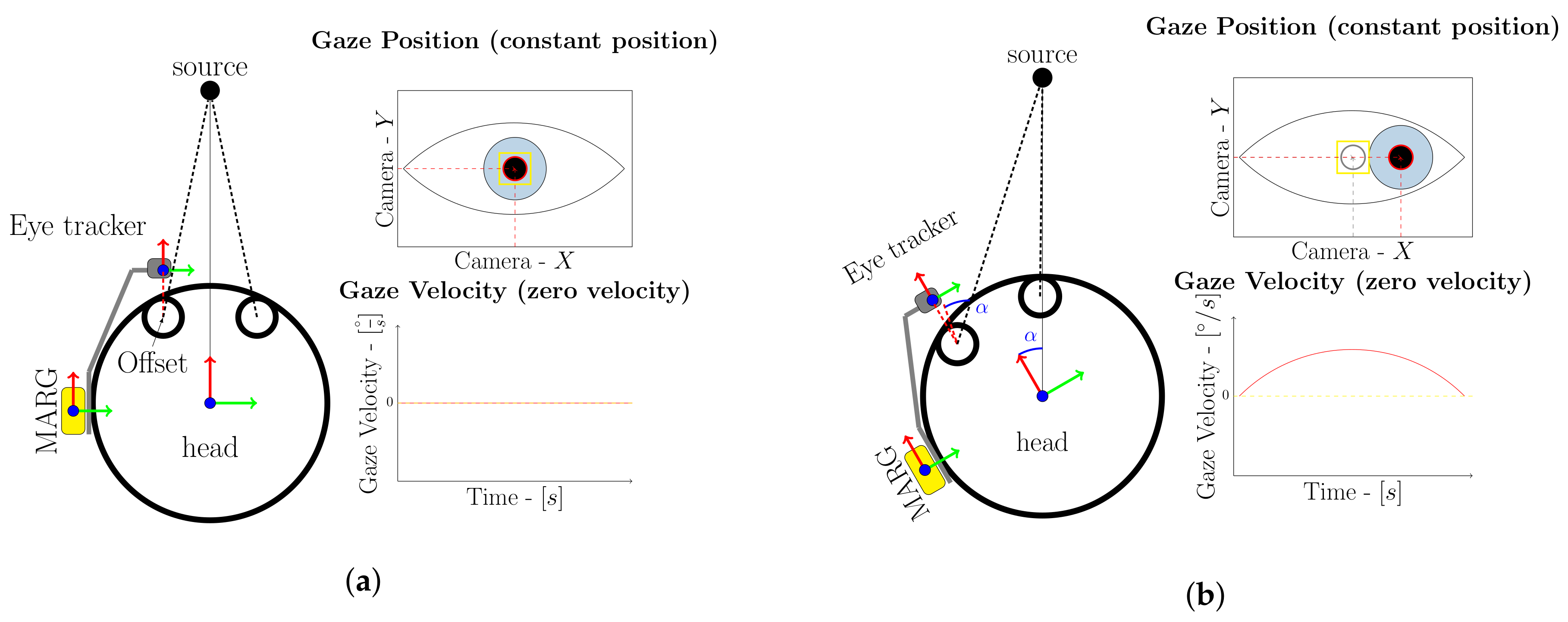
2. Working Principle
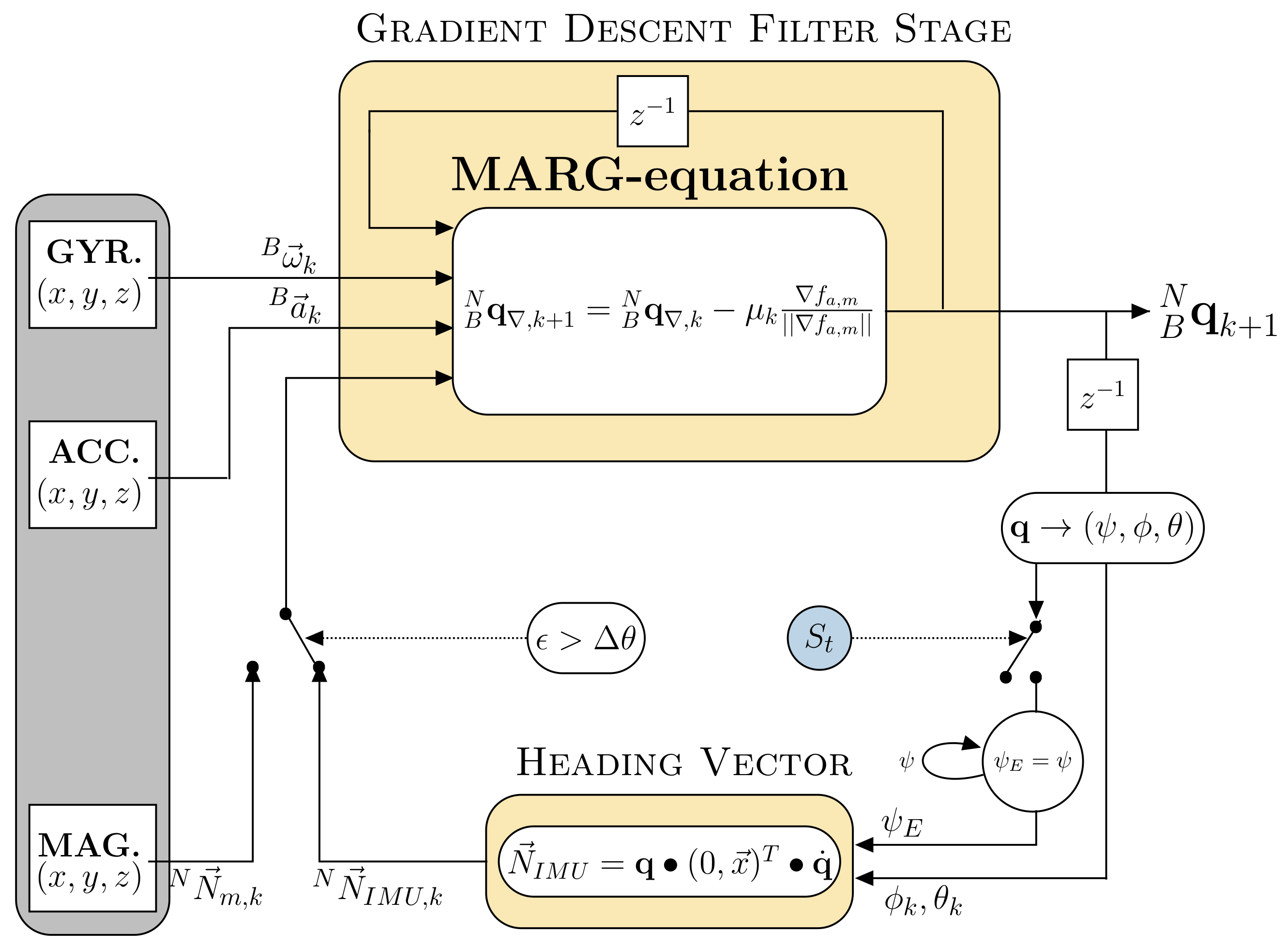
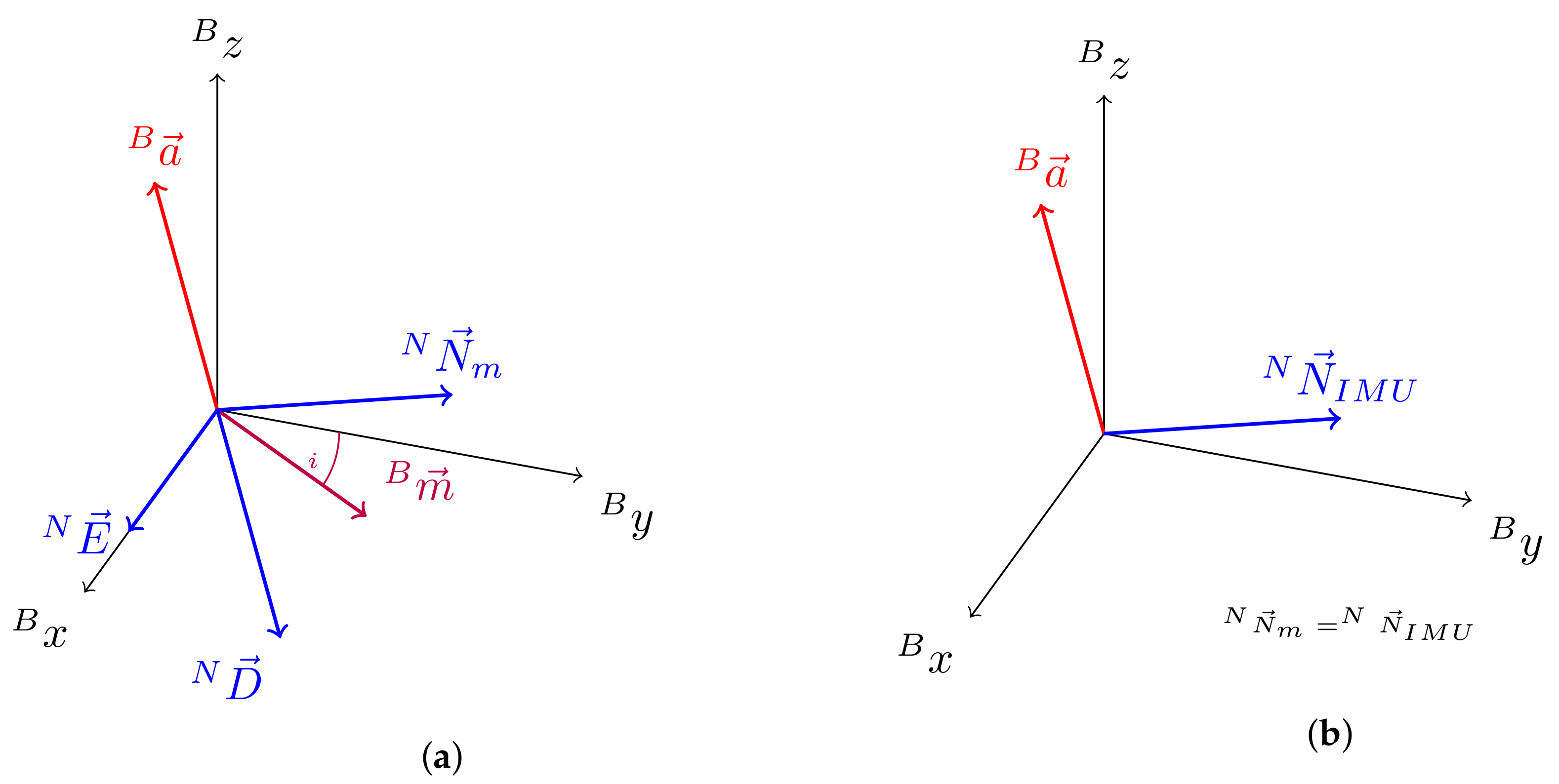
3. Data Fusion Process
3.1. Visual Zero Rotation Detection
3.2. MARG-Sensor Datafusion
4. Interface Setup
5. Experimental Setup
6. Results and Discussion
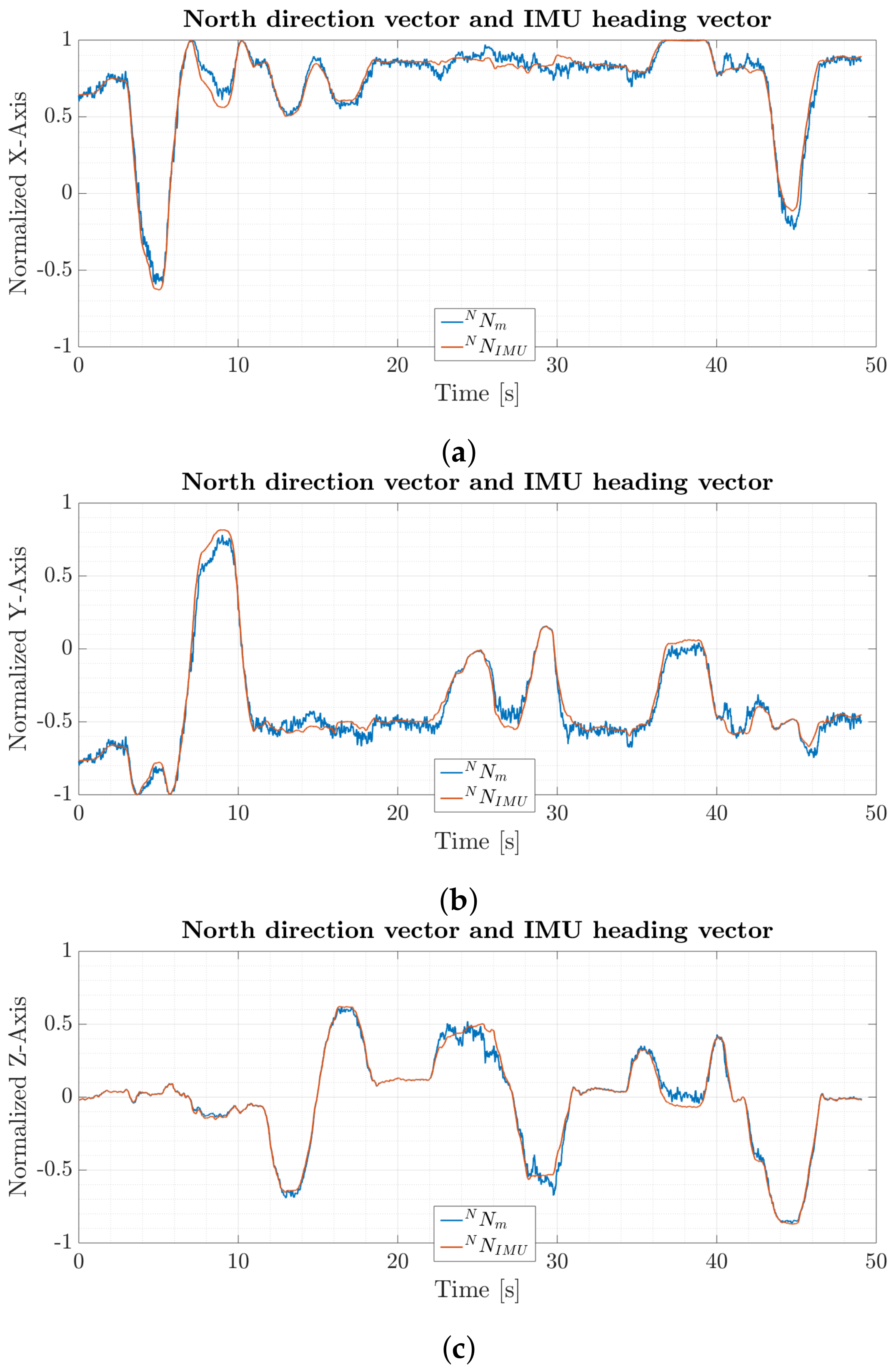
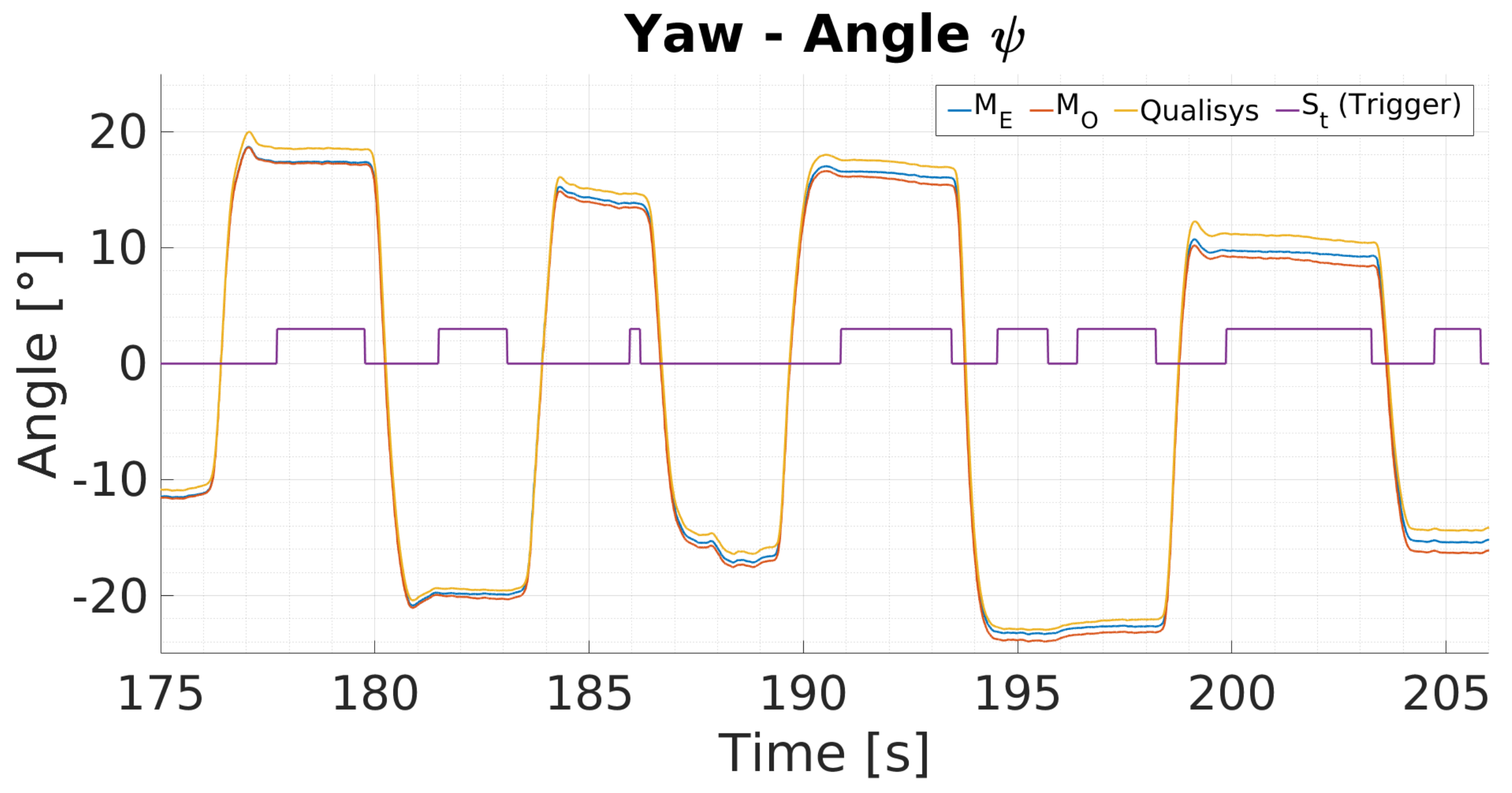
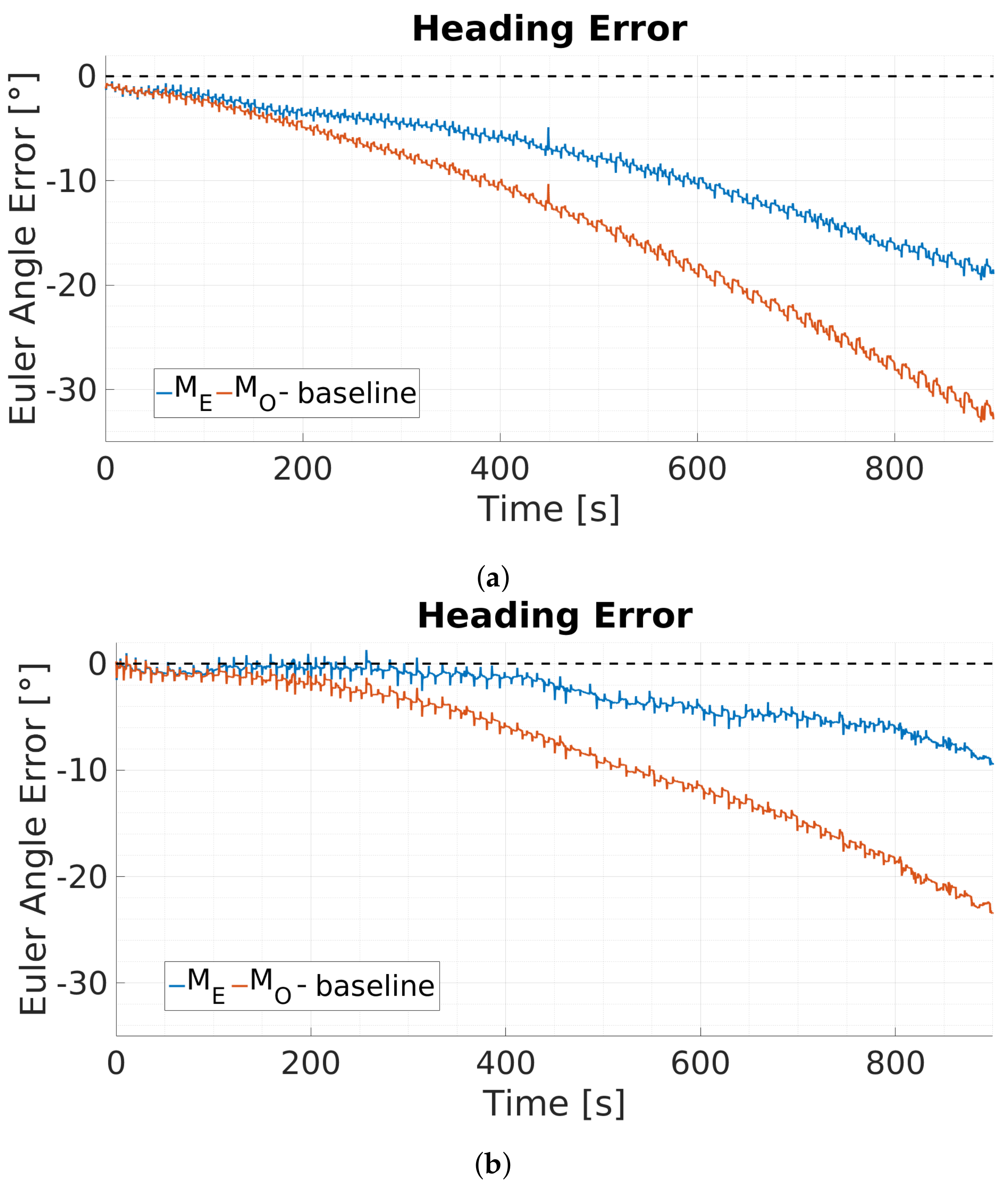
6.1. Interchangeable North Direction Vector Substitutes
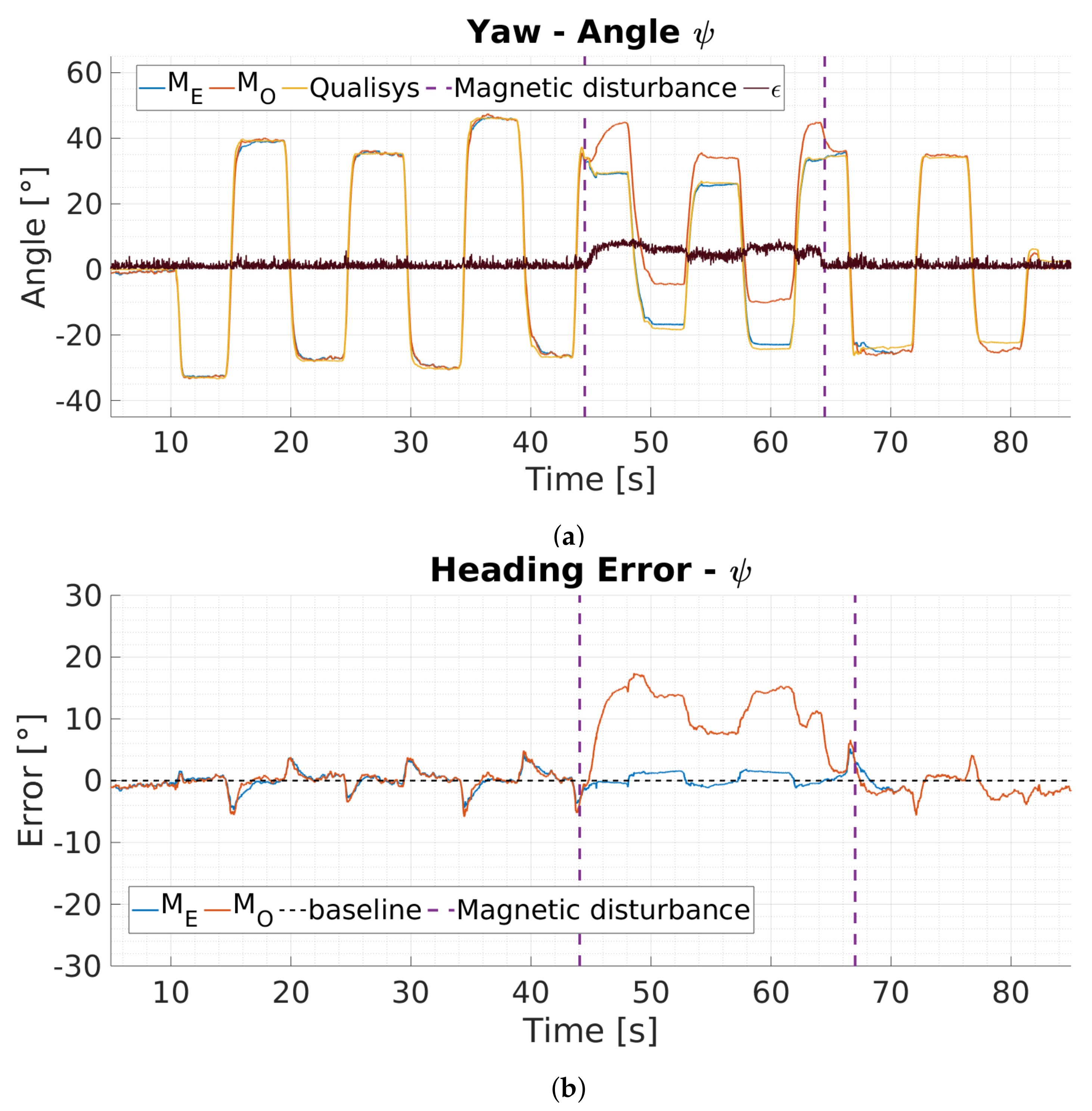
6.2. Magnetic Disturbance Detection
6.3. MARG-Sensor Data Fusion Approach Using Visual Fixations
7. Conclusions
Limitations
8. Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MARG | MagneticAngularate Gravity sensor |
| IMU | Inertial Measurement Unit |
| GDA | Gradient Descent Algorithm |
| MEMS | Micro-Electro-Mechanical Systems |
| API | Application Programming Interface |
| NED | North East Down |
| MCU | Microcontroller Unit |
| dc-bias | direct current bias |
References
- Rudigkeit, N.; Gebhard, M. AMiCUS—A Head Motion-Based Interface for Control of an Assistive Robot. Sensors 2019, 19, 2836. [Google Scholar] [CrossRef] [PubMed]
- Jackowski, A.; Gebhard, M.; Thietje, R. Head Motion and Head Gesture-Based Robot Control: A Usability Study. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Alsharif, S.; Kuzmicheva, O.; Gräser, A. Gaze Gesture-Based Human Robot Interface. Technische Unterstützungssysteme die die Menschen Wirklich Wollen 2016, 12, 339. [Google Scholar]
- Wendel, J. Integrierte Navigationssysteme: Sensordatenfusion, GPS und Inertiale Navigation; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Shiau, J.K.; Huang, C.X.; Chang, M.Y. Noise characteristics of MEMS gyro’s null drift and temperature compensation. J. Appl. Sci. Eng. 2012, 15, 239–246. [Google Scholar]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. A linear Kalman filter for MARG orientation estimation using the algebraic quaternion algorithm. IEEE Trans. Instrum. Meas. 2016, 65, 467–481. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Elkaim, G.; Powell, J.D.; Parkinson, B. A non-linear, two-step estimation algorithm for calibrating solid-state strapdown magnetometers. In Proceedings of the 8th St. Petersburg International Conference on Integrated Navigation Systems (IEEE/AIAA), St. Petersburg, Russia, 28–30 May 2001. [Google Scholar]
- Wöhle, L.; Gebhard, M. A robust quaternion based Kalman filter using a gradient descent algorithm for orientation measurement. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors; Technical Report; Xsens Motion Technologies BV: Enschede, The Netherlands, 8 April 2009; pp. 1–9. [Google Scholar]
- Madgwick, S.O.; Harrison, A.J.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the IEEE International Conference on Rehabilitation Robotics (ICORR), Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Effect of local magnetic field disturbances on inertial measurement units accuracy. Appl. Ergon. 2017, 63, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Sun, Z.; Zhang, W.; Chen, Q. Attitude and gyro bias estimation by the rotation of an inertial measurement unit. Meas. Sci. Technol. 2015, 26, 125102. [Google Scholar] [CrossRef]
- Wu, Y.; Zou, D.; Liu, P.; Yu, W. Dynamic Magnetometer Calibration and Alignment to Inertial Sensors by Kalman Filtering. IEEE Trans. Control Syst. Technol. 2018, 26, 716–723. [Google Scholar] [CrossRef]
- Aqel, M.O.; Marhaban, M.H.; Saripan, M.I.; Ismail, N.B. Review of visual odometry: Types, approaches, challenges, and applications. SpringerPlus 2016, 5, 1897. [Google Scholar] [CrossRef] [PubMed]
- Valenti, R.; Sebe, N.; Gevers, T. What are you looking at? Int. J. Comput. Vis. 2012, 98, 324–334. [Google Scholar] [CrossRef]
- Kassner, M.; Patera, W.; Bulling, A. Pupil: An Open Source Platform for Pervasive Eye Tracking and Mobile Gaze-based Interaction. In Adjunct Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing; ACM: New York, NY, USA, 2014; pp. 1151–1160. [Google Scholar]
- Wöhle, L.; Miller, S.; Gerken, J.; Gebhard, M. A Robust Interface for Head Motion based Control of a Robot Arm using MARG and Visual Sensors. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Pupil Labs GmbH. Pupil Core. Open Source Eye Tracking Platform Home Page. Available online: https://pupil-labs.com/products/core/ (accessed on 12 April 2020).
- Larsson, L.; Schwaller, A.; Holmqvist, K.; Nyström, M.; Stridh, M. Compensation of head movements in mobile eye-tracking data using an inertial measurement unit. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing: Adjunct Publication, New York, NY, USA, 13–17 September 2014; pp. 1161–1167. [Google Scholar] [CrossRef]
- Salvucci, D.D.; Goldberg, J.H. Identifying fixations and saccades in eye-tracking protocols. In Proceedings of the 2000 Symposium on Eye Tracking Research & Applications, Palm Beach Gardens, FL, USA, 6–8 November 2000; pp. 71–78. [Google Scholar] [CrossRef]
- Duchowski, A.T.; Jörg, S. Eye animation. In Handbook of Human Motion; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–19. [Google Scholar]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Real Time Engineers Ltd. FreeRTOS. Real-Time Operating System for Microcontrollers. Available online: https://www.freertos.org/Documentation/RTOS_book.html (accessed on 12 April 2020).
- STMicroelectronics. Parameters and Calibration of a Low-g 3-Axis Accelerometer, Application Note 4508. Available online: https://www.st.com/resource/en/application_note/dm00119044-parameters-and-calibration-of-a-lowg-3axis-accelerometer-stmicroelectronics.pdf (accessed on 12 April 2020).
- Gebre-Egziabher, D.; Elkaim, G.H.; David Powell, J.; Parkinson, B.W. Calibration of strapdown magnetometers in magnetic field domain. J. Aerosp. Eng. 2006, 19, 87–102. [Google Scholar] [CrossRef]

| 1. | |||
| 2. | |||
| 3. | |||
| 4. | |||
| 5. | |||
| 6. | |||
| average |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wöhle, L.; Gebhard, M. SteadEye-Head—Improving MARG-Sensor Based Head Orientation Measurements Through Eye Tracking Data. Sensors 2020, 20, 2759. https://doi.org/10.3390/s20102759
Wöhle L, Gebhard M. SteadEye-Head—Improving MARG-Sensor Based Head Orientation Measurements Through Eye Tracking Data. Sensors. 2020; 20(10):2759. https://doi.org/10.3390/s20102759
Chicago/Turabian StyleWöhle, Lukas, and Marion Gebhard. 2020. "SteadEye-Head—Improving MARG-Sensor Based Head Orientation Measurements Through Eye Tracking Data" Sensors 20, no. 10: 2759. https://doi.org/10.3390/s20102759
APA StyleWöhle, L., & Gebhard, M. (2020). SteadEye-Head—Improving MARG-Sensor Based Head Orientation Measurements Through Eye Tracking Data. Sensors, 20(10), 2759. https://doi.org/10.3390/s20102759





