Performance Bound for Joint Multiple Parameter Target Estimation in Sparse Stepped-Frequency Radar: A Comparison Analysis
Abstract
:1. Introduction
2. Signal Model
3. CRLB of Basic LSF and SSF Signals—Time Delay And Doppler Stretch
3.1. CRLB of SSF-Chirp Signals
3.2. SSF-Rect Signals
4. CRLB of Joint Multiple Parameter Estimation
4.1. Basic Model of CRLB
4.2. Series Expressions of Partial Derivative
4.3. Derivations of the FIM
5. CRLB of Sparse Based Estimator—Compressive Sensing
6. Experiments and Discussion
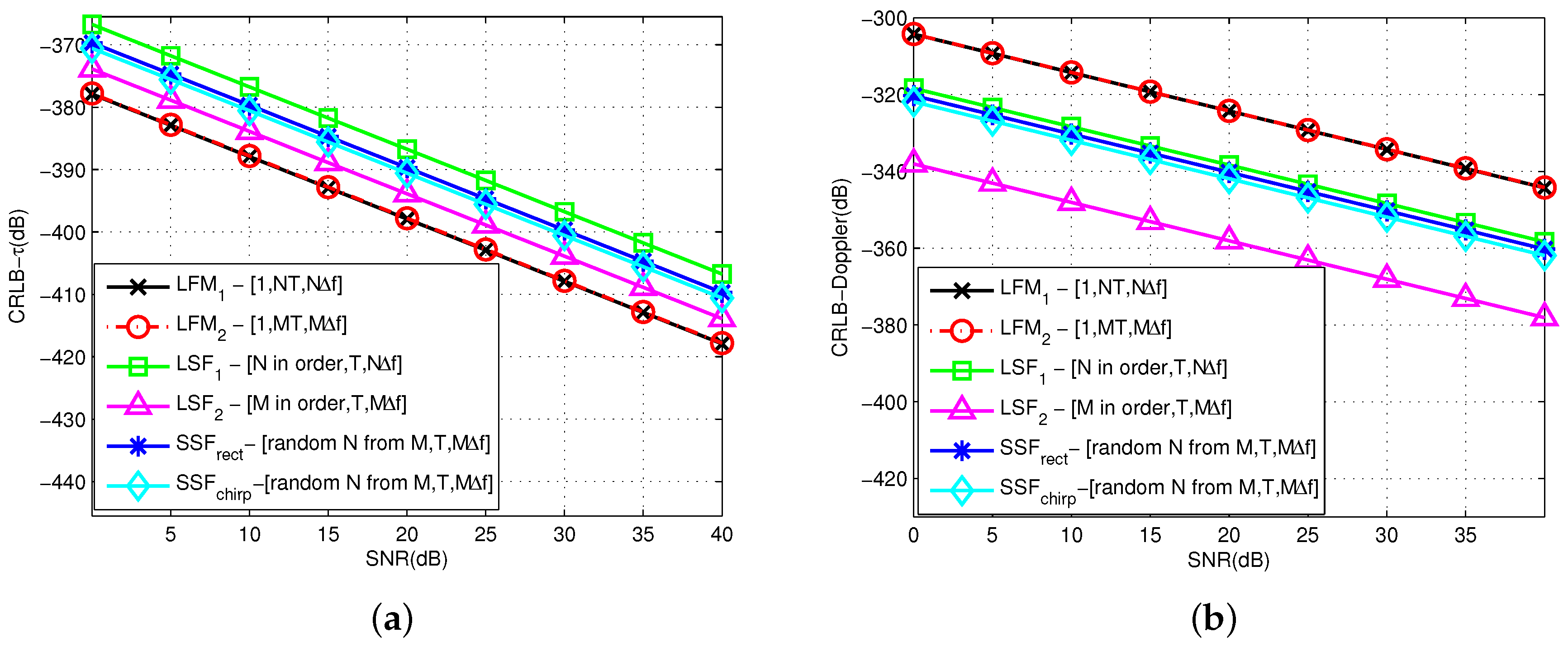
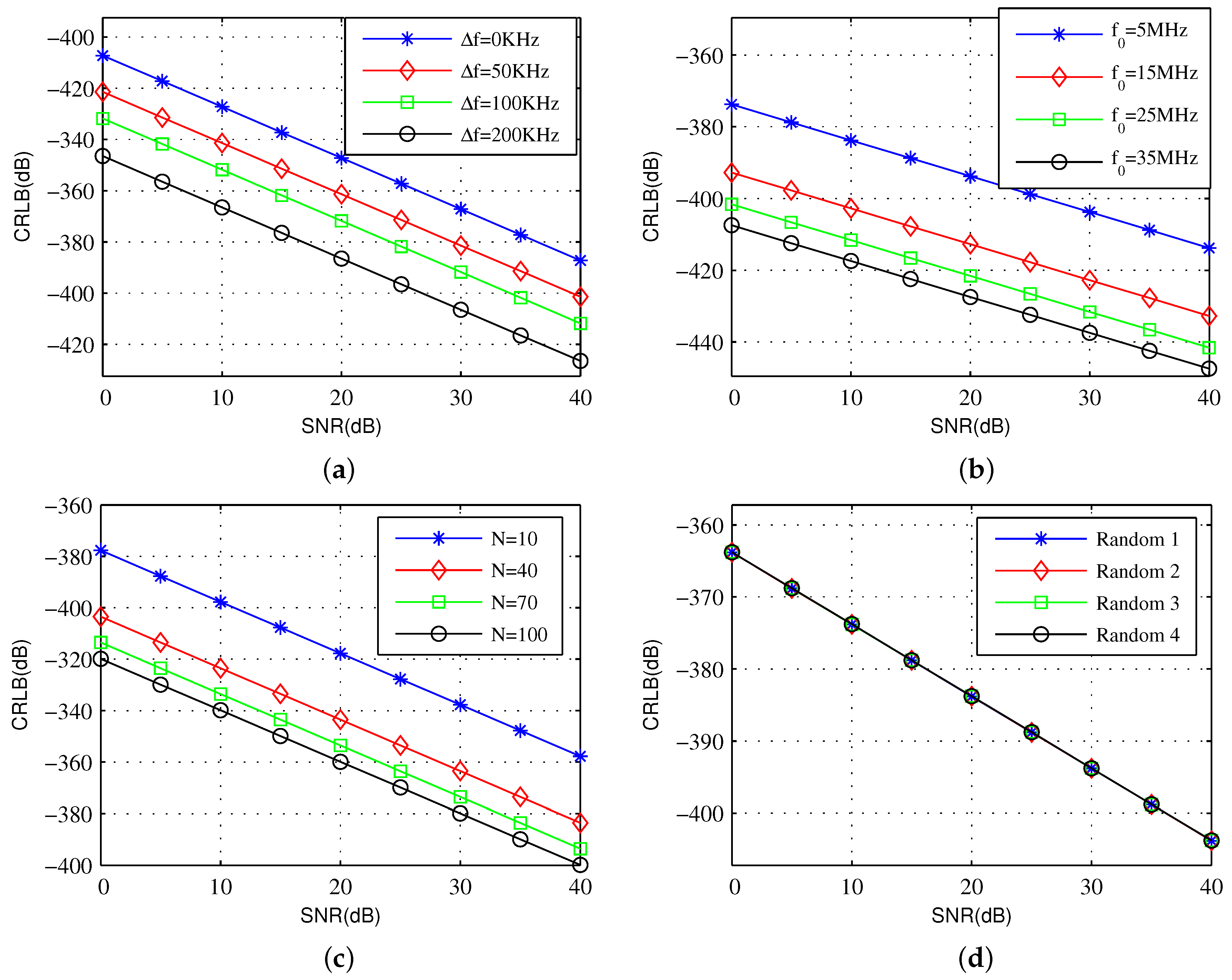
6.1. CRLB Comparison with Different Waveforms
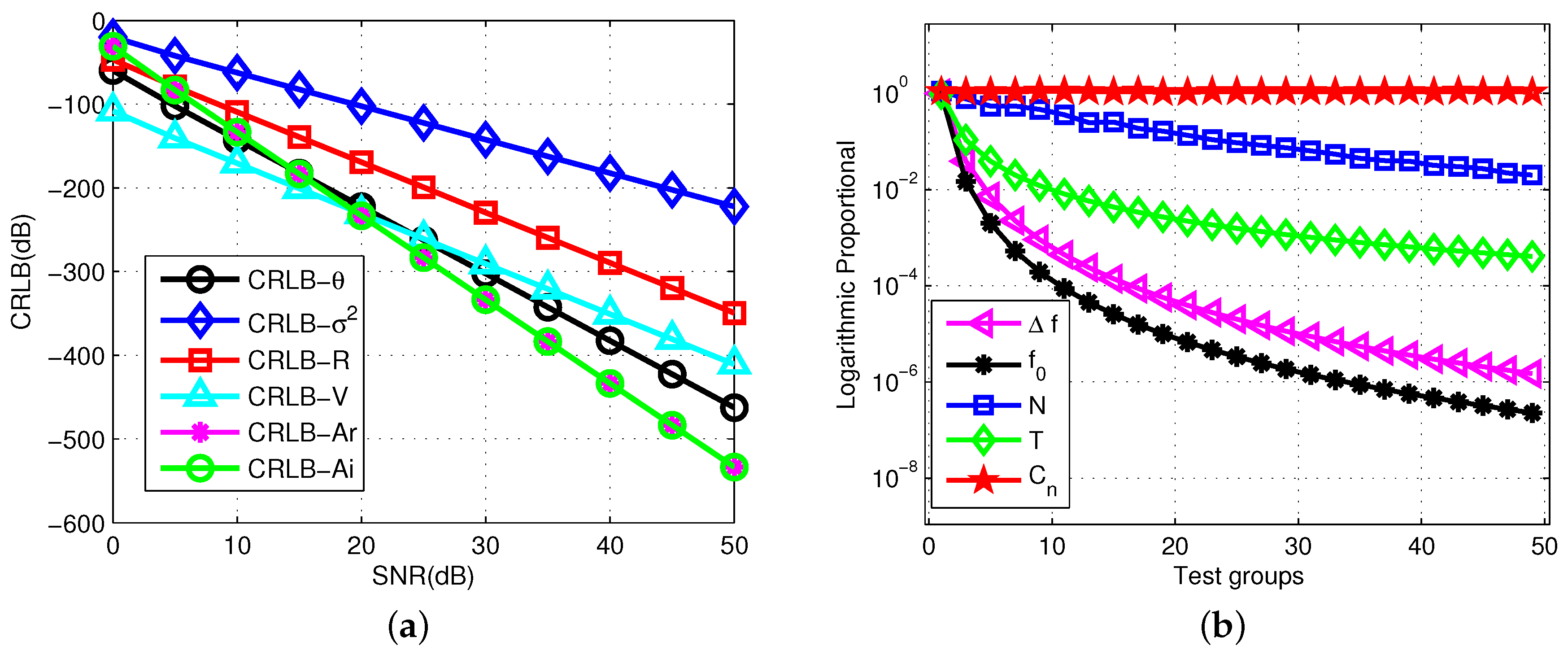
6.2. Comparison of Different CRLBs
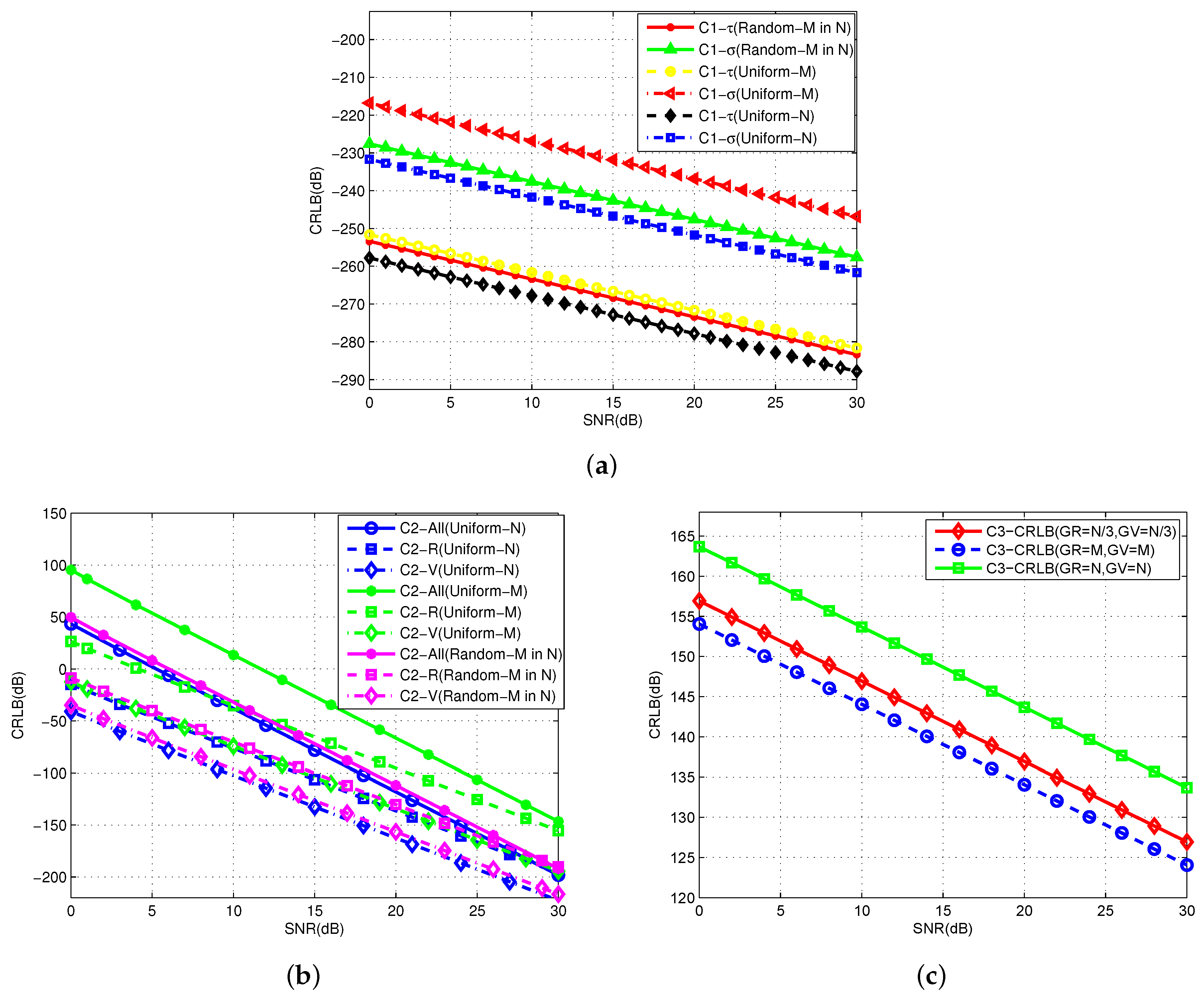
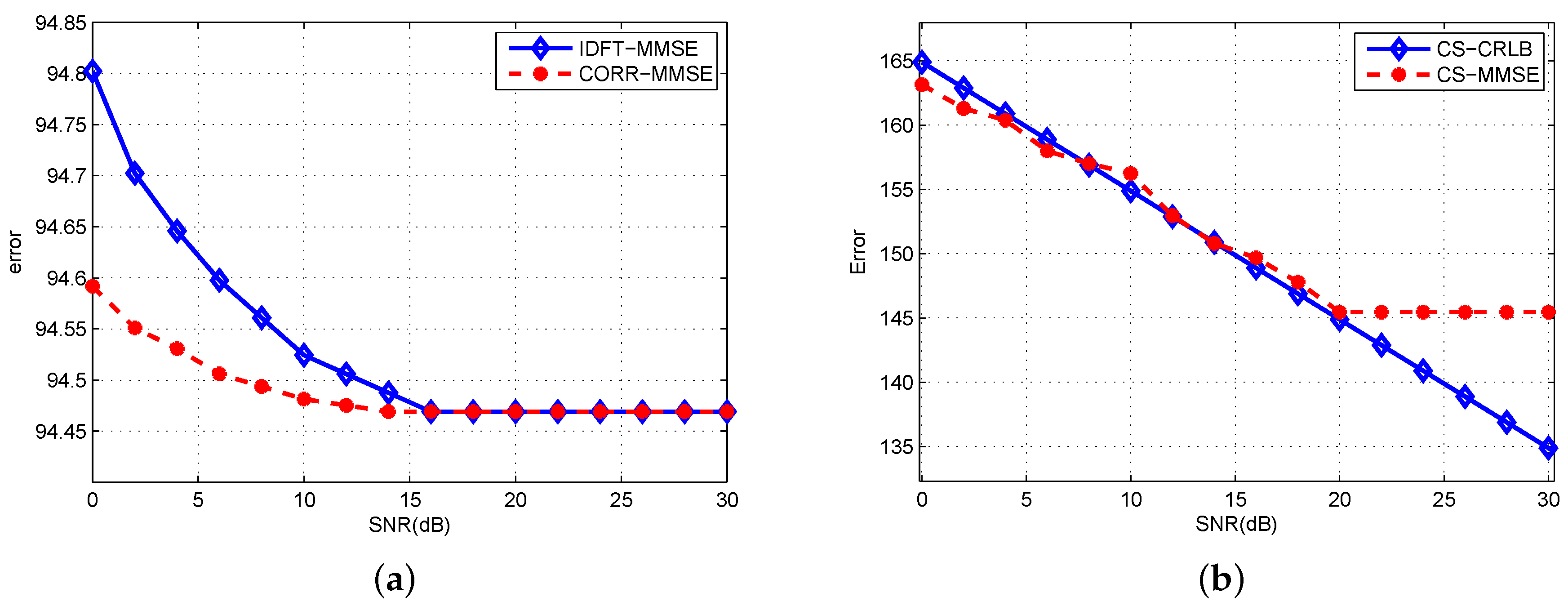
6.3. CRLBs Using Different Estimators
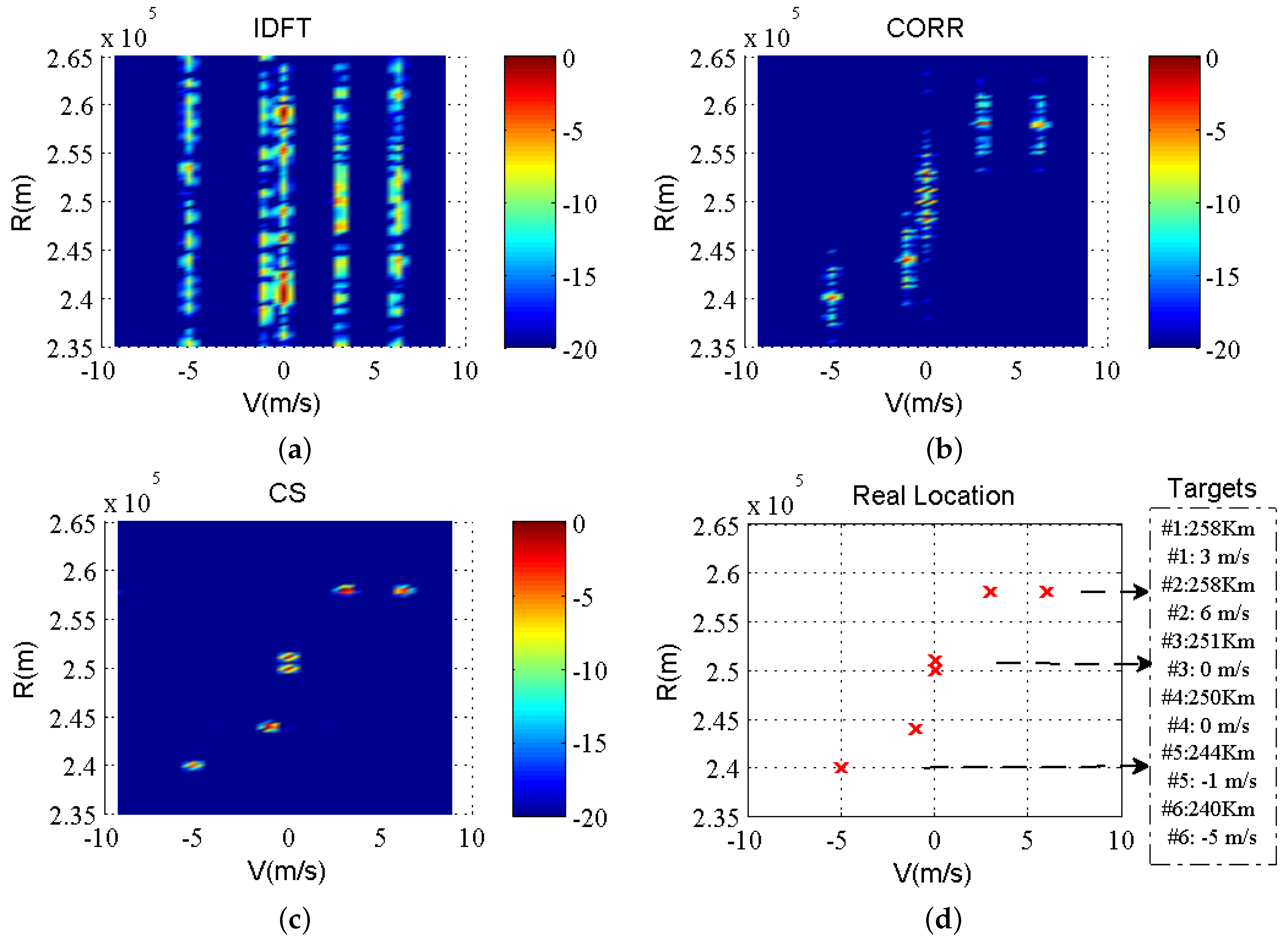
6.4. RD Comparison between Different Methods
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Scharf, L.; Mcwhorter, L. Geometry of the Cramér-Rao bound. In Proceedings of the IEEE 6th SP Workshop on Statistic Signal and Array Process, Victoria, BC, Canada, 7–9 October 1992; pp. 5–8. [Google Scholar]
- Jin, Q.; Wong, K.; Luo, Z. The estimation of time delay and Doppler stretch of wideband signals. IEEE Trans. Signal Process. 1995, 43, 904–916. [Google Scholar] [CrossRef]
- Shi, C.; Salous, S.; Wang, F.; Zhou, J. Cramér-Rao Lower Bound Evaluation for Linear Frequency Modulation Based Active Radar Networks Operating in a Rice Fading Environment. Sensors 2016, 16, 2072. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Wang, F.; Salous, S.; Zhou, J. Cramér-Rao lower bounds for joint target parameter estimation in FM-based distributed passive radar network with antenna arrays. Radio Sci. 2018, 53, 314–333. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Zhou, J. Cramér-rao bound analysis for joint target location and velocity estimation in frequency modulation based passive radar networks. IET Signal Process. 2016, 10, 780–790. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Salous, S. Performance Analysis for Joint Target Parameter Estimation in UMTS-Based Passive Multistatic Radar with Antenna Arrays Using Modified Cramer-Rao Lower Bounds. Sensors 2017, 17, 2379. [Google Scholar] [CrossRef] [PubMed]
- Tilli, E.; Ortenzi, L.; Prodi, F. On the use of HRR data to improve target kinematics estimation: CRLB computation and comparison with simulated results. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 10–14 May 2010; pp. 380–384. [Google Scholar]
- Xiong, J.; Ouyang, X.; Luo, L. A novel Cramér-rao lower bound of time difference of arrival for frequence hopping signals. In Proceedings of the 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; pp. 1741–1744. [Google Scholar]
- Zhang, N.; Zhao, T.; Huang, T. Cramér-rao lower bounds of joint time delay and Doppler-stretch estimation with random stepped-frequency signals. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 647–651. [Google Scholar]
- Zhao, T.; Zhang, N.; Huang, T. Performance analysis of joint time delay and Doppler-stretch estimation with random stepped-frequency signals. In Proceedings of the IEEE International Conference on Digital Signal Processing, Beijing, China, 16–18 October 2016; pp. 594–598. [Google Scholar]
- Zhou, J.; Zhao, H.; Shi, Z. Analytic performance bounds on estimates of scattering center parameters. Trans. Aerosp. Electron. Syst. 2007, 43, 813–826. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, H.; Shi, Z. Performance Analysis of 1D Scattering Center Extraction From Wideband Radar Measurements. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2006), Toulouse, France, 14–19 May 2006. [Google Scholar]
- Wei, H.; Ye, S.; Wan, Q. Influence of phase on Cramer-Rao lower bounds for joint time delay and Doppler stretch estimation. In Proceedings of the 2007 9th International Symposium on Signal Processing and Its Applications, Sharjah, UAE, 12–15 February 2007; pp. 1–4. [Google Scholar]
- Gogolev, I.; Yashin, G. Cramér-rao lower bound of Doppler stretch and delay in wideband signal model. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 1–3 February 2017. [Google Scholar]
- He, L.; Kassam, S.; Ahmad, F. Sparse Stepped-Frequency Waveform Design for Through-the-Wall Radar Imaging. IET Digit. Libr. 2011, 922–938. [Google Scholar]
- Zhu, F.; Zhang, Q.; Lei, Q. Reconstruction of Moving Target’s HRRP Using Sparse Frequency-Stepped Chirp Signal. IEEE Sens. J. 2011, 11, 2327–2334. [Google Scholar]
- Zhang, L.; Qiao, Z.; Xing, M. High-Resolution ISAR Imaging with Sparse Stepped-Frequency Waveforms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4630–4651. [Google Scholar] [CrossRef]
- Axelsson, S. Analysis of Random Step Frequency Radar and Comparison with Experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 890–904. [Google Scholar] [CrossRef]
- Mahdi, S.; Sergiy, A. Cramér-rao Bound for Sparse Signals Fitting the Low-Rank Model with Small Number of Parameters. IEEE Signal Process. Lett. 2015, 22, 1497–1501. [Google Scholar]
- Yun, S.; Kim, S. Analysis of Cramér-rao Lower Bound for time delay estimation using UWB pulses. In Proceedings of the Ubiquitous Positioning, Indoor Navigation, and Location Based Service, Helsinki, Finland, 3–4 October 2012; pp. 1–5. [Google Scholar]
- Zhou, J.; Zhao, H.; Fu, Q. Performance analysis of one dimensional radar imaging based on sparse and non-uniform frequency samplings. In Proceedings of the IET International Conference on Radar Systems, Glasgow, UK, 22–25 October 2012; pp. 1–7. [Google Scholar]
- Zhao, T.; Huang, T. Cramér-rao Lower Bounds for the Joint Delay-Doppler Estimation of an Extended Target. IEEE Trans. Signal Process. 2016, 64, 1562–1573. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Meng, H. Adaptive Compressed Sensing via Minimizing Cramér-rao Bound. IEEE Signal Process. Lett. 2014, 21, 270–274. [Google Scholar] [CrossRef]
- Benhaim, Z.; Eldar, Y. The Cramér-Rao Bound for Estimating a Sparse Parameter Vector. IEEE Trans. Signal Process. 2010, 58, 3384–3389. [Google Scholar] [CrossRef]
- Kalouptsidis, N.; Tarokh, V.; Babadi, B. Asymptotic Achievability of the Cramér-Rao Bound for Noisy Compressive Sampling. IEEE Trans. Signal Process. 2009, 57, 1233–1236. [Google Scholar]
| Variables | Initial Value | the Value of Groups | Value Range |
|---|---|---|---|
| (kHz) | |||
| (MHz) | |||
| N | |||
| T(ms) | |||
| Random | Random |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Zhang, X.; Yang, Q.; Ye, L.; Zhao, M. Performance Bound for Joint Multiple Parameter Target Estimation in Sparse Stepped-Frequency Radar: A Comparison Analysis. Sensors 2019, 19, 2002. https://doi.org/10.3390/s19092002
Chen Q, Zhang X, Yang Q, Ye L, Zhao M. Performance Bound for Joint Multiple Parameter Target Estimation in Sparse Stepped-Frequency Radar: A Comparison Analysis. Sensors. 2019; 19(9):2002. https://doi.org/10.3390/s19092002
Chicago/Turabian StyleChen, Qiushi, Xin Zhang, Qiang Yang, Lei Ye, and Mengxiao Zhao. 2019. "Performance Bound for Joint Multiple Parameter Target Estimation in Sparse Stepped-Frequency Radar: A Comparison Analysis" Sensors 19, no. 9: 2002. https://doi.org/10.3390/s19092002
APA StyleChen, Q., Zhang, X., Yang, Q., Ye, L., & Zhao, M. (2019). Performance Bound for Joint Multiple Parameter Target Estimation in Sparse Stepped-Frequency Radar: A Comparison Analysis. Sensors, 19(9), 2002. https://doi.org/10.3390/s19092002





