Distributed Acoustic Sensing of Strain at Earth Tide Frequencies
Abstract
1. Introduction
2. Materials and Methods
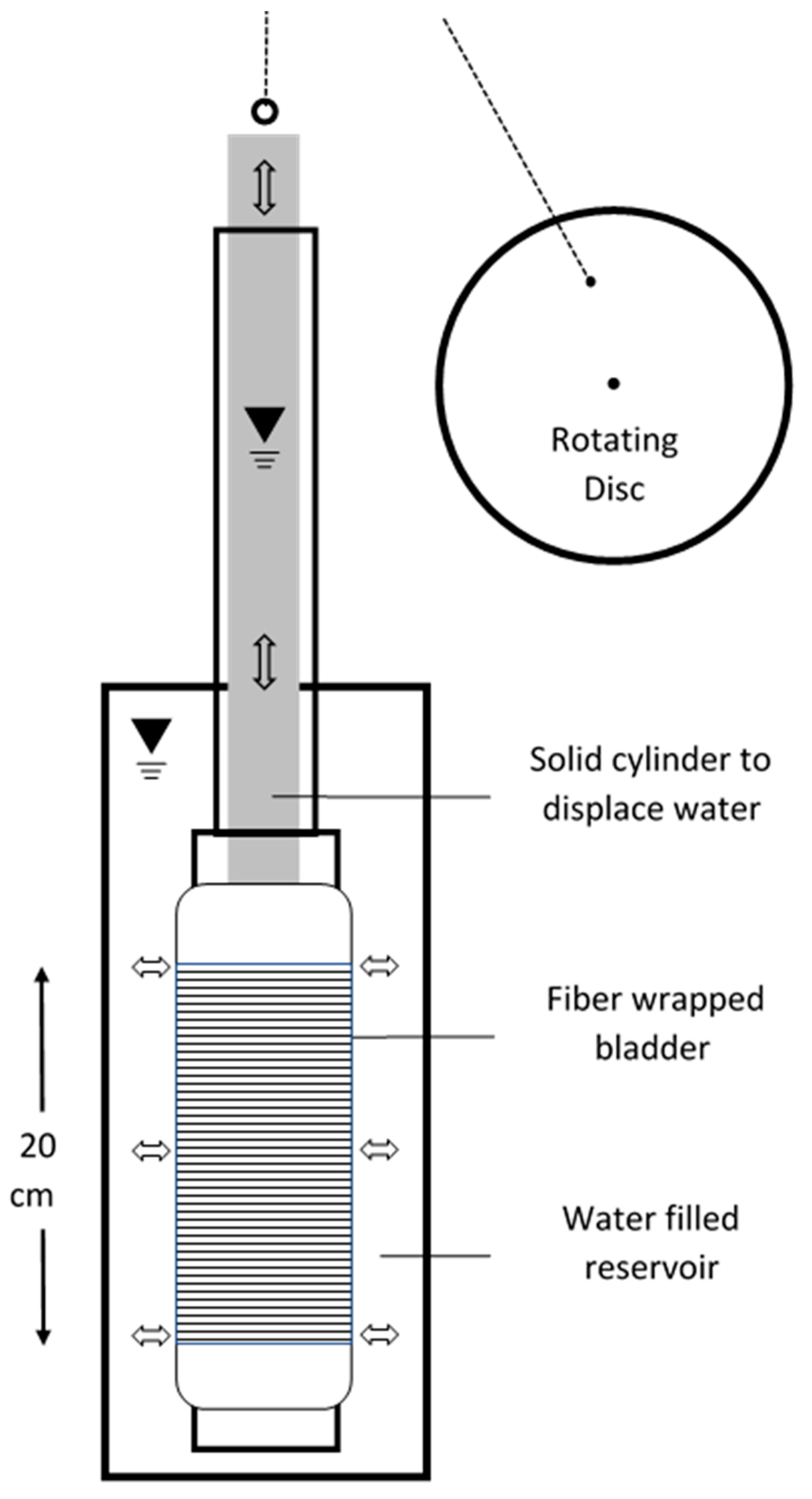
2.1. Sensor Principles
2.2. Experimental Setup
2.3. Data Processing
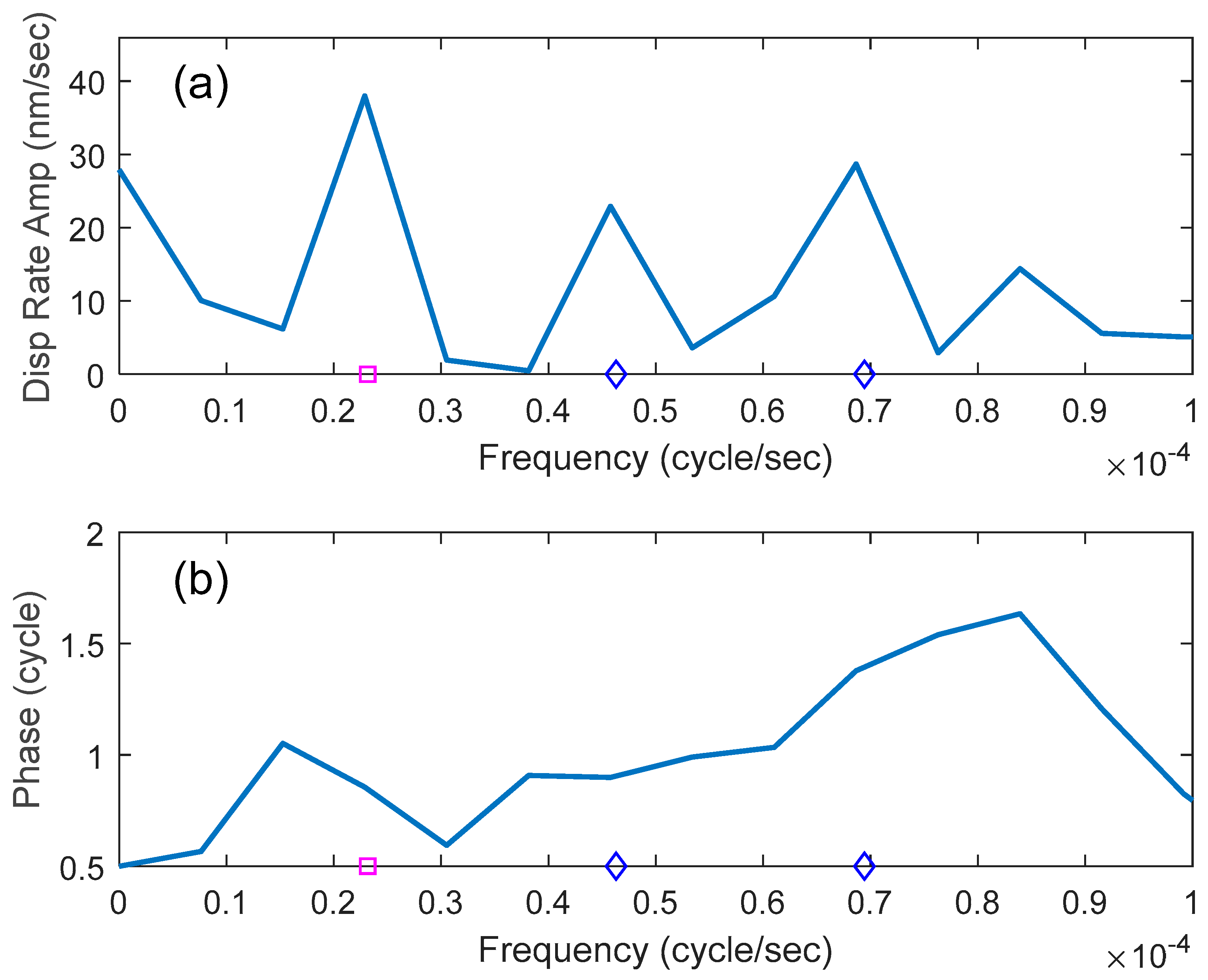
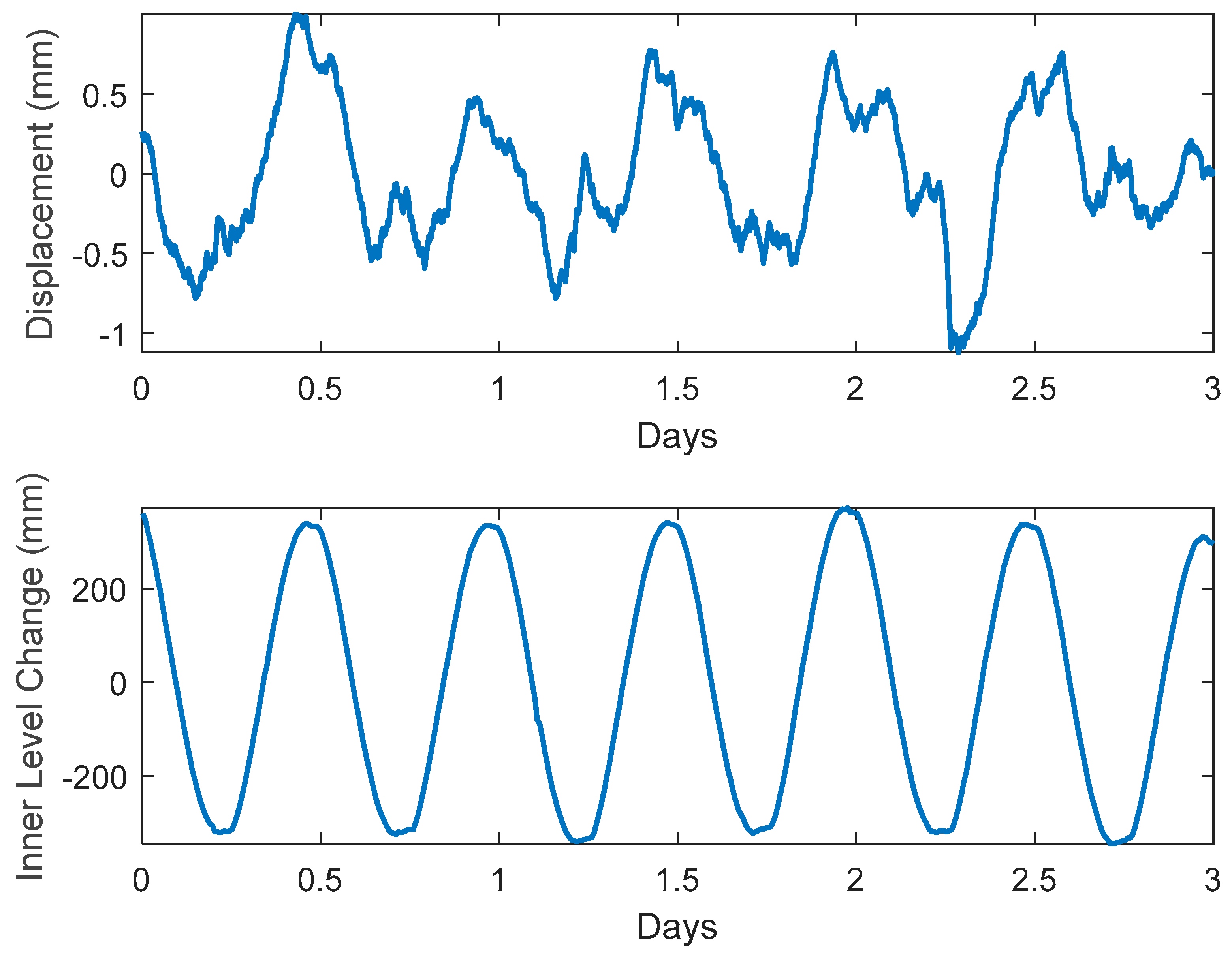
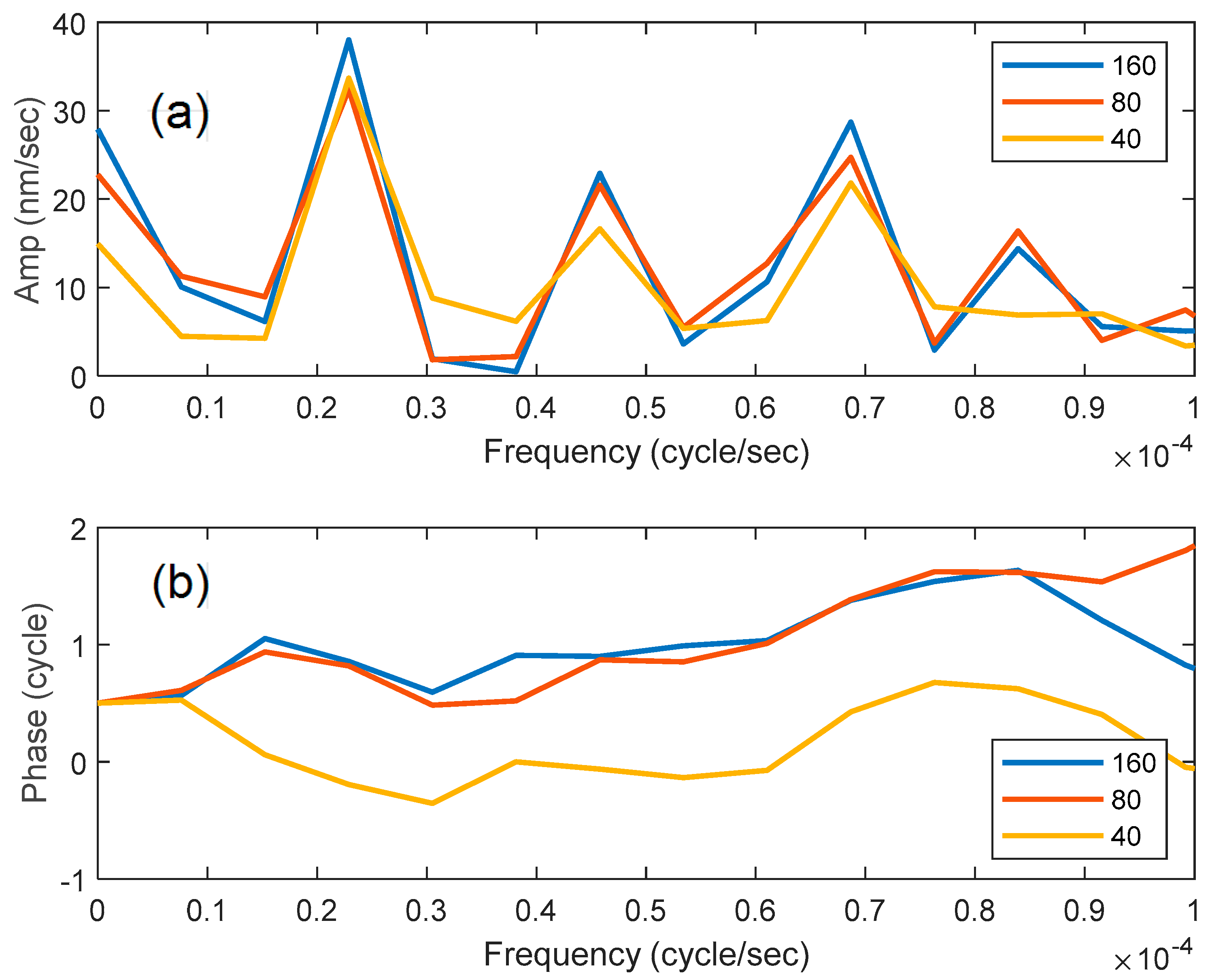
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Agnew, D.C. 3.06 Earth Tides. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 151–178. [Google Scholar]
- Bower, D.R. Bedrock fracture parameters from the interpretation of well tides. J. Geophys. Res. Solid Earth 1983, 88, 5025–5035. [Google Scholar] [CrossRef]
- Burbey, T.J. Fracture characterization using Earth tide analysis. J. Hydrol. 2010, 380, 237–246. [Google Scholar] [CrossRef]
- Hisz, D.B.; Murdoch, L.C.; Germanovich, L.N. A portable borehole extensometer and tiltmeter for characterizing aquifers. Water Resour. Res. 2013, 49, 7900–7910. [Google Scholar] [CrossRef]
- Allègre, V.; Brodsky, E.E.; Xue, L.; Nale, S.M.; Parker, B.L.; Cherry, J.A. Using earth-tide induced water pressure changes to measure in situ permeability: A comparison with long-term pumping tests. Water Resour. Res. 2016, 52, 3113–3126. [Google Scholar] [CrossRef]
- Burbey, T.J.; Hisz, D.; Murdoch, L.C.; Zhang, M. Quantifying fractured crystalline-rock properties using well tests, earth tides and barometric effects. J. Hydrol. 2012, 414, 317–328. [Google Scholar] [CrossRef]
- Becker, M.W.; Coleman, T.; Ciervo, C.; Cole, M.; Mondanos, M. Fluid pressure sensing with fiber-optic distributed acoustic sensing. Lead. Edge 2017, 36, 1018–1023. [Google Scholar] [CrossRef]
- Becker, M.W.; Ciervo, C.; Coleman, T. A Slimhole Approach to Measuring Distributed Hydromechanical Strain in Fractured Geothermal Reservoirs. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering Stanford University, Palo Alto, CA, USA, 12–14 February 2018. [Google Scholar]
- Becker, M.W.; Cole, M.; Ciervo, C.; Coleman, T.; Mondanos, M.J. Measuring Hydraulic Connection in Fractured Bedrock with Periodic Hydraulic Tests and Distributed Acoustic Sensing. In Proceedings of the 41st Workshop on Geothermal Reservoir Engineering Stanford University, Palo Alto, CA, USA, 22–24 February 2016. [Google Scholar]
- Becker, M.W.; Ciervo, C.; Cole, M.; Coleman, T.; Mondanos, M. Fracture hydromechanical response measured by fiber optic distributed acoustic sensing at milliHertz frequencies. Geophys. Res. Lett. 2017, 44, 7295–7302. [Google Scholar] [CrossRef]
- Sato, K. Monitoring the underground migration of sequestered carbon dioxide using Earth tides. Energy Convers. Manage. 2006, 47, 2414–2423. [Google Scholar] [CrossRef]
- Johannessen, K.; Drakeley, B.K.; Farhadiroushan, M. Distributed Acoustic Sensing—A New Way of Listening to Your Well/Reservoir. In Proceedings of the SPE Intelligent Energy International, Utrecht, The Netherlands, 27–29 March 2012. [Google Scholar] [CrossRef]
- Mestayer, J.; Cox, B.; Wills, P.; Kiyashchenko, D.; Lopez, J.; Costello, M.; Bourne, S.; Ugueto, G.; Lupton, R.; Solano, G.; et al. Field Trials of Distributed Acoustic Sensing for Geophysical Monitoring. Available online: https://library.seg.org/doi/abs/10.1190/1.3628095 (accessed on 19 March 2019).
- Parker, T.; Shatalin, S.; Farhadiroushan, M. Distributed acoustic sensing—A new tool for seismic applications. First Break 2014, 32, 61–69. [Google Scholar] [CrossRef]
- Hull, R.; Meek, R.; Bello, H.; Miller, D. Case history of DAS fiber-based microseismic and strain data, monitoring horizontal hydraulic stimulations using various tools to highlight physical deformation processes (Part A). In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; pp. 3050–3062. [Google Scholar]
- Daley, T.M.; Freifeld, B.; Ajo-Franklin, J.; Dou, S.; Pevzner, R.; Shulakova, V.; Kashika, S.; Miller, D.; Goetz, J.; Henninges, J.; et al. Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring. Lead. Edge 2013, 32, 699–706. [Google Scholar] [CrossRef]
- Miah, K.; Potter, D. A Review of Hybrid Fiber-Optic Distributed Simultaneous Vibration and Temperature Sensing Technology and Its Geophysical Applications. Sensors 2017, 17, 2511. [Google Scholar] [CrossRef] [PubMed]
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Schenato, L. A Review of Distributed Fibre Optic Sensors for Geo-Hydrological Applications. Appl. Sci. 2017, 7, 896. [Google Scholar] [CrossRef]
- Daley, T.M.; Miller, D.E.; Dodds, K.; Cook, P.; Freifeld, B.M. Field testing of modular borehole monitoring with simultaneous distributed acoustic sensing and geophone vertical seismic profiles at Citronelle, Alabama. Geophys. Prospect. 2015. [Google Scholar] [CrossRef]
- Roeloffs, E. Tidal calibration of Plate Boundary Observatory borehole strainmeters: Roles of vertical and shear coupling. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Silixa Ltd. Case Study: High-Resolution, Far-Offset VSP Survey with Carina® Sensing System for Permanent CO2 Storage Monitoring in Otway, Australia Silixa Ltd. Available online: https://silixa.com/wp-content/uploads/Case-Study-High-resolution-far-offset-VSP-survey-with-Carina-Sensing-System2.pdf (accessed on 24 April 2019).
- Langaas, K.; Nilsen, K.I.; Skjaeveland, S.M. Tidal Pressure Response and Surveillance of Water Encroachment. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Hanson, J.M.; Owen, L.B. Fracture Orientation Analysis by the Solid Earth Tidal Strain Method. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 26–29 September 1982. [Google Scholar]
| Symbol | Origin | Period (day) | Amplitude (mm) |
|---|---|---|---|
| Long-period components | |||
| SSa | Solar declinational | 182.6 | 31 |
| Mm | Lunar elliptic | 27.6 | 35 |
| Mf | Lunar declinational | 13.7 | 67 |
| Diurnal components | |||
| O1 | Lunar principal | 1.08 | 262 |
| P1 | Solar principal | 1.00 | 122 |
| mK1 + sK1 | Lunar-solar declinational | 1.00 | 369 |
| Semi-diurnal components | |||
| N2 | Lunar major elliptic of M2 | 0.527 | 121 |
| M2 | Lunar principal | 0.518 | 632 |
| S2 | Solar principal | 0.500 | 294 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, M.W.; Coleman, T.I. Distributed Acoustic Sensing of Strain at Earth Tide Frequencies. Sensors 2019, 19, 1975. https://doi.org/10.3390/s19091975
Becker MW, Coleman TI. Distributed Acoustic Sensing of Strain at Earth Tide Frequencies. Sensors. 2019; 19(9):1975. https://doi.org/10.3390/s19091975
Chicago/Turabian StyleBecker, Matthew W., and Thomas I. Coleman. 2019. "Distributed Acoustic Sensing of Strain at Earth Tide Frequencies" Sensors 19, no. 9: 1975. https://doi.org/10.3390/s19091975
APA StyleBecker, M. W., & Coleman, T. I. (2019). Distributed Acoustic Sensing of Strain at Earth Tide Frequencies. Sensors, 19(9), 1975. https://doi.org/10.3390/s19091975




