Building Corner Detection in Aerial Images with Fully Convolutional Networks
Abstract
1. Introduction
2. Semantic Image Segmentation with the DeepLab
2.1. Atrous Convolution
2.2. Multiscale Processing
2.3. Fully Connected Conditional Random Fields
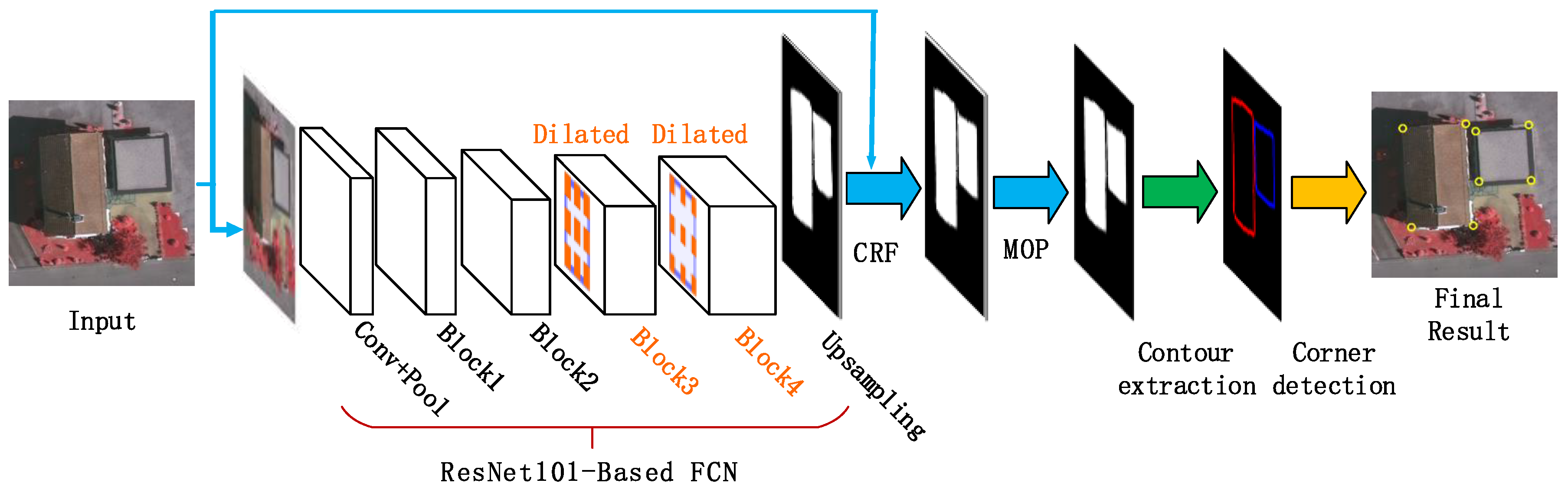
3. Proposed Algorithm for Building Corner Detection
3.1. Dataset of Aerial Images
3.2. Building Segmentation
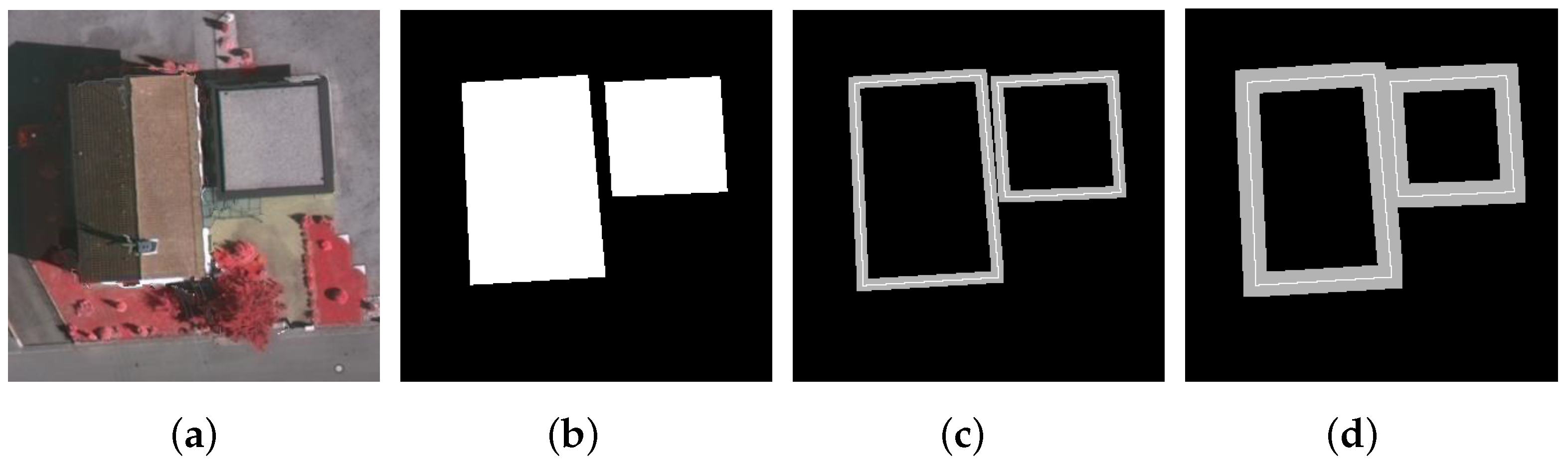
3.3. Building Contour Extraction
3.4. Building Corner Detection
- Step 1.
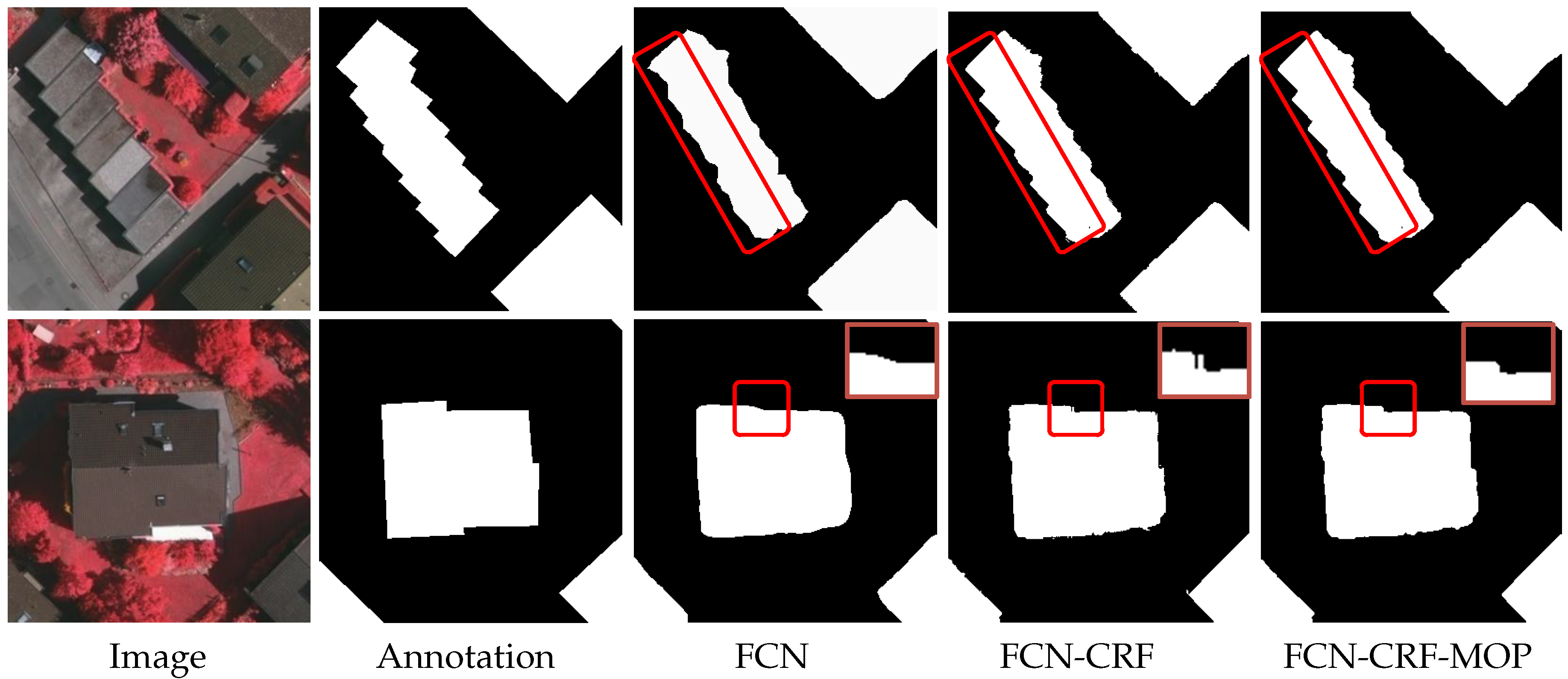
- Building region segmentation. With the trained DeepLab model, a building region segmentation of the input image is conducted using the FCNs (a ResNet-101 re-purposed by atrous convolution), followed by the exploitation of a CRF step and the morphological opening operation (MOP) to improve segmentation accuracy.
- Step 2.
- Building contour extraction. The Matlab function bwboundaries is employed to extract the contour curves on the segmentation map of building regions.
- Step 3.
- Building corner detection. Based on a scale-space representation of each building boundary, corner points are recognized at a coarse scale and then tracked back to the finest scale to improve their locations.
4. Experimental Results and Discussions
4.1. Evaluation Metrics
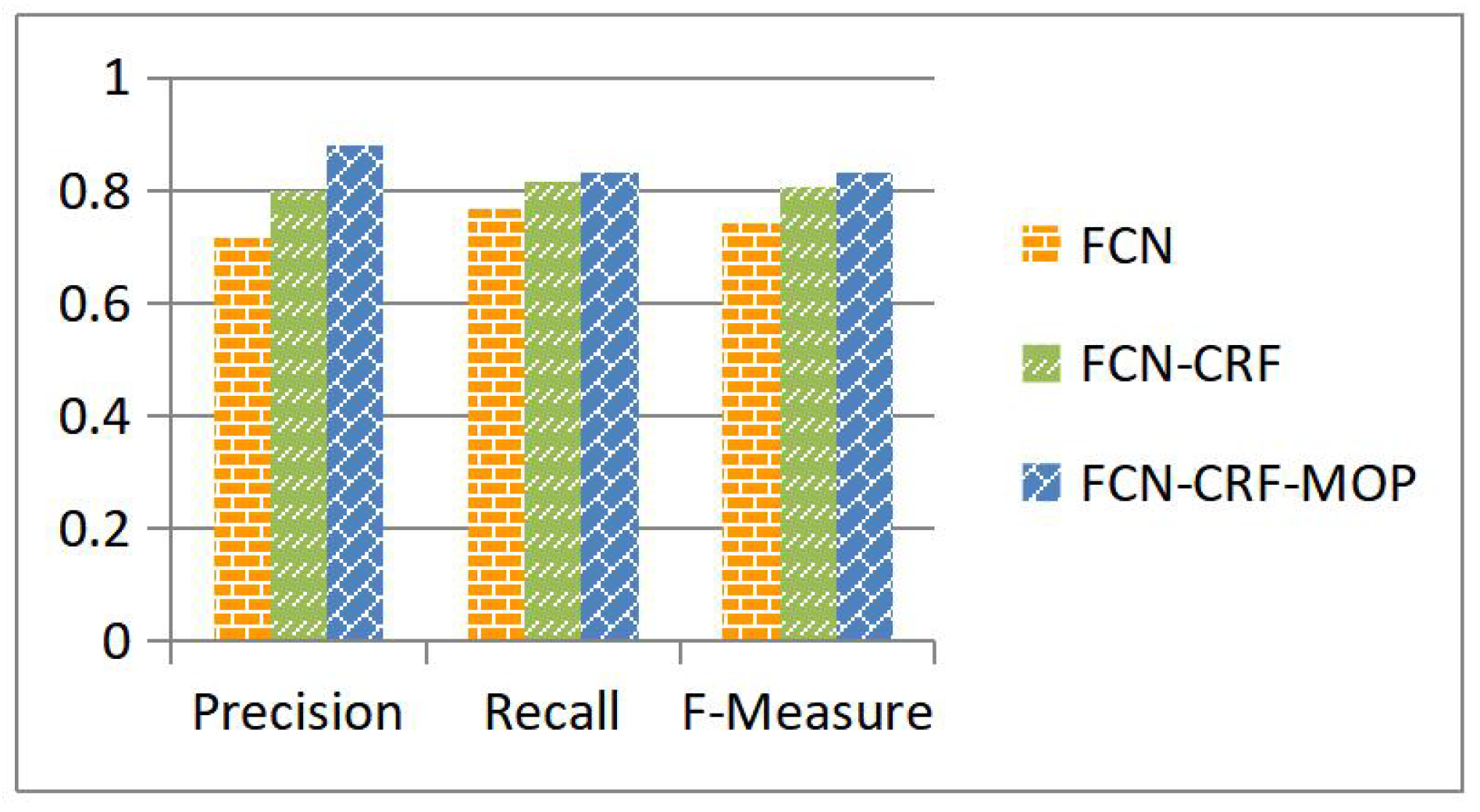
4.2. Verification of the FCN-CRF-MOP Model
4.3. Verification of Our Corner Detection Scheme
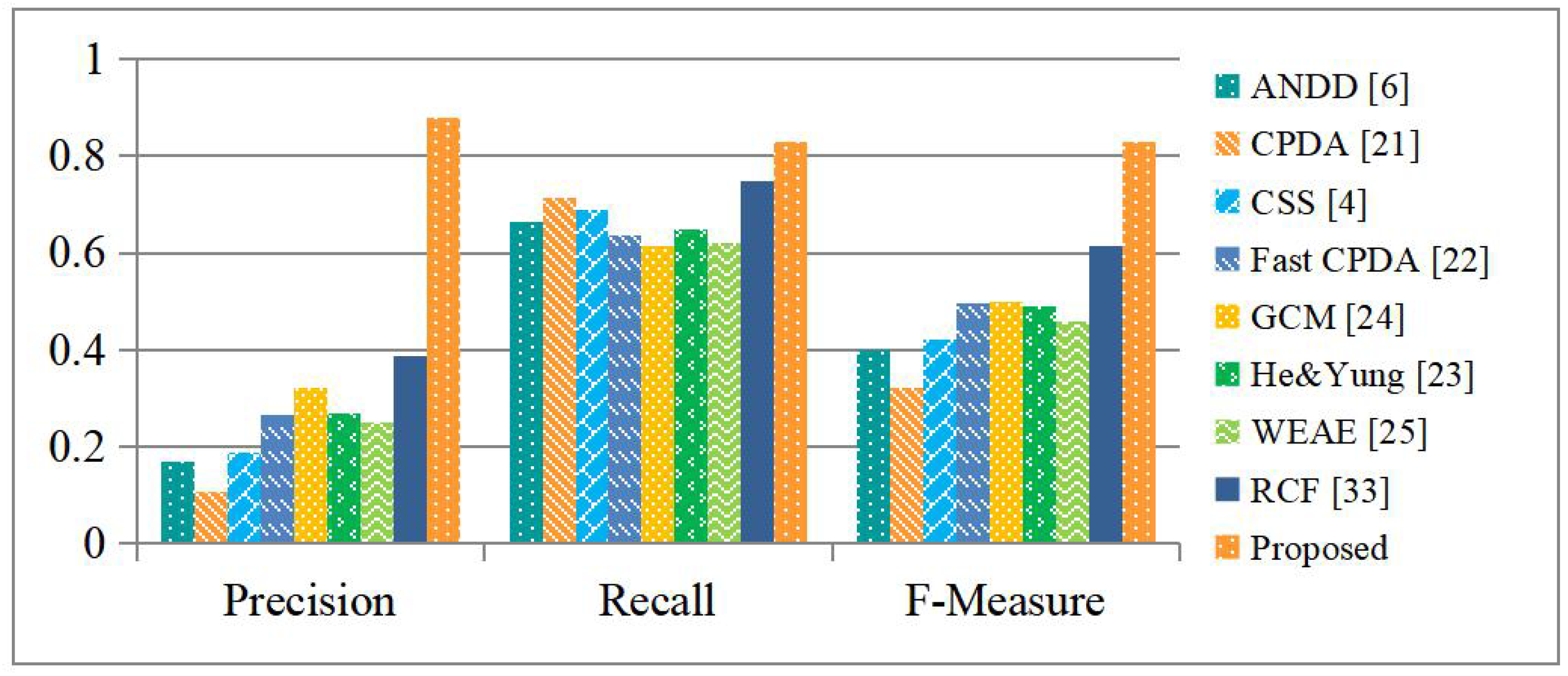
4.4. Objective Evaluation
4.5. Subjective Evaluation
4.6. Computational Complexity
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jung, J.; Sohn, G.; Bang, K.; Wichmann, A.; Armenakis, C.; Kada, M. Matching aerial images to 3d building models using context-based geometric hashing. Sensors 2016, 16, 932. [Google Scholar] [CrossRef]
- Bansal, M.; Daniilidis, K. Geometric Urban Geo-localization. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Detection (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3978–3985. [Google Scholar]
- Im, J.H.; Im, S.H.; Jee, G.I. Vertical corner feature based precise vehicle localization using 3d lidar in urban area. Sensors 2016, 16, 1268. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Mokhtarian, F.; Suomela, R. Robust image corner detection through curvature scale space. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1376–1381. [Google Scholar] [CrossRef]
- Teng, S.W.; Sadat, R.M.N.; Lu, G. Effective and efficient contour-based corner detectors. Pattern Recognit. 2015, 48, 2185–2197. [Google Scholar] [CrossRef]
- Kahaki, S.M.M.; Nordin, M.J.; Ashtari, A.H. Contour-based corner detection and classification by using mean projection transform. Sensors 2014, 14, 4126–4143. [Google Scholar] [CrossRef]
- Shui, P.L.; Zhang, W.C. Corner detection and classification using anisotropic directional derivative representations. IEEE Trans. Image Process. 2013, 22, 3204–3218. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, D.; Huang, S.; Zhang, X.; Tu, L.; Ren, Z. Robust corner detection using the eigenvector-based angle estimator. J. Visual Commun. Image Represent. 2017, 45, 181–193. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, CA, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Detection (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Detection (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuill, A.L. Deeplab Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Chen, L.C.; Yang, Y.; Wang, J.; Xu, W.; Yuille, A.L. Attention to scale: Scale-aware semantic image segmentation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Detection (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3640–3649. [Google Scholar]
- Arnab, A.; Jayasumana, S.; Zheng, S.; Torr, P.H. Higher order conditional random fields in deep neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 524–540. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv 2013, arXiv:1312.6229. [Google Scholar]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The isprs benchmark on urban object classification and 3d building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 293–298. [Google Scholar] [CrossRef]
- Marmanis, D.; Wegner, J.D.; Galliani, S.; Schindler, K.; Datcu, M.; Stilla, U. Semantic segmentation of aerial images with an ensemble of cnns. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 473–480. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Kohli, P.; Torr, P.H.S. Robust higher order potentials for enforcing label consistency. Int. J. Comput. Vis. 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Zhong, B.; Ma, K.-K.; Liao, W. Scale-space behavior of planar-curve corners. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 1517–1524. [Google Scholar] [CrossRef]
- Rattarangsi, A.; Chin, R.T. Scale-Based Detection of Corners of Planar Curves. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 430–449. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, M.M.; Hu, X.; Bian, J.W.; Zhang, L.; Bai, X.; Tang, J. Richer convolutional features for edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G. Robust image corner detection based on the chord-to-point distance accumulation technique. IEEE Trans. Multimedia. 2008, 10, 1059–1072. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G.; Fraser, C.S.; Ravanbakhsh, M. A fast corner detector based on the chordto-point distance accumulation technique. In Proceedings of the Digital Image Computing: Techniques and Applications, Melbourne, Australia, 1–3 December 2009; pp. 519–525. [Google Scholar]
- He, X.C.; Yung, N.H.C. Corner detector based on global and local curvature properties. Opt. Eng. 2008, 47, 057008. [Google Scholar]
- Zhang, X.H.; Wang, H.X.; Smith, A.W.B.; Xu, L.; Lovell, B.C.; Yang, D. Corner detection based on gradient correlation matrices of planar curves. Pattern Recognit. 2010, 47, 1207–1223. [Google Scholar] [CrossRef]




| Segmentation Method | Mean IoU (%) |
|---|---|
| FCN | 92.83 |
| FCN-CRF | 93.16 |
| FCN-CRF-MOP (Proposed) | 93.21 |
| Segmentation Method | Trimap Width (Pixels) | |||||
|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | |
| FCN | 72.59 | 83.70 | 88.15 | 90.50 | 91.95 | 92.90 |
| FCN-CRF | 74.98 | 84.91 | 88.98 | 91.14 | 92.46 | 93.33 |
| FCN-CRF-MOP (Proposed) | 75.12 | 85.00 | 89.05 | 91.50 | 92.50 | 93.36 |
| Detectors | ANDD | CPDA | CSS | Fast CPDA | GCM | He & Yung | WEAE |
|---|---|---|---|---|---|---|---|
| 0.2 | 0.21 | – | 0.12 | 0.0095 | 1.8 | 146 | |
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Detectors | ANDD | CPDA | CSS | Fast CPDA | GCM | He & Yung | WEAE | RCF | Proposed |
|---|---|---|---|---|---|---|---|---|---|
| Time (s) | 1.03 | 0.14 | 0.13 | 0.04 | 0.04 | 0.05 | 0.06 | 0.2 | 0.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Zhong, B.; Sun, X. Building Corner Detection in Aerial Images with Fully Convolutional Networks. Sensors 2019, 19, 1915. https://doi.org/10.3390/s19081915
Song W, Zhong B, Sun X. Building Corner Detection in Aerial Images with Fully Convolutional Networks. Sensors. 2019; 19(8):1915. https://doi.org/10.3390/s19081915
Chicago/Turabian StyleSong, Weigang, Baojiang Zhong, and Xun Sun. 2019. "Building Corner Detection in Aerial Images with Fully Convolutional Networks" Sensors 19, no. 8: 1915. https://doi.org/10.3390/s19081915
APA StyleSong, W., Zhong, B., & Sun, X. (2019). Building Corner Detection in Aerial Images with Fully Convolutional Networks. Sensors, 19(8), 1915. https://doi.org/10.3390/s19081915




