Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles
Abstract
1. Introduction
1.1. Related Work
1.2. Organization and Contributions
- This paper solves the shortest path and obstacle avoidance problem by proposing a novel path planning algorithm, termed OABAS algorithm.
- A linear loss function is designed as a cost function of the OABAS algorithm according to the constraints of UAVs.
- The proposed algorithm is applied to the UAV model and compared with the existing algorithms to verify the feasibility and efficiency.
2. Preliminaries
2.1. Path Definition and Generation
Navigation: the task of navigation is to move a robot from one location to another. In the process of navigation, the robot movement needs a path that is gradually determined. During the navigation, it is often necessary to rely on the sensor data to update the information about position of the surrounding obstacles and to update the position and direction information of the robot.
Path planning: in general, the work that path planning needs to do is to collect relevant data information and generate available paths based on constraints. We use the cost function to constrain the path. The cost function can generally be determined by the length of the path, possibility of collides with obstacles, the load of the robot, and other conditions that cause danger. From this, it can be inferred that reducing the numerical value of the cost function can plan an efficient, feasible and safe path.
2.2. Obstacle Sensing and Avoidance in Path Planning
3. Methodology
3.1. Path Representation
3.2. Cost Function
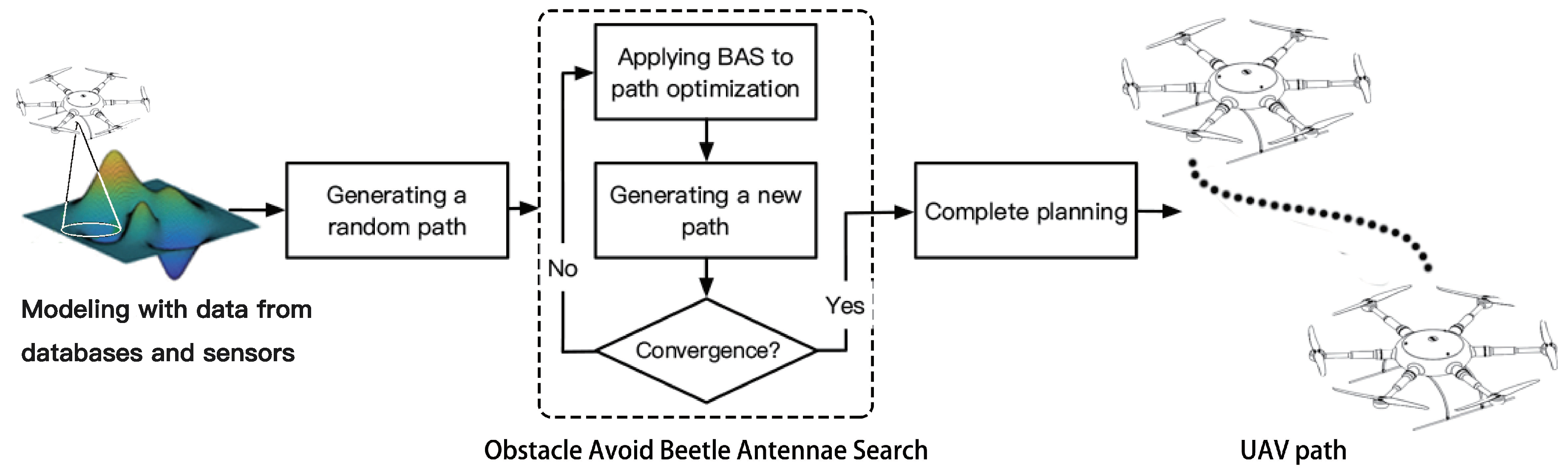
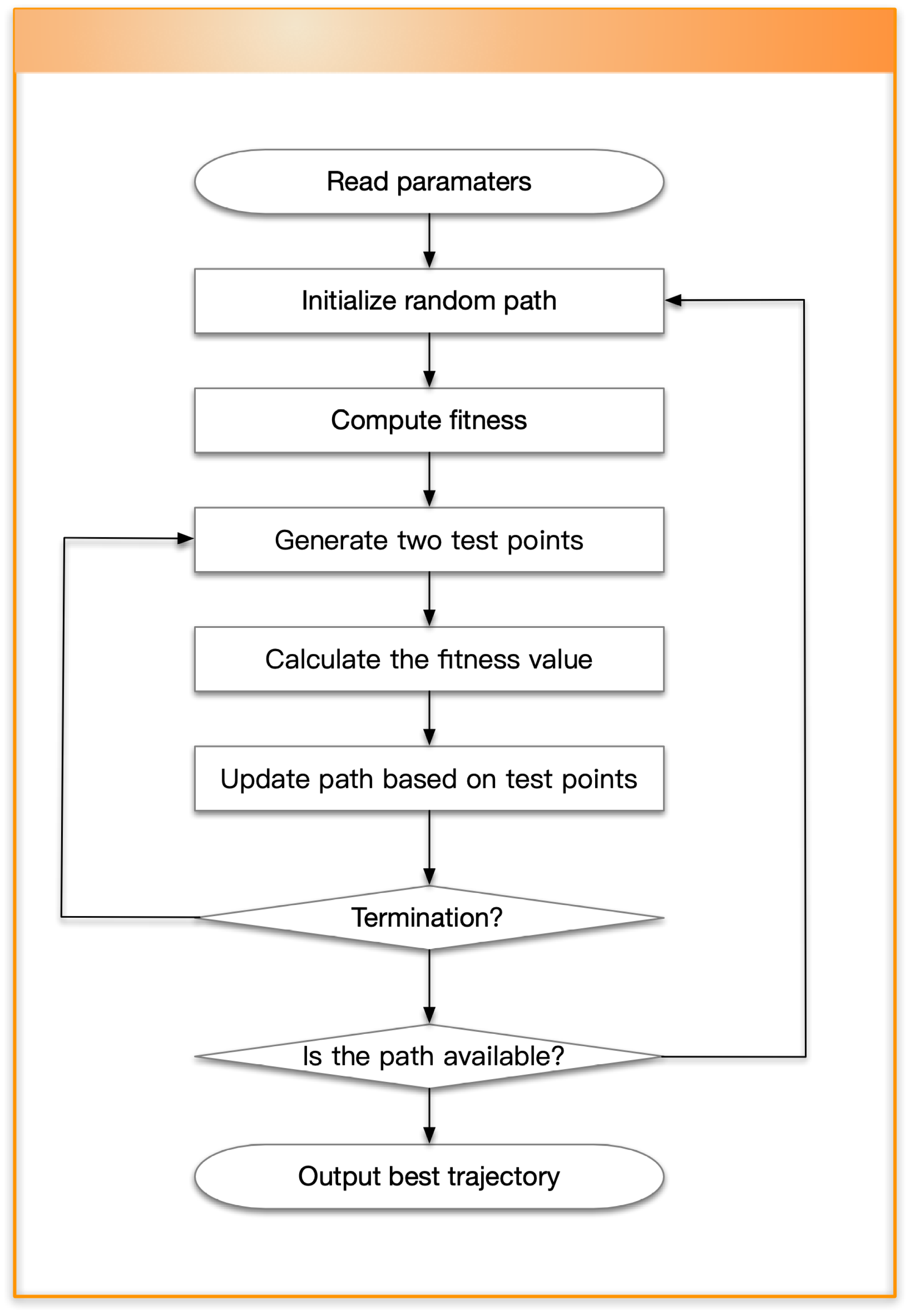
3.3. OABAS Algorithm
| Algorithm 1: Obstacle avoidance beetle antennae search (OABAS) algorithm for path planning of UAVs. |
 |
4. Simulation Studies and Experimental Results
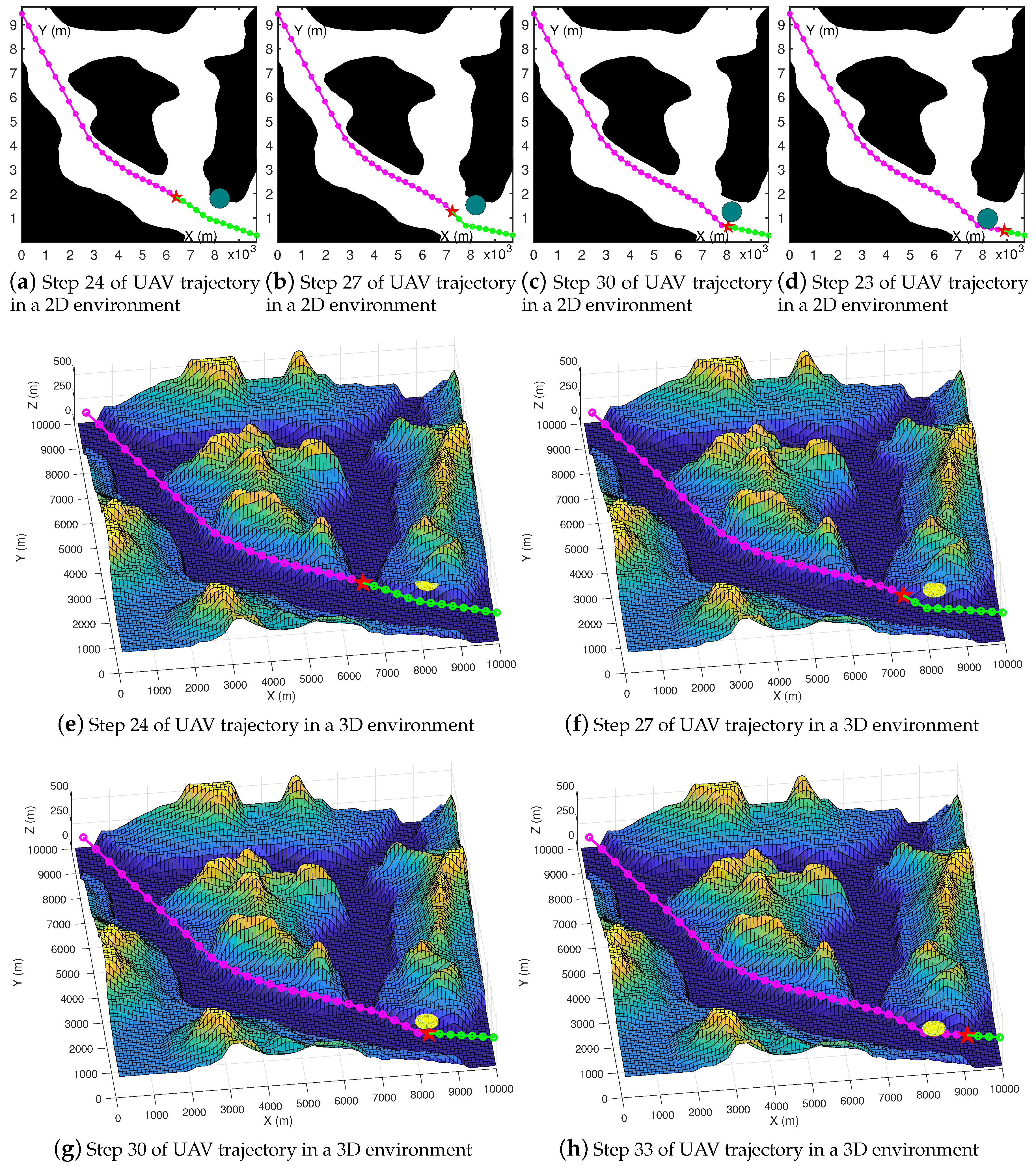
4.1. UAV Path Planning in Different Environments
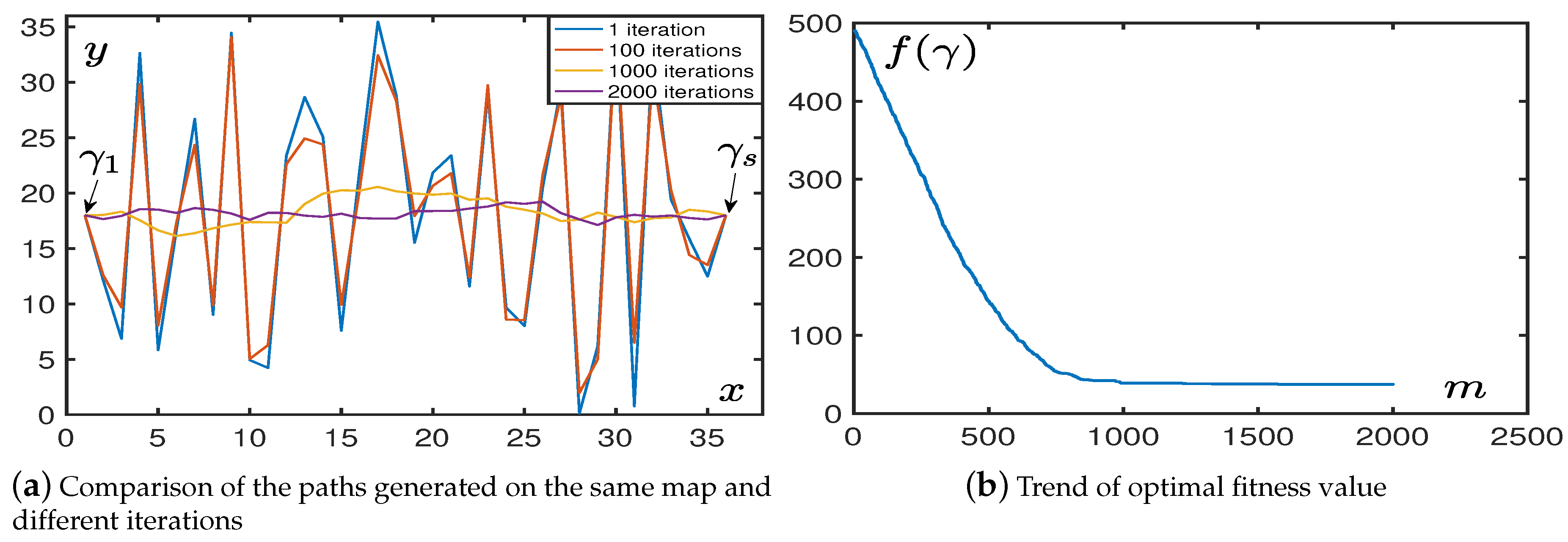
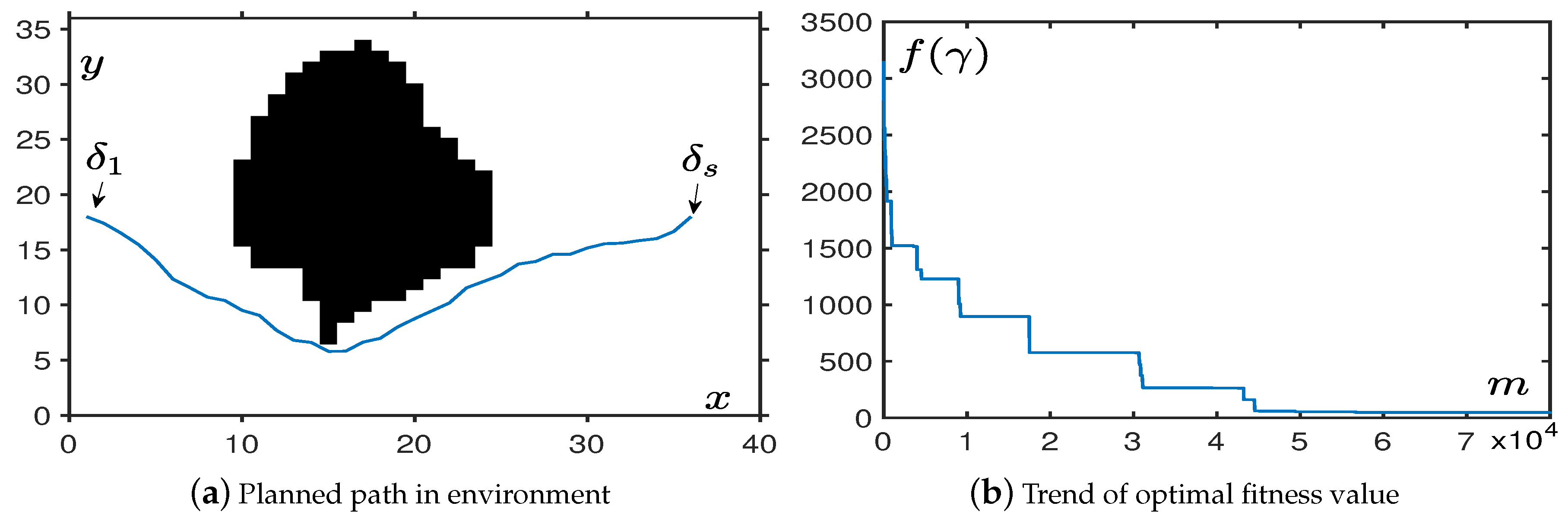
4.1.1. In Obstacle-Free Environment
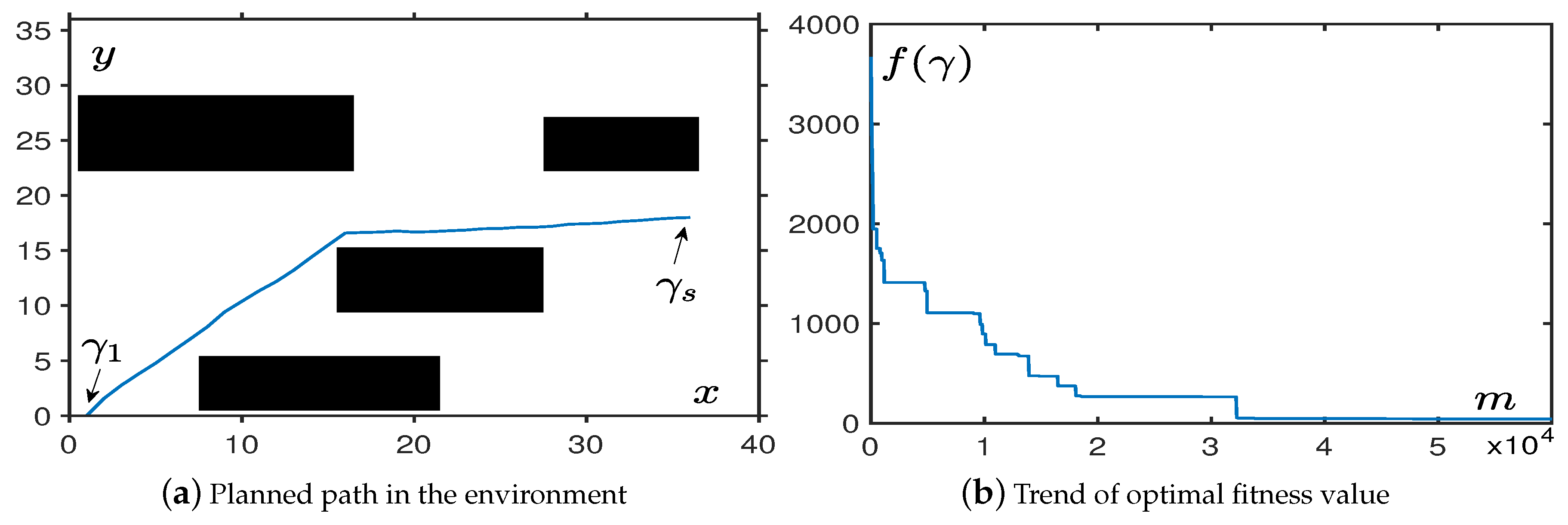
4.1.2. In Regular Obstacles Environment
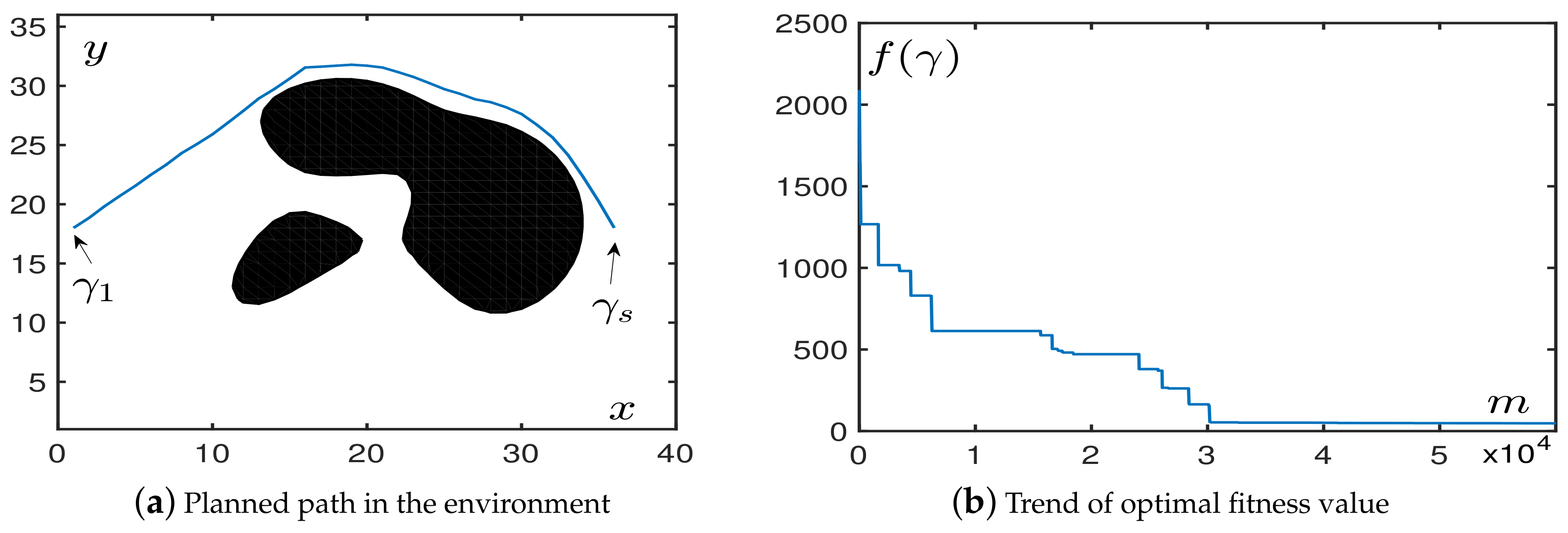
4.1.3. In Irregular Obstacle Environments
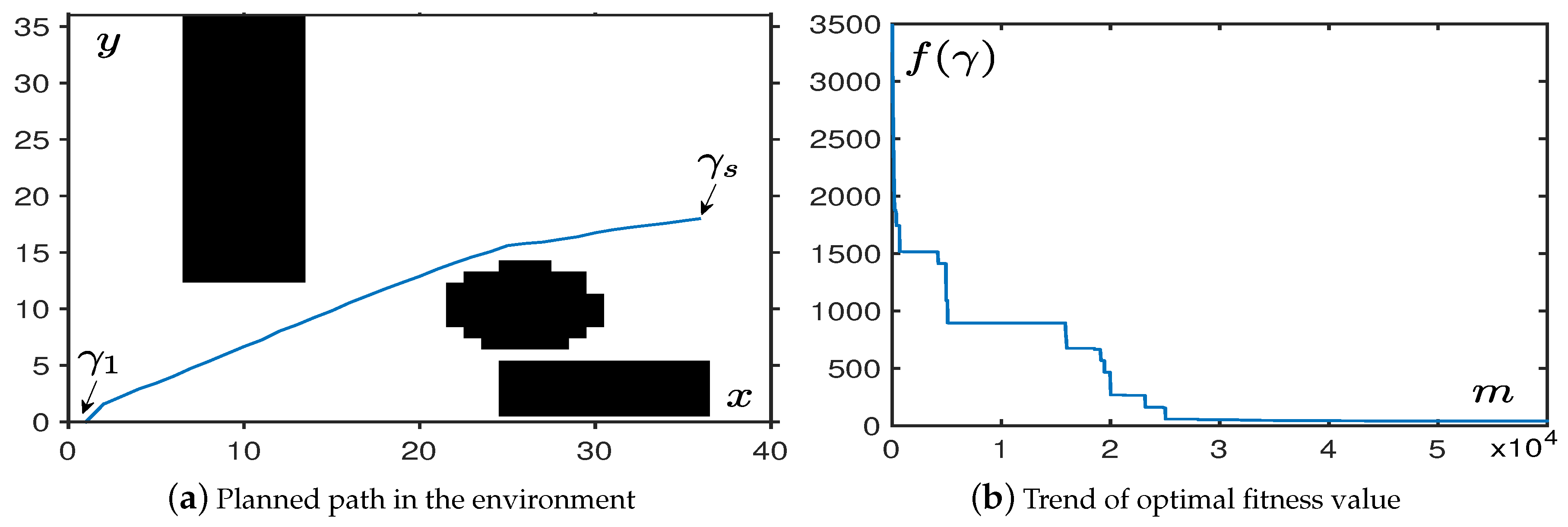
4.1.4. In Mixed Obstacle Environments
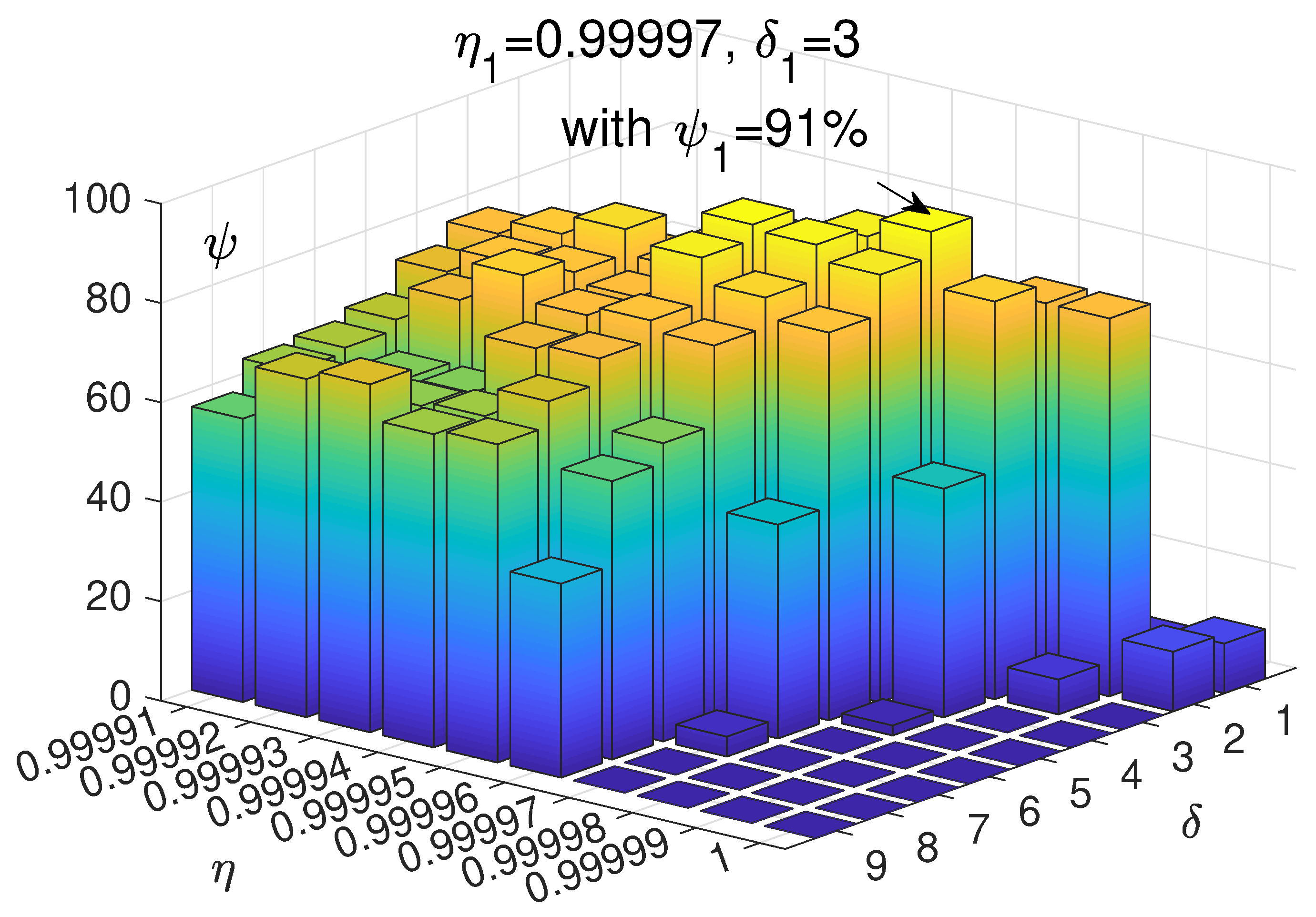
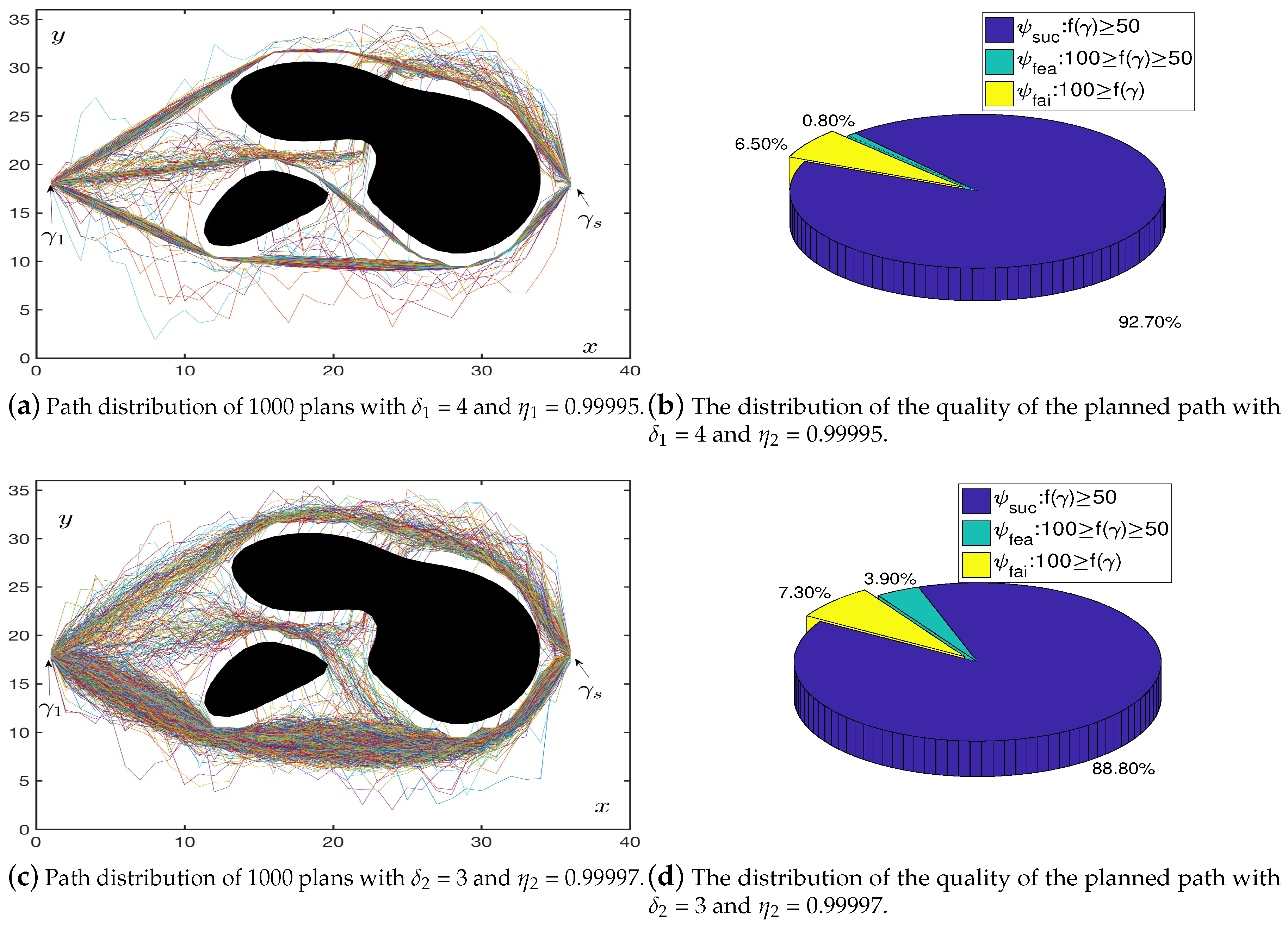
4.2. Cycle Batch Tests
4.3. Comparisons with PSO and ABC
4.4. Tested Results on High-Resolution Maps with Various Types of Obstacles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cai, G.; Dias, J.; Seneviratne, L. A Survey of Small-Scale Unmanned Aerial Vehicles: Recent Advances and Future Development Trends. Unmanned Syst. 2014, 02, 175–199. [Google Scholar] [CrossRef]
- Ahmad, K.Y.; AlMajali, A.; Ghalyon, S.A.; Dweik, W.; Mohd, B.J. Analyzing Cyber-Physical Threats on Robotic Platforms. Sensors 2018, 18, 1643. [Google Scholar] [CrossRef]
- Gupta, S.G.; Ghonge, M.M.; Jawandhiya, P. Review of unmanned aircraft system (UAS). Int. J. Adv. Res. Comput. Eng. Technol. 2013, 2, 1646–1658. [Google Scholar]
- Guerrero-Castellanos, J.; Madrigal-Sastre, H.; Durand, S.; Torres, L.; Muñoz-Hernández, G. A robust nonlinear observer for real-time attitude estimation using low-cost MEMS inertial sensors. Sensors 2013, 13, 15138–15158. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Kapila, V. Optimal path planning for unmanned air vehicles with kinematic and tactical constraints. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 1301–1306. [Google Scholar]
- De La Iglesia, I.; Hernandez-Jayo, U.; Osaba, E.; Carballedo, R. Smart Bandwidth Assignation in an Underlay Cellular Network for Internet of Vehicles. Sensors 2017, 17, 2217. [Google Scholar] [CrossRef]
- Jin, L.; Li, S. Distributed task allocation of multiple robots: A control perspective. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 693–701. [Google Scholar] [CrossRef]
- Yan, F.; Liu, Y.S.; Xiao, J.Z. Path Planning in Complex 3D Environments Using a Probabilistic Roadmap Method. Int. J. Autom. Comput. 2013, 10, 525–533. [Google Scholar] [CrossRef]
- Cho, Y.; Kim, D.; Kim, D.S. Topology representation for the Voronoi diagram of 3D spheres. Int. J. CAD/CAM 2009, 5, 59–68. [Google Scholar]
- Geraerts, R. Planning short paths with clearance using explicit corridors. In Proceedings of the 2010 IEEE International Conference on Communication, Cape Town, South Africa, 23–27 May 2010; pp. 1997–2004. [Google Scholar]
- Vadakkepat, P.; Tan, K.C.; Ming-Liang, W. Evolutionary artificial potential fields and their application in real time robot path planning. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 256–263. [Google Scholar]
- Musliman, I.A.; Rahman, A.A.; Coors, V. Implementing 3D network analysis in 3D GIS. Int. Arch. ISPRS 2008, 37, 913–918. [Google Scholar]
- Carsten, J.; Ferguson, D.; Stentz, A. 3d field d: Improved path planning and replanning in three dimensions. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3381–3386. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- De Filippis, L.; Guglieri, G.; Quagliotti, F. Path planning strategies for UAVS in 3D environments. J. Intell. Robot. Syst. 2012, 65, 247–264. [Google Scholar] [CrossRef]
- Valente, J.; Del Cerro, J.; Barrientos, A.; Sanz, D. Aerial coverage optimization in precision agriculture management: A musical harmony inspired approach. Comput. Electron. Agric. 2013, 99, 153–159. [Google Scholar] [CrossRef]
- Miller, B.; Stepanyan, K.; Miller, A.; Andreev, M. 3D path planning in a threat environment. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6864–6869. [Google Scholar]
- Chamseddine, A.; Zhang, Y.; Rabbath, C.A.; Join, C.; Theilliol, D. Flatness-based trajectory planning/replanning for a quadrotor unmanned aerial vehicle. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2832–2848. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wu, Q. Rejecting Chaotic Disturbances Using a Super-Exponential-Zeroing Neurodynamic Approach for Synchronization of Chaotic Sensor Systems. Sensors 2019, 19, 74. [Google Scholar] [CrossRef] [PubMed]
- Volkan Pehlivanoglu, Y.; Baysal, O.; Hacioglu, A. Path planning for autonomous UAV via vibrational genetic algorithm. Aircr. Eng. Aerosp. Technol. 2007, 79, 352–359. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S.; Zhang, Y. Modified ZNN for time-varying quadratic programming with inherent tolerance to noises and its application to kinematic redundancy resolution of robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 6978–6988. [Google Scholar] [CrossRef]
- Okdem, S.; Karaboga, D. Routing in wireless sensor networks using an ant colony optimization (ACO) router chip. Sensors 2009, 9, 909–921. [Google Scholar] [CrossRef] [PubMed]
- Hassanzadeh, I.; Madani, K.; Badamchizadeh, M.A. Mobile robot path planning based on shuffled frog leaping optimization algorithm. In Proceedings of the 2010 IEEE International Conference on Automation Science and Engineering, Toronto, ON, Canada, 21–24 August 2010; pp. 680–685. [Google Scholar]
- Liu, L.; Zhang, S. Voronoi diagram and GIS-based 3D path planning. In Proceedings of the 2009 17th International Conference on Geoinformatics, Washington, DC, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Schøler, F.; la Cour-Harbo, A.; Bisgaard, M. Generating approximative minimum length paths in 3D for UAVs. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium IEEE, Alcala de Henares, Spain, 3–7 June 2012; pp. 229–233. [Google Scholar]
- Chen, D.; Zhang, Y.; Li, S. Zeroing neural-dynamics approach and its robust and rapid solution for parallel robot manipulators against superposition of multiple disturbances. Neurocomputing 2018, 275, 845–858. [Google Scholar] [CrossRef]
- Kroumov, V.; Yu, J.; Shibayama, K. 3D path planning for mobile robots using simulated annealing neural network. Int. J. Innov. Comput. Inf. Control 2010, 6, 2885–2899. [Google Scholar]
- Passino, K.M. Bacterial foraging optimization. Int. J. Swarm Intell. Res. (IJSIR) 2010, 1, 1–16. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin, Germany, 2010; pp. 65–74. [Google Scholar]
- Li, S.; He, J.; Li, Y.; Rafique, M.U. Distributed recurrent neural networks for cooperative control of manipulators: A game-theoretic perspective. IEEE Trans. Neural Networks Learn. Syst. 2017, 28, 415–426. [Google Scholar] [CrossRef] [PubMed]
- Gawel, A.; Dubé, R.; Surmann, H.; Nieto, J.; Siegwart, R.; Cadena, C. 3D registration of aerial and ground robots for disaster response: An evaluation of features, descriptors, and transformation estimation. In Proceedings of the SSRR 2017-IEEE International Symposium on Safety, Security and Rescue Robotics, Shanghai, China, 11–13 October 2017; pp. 27–34. [Google Scholar]
- Xu, C.; Duan, H.; Liu, F. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning. Aerosp. Sci. Technol. 2010, 14, 535–541. [Google Scholar] [CrossRef]
- Duan, H.; Yu, Y.; Zhang, X.; Shao, S. Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Duan, H.B.; Zhang, X.Y.; Wu, J.; Ma, G.J. Max-Min Adaptive Ant Colony Optimization Approach to Multi-UAVs Coordinated Trajectory Replanning in Dynamic and Uncertain Environments. J. Bionic Eng. 2009, 6, 161–173. [Google Scholar] [CrossRef]
- Mittal, S.; Deb, K. Three-dimensional offline path planning for UAVs using multiobjective evolutionary algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3195–3202. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- Hoffman, K.L.; Padberg, M. Traveling Salesman Problem (TSP) Traveling Salesman Problem. In Encyclopedia of Operations Research and Management Science; Springer: Berlin, Germany, 2001; pp. 849–853. [Google Scholar]
- Eiselt, H.A.; Gendreau, M.; Laporte, G. Arc routing problems, part I: The Chinese postman problem. Oper. Res. 1995, 43, 231–242. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Y. A hybrid multi-objective scheme applied to redundant robot manipulators. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1337–1350. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Jin, L. Kinematic control of redundant manipulators using neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2243–2254. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Xu, F.; Yan, L. New Pseudoinverse-Based Path-Planning Scheme With PID Characteristic for Redundant Robot Manipulators in the Presence of Noise. IEEE Trans. Control Syst. Technol. 2017, 26, 2008–2019. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Y. Robust Zeroing Neural-Dynamics and Its Time-Varying Disturbances Suppression Model Applied to Mobile Robot Manipulators. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4385–4397. [Google Scholar]
- Chen, D.; Zhang, Y.; Li, S. Tracking Control of Robot Manipulators with Unknown Models: A Jacobian-Matrix-Adaption Method. IEEE Trans. Ind. Infor. 2018, 14, 3044–3053. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Seet, B.C.; Liu, G.; Lee, B.S.; Foh, C.H.; Wong, K.J.; Lee, K.K. A-STAR: A mobile ad hoc routing strategy for metropolis vehicular communications. Lect. Notes Comput. Sci. 2004, 3042, 989–999. [Google Scholar]
- Nikolos, I.K.; Zografos, E.S.; Brintaki, A.N. UAV path planning using evolutionary algorithms. In Innovations in Intelligent Machines-1; Springer: Berlin, Germany, 2007; pp. 77–111. [Google Scholar]
- Menon, P.K.A.; Cheng, V.L.; Kim, E. Optimal trajectory synthesis for terrain-following flight. J. Guid. Control. Dyn. 1991, 14, 807–813. [Google Scholar] [CrossRef]
- Choset, H.M.; Hutchinson, S.; Lynch, K.M.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementation; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Schøler, F. 3d path Planning for autonomous Aerial Vehicles in Constrained Spaces. Ph.D. Thesis, Section of Automation & Control, Department of Electronic Systems, Aalborg University, Aalborg, Denmark, 2012. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Yang, L.; Qi, J.; Xiao, J.; Yong, X. A literature review of UAV 3D path planning. In Proceedings of the WCICA 2014-The 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 2376–2381. [Google Scholar]
- Asseo, S.J. Terrain following/terrain avoidance path optimization using the method of steepest descent. In Proceedings of the IEEE 1988 National Aerospace and Electronics Conference, NAECON 1988, Dayton, OH, USA, 23–27 May 1988; pp. 1128–1136. [Google Scholar]
- Wendl, M.; Katt, D.; Young, G. Advanced automatic terrain following/terrain avoidance control concepts study. In Proceedings of the IEEE 1982 National Aerospace and Electronics Conference, NAECON 1982, Dayton, OH, USA, 18–20 May 1982; pp. 18–20. [Google Scholar]
- Harrington, W. TF/TA System Design Evaluation Using Pilot-in-the-Loop Simulations: The Cockpit Design Challenge. In Proceedings of the 1984 SAE Aerospace Congress & Exposition, Long Beach, CA, USA, 15–18 October 1984. [Google Scholar]
- Avellar, G.; Pereira, G.; Pimenta, L.; Iscold, P. Multi-UAV routing for area coverage and remote sensing with minimum time. Sensors 2015, 15, 27783–27803. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. Int. J. Robot. Control 2018, 1, 1–2. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Anderson, J.D.; Hunter, L.P. Introduction to flight. Phys. Today 1987, 40, 125. [Google Scholar] [CrossRef]
- Har-Peled, S.; Mazumdar, S. Fast algorithms for computing the smallest k-enclosing circle. Algorithmica 2005, 41, 147–157. [Google Scholar] [CrossRef]

| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 10,503 | 0.029 | 35.51 | 35.30 | 0.010 | Yes |
| 1.0 | 20418 | 0.057 | 35.47 | 35.29 | 0.008 | Yes |
| 1.5 | 23,873 | 0.067 | 35.60 | 35.40 | 0.010 | Yes |
| 2.0 | 24,077 | 0.067 | 35.92 | 35.54 | 0.035 | Yes |
| 2.5 | 24,122 | 0.067 | 36.40 | 35.85 | 0.077 | Yes |
| 3.0 | 23,957 | 0.067 | 36.97 | 36.03 | 0.105 | Yes |
| 3.5 | 24,128 | 0.067 | 37.53 | 36.31 | 0.265 | Yes |
| 4.0 | 24,031 | 0.067 | 38.24 | 36.98 | 0.366 | Yes |
| 4.5 | 24,243 | 0.068 | 39.11 | 37.70 | 0.816 | Yes |
| 5.0 | 24,103 | 0.067 | 40.05 | 37.50 | 1.131 | Yes |
| 5.5 | 24,085 | 0.067 | 40.76 | 38.48 | 1.429 | Yes |
| 6.0 | 24,186 | 0.067 | 41.59 | 39.56 | 1.145 | Yes |
| 6.5 | 24,115 | 0.067 | 42.60 | 39.36 | 3.033 | Yes |
| 7.0 | 24,039 | 0.067 | 43.74 | 41.14 | 1.910 | Yes |
| 7.5 | 24,105 | 0.067 | 44.82 | 41.76 | 3.693 | Yes |
| 8.0 | 24,141 | 0.067 | 46.79 | 42.03 | 7.127 | Yes |
| 8.5 | 24,269 | 0.068 | 47.21 | 43.74 | 4.717 | Yes |
| 9.0 | 24,195 | 0.067 | 48.56 | 44.02 | 6.020 | Yes |
| 9.5 | 24,155 | 0.067 | 49.69 | 45.13 | 7.214 | Yes |
| 10 | 24,055 | 0.067 | 50.98 | 45.00 | 8.315 | No |
| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 6819 | 0.019 | 858.32 | 557.84 | No | |
| 1.0 | 4532 | 0.013 | 620.79 | 38.25 | No | |
| 1.5 | 7898 | 0.022 | 228.38 | 37.28 | No | |
| 2.0 | 12,284 | 0.035 | 104.18 | 37.33 | No | |
| 2.5 | 17,209 | 0.049 | 70.35 | 37.83 | Yes | |
| 3.0 | 19,065 | 0.054 | 55.54 | 37.71 | Yes | |
| 3.5 | 19,984 | 0.057 | 58.37 | 38.61 | Yes | |
| 4.0 | 21,096 | 0.060 | 53.17 | 39.17 | Yes | |
| 4.5 | 22,111 | 0.063 | 49.58 | 39.73 | Yes | |
| 5.0 | 22,851 | 0.065 | 53.79 | 39.80 | Yes | |
| 5.5 | 22,893 | 0.065 | 53.80 | 41.49 | Yes | |
| 6.0 | 23,313 | 0.066 | 51.11 | 41.58 | Yes | |
| 6.5 | 23,143 | 0.066 | 68.48 | 42.31 | Yes | |
| 7.0 | 23,556 | 0.067 | 68.72 | 42.66 | Yes | |
| 7.5 | 23,436 | 0.066 | 59.53 | 43.64 | Yes | |
| 8.0 | 23,476 | 0.067 | 75.87 | 44.90 | Yes | |
| 8.5 | 23,664 | 0.067 | 86.04 | 45.65 | Yes | |
| 9.0 | 23,605 | 0.067 | 114.23 | 47.07 | No | |
| 9.5 | 23,595 | 0.067 | 132.36 | 50.07 | No | |
| 10 | 23,508 | 0.067 | 153.99 | 51.96 | No |
| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 4897 | 0.014 | 46.04 | 42.41 | Yes | |
| 1.0 | 6292 | 0.018 | 46.31 | 42.78 | Yes | |
| 1.5 | 9382 | 0.027 | 51.73 | 42.83 | Yes | |
| 2.0 | 12,627 | 0.036 | 50.30 | 42.38 | Yes | |
| 2.5 | 15,906 | 0.045 | 48.06 | 42.84 | Yes | |
| 3.0 | 18,766 | 0.053 | 51.87 | 42.77 | Yes | |
| 3.5 | 20,210 | 0.057 | 55.10 | 43.29 | Yes | |
| 4.0 | 21,267 | 0.060 | 54.54 | 43.75 | Yes | |
| 4.5 | 22,036 | 0.063 | 62.07 | 43.74 | Yes | |
| 5.0 | 22,445 | 0.064 | 71.34 | 44.34 | Yes | |
| 5.5 | 23,327 | 0.066 | 66.52 | 44.60 | Yes | |
| 6.0 | 23,063 | 0.065 | 93.94 | 46.28 | Yes | |
| 6.5 | 23,468 | 0.067 | 116.06 | 46.03 | No | |
| 7.0 | 22,938 | 0.065 | 176.84 | 47.59 | No | |
| 7.5 | 23,541 | 0.067 | 147.41 | 49.04 | No | |
| 8.0 | 23,613 | 0.067 | 181.11 | 47.65 | No | |
| 8.5 | 23,581 | 0.067 | 164.87 | 50.87 | No | |
| 9.0 | 23,522 | 0.067 | 302.28 | 54.17 | No | |
| 9.5 | 23,794 | 0.067 | 267.42 | 54.26 | No | |
| 10 | 23,399 | 0.066 | 393.70 | 54.07 | No |
| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 2076 | 0.006 | 839.27 | 440.39 | No | |
| 1.0 | 4833 | 0.014 | 578.47 | 45.59 | No | |
| 1.5 | 9304 | 0.026 | 235.70 | 45.79 | No | |
| 2.0 | 15,680 | 0.044 | 185.26 | 45.01 | No | |
| 2.5 | 21454 | 0.061 | 117.10 | 45.91 | Yes | |
| 3.0 | 27,507 | 0.078 | 127.29 | 45.32 | Yes | |
| 3.5 | 31,483 | 0.089 | 136.02 | 45.31 | Yes | |
| 4.0 | 35,306 | 0.100 | 137.72 | 45.12 | Yes | |
| 4.5 | 37,304 | 0.106 | 187.19 | 44.38 | Yes | |
| 5.0 | 44,019 | 0.125 | 136.82 | 44.42 | Yes | |
| 5.5 | 47,124 | 0.134 | 130.63 | 45.73 | Yes | |
| 6.0 | 48,738 | 0.138 | 159.98 | 44.61 | No | |
| 6.5 | 50,540 | 0.143 | 145.77 | 45.68 | Yes | |
| 7.0 | 53,528 | 0.152 | 134.59 | 45.33 | Yes | |
| 7.5 | 55,753 | 0.158 | 157.71 | 45.14 | No | |
| 8.0 | 58,812 | 0.167 | 129.98 | 45.34 | Yes | |
| 8.5 | 59,677 | 0.169 | 185.15 | 45.04 | No | |
| 9.0 | 62,318 | 0.177 | 178.01 | 45.54 | No | |
| 9.5 | 64,671 | 0.183 | 145.06 | 46.25 | Yes | |
| 10 | 66,818 | 0.190 | 153.18 | 45.71 | No |
| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 17,100 | 0.049 | 1131.63 | 1011.86 | No | |
| 1.0 | 14,902 | 0.042 | 1029.72 | 667.69 | No | |
| 1.5 | 8053 | 0.023 | 700.90 | 44.30 | No | |
| 2.0 | 12,208 | 0.035 | 324.22 | 44.21 | No | |
| 2.5 | 18,918 | 0.054 | 112.02 | 43.19 | No | |
| 3.0 | 23,355 | 0.066 | 107.40 | 43.46 | No | |
| 3.5 | 29,487 | 0.084 | 92.42 | 44.40 | Yes | |
| 4.0 | 35,404 | 0.100 | 75.76 | 43.80 | Yes | |
| 4.5 | 38,980 | 0.111 | 77.82 | 43.39 | Yes | |
| 5.0 | 41,242 | 0.117 | 93.62 | 43.02 | Yes | |
| 5.5 | 44,172 | 0.125 | 83.76 | 43.41 | Yes | |
| 6.0 | 48,920 | 0.139 | 86.69 | 43.28 | Yes | |
| 6.5 | 50,991 | 0.145 | 83.37 | 44.16 | Yes | |
| 7.0 | 52,113 | 0.148 | 82.61 | 44.49 | Yes | |
| 7.5 | 57,042 | 0.162 | 86.57 | 44.02 | Yes | |
| 8.0 | 55,957 | 0.159 | 96.58 | 44.46 | Yes | |
| 8.5 | 58,915 | 0.167 | 79.12 | 44.29 | Yes | |
| 9.0 | 61,916 | 0.176 | 84.94 | 42.79 | Yes | |
| 9.5 | 62,468 | 0.177 | 101.00 | 44.37 | No | |
| 10 | 66,231 | 0.188 | 70.62 | 44.01 | Yes |
| Con. | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 12,488 | 0.035 | 40.53 | 39.97 | 0.11 | Yes |
| 1.0 | 17,521 | 0.050 | 40.22 | 39.91 | 0.08 | Yes |
| 1.5 | 21,086 | 0.060 | 40.40 | 39.99 | 0.22 | Yes |
| 2.0 | 21,694 | 0.062 | 40.95 | 40.10 | 2.12 | Yes |
| 2.5 | 22,186 | 0.063 | 44.53 | 40.42 | Yes | |
| 3.0 | 22,336 | 0.063 | 47.37 | 40.49 | Yes | |
| 3.5 | 23,226 | 0.066 | 43.37 | 41.07 | Yes | |
| 4.0 | 23,170 | 0.066 | 49.39 | 41.67 | Yes | |
| 4.5 | 23,319 | 0.066 | 49.12 | 42.22 | Yes | |
| 5.0 | 23,189 | 0.066 | 58.41 | 42.75 | Yes | |
| 5.5 | 23,420 | 0.066 | 73.59 | 43.10 | Yes | |
| 6.0 | 23,131 | 0.066 | 67.96 | 42.91 | Yes | |
| 6.5 | 23,575 | 0.067 | 86.27 | 42.75 | Yes | |
| 7.0 | 23,796 | 0.067 | 100.55 | 44.47 | No | |
| 7.5 | 23,672 | 0.067 | 133.62 | 45.15 | No | |
| 8.0 | 23,706 | 0.067 | 135.61 | 46.58 | No | |
| 8.5 | 23,769 | 0.067 | 158.27 | 47.54 | No | |
| 9.0 | 23,803 | 0.068 | 205.10 | 50.41 | No | |
| 9.5 | 23,882 | 0.068 | 248.31 | 50.15 | No | |
| 10 | 23,799 | 0.068 | 395.42 | 51.71 | No |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.99991 | 0 | 35 | 67 | 76 | 72 | 66 | 64 | 63 | 57 | |
| 0.99992 | 0 | 35 | 72 | 79 | 77 | 73 | 61 | 58 | 68 | |
| 0.99993 | 2 | 43 | 73 | 83 | 78 | 81 | 61 | 62 | 70 | |
| 0.99994 | 1 | 51 | 79 | 78 | 76 | 76 | 73 | 63 | 63 | |
| 0.99995 | 1 | 49 | 82 | 90 | 87 | 78 | 74 | 69 | 64 | |
| 0.99996 | 1 | 55 | 87 | 89 | 82 | 76 | 60 | 56 | 39 | |
| 0.99997 | 1 | 66 | 91 | 86 | 78 | 43 | 4 | 0 | 0 | |
| 0.99998 | 2 | 76 | 80 | 46 | 2 | 0 | 0 | 0 | 0 | |
| 0.99999 | 7 | 76 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1.00000 | 10 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Type of Obstacles | Algorithms | (%) | ||
|---|---|---|---|---|
| Single regular | OABAS | 0.059 | 17.63 | 100 |
| PSO | 0.606 | 19.54 | 100 | |
| ABC | 0.356 | 17.29 | 100 | |
| Multiple regular | OABAS | 0.083 | 17.37 | 97 |
| PSO | 2.254 | 19.30 | 97 | |
| ABC | 0.279 | 17.32 | 100 | |
| Single irregular | OABAS | 0.102 | 21.16 | 100 |
| PSO | 7.670 | 22.68 | 87 | |
| ABC | 0.450 | 19.29 | 100 | |
| Multiple irregular | OABAS | 0.065 | 19.69 | 100 |
| PSO | 17.285 | 19.52 | 63 | |
| ABC | 0.571 | 19.90 | 100 | |
| Mixed | OABAS | 0.088 | 19.56 | 100 |
| PSO | 0.536 | 21.54 | 98 | |
| ABC | 0.325 | 21.64 | 100 |
| Type of Obstacles | Algorithms | (%) | ||
|---|---|---|---|---|
| Single regular | OABAS | 0.301 | 36.94 | 100 |
| PSO | NA | 57.04 | 52 | |
| ABC | 49.729 | 40.47 | 96 | |
| Multiple regular | OABAS | 0.371 | 41.77 | 99 |
| PSO | NA | 51.18 | 38 | |
| ABC | 32.382 | 48.48 | 100 | |
| Single irregular | OABAS | 0.406 | 46.01 | 99 |
| PSO | 184.593 | 44.44 | 39 | |
| ABC | 35.434 | 40.91 | 100 | |
| Multiple irregular | OABAS | 0.428 | 41.71 | 95 |
| PSO | 251.506 | 40.88 | 12 | |
| ABC | 56.813 | 41.36 | 48 | |
| Mixed | OABAS | 0.345 | 39.91 | 100 |
| PSO | NA | 57.04 | 92 | |
| ABC | 46.956 | 48.93 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Shen, X.; Jin, Y.; Chen, Z.; Li, S.; Khan, A.H.; Chen, D. Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles. Sensors 2019, 19, 1758. https://doi.org/10.3390/s19081758
Wu Q, Shen X, Jin Y, Chen Z, Li S, Khan AH, Chen D. Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles. Sensors. 2019; 19(8):1758. https://doi.org/10.3390/s19081758
Chicago/Turabian StyleWu, Qing, Xudong Shen, Yuanzhe Jin, Zeyu Chen, Shuai Li, Ameer Hamza Khan, and Dechao Chen. 2019. "Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles" Sensors 19, no. 8: 1758. https://doi.org/10.3390/s19081758
APA StyleWu, Q., Shen, X., Jin, Y., Chen, Z., Li, S., Khan, A. H., & Chen, D. (2019). Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles. Sensors, 19(8), 1758. https://doi.org/10.3390/s19081758







