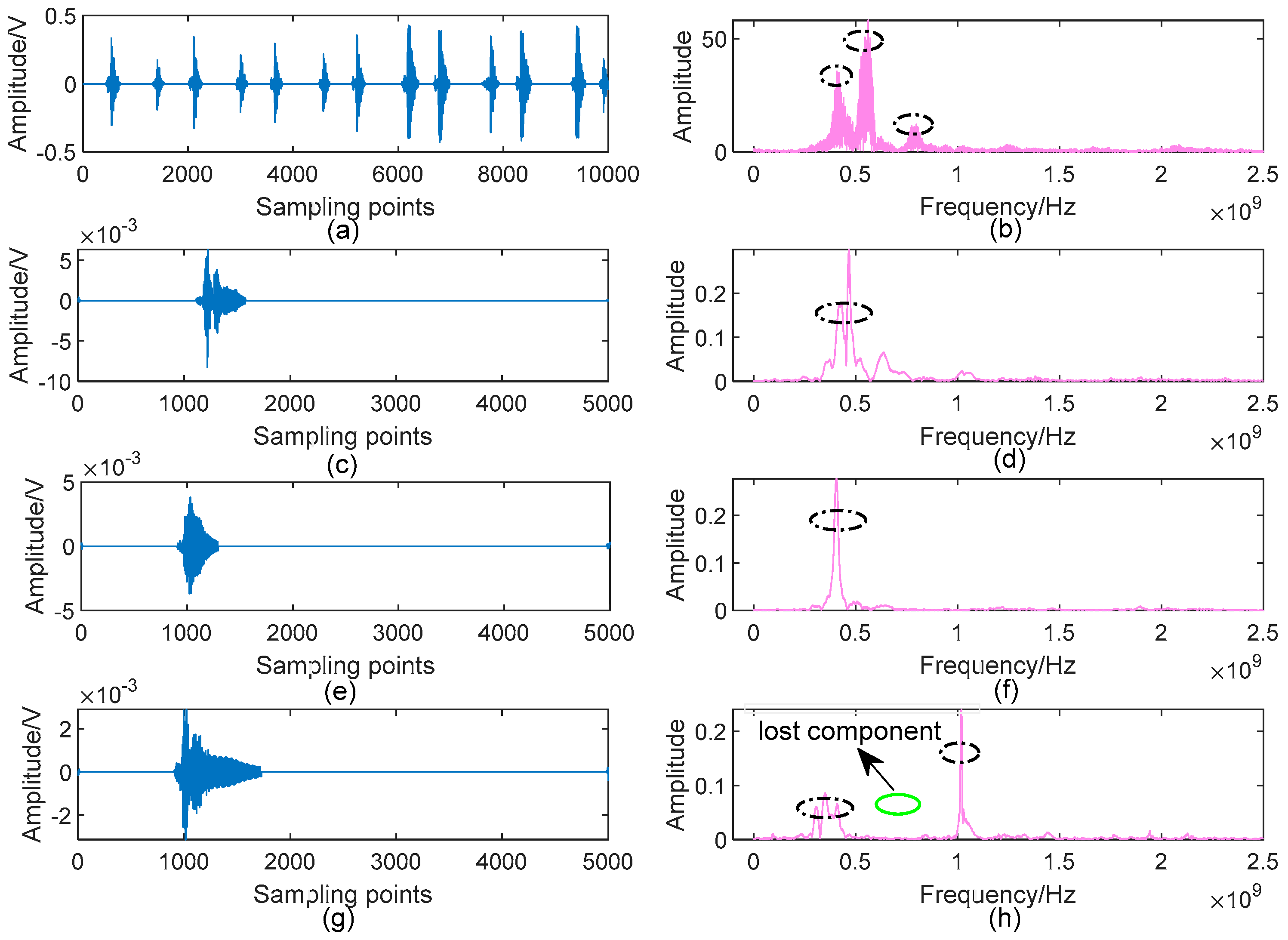
1. Introduction
Power systems constitute critical societal infrastructure, and play an increasingly important role in the development of the national economy and the improvement of the population’s living standard [
1]. Accompanying inevitable technological advances, the probability of failure of electrical equipment and the resulting damage will also increase greatly. Therefore, timely and accurate monitoring of the operating status of electrical equipment plays a vital role to ensure its safe and stable operation, and to prevent large-scale blackouts. In most cases, high-voltage electrical equipment is accompanied by partial discharge (PD) phenomenon before catastrophic failure [
2,
3,
4]. Among various PD detection methods, the ultra-high frequency (UHF) technique has been widely used due to its superior performance in location [
5], type recognition [
6] and severity evaluation of PD faults [
7]. However, the complicated and unpredictable electromagnetic environment in a substation may cause the PD signals to be contaminated by noise, leading to an incorrect diagnosis. Hence, a reliable noise suppression method is a prerequisite for the accurate detection and diagnosis of PD [
8].
Up to now, various methods for PD signal denoising have been reported, most of which are designed to deal with a particular noise type (e.g., white noise or narrow band noise). To our best knowledge, most state of the art PD denoising methods are based on signal decomposition technologies, such as the wavelet transform (WT), empirical mode decomposition (EMD), singular value decomposition (SVD) and sparse decomposition, etc. For example, the WT-based denoising methods was studied comprehensively in [
9]. Recently, the dual-tree complex WT was introduced for PD denoising, and it shows superior performance in comparing with traditional WT and SVD [
10]. Although the WT-based method has been widely accepted as a promising tool for denoising, the performance of WT relies heavily on the selection of wavelet basis, decomposition levels and threshold, especially when the composition of PD signal is complex or the PD component is relatively weak. An improper selection of these parameters may lead to the loss of some effective components. Different from WT, EMD and SVD are non-parametric signal analysis tools which can be implemented without pre-defined basis functions. In [
11], a discrete spectral interference suppressing method was developed based on bivariate EMD, and it showed superior performance over WT in PD denoising. Authors in [
12] also introduced the EMD algorithm into ultrasonic PD signals, and the denoising result was satisfied. Besides, some improved version of EMD like ensemble EMD (EEMD) [
13] or complete ensemble EMD (CEEMD) [
14] also perform well in noise suppression. However, all these EMD-based methods are essentially a kind of recursive algorithm, which suffers the following deficiencies: (i) the previous estimation error will be passed to the following results, namely error accumulation; (ii) mode mixing will exist when dealing with multi-components and strong nonlinear signals; (iii) there are end effects in this kind of algorithms. Another attractive decomposition method is SVD. An adaptive SVD method was proposed in [
15], and its key innovation was that it can select and remove those singular values (SVs) relating to white noise automatically. To improve the efficiency of traditional SVD, a sliding SVD was presented in [
16]. It provides a fully automatic data-driven component extraction scheme and a sliding window-based SVD (just like the Short Time Fourier Transform). Nevertheless, because the selected SVs are still mixed with small amount of white noise, using SVD alone may result in unsatisfactory denoising results. In addition, when the original signal contains multiple components, it will become difficult for SVD to distinguish other components except the white noise. Another new denoising method based on sparse decomposition was proposed by designing PD-correlated atom and overcomplete dictionary [
17], and superior results could be achieved over traditional WT methods in noise suppression and waveform distortion.
Recently, a completely non-recursive mode decomposition method, namely the variational mode decomposition (VMD) was developed [
18]. With this method, the original signal can be decomposed into a set of amplitude modulation-frequency modulation functions (AM-FM), which are band-limited and frequency-unmixed. Due to its superior performance over traditional methods like WT and EMD, researchers in various fields such as machinery [
19], biomedicine [
20], geology [
21] and so on, have begun to apply VMD extensively. However, the original author also pointed out that the performance of VMD will be affected by the following three parameters: the number of modes
K, the quadratic penalty term
a and the time-step of the dual ascent
τ [
18]. Some guidelines for choosing these parameters were discussed in [
18], for example,
τ is suggested to be zero when the noise level is high. Moreover, a relatively moderate value of
a recommended by the author is 2000. Thus, the determination of
K is the key problem when employing VMD.
This paper aims to remove various interferences in UHF PD signal and preserve its key features at the same time. To achieve this goal, a new denoising method, namely the adaptive variational mode decomposition and singular spectrum analysis (AVMDSSA), is developed, and the main steps are outlined as follows:
- (i)
An automatic VMD algorithm is presented based on a mode-mixing judgement criterion. With the optimal K, the original PD signal can be decomposed into BLIMFs at high accuracy.
- (ii)
Considering that BLIMFs containing PD components will exhibit the shape of pulse, a kurtosis-based method is employed to pick out those valuable BLIMFs (i.e., eBLIMFs).
- (iii)
For each selected eBLIMF, the dominant singular values (DSVs) are retained at first. Then, they will be used to reconstruct PD signal by diagonal averaging. Next, the rescaling thresholding technique [
9] is applied to further remove the residual white noise in each eBLIMF. Finally, the denoised UHF PD signal is obtained by adding up all these denoised eBLIMFs.
The rest of this paper is organized as follows:
Section 2 reviews the mathematical background. The proposed method is detailed in
Section 3. Simulative case, laboratorial case and field case are respectively analyzed in
Section 4,
Section 5 and
Section 6. Main contributions and some open questions of our paper is discussed in
Section 7. Finally, the conclusion is drawn in
Section 8.
3. Proposed Denoising Method
3.1. Adaptive VMD
As discussed before, the performance of VMD is heavily dependent on the choice of its parameters, especially for the number of modes
. Some related studies have discussed the parameter selection problem of VMD, which mainly focus on optimizing by heuristic optimization algorithms. For example, a searching method for quadratic penalty term
and mode number
is presented in [
24] based on the artificial fish swarm (AFS) algorithm. Besides, the particle swarm optimization (PSO) algorithm has also been applied to VMD in [
8]. Although these methods can obtain appropriate parameters to some extent, they may need to go through many iterations before convergence. Moreover, one may have to set initial parameters of heuristic optimization algorithms manually, making the VMD method more complicated.
In this paper, the quadratic penalty term
a and time-step of the dual ascent
τ are respectively set to 2000 and 0, and we focus on the optimization method of the mode number
K. The basic idea behind this adaptive VMD (AVMD) method is simple and straight: increase the value of
K (starting from 2) step by step and obtain the BLIMFs by VMD during each step. When there is no mode mixing happened in all BLIMFs for a certain
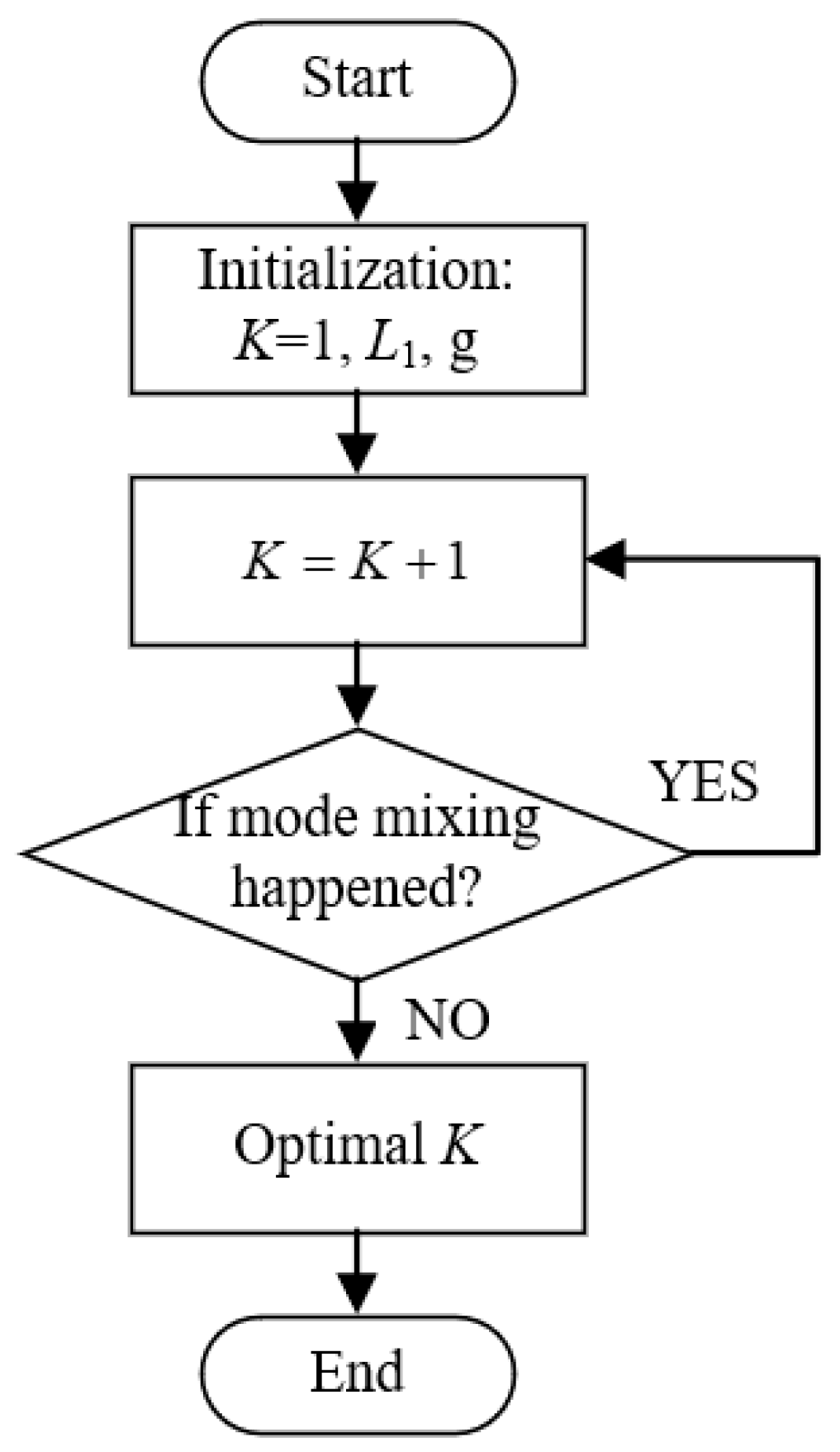
K, then this value is considered as optimal. Based on this concept, the schematic diagram of the proposed method is demonstrated in
Figure 1.
As can be seen from
Figure 1, the key of this method is to determine whether there is mode mixing occurred in decomposed BLIMFs. For this purpose, the first important task is to find out the local maximum points (LMPs) of BLIMF spectrum, which are considered to belong to the potential effective components. This can be achieved by the following two steps:
(i) Preliminary screening
To begin with, the frequency spectrum is divided into several consecutive segments, and each segment has the same length L1 (the last segment may not). Then, the maximal point in each segment will be picked out to form a new sequence , where denotes the maximal point of the nth segment, and is the number of segments.
(ii) Peaks confirmation
After the previous process, it is easy to find that the LMPs of the frequency spectrum must be the points within segmax. Therefore, the LMPs can be obtained easily by searching the peak points of segmax, remarked as pks.
Due to the influences of potential multiple components or interfering noise, the number of pks is likely to be more than one. Consequently, the remaining problem is to determine whether other points in pks except for the maximum are active components. Denote the maximal point of pks as max_temp, then the proposed rules for mode-mixing determination is given as follows: for any point in pks except for max_temp, if the distance between max_temp and this point is larger than a pre-set value, and in the meanwhile, the amplitude of this point is higher than a pre-set value, then the corresponding frequency component at this point is considered as active. If the point satisfying the above conditions exists, it will imply that there are at least two active components in the current BLIMF (including max_temp). Obviously, this means mode-mixing has occurred. The pseudocode of this judgment algorithm is detailed in Algorithm 1.
| Algorithm 1: Pseudo-code of the proposed mode-mixing judgement method |
![Sensors 19 01594 i001 Sensors 19 01594 i001]() |
Follow the workflow in
Figure 1 and the decision rule in Algorithm 1, the optimal mode number
K can be obtained in just a few steps.
3.2. Effective BLIMF Selection
Based on the AVMD algorithm presented in the previous section, the PD signal is decomposed into
K BLIMFs, and each BLIMF contains only one active component. However, not all these active components are PD components. In fact, the generating mechanism of PD electromagnetic signal and its propagation path determine that it exhibits characteristics of damped oscillation and steep rising edge in the time domain, while narrowband periodic noise or white noise does not show such characteristic. Therefore, in this paper, BLIMF with following features is defined as effective BLIMF (abbreviate as eBLIMF): (i) with central frequency in UHF band (i.e., higher than 0.3GHz); (ii) exhibits damped oscillation in time domain; (iii) has steep rising edge. Based on the above analysis, the kurtosis operator which is sensitive to abrupt change is selected as the indicator, and the decision rule is formulated as:
where
is a pre-set threshold.
f0( ) is the central frequency operator, and
kurtosis( ) is the kurtosis operator, which is calculated as:
where
is a discrete signal defined in
Section 2.2, and
denotes its mean value.
3.3. SSA-based Shrinkage method
In this section, a denoising algorithm based on SSA and shrinkage method is designed. For each eBLIMF, the Hankel matrix is constructed and be decomposed into several sub-space matrices
Ai by SVD. Since there is only one dominant component in each eBLIMF, the grouping step described in
Section 2.2 becomes easy. Assume the SVs are sorted in descending order, and the ratio of each SV to the sum of all SVs are denoted as
(
R is the rank of Hankel matrix), a common way to choose DSVs is to compute the cumulative sum of
until its value reached a proper threshold
. This process can be expressed as:
Therefore, the first
SVs are decided as DSVs. For each DSV, its corresponding sub-space matrices
Ai is computed by Equation (9), then the reconstructed signal
based on
Ai can be obtained by the diagonal averaging method. In order to further suppress the white noise in
, the shrinkage technology typically used in WT-based denoising is employed [
9]. Specifically, the multiplicative threshold rescaling scheme with
sqtwolog rule is adopted, which is expressed as:
where
is the length of
,
is the set of DSVs,
is the threshold of
. Afterwards, the hard threshold function is applied to denoise the recovered signal
, given by:
where
is the
jth element of
. At last, for all DSVs, the denoised
are added to form the denoised eBLIMF:
In Equation (15),
is the
jth element of the denoised eBLIMF, and
has been explained in Equation (12). The whole procedure of SSA-based shrinkage method is illustrated in Algorithm 2.
| Algorithm 2: Pseudo-code of thr proposed SSA-based Shrinkage denoising method |
![Sensors 19 01594 i002 Sensors 19 01594 i002]() |
3.4. Implementation Procedure of Proposed AVMDSSA Method
Based on the above descriptions, the schematic diagram of AVMDSSA method is demonstrated in
Figure 2, and the overall process is summarized as follows:
- (i)
Optimization of the number of modes K by gradually increasing its value and judging whether there is mode-mixing happened in each BLIMF at every step.
- (ii)
Decompose the UHF PD signal into a set of BLIMFs by VMD with the optimal K parameter, then a kurtosis-based selection method is employed to pick out the eBLIMFs.
- (iii)
For each eBLIMF, the SSA-based Shrinkage denoising method is applied to suppress the white noise, and summation of all denoised eBLIMFs will recover the denoised UHF PD signal.
6. Field Case Study
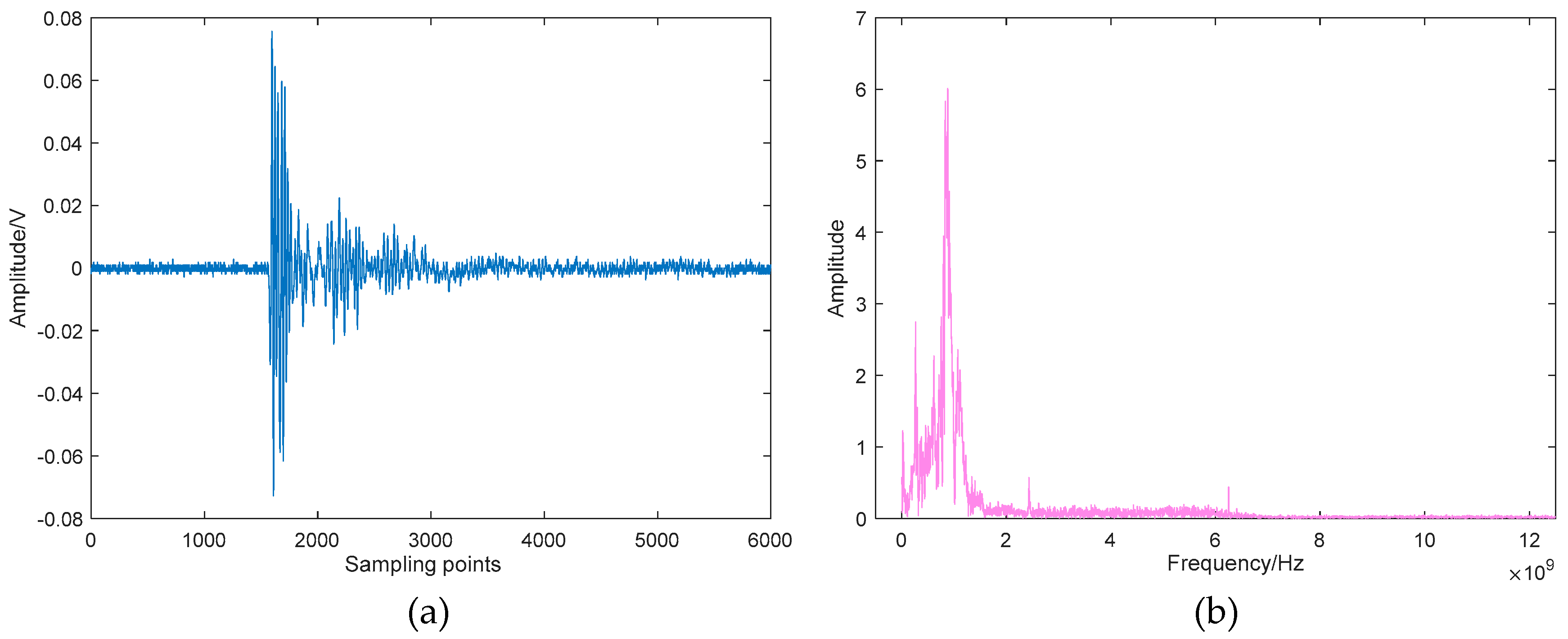
In this section, the field UHF PD data from a 220 kV current transformer are analyzed. The suspected PD signal radiates outward through the resin sprue on the basin insulator, and then be coupled by the UHF sensor and sent to the oscilloscope (25 GS/s, 6GHz) for sampling and storage. The picture of the field test is given in
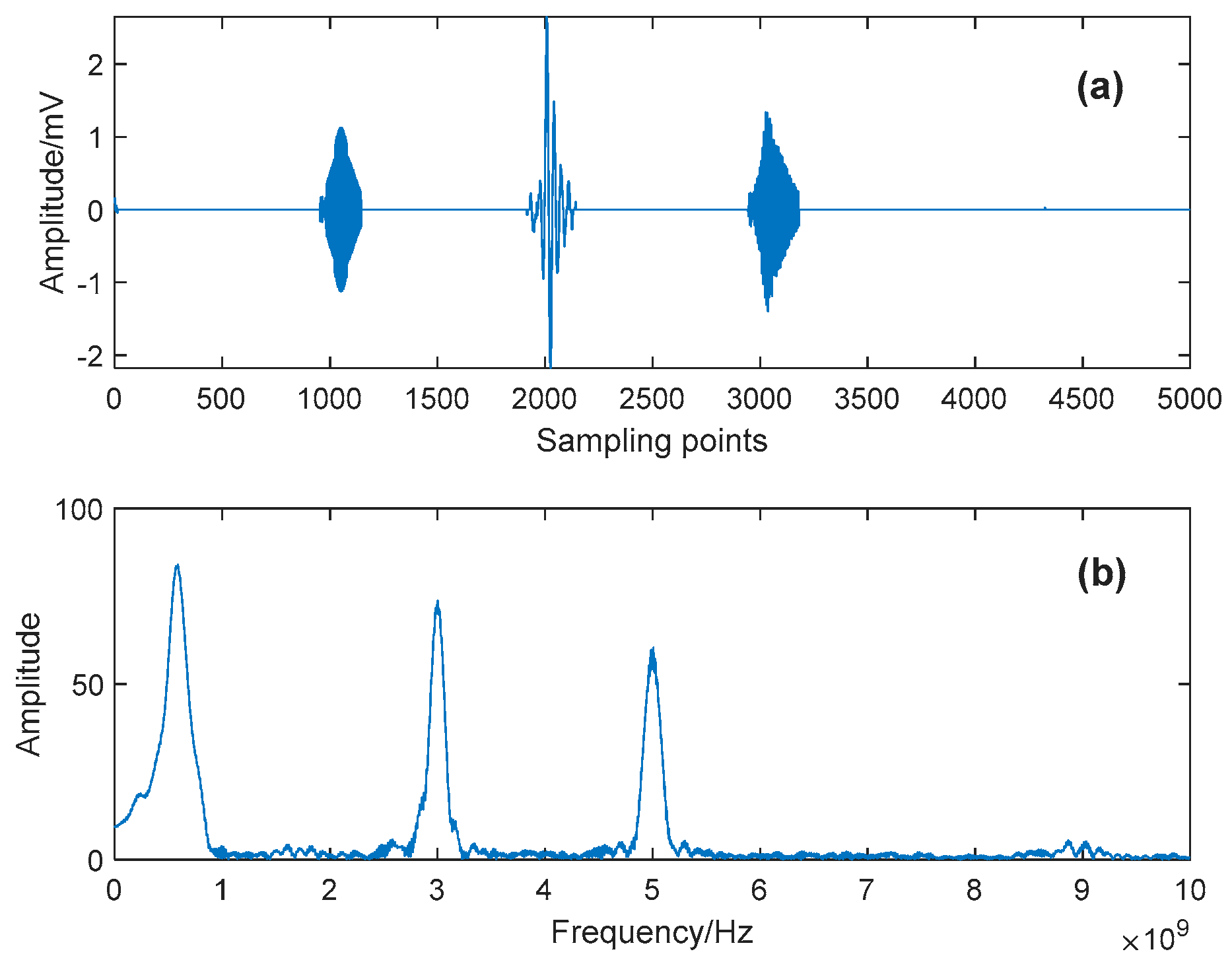
Figure 16, and the typical time-domain waveform and its spectrum are depicted in
Figure 17. As can be seen, although the metal shell of GIS can shield most of the external interferences, the captured signal still has a complex composition, which makes the denoising work more challenging.
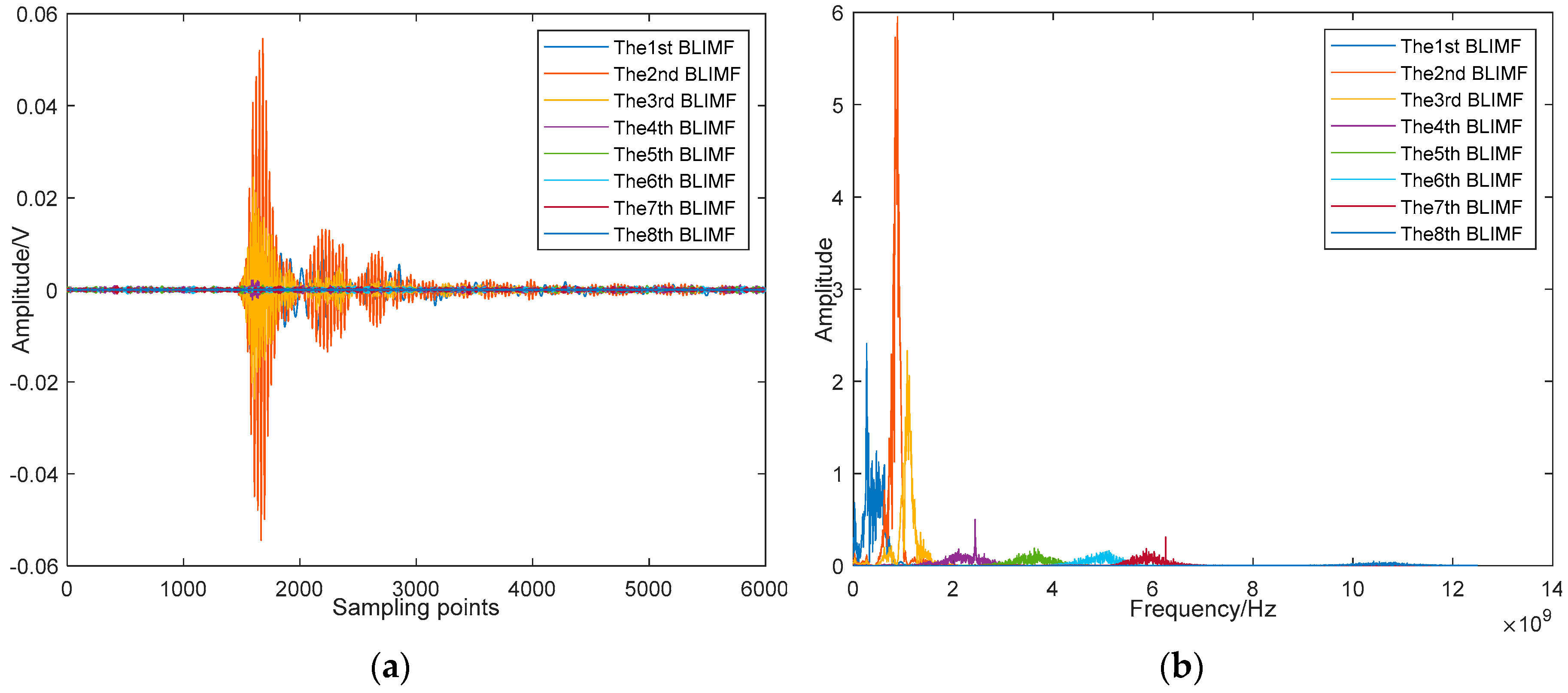
By using the proposed method, the mode number of VMD is optimized first, and the optimal value of
K is 8 in this example.
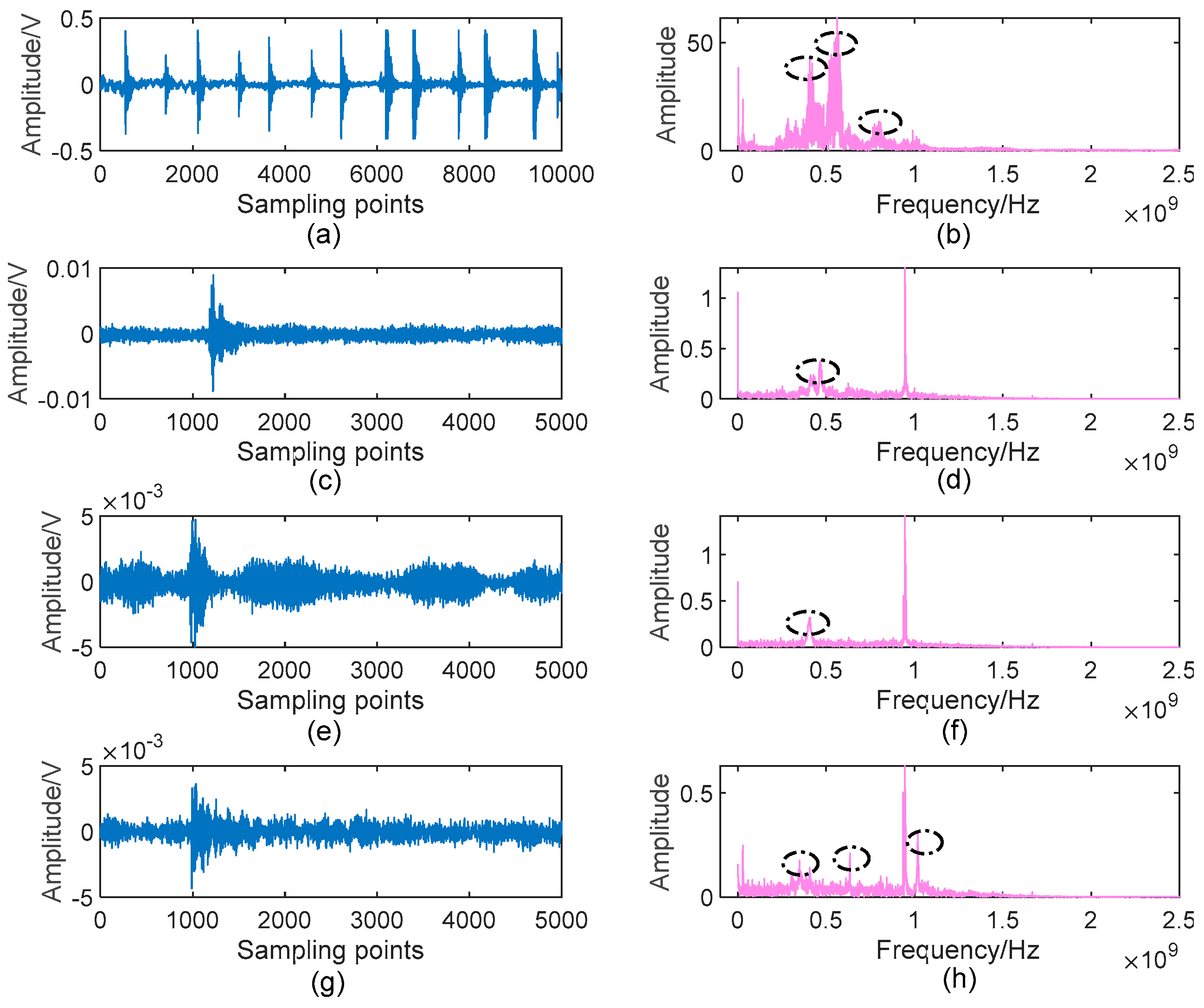
Figure 18 shows the decomposed BLIMFs of the above signal by applying the optimal VMD. A comparison between
Figure 17b and
Figure 18b shows that there are no active frequency components mixing or missing, which means the decomposition is complete. Next, the eBLIMFs will be decided according to Equation (10) by calculating their central frequencies and kurtosis values. Results of this step are listed in
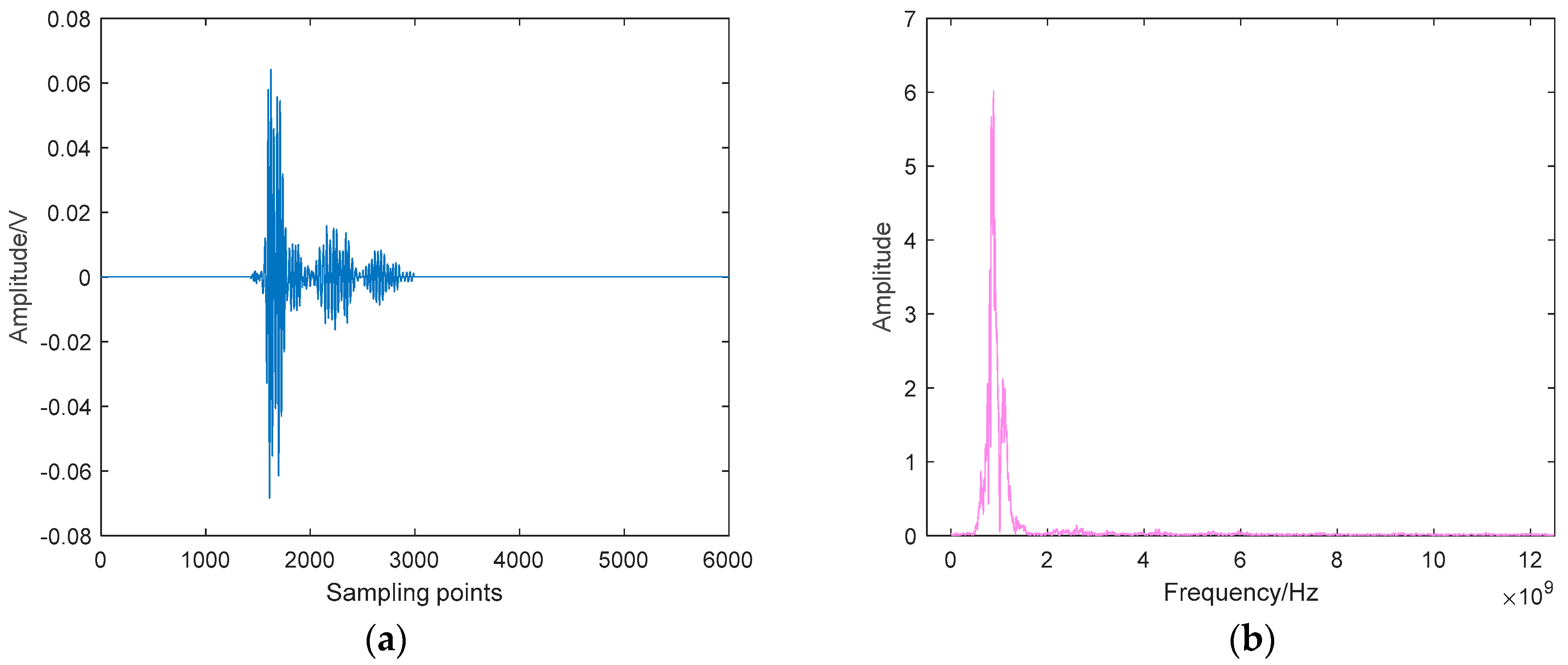
Table 5, in which can we see that only BLIMF2 and BLIMF3 are judged as eBLIMFs. At last, the SSA-based Shrinkage scheme is used to further remove the white noise in each eBLIMF. The final denoising result is shown in
Figure 19.
Again, we use the newly designed indices to evaluate the performance of AVMDSSA under this field situation. The average computation results of fifty measured signals are as follow: Index1: 0.4860; Index2: 0.9723. This result demonstrates that the AVMDSSA method can effectively reduce the uncertainty of the measured data. And what’s more, there is almost no loss of the characteristic components after the denoising process, which is critical to the subsequent processing and diagnosis.
7. Discussion
In this paper, a novel denoising method namely AVMDSSA is developed. To comprehensively evaluate the performance of AVMDSSA, three case studies are conducted, and we discuss the results as follows:
(i) Simulative case
In the simulative case study, complex UHF PD signals with heavy noise are simulated. One can easily see from
Figure 4b,d that if the decomposition by VMD is incomplete (i.e., the value of
K is smaller than the actual number of active components in the raw signal), there will be multiple local maximum points in the BLIMF. On the contrary, every decomposed BLIMF should contain only one active component if
K is equal to the number of actual components, as can be seen from
Figure 5. The optimization process by the proposed AVMD algorithm is given in
Table 3. After the selection of eBLIMFs and an SSA-based shrinkage algorithm, the final denoising result is obtained. Comparing
Figure 7 with
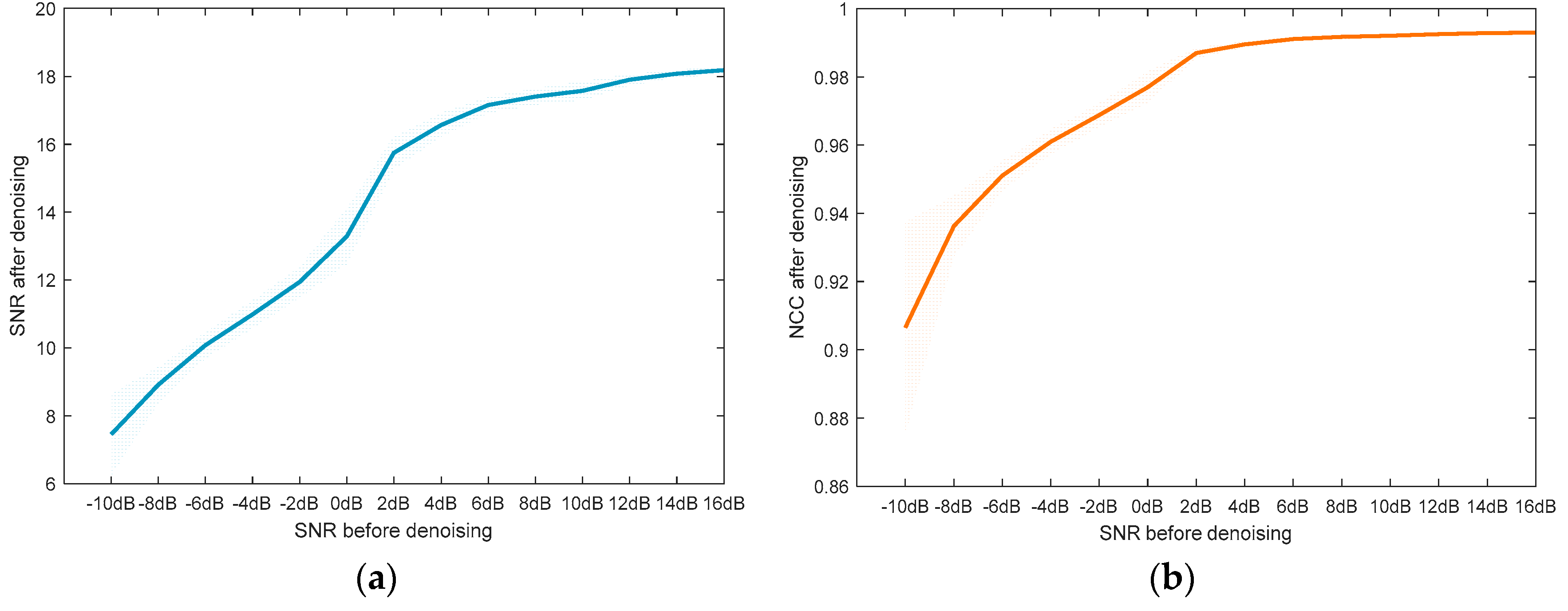
Figure 9, one can readily observe the superiority of AVMDSSA over other methods. In addition, the results of the noise robustness tests (depicted in
Figure 8) and quantitative comparison (depicted in
Figure 10) are all demonstrate the effectiveness of our method.
(ii) Laboratorial case
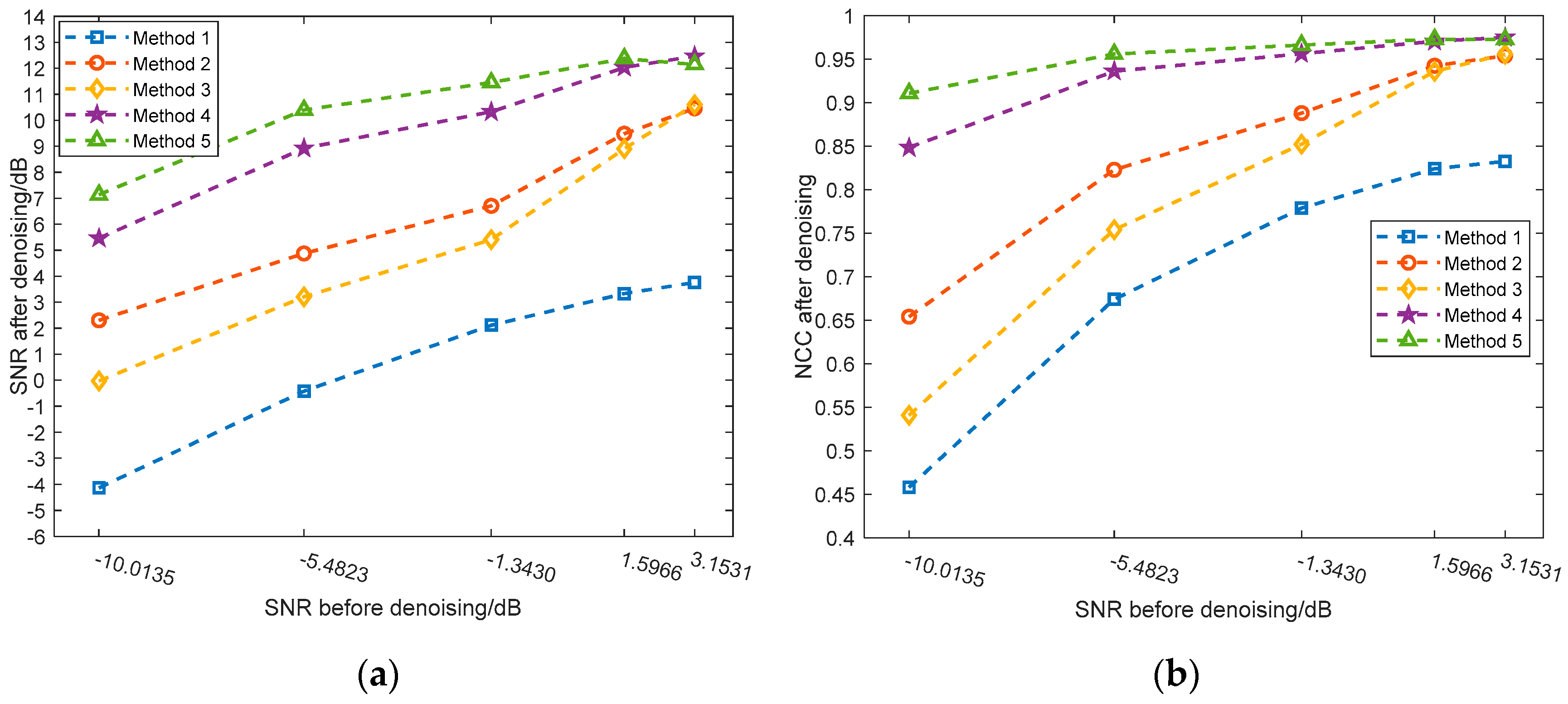
To examine the performance of AVMDSSA by real UHF PD signal, four kinds of laboratorial PD data are collected. In addition, we define two new evaluation indices for denoising method from the perspective of noise suppression and feature retention, respectively. The effectiveness of the proposed AVMDSSA method is readily shown in
Figure 14, even for the signal that contains multiple PD components. By using the newly defined indices for each method, we can conclude from
Table 4 that AVMDSSA shows the best performance (lowest
Index1, highest
Index2).
(iii) Field Case
The UHF PD signals from a real high-voltage current transformer are also employed in this paper, and the denoising results shown in
Figure 19 are satisfactory, suggesting that our method has the application potential in practical scenarios.
The above discussions prove the effectiveness of the presented method. Moreover, it is worth mentioning that all the denoising results of AVMDSSA are obtained by using the same parameters listed in
Table 2, which indicates the robustness of this method.
Compared with our previous denoising study in reference [
8], contributions in this work are summarized as follows: (i) the parameter optimization method adopted in this paper has more explicit physical meaning and faster searching speed; (ii) the SSA-based shrinkage method developed in this work shows better denoising performance compared with the Wavelet Shrinkage method used in [
8]; (iii) more comprehensive assessment of the denoising method is given in this study, including the noise robustness test, newly designed evaluation indices, and the field test. All these advancements show that the current method achieves much improvement compared to our previous work.
Despite all the advantages, we should admit that the efficiency of AVMDSSA needs to be improved. For example, the average time consumption of AVMDSSA for a signal with length of 5000 is 3.6 s (hardware: Intel Core i5 CPU, 16 GB RAM; software: MATLAB 2018b), while this value can rise to more than 10 s when dealing with a signal with length of 10000. Such high computational cost mainly comes from the SVD algorithm used in SSA. To a certain extent, this restricts the real-time application of our method in embedded hardware. However, for offline applications that are not very sensitive to computational complexity, the proposed method still shows great advantages.
To suppress the electromagnetic interference in PD signals more thoroughly, improvements in hardware design are also important. For example, a reliable metal shell for the UHF sensor will prevent the external noise from coupling into the detection system to a large extent. Besides, considering that the optical fiber is a kind of ideal transmission medium due to its advantages such as high sensitivity, immunity to electromagnetic interference and stability in harsh environments, it can be used in the data transmission module of the PD detection system. In summary, only when the noise suppression measures are taken into account in both of hardware and software design, can the PD detection system play a more stable and reliable role in practice.