Biocompatible Cantilevers for Mechanical Characterization of Zebrafish Embryos using Image Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design of the System
2.1.1. Microtweezers
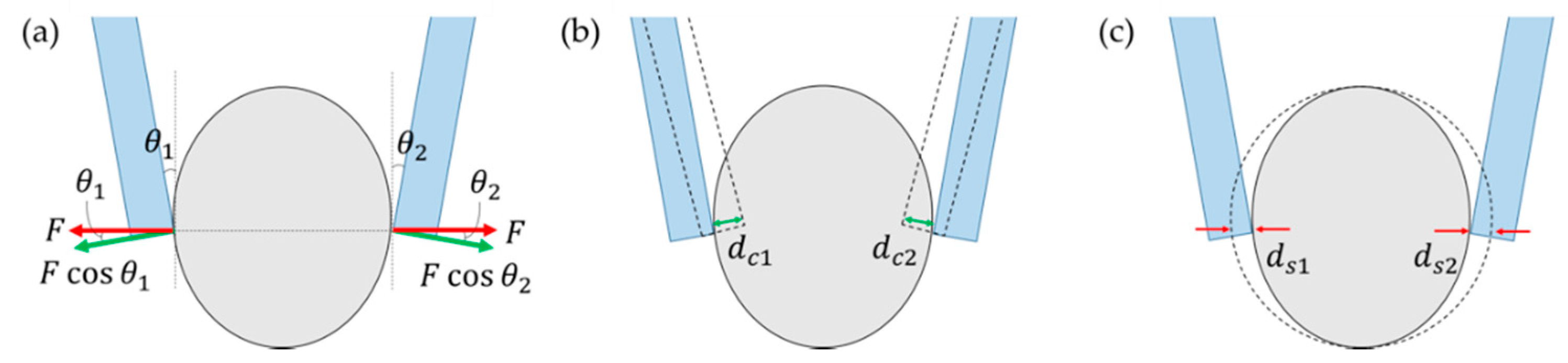
2.1.2. Principle of Force Sensing
2.1.3. Stiffness Analysis Using Pattern Matching and Tracking
2.2. Cantilever
2.2.1. Cantilever Fabrication
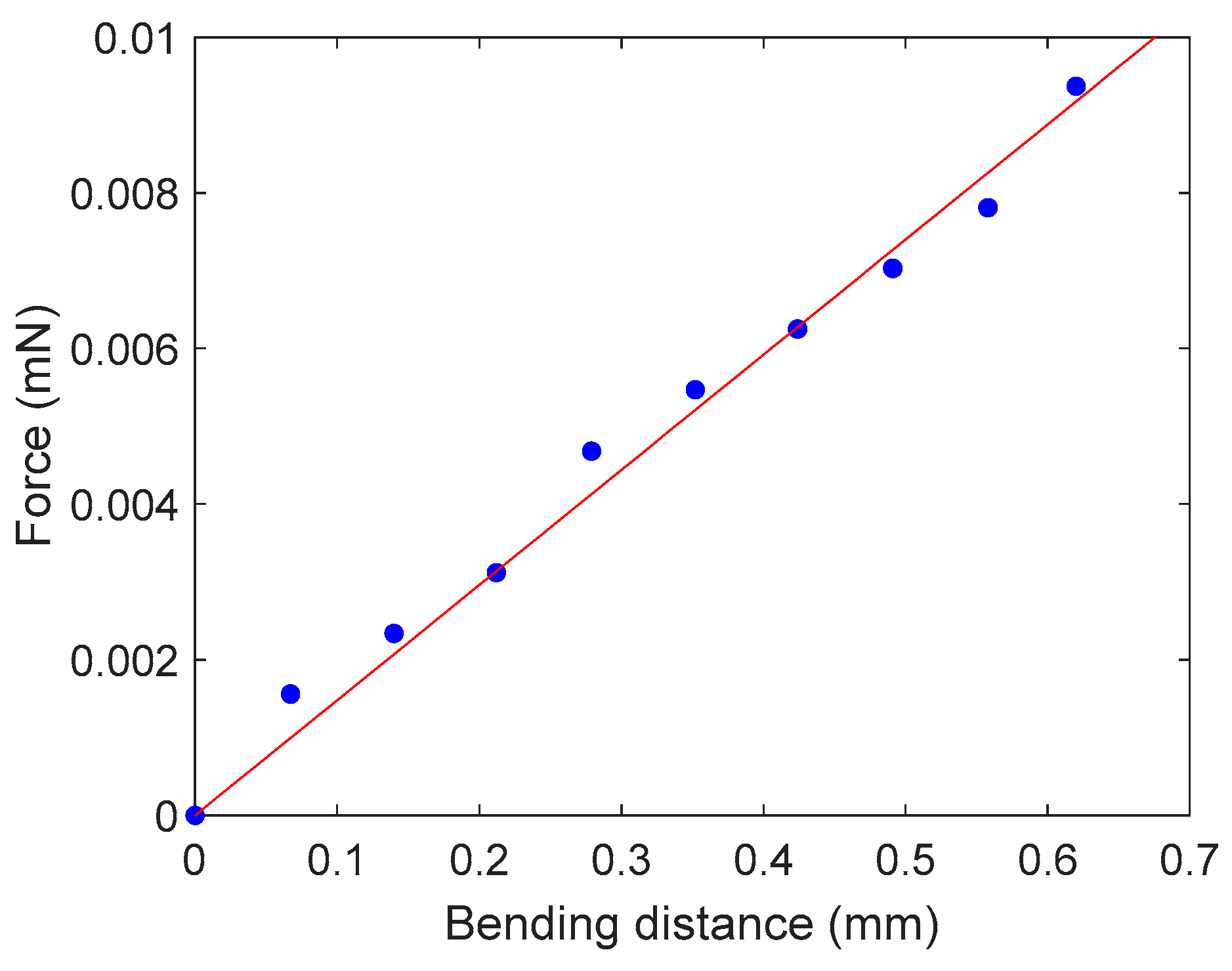
2.2.2. Cantilever Calibration
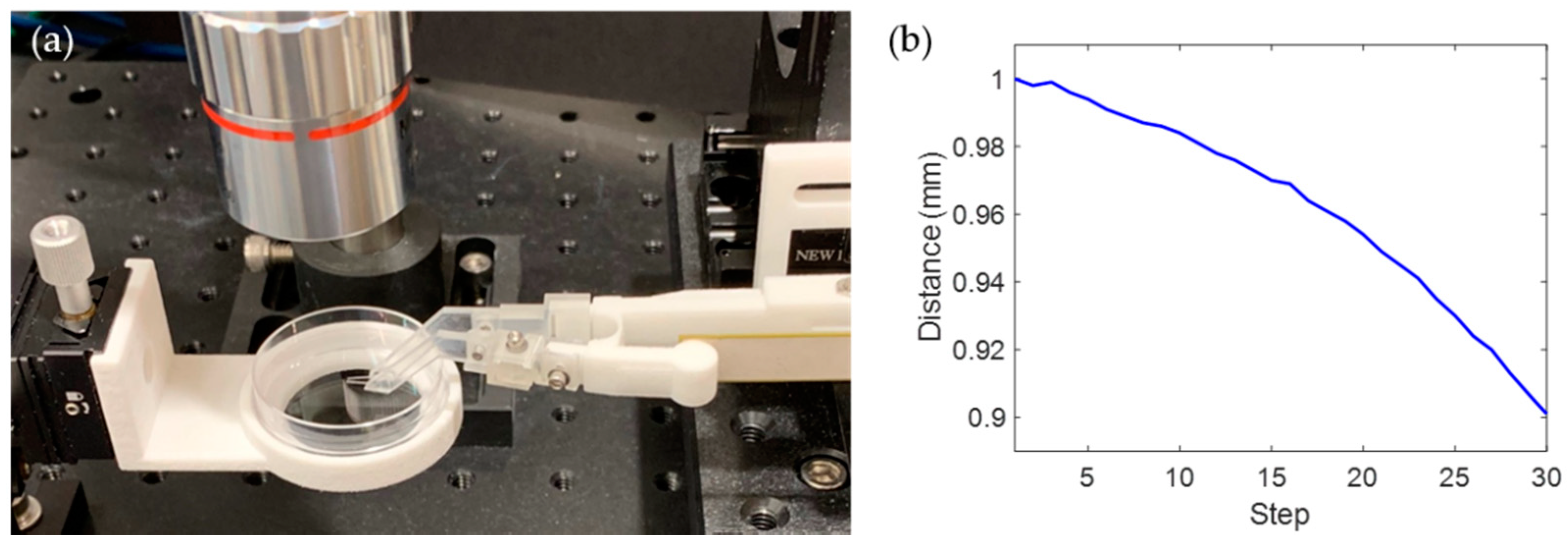
2.3. Experimental Setup
2.4. Preparation of Zebrafish Embryos
3. Results
3.1. Cantilever Calibration
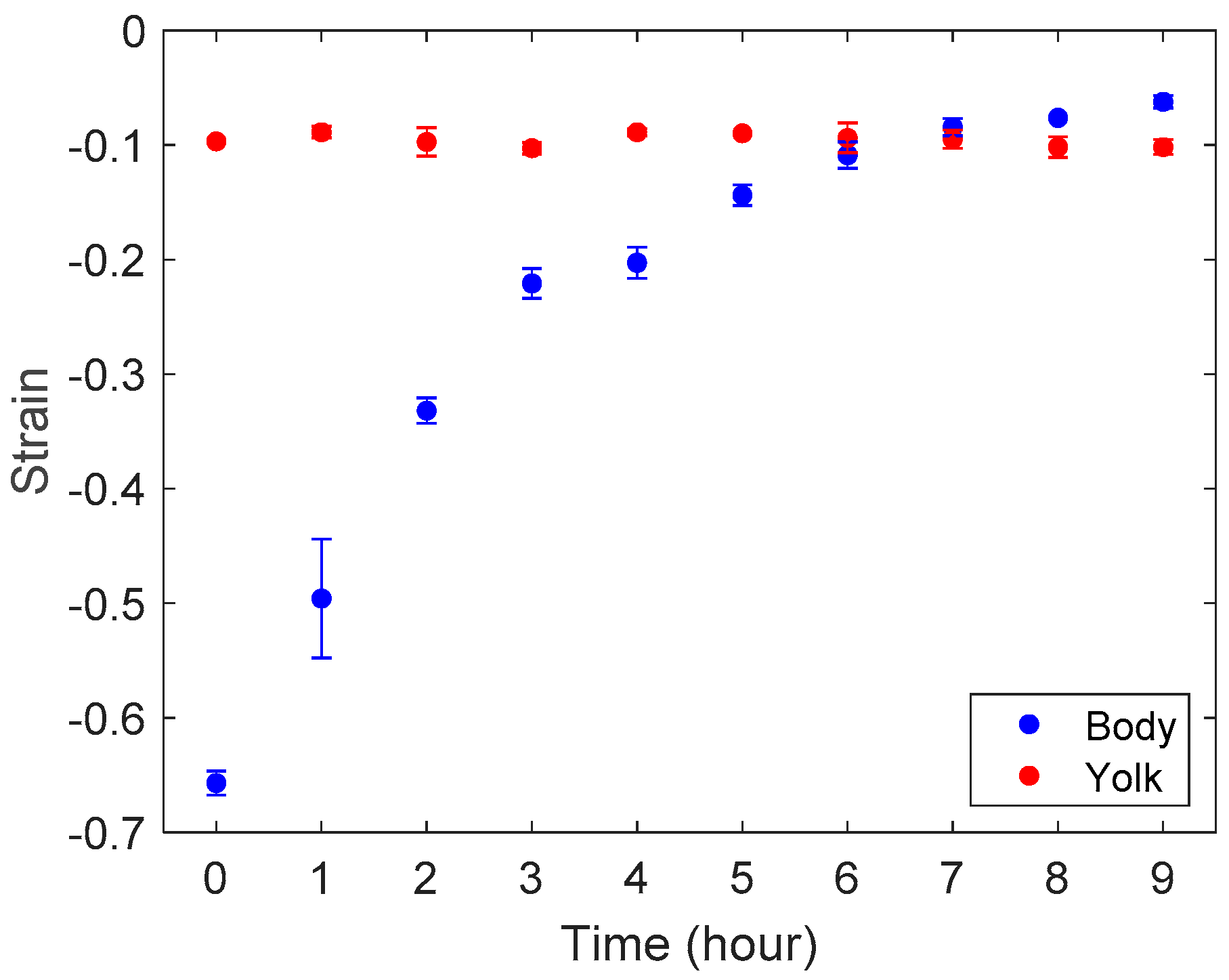
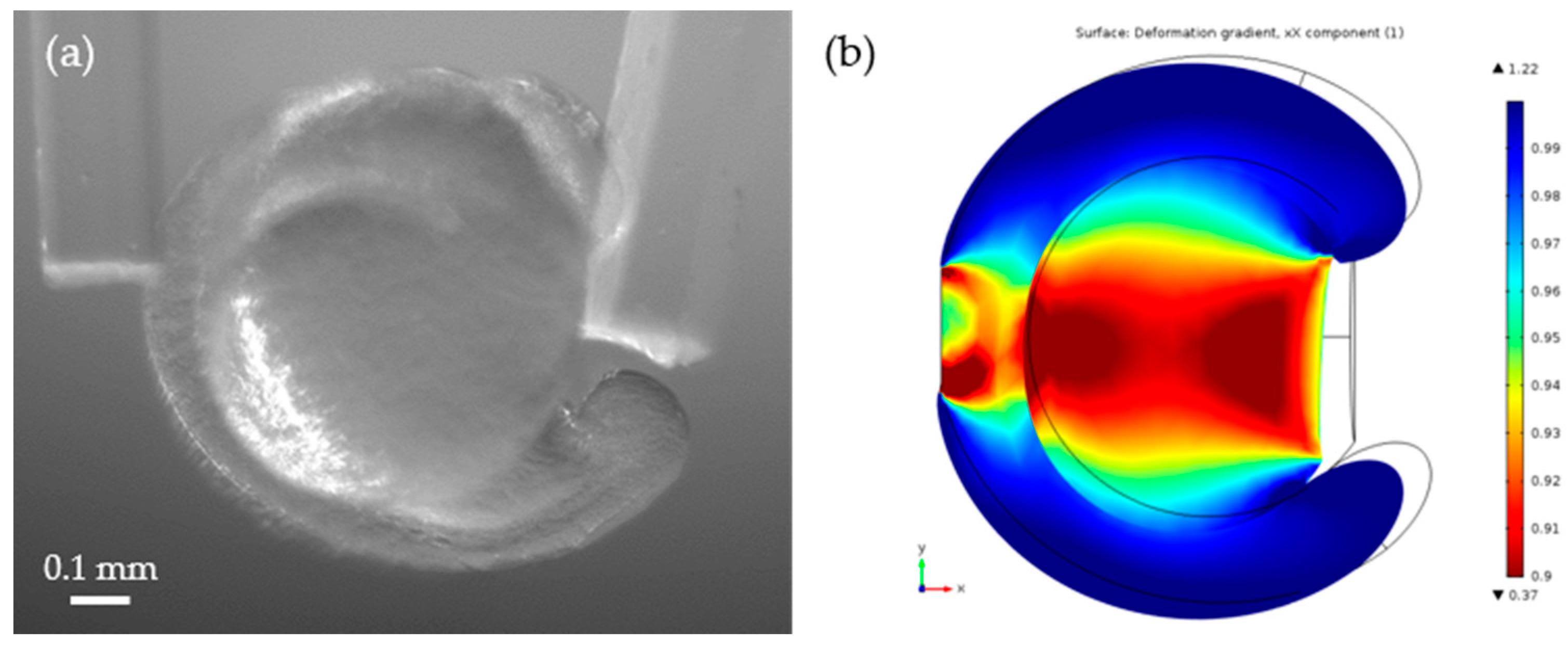
3.2. Stiffness Analysis of Zebrafish Embryo
3.3. Young’s Modulus Estimation Using a Finite Element Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ivascu, A.; Kubbies, M. Diversity of Cell-Mediated Adhesions in Breast Cancer Spheroids. Int. J. Oncol. 2007, 31, 1403. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Lin, B.; Qin, J. Carcinoma-Associated Fibroblasts Promoted Tumor Spheroid Invasion on a Microfluidic 3D Co-Culture Device. Lab Chip 2010, 10, 1671. [Google Scholar] [CrossRef] [PubMed]
- Mehta, G.; Hsiao, A.Y.; Ingram, M.; Luker, G.D.; Takayama, S. Opportunities and Challenges for use of Tumor Spheroids as Models to Test Drug Delivery and Efficacy. J. Control. Release 2012, 164, 192–204. [Google Scholar] [CrossRef] [PubMed]
- Vargo-Gogola, T.; Rosen, J.M. Modelling Breast Cancer: One Size does Not Fit All. Nat. Rev. Cancer 2007, 7, 659–672. [Google Scholar] [CrossRef]
- Zietarska, M.; Maugard, C.M.; Filali-Mouhim, A.; Alam-Fahmy, M.; Tonin, P.N.; Provencher, D.M.; Mes-Masson, A. Molecular Description of a 3D in Vitro Model for the Study of Epithelial Ovarian Cancer (EOC). Mol. Carcinog. 2007, 46, 872–885. [Google Scholar] [CrossRef]
- Guttilla, I.; Phoenix, K.; Hong, X.; Tirnauer, J.; Claffey, K.; White, B. Prolonged Mammosphere Culture of MCF-7 Cells Induces an EMT and Repression of the Estrogen Receptor by microRNAs. Breast Cancer Res. Treat. 2012, 132, 75–85. [Google Scholar] [CrossRef]
- DiMarco, R.L.; Su, J.; Yan, K.S.; Dewi, R.; Kuo, C.J.; Heilshorn, S.C. Engineering of Three-Dimensional Microenvironments to Promote Contractile Behavior in Primary Intestinal Organoids. Integr. Biol. Quant. Biosci. Nano Macro 2014, 6, 127. [Google Scholar] [CrossRef]
- Mondrinos, M.J.; Finck, C.M.; Jones, P.L.; Lelkes, P.I. Engineering De Novo Assembly of Fetal Pulmonary Organoids. Tissue Eng. 2014, 20, 2892–2907. [Google Scholar] [CrossRef]
- Tamai, M.; Adachi, E.; Tagawa, Y. Characterization of a Liver Organoid Tissue Composed of Hepatocytes and Fibroblasts in Dense Collagen Fibrils. Tissue Eng. Part A 2013, 19, 2527–2535. [Google Scholar] [CrossRef]
- Wetering, M.v.d.; Clevers, H.; Bartfeld, S.; Vries, R.; Bayram, T.; Peters, P.J.; Huch, M.; Kujala, P.; Begthel, H. In Vitro Expansion of Human Gastric Epithelial Stem Cells and their Responses to Bacterial Infection. Gastroenterology 2015, 148, 136. [Google Scholar]
- Yamaguchi, S.; Morizane, R.; Homma, K.; Monkawa, T.; Suzuki, S.; Fujii, S.; Koda, M.; Hiratsuka, K.; Yamashita, M.; Yoshida, T.; et al. Generation of Kidney Tubular Organoids from Human Pluripotent Stem Cells. Sci. Rep. 2016, 6, 38353. [Google Scholar] [CrossRef]
- Chen, P.; Lin, S.; Xu, G.; Li, B.; Feng, X. Three-Dimensional Collective Cell Motions in an Acinus-Like Lumen. J. Biomech. 2019, 84, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Guirao, B.; Bellaïche, Y. Biomechanics of Cell Rearrangements in Drosophila. Curr. Opin. Cell Biol. 2017, 48, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Mohagheghian, E.; Luo, J.; Chen, J.; Chaudhary, G.; Chen, J.; Sun, J.; Ewoldt, R.H.; Wang, N. Quantifying Compressive Forces between Living Cell Layers and within Tissues using Elastic Round Microgels. Nat. Commun. 2018, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Faria, E.C.; Ma, N.; Gazi, E.; Gardner, P.; Brown, M.; Clarke, N.W.; Snook, R.D. Measurement of Elastic Properties of Prostate Cancer Cells using AFM. Analyst 2008, 133, 1498–1500. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.S.; Lee, G.Y.H.; Ong, C.N.; Lim, C.T. AFM Indentation Study of Breast Cancer Cells. Biochem. Biophys. Res. Commun. 2008, 374, 609–613. [Google Scholar] [CrossRef] [PubMed]
- Plodinec, M.; Loparic, M.; Monnier, C.A.; Obermann, E.C.; Zanetti-Dallenbach, R.; Oertle, P.; Hyotyla, J.T.; Aebi, U.; Bentires-Alj, M.; Lim, R.Y.H.; et al. The Nanomechanical Signature of Breast Cancer. Nat. Nanotechnol. 2012, 7, 757–765. [Google Scholar] [CrossRef]
- Tortonese, M.; Barrett, R.C.; Quate, C.F. Atomic Resolution with an Atomic Force Microscope using Piezoresistive Detection. Appl. Phys. Lett. 1993, 62, 834–836. [Google Scholar] [CrossRef]
- Harley, J.A.; Kenny, T.W. High-Sensitivity Piezoresistive Cantilevers Under 1000 Ã… Thick. Appl. Phys. Lett. 1999, 75, 289–291. [Google Scholar] [CrossRef]
- Behrens, I.; Doering, L.; Peiner, E. Piezoresistive Cantilever as Portable Micro Force Calibration Standard. J. Micromech. Microeng. 2003, 13, S177. [Google Scholar] [CrossRef]
- Peiner, E.; Tibrewala, A.; Bandorf, R.; Biehl, S.; Lüthje, H.; Doering, L. Micro Force Sensor with Piezoresistive Amorphous Carbon Strain Gauge. Sens. Actuators A. Phys. 2006, 130, 75–82. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, P.C.Y.; Lin, W. Force Sensing and Control in Micromanipulation. IEEE Trans. Syst. Manand Cybern. Part C 2006, 36, 713–724. [Google Scholar] [CrossRef]
- Onoe, H.; Gel, M.; Hoshino, K.; Matsumoto, K.; Shimoyama, I. Direct Measurement of the Binding Force between Microfabricated Particles and a Planar Surface in Aqueous Solution by Force-Sensing Piezoresistive Cantilevers. Langmuir ACS J. Surf. Colloids 2005, 21, 11251–11261. [Google Scholar] [CrossRef]
- Jaiswal, D.; Cowley, N.; Bian, Z.; Zheng, G.; Claffey, K.P.; Hoshino, K. Stiffness Analysis of 3D Spheroids using Microtweezers. PLoS ONE 2017, 12, e0188346. [Google Scholar] [CrossRef]
- Tao, S.L.; Popat, K.C.; Norman, J.J.; Desai, T.A. Surface Modification of SU-8 for Enhanced Biofunctionality and Nonfouling Properties. Langmuir ACS J. Surf. Colloids 2008, 24, 2631–2636. [Google Scholar] [CrossRef] [PubMed]
- Ingham, P.W. The Power of the Zebrafish for Disease Analysis. Hum. Mol. Genet. 2009, 18, R112. [Google Scholar] [CrossRef]
- Seto, S.; Kiat, H.; Lee, S.M.Y.; Bensoussan, A.; Sun, Y.; Hoi, M.P.M.; Chang, D. Zebrafish Models of Cardiovascular Diseases and their Applications in Herbal Medicine Research. Eur. J. Pharmacol. 2015, 768, 77–86. [Google Scholar] [CrossRef]
- Kimmel, C.B.; Ballard, W.W.; Kimmel, S.R.; Ullmann, B.; Schilling, T.F. Stages of Embryonic Development of the Zebrafish. Dev. Dyn. Off. Publ. Am. Assoc. Anat. 1995, 203, 253–310. [Google Scholar] [CrossRef]
- Stickney, H.L.; Barresi, M.J.; Devoto, S.H. Somite Development in Zebrafish. Dev. Dyn. Off. Publ. Am. Assoc. Anat. 2000, 219, 287–303. [Google Scholar] [CrossRef]
- Liu, M.; Sun, J.; Chen, Q. Influences of Heating Temperature on Mechanical Properties of Polydimethylsiloxane. Sens. Actuators A. Phys. 2009, 151, 42–45. [Google Scholar] [CrossRef]
- Liu, M.; Sun, J.; Sun, Y.; Bock, C.; Chen, Q. Thickness-Dependent Mechanical Properties of Polydimethylsiloxane Membranes. J. Micromech. Microeng. 2009, 19, 035028. [Google Scholar] [CrossRef]
- Khanafer, K.; Duprey, A.; Schlicht, M.; Berguer, R. Effects of Strain Rate, Mixing Ratio, and Stress-Strain Definition on the Mechanical Behavior of the Polydimethylsiloxane (PDMS) Material as Related to its Biological Applications. Biomed. Microdevices 2009, 11, 503–508. [Google Scholar] [CrossRef] [PubMed]
- Hocheng, H.; Chen, C.; Chou, Y.; Lin, C. Study of Novel Electrical Routing and Integrated Packaging on Bio-Compatible Flexible Substrates. Microsyst. Technol. 2010, 16, 423–430. [Google Scholar] [CrossRef]
- Engineering ToolBox, Young’s Modulus—Tensile and Yield Strength for common Materials. Available online: https://Www.Engineeringtoolbox.Com/Young-Modulus-d_417.Html (accessed on 19 December 2018).
- Lam, R.H.W.; Weng, S.; Lu, W.; Fu, J. Live-Cell Subcellular Measurement of Cell Stiffness using a Microengineered Stretchable Micropost Array Membrane. Integr. Biol. Quant. Biosci. Nano Macro 2012, 4, 1289–1298. [Google Scholar] [CrossRef]
- Canović, E.; Seidl, D.; Polio, S.; Oberai, A.; Barbone, P.; Stamenović, D.; Smith, M. Biomechanical Imaging of Cell Stiffness and Prestress with Subcellular Resolution. Biomech. Model. Mechanobiol. 2014, 13, 665–678. [Google Scholar] [CrossRef]
- Kamgoué, A.; Ohayon, J.; Tracqui, P. Estimation of Cell Young’s Modulus of Adherent Cells Probed by Optical and Magnetic Tweezers: Influence of Cell Thickness and Bead Immersion. J. Biomech. Eng. 2007, 129, 523–530. [Google Scholar] [CrossRef]
- Lekka, M.; Laidler, P.; Gil, D.; Lekki, J.; Stachura, Z.; Hrynkiewicz, A.Z. Elasticity of Normal and Cancerous Human Bladder Cells Studied by Scanning Force Microscopy. Eur. Biophys. J. 1999, 28, 312–316. [Google Scholar] [CrossRef]




| Length (mm) | Width (mm) | Thickness (mm) | |
|---|---|---|---|
| Average | 3.47 | 0.261 | 0.183 |
| Standard deviation | 0.16 | 0.015 | 0.044 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomizawa, Y.; Dixit, K.; Daggett, D.; Hoshino, K. Biocompatible Cantilevers for Mechanical Characterization of Zebrafish Embryos using Image Analysis. Sensors 2019, 19, 1506. https://doi.org/10.3390/s19071506
Tomizawa Y, Dixit K, Daggett D, Hoshino K. Biocompatible Cantilevers for Mechanical Characterization of Zebrafish Embryos using Image Analysis. Sensors. 2019; 19(7):1506. https://doi.org/10.3390/s19071506
Chicago/Turabian StyleTomizawa, Yuji, Krishna Dixit, David Daggett, and Kazunori Hoshino. 2019. "Biocompatible Cantilevers for Mechanical Characterization of Zebrafish Embryos using Image Analysis" Sensors 19, no. 7: 1506. https://doi.org/10.3390/s19071506
APA StyleTomizawa, Y., Dixit, K., Daggett, D., & Hoshino, K. (2019). Biocompatible Cantilevers for Mechanical Characterization of Zebrafish Embryos using Image Analysis. Sensors, 19(7), 1506. https://doi.org/10.3390/s19071506





