Exploiting Impact of Hardware Impairments in NOMA: Adaptive Transmission Mode in FD/HD and Application in Internet-of-Things
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions and Organization
- Considering the cooperative relaying NOMA system as in [34], the outage performance and ergodic capacity for the near user and the far users under impacts of residual hardware impairment (RHI) are examined under Rayleigh fading environment.
- We also propose two adaptive schemes considering the trade-offs between FD and HD NOMA relaying and between NOMA and OMA FD relaying, respectively.
- Comparison study is performed for two typical users, i.e., near user and far user in NOMA, for both outage performance and ergodic capacity. These performance metric are employed by controlling level of hardware noise, residual interference due to FD mode to adapt requirements of wireless system.
- Extensive Monte Carlo simulation results are presented in order to corroborate the derived exact and asymptotic expressions.
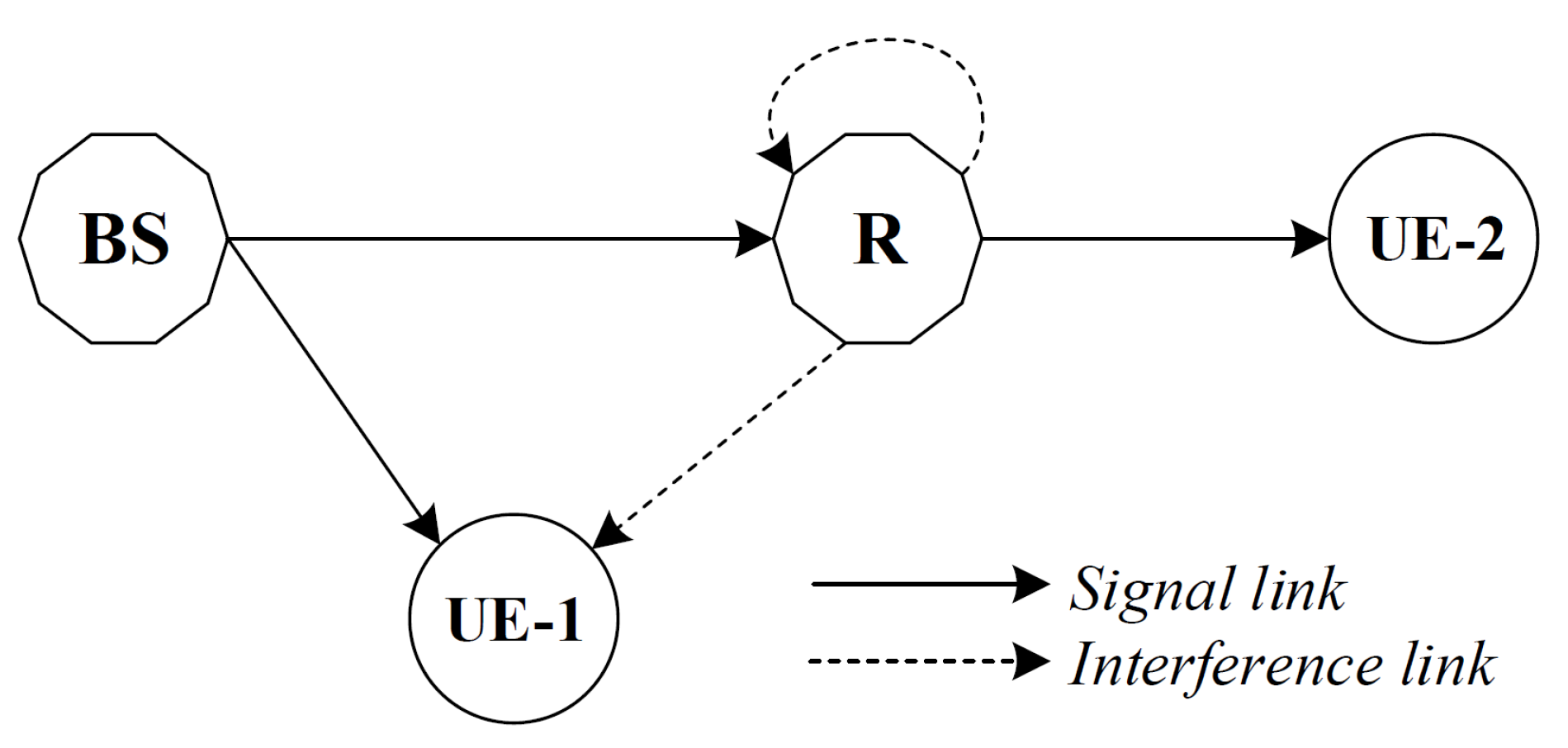
2. System Model
2.1. Transceiver Hardware Impairment Model
2.2. Signal Model for NOMA FD Relaying Networks
2.2.1. UE–1 Analysis
2.2.2. UE–2 Analysis
3. NOMA with Full-Duplex Cooperative Relaying System
3.1. Outage Probability Analysis
3.1.1. Outage Probability of UE-1 in FD Mode
3.1.2. Outage Probability of UE–2 in FD Mode
3.1.3. Overall System Outage Probability of FD Mode
3.2. Ergodic Capacity Analysis
4. NOMA with Half-Duplex Cooperative Relaying System
4.1. Outage Probability Analysis for HD Mode
4.1.1. Outage Probability of UE–1 for HD Network
4.1.2. Outage Probability of UE–2 in HD Mode
4.1.3. Overall System Outage Probability of HD Mode
4.2. Ergodic Capacity
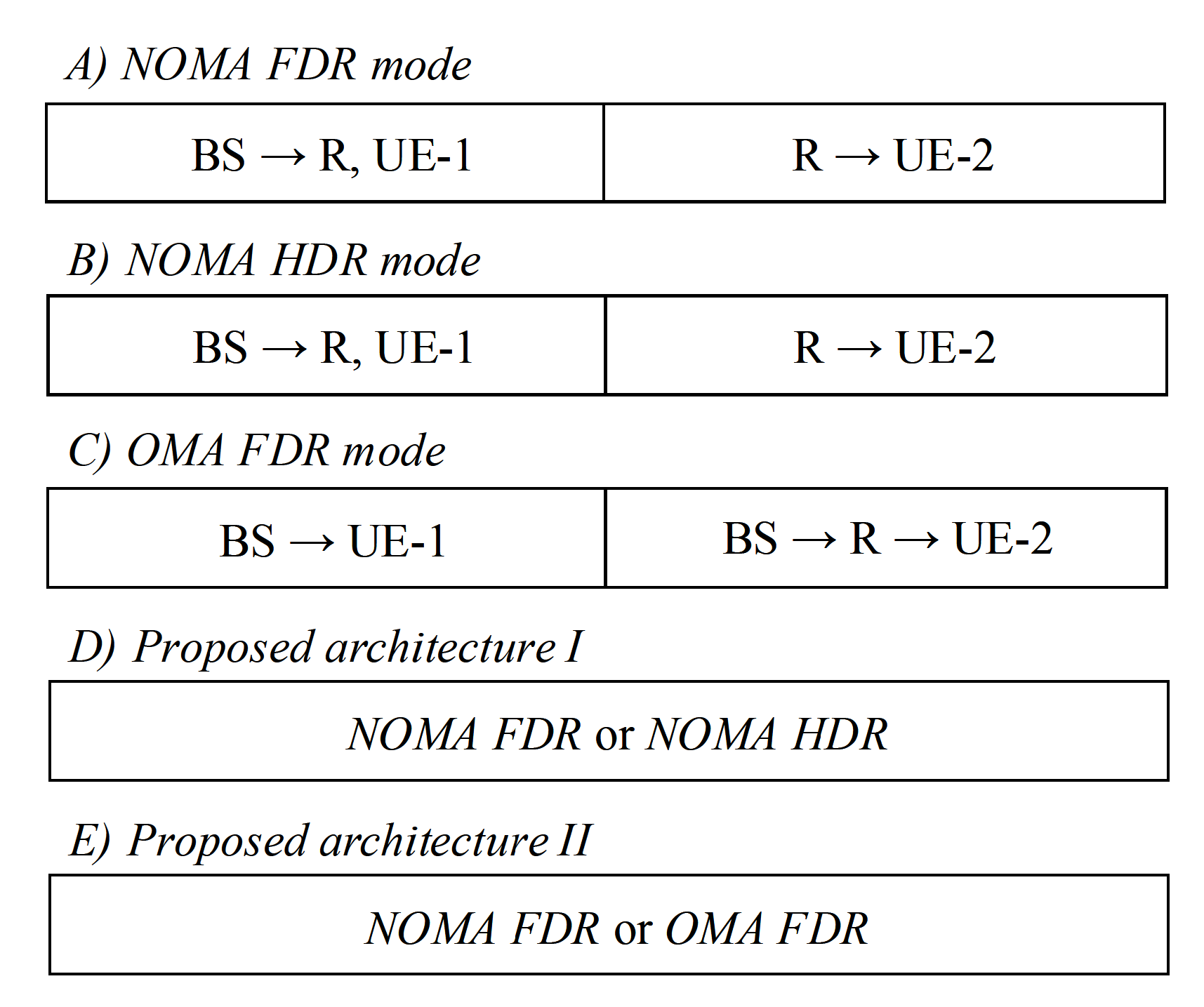
5. Adaptive Transmission Mode
5.1. Architecture 1: FD-HD Trade-Off for Cooperative NOMA Network
5.1.1. Outage Probability of UE–1 in A-I Scheme
5.1.2. Outage Probability of UE–2 in A-I Scheme
5.1.3. Overall system Outage of A-I Scheme
5.2. Architecture 2: NOMA-OMA Trade-Off for Cooperative FD Network
5.2.1. OMA FD Relaying Scheme
5.2.2. Architecture II
5.2.3. Outage Probability of UE–1 in A-II Scheme
5.2.4. Outage Probability of U–2 in A-II Scheme
5.2.5. Overall system Outage of A-II scheme
6. Simulation Results and Discussions
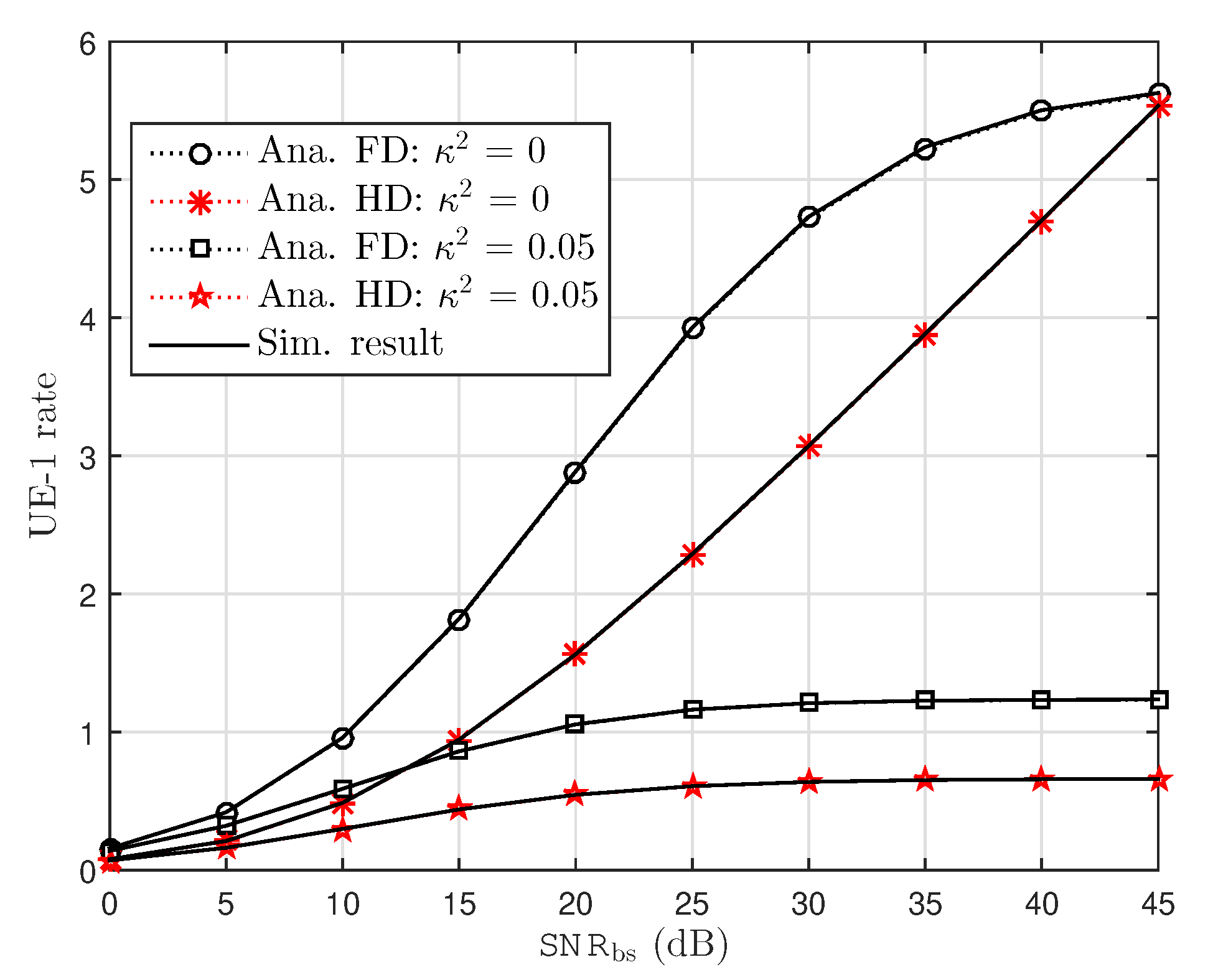
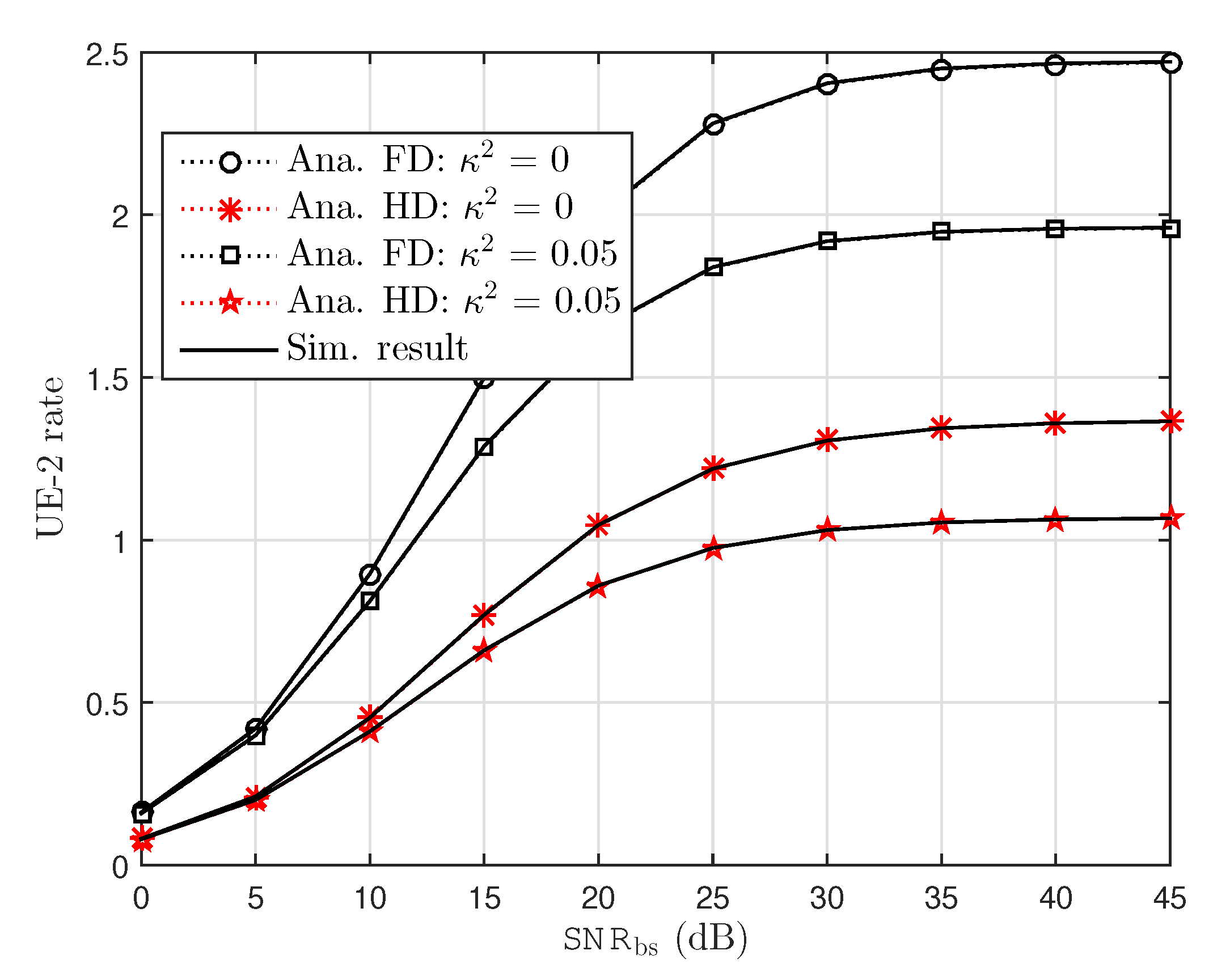
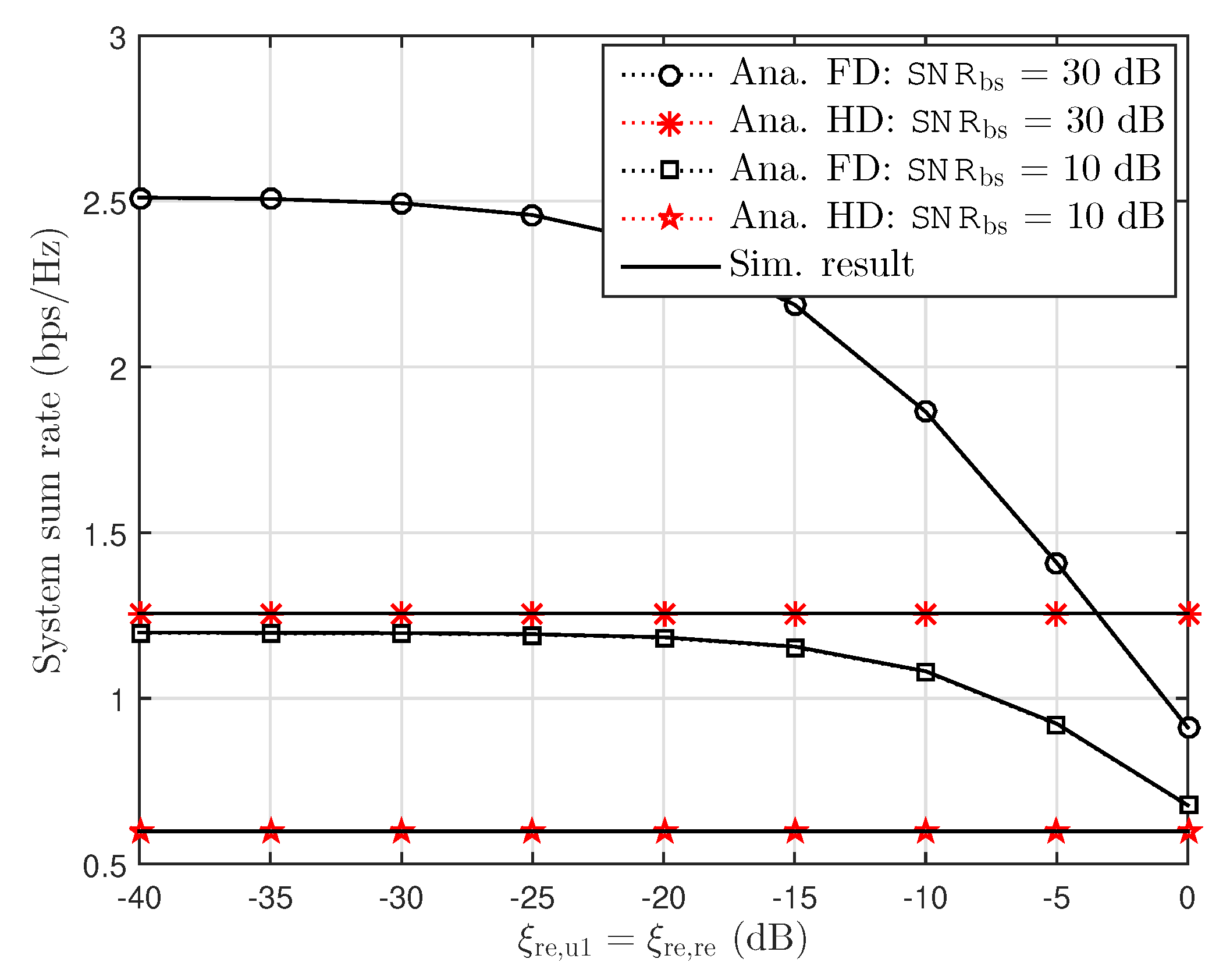
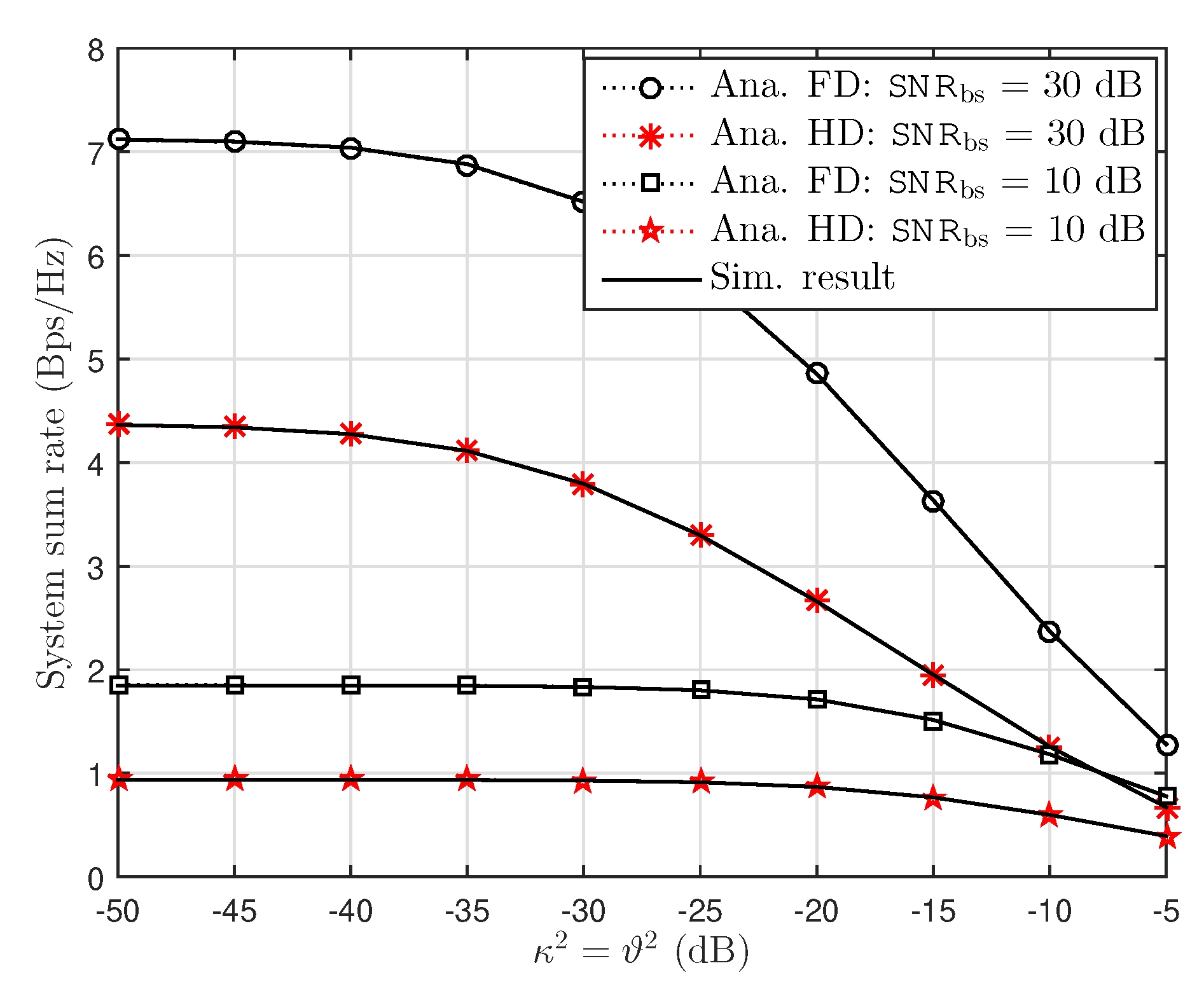
6.1. Ergodic Capacity Examinations
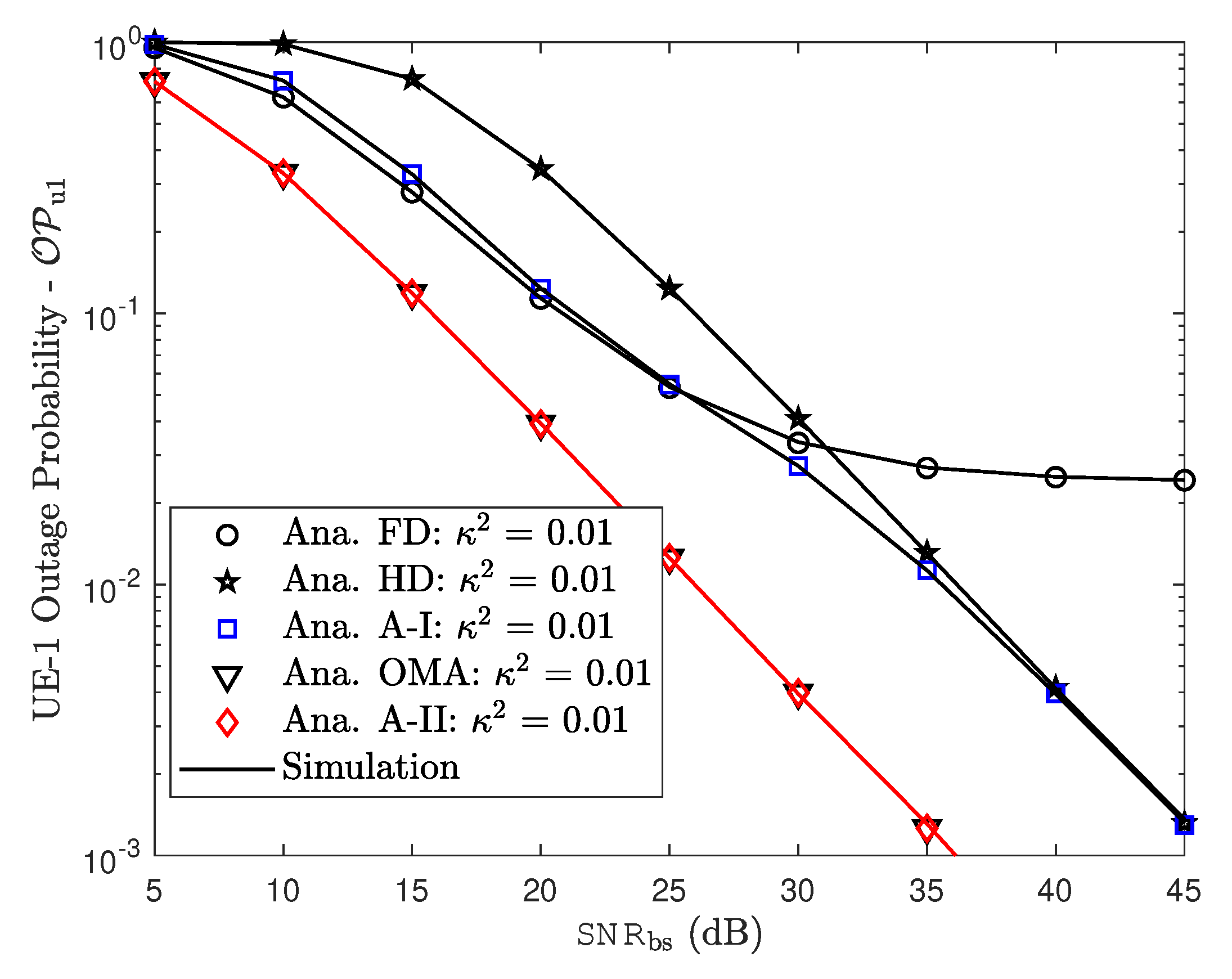
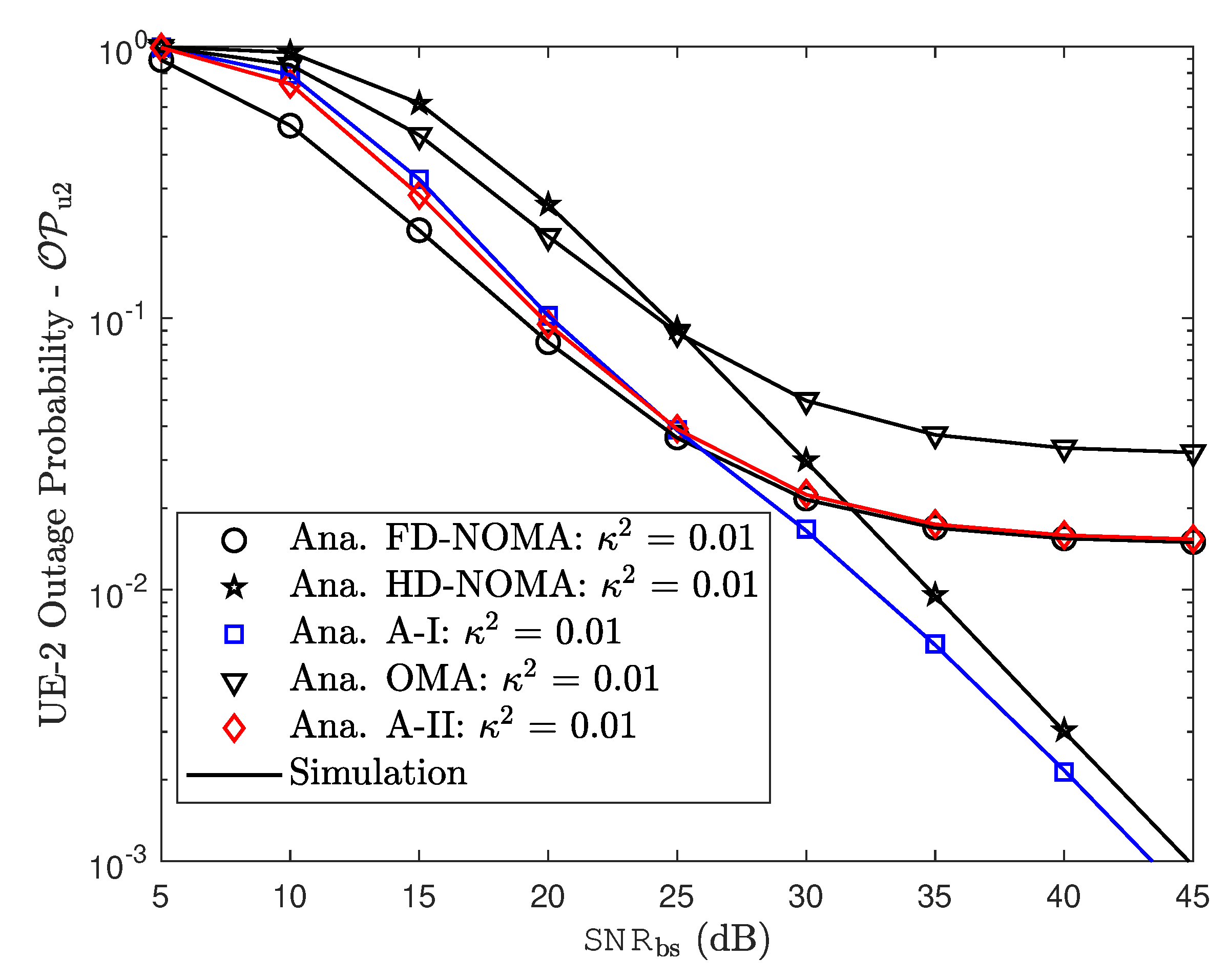
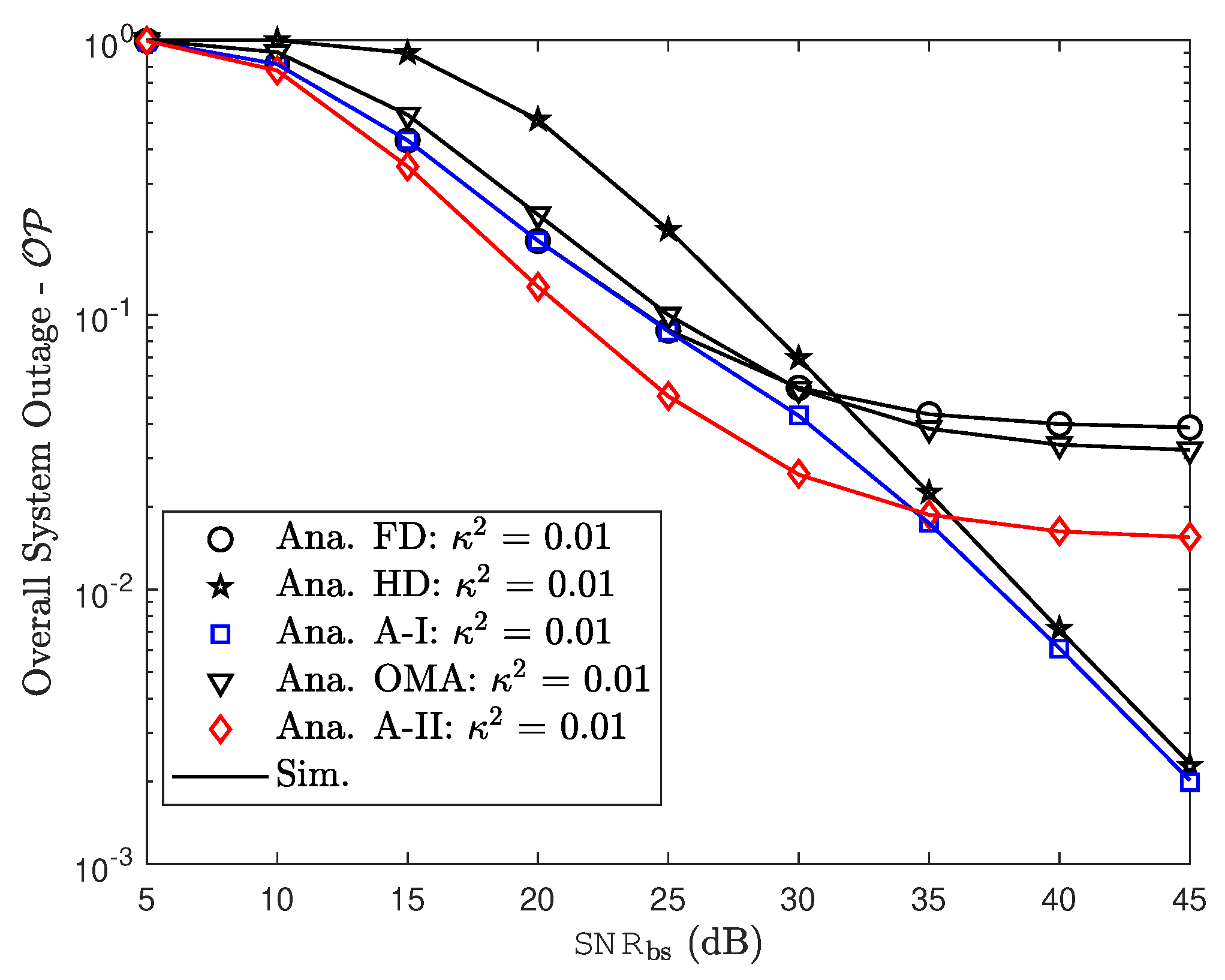
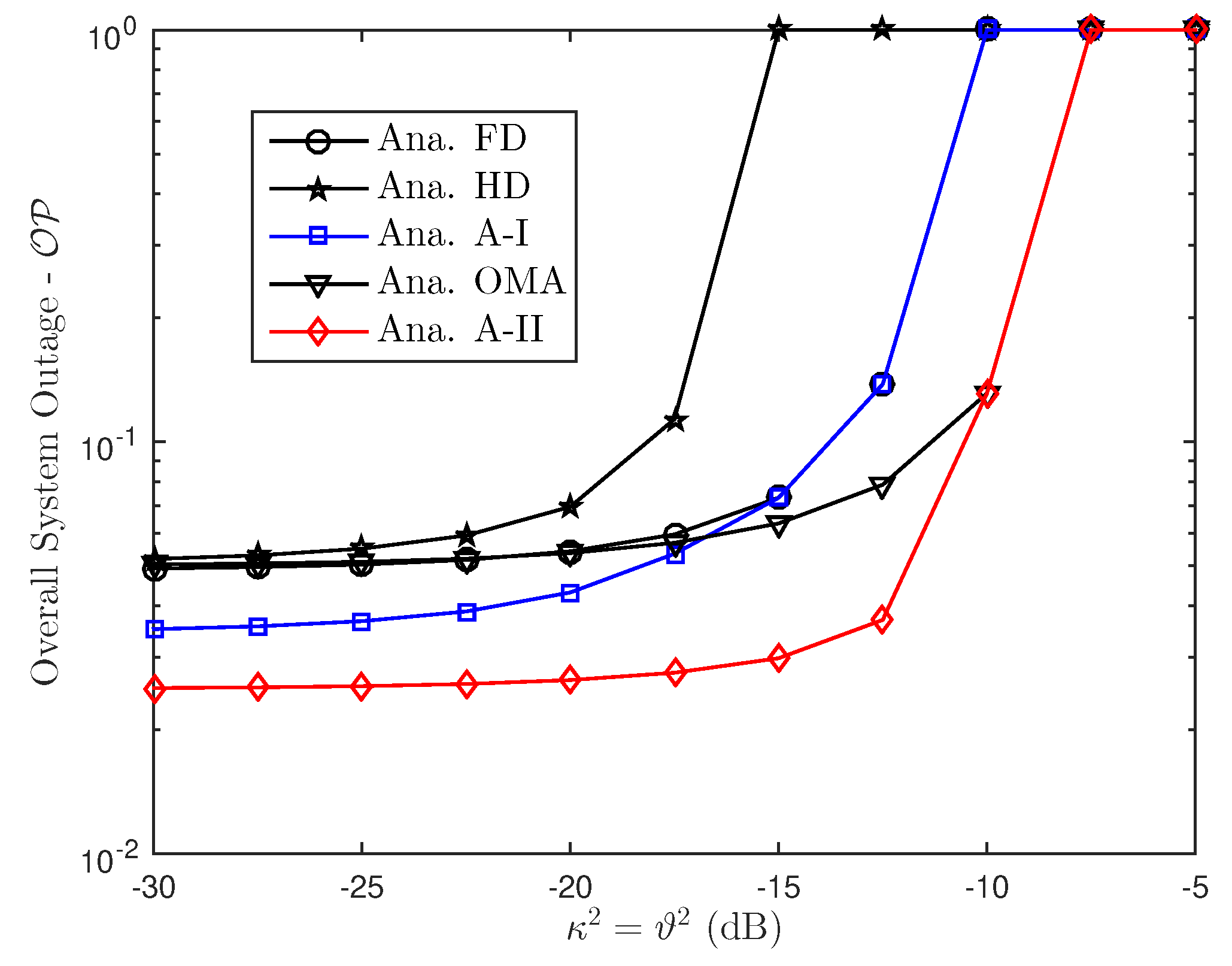
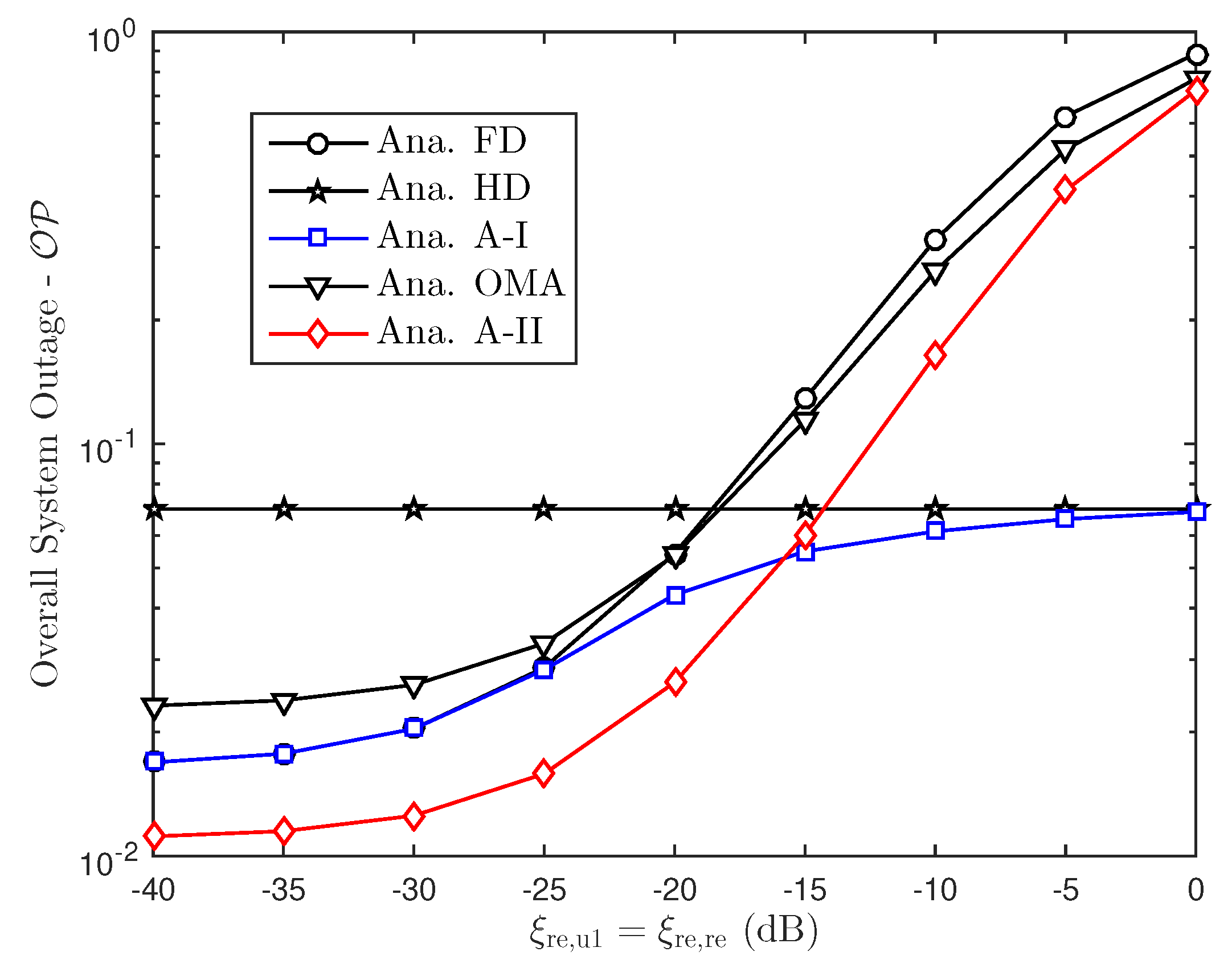
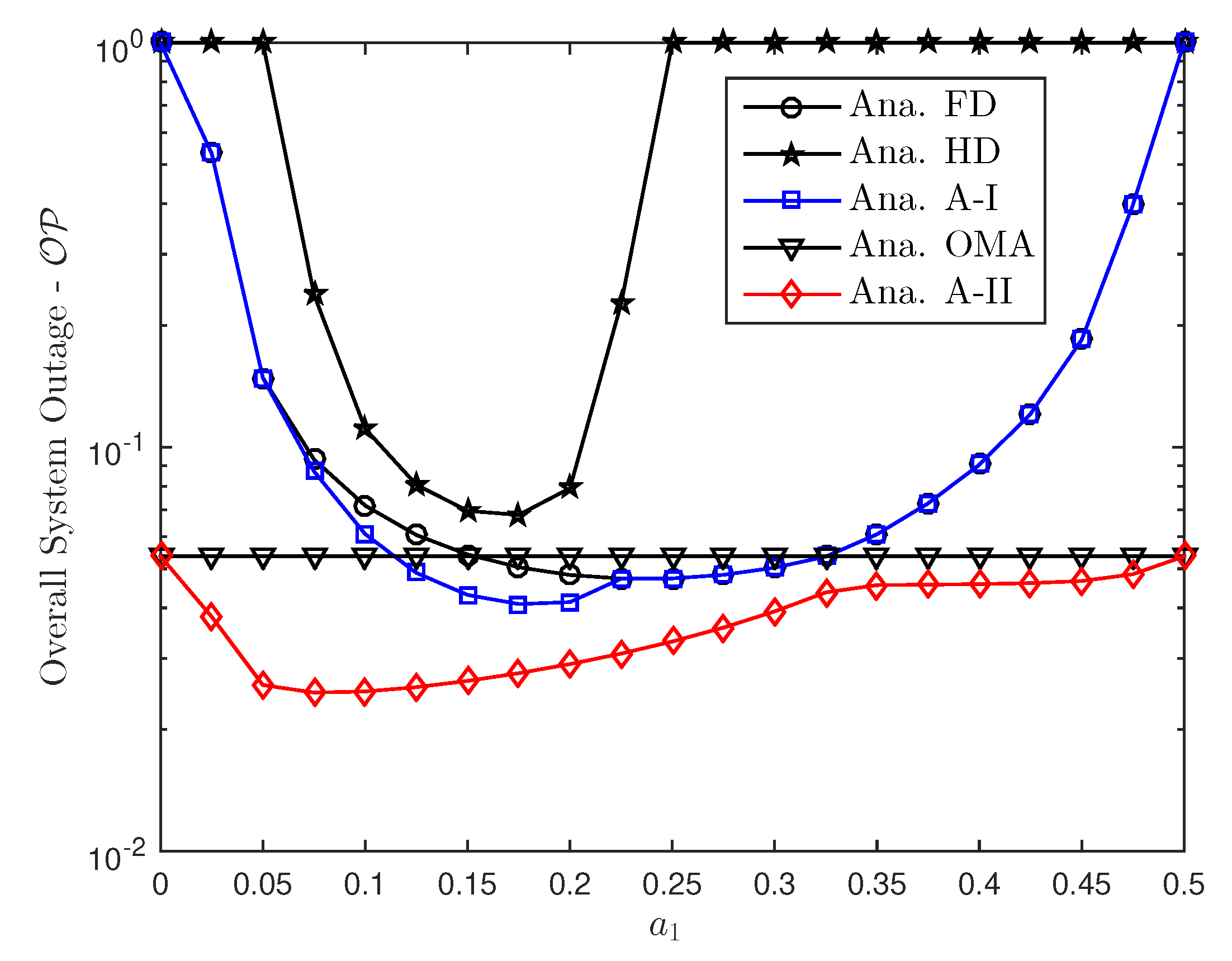
6.2. Outage Probability Examinations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Lemma 1
Appendix B. Proof of Proposition 1
Appendix C. Proof of Proposition 2
Appendix D. Proof of Proposition 3
Appendix D.1. Ergodic Capacity of UE–1
Appendix D.2. Ergodic Capacity of UE–2
Appendix E. Proof of Proposition 4
Appendix F. Proof of Proposition 5
References
- Chen, J.; Yang, L.; Alouini, M. Performance analysis of cooperative NOMA schemes in spatially random relaying networks. IEEE Access. 2018, 6, 33159–33168. [Google Scholar] [CrossRef]
- Do, D.-T.; Le, C.-B. Application of NOMA in Wireless System with Wireless Power Transfer Scheme: Outage and Ergodic Capacity Performance Analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef] [PubMed]
- Do, D.-T.; Van Nguyen, M.-S.; Hoang, T.-A.; Voznak, M. NOMA-Assisted Multiple Access Scheme for IoT Deployment: Relay Selection Model and Secrecy Performance Improvement. Sensors 2019, 19, 736. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Poor, H.V. Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Do, D.-T.; Nguyen, H.-S.; Voznak, M.; Nguyen, T.-S. Wireless powered relaying networks under imperfect channel state information: system performance and optimal policy for instantaneous rate. Radioengineering 2017, 26, 869–877. [Google Scholar] [CrossRef]
- Kieu, T.N.; Do, D.-T.; Nguyen, X.-X.; Nhat, T.N.; Duy, H.H. Wireless information and power transfer for full duplex relaying networks: performance analysis. In AETA 2015: Recent Advances in Electrical Engineering and Related Sciences; Duy, V.H., Dao, T.T., Zelinka, I., Choi, H.-S., Chadli, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 53–62. [Google Scholar]
- Wang, J.; Peng, Q.; Huang, Y.; Wang, H.; You, X. Convexity of weighted 345 sum rate maximization in NOMA systems. IEEE Signal Process. Lett. 2017, 24, 1323–1327. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-duplex device-to-device- aided cooperative non-orthogonal multiple access. IEEE Trans. Veh. Technol. 2017, 66, 4467–4471. [Google Scholar] [CrossRef]
- Chen, S.; Ren, B.; Gao, Q.; Kang, S.; Sun, S.; Niu, K. Pattern Division Multiple Access—A Novel Non-orthogonal Multiple Access for Fifth-Generation Radio Networks. IEEE Trans.Veh. Technol. 2017, 66, 3185–3196. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Zheng, T.; Yang, Q. Energy-Efficient Transmission Design in Non-orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2017, 66, 2852–2857. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Elkashlan, M.; Yuan, J. Non-orthogonal multiple access in large-scale underlay cognitive radio networks. IEEE Trans. Veh. Technol. 2016, 65, 10152–10157. [Google Scholar] [CrossRef]
- Lv, L.; Ni, Q.; Ding, Z.; Chen, J. Application of non-orthogonal multiple access in cooperative spectrum-sharing networks over Nakagami- m fading channels. IEEE Trans. Veh. Technol. 2017, 66, 5506–5511. [Google Scholar] [CrossRef]
- Ding, Z.; Dai, H.; Poor, H.V. Relay selection for cooperative NOMA. IEEE Wireless Commun. Lett. 2016, 5, 416–419. [Google Scholar] [CrossRef]
- Deng, D.; Fan, L.; Lei, X.; Tan, W.; Xie, D. Joint user and relay selection for cooperative NOMA networks. IEEE Access. 2017, 5, 20220–20227. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Gao, Y.; Hanzo, L. Enhancing the physical layer security of non-orthogonal multiple access in large-scale networks. IEEE Trans. Wirel. Commun. 2016, 16, 1656–1672. [Google Scholar] [CrossRef]
- Sharma, P.; Garg, P. Achieving high data rates through full duplex relaying in multicell environments. Trans. Emerging Telecommun. Technol. 2016, 27, 111–121. [Google Scholar] [CrossRef]
- Nguyen, X.-X.; Do, D.-T. Optimal Power Allocation and Throughput Performance of Full-Duplex DF Relaying Networks with Wireless Power Transfer-Aware Channel. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 152. [Google Scholar] [CrossRef]
- Nguyen, X.-X.; Do, D.-T. Maximum harvested energy policy in full-duplex relaying networks with SWIPT. Int. J. Commun. Syst. 2017, 30, e3359. [Google Scholar] [CrossRef]
- Sharma, P.K.; Garg, P. Performance analysis of full duplex decode-and-forward cooperative relaying over Nakagami-m fading channels. Trans. Emerg. Telecommun. Technol. 2014, 25, 905–913. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. On the coexistence between full-duplex and NOMA. IEEE Wirel. Commun. Lett. 2018, 7, 692–695. [Google Scholar] [CrossRef]
- Shahab, M.B.; Shin, S.Y. Time shared half/full-duplex cooperative NOMA with clustered cell edge users. IEEE Wireless Commun. Lett. 2018, 22, 1794–1797. [Google Scholar] [CrossRef]
- Sun, Y.; Ng, D.W.K.; Ding, Z.; Schober, R. Optimal joint power and subcarrier allocation for full-duplex multicarrier non-orthogonal multiple access systems. IEEE Trans. Commun. 2017, 65, 1077–1091. [Google Scholar] [CrossRef]
- Elbamby, M.S.; Bennis, M.; Saad, W.; Debbah, M.; Latva-ahom, M. Resource optimization and power allocation in in-band full duplex-enabled non-orthogonal multiple access networks. IEEE J. Sel. Areas Commun. 2017, 35, 2860–2873. [Google Scholar] [CrossRef]
- Schenk, T. RF Imperfections in High-Rate Wireless Systems: Impact and Digital Compensation, 1st ed.; Springer: Cham, Switzerland, 2008. [Google Scholar]
- Do, D.-T. Energy-aware two-way relaying networks under imperfect hardware: optimal throughput design and analysis. Telecommun. Syst. 2016, 62, 449–459. [Google Scholar] [CrossRef]
- Li, J.; Matthaiou, M.; Svensson, T. I/Q imbalance in two-way af relaying. IEEE Trans. Commun. 2014, 62, 2271–2285. [Google Scholar] [CrossRef]
- Do, D.-T. Power Switching Protocol for Two-way Relaying Network under Hardware Impairments. Radioengineering 2015, 24, 765–771. [Google Scholar] [CrossRef]
- Maletic, N.; Cabarkapa, M.; Neskovic, N.; Budimir, D. Hardware impairments impact on fixed-gain AF relaying performance in Nakagami-m fading. Electron. Lett. 2016, 52, 121–122. [Google Scholar] [CrossRef]
- Balti, E.; Guizani, M. Impact of Non-Linear High-Power Amplifiers on Cooperative Relaying Systems. IEEE Trans. Commun. 2017, 65, 4163–4175. [Google Scholar] [CrossRef]
- Selim, B.; Muhaidat, S.; Sofotasios, P.C.; Sharif, B.S.; Stouraitis, T.; Karagiannidis, G.K.; Al-Dhahir, N. Performance analysis of non-orthogonal multiple access under I/Q imbalance. IEEE Access. 2018, 6, 18453–18468. [Google Scholar] [CrossRef]
- Ding, F.; Wang, H.; Zhang, S.; Dai, M. Impact of residual hardware impairments on non-orthogonal multiple access based amplify-and-forward relaying networks. IEEE Access. 2018, 6, 15117–15131. [Google Scholar] [CrossRef]
- Nguyen, T.-L.; Do, D.-T. Exploiting Impacts of Intercell Interference on SWIPT-assisted Non-orthogonal Multiple Access. Wireless Commun. Mob. Comp. 2018, 2018, 2525492. [Google Scholar] [CrossRef]
- Kader, M.F.; Shin, S.Y. Coordinated direct and relay transmission using uplink NOMA. IEEE‘ Commun. Lett. 2018, 7, 400–403. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, Z. Non-orthogonal multiple access with cooperative full- duplex relaying. IEEE Commun. Lett. 2016, 20, 2478–2481. [Google Scholar] [CrossRef]
- Matthaiou, M.; Papadogiannis, A.; Bjornson, E.; Debbah, M. Two-way relaying under the presence of relay transceiver hardware impairments. IEEE Commun. Lett. 2013, 17, 1136–1139. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, C.-B.; Do, D.-T.; Voznak, M. Exploiting Impact of Hardware Impairments in NOMA: Adaptive Transmission Mode in FD/HD and Application in Internet-of-Things. Sensors 2019, 19, 1293. https://doi.org/10.3390/s19061293
Le C-B, Do D-T, Voznak M. Exploiting Impact of Hardware Impairments in NOMA: Adaptive Transmission Mode in FD/HD and Application in Internet-of-Things. Sensors. 2019; 19(6):1293. https://doi.org/10.3390/s19061293
Chicago/Turabian StyleLe, Chi-Bao, Dinh-Thuan Do, and Miroslav Voznak. 2019. "Exploiting Impact of Hardware Impairments in NOMA: Adaptive Transmission Mode in FD/HD and Application in Internet-of-Things" Sensors 19, no. 6: 1293. https://doi.org/10.3390/s19061293
APA StyleLe, C.-B., Do, D.-T., & Voznak, M. (2019). Exploiting Impact of Hardware Impairments in NOMA: Adaptive Transmission Mode in FD/HD and Application in Internet-of-Things. Sensors, 19(6), 1293. https://doi.org/10.3390/s19061293






