Electrical Properties of Two-Dimensional Materials Used in Gas Sensors
Abstract
1. Introduction
2. Two-Dimensional Materials Used in Gas Sensors
2.1. Two-Dimensional Materials for Gas Sensing
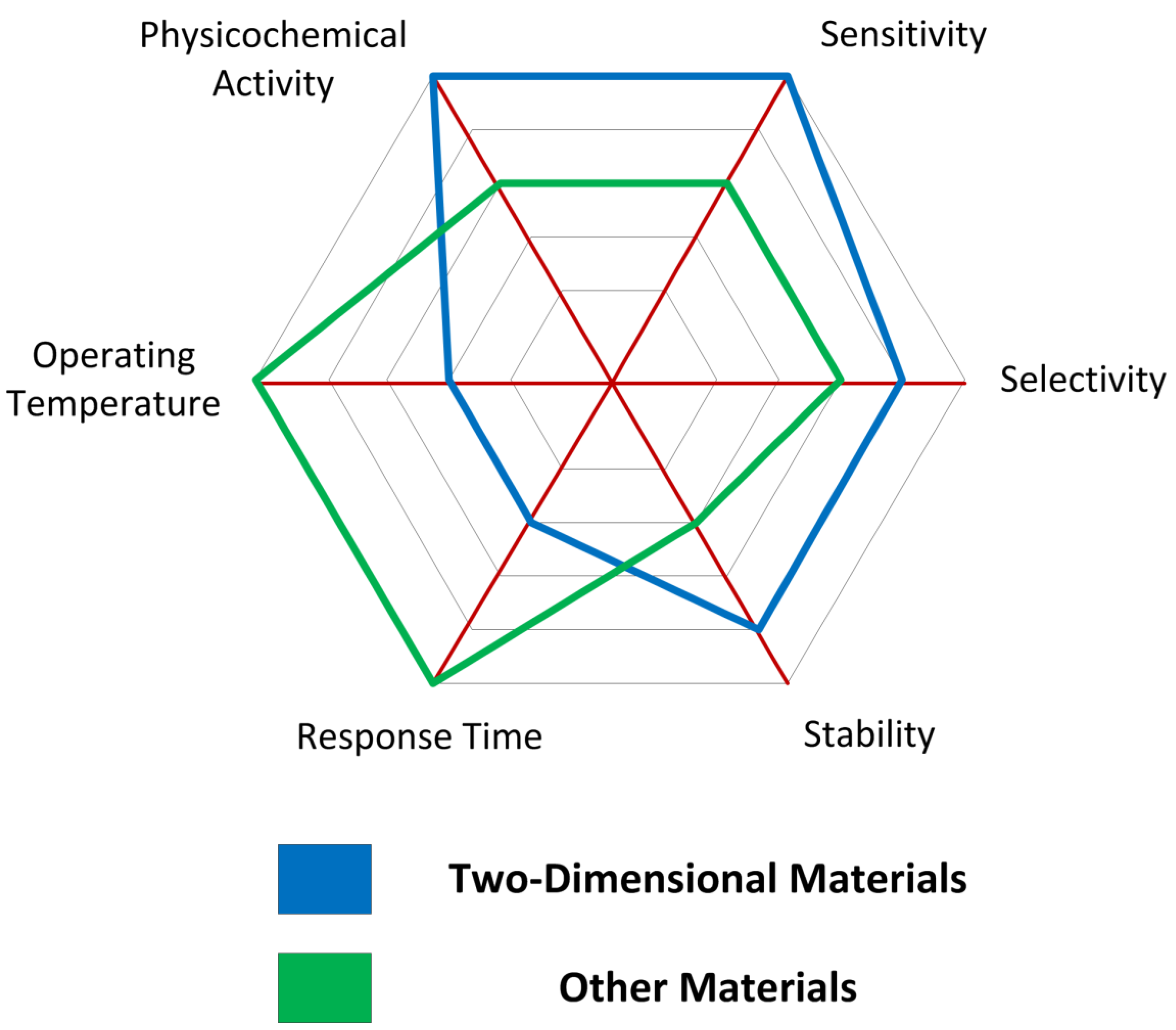
2.2. Advantages of Two-Dimensional Materials for Gas Sensing
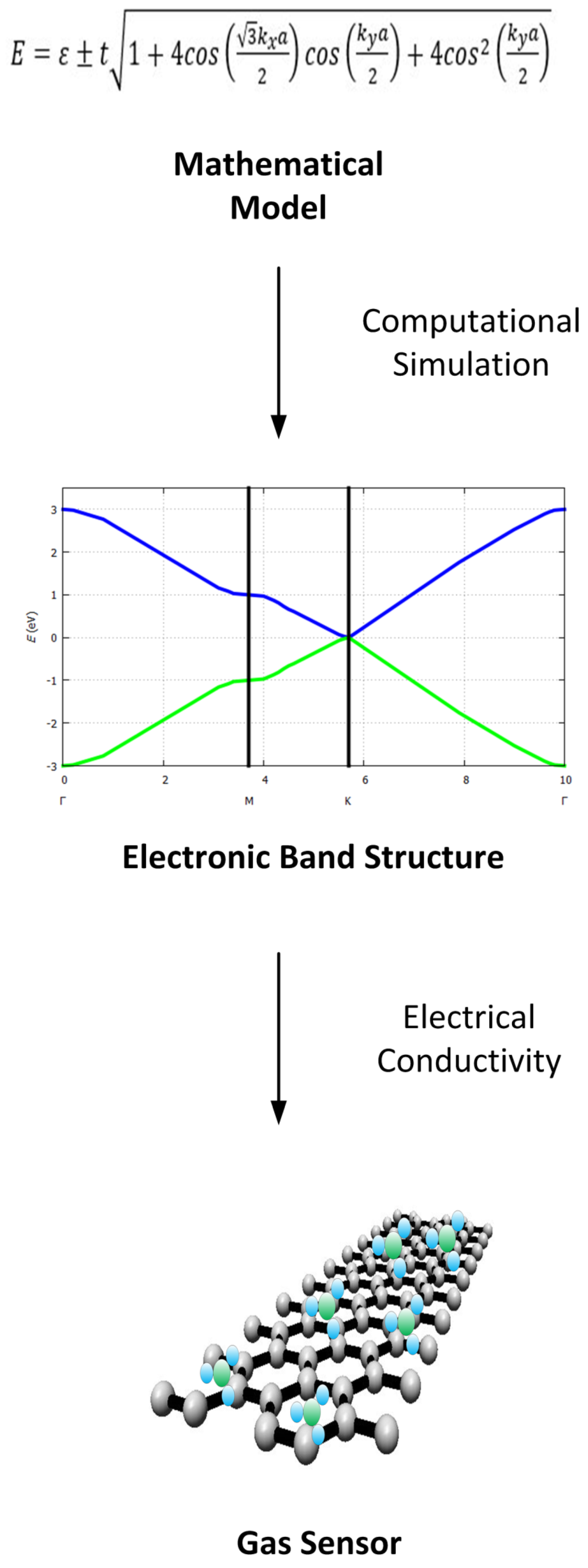
3. Electronic Band Structure for Two-Dimensional Materials
3.1. First Brillouin Zone of Two-Dimensional Materials
3.1.1. First Brillouin Zone for materials with Hexagonal Crystalline Lattices
3.1.2. First Brillouin Zone for Materials with Orthorhombic Crystalline Lattices
3.1.3. First Brillouin Zone for Materials with Triclinic Crystalline Lattices
3.1.4. First Brillouin Zone for Materials with Monoclinic Crystalline Lattices
3.2. Tight-Binding Model for Two-Dimensional Materials
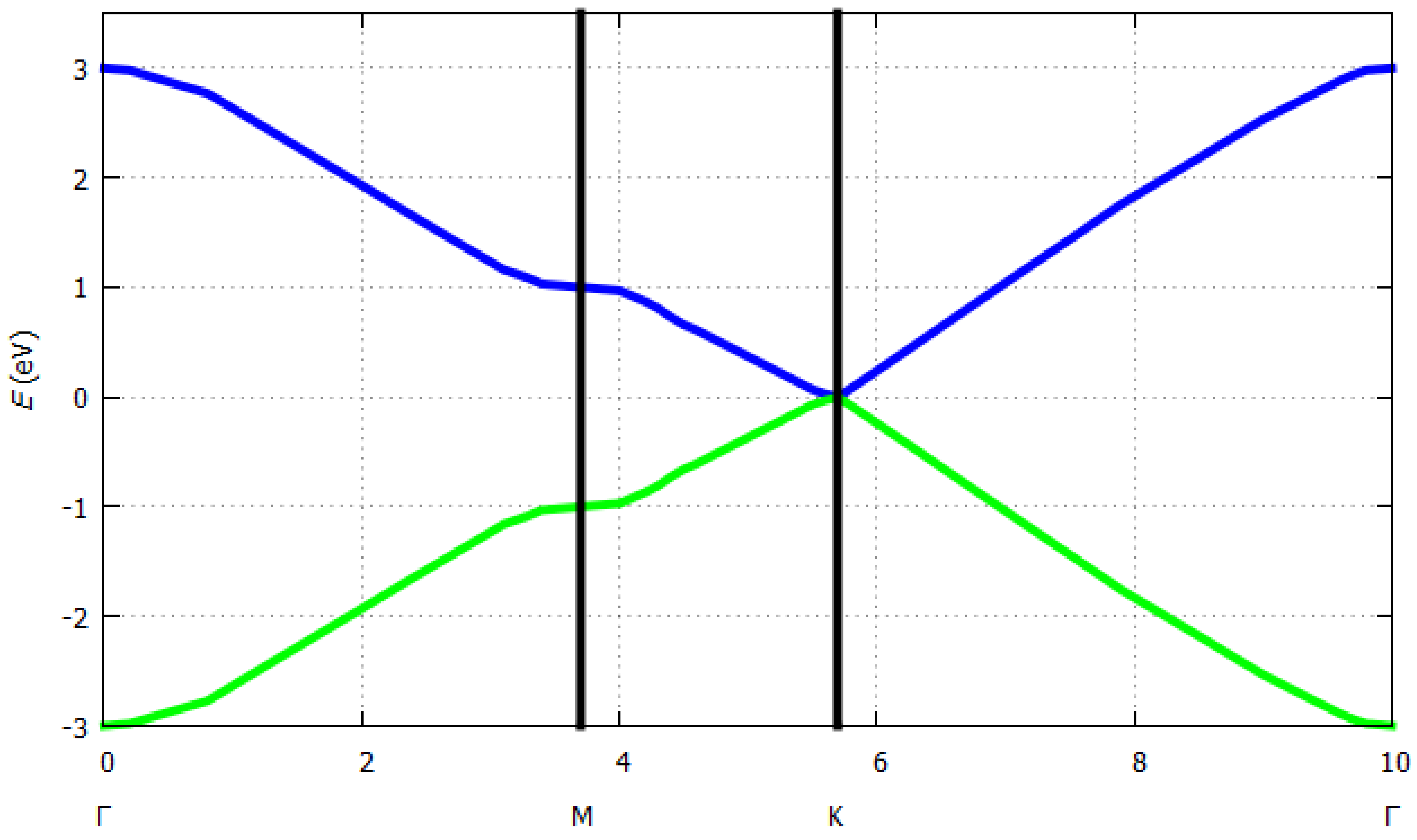
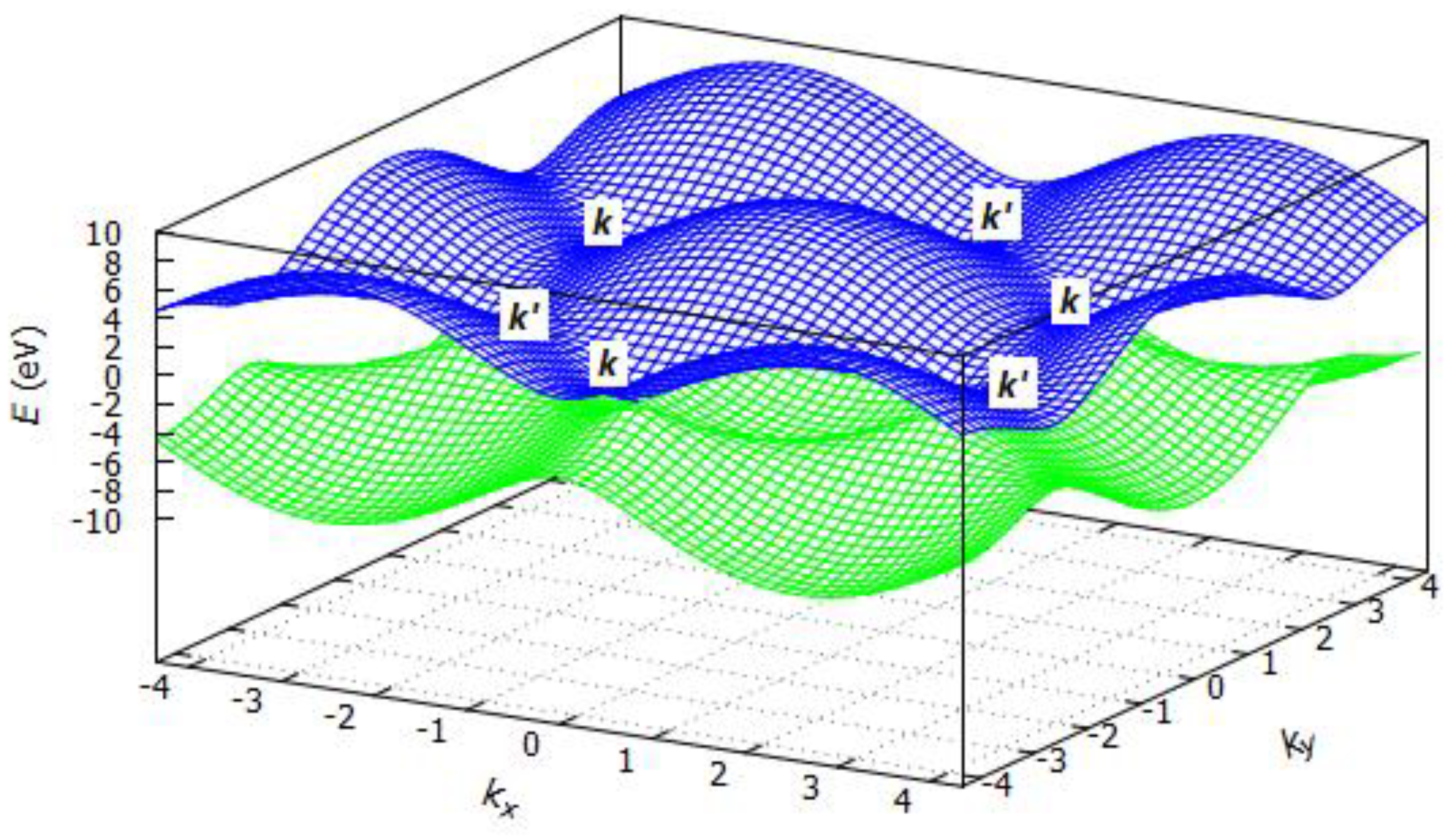
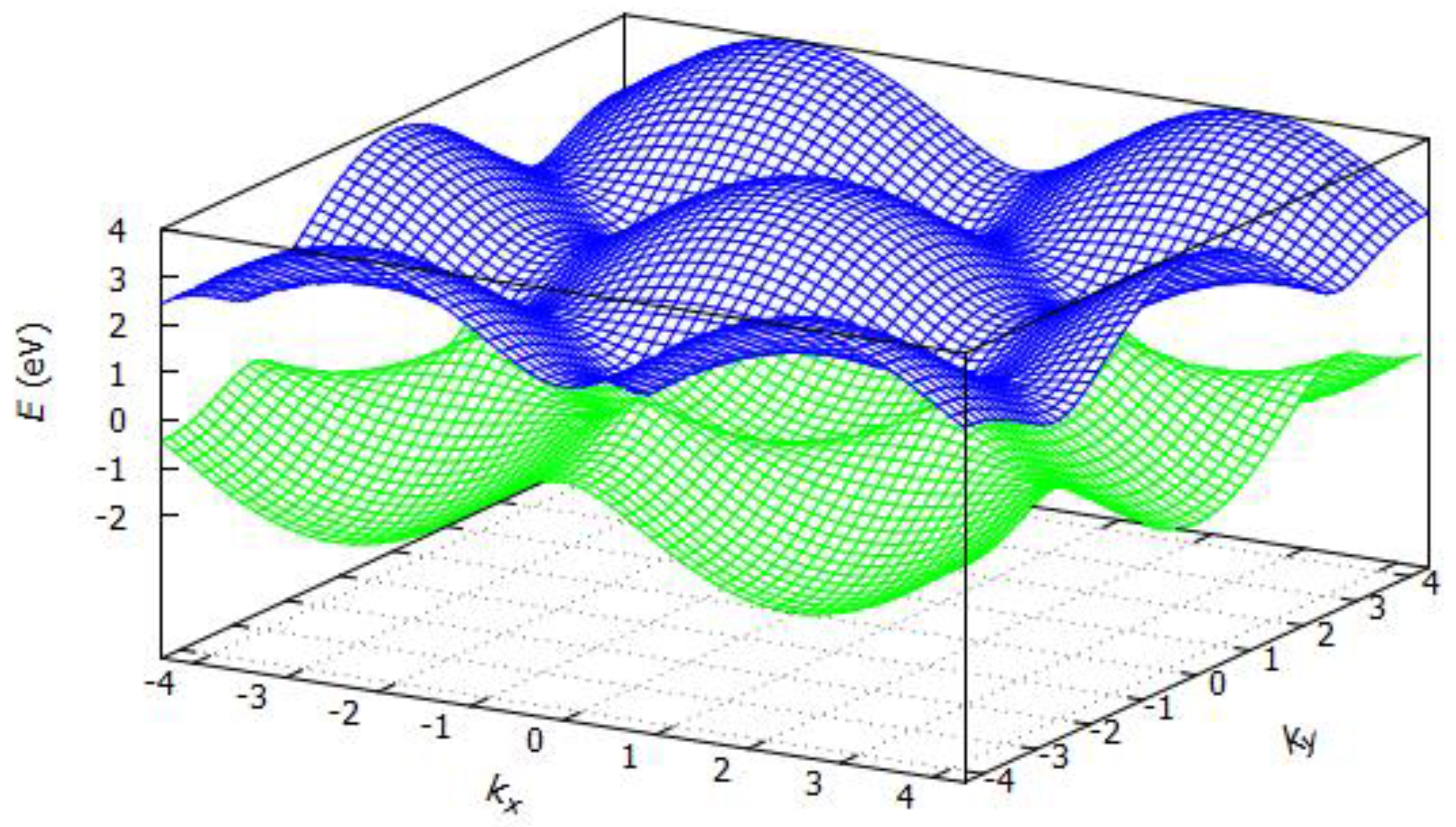
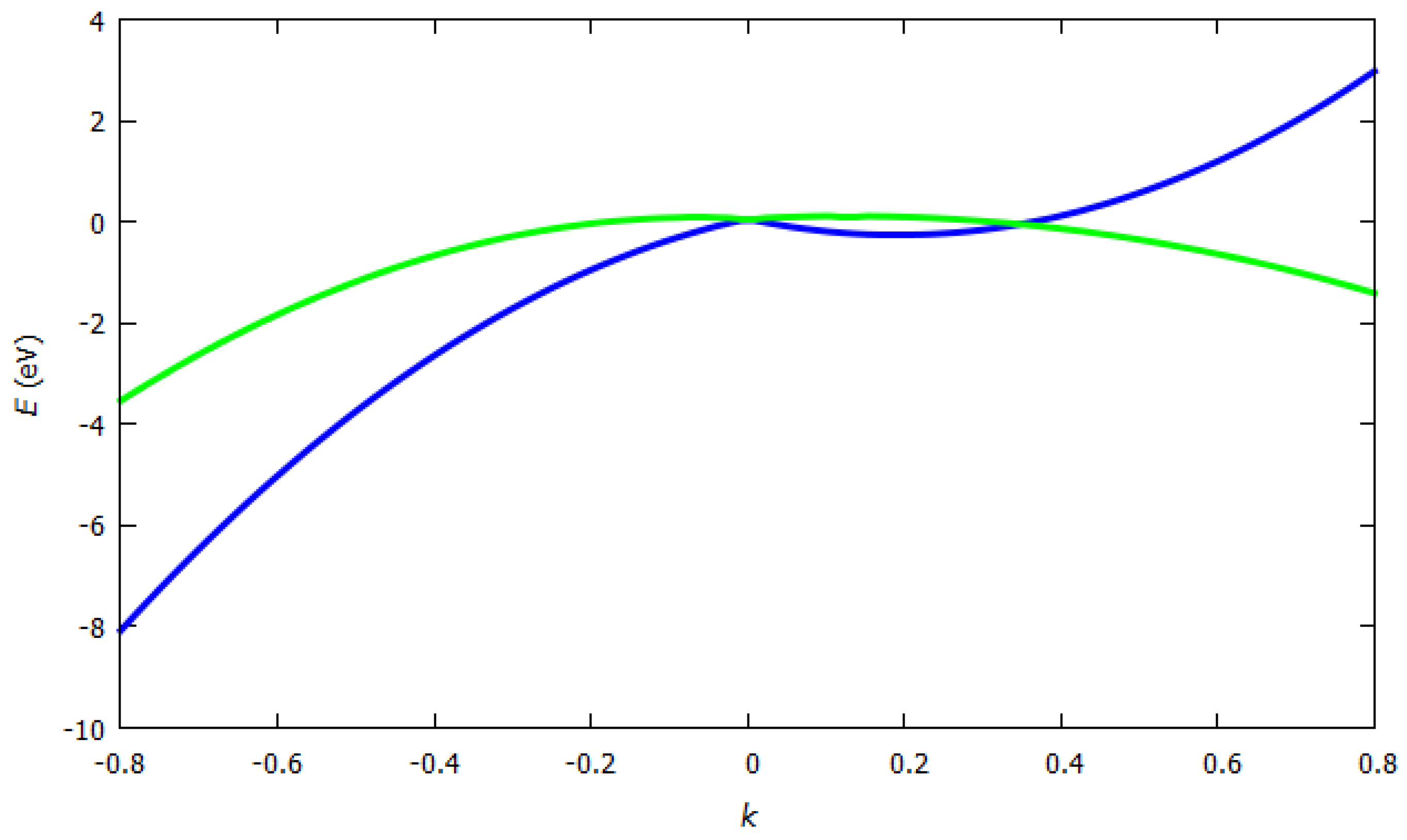
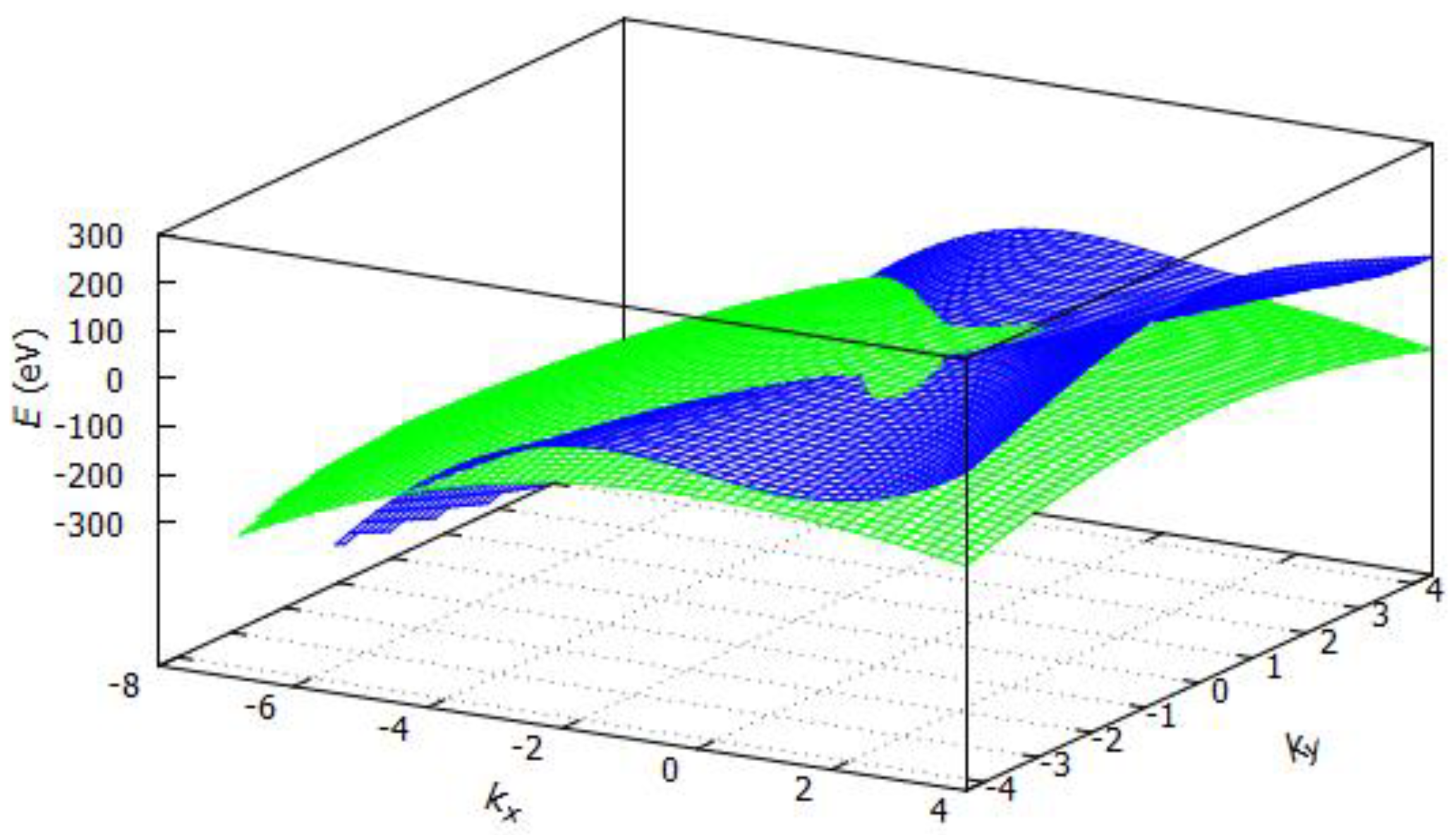
3.2.1. Band Structure of Graphene
3.2.2. Band Structure of Hexagonal Boron Nitride (h-BN)
3.2.3. Band Structure of Silicene
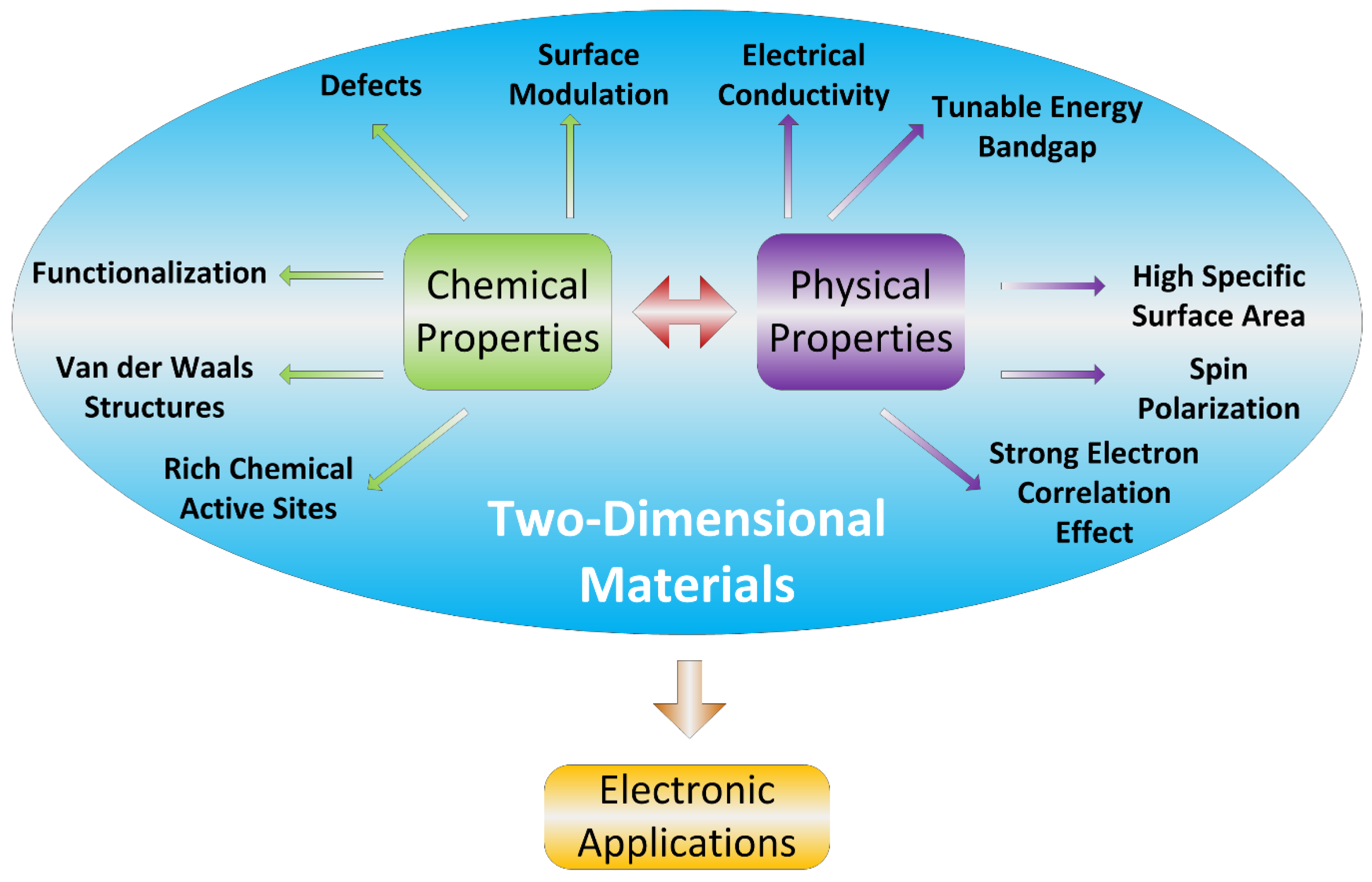
4. Why Study Electrical Properties of the 2D Materials for Gas Sensors?
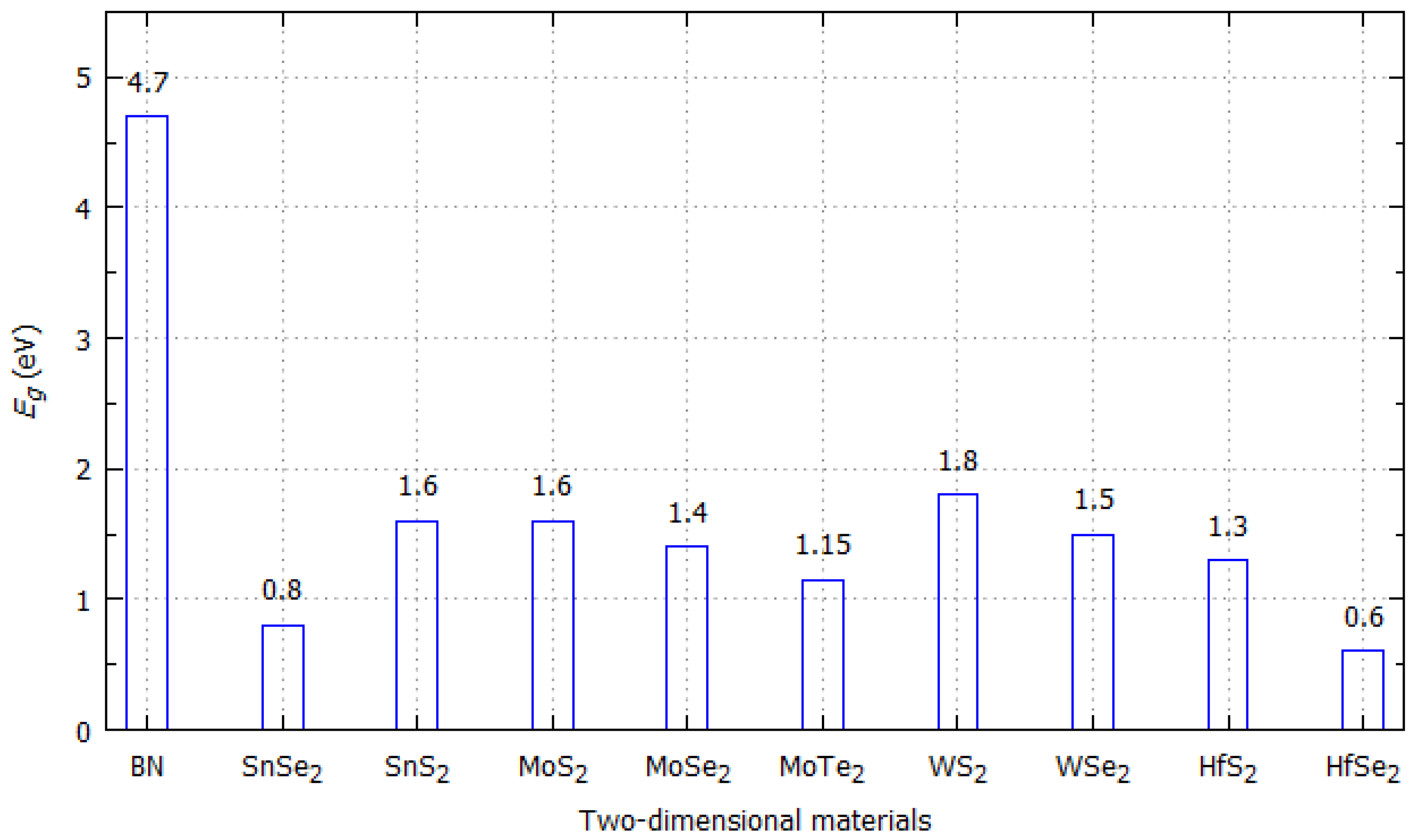
4.1. Correlation between Band Gap and/or Electronic Band Structure and Electrical Conductivity
4.2. Correlation between Gas Sensing Characteristics and Electronic Band Structure
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Zhang, L.; Huang, L.; Li, L.; Meng, L.; Gao, M.; Huan, Q.; Lin, X.; Wang, Y.; Du, S.; et al. Construction of 2D Atomic Crystals on Transition Metal Surfaces: Graphene, Silicene, and Hafnene. Small 2014, 10, 2215–2225. [Google Scholar] [CrossRef] [PubMed]
- Balendhran, S.; Walia, S.; Nili, H.; Sriram, S.; Bhaskaran, M. Elemental Analogues of Graphene: Silicene, Germanene, Stanene, and Phosphorene. Small 2015, 11, 640–652. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Wang, H.; Fu, W.; Gong, Y.; Zhou, W.; Ajayan, P.M.; Lou, J.; Liu, Z. Band Engineering for Novel Two-Dimensional Atomic Layers. Small 2015, 11, 1868–1884. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Wang, C.; Pan, A.; Yu, R.; Duan, X. Two-Dimensional Transition Metal Dichalcogenides as Atomically Thin Semiconductors: Opportunities and Challenges. Chem. Soc. Rev. 2015, 44, 8859–8876. [Google Scholar] [CrossRef] [PubMed]
- Naguib, M.; Gogotsi, Y. Synthesis of Two-Dimensional Materials by Selective Extraction. Acc. Chem. Res. 2015, 48, 128–135. [Google Scholar] [CrossRef]
- Vargas-Bernal, R. The Next Generation of Nanomaterials for Designing Analog Integrated Circuits. In Analog Circuits: Fundamentals, Synthesis and Performance; Tlelo-Cuautle, E., Fakhfakh, M., de la Fraga, L.G., Eds.; Nova Science Publishers: New York, NY, USA, 2016; pp. 3–21. ISBN 978-1-53610-969-6. [Google Scholar]
- Dai, J.; Li, M.; Zeng, X.C. Group IVB Transition Metal Trichalcogenides: A New Class of 2D Layered Materials beyond Graphene. WIREs Comput. Mol. Sci. 2016, 6, 211–222. [Google Scholar] [CrossRef]
- Vargas-Bernal, R. Graphene against Other Two-Dimensional Materials: A Comparative Study on the Basis of Electronic Applications. In Two-Dimensional Materials: Synthesis, Characterization and Potential Applications; Nayak, P.K., Ed.; Intech: Rijeka, Croatia, 2016; pp. 103–121. ISBN 978-953-51-2555-6. [Google Scholar]
- Wasala, M.; Sirikumara, H.I.; Sapkota, Y.R.; Hofer, S.; Mazumdar, D.; Jakasekera, T.; Talapatra, S. Recent Advances in Investigations of the Electronic and Optoelectronic Properties of Group III, IV, and V Selenide based Binary Layered Compounds. J. Mater. Chem. C 2017, 5, 11214–11225. [Google Scholar] [CrossRef]
- Kong, X.; Liu, Q.; Zhang, C.; Peng, Z.; Chen, Q. Elemental Two-Dimensional Nanosheets Beyond Graphene. Chem. Soc. Rev. 2017, 46, 2127–2157. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, S.; Chen, Z.; Wang, Y.; Gao, H.; Gómez-Herrero, J.; Ares, P.; Zamora, F.; Zhu, Z.; Zeng, H. Recent Progress in 2D Group-VA Semiconductors: From Theory to Experiment. Chem. Soc. Rev. 2018, 47, 982–1021. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, Z.; Duan, X.; Duan, X. Chemical Synthesis of Two-Dimensional Atomic Crystals, Heterostructures and Superlattices. Chem. Soc. Rev. 2018, 47, 3129–3151. [Google Scholar] [CrossRef]
- Shi, E.; Gao, Y.; Finkenauer, B.P.; Akriti; Coffrey, A.H.; Dou, L. Two-Dimensional Halide Perovskite Nanomaterials and Heterostructures. Chem. Soc. Rev. 2018, 47, 6046–6072. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, B.; Zou, X.; Cheng, H.M. Chemical Vapor Deposition Growth and Applications of Two-Dimensional Materials and Their Heterostructures. Chem. Rev. 2018, 118, 6091–6133. [Google Scholar] [CrossRef]
- Yu, J.; Hu, X. Large-Scale Synthesis of 2D Metal Dichalcogenides. J. Mater. Chem. C 2018, 6, 4627–4640. [Google Scholar] [CrossRef]
- Basu, S.; Bhattacharyya, P. Recent Developments on Graphene and Graphene Oxide based Solid State Gas Sensors. Sens. Actuators B Chem. 2012, 173, 1–21. [Google Scholar] [CrossRef]
- Vargas-Bernal, R.; Herrera-Pérez, G. Importance of the Nanostructured Ceramic Materials on Gas Sensing. In Nanotechnology for Optics and Sensors; Aliofkhazraei, M., Ed.; One Central Press: Cheshire, UK, 2014; pp. 1–34. ISBN 978-1-910086-09-4. [Google Scholar]
- Varghese, S.S.; Varghese, S.H.; Swaminathan, S.; Singh, K.K.; Mittal, V. Two-Dimensional Materials for Sensing: Graphene and Beyond. Electronics 2015, 4, 651–687. [Google Scholar] [CrossRef]
- Schmidt, H.; Giustiniano, F.; Eda, G. Electronic Transport Properties of Transition Metal Dichalcogenide Field-Effect Devices: Surface and Interface Effects. Chem. Soc. Rev. 2015, 44, 7715–7736. [Google Scholar] [CrossRef]
- Sarkar, D.; Xie, X.; Kang, J.; Zhang, H.; Liu, W.; Navarrete, J.; Moskovits, M.; Banerjee, K. Functionalization of Transition Metal Dichalcogenides with Metallic Nanoparticles: Implications for Doping and Gas-Sensing. Nano Lett. 2015, 15, 2852–2862. [Google Scholar] [CrossRef]
- Yang, W.; Li, H.; Zhai, T. Two-Dimensional Layered Nanomaterials for Gas-Sensing Applications. Inorg. Chem. Front. 2016, 3, 433–451. [Google Scholar] [CrossRef]
- Akbari, E.; Buntat, Z.; Afroozeh, A.; Pourmand, S.E.; Farhang, Y.; Sanati, P. Silicene and Graphene Nano Materials in Gas Sensing Mechanism. RSC Adv. 2016, 6, 81647–81653. [Google Scholar] [CrossRef]
- Vargas-Bernal, R. Modeling, Design and Applications of the Gas Sensors based on Graphene and Carbon Nanotubes. In Handbook of Research on Nanoelectronic Sensor Modeling and Applications; Ahmadi, M.T., Ismail, R., Anwar, S., Eds.; IGI Global: Hershey, PA, USA, 2016; pp. 187–213. ISBN 978-1-5225-0736-9. [Google Scholar] [CrossRef]
- Mao, S.; Chang, J.; Pu, H.; Lu, G.; He, Q.; Zhang, H.; Chen, J. Two-Dimensional Nanomaterial-based Field-Effect Transistors for Chemical and Biological Sensing. Chem. Soc. Rev. 2017, 46, 6872–6904. [Google Scholar] [CrossRef]
- Liu, X.; Ma, T.; Pinna, N.; Zhang, J. Two-Dimensional Nanostructured Materials for Gas Sensing. Adv. Funct. Mater. 2017, 27, 1702168. [Google Scholar] [CrossRef]
- Tung, T.T.; Nine, M.J.; Krebsz, M.; Pasinszki, T.; Coghlan, C.J.; Tran, D.N.H.; Losic, D. Recent Advances in Sensing Applications of Graphene Assemblies and Their Composites. Adv. Funct. Mater. 2017, 27, 1702891. [Google Scholar] [CrossRef]
- Ping, J.; Fan, Z.; Sindoro, M.; Ying, Y.; Zhang, H. Recent Advances in Sensing Applications of Two-Dimensional Transition Metal Dichalcogenides Nanosheets and Their Composites. Adv. Funct. Mater. 2017, 27, 1605817. [Google Scholar] [CrossRef]
- Tang, X.; Du, A.; Kou, L. Gas Sensing and Capturing based on Two-Dimensional Layered Materials: Overview from Theoretical Perspective. WIREs Comput. Mol. Sci. 2018, 8, e1631. [Google Scholar] [CrossRef]
- Gablech, I.; Pekárek, J.; Klempa, J.; Svatoš, V.; Sejedi-Moghaddam, A.; Neužil, P.; Pumera, M. Monoelemental 2D Materials-based Field Effect Transistors for Sensing and Biosensing: Phosphorene, Antimonene, Arsenene, Silicene, and Germanene go beyond Graphene. Trends Analyt. Chem. 2018, 105, 251–262. [Google Scholar] [CrossRef]
- Anichi, C.; Czepa, W.; Pakulski, D.; Aliprandi, A.; Ciesielski, A.; Samori, P. Chemical Sensing with 2D Materials. Chem. Soc. Rev. 2018, 47, 4860–4908. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.J.; Kim, I.D. Recent Developments in 2D Nanomaterials for Chemiresistive-Type Gas Sensors. Electron. Mater. Lett. 2018, 14, 221–260. [Google Scholar] [CrossRef]
- Donarelli, M.; Ottaviano, L. 2D Materials for Gas Sensing Applications: A Review on Graphene Oxide, MoS2, WS2 and Phosphorene. Sensors 2018, 18, 3638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Chen, Y.B.; Zhou, K.G.; Liu, C.H.; Zeng, J.; Zhang, H.L.; Peng, Y. Improving Gas Sensing Properties of Graphene by Introducing Dopants and Defects: A First-Principles Study. Nanotechnology 2009, 20, 185504. [Google Scholar] [CrossRef]
- Karaduman, I.; Er, E.; Çelikkan, H.; Acar, S. A New Generation Gas Sensing Material based on High-Quality Graphene. Sens. Actuators B Chem. 2015, 221, 1188–1194. [Google Scholar] [CrossRef]
- Singh, E.; Meyyappan, M.; Nalwa, H.S. Flexible Graphene-based Wearable Gas and Chemical Sensors. ACS Appl. Mater. Interfaces 2017, 9, 34544–34586. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, J.; Umar, A.; Wang, Y.; Li, H.; Zhou, G. Three-Dimensional Crumpled Graphene-based Nanosheets with Ultrahigh NO2 Gas Sensibility. ACS Appl. Mater. Interfaces 2017, 9, 11819–11827. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.K.; Singh, D.; Rajput, K.; Sonvane, Y. Germanene: A New Electronic Gas Sensing Material. RSC Adv. 2016, 6, 102264–102271. [Google Scholar] [CrossRef]
- Xia, W.; Hu, W.; Li, Z.; Yang, J. A First-Principles Study of Gas Adsorption on Germanene. Phys. Chem. Chem. Phys. 2014, 16, 22495–22498. [Google Scholar] [CrossRef] [PubMed]
- Bayani, A.H.; Dideban, D.; Moezi, N. Hydrogen Sensitive Field-Effect Transistor based on Germanene Nanoribbon and Optical Properties of Hydrogenated Germanene. J. Comput. Electron. 2016, 15, 381–388. [Google Scholar] [CrossRef]
- Monshi, M.M.; Aghaei, S.M.; Clizo, I. Doping and Defect-induced Germanene: A Superior Media for Sensing H2S, SO2, and CO2 Gas Molecules. Surf. Sci. 2017, 665, 96–102. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. NO2 Adsorption Behaviour on Germanene Nanosheet—A First-Principles Investigation. Superlattices Microstruct. 2017, 101, 160–171. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. CO and NO Monitoring using Pristine Germanene Nanosheets: DFT Study. J. Mol. Liq. 2017, 234, 355–363. [Google Scholar] [CrossRef]
- Pang, Q.; Li, L.; Gao, D.L.; Chai, R.P.; Zhang, C.L.; Song, Y.L. Tuning the Electronic and Magnetic Properties of Germanene by Surface Adsorption of Small Nitrogen-based Molecules. Phys. E Low Dimens. Syst. Nanostruct. 2017, 88, 237–242. [Google Scholar] [CrossRef]
- Nagarajan, V.; Bhattacharyya, A.; Chandiramouli, R. Adsorption of Ammonia Molecules and Humidity on Germanane Nanosheet—A Density Functional Study. J. Mol. Graph. Model. 2018, 79, 149–156. [Google Scholar] [CrossRef]
- Prasongkit, J.; Amorim, R.G.; Chakraborty, S.; Ahuja, R.; Scheicher, R.H.; Amornkitbamrung, V. Highly Sensitive and Selective Gas Detection based on Silicene. J. Phys. Chem. C 2015, 119, 16934–16940. [Google Scholar] [CrossRef]
- Chandiramouli, R.; Srivastava, A.; Nagarajan, V. NO Adsorption Studies on Silicene Nanosheet: DFT Investigation. Appl. Surf. Sci. 2015, 351, 662–672. [Google Scholar] [CrossRef]
- Walia, G.K.; Randhawa, D.K.K. Adsorption and Dissociation of Sulfur-based Toxic Gas Molecules on Silicene Nanoribbons: A Quest for High-Performance Gas Sensors and Catalysts. J. Mol. Model. 2018, 24, 94. [Google Scholar] [CrossRef]
- Chen, X.; Tan, C.; Yang, Q.; Meng, R.; Liang, Q.; Cai, M.; Zhang, S.; Jiang, J. Ab Initio Study of the Adsorption of Small Molecules on Stanene. J. Phys. Chem. C 2016, 120, 13987–13994. [Google Scholar] [CrossRef]
- Garg, P.; Choudhuri, I.; Pathak, B. Stanene based Gas Sensors: Effect of Spin-Orbit Coupling. Phys. Chem. Chem. Phys. 2017, 19, 31325–31334. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Zhao, R.; Zhao, M.; Zhao, X.; An, Y.; Dai, X.; Xia, C. Effects of Applied Strain and Electric Field on Small-Molecule Sensing by Stanene Monolayers. J. Mater. Sci. 2017, 52, 5083–5096. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. Adsorption Behavior of NH3 and NO2 Molecules on Stanene and Stanene Nanosheets—A Density Functional Theory Study. Chem. Phys. Lett. 2018, 695, 162–169. [Google Scholar] [CrossRef]
- Liu, N.; Zhou, S. Gas Adsorption on Monolayer Blue Phosphorus: Implications for Environmental Stability and Gas Sensors. Nanotechnology 2017, 28, 175708. [Google Scholar] [CrossRef]
- Mayorga-Martinez, C.C.; Sofer, Z.; Pumera, M. Layered Black Phosphorus as a Selective Vapor Sensor. Angew. Chem. Int. Edit. 2015, 54, 14317–14320. [Google Scholar] [CrossRef] [PubMed]
- Cui, S.; Pu, H.; Wells, S.A.; Wen, Z.; Mao, S.; Chang, J.; Hersam, M.C.; Chen, J. Ultrahigh Sensitivity and Layer-Dependent Sensing Performance of Phosphorene-based Gas Sensors. Nat. Commun. 2015, 6, 8632. [Google Scholar] [CrossRef]
- Yang, Q.; Meng, R.S.; Jiang, J.K.; Liang, Q.H.; Tan, C.J.; Cai, M.; Sun, X.; Yang, D.G.; Ren, T.L.; Chen, X.P. First-Principles Study of Sulfur Dioxide Sensor based on Phosphorenes. IEEE Electron Device Lett. 2016, 37, 660–662. [Google Scholar] [CrossRef]
- Lalitha, M.; Nataraj, Y.; Lakshmipathi, S. Calcium Decorated and Doped Phosphorene for Gas Adsorption. Appl. Surf. Sci. 2016, 377, 311–323. [Google Scholar] [CrossRef]
- Mahabal, M.S.; Deshpande, M.D.; Hussain, T.; Ahuja, R. Sensing Characteristics of Phosphorene Monolayers toward PH3 and AsH3 Gases upon the Introduction of Vacancy Defects. J. Phys. Chem. C 2016, 120, 20428–20436. [Google Scholar] [CrossRef]
- Pang, J.; Yang, Q.; Ma, X.; Wang, L.; Tan, C.; Xiong, D.; Ye, H.; Chen, X. DFT Coupled with NEGF Study of Ultra-Sensitive HCN and HNC Gases Detection and Distinct I-V Response based on Phosphorene. Phys. Chem. Chem. Phys. 2017, 19, 30852–30860. [Google Scholar] [CrossRef] [PubMed]
- Pumera, M. Phosphorene and Black Phosphorus for Sensing and Biosensing. Trends Anal. Chem. 2017, 93, 1–6. [Google Scholar] [CrossRef]
- Guo, S.; Yuan, L.; Liu, X.; Zhou, W.; Song, X.; Zhang, S. First-Principles Study of SO2 Sensors based on Phosphorene and Its Isoelectronic Counterparts: GeS, GeSe, SnS, SnSe. Chem. Phys. Lett. 2017, 686, 83–87. [Google Scholar] [CrossRef]
- Khan, M.S.; Srivastava, A.; Pandey, R. Electronic Properties of a Pristine and NH3/NO2 Adsorbed Buckled Arsenene Monolayer. RSC Adv. 2016, 6, 72634–72642. [Google Scholar] [CrossRef]
- Chen, X.P.; Wang, L.M.; Sun, X.; Meng, R.S.; Xiao, J.; Ye, H.Y.; Zhang, G.Q. Sulfur Dioxide and Nitrogen Dioxide Gas Sensor based on Arsenene: A First-Principle Study. IEEE Electron Device Lett. 2017, 38, 661–664. [Google Scholar] [CrossRef]
- Liu, C.; Liu, C.S.; Yan, X. Arsenene as a Promising Candidate for NO and NO2 Sensor: A First-Principles Study. Phy. Lett. A 2017, 381, 1092–1096. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. Investigation on Adsorption Properties of CO and NO Gas Molecules on Aluminene Nanosheet: A Density Functional Application. Mater. Sci. Eng. B 2018, 229, 193–200. [Google Scholar] [CrossRef]
- Meng, R.S.; Cai, M.; Jiang, J.K.; Liang, Q.H.; Sun, X.; Yang, Q.; Tan, C.J.; Chen, X.P. First Principles Investigation of Small Molecules Adsorption on Antimonene. IEEE Electron Device Lett. 2017, 38, 134–137. [Google Scholar] [CrossRef]
- Li, T.T.; He, C.; Zhang, W.X. Electric Field Improved the Sensitivity of CO on substitutionally doped Antimonene. Appl. Surf. Sci. 2018, 427(Part A), 388–395. [Google Scholar] [CrossRef]
- Kistanov, A.A.; Cai, Y.; Kripalani, D.R.; Zhou, K.; Dmitriev, S.V.; Zhang, Y.W. A First-Principles Study on the Adsorption of Small Molecules on Antimonene: Oxidation Tendency and Stability. J. Mater. Chem. C 2018, 6, 4308–4317. [Google Scholar] [CrossRef]
- Srivastava, A.; Khan, M.S.; Ahuja, R. Electron Transport in NH3/NO2 Sensed Buckled Antimonene. Solid State Commun. 2018, 272, 1–7. [Google Scholar] [CrossRef]
- Shukla, V.; Wärma, J.; Jena, N.K.; Grigoriev, A.; Ahuja, R. Toward the Realization of 2D Borophene based Gas Sensor. J. Phys. Chem. C. 2017, 121, 26868–26876. [Google Scholar] [CrossRef]
- Huang, C.S.; Murat, A.; Babar, V.; Montes, E.; Schwingenschlögl, U. Adsorption of the Gas Molecules NH3, NO, NO2, and CO on Borophene. J. Phys. Chem. C 2018, 122, 14665–14670. [Google Scholar] [CrossRef]
- O’Brien, M.; Lee, K.; Morrish, R.; Berner, N.C.; McEvoy, N.; Wolden, C.A.; Duesberg, G.S. Plasma assisted Synthesis of WS2 for Gas Sensing Applications. Chem. Phys. Lett. 2014, 615, 6–10. [Google Scholar] [CrossRef]
- Kuru, C.; Choi, D.; Kargar, A.; Liu, C.H.; Yavuz, S.; Choi, C.; Jin, S.; Bandaru, P.R. High-Performance Flexible Hydrogen Sensor made of WS2 Nanosheet-Pd Nanoparticle Composite Film. Nanotechnology 2016, 27, 195501. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Wang, J.; Zhang, J. WS2 Nanoflakes based Selective Ammonia Sensors at Room Temperature. Sens. Actuators B Chem. 2017, 240, 273–277. [Google Scholar] [CrossRef]
- Ko, K.Y.; Park, K.; Lee, S.; Kim, Y.; Woo, W.J.; Kim, D.; Song, J.-G.; Park, J.; Kim, H. Recovery Improvement for Large-Area Tungsten Diselenide Gas Sensors. ACS Appl. Mater. Interfaces 2018, 10, 23910–23917. [Google Scholar] [CrossRef]
- Li, H.; Yin, Z.; He, Q.; Li, H.; Huang, X.; Lu, G.; Fam, D.W.H.; Tok, A.I.Y.; Zhang, Q.; Zhang, H. Fabrication of Single- and Multilayer MoS2 Film-based Field-Effect Transistors for Sensing NO at Room Temperature. Small 2012, 8, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Cho, B.; Hahm, M.G.; Choi, M.; Yoon, J.; Kim, A.R.; Lee, Y.J.; Park, S.G.; Kwon, J.D.; Kim, C.S.; Song, M.; et al. Charge-Transfer-based Gas Sensing using Atomic-Layer MoS2. Sci. Rep. 2015, 5, 8052. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.Y.; Kim, S.J.; Lee, Y.; Kim, J.S.; Jung, W.B.; Yoo, H.W.; Kim, J.; Jung, H.T. Highly Enhanced Gas Adsorption Properties in Vertically Aligned MoS2 Layers. ACS Nano 2015, 9, 9314–9321. [Google Scholar] [CrossRef]
- Shokri, A.; Salmi, N. Gas Sensor based on MoS2 Monolayer. Sens. Actuators B Chem. 2016, 236, 378–385. [Google Scholar] [CrossRef]
- Kang, M.A.; Han, J.K.; Cho, S.Y.; Bu, S.D.; Park, C.Y.; Myung, S.; Song, W.; Lee, S.S.; Lim, J.; An, K.S. Strain-Gradient Effect in Gas Sensors based on Three-Dimensional Hollow Molybdenum Disulfide Nanoflakes. ACS Appl. Mater. Interfaces 2017, 9, 43799–43806. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.Y.; Kim, Y.; Chung, H.S.; Kim, A.R.; Kwon, J.D.; Park, J.; Kim, Y.L.; Kwon, S.H.; Hahm, M.G.; Cho, B. Effect of Nb Doping on Chemical Sensing Performance of Two-Dimensional Layered MoSe2. ACS Appl. Mater. Interfaces 2017, 9, 3817–3823. [Google Scholar] [CrossRef]
- Nagarajan, V.; Chandiramouli, R. MoSe2 Nanosheets for Detection of Methanol and Ethanol Vapors: A DFT Study. J. Mol. Graph. Model. 2018, 81, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Mirabelli, G.; McGeough, C.; Schmidt, M.; McCarthy, E.K.; Monaghan, S.; Povey, I.M.; McCarthy, M.; Gity, F.; Nagle, R.; Hughes, G.; et al. Air Sensitivity of MoS2, MoSe2, MoTe2, HfS2, and HfSe2. J. Appl. Phys. 2016, 120, 125102. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhou, K.G.; Gou, X.C.; Xie, K.F.; Zhang, H.L.; Peng, Y. Effects of Dopant and Defect on the Adsorption of Carbon Monoxide on Graphitic Boron Nitride Sheet: A First-Principles Study. Chem. Phys. Lett. 2010, 484, 266–270. [Google Scholar] [CrossRef]
- Sajjad, M.; Feng, P. Study the Gas Sensing Properties of Boron Nitride Nanosheets. Mater. Res. Bull. 2014, 49, 35–38. [Google Scholar] [CrossRef]
- Srivastava, A.; Bhat, C.; Jain, S.K.; Mishra, P.K.; Brajpuriya, R. Electronic Transport Properties of BN Sheet on Adsorption of Ammonia (NH3) Gas. J. Mol. Model. 2015, 21, 39. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Yang, Z. First Principles Study of the Gas Sensing 2D GeTe: Atomic, Electronic and Transport Properties. J. Phys. D 2018, 51, 345304. [Google Scholar] [CrossRef]
- Mao, Y.; Long, L.; Yuan, J.; Zhong, J.; Zhao, H. Toxic Gases Molecules (NH3, SO2 and NO2) Adsorption on GeSe Monolayer with Point Defects Engineering. Chem. Phys. Lett. 2018, 706, 501–508. [Google Scholar] [CrossRef]
- Liu, L.; Yang, Q.; Wang, Z.; Ye, H.; Chen, X.; Fan, X.; Zhang, G. High Selective Gas Detection for Small Molecules based on Germanium Selenide Monolayer. Appl. Surf. Sci. 2018, 433, 575–581. [Google Scholar] [CrossRef]
- Ma, S.; Yuan, D.; Wang, Y.; Jiao, Z. Monolayer GeS as a Potential Candidate for NO2 Gas Sensors and Capturers. J. Mat. Chem. C 2018, 6, 8082–8091. [Google Scholar] [CrossRef]
- Sun, X.; Yang, Q.; Meng, R.; Tan, C.; Liang, Q.; Jiang, J.; Ye, H.; Chen, X. Adsorption of Gas Molecules on Graphene-like InN Monolayer: A First-Principle Study. Appl. Surf. Sci. 2017, 404, 291–299. [Google Scholar] [CrossRef]
- Ma, D.; Ju, W.; Tang, Y.; Chen, Y. First-Principles Study of the Small Molecule Adsorption on the InSe Monolayer. Appl. Surf. Sci. 2017, 426, 244–252. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, G.; Zhang, Y.W. Charge Transfer and Functionalization of Monolayer InSe by Physisorption of Small Molecules for Gas Sensing. J. Phys. Chem. C 2017, 121, 10182–10193. [Google Scholar] [CrossRef]
- Ou, J.Z.; Ge, W.; Carey, B.; Daeneke, T.; Rotbart, A.; Shan, W.; Wang, Y.; Fu, Z.; Chrimes, A.F.; Wlodarski, W.; et al. Physisorption-based Charge Transfer in Two-Dimensional SnS2 for Selective and Reversible NO2 Gas Sensing. ACS Nano 2015, 9, 10313–10323. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Leonardi, S.G.; Bonavita, A.; Neri, G.; Wlodarski, W. Two-Dimensional (2D) SnS2-based Oxygen Sensor. Procedia Eng. 2016, 168, 1102–1105. [Google Scholar] [CrossRef]
- Qin, Z.; Xu, K.; Yue, H.; Wang, H.; Zhang, J.; Ouyang, C.; Xie, C.; Zeng, D. Enhanced Room-Temperature NH3 Gas Sensing by 2D SnS2 with Sulfur Vacancies Synthesized by Chemical Exfoliation. Sens. Actuators B Chem. 2018, 262, 771–779. [Google Scholar] [CrossRef]
- Chen, M.; Li, Z.; Li, W.; Shan, C.; Li, W.; Li, K.; Gu, G.; Feng, Y.; Zhong, G.; Wei, L. Large-Scale Synthesis of Single-Crystalline Self-Standing SnSe2 Nanoplate Arrays for Wearable Gas Sensors. Nanotechnology 2018, 29, 455501. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Li, Y.C.; Yu, X.F.; Cheng, J.B. MXenes: Reusable Materials for NH3 Sensor or Capturer by Controlling the Charge Injection. Sens. Actuators B Chem. 2016, 235, 103–109. [Google Scholar] [CrossRef]
- Kim, S.J.; Koh, H.J.; Ren, C.E.; Kwon, O.; Maleski, K.; Cho, S.Y.; Anasori, B.; Kim, C.K.; Choi, Y.K.; Kim, J.; et al. Metallic Ti3C2Tx MXene Gas Sensors with Ultrahigh Signal-to-Noise Ratio. ACS Nano 2018, 12, 986–993. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Yuan, D.; Jiao, Z.; Wang, T.; Dai, X. Monolayer Sc2CO2: A Promising Candidate as a SO2 Gas Sensor or Capturer. J. Phys. Chem. C 2017, 121, 24077–24084. [Google Scholar] [CrossRef]
- Yu, J.; Khazaei, M.; Umezawa, N.; Wang, J. Evolutionary Structure Prediction of Two-Dimensional IrB14: A Promising Gas Sensor Material. J. Phys. Chem. C 2018, 6, 5803–5811. [Google Scholar] [CrossRef]
- Cho, B.; Yoon, J.; Lim, S.K.; Kim, A.R.; Kim, D.H.; Park, S.G.; Kwon, J.D.; Lee, Y.J.; Lee, K.H.; Lee, B.H.; et al. Chemical Sensing of 2D Graphene/MoS2 Heterostructure Device. ACS Appl. Mater. Interfaces 2015, 7, 16775–16780. [Google Scholar] [CrossRef]
- Yang, W.; Wan, P.; Zhou, X.; Hu, J.; Guan, Y.; Feng, L. Additive-Free Synthesis of In2O3 Cubes Embedded into Graphene Sheets and Their Enhanced NO2 Sensing Performance at Room Temperature. ACS Appl. Mater. Interfaces 2014, 6, 21093–21100. [Google Scholar] [CrossRef]
- Shanmugasundaram, A.; Gundimeda, V.; Hou, T.; Lee, D.W. Realizing Synergy between In2O3 Nanocubes and Nitrogen-Doped Reduced Graphene Oxide: An Excellent Nanocomposite for the Selective and Sensitive Detection of CO at Ambient Temperatures. ACS Appl. Mater. Interfaces 2017, 9, 31728–31740. [Google Scholar] [CrossRef]
- Abbasi, A.; Sardroodi, J.J. An Innovative Method for the Removal of Toxic SOx Molecules from Environment by TiO2/Stanene Nanocomposite: A First-Principles Study. J. Inorg. Organomet. Polym. 2018, 28, 1901–1913. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, Y.; Jiang, C.; Zhang, Y. Room Temperature Hydrogen Gas Sensor based on Palladium decorated Tin Oxide/Molybdenum Disulfide Ternary Hybrid via Hydrothermal Route. Sens. Actuators B Chem. 2017, 242, 15–24. [Google Scholar] [CrossRef]
- Triet, N.M.; Duy, L.T.; Hwang, B.U.; Hanif, A.; Siddiqui, S.; Park, K.H.; Cho, C.Y.; Lee, N.E. High-Performance Schottky Diode Gas Sensor based on the Heterojunction of Three-Dimensional Nanohybrids of Reduced Graphene Oxide-Vertical ZnO Nanorods on AlGaN/GaN Layer. ACS Appl. Mater. Interfaces 2017, 9, 30722–30732. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Katz, H.E. Hybrid of P3HT and ZnO@GO Nanostructured Particles for Increased NO2 Sensing Response. J. Mater. Chem. C 2017, 5, 2160–2166. [Google Scholar] [CrossRef]
- Thanh, T.D.; Chuong, N.D.; Hien, H.V.; Kshetri, T.; Tuan, L.H.; Kim, N.H.; Lee, J.H. Recent Advances in Two-Dimensional Transition Metal Dichalcogenides-Graphene Heterostructured Materials for Electrochemical Applications. Prog. Mater. Sci. 2018, 96, 51–85. [Google Scholar] [CrossRef]
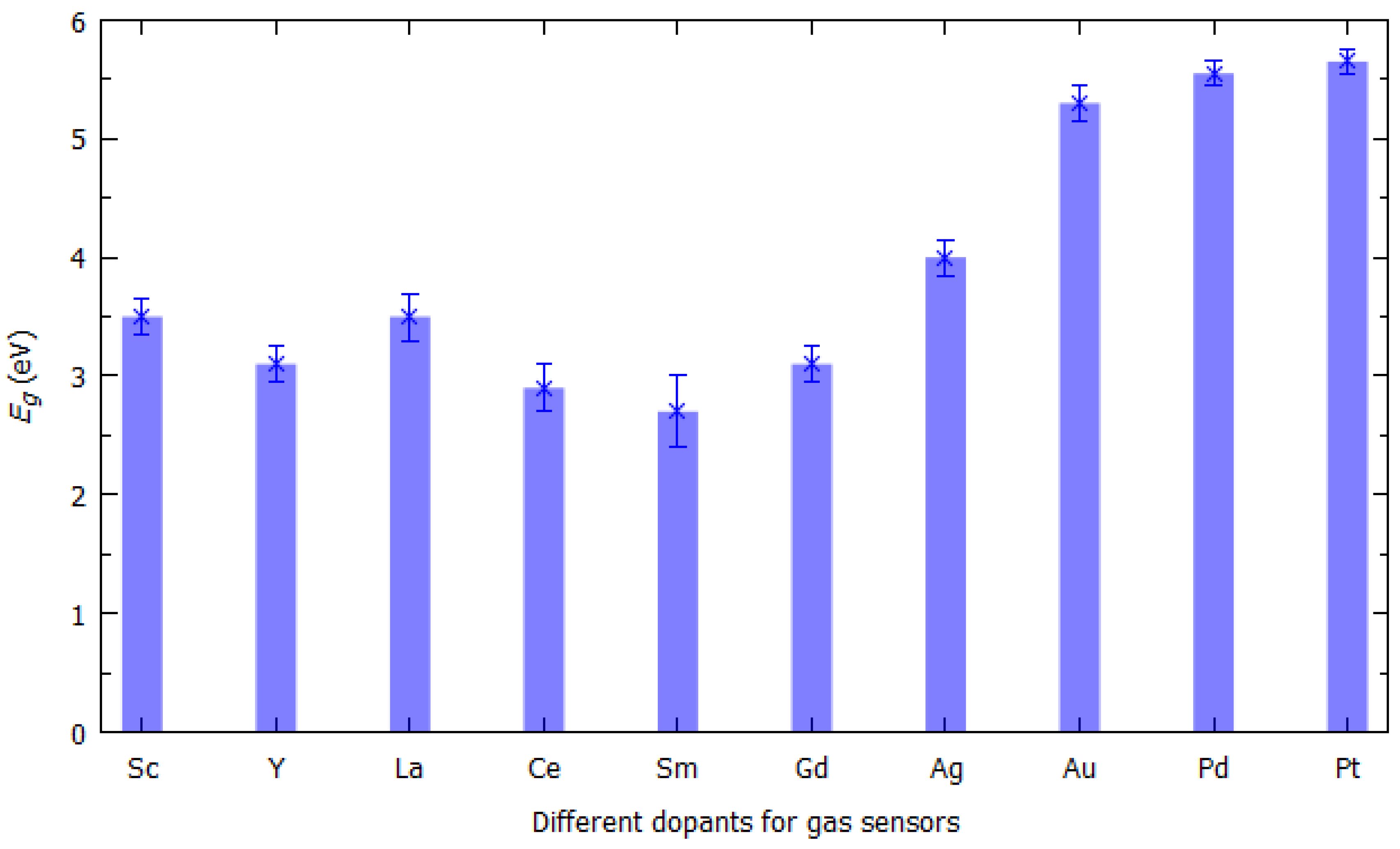
- Nieuwenhuys, B.E.; Van Aardenne, O.G.; Sachtler, W.M.H. Absorption of Xenon on Group VIII and ib Metals studied by Photoelectric Work Function Measurements. Chem. Phym. 1974, 5, 418–428. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, C.; Wei, S.-H. Gas Sensing in 2D Materials. Appl. Phys. Rev. 2017, 4, 021304. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 0-471-68057-5. [Google Scholar]
- Harrison, W.A. Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond; Dover Publications: Mineola, NY, USA, 1989; pp. 31–58. ISBN 978-0486660219. [Google Scholar]
- Ladd, M.; Palmer, R. Structure Determination by X-Ray Crystallography: Analysis by X-rays and Neutrons; Springer: Berlin, Germany, 2013; pp. 51–110. ISBN 978-1-4614-3956-1. [Google Scholar]
- Setyawan, W.; Curtarolo, S. High-throughput Electronic Band Structure Calculations: Challenges and Tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Castro-Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The Electronic Properties of Graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Ribeiro, R.M.; Peres, N.M.R. Stability of Boron Nitride Bilayers: Ground-State Energies, Interlayer Distances, and Tight-Binding Description. Phys. Rev. B 2011, 83, 235312. [Google Scholar] [CrossRef]
- Gert, A.V.; Nestoklon, M.O.; Yassievich, I.N. Band Structure of Silicene in the Tight Binding Approximation. J. Exp. Theor. Phys. 2015, 121, 115–121. [Google Scholar] [CrossRef]
- Takahashi, L.; Takahashi, K. Low Temperature Pollutant Trapping and Dissociation over Two-Dimensional Tin. Phys. Chem. Chem. Phys. 2015, 17, 21394–21396. [Google Scholar] [CrossRef]
- Lin, Y.; Connell, J.W. Advances in 2D Boron Nitride Nanostructures: Nanosheets, Nanoribbons, Nanomeshes, and Hybrids with Graphene. Nanoscale 2012, 4, 6908–6939. [Google Scholar] [CrossRef] [PubMed]
- Lebègue, S.; Björkman, T.; Klintenberg, M.; Nieminen, R.M.; Erikson, O. Two-Dimensional Materials from Data Filtering and Ab Initio Calculations. Phys. Rev. X 2013, 3, 031002. [Google Scholar] [CrossRef]
- Garg, P.; Choudhuri, I.; Mahata, A.; Pathak, B. Band Gap Opening in Stanene induced by Patterned B-N Doping. Phys. Chem. Chem. Phys. 2017, 19, 3660–3669. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Galli, G. Electronic Properties of MoS2 Nanoparticles. J. Phys. Chem. C 2007, 111, 16192–16196. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Potyrailo, R.A.; Surman, C.; Nagraj, N.; Burns, A. Materials and Transducers toward Selective Wireless Gas Sensing. Chem. Rev. 2011, 111, 7315–7354. [Google Scholar] [CrossRef] [PubMed]



| Two-Dimensional Material | BAND GAP | Electrical Properties | Crystal Structure | Unit Cell Parameters |
|---|---|---|---|---|
| Graphene | 0 eV | Metal | Hexagonal | a = b = 0.2612 nm, c = 0.6079 nm, α = β = 90°, γ = 120° |
| Germanene | 0.26 eV | Semimetal | Hexagonal | a = b = 0.249 nm, c = 0.268 nm, α = β = 90°, γ = 120° |
| Silicene | 0.1 eV | Semimetal | Hexagonal | a = b = 0.382 nm, c = 0.45 nm, α = β = 90°, γ = 120° |
| Borophene (striped) | 2 eV | Semimetal | Orthorhombic | a = 0.161, b = 0.286 nm, c = 0.911 nm, α = β = 90°, γ = 120° |
| Stanene | 0.074 eV | Semimetal | Hexagonal | a = b = 0.468 nm, c = 0.283 nm, α = β = 90°, γ = 120° |
| Aluminene | 1.618 eV | Semiconductor | Hexagonal | a = b = 0.449 nm, c = 0.259 nm, α = β = 90°, γ = 120° |
| Bismuthene | 0.8 eV | Semimetal | Hexagonal | a = b = 0.449 nm, c = 0.259 nm, α = β = 90°, γ = 120° |
| Antimonene (β phase) | 0.8–1.44 eV | Semimetal/Semiconductor | Hexagonal | a = b = 0.401 nm, c = 0.284 nm, α = β = 90°, γ = 120° |
| Two-Dimensional Material | Band Gap | Electrical Properties | Crystal Structure | Unit Cell Parameters |
|---|---|---|---|---|
| Diarsenic tritelluride As2Te3 (α phase) | 0.2–0.3 eV | Semiconductor (indirect band gap), Topological insulator, Thermoelectric material | Monoclinic C | a = 1.430 nm, b = 0.403 nm, c = 0.986 nm, α = γ = 90°, β = 95.40° |
| Black phosphorus (BP) | 0.3 eV | Semiconductor (direct band gap) | Orthorhombic C | a = 0.331 nm, b = 1.048 nm, c = 0.437 nm, α = β = γ = 90° |
| Hexagonal Boron Nitride (h-BN) | 5.9 eV | Insulator/Semiconductor (direct band gap) | Hexagonal | a = b = 0.2502 nm, c = 0.6617 nm, α = β = 90°, γ = 120° |
| Dibismuth trisulphide (Bi2S3) | 1.3–1.45 eV | Semiconductor (direct band gap) | Orthorhombic | a = 0.4025 nm, b = 1.117 nm, c = 1.135 nm, α = β = γ = 90° |
| Gallium sulfide GaS (α phase) | 2.6 eV | Semiconductor (indirect band gap) | Hexagonal | a = 0.360 nm, b = 0.640 nm, c = 1.544 nm, α = β = 90°, γ = 120° |
| Gallium selenide GaSe (2H phase) | 2.1 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.374 nm, c = 1.592 nm, α = β = 90°, γ = 120° |
| Germanium sulfide (GeS) | 1.6 eV | Semiconductor (indirect band gap) | Orthorhombic | a = 1.450 nm, b = 0.364 nm, c = 0.430 nm, α = β = γ = 90° |
| Hafnium Disulfide (HfS2) | 2 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.363 nm, c = 0.586 nm, α = β = 90°, γ = 120° |
| Hafnium Diselenide (HfSe2) | 1.1 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.3745 nm, c = 0.616 nm, α = β = 90°, γ = 120° |
| Indium Selenide (In2Se3) (2H phase, α-phase) | 1.14 eV | Semiconductor (direct band gap) | Hexagonal | a = b = 0.398 nm, c = 18.89 nm, α = β = 90°, γ = 120° |
| Molybdenum Disulfide (MoS2) (2H phase) | 1.6 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.315 nm, c = 1.229 nm, α = β = 90°, γ = 120° |
| Molybdenum Ditelluride (2H phase) | 1.2 eV | n-type Semiconductor (indirect band gap) | Hexagonal | a = b = 0.353 nm, c = 1.396 nm, α = β = 90°, γ = 120° |
| Molybdenum Diselenide (MoSe2) (2H phase) | 1.2 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.329 nm, c = 1.289 nm, α = β = 90°, γ = 120° |
| Molybdenum Sulfide Selenide Alloy (MoSSe) | 1.4 eV | Semiconductor (indirect band gap or direct band gap) | Hexagonal | a = b = 0.31–0.33 nm, c = 1.21–1.29 nm, α = β = 90°, γ = 120° |
| Molybdenum Tungsten Diselenide Alloy (MoWSe2) | 1.2–1.3 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.31–0.33 nm, c = 1.21–1.30 nm, α = β = 90°, γ = 120° |
| Rhenium Disulphide (ReS2) | 1.35 eV | Semiconductor (direct band gap) | Triclinic | a = 0.634 nm, b = 0.640 nm, c = 0.645 nm, α = 106.74°, β = 119.03°, γ = 89.97° |
| Rhenium Diselenide (ReSe2) | 1.1 eV | Semiconductor (direct band gap) | Triclinic | a = 0.658 nm, b = 0.670 nm, c = 0.672 nm, α = 91.75°, β = 105°, γ = 118.9° |
| Antimony Telluride (Sb2Te3) | 0.340–0.515 eV | Semiconductor (direct band gap), topological insulator, thermoelectric material | Hexagonal | a = b = 0.425 nm, c = 3.048 nm, α = β = 90°, γ = 120° |
| Tin Disulfide (SnS2) (2H phase) | 2.2 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.364 nm, c = 0.589 nm, α = β = 90°, γ = 120° |
| Tin Diselenide (SnSe2) | 2–3 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.381 nm, c = 0.614 nm, α = β = 90°, γ = 120° |
| Tantalum Disulfide (TaS2) (1T phase) | 1 eV | Semiconductor (direct band gap), Charge density waves (CDW) system, Mott phase | Hexagonal | a = b = 0.336 nm, c = 0.590 nm, α = β = 90°, γ = 120° |
| Tungsten Disulfide (WS2) (2H phase | 1.3 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.315 nm, c = 1.227 nm, α = β = 90°, γ = 120° |
| Tungsten Diselenide (WSe2) | 1.3 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.328 nm, c = 1.298 nm, α = β = 90°, γ = 120° |
| Zirconium Diselenide (ZrSe2) | 1 eV | Semiconductor (indirect band gap) | Hexagonal | a = b = 0.377 nm, c = 0.614 nm, α = β = 90°, γ = 120° |
| Zirconium Triselenide (ZrSe3) | 1.1 eV | Semiconductor (indirect band gap) | Monoclinic P | a = 0.541 nm, b = 0.375 nm, c = 0.944 nm, α = β = 90°, γ = 97.50° |
| Two-Dimensional Material | Detected Gases | References |
|---|---|---|
| Graphene | CO, NO, NO2, NH3 | [33] |
| CO, NO | [34] | |
| NO2, NH3, H2, H2S, CO2, SO2 | [35] | |
| NO2 | [36] | |
| Germanene | NH3, SO2, NO2 | [37] |
| N2, CO, CO2, NH3, NO, NO2, O2 | [38] | |
| H2 | [39] | |
| H2S, SO2, CO2 | [40] | |
| NO2 | [41] | |
| CO, NO | [42] | |
| N2, NO, NO2, NH3 | [43] | |
| Germanane | NH3 | [44] |
| Silicene | NO, NO2 | [45] |
| NO | [46] | |
| H2S, SO2 | [47] | |
| Stanene | CO, NH3, H2S, O2, NO, NO2 | [48] |
| NO, NO2, NH3, N2O | [49] | |
| NH3, CO, NO, NO2 | [50] | |
| NH3, NO2 | [51] | |
| Blue Phosphorene | O2, NO, SO2, NH3, NO2, CO2, H2S, CO, N2 | [52] |
| Black Phosphorene | CH3OH | [53] |
| NO2 | [54] | |
| SO2 | [55] | |
| CH4, CO2, H2, NH3 | [56] | |
| PH3, AsH3 | [57] | |
| HCN, HNC | [58] | |
| NO2 | [59] | |
| SO2 | [60] | |
| Arsenene | NH3, NO2 | [61] |
| SO2, NO2 | [62] | |
| NO, NO2 | [63] | |
| Aluminene | CO, NO | [64] |
| Antimonene | NH3, SO2, NO, NO2 | [65] |
| CO | [66] | |
| CO, NO, NO2, O2, NH3, H2 | [67] | |
| NH3, NO2 | [68] | |
| Borophene | CO, NO, NO2, NH3, CO2 | [69] |
| NH3, NO, NO2, CO | [70] | |
| WS2 | NH3 | [71] |
| H2 | [72] | |
| NH3, CH2O, CH3CH2OH, C6H6, C3H6O | [73] | |
| WSe2 | NO2, NH3, CO2, C3H6O | [74] |
| MoS2 | NO | [75] |
| NO2, NH3 | [76] | |
| NO2 | [77] | |
| CO, CO2, NO | [78] | |
| NH3, NO2 | [79] | |
| MoSe2 | NO2 | [80] |
| CH3OH, CH3CH2OH | [81] | |
| MoTe2 | O2 | [82] |
| Boron Nitride (BN) | CO | [83] |
| CH4 | [84] | |
| NH3 | [85] | |
| GeTe | NO | [86] |
| GeSe | NH3, SO2, NO2 | [87] |
| O2, NH3, SO2, H2, CO2, H2S, NO2, CH4, NO, CO | [88] | |
| GeS | NO2 | [89] |
| InN | CO, NH3, H2S, NO2, NO, SO2 | [90] |
| InSe | CO, NH3, N2, NO2, NO, and O2 | [91] |
| CO, NO, NO2, H2S, N2, O2, NH3, H2 | [92] | |
| SnS2 | NO2 | [93] |
| O2 | [94] | |
| NH3 | [95] | |
| SnSe2 | CH4 | [96] |
| HfS2 | O2 | [82] |
| HfSe2 | O2 | [82] |
| M2CO2, M = Sc, Ti, Zr, and Hf | NH3 | [97] |
| Ti3C2(OH)2 | Volatile organic compounds (VOCs) | [98] |
| Sc2CO2 | SO2 | [99] |
| IrB14 | CO, CO2 | [100] |
| Material | Detected Gases | References |
|---|---|---|
| Graphene/Molybdenum Disulfide (MoS2) | NO2 | [101] |
| Indium Oxide (In2O3)—Graphene | NO2 | [102] |
| Indium Oxide (In2O3)—Nitrogen-doped Reduced Graphene Oxide (N-RGO) | CO | [103] |
| Titania (TiO2)/Stanene | SOx | [104] |
| Palladium—Tin Oxide—Molybdenum Disulfide (Pd-SnO2/MoS2) | H2 | [105] |
| Reduced Graphene Oxide—Zinc Oxide—Aluminum Gallium Nitride/Gallium Nitride (RGO-ZnO-AlGaN/GaN) | NO2, SO2, HCHO | [106] |
| Poly(3-hexylthiophene)—Zinc Oxide–Graphene Oxide (P3HT-ZnO@GO) | NO2 | [107] |
| Crystal System | Relations | |
|---|---|---|
| Lattice Constants | Interaxial Angles | |
| Cubic | a = b = c | α = β = γ = 90° |
| Tetragonal | a = b ≠ c | α = β = γ = 90° |
| Orthorhombic | a ≠ b ≠ c | α = β = γ = 90° |
| Monoclinic | a ≠ b ≠ c | α = γ, β ≠ 90° |
| Triclinic | a ≠ b ≠ c | α ≠ β ≠ γ ≠ 90° |
| Trigonal (Rhombohedral) | a = b = c | α = β = γ ≠ 90° |
| Hexagonal | a = b ≠ c | α = β, γ = 120° |
| Symbol | Description |
|---|---|
| Γ | Center of the Brillouin zone |
| A | Center of a hexagonal face |
| H | Corner point |
| K | Middle of an edge joining two rectangular faces |
| L | Middle of an edge joining a hexagonal and a rectangular face |
| M | Center of a rectangular face |
| Crystalline Lattice | First Brillouin Zone |
|---|---|
| Hexagonal |  |
| Orthorhombic |  |
| Monoclinic (P and C) |  |
| Triclinic | 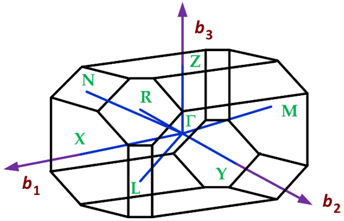 |
| Symmetry Points | [kx, ky, kz] | Point Group |
|---|---|---|
| Γ: (0, 0, 0) | [0, 0, 0] | 6/mmm |
| A: (0, 0, 1/2) | [0, 0, π/c] | 6/mmm |
| K: (2/3, 1/3, 0) | [4π/3a, 0, 0] | 2m |
| H: (2/3, 1/3, 1/2) | [4π/3a, 0, π/c] | 2m |
| M: (1/2, 0, 0) | [π/a, -π/a, 0] | mmm |
| L: (1/2, 0, 1/2) | [π/a, -π/a, π/c] | mmm |
| Symmetry Points | [kx, ky, kz] | Point Group |
|---|---|---|
| Γ: (0, 0, 0) | [0, 0, 0] | mmm |
| Y: (1/2, 1/2, 0) | [π/a, 0, 0] | mmm |
| Y’ or Y1: (−1/2, 1/2, 0) | [0, π/b, 0] | mmm |
| Z: (0, 0, 1/2) | [0, 0, π/c] | mmm |
| T: (1/2, 1/2, 1/2) | [π/a, 0, π/c] | mmm |
| T’ o T1: (−1/2, 1/2, 1/2) | [0, π/b, π/c] | mmm |
| S: (0, 1/2, 0) | [π/2a, π/2b, 0] | 2/m |
| R: (0, 1/2, 1/2) | [π/2a, π/2b, π/c] | 2/m |
| Symmetry Points |
|---|
| Γ |
| L |
| M |
| N |
| R |
| X |
| Y |
| Z |
| Symmetry Points | [kx, ky, kz] |
|---|---|
| Γ | [0, 0, 0] |
| X | [2π/a, −2π/atanγ, 0] |
| Y | [0, 2π/bsinγ, 0] |
| Z | [0, 0, 2π/c] |
| A | [2π/a, −2π/atanγ, 2π/c] |
| D | [0, 2π/bsinγ, 2π/c] |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas-Bernal, R. Electrical Properties of Two-Dimensional Materials Used in Gas Sensors. Sensors 2019, 19, 1295. https://doi.org/10.3390/s19061295
Vargas-Bernal R. Electrical Properties of Two-Dimensional Materials Used in Gas Sensors. Sensors. 2019; 19(6):1295. https://doi.org/10.3390/s19061295
Chicago/Turabian StyleVargas-Bernal, Rafael. 2019. "Electrical Properties of Two-Dimensional Materials Used in Gas Sensors" Sensors 19, no. 6: 1295. https://doi.org/10.3390/s19061295
APA StyleVargas-Bernal, R. (2019). Electrical Properties of Two-Dimensional Materials Used in Gas Sensors. Sensors, 19(6), 1295. https://doi.org/10.3390/s19061295





