Time Series Data Fusion Based on Evidence Theory and OWA Operator
Abstract
1. Introduction
2. Preliminaries
2.1. Evidence Theory
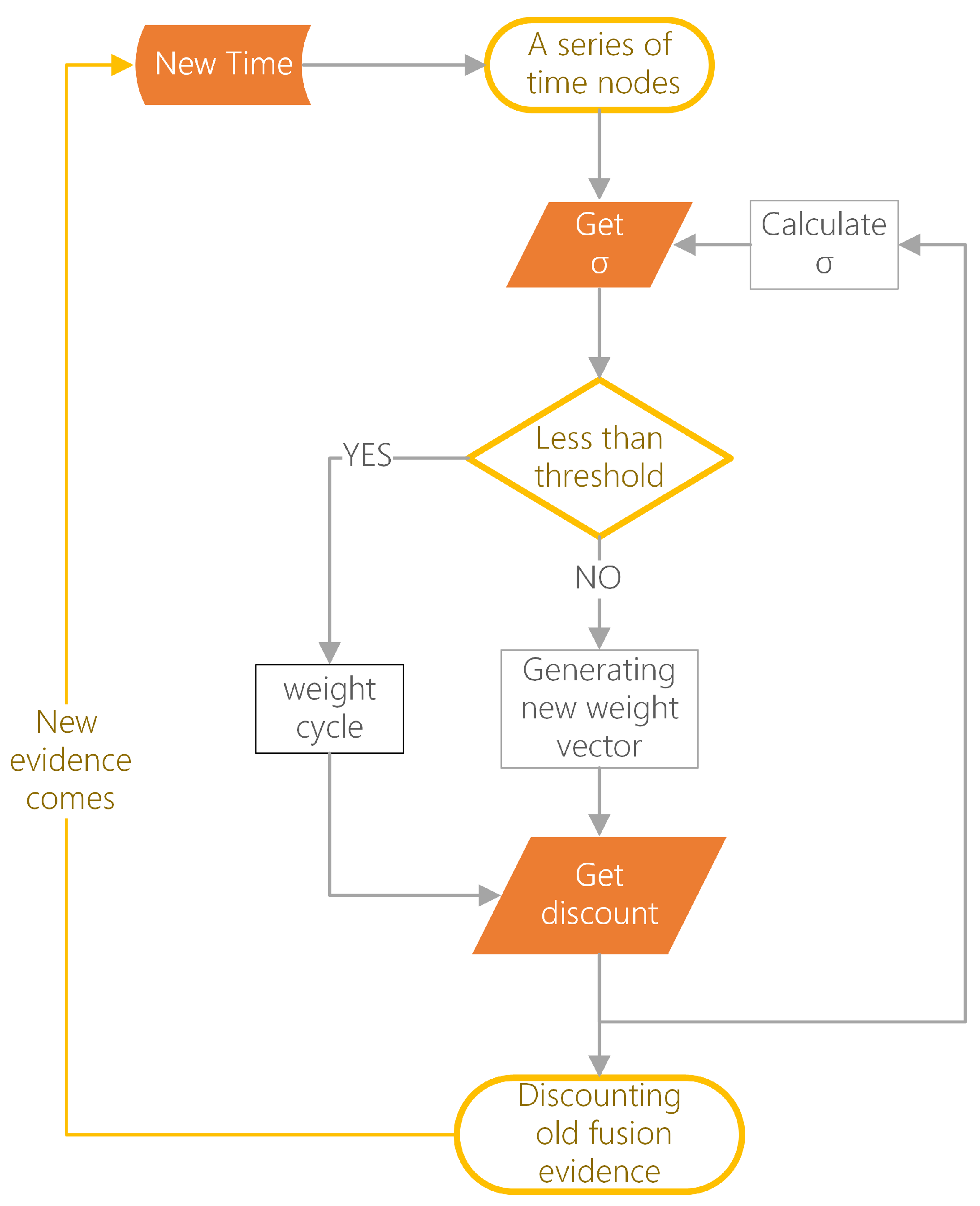
2.2. The Credibility Decay Model
2.3. The Ordered Weighted Aggregation Operator
- .
3. A New CDM Based on OWA
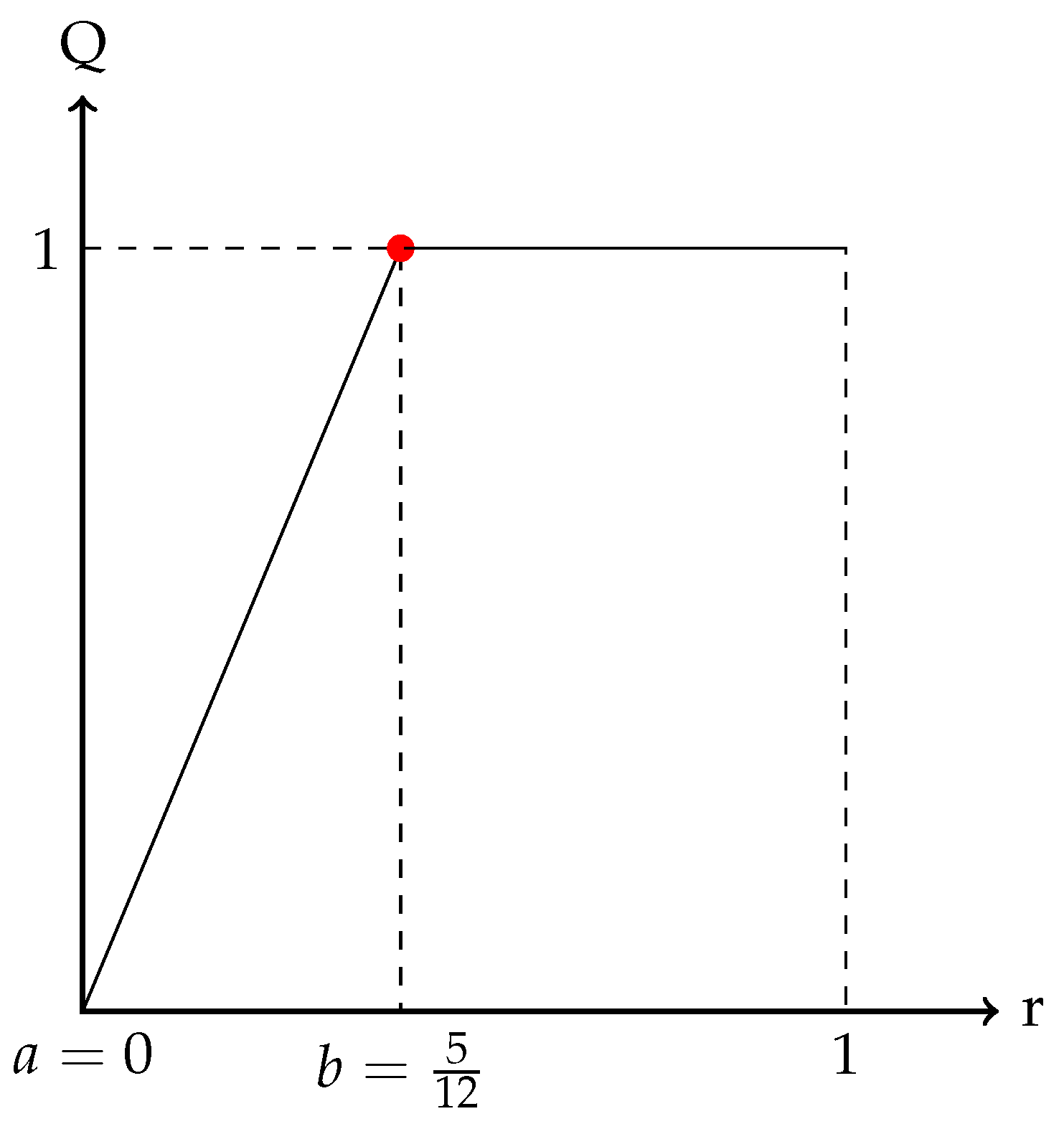
- a must equal to 0, otherwise may equal to 0.
- When b closes to 0, more satisfaction is given to the newest fusion evidence.
- When b closes to 1, less satisfaction is given to the newest fusion evidence.
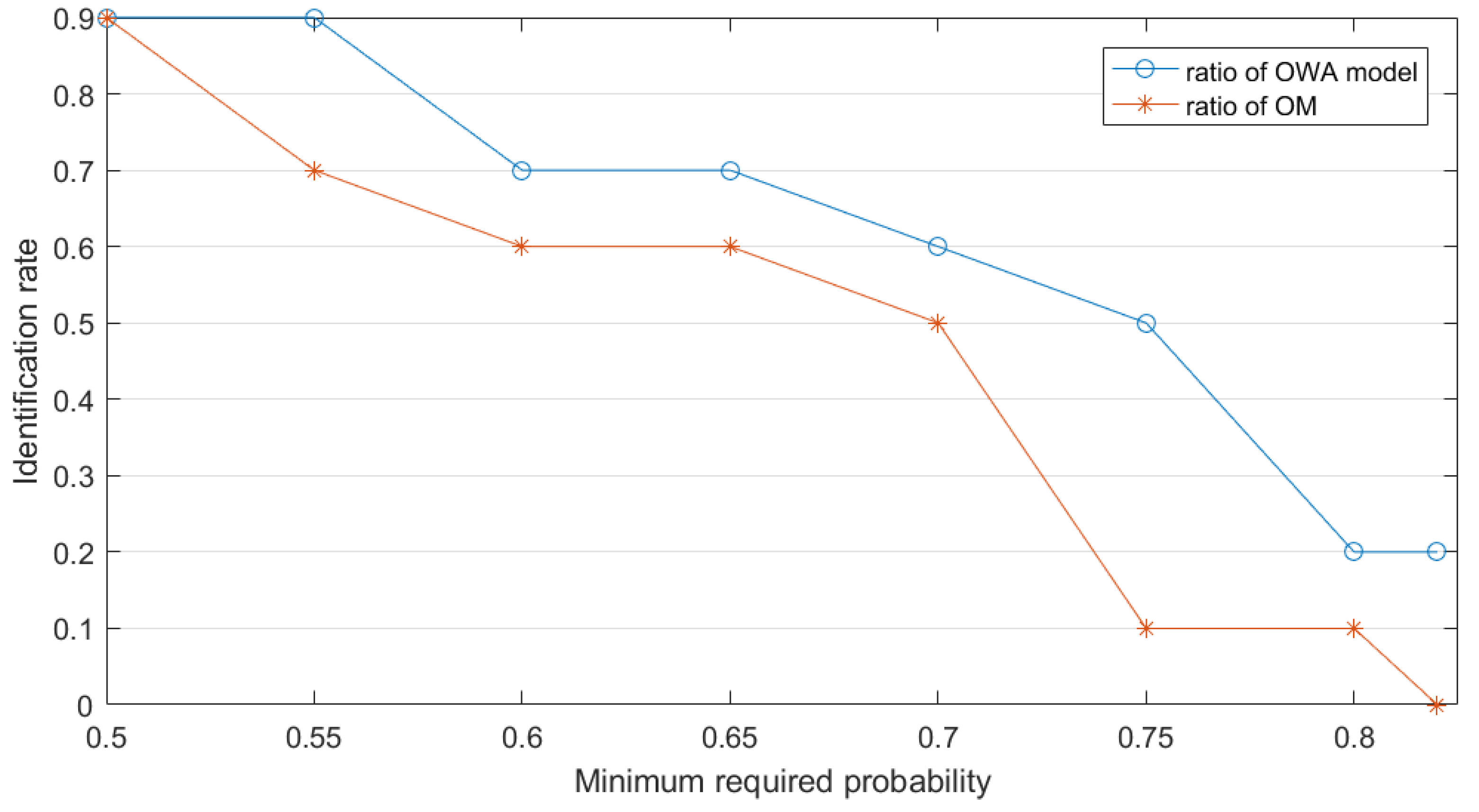
4. Application
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: New York, NY, USA, 2008; pp. 57–72. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Yager, R.R. On the Dempster-Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar]
- Smets, P. The combination of evidence in the transferable belief model. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 447–458. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar]
- Lefevre, E.; Colot, O.; Vannoorenberghe, P. Belief function combination and conflict management. Inf. Fusion 2002, 3, 149–162. [Google Scholar]
- Haenni, R. Are alternatives to Dempster’s rule of combination real alternatives? Comments on about the belief function combination and the conflict management problem?—Lefevre et al. Inf. Fusion 2002, 3, 237–239. [Google Scholar]
- Zhang, H.; Deng, Y. Engine fault diagnosis based on sensor data fusion considering information quality and evidence theory. Adva. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Chen, L.; Deng, Y. A new failure mode and effects analysis model using Dempster-Shafer evidence theory and grey relational projection method. Eng. Appl. Artif. Intell. 2018, 76, 13–20. [Google Scholar]
- Janghorbani, A.; Moradi, M.H. Fuzzy evidential network and its application as medical prognosis and diagnosis models. J. Biomed. Inform. 2017, 72, 96–107. [Google Scholar]
- Chen, L.; Diao, L.; Sang, J. Weighted Evidence Combination Rule Based on Evidence Distance and Uncertainty Measure: An Application in Fault Diagnosis. Math. Probl. Eng. 2018, 2018, 5858272. [Google Scholar]
- Han, Y.; Deng, Y. A hybrid intelligent model for Assessment of critical success factors in high risk emergency system. J. Ambient Intell. Hum. Comput. 2018, 9, 1933–1953. [Google Scholar] [CrossRef]
- Chen, L.; Deng, X. A Modified Method for Evaluating Sustainable Transport Solutions Based on AHP and Dempster-Shafer Evidence Theory. Appl. Sci. 2018, 8, 563. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Dependence assessment in human reliability analysis using an evidential network approach extended by belief rules and uncertainty measures. Annal. Nuclear Energy 2018, 117, 183–193. [Google Scholar]
- Dahooie, J.H.; Zavadskas, E.K.; Abolhasani, M.; Vanaki, A.; Turskis, Z. A Novel Approach for Evaluation of Projects Using an Interval–Valued Fuzzy Additive Ratio Assessment ARAS Method: A Case Study of Oil and Gas Well Drilling Projects. Symmetry 2018, 10, 45. [Google Scholar] [CrossRef]
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar]
- Seiti, H.; Hafezalkotob, A.; Najafi, S.; Khalaj, M. A risk-based fuzzy evidential framework for FMEA analysis under uncertainty: An interval-valued DS approach. J. Intell. Fuzzy Syst. 2018, 35, 1–12. [Google Scholar]
- Behrouz, M.; Alimohammadi, S. Uncertainty Analysis of Flood Control Measures Including Epistemic and Aleatory Uncertainties: Probability Theory and Evidence Theory. J. Hydrol. Eng. 2018, 23, 04018033. [Google Scholar]
- Wu, B.; Yan, X.; Wang, Y.; Soares, C.G. An Evidential Reasoning-Based CREAM to Human Reliability Analysis in Maritime Accident Process. Risk Anal. 2017, 37, 1936–1957. [Google Scholar]
- Li, M.; Zhang, Q.; Deng, Y. Evidential identification of influential nodes in network of networks. Chaos Solitons Fractals 2018, 117, 283–296. [Google Scholar]
- Han, Y.; Deng, Y. An enhanced fuzzy evidential DEMATEL method with its application to identify critical success factors. Soft Comput. 2018, 22, 5073–5090. [Google Scholar]
- Lachaize, M.; Le Hégarat-Mascle, S.; Aldea, E.; Maitrot, A.; Reynaud, R. Evidential framework for Error Correcting Output Code classification. Eng. Appl. Artif. Intell. 2018, 73, 10–21. [Google Scholar]
- Su, Z.g.; Denoeux, T.; Hao, Y.s.; Zhao, M. Evidential K-NN classification with enhanced performance via optimizing a class of parametric conjunctive t-rules. Knowl-Based Syst. 2018, 142, 7–16. [Google Scholar]
- Xu, X.; Zheng, J.; Yang, J.B.; Xu, D.L.; Chen, Y.W. Data classification using evidence reasoning rule. Knowl-Based Syst. 2017, 116, 144–151. [Google Scholar]
- Han, Y.; Deng, Y. An Evidential Fractal AHP target recognition method. Def. Sci. J. 2018, 68, 367–373. [Google Scholar]
- He, Z.; Jiang, W. An evidential dynamical model to predict the interference effect of categorization on decision making. Knowl-Based Syst. 2018, 150, 139–149. [Google Scholar]
- Xiao, F. A Hybrid Fuzzy Soft Sets Decision Making Method in Medical Diagnosis. IEEE Access 2018, 6, 25300–25312. [Google Scholar]
- Xiao, F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Eng. Appl. Artif. Intell. 2018, 71, 216–225. [Google Scholar]
- Zhu, W.; Ku, Q.; Wu, Y.; Zhang, H.; Sun, Y.; Zhang, C. A research into the evidence reasoning theory of two-dimensional framework and its application. Kybernetes 2018, 47, 873–887. [Google Scholar]
- Han, Y.; Deng, Y. A novel matrix game with payoffs of Maxitive Belief Structure. Int. J. Intell. Syst. 2019, 34, 690–706. [Google Scholar]
- Fei, L.; Deng, Y. A new divergence measure for basic probability assignment and its applications in extremely uncertain environments. Int. J. Intell. Syst. 2019, 34, 584–600. [Google Scholar] [CrossRef]
- Xu, X.; Li, S.; Song, X.; Wen, C.; Xu, D. The optimal design of industrial alarm systems based on evidence theory. Control Eng. Pract. 2016, 46, 142–156. [Google Scholar]
- Zhou, Y.; Tao, X.; Luan, L.; Wang, Z. Safety justification of train movement dynamic processes using evidence theory and reference models. Knowl-Based Syst. 2018, 139, 78–88. [Google Scholar]
- Du, Y.W.; Shan, Y.K.; Li, C.X.; Wang, R. Mass Collaboration-Driven Method for Recommending Product Ideas Based on Dempster-Shafer Theory of Evidence. Math. Probl. Eng. 2018, 2018, 1980152. [Google Scholar]
- Yin, L.; Deng, X.; Deng, Y. The negation of a basic probability assignment. IEEE Trans. Fuzzy Syst. 2019, 27, 135–143. [Google Scholar]
- Yager, R.R.; Alajlan, N. Maxitive Belief Structures and Imprecise Possibility Distributions. IEEE Trans. Fuzzy Syst. 2017, 25, 768–774. [Google Scholar]
- Zhou, X.; Hu, Y.; Deng, Y.; Chan, F.T.S.; Ishizaka, A. A DEMATEL-Based Completion Method for Incomplete Pairwise Comparison Matrix in AHP. Annal. Oper. Res. 2018, 271, 1045–1066. [Google Scholar]
- Li, Y.; Deng, Y. Generalized Ordered Propositions Fusion Based on Belief Entropy. Int. J. Comput. Commun. Control 2018, 13, 792–807. [Google Scholar]
- Pan, L.; Deng, Y. A New Belief Entropy to Measure Uncertainty of Basic Probability Assignments Based on Belief Function and Plausibility Function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W.; Wang, Z. Zero-sum polymatrix games with link uncertainty: A Dempster-Shafer theory solution. Appl. Math. Comput. 2019, 340, 101–112. [Google Scholar]
- Xiao, F. An Improved Method for Combining Conflicting Evidences Based on the Similarity Measure and Belief Function Entropy. Int. J. Fuzzy Syst. 2018, 20, 1256–1266. [Google Scholar]
- Cao, Z.; Lin, C.T. Inherent Fuzzy Entropy for the Improvement of EEG Complexity Evaluation. IEEE Trans. Fuzzy Syst. 2018, 26, 1032–1035. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xing, Y. Credibility decay model in temporal evidence combination. Inf. Process. Lett. 2015, 115, 248–252. [Google Scholar]
- Smets, P. Analyzing the combination of conflicting belief functions. Inf. Fusion 2007, 8, 387–412. [Google Scholar]
- Wang, J.; Liu, F. Temporal evidence combination method for multi-sensor target recognition based on DS theory and IFS. J. Syst. Eng. Electron. 2017, 28, 1114–1125. [Google Scholar]
- Xu, P.; Zhang, R.; Deng, Y. A Novel Visibility Graph Transformation of Time Series into Weighted Networks. Chaos Solitons Fractals 2018, 117, 201–208. [Google Scholar]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar]
- Lu, F.; Jiang, C.; Huang, J.; Wang, Y.; You, C. A novel data hierarchical fusion method for gas turbine engine performance fault diagnosis. Energies 2016, 9, 828. [Google Scholar]
- Axenie, C.; Richter, C.; Conradt, J. A Self-Synthesis Approach to Perceptual Learning for Multisensory Fusion in Robotics. Sensors 2016, 16, 1751. [Google Scholar]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar]
- Yager, R.R. Applications and extensions of OWA aggregations. Int. J. Man-Mach. Stud. 1992, 37, 103–122. [Google Scholar]
- Kang, B.; Deng, Y.; Hewage, K.; Sadiq, R. Generating Z- number based on OWA weights using maximum entropy. Int. J. Intell. Syst. 2018, 33, 1745–1755. [Google Scholar]
- Fei, L.; Wang, H.; Chen, L.; Deng, Y. A new vector valued similarity measure for intuitionistic fuzzy sets based on OWA operators. Iran. J. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zavadskas, E.K.; Awang, S.R.; Zare, H.; Jamal, N.M. Decision making methods based on fuzzy aggregation operators: Three decades review from 1986 to 2017. Int. J. Inf. Technol. Decis. Making 2018, 17, 391–466. [Google Scholar]
- Seiti, H.; Hafezalkotob, A. Developing the R-TOPSIS methodology for risk-based preventive maintenance planning: A case study in rolling mill company. Comput. Ind. Eng. 2019, 128, 622–636. [Google Scholar]
- Dutta, P.; Hazarika, G. Construction of families of probability boxes and corresponding membership functions at different fractiles. Expert Syst. 2017, 34, e12202. [Google Scholar]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antucheviciene, J. Supplier evaluation and selection in fuzzy environments: a review of MADM approaches. Econ. Res-Ekonomska Istraživanja 2017, 30, 1073–1118. [Google Scholar]
- Yin, L.; Deng, Y. Toward uncertainty of weighted networks: An entropy-based model. Phys. A Stat. Mech. Appl. 2018, 508, 176–186. [Google Scholar] [CrossRef]
- Fei, L.; Zhang, Q.; Deng, Y. Identifying influential nodes in complex networks based on the inverse-square law. Phys. A Stat. Mech. Appl. 2018, 512, 1044–1059. [Google Scholar] [CrossRef]
- Yang, H.; Deng, Y.; Jones, J. Network Division Method Based on Cellular Growth and Physarum-inspired Network Adaptation. Int. J. Unconv. Comput. 2018, 13, 477–491. [Google Scholar]
- Song, Y.; Wang, X.; Lei, L.; Yue, S. Uncertainty measure for interval-valued belief structures. Measurement 2016, 80, 241–250. [Google Scholar]
- Wang, X.; Song, Y. Uncertainty measure in evidence theory with its applications. Appl. Intell. 2017. [Google Scholar] [CrossRef]
- Deng, X. Analyzing the monotonicity of belief interval based uncertainty measures in belief function theory. Int. J. Intell. Syst. 2018, 33, 1869–1879. [Google Scholar]
- Sun, R.; Deng, Y. A new method to identify incomplete frame of discernment in evidence theory. IEEE Access 2019, 7, 15547–15555. [Google Scholar]
- Xiao, F. A multiple criteria decision-making method based on D numbers and belief entropy. Int. J. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Yager, R.R. Fuzzy rule bases with generalized belief structure inputs. Eng. Appl. Artif. Intell. 2018, 72, 93–98. [Google Scholar]
- Seiti, H.; Hafezalkotob, A. Developing pessimistic-optimistic risk-based methods for multi-sensor fusion: An interval-valued evidence theory approach. Appl. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Shi, F.; Su, X.; Qian, H.; Yang, N.; Han, W. Research on the Fusion of Dependent Evidence Based on Rank Correlation Coefficient. Sensors 2017, 17, 2362. [Google Scholar]
- Mönks, U.; Dörksen, H.; Lohweg, V.; Hübner, M. Information fusion of conflicting input data. Sensors 2016, 16, 1798. [Google Scholar]
- Sun, G.; Guan, X.; Yi, X.; Zhao, J. Conflict Evidence Measurement Based on the Weighted Separate Union Kernel Correlation Coefficient. IEEE Access 2018, 6, 30458–30472. [Google Scholar]
- Wang, Y.; Deng, Y. Base belief function: an efficient method of conflict management. J. Ambient Intell. Hum. Comput. 2018. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, Y. Combining conflicting evidence using the DEMATEL method. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Yang, J.B.; Xu, D.L. Evidential reasoning rule for evidence combination. Artif. Intell. 2013. [Google Scholar] [CrossRef]
- Dutta, P. An uncertainty measure and fusion rule for conflict evidences of big data via Dempster–Shafer theory. Int. J. Image Data Fusion 2018, 9, 152–169. [Google Scholar] [CrossRef]
- Smets, P.; Kennes, R. The transferable belief model. Artif. Intell. 1994, 66, 191–234. [Google Scholar]
- Xu, Z. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Inf. Sci. 2004, 168, 171–184. [Google Scholar]
- Calvo, T.; Mayor, G.; Mesiar, R. Aggregation Operators: New Trends and Applications; Physica: Ringwood, Australia, 2012; Volume 97. [Google Scholar]
- Zadeh, L.A. A computational approach to fuzzy quantifiers in natural languages. Comput. Math. Appl. 1983, 9, 149–184. [Google Scholar]
| Time Node | (Credibility ) | (Effect Degree) |
|---|---|---|
| = 1 s | - | - |
| = 4 s | 1.000 | 1.000 |
| = 7 s | 0.800 | 0.800 |
| = 17 s | 0.600 | 0.480 |
| = 20 s | 0.480 | 0.230 |
| = 23 s | 0.400 | 0.092 |
| = 25 s | 0.343 | 0.032 |
| = 29 s | 0.300 | 0.009 |
| = 39 s | 1.000 | 0.009 |
| = 42 s | 0.800 | 0.002 |
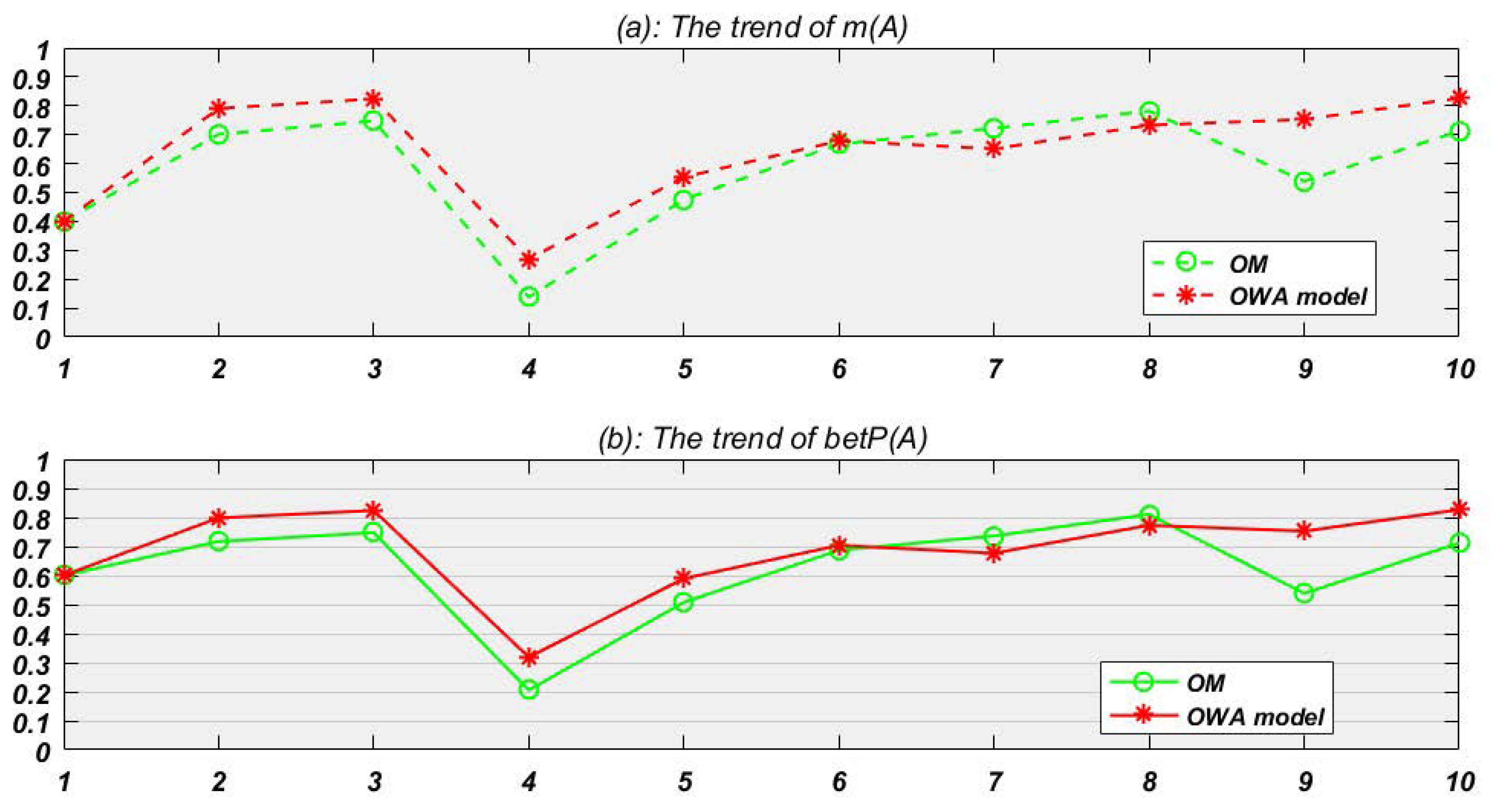
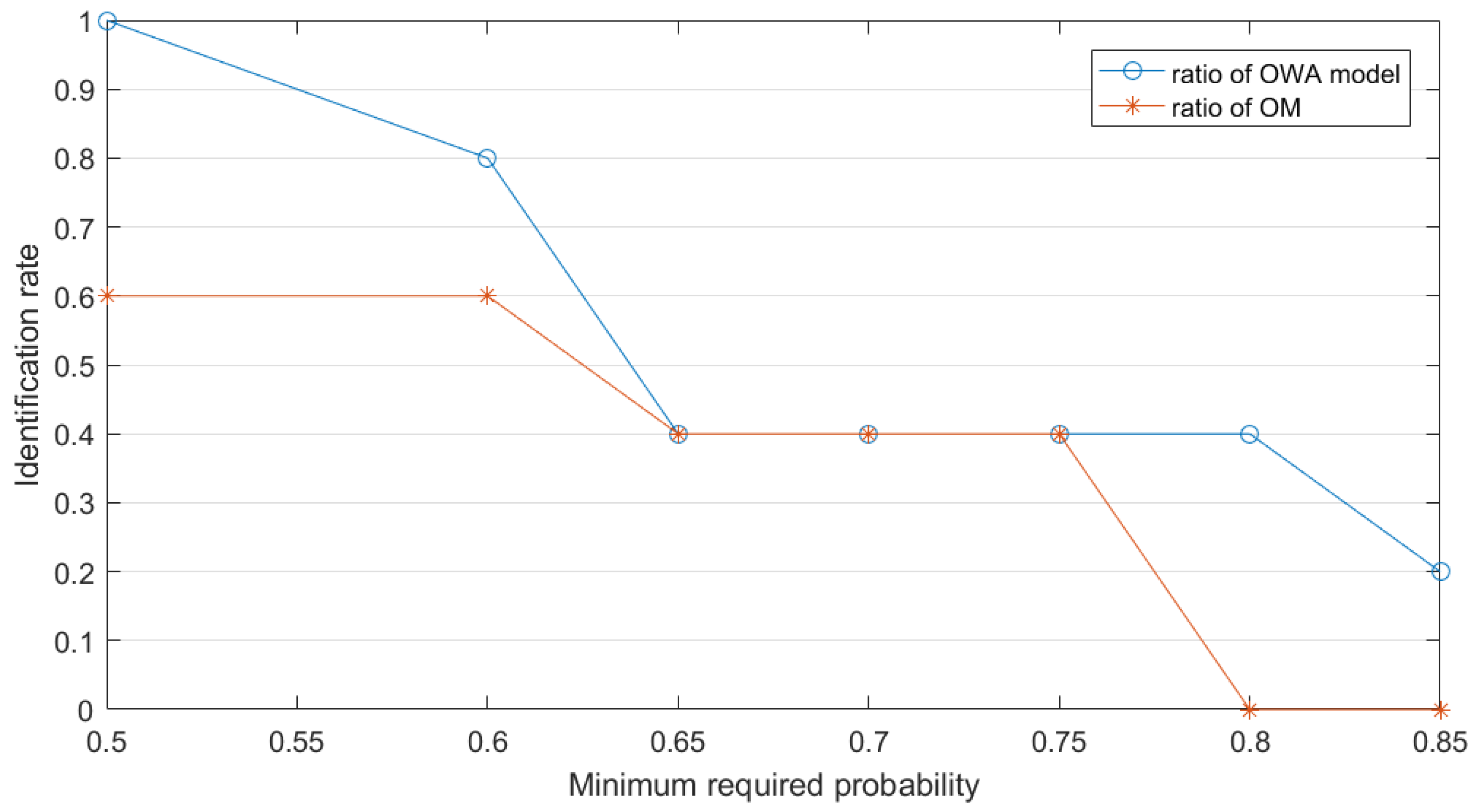
| m(A) | m(B) | m(C) | m(AB) | m(AC) | m(BC) | m() | in OWA Model | in OM | |
|---|---|---|---|---|---|---|---|---|---|
| = 1 s | 0.4 | 0.1 | 0.1 | 0.2 | 0.2 | 0 | 0 | - | - |
| = 4 s | 0.6 | 0.2 | 0.1 | 0 | 0.05 | 0.05 | 0 | 1 | 0.638 |
| = 7 s | 0.65 | 0.15 | 0 | 0 | 0 | 0.2 | 0 | 0.8 | 0.638 |
| = 17 s | 0.1 | 0.75 | 0 | 0.15 | 0 | 0 | 0 | 0.6 | 0.223 |
| = 20 s | 0.6 | 0.3 | 0 | 0.1 | 0 | 0 | 0 | 0.48 | 0.638 |
| = 23 s | 0.65 | 0.25 | 0 | 0 | 0 | 0 | 0.1 | 0.4 | 0.638 |
| = 25 s | 0.6 | 0.3 | 0 | 0 | 0 | 0 | 0.1 | 0.343 | 0.741 |
| = 29 s | 0.7 | 0.2 | 0 | 0.1 | 0 | 0 | 0 | 0.3 | 0.549 |
| = 39 s | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 1 | 0.223 |
| = 42 s | 0.65 | 0.1 | 0.15 | 0 | 0 | 0.1 | 0 | 0.8 | 0.638 |
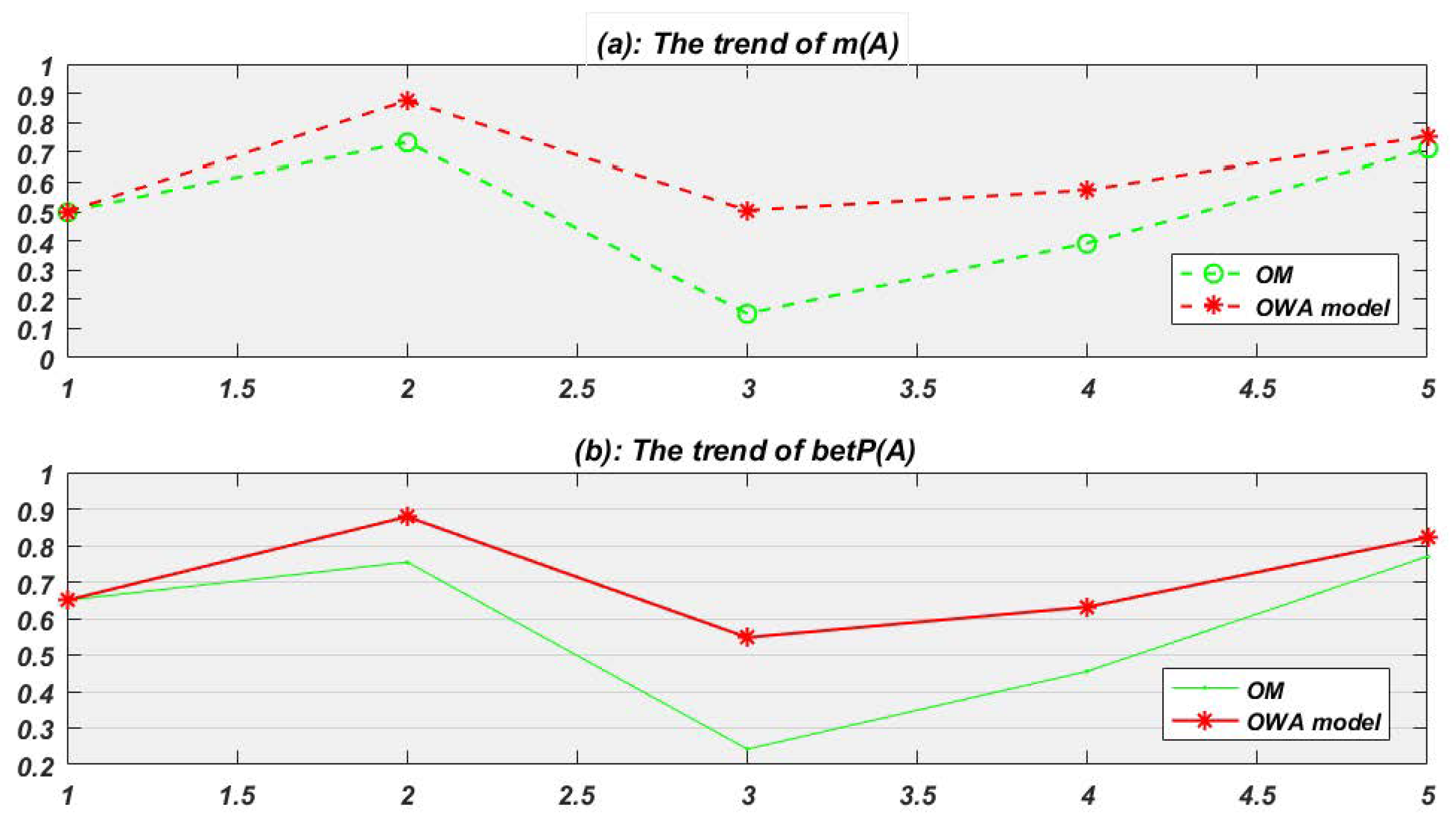
| Time Node | BPA | in OWA Model | in OM |
|---|---|---|---|
| = 1 s | m(A) = 0.5, m(B) = 0.1 | ||
| m(C) = 0.1, m(AB) = 0.2 | - | - | |
| m(AC) = 0.1 | |||
| = 10 s | m(A) = 0.7, m(B) = 0.1 | ||
| m(C) = 0.1, m(AC) = 0.05 | 1.00 | 0.259 | |
| m(BC) = 0.05 | |||
| = 20 s | m(A) = 0.1, m(B) = 0.7 | 0.80 | 0.223 |
| m(AB) = 0.2 | |||
| = 22 s | m(A) = 0.5, m(B) = 0.2 | 0.60 | 0.741 |
| m(ABC) = 0.3 | |||
| = 30 s | m(A) = 0.7, m(B) = 0.1 | 0.48 | 0.638 |
| m(AB) = 0.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Xiao, F. Time Series Data Fusion Based on Evidence Theory and OWA Operator. Sensors 2019, 19, 1171. https://doi.org/10.3390/s19051171
Liu G, Xiao F. Time Series Data Fusion Based on Evidence Theory and OWA Operator. Sensors. 2019; 19(5):1171. https://doi.org/10.3390/s19051171
Chicago/Turabian StyleLiu, Gang, and Fuyuan Xiao. 2019. "Time Series Data Fusion Based on Evidence Theory and OWA Operator" Sensors 19, no. 5: 1171. https://doi.org/10.3390/s19051171
APA StyleLiu, G., & Xiao, F. (2019). Time Series Data Fusion Based on Evidence Theory and OWA Operator. Sensors, 19(5), 1171. https://doi.org/10.3390/s19051171





